Density Functional Treatment of Photoionization of Sodium Clusters: Effects of Cluster Size and Exchange–Correlation Framework
Abstract
:1. Introduction
2. Theoretical Methodology
2.1. DFT Exchange–Correlation Functionals
2.2. LR-TDDFT Dynamical Response
3. Results and Discussion
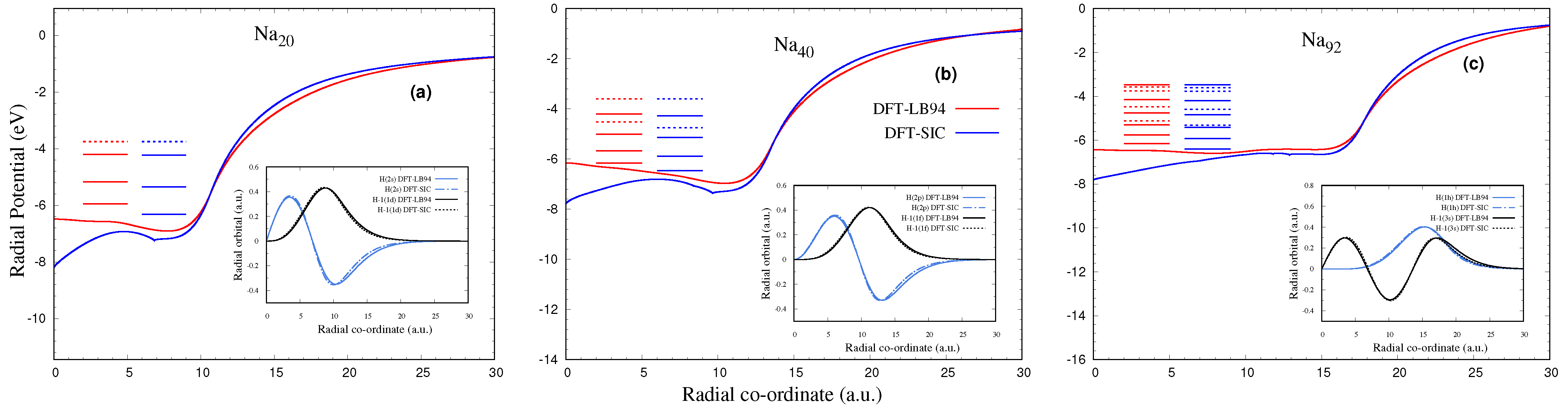
3.1. Ground State Structure
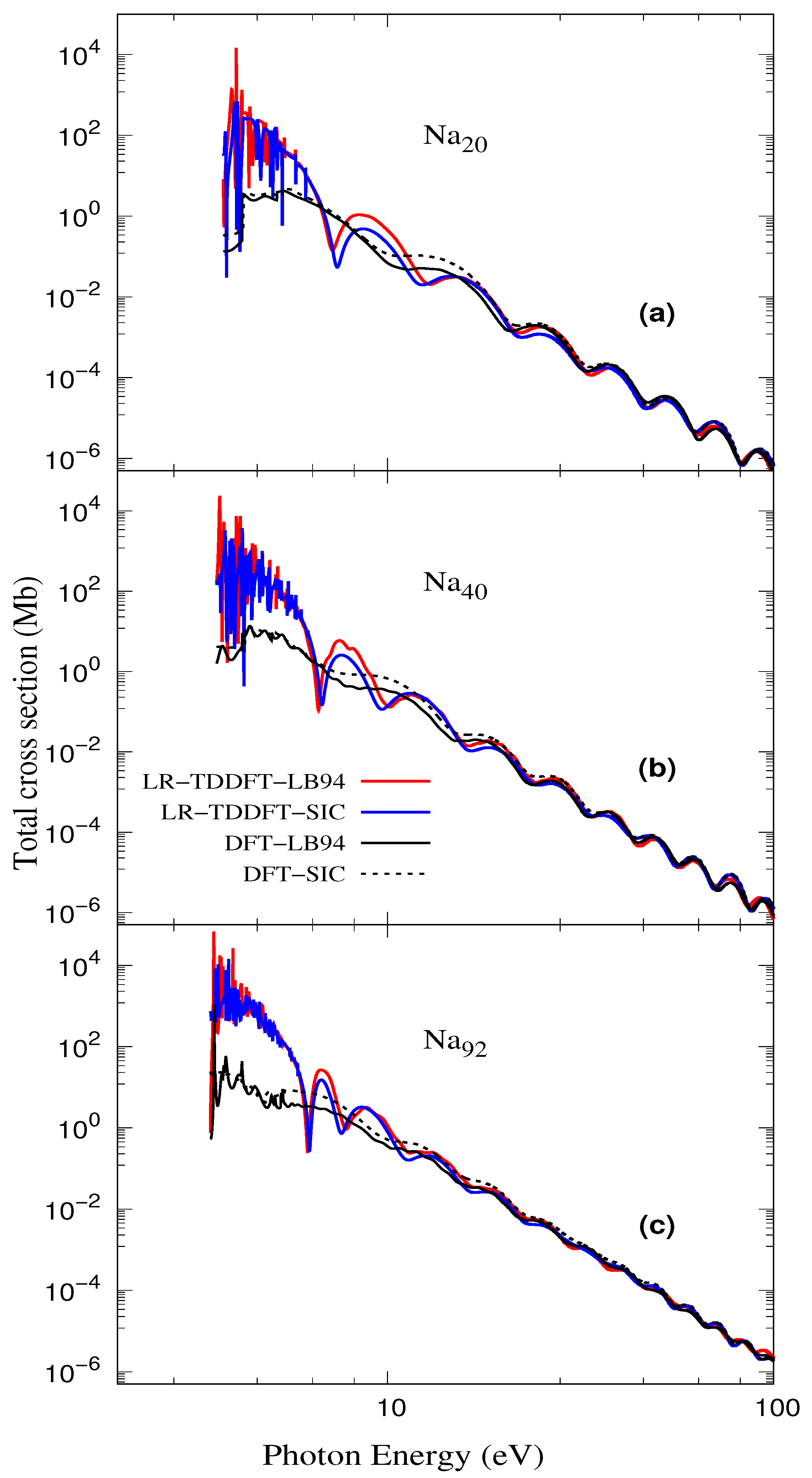
3.2. Total Photoionization Cross-Section
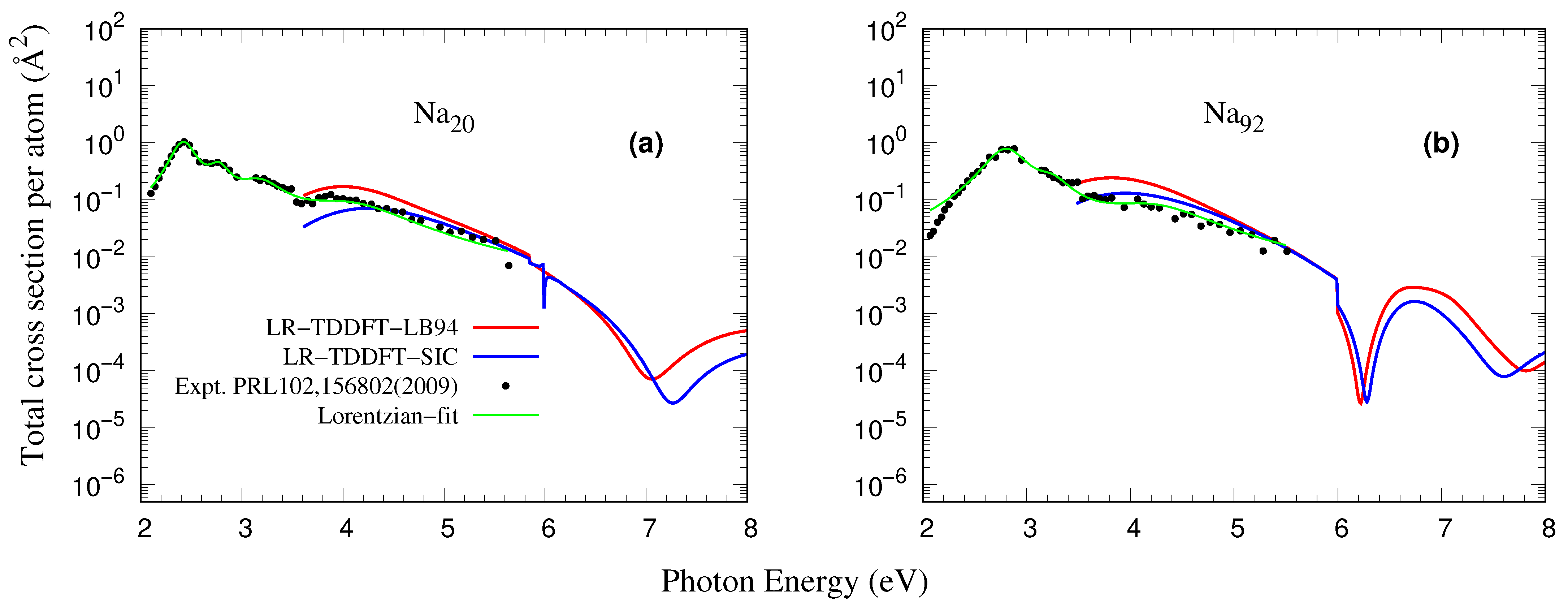
3.3. Comparison with Experiments
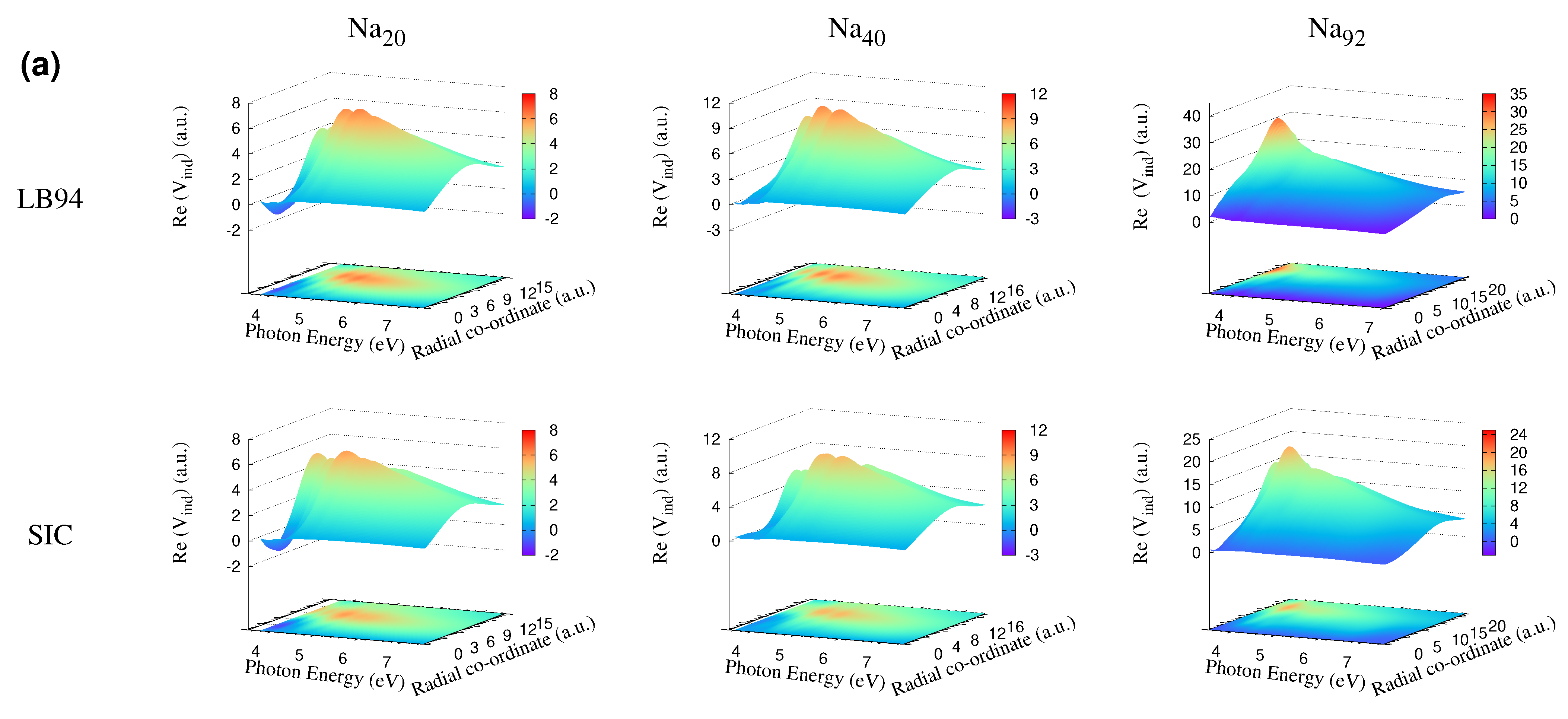
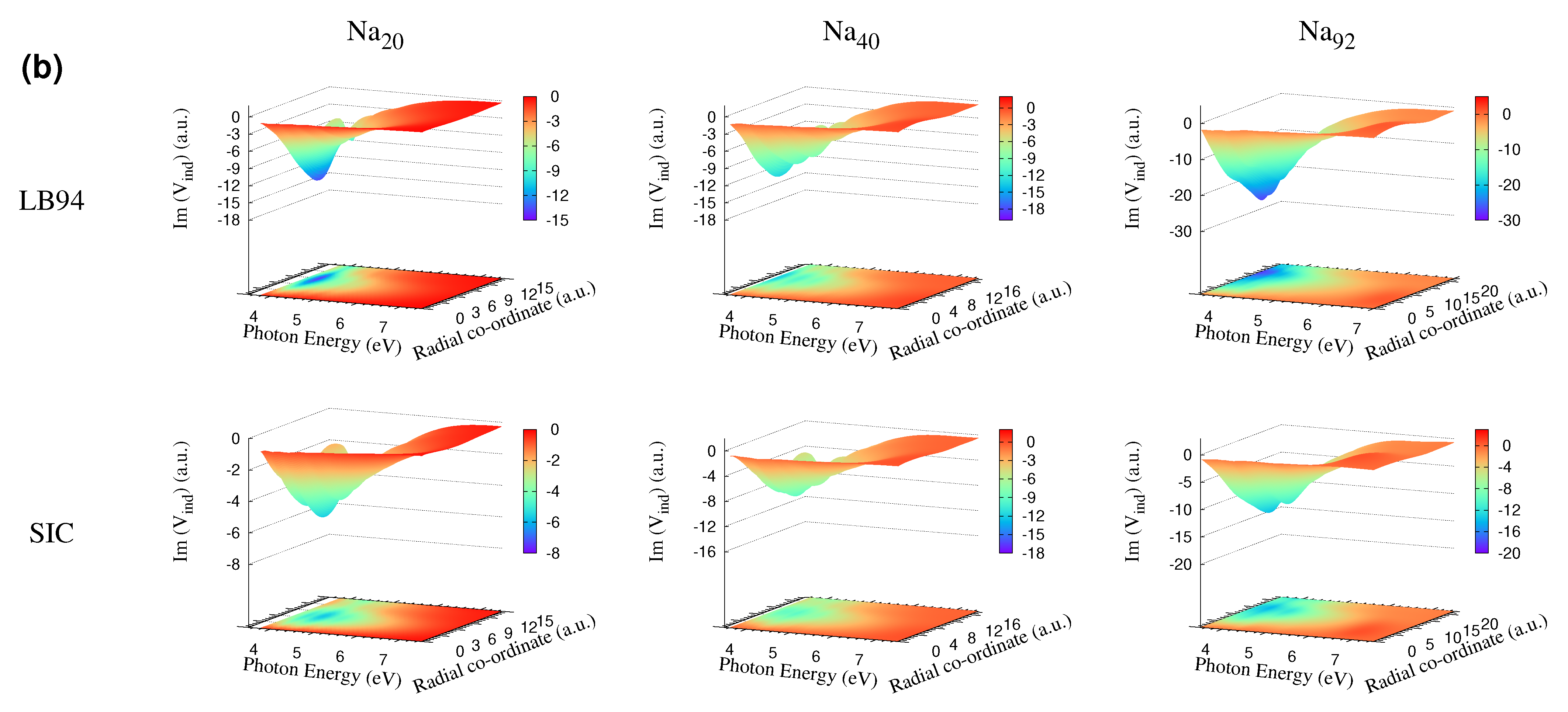
3.4. Self-Consistent Induced Potential
4. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Reinhard, P.G.; Suraud, E.; Dinh, P.M. An Introduction to Cluster Science; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Jena, P.; Sun, Q. Super atomic clusters: Design rules and potential for building blocks of materials. Chem. Rev. 2018, 118, 5755–5870. [Google Scholar]
- Castleman, A., Jr.; Khanna, S. Clusters, superatoms, and building blocks of new materials. J. Phys. Chem. C 2009, 113, 2664–2675. [Google Scholar] [CrossRef]
- Kawabata, A.; Kubo, R. Electronic properties of fine metallic particles. II. Plasma resonance absorption. J. Phys. Soc. Jpn. 1966, 21, 1765–1772. [Google Scholar] [CrossRef]
- Kreibig, U.; Vollmer, M. Optical Properties of Metal Clusters; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 25. [Google Scholar]
- Xia, C.; Yin, C.; Kresin, V.V. Photoabsorption by volume plasmons in metal nanoclusters. Phys. Rev. Lett. 2009, 102, 156802. [Google Scholar] [CrossRef] [PubMed]
- Madjet, M.E.A.; Chakraborty, H. Collective resonances in the photoresponse of metallic nanoclusters. J. Phys. Conf. Ser. 2009, 194, 022103. [Google Scholar] [CrossRef]
- Ekardt, W. Size-dependent photoabsorption and photoemission of small metal particles. Phys. Rev. B 1985, 31, 6360. [Google Scholar] [CrossRef]
- Sun, W.G.; Wang, J.J.; Lu, C.; Xia, X.X.; Kuang, X.Y.; Hermann, A. Evolution of the structural and electronic properties of medium-sized sodium clusters: A honeycomb-like Na20 cluster. Inorg. Chem. 2017, 56, 1241–1248. [Google Scholar] [CrossRef] [PubMed]
- Miroshnichenko, A.E.; Flach, S.; Kivshar, Y.S. Fano resonances in nanoscale structures. Rev. Mod. Phys. 2010, 82, 2257. [Google Scholar] [CrossRef]
- Luk’Yanchuk, B.; Zheludev, N.I.; Maier, S.A.; Halas, N.J.; Nordlander, P.; Giessen, H.; Chong, C.T. The Fano resonance in plasmonic nanostructures and metamaterials. Nat. Mater. 2010, 9, 707–715. [Google Scholar] [CrossRef] [PubMed]
- Cederbaum, L.; Zobeley, J.; Tarantelli, F. Giant intermolecular decay and fragmentation of clusters. Phys. Rev. Lett. 1997, 79, 4778. [Google Scholar] [CrossRef]
- Marburger, S.; Kugeler, O.; Hergenhahn, U.; Möller, T. Experimental evidence for interatomic Coulombic decay in Ne clusters. Phys. Rev. Lett. 2003, 90, 203401. [Google Scholar] [CrossRef]
- De, R.; Magrakvelidze, M.; Madjet, M.E.; Manson, S.T.; Chakraborty, H.S. First prediction of inter-Coulombic decay of C60 inner vacancies through the continuum of confined atoms. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 11LT01. [Google Scholar] [CrossRef]
- Shaik, R.; Varma, H.R.; Madjet, M.E.A.; Zheng, F.; Frauenheim, T.; Chakraborty, H.S. Plasmonic Resonant Intercluster Coulombic Decay. Phys. Rev. Lett. 2023, 130, 233201. [Google Scholar] [CrossRef] [PubMed]
- Jänkälä, K.; Tchaplyguine, M.; Mikkelä, M.H.; Björneholm, O.; Huttula, M. Photon energy dependent valence band response of metallic nanoparticles. Phys. Rev. Lett. 2011, 107, 183401. [Google Scholar] [CrossRef]
- Frank, O.; Rost, J.M. From collectivity to the single-particle picture in the photoionization of clusters. Phys. Rev. A 1999, 60, 392. [Google Scholar] [CrossRef]
- Frank, O.; Rost, J.M. Diffraction effects in the photoionization of clusters. Chem. Phys. Lett. 1997, 271, 367–371. [Google Scholar] [CrossRef]
- Mirin, N.A.; Bao, K.; Nordlander, P. Fano resonances in plasmonic nanoparticle aggregates. J. Phys. Chem. A 2009, 113, 4028–4034. [Google Scholar] [CrossRef]
- Cole, J.R.; Halas, N. Optimized plasmonic nanoparticle distributions for solar spectrum harvesting. Appl. Phys. Lett. 2006, 89, 153120. [Google Scholar] [CrossRef]
- Dragan, A.I.; Geddes, C.D. Metal-enhanced fluorescence: The role of quantum yield, Q, in enhanced fluorescence. Appl. Phys. Lett. 2012, 100, 093115. [Google Scholar] [CrossRef]
- Liao, H.; Nehl, C.L.; Hafner, J.H. Biomedical Applications of Plasmon Resonant Metal Nanoparticles; Nanomedicine: London, UK, 2006; Volume 1, pp. 201–208. [Google Scholar]
- Huang, X.; Jain, P.K.; El-Sayed, I.H.; El-Sayed, M.A. Plasmonic photothermal therapy (PPTT) using gold nanoparticles. Lasers Med. Sci. 2008, 23, 217–228. [Google Scholar] [CrossRef]
- De Heer, W.A. The physics of simple metal clusters: Experimental aspects and simple models. Rev. Mod. Phys. 1993, 65, 611. [Google Scholar] [CrossRef]
- Brack, M. The physics of simple metal clusters: Self-consistent jellium model and semiclassical approaches. Rev. Mod. Phys. 1993, 65, 677. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244. [Google Scholar] [CrossRef] [PubMed]
- Klüpfel, P.; Dinh, P.M.; Reinhard, P.G.; Suraud, E. Koopmans’ condition in self-interaction-corrected density-functional theory. Phys. Rev. A 2013, 88, 052501. [Google Scholar] [CrossRef]
- Saito, S.; Bertsch, G.F.; Tománek, D. Collective electronic excitations in small metal clusters. Phys. Rev. B 1991, 43, 6804. [Google Scholar] [CrossRef]
- Van Leeuwen, R.; Baerends, E. Exchange-correlation potential with correct asymptotic behavior. Phys. Rev. A 1994, 49, 2421. [Google Scholar] [CrossRef]
- Choi, J.; Chang, E.; Anstine, D.M.; Madjet, M.E.A.; Chakraborty, H.S. Effects of exchange-correlation potentials on the density-functional description of C60 versus C240 photoionization. Phys. Rev. A 2017, 95, 023404. [Google Scholar] [CrossRef]
- Shaik, R.; Varma, H.R.; Chakraborty, H.S. Collective effects in photoionization of sodium clusters: Plasmon resonance spill, induced attractive force and correlation minimum. J. Phys. B At. Mol. Opt. Phys. 2021, 54, 125101. [Google Scholar] [CrossRef]
- Madjet, M.E.; Chakraborty, H.S.; Rost, J.M.; Manson, S.T. Photoionization of C60: A model study. J. Phys. B At. Mol. Opt. Phys. 2008, 41, 105101. [Google Scholar] [CrossRef]
- Chandezon, F.; Bjørnholm, S.; Borggreen, J.; Hansen, K. Electronic shell energies and deformations in large sodium clusters from evaporation spectra. Phys. Rev. B 1997, 55, 5485. [Google Scholar] [CrossRef]
- Gunnarsson, O.; Lundqvist, B.I. Exchange and correlation in atoms, molecules, and solids by the spin-density-functional formalism. Phys. Rev. B 1976, 13, 4274. [Google Scholar] [CrossRef]
- Oliver, G.; Perdew, J. Spin-density gradient expansion for the kinetic energy. Phys. Rev. A 1979, 20, 397. [Google Scholar] [CrossRef]
- Marques, M.A.; Castro, A.; Rubio, A. Assessment of exchange-correlation functionals for the calculation of dynamical properties of small clusters in time-dependent density functional theory. J. Chem. Phys. 2001, 115, 3006–3014. [Google Scholar] [CrossRef]
- Petersilka, M.; Gossmann, U.; Gross, E. Excitation energies from time-dependent density-functional theory. Phys. Rev. Lett. 1996, 76, 1212. [Google Scholar] [CrossRef]
- Bertsch, G. An RPA program for jellium spheres. Comput. Phys. Commun. 1990, 60, 247–255. [Google Scholar] [CrossRef]
- Parr, R.G.; Weitao, Y. Density Functional Theory of Atoms and Molecules; International series of monographs on Chemistry. 16; Oxford Science Publications: Oxford, UK, 1989; pp. 271–272. [Google Scholar]
- Madjet, M.; Chakraborty, H.S.; Rost, J.M. Spurious oscillations from local self-interaction correction in high-energy photoionization calculations for metal clusters. J. Phys. B At. Mol. Opt. Phys. 2001, 34, L345. [Google Scholar] [CrossRef]
- Bachau, H.; Frank, O.; Rost, J.M. Photoionization of alkali metal clusters. Z. Phys. D At. Mol. Clust. 1996, 38, 59–64. [Google Scholar]
- Fano, U. Effects of configuration interaction on intensities and phase shifts. Phys. Rev. 1961, 124, 1866. [Google Scholar] [CrossRef]
- Bertsch, G.; Tománek, D. Thermal line broadening in small metal clusters. Phys. Rev. B 1989, 40, 2749. [Google Scholar] [CrossRef]
- Koskinen, M.; Manninen, M. Photoionization of metal clusters. Phys. Rev. B 1996, 54, 14796. [Google Scholar] [CrossRef] [PubMed]
- Bartels, C.; Hock, C.; Huwer, J.; Kuhnen, R.; Schwobel, J.; Von Issendorff, B. Probing the angular momentum character of the valence orbitals of free sodium nanoclusters. Science 2009, 323, 1323–1327. [Google Scholar] [CrossRef]
- Wrigge, G.; Hoffmann, M.A.; Issendorff, B.V. Photoelectron spectroscopy of sodium clusters: Direct observation of the electronic shell structure. Phys. Rev. A 2002, 65, 063201. [Google Scholar] [CrossRef]
- Solov’yov, A.V.; Polozkov, R.G.; Ivanov, V.K. Angle-resolved photoelectron spectra of metal cluster anions within a many-body-theory approach. Phys. Rev. A 2010, 81, 021202. [Google Scholar] [CrossRef]
- Polozkov, R.; Ivanov, V.; Verkhovtsev, A.; Korol, A.; Solov’yov, A. New applications of the jellium model for the study of atomic clusters. J. Phys. Conf. Ser. 2013, 438, 012009. [Google Scholar] [CrossRef]
- Zangwill, A.; Soven, P. Local field effects in photoabsorption. J. Vac. Sci. Technol. 1980, 17, 159–163. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shaik, R.; Varma, H.R.; Chakraborty, H.S. Density Functional Treatment of Photoionization of Sodium Clusters: Effects of Cluster Size and Exchange–Correlation Framework. Atoms 2023, 11, 114. https://doi.org/10.3390/atoms11080114
Shaik R, Varma HR, Chakraborty HS. Density Functional Treatment of Photoionization of Sodium Clusters: Effects of Cluster Size and Exchange–Correlation Framework. Atoms. 2023; 11(8):114. https://doi.org/10.3390/atoms11080114
Chicago/Turabian StyleShaik, Rasheed, Hari R. Varma, and Himadri S. Chakraborty. 2023. "Density Functional Treatment of Photoionization of Sodium Clusters: Effects of Cluster Size and Exchange–Correlation Framework" Atoms 11, no. 8: 114. https://doi.org/10.3390/atoms11080114
APA StyleShaik, R., Varma, H. R., & Chakraborty, H. S. (2023). Density Functional Treatment of Photoionization of Sodium Clusters: Effects of Cluster Size and Exchange–Correlation Framework. Atoms, 11(8), 114. https://doi.org/10.3390/atoms11080114







