Abstract
The spin-orbit interaction is quite small compared to electrostatic forces in atoms. Nevertheless, this small interaction can have large consequences. Several examples of the importance of the spin-orbit force in atomic photoionization are presented and explained.
1. Introduction
More than a half-century ago, Ugo Fano pointed out that the small spin-orbit interaction had significant implications for atomic physics [1]. Photoelectron spin polarization and the splitting of inner and outer atomic energy levels were considered in his comment. Over the intervening half-century, there have been a number of new aspects of the importance of the spin-orbit interaction that have been investigated, both experimentally and theoretically, that exemplify and amplify the earlier observations. In this short review, we shall discuss several more recent examples of the large influence of the spin-orbit interaction in various aspects of atomic photoionization.
2. Spin-Orbit Splitting of Cooper Minima
Cooper minima [2], zeros or near-zeros in dipole photoionization matrix elements are ubiquitous features in valence and near-valence shell photoionization cross sections of atoms over the entire periodic table [3]. These Cooper minima occur in ground state photoionization only in the l → l + 1 dipole channels. Typically, the Cooper minima have significant influence on the energy dependence of the photoionization cross section and the spectral distribution of oscillator strength over a broad energy region around the location of the minimum [4]. From a simple single-particle point of view, a Cooper minimum occurs at an energy where the overlap between the initial and final state wave functions in the dipole matrix element is such that the positive and negative contributions just cancel each other out, resulting in a zero in the matrix element, as a function of energy. For photoionization from an nl atomic subshell with l ≠ 0, the cross section never can go to zero because of the existence of the l → l − 1 channel that does not have a Cooper minimum. However, for ns subshell photoionization, there is the possibility of a zero-cross section since no l → l − 1 photoionization channel exists. However, owing to the spin-orbit interaction, a single ns → εp transition splits into two.
This splitting of Cooper minima by the spin-orbit interaction was first found by Seaton [5], where the ns → εp1/2 and ns → εp3/2 dipole matrix elements in the alkali atoms exhibit their Cooper minima at slightly different energies so that the sum of the cross sections of the two channels never vanished, thereby leading to the non-zero photoionization cross section Cooper minimum observed experimentally in the alkali atoms.
For non-s states, the Cooper minima split into three owing to the spin-orbit splitting of the bound states in addition to the splitting of the continuum states [6,7,8,9]. These splittings of the Cooper minima are very much larger than the initial state spin-orbit splittings. For high-Z atoms, the splittings become quite significant indeed. For example, for the uranium atom, the calculated 6p spin-orbit splitting is 9.5 eV, but the Cooper minima are split by more than 200 eV [6]. From a physical standpoint, these effects result from the spin-orbit force being attractive for (both discrete and continuum) j = l − 1/2 states and repulsive for j = l + 1/2 states.
For superheavy elements, the splittings are magnified even further [10], as seen in Table 1 where the splittings of the 6s Cooper minima, calculated using the relativistic-random-phase approximation (RRPA), including coupling among all relevant channels, increase from 0.47 a.u. for Hg (Z = 80) to 167.50 a.u (more than 4 keV) for Og (Z = 118), the heaviest known atom. Now, for initial ns states, there is no spin-orbit splitting, so this effect is entirely the result of the spin-orbit interaction in the final continuum states. Thus, while the vast majority of studies of the spin-orbit interaction are for discrete (bound) states, it must be emphasized that there are important effects on continuum (unbound) state wave functions as well.

Table 1.
Positions of Cooper minima in 6s subshells in photoelectron energy (a.u.).
In any case, all this is as a result of the spin-orbit interaction.
3. Photoelectron Angular Distributions from s-States
Within the framework of the dipole approximation, generally valid for low photon energy, the photoemission angular distribution of atomic subshell i for incident linearly polarized light is given by [11] the following:
where is the subshell cross section, is the angle between the photon polarization and the photoelectron momentum. Non-relativistically, for ns subshells of closed-shell, 1S0 atoms, βns = 2 and is energy-independent. This is because there is only one possible final state for the ns → εp process, leading to a 1P1 final state of the residual ion-plus-photoelectron system. Using a relativistic formulation, however, the possible transitions are ns → εp1/2 and ns → εp3/2, which can interfere, leading to an energy-dependent βns [11]. Looked at another way, the final states of the system are the possible J = 1 states 1P1 and 3P1, which are the eigenchannels of the final states. Clearly, the transition to the triplet final state involves a spin flip and can only be effected by the spin-orbit interaction.
An extremely useful way to look at photoelectron angular distributions involves the use of the angular momentum transfer analysis of Dill and Fano [12]. The angular momentum transfer is defined generally as jt = Jc + s + J0, where Jc and J0 are the angular momenta of the ion core and initial state, respectively, and s is the photoelectron spin. The utility of this analysis is that there is a β for each allowed value of jt and these add up incoherently to calculate the observed β. Now, it turns out that the transition to the 1P1 corresponds to jt = 0 and leads to βns = 2, but the transition to 3P1 corresponds to jt = 1, which is what is known as a parity-unfavored transition, leading to βns = −1 [11,12]. Then, βns is a linear combination of these values, 2 and −1, weighted by their cross sections, i.e.,
βns = [2σ(1P1) − σ(3P1)]/[σ(1P1) + σ(3P1)].
These effects are particularly enhanced near Cooper minima, where the singlet cross section becomes quite small. As an example, in Figure 1, the situation for Xe 5s, calculated using the fully relativistic RRPA, is shown [13]. It is seen that the cross section exhibits a Cooper minimum and, in that energy region, βns is seen to deviate from the value of 2 and to be strongly energy-dependent. Parenthetically, note that this behavior has also been validated in the laboratory [13].
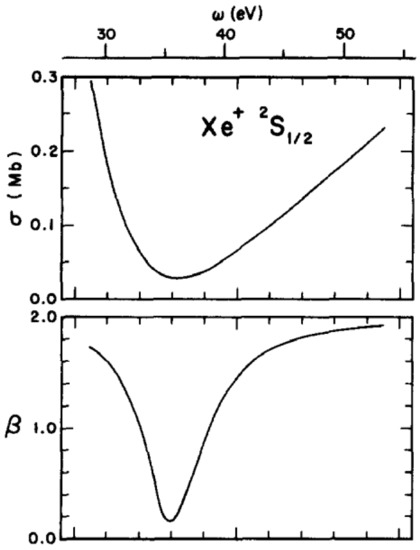
Figure 1.
Xe 5s photoionization cross section (upper curve) and β parameter (lower curve) vs. photon energy, ω, calculated using relativistic-random-phase approximation (RRPA) [13].
It is thus evident that the small spin-orbit force changes the ns photoelectron angular distribution markedly.
4. Branching Ratios at High Energy
Atomic nl subshells with l ≠ 0 are split into doublets with j = l ± ½ owing to the spin-orbit interaction; these splittings are quite small compared to the binding energies of the nl subshells. Thus, in a photoionization process at a given photon energy, the photoelectrons from the split subshells have slightly different energies and this gives the branching ratios of the j = l ± ½ cross sections an energy dependence, even if the dynamics of the two are the same; this is known as the kinetic energy effect. At high energies, where the cross sections vary slowly with energy, this small energy difference is no longer of any consequence, and it was expected earlier that the branching ratios for the j = l + ½/j = l − ½ cross should approach the non-relativistic value of (l + 1)/l, which simply reflects the occupation numbers of the spin-orbit-split nl subshell [14]. However, it was later shown that relativistic interactions, particularly spin-orbit, affect not only the energies, causing a splitting, but the initial state wave functions too, and this causes the ratio to drop below the statistical value at high energies [15,16]. In addition, this prediction has recently been verified experimentally [17]. In fact, the nlj wave functions for j = l ± ½ are essentially the same for intermediate and large r, but differ considerably for small r. The Dirac equation shows that the ratios of the nll−1/2:nll+1/2 probability densities diverge as Z2/r2 as r → 0 [18].
Now, the relevant region for the dipole matrix element moves to smaller and smaller r with increasing energy, and this can be understood both mathematically and physically [19]. From a mathematical standpoint, with increasing photoelectron energy, the continuum wave function (the final state of the photoelectron after photoabsorption) becomes increasingly oscillatory, resulting in a net cancellation of the matrix element beyond the first node of the continuum wave function. This node moves towards the nucleus with increasing energy, thereby causing the matrix element to be generated in a region increasingly close to the nucleus as the energy increases. From a physical point of view, both energy and linear momentum must be conserved in the photoionization process. High-energy photoabsorption entails a lot of linear momentum which must be transferred to the residual atom, where most of the mass is at the nucleus. Thus, to take up this momentum, the absorption is most likely to take place near the nucleus, i.e., at small r. From these arguments, it is evident that the branching ratios do not reach a limit but continually decrease as a function of photon energy.
As an example, the theoretical results for Kr 2p, 3p, 4p and 3d branching ratios are shown in Figure 2 [19], where it is seen that all of the branching ratios decrease with energy. These calculations were performed using RRPA which was modified to be able to deal with high energies. This required modifying the integration mesh by increasing both the number and density of the mesh points to be able to deal accurately with the extremely oscillatory high-energy continuum wave functions. At the highest energies, the np ratios are between 1.7 and 1.8, well below the statistical value of 2.0 for np-states. The 3d branching ratio is also decreasing below the statistical value of 1.5 but much more slowly. This occurs because in nd-states, where the main transition is nd → εf; the f-wave centrifugal barrier keeps the continuum wave function away from the small-r region where the initial state wave functions differ.
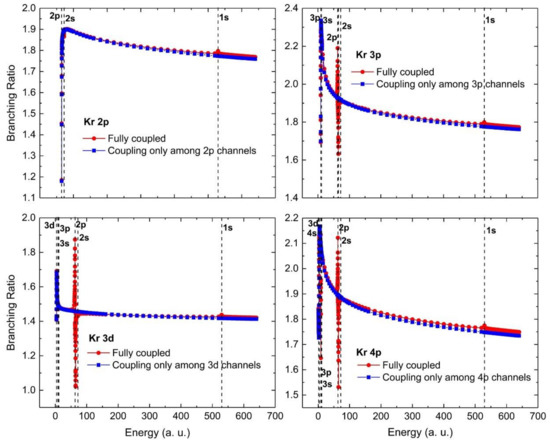
Figure 2.
Photoionization cross section branching ratios for Kr np3/2/np1/2 and 3d5/2/3d3/2 calculated using RRPA with full coupling (red dots) and with only intrashell coupling as indicated (blue squares). The vertical dashed lines indicate the thresholds.
Parenthetically, also seen in Figure 2 is the fact that in the vicinity of inner-shell thresholds, the branching ratios experience excursions from smooth behavior. This is due to interchannel coupling between the inner-shell photoionization channels and the channels involved in the branching ratio; this is evident by noting that this structure completely disappears when the interchannel coupling interactions are omitted, as shown in Figure 2. In any case, this is another example of the small spin-orbit force having a significant effect.
5. Final Remarks
The above examples are in no way exhaustive; they are illustrative of a few of the consequences of the small spin-orbit force on the atomic photoionization process. These suggest that the spin-flip channels, engendered by the spin-orbit force, will also be important in attosecond photoemission time delay, which has been the focus of quite a number of investigations over the past decade or so (see, for example, [20,21,22] and references therein), particularly in the neighborhood of Cooper minima where, the non-spinflip channel amplitudes become quite small. In addition, as pointed out by Fano [1], there are also implications in other aspects of atomic physics. Furthermore, there is nothing special about atoms; the same implications are also true for atomic ions (both positive and negative), molecules and condensed matter, i.e., over a broad range of AMO physics and chemistry. This note is to remind us that as calculations and experiments become more detailed and dig deeper into AMO structure and processes, in many cases, it can be crucial to include the spin-orbit interaction into the mix to properly calculate and understand what might be going on.
Funding
This work was supported by the US Department of Energy, Office of Basic Sciences, Division of Chemical Science, Geosciences and Biosciences under Grant No. DE-FG02-03ER15428.
Conflicts of Interest
The author declares no conflict of interest.
References
- Fano, U. Spin-Orbit Coupling: A Weak Force with Conspicuous Effects. Comments At. Molec. Phys. 1970, 2, 30–36. [Google Scholar]
- Cooper, J.W. Photoionization from Outer Atomic Subshells. A Model Study. Phys. Rev. 1962, 128, 681–693. [Google Scholar] [CrossRef]
- Manson, S.T. Systematics of zeros in dipole matrix elements for photoionizing transitions: Nonrelativistic calculations. Phys. Rev. A 1985, 31, 3698–3703. [Google Scholar] [CrossRef] [PubMed]
- Starace, A.F. Theory of Atomic Photoionization. In Handbuch der Physik; Mehlhorn, W., Ed.; Springer: Berlin/Heidelberg, Germany, 1882; Volume 32, pp. 1–121. [Google Scholar]
- Seaton, M.J. A comparison of theory and experiment for photo-ionization cross-sections II. Sodium and the alkali metals. Proc. Roy. Soc. Lond. Sect. A 1951, 208, 418–430. [Google Scholar]
- Kim, Y.S.; Ron, A.; Pratt, R.H.; Tambe, B.R.; Manson, S.T. Relativistic Effects in the Photoionization of High Z Elements: Splitting and Shifts in Minima. Phys. Rev. Lett. 1981, 46, 1326–1329. [Google Scholar] [CrossRef]
- Deshmukh, P.C.; Radojevic, V.; Manson, S.T. Relativistic Splitting of Cooper Minima in Radon: A Relativistic Random Phase Approximation Study. Phys. Lett. A 1986, 117, 293–296. [Google Scholar] [CrossRef]
- Deshmukh, P.C.; Tambe, B.; Manson, S.T. Relativistic Effects in the Photoionisation of Heavy Atoms: Cooper Minima. Aust. J. Phys. 1986, 39, 679–686. [Google Scholar] [CrossRef]
- Yin, R.Y.; Pratt, R.H. Survey of relativistic Cooper minima. Phys. Rev. A 1987, 35, 1149–1153. [Google Scholar] [CrossRef] [PubMed]
- Baral, S.; Saha, S.; Dubey, K.A.; Jose, J.; Deshmukh, P.C.; Razavi, A.K.; Manson, S.T. Unusual behavior of Cooper minima of ns subshells in high-Z atoms. Phys. Rev. A 2022, 105, 062819. [Google Scholar] [CrossRef]
- Manson, S.T.; Starace, A.F. Photoelectron Angular Distributions: Energy Dependence for s Subshells. Rev. Mod. Phys. 1982, 54, 389–406. [Google Scholar] [CrossRef]
- Fano, U.; Dill, D. Angular Momentum Transfer in the Theory of Angular Distributions. Phys. Rev. A 1972, 6, 185–192. [Google Scholar] [CrossRef]
- Huang, K.-N.; Johnson, W.; Cheng, K. Theoretical photoionization parameters for the noble gases argon, krypton, and xenon. At. Data Nucl. Data Tables 1981, 26, 33–45. [Google Scholar] [CrossRef]
- James, A.R.; Samson, J.; Gardner, L.; Starace, A.F. 2P3/2: 2P1/2 partial photoionization cross-section ratios in the rare gases. Phys. Rev. A 1975, 12, 1459–1463. [Google Scholar]
- Ron, A.; Kim, Y.S.; Pratt, R.H. Subshell branching ratios of partial photoionization cross sections. Phys. Rev. A 1981, 24, 1260–1263. [Google Scholar] [CrossRef]
- Kim, Y.S.; Pratt, R.H.; Ron, A. Nonstatistical behavior of photoeffect subshell branching ratios at high energies. Phys. Rev. A 1981, 24, 1889–1893. [Google Scholar] [CrossRef]
- Püttner, R.; Martins, J.B.; Marchenko, T.; Travnikova, O.; Guillemin, R.; Journel, L.; Ismail, I.; Goldsztejn, G.; Koulentianos, D.; Céolin, D.; et al. Nonstatistical Behavior of the Photoionization of Spin-Orbit Doublets. J. Phys. B 2021, 54, 085001. [Google Scholar] [CrossRef]
- Bethe, H.A.; Salpeter, E.E. Quantum Mechanics of One- and Two-Electron Atoms; Springer: Berlin/Heidelberg, Germany, 1957; p. 63ff. [Google Scholar]
- Munasinghe, C.R.; Deshmukh, P.C.; Manson, S.T. Photoionization branching ratios of spin-orbit doublets far above thresholds: Interchannel and relativistic effects in the noble gases. Phys. Rev. A 2022, 106, 013102. [Google Scholar] [CrossRef]
- Pazourek, R.; Nagele, S.; Burgdörfer, J. Attosecond chronoscopy of photoemission. Rev. Mod. Phys. 2015, 87, 765–802. [Google Scholar] [CrossRef]
- Deshmukh, P.C.; Banerjee, S.; Mandal, A.; Manson, S.T. Wigner-Eisenbud-Smith Time Delay in Atom-Laser Interactions. Eur. Phys. J. Spec. Top. 2021, 230, 4151–4164. [Google Scholar] [CrossRef]
- Kheifets, A.S. Wigner time delay in atomic photoionization. J. Phys. B 2023, 56, 022001. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).