Towards Understanding Incomplete Fusion Reactions at Low Beam Energies: Modified Sum Rule Model
Abstract
1. Introduction
2. Experiments
3. Results and Discussion
3.1. Disentangling CF and ICF
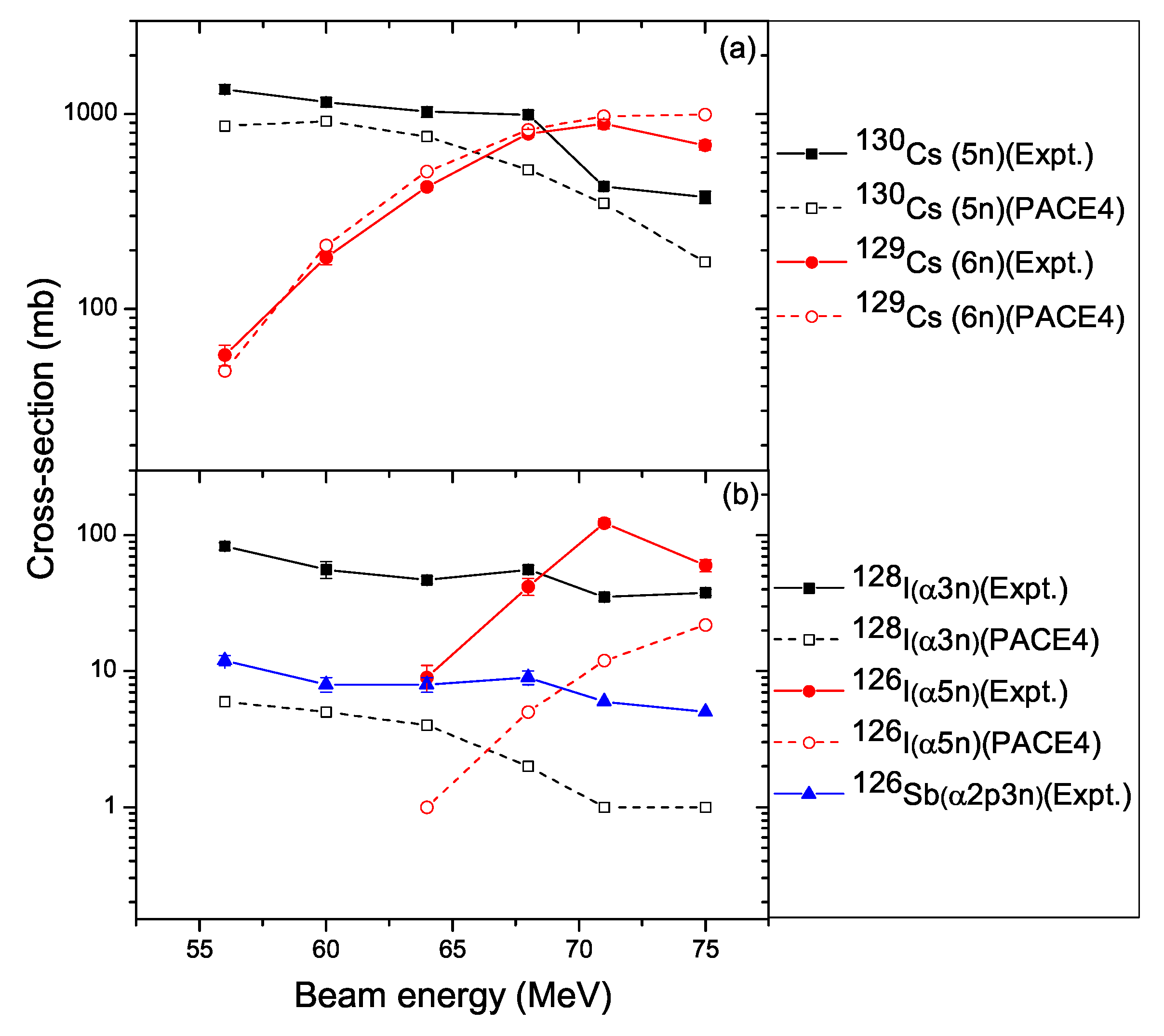
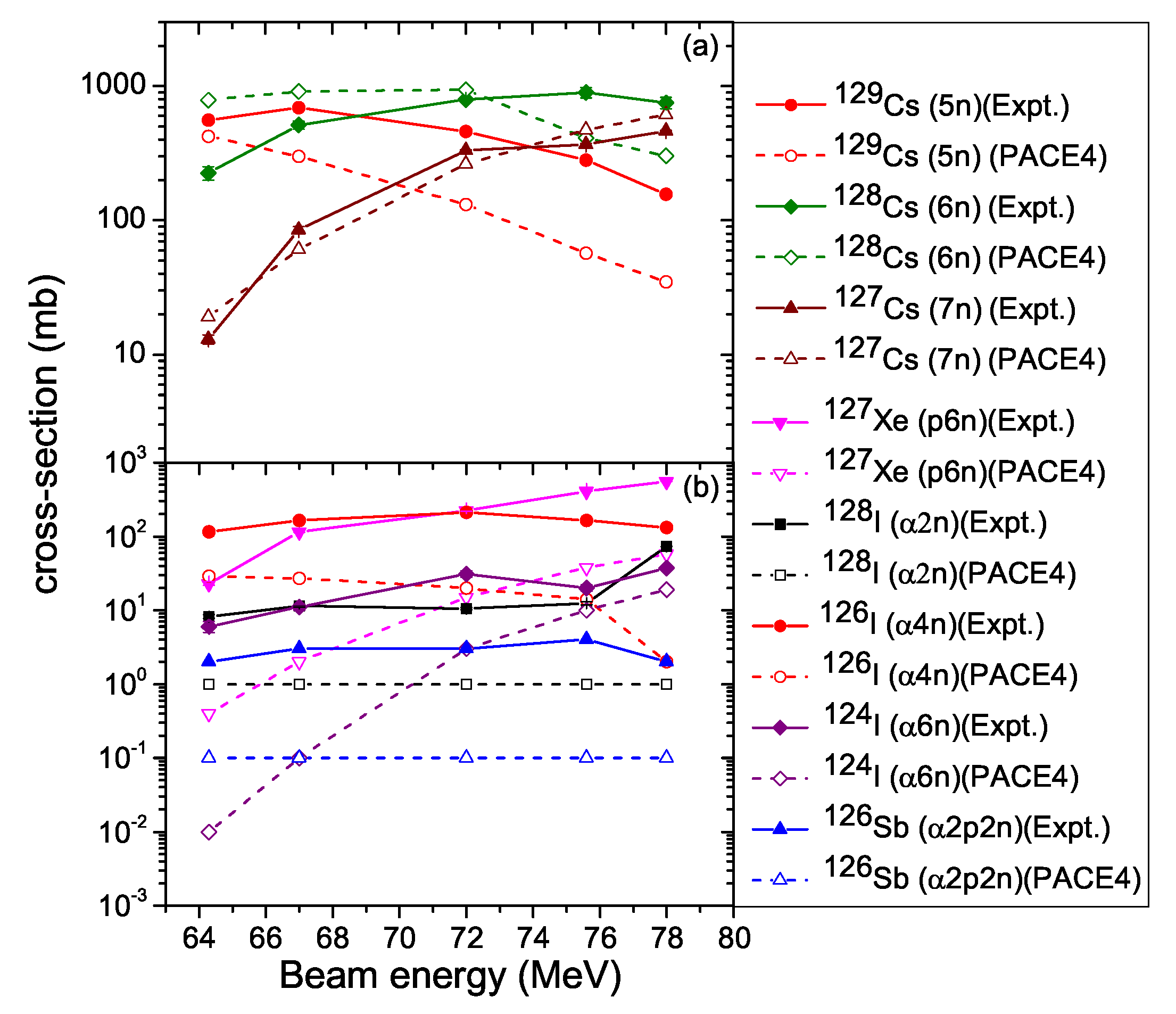
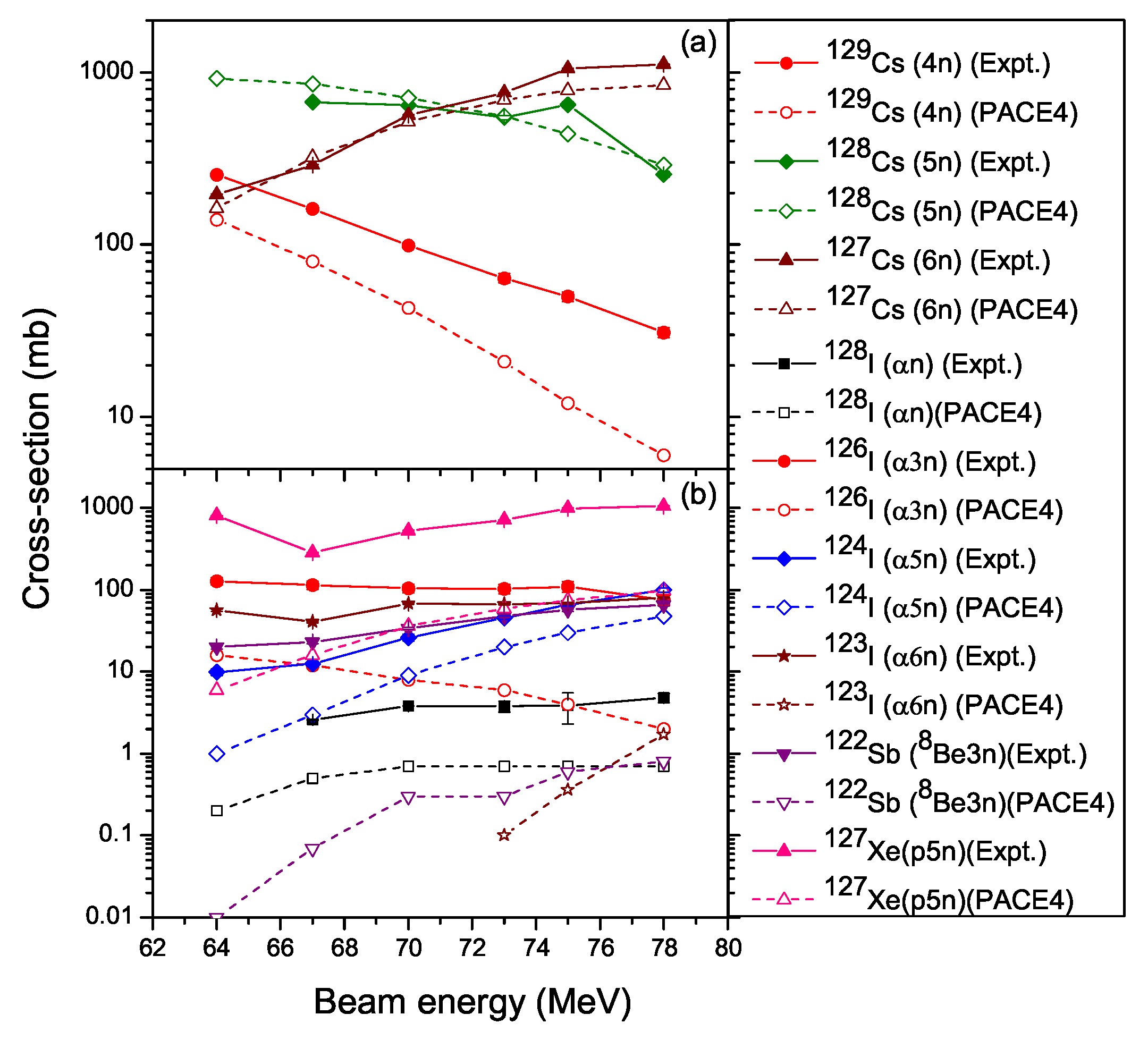
3.2. Excitation Functions
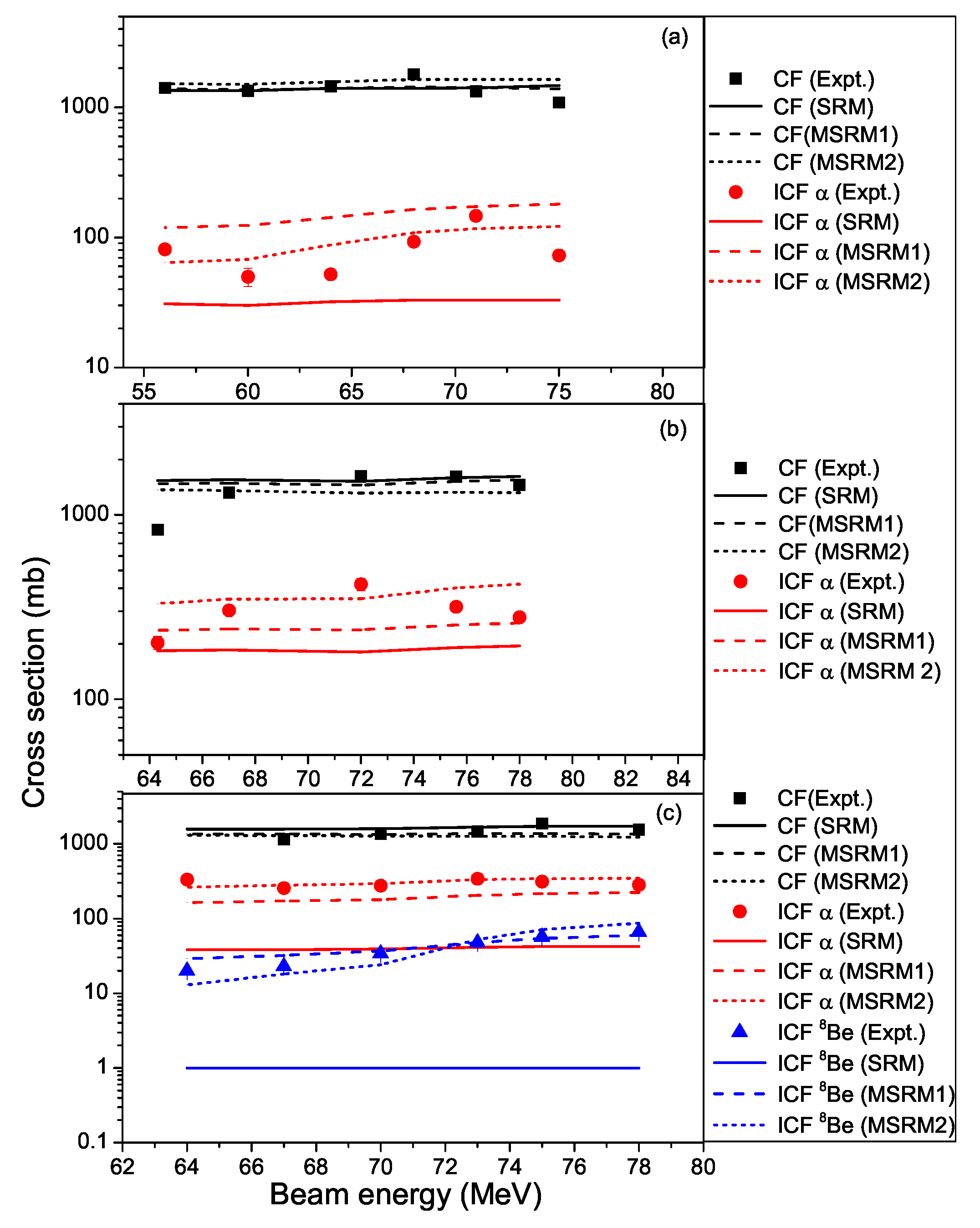
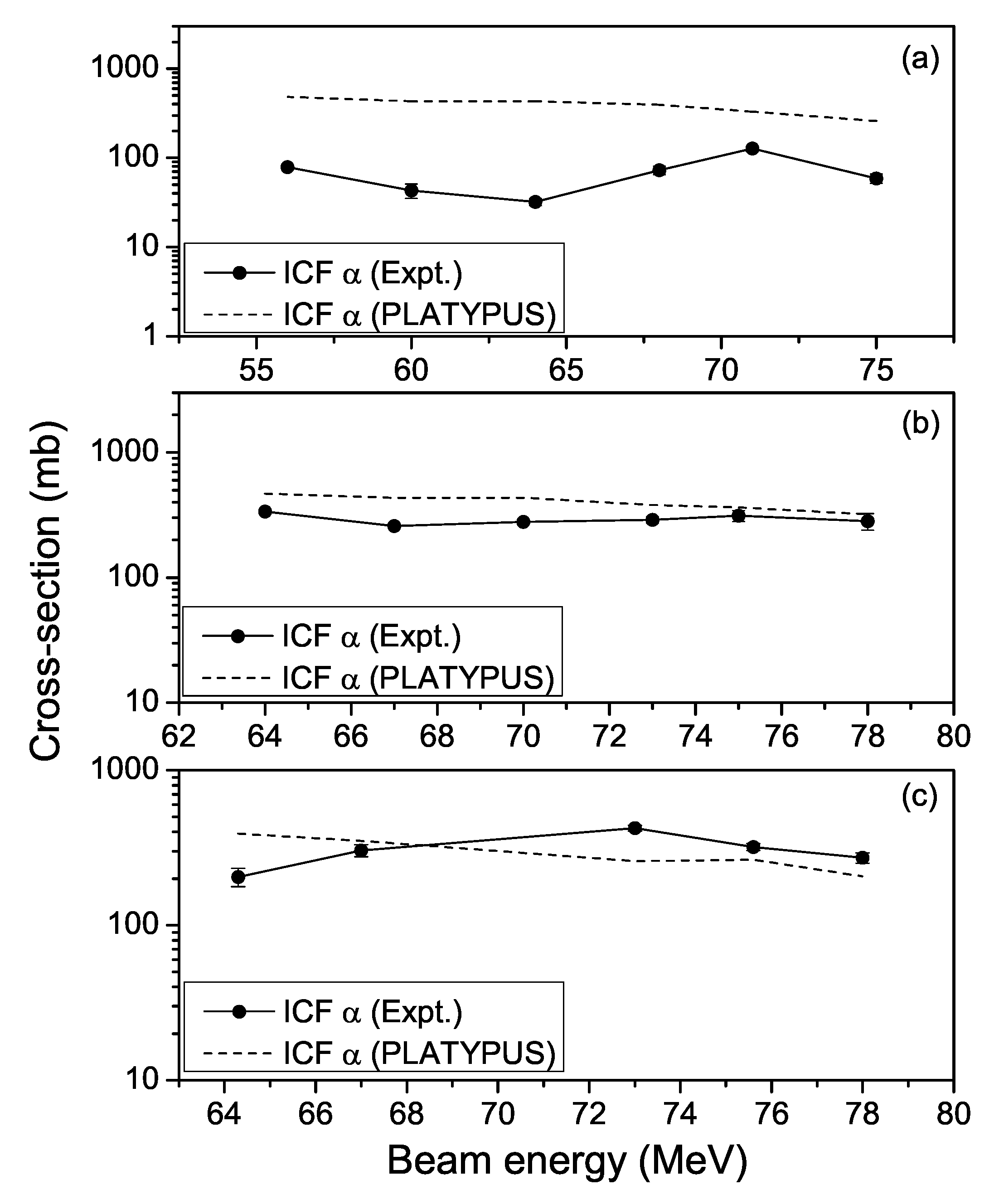
3.2.1. Reaction: B+Sn
3.2.2. Reaction: B+Sn
3.2.3. Reaction: B+Sn
4. Theoretical Discussion
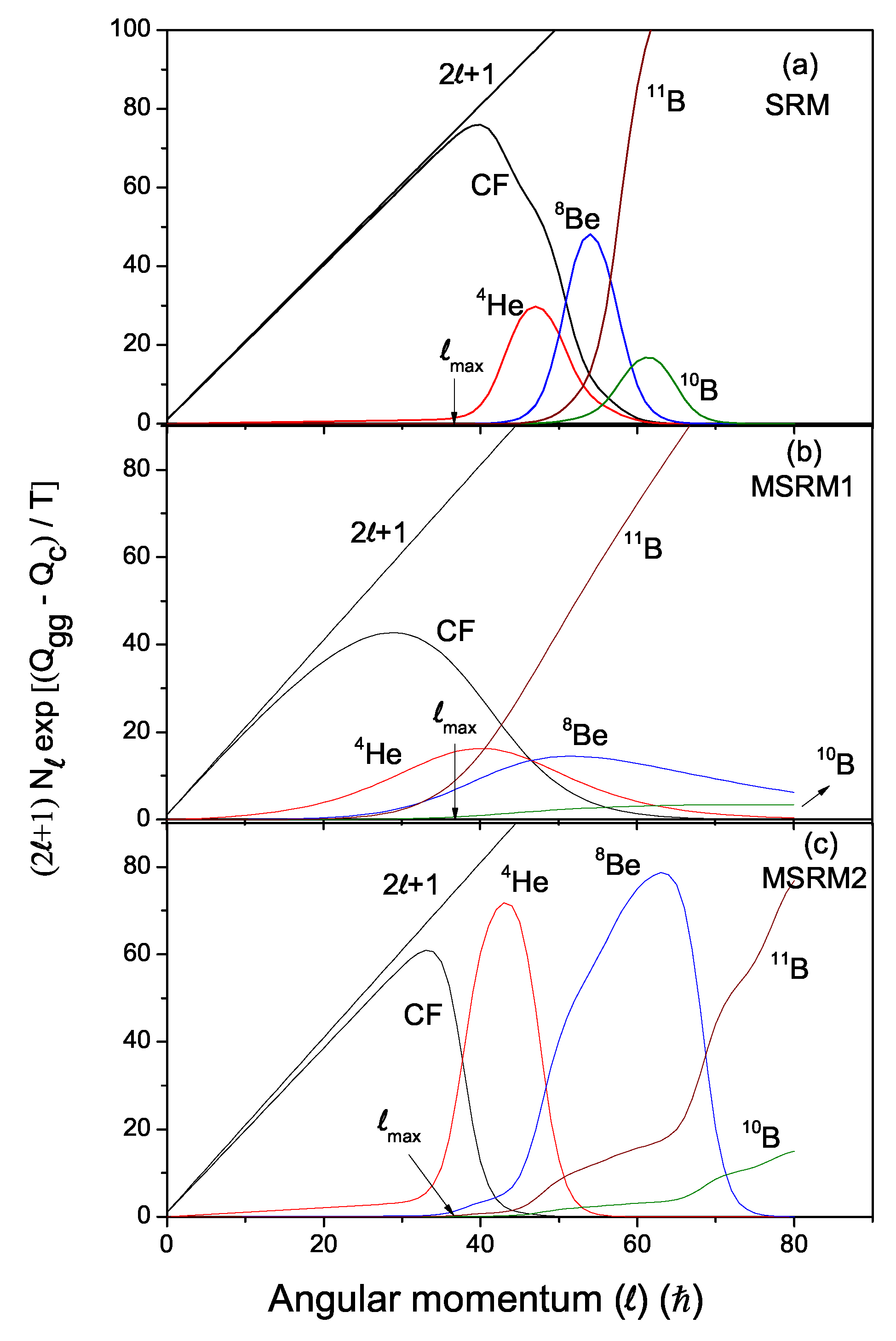
4.1. Sum Rule Model (SRM)
4.2. Modified Sum Rule Model-1 (MSRM1)
4.3. Modified Sum Rule Model-2 (MSRM2)
4.4. 3D Stochastic Breakup Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CF | Complete fusion reaction |
| ICF | Incomplete fusion reaction |
| PACE4 | Projection angular-momentum-coupled evaporation (version-4) |
| SRM | Sum rule model |
References
- Hodgson, P.E.; Gadioli, E.; Gadioli Erba, E. Introductory Nuclear Physics; Oxford Science Publications, Clarendon Press: New York, NY, USA, 1997; pp. 417–537. [Google Scholar]
- Britt, H.C.; Quinton, A.R. Alpha particles and protons emitted in the bombardment of Au197 and Bi209 by C12, N14, and O16 projectiles. Phys. Rev. 1961, 124, 877–887. [Google Scholar] [CrossRef]
- Kaufmann, R.; Wolfgang, R. Nucleon Transfer Reactions in Grazing Collisions of Heavy Ions. Phys. Rev. 1961, 121, 192–205. [Google Scholar] [CrossRef]
- Inamura, T.; Ishihara, M.; Fukuda, T.; Shimoda, T.; Hiruta, H. Gamma-rays from an Incomplete fusion reaction induced by 95 MeV 14N. Phys. Lett. B 1977, 68, 51–54. [Google Scholar] [CrossRef]
- Udagawa, T.; Tamura, T. Breakup-fusion description of massive transfer reactions with emission of fast light particles. Phys. Rev. Lett. 1980, 45, 1311–1314. [Google Scholar] [CrossRef]
- Udagawa, T.; Price, D.; Tamura, T. Exact-finite-range DWBA calculations of massive transfer reactions treated as break-up fusion reactions. Phys. Lett. B 1982, 116, 311–314. [Google Scholar] [CrossRef]
- Takada, E.; Shimoda, T.; Takahashi, N.; Yamaya, T.; Nagatani, K.; Udagawa, T.; Tamura, T. Projectile break-up reaction and evidence of a brakup-fusion mechanism. Phys. Rev. C 1981, 23, 772–779. [Google Scholar] [CrossRef]
- Wilczyński, J.; Siwek-Wilczyńska, K.; ven Driel, J.; Gonggrijp, S.; Hageman, D.C.J.M.; Janssens, R.V.F.; Łukasiak, J.; Siemssen, R.H. Incomplete-Fusion reactions in the 14N+159Tb System and a “Sum-Rule Model” for Fusion and Incomplete-Fusion Reactions. Phys. Rev. Lett. 1980, 45, 606–609. [Google Scholar] [CrossRef]
- Blann, M. Hybrid model for Pre-equilibrium decay in Nuclear reactions. Phys. Rev. Lett. 1971, 27, 337–340. [Google Scholar] [CrossRef]
- Weiner, R.; Weström, M. Diffusion of heat in nuclear matter and preequilibrium phenomena. Nucl. Phys. A 1977, 286, 282–296. [Google Scholar] [CrossRef]
- Bondorf, J.P.; De, J.N.; Fái, G.; Karvinen, O.T.; Jakobsson, B.; Randrup, J. Prompty emitted particles in nuclear collisions. Nucl. Phys. A 1980, 333, 285–301. [Google Scholar] [CrossRef]
- Harvey, B.G.; Murphy, M.J. Dynamics of heavy-ion transfer reactions. Phys. Lett. B 1983, 130, 373–377. [Google Scholar] [CrossRef]
- Harvey, B.G. A microscopic calculation of fragment formation in nucleus-nucleus collisions. Nucl. Phys. A 1985, 444, 498–518. [Google Scholar] [CrossRef]
- Abul-Magd, A.Y. Entrance-Channel angular momentum dependence of mass transfer between heavy ions. Z. Phys. A 1980, 298, 143–147. [Google Scholar] [CrossRef]
- Simbel, M.H.; Abul-Magd, A.Y. Influence of angular momentum dependence of charge transfer in deeply inelastic collisions on fragment kinetic energies. Z. Phys. A 1980, 294, 277–280. [Google Scholar] [CrossRef]
- Zagrebaev, V.I. Semicalssical theory of direct and deep inelastic heavy ion collisions. Ann. Phys. 1990, 197, 33–93. [Google Scholar] [CrossRef]
- Diaz-Torres, A.; Hinde, D.J.; Tostevin, J.A.; Dasgupta, M.; Gasques, L.R. Relating breakup and incomplete fusion of weakly bound nuclei through a classical trajectory model with stochastic breakup. Phys. Rev. Lett. 2007, 98, 152701. [Google Scholar] [CrossRef]
- Diaz-Torres, A. Modelling incomplete fusion dynamics of weakly bound nuclei at near-barrier energies. J. Phys. G Nucl. Part. Phys. 2010, 37, 075109. [Google Scholar] [CrossRef]
- Tserruya, I.; Steiner, V.; Fraenkel, Z.; Jacobs, P.; Kovar, D.G.; Henning, W.; Vineyard, M.F.; Glagola, B.G. Incomplete fusion reactions induced by 12C at 5.5-10 MeV/nucleon. Phys. Rev. Lett. 1988, 60, 14–17. [Google Scholar] [CrossRef]
- Gerschel, C. Incomplete fusion reactions. Nucl. Phys. A 1982, 387, 297c–312c. [Google Scholar] [CrossRef]
- Morgenstern, H.; Bohne, W.; Galster, W.; Grabisch, K.; Kyanowski, A. Influence of the mass asymmetry on the onset of incomplete and the limit to complete fusion. Phys. Rev. Lett. 1984, 52, 1104–1107. [Google Scholar] [CrossRef]
- Singh, P.P.; Singh, B.P.; Sharma, M.K.; Unnati; Singh, D.P.; Prasad, R.; Kumar, R.; Golda, K.S. Influence of incomplete fusion on complete fusion: Observation of a large incomplete fusion fraction at E ≈ 5-7 MeV/nucleon. Phys. Rev. C 2008, 77, 014607. [Google Scholar] [CrossRef]
- Rafiei, R.; du Rietz, R.; Luong, D.H.; Hinde, D.J.; Dasgupta, M.; Evers, M.; Diaz-Torres, A. Mechanisms and systematics of breakup in reactions of 9Be at near-barrier energies. Phys. Rev. C 2010, 81, 024601. [Google Scholar] [CrossRef]
- Gasques, L.R.; Hinde, D.J.; Dasgupta, M.; Mukherjee, A.; Thomas, R.G. Suppresion of complete fusion due to breakup in the reaction 10,11B+209Bi. Phys. Rev. C 2009, 79, 034605. [Google Scholar] [CrossRef]
- Hinde, D.J.; Dasgupta, M.; Mukherjee, A. Severe inhibition of fusion by quassifission in reactions forming 220Th. Phys. Rev. Lett. 2002, 89, 272701. [Google Scholar] [CrossRef]
- Gomes, P.R.S.; Linares, R.; Lubian, J.; Lopes, C.C.; Cardozo, E.N.; Pereira, B.H.F.; Padron, I. Search for systematic behavior of incomplete-fusion probabiity and complete-fusion suppression induced by 9Be on different targets. Phys. Rev. C 2011, 84, 014615. [Google Scholar] [CrossRef]
- Shuaib, M.; Sharma, V.R.; Yadav, A.; Singh, P.P.; Sharma, M.K.; Singh, D.P. Incomplete fusion studies in the 19F+159Tb system at low energies and its correlation with various systematics. Phys. Rev. C 2016, 94, 014613. [Google Scholar]
- Mullins, S.M.; Dracoulis, G.D.; Byrne, A.P.; McGoram, T.R.; Bayer, S.; Bark, R.A.; Newman, R.T.; Seale, W.A.; Kondev, F.G. Rotational and intrinsic states above the Kπ = 25/2−, T1/2 = 25 day isomer in 179Hf. Phys. Rev. C 2000, 61, 044315. [Google Scholar] [CrossRef]
- Lane, G.J.; Dracoulis, G.D.; Byrne, P.; Poletti, A.R.; McGoram, T.R. Population of high-spin states in 234U by an incomplete-fusion reaction. Phys. Rev. C 1999, 60, 067301. [Google Scholar] [CrossRef]
- Dracoulis, G.D.; Byrne, A.P.; Kibédi, T.; McGoram, T.R.; Mullins, S.M. Incomplete fusion as a spectroscopic tool. Phys. G Nucl. Part. Phys. 1997, 23, 1191. [Google Scholar] [CrossRef]
- Jungclaus, A.; Binder, B.; Dietrich, A.; Härtlein, T.; Bauer, H.; Gund, C.; Pansegrau, D.; Schwalm, D.; Egido, J.L.; Sun, Y.; et al. Backbending region study in 160,162Dy using incomplete fusion reactions. Phys. Rev. C 2002, 66, 014312. [Google Scholar] [CrossRef]
- Jungclaus, A.; Binder, B.; Dietrich, A.; Härtlein, T.; Bauer, H.; Gund, C.; Pansegrau, D.; Schwalm, D.; Bazzacco, D.; Farnea, E.; et al. Excited bands and signature dependent electromagnetic decay properties in neutron-rich 159,161,163Dy. Phys. Rev. C. 2003, 67, 034302. [Google Scholar] [CrossRef]
- Kumar, K.; Ali, S.; Ahmad, T.; Rizvi, I.A.; Agarwal, A.; Kumar, R.; Chaubey, A.K. Low energy incomplete fusion: Observation of a significant incomplete fusion fraction at ℓ < ℓcrit. EPJ Web Conf. 2015, 86, 00011. [Google Scholar]
- Singh, D.P.; Yadav, A.; Bala, I.; Raghav, A.; Shuaib, M.; Kumar, P.; Singh, P.P.; Unnati; Sharma, M.K.; Sharma, V.R.; et al. Observation of incomplete fusion at low angular momenta. EPJ Web Conf. 2015, 86, 50. [Google Scholar] [CrossRef]
- Tricoire, H.; Gerschel, C.; Gillibert, A.; Perrin, N. Evidence for large angular momentum window associated with incomplete fusion reactions. Z. Phys. A-At. Nucl. 1986, 323, 163–171. [Google Scholar] [CrossRef]
- Utsunomiya, H.; Nomura, T.; Ishihara, M.; Sugitate, T.; Ieki, K.; Kohmoto, S. Angular-momentum transfer and alignement following preequilibrium α-partilce emission in the reaction 209Bi + 14N. Phys. Lett. B 1981, 105, 135–139. [Google Scholar] [CrossRef]
- Bhujang, B.; Das, P.; Singh, R.P.; Tripathi, R.; Tomar, B.S. Incomplete fusion studies near Coulomb barrier: A modified sum rule model. J. Phys. Conf. Ser. 2013, 420, 012128. [Google Scholar] [CrossRef]
- Kumar, A.; Tripathi, R.; Sodaye, S.; Sudarshan, K.; Pujari, P.K. Angular distributions and cross-sections of projectile-like fragments in the 19F+159Tb reaction. Eur. J. Phys. 2013, 49, 3. [Google Scholar] [CrossRef]
- National Nuclear Data Center. Available online: http://www.nndc.bnl.gov (accessed on 23 May 2023).
- RADWARE. Available online: http://radware.phy.ornl.gov (accessed on 23 May 2023).
- Gavron, A. Statistical model calculations in heavy ion reactions. Phys. Rev. C 1980, 21, 230–236. [Google Scholar] [CrossRef]
- Bass, R. Nucleus-Nucleus potential deduced from experimental fusion cross sections. Phys. Rev. Lett. 1977, 39, 265–268. [Google Scholar] [CrossRef]
- Cavinato, M.; Fabrici, E.; Gadioli, E.; Gadoli Erba, E.; Vergani, P.; Crippa, M.; Colombo, G.; Redaelli, I.; Ripamonti, M. Study of reactions occurring in the fusion of 12C and 16O with heavy nuclei at incident erergies below 10 MeV/nucleon. Phys. Rev. C 1995, 52, 2577–2590. [Google Scholar] [CrossRef]
- Siwek-Wilczyńska, K.; du Marchie van Voorthuysen, E.H.; van Popta, J.; Siemssen, R.H.; Wilczyński, J. Incomplete fusion in 12C+160Gd collisions interpreted in terms of a generalized concept of critical angular momentum. Phys. Rev. Lett. 1979, 42, 1599–1602. [Google Scholar] [CrossRef]
- Wilczyński, J.; Siwek-Wilczyńska, K. Determination of the nucleus-nucleus potential from boundary conditions. Phys. Lett. B 1975, 55, 270–272. [Google Scholar] [CrossRef]
- Siwek-Wilczyńska, K.; Wilczyński, J. A test of the nucleus-nucleus potential using fusion excitation functions. Phys. Lett. B 1978, 74, 313–315. [Google Scholar] [CrossRef]
- Wilczyński, J. Calculations of the critical angular momentum in the entrance reaction channel. Nucl. Phys. A 1973, 216, 386–394. [Google Scholar] [CrossRef]
- Myers, W.D. Geometric properties of Leptodermous distributions with applications to nuclei. Nucl. Phys. A 1973, 204, 465–484. [Google Scholar] [CrossRef]
- Siwek-Wilczyńska, K.; du Marchie van Voorthuysen, E.H.; van Popta, J.; Siemssen, R.H.; Wilczyński, J. Incomplete fusion in 12C+160Gd collisions. Nucl. Phys. A 1979, 330, 150–172. [Google Scholar] [CrossRef]
- Mukherjee, A.; Pradhan, M.K. Influence of projectile breakup on complete fusion. Pramana J. Phys. 2010, 75, 99–107. [Google Scholar] [CrossRef]
- Tripathi, R.; Sudarshan, K.; Sodaye, S.; Reddy, A.V.R.; Goswami, A.; Nayak, B.K.; Sharma, S.K. Cross sections of projectile-like fragments in the reaction 19F + 66Zn in the beam energy range of 3–6 MeV/nucleon. Phys. Rev. C 2009, 79, 064604. [Google Scholar] [CrossRef]
- Goldstein, H. Classical Mechanics, 2nd ed.; Narosa Publishing House: New Delhi, India, 2001. [Google Scholar]
- Glas, D.; Mosel, U. On the critical distance in fusion reactions. Nucl. Phys. A 1975, 237, 429–440. [Google Scholar] [CrossRef]
- Hagino, K.; Vitturi, A.; Dasso, C.H.; Lenzi, S.M. Role of breakup processes in fusion enhancement of drip-line nuclei at energies below the Coulomb barrier. Phys. Rev. C 2000, 61, 037602. [Google Scholar] [CrossRef]
- Diaz-Torres, A. PLATYPUS: A code for reaction dynamics of weakly-bound nuclei at near-barrier energies within a classical dynamical model. Comp. Phys. Comm. 2011, 182, 1100–1104. [Google Scholar] [CrossRef]
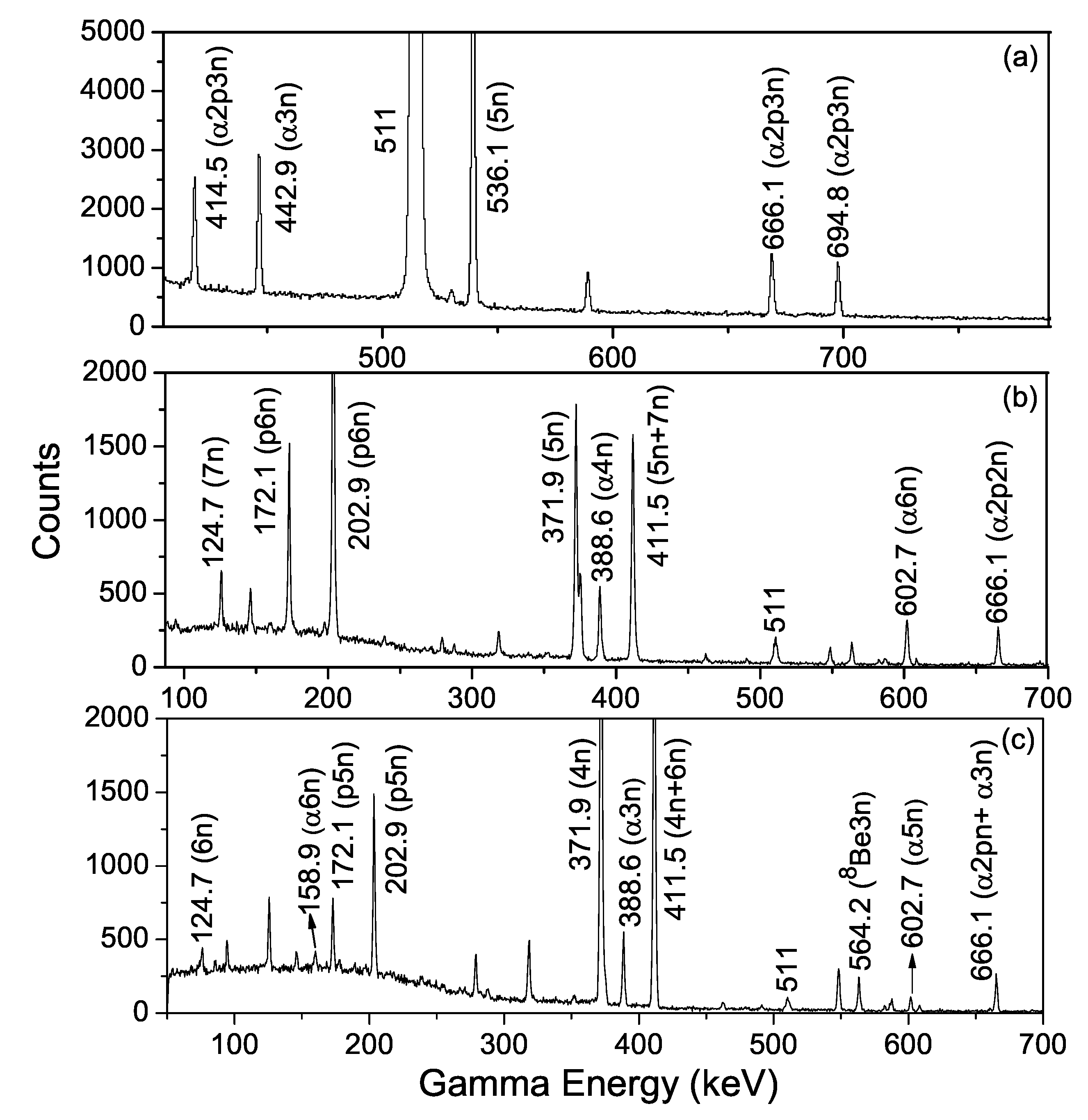
| Evaporation Residues | Decay Mode (%) | BSn | BSn | BSn | E (keV) | (%) | |
|---|---|---|---|---|---|---|---|
| Cs | EC 98.4 | 29.21 m | 5n | - | - | 536.1 | 3.8 |
| Cs | EC 100 | 32.06 h | 6n | 5n | 4n | 371.9 | 30.6 |
| Cs | EC 100 | 3.66 m | - | 6n | 5n | 442.9 | 26.8 |
| Cs | 100 | 6.25 h | - | 7n | 6n | 124.7 | 11.37 |
| Xe | EC 100 | 36.4 d | - | 202.9 | 68.7 | ||
| I | 93.10 | 25 m | 442.9 | 12.62 | |||
| I | 47.3 | 12.93 d | 388.6 | 35.6 | |||
| EC 52.7 | 12.93 d | 666.3 | 32.6 | ||||
| I | EC 100 | 4.176 d | - | 602.7 | 62.9 | ||
| I | EC 100 | 13.22 h | - | - | 158.9 | 83.3 | |
| Sb | 86.4 | 19.15 m | 666.1 | 86 | |||
| 100 | 12.35 d | 666.1 | 99.6 | ||||
| Sb | 97.59 | 2.734 d | - | - | Be | 564.2 | 70.67 |
| Parameter | SRM | MSRM1 | MSRM2 |
|---|---|---|---|
| 0.92 MeVfm | 0.92 MeVfm | 0.92 MeVfm | |
| T | 3 MeV | 3 MeV | 3.5 MeV |
| 0.06 fm | 0.06 fm | 0.05 fm | |
| 2 ℏ | 2 ℏ | 1.4 ℏ | |
| - | 0.021 | - | |
| - | - | 0.71 | |
| 1.05 fm | 1.05 fm | 1.08 fm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhujang, B.; Das, P. Towards Understanding Incomplete Fusion Reactions at Low Beam Energies: Modified Sum Rule Model. Atoms 2023, 11, 106. https://doi.org/10.3390/atoms11070106
Bhujang B, Das P. Towards Understanding Incomplete Fusion Reactions at Low Beam Energies: Modified Sum Rule Model. Atoms. 2023; 11(7):106. https://doi.org/10.3390/atoms11070106
Chicago/Turabian StyleBhujang, Bhushan, and Pragya Das. 2023. "Towards Understanding Incomplete Fusion Reactions at Low Beam Energies: Modified Sum Rule Model" Atoms 11, no. 7: 106. https://doi.org/10.3390/atoms11070106
APA StyleBhujang, B., & Das, P. (2023). Towards Understanding Incomplete Fusion Reactions at Low Beam Energies: Modified Sum Rule Model. Atoms, 11(7), 106. https://doi.org/10.3390/atoms11070106






