Quantum Fisher Information of Three-Level Atom under the Influence of the Stark Effect and Intrinsic Dechorence
Abstract
1. Introduction
2. Hamiltonian Model
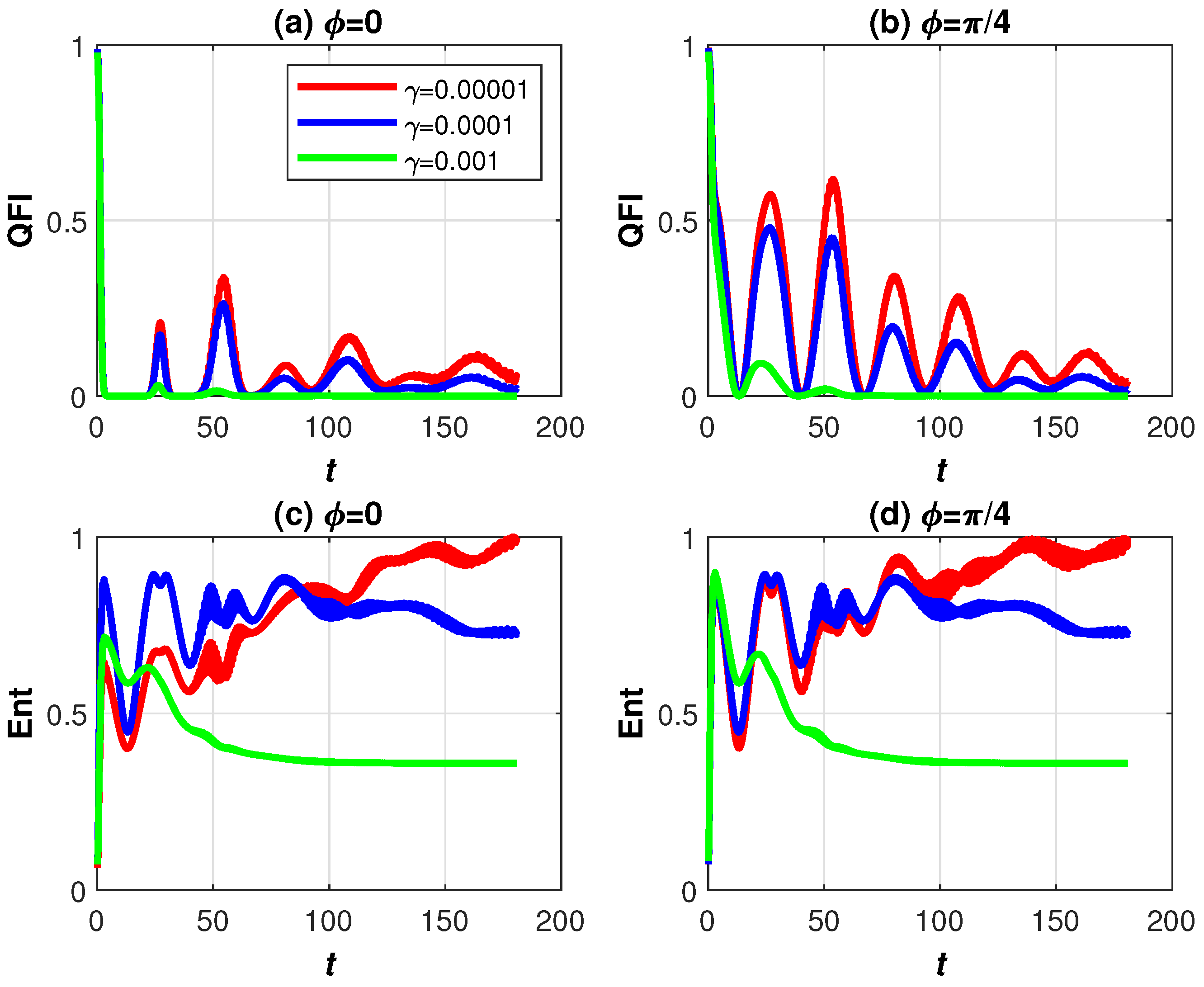
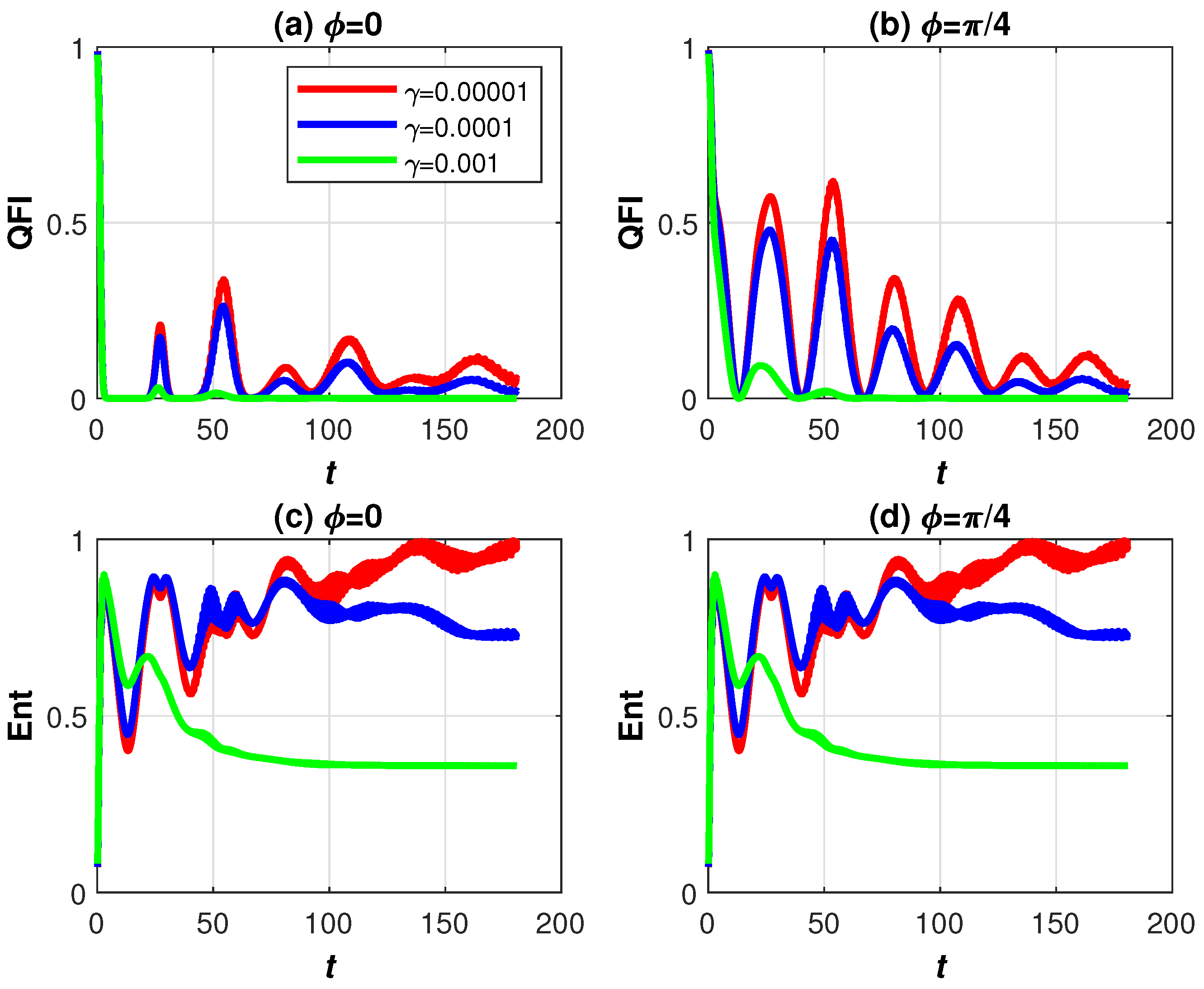
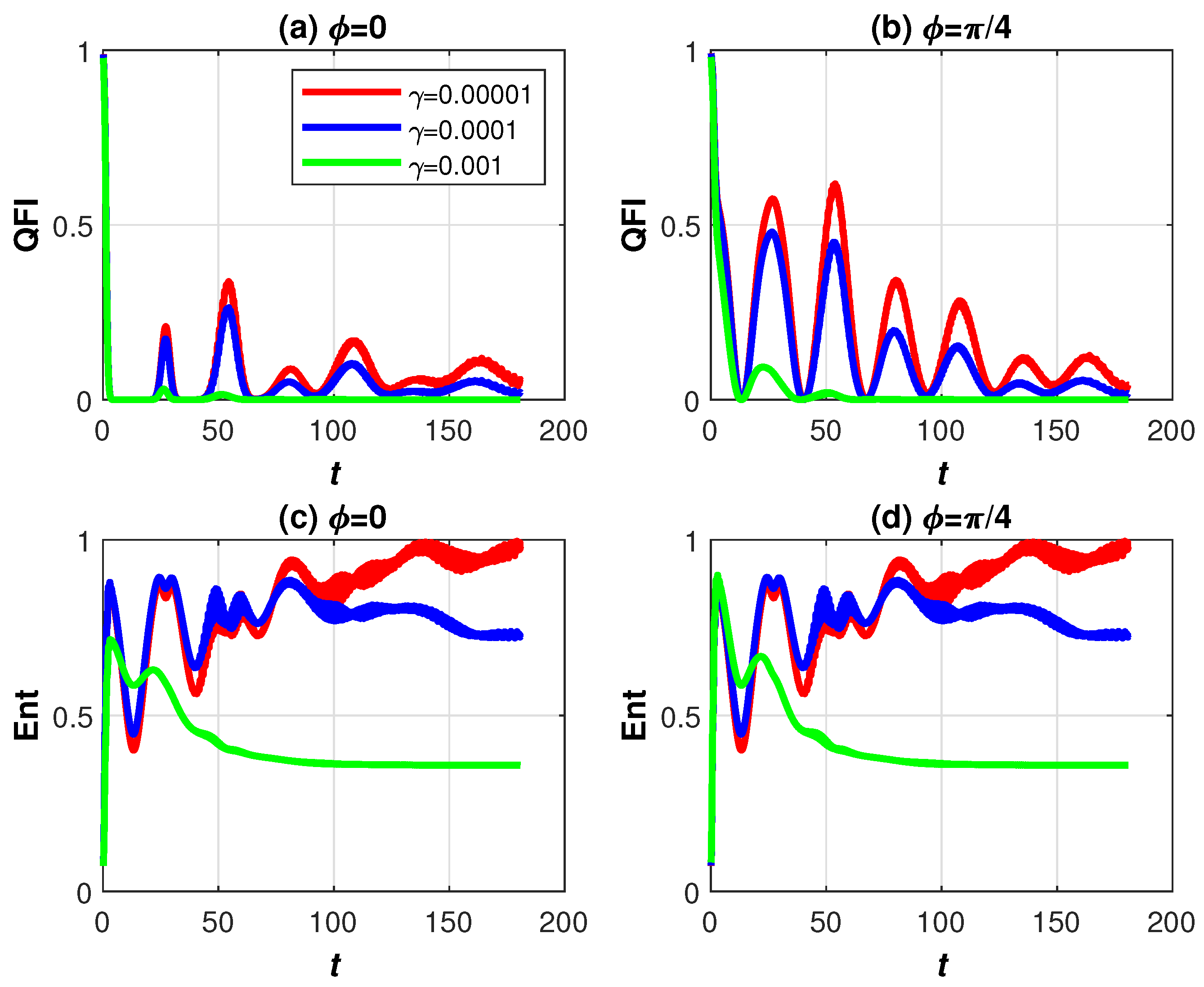
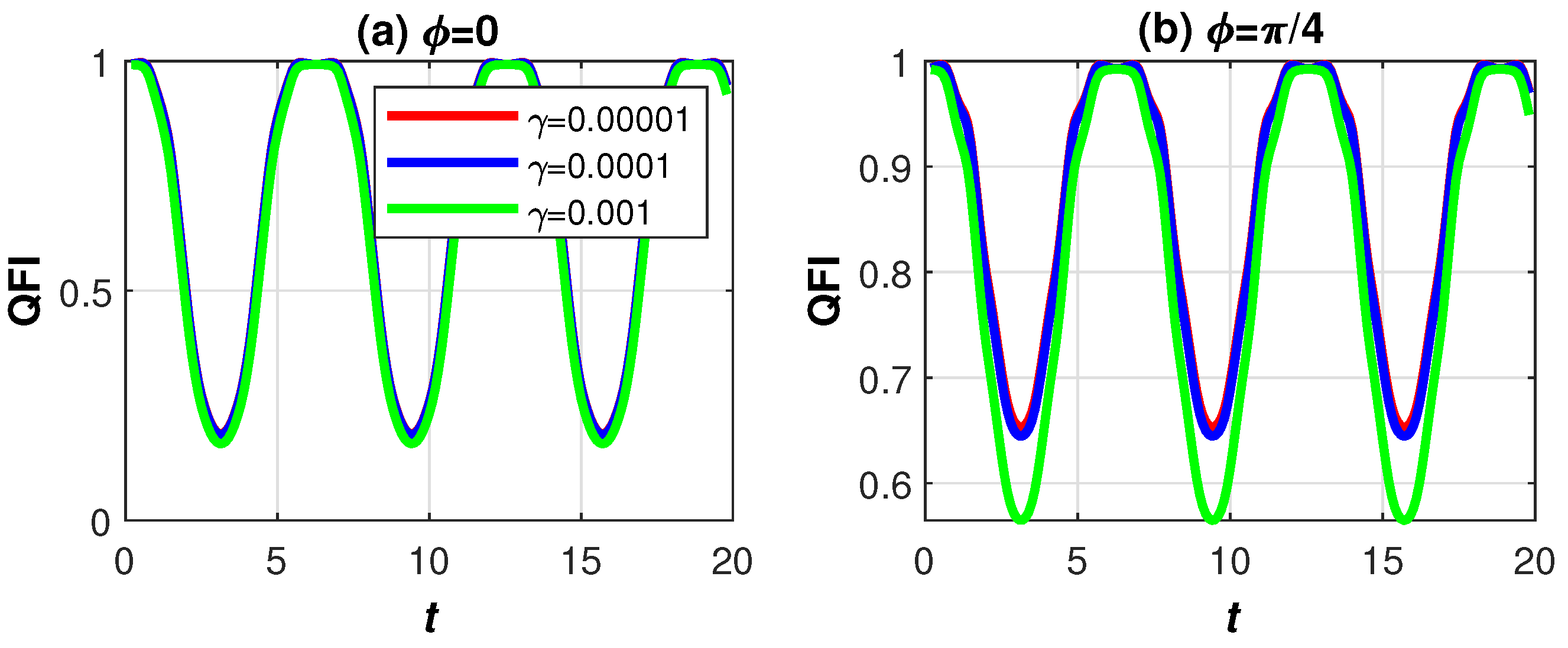
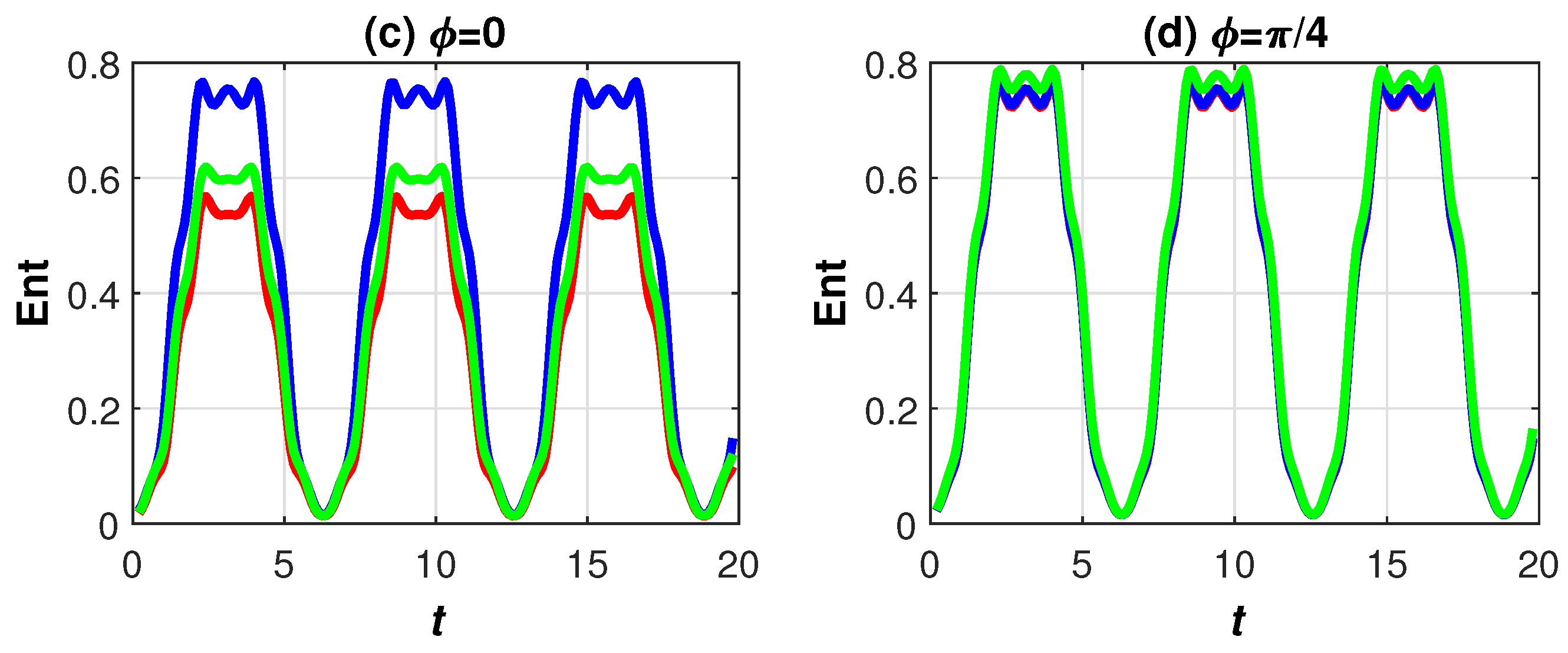
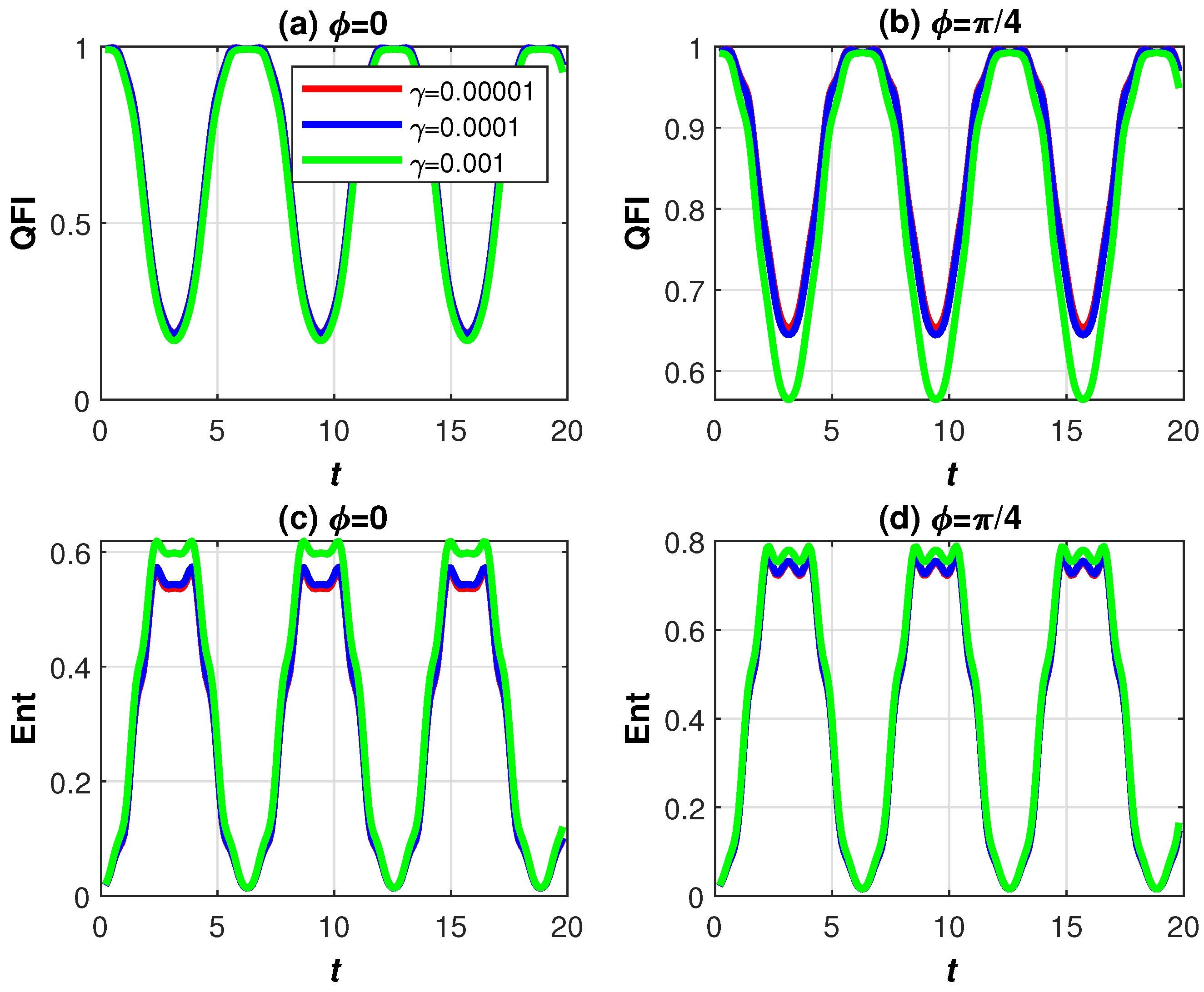
3. Numerical Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Englert, B.-G.; Metwally, N. Kinematics of qubit pairs. In Mathematics of Quantum Computation; Brylinski, R., Chen, G., Eds.; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2002; pp. 25–75. [Google Scholar]
- Phoenix, S.J.D.; Knight, P.L. Fluctuations and entropy in models of quantum optical resonance. Ann. Phys. 1988, 186, 381–407. [Google Scholar] [CrossRef]
- Phoenix, S.J.D.; Knight, P.L. Establishment of an entangled atom-field state in the Jaynes–Cummings model. Phys. Rev. A 1991, 44, 6023–6029. [Google Scholar] [CrossRef]
- Vedral, V.; Plenio, M.B.; Rippin, M.A.; Knight, P.L. Quantifying entanglement. Phys. Rev. Lett. 1997, 78, 2275–2279. [Google Scholar] [CrossRef]
- Metwally, N. Quantum dense coding and dynamics of information over Bloch channels. J. Phys. A 2011, 44, 055305. [Google Scholar] [CrossRef]
- Obada, A.S.; Ahmed, M.M.A.; Faramawy, F.K.; Khalil, E.M. Entropy and entanglement of the nonlinear Jaynes–Cummings model. Chin. J. Phys. 2004, 42, 79–91. [Google Scholar]
- Hines, A.P.; Dawson, C.M.; McKenzie, R.H.; Milburn, G.J. Entanglement and bifurcations in Jahn–Teller models. Phys. Rev. A 2004, 70, 022303. [Google Scholar] [CrossRef]
- Jia, X.; Subramaniam, A.R.; Gruzberg, I.A.; Chakravarty, S. Entanglement entropy and multifractality at localization transitions. Phys. Rev. B 2008, 77, 014208. [Google Scholar] [CrossRef]
- Abdelghany, R.A.; Mohamed, A.B.; Tammam, M.; Kuo, W.; Eleuch, H. Tripartite entropic uncertainty relation under phase decoherence. Sci. Rep. 2021, 11, 11830. [Google Scholar] [CrossRef] [PubMed]
- Dattoli, G.; Gallardo, J.; Torre, A. Binomialstatesofthe quantized radiation field: Comment. J. Opt. Soc. Am. B 1987, 4, 185–187. [Google Scholar] [CrossRef]
- Verma, A.; Sharma, N.K.; Pathak, A. Higher order antibunching in intermediate states. Phys. Lett. A 2008, 372, 5542–5551. [Google Scholar] [CrossRef]
- Agarwal, G.S.; Tara, K. Nonclassical properties of states generated by the excitations on a coherent state. Phys. Rev. A 1991, 43, 492–497. [Google Scholar] [CrossRef]
- Tavassoly, M.K.; Hekmatara, H. Entanglement and other nonclassical properties of two two-level atoms interacting with a two-mode binomial field: Constant and intensity-dependent coupling regimes. Commun. Theor. Phys. 2015, 64, 439–446. [Google Scholar] [CrossRef]
- Torres-Arenas, A.J.; Dong, Q.; Sun, G.H.; Qiang, W.C.; Dong, S.H. Entanglement measures of W-state in noninertial frames. Phys. Lett. B 2019, 789, 93–105. [Google Scholar] [CrossRef]
- Qiang, W.C.; Dong, Q.; Mercado Sanchez, M.A.; Sun, G.H.; Dong, S.H. Entanglement property of the Werner state in accelerated frames. Quantum Inf. Process. 2019, 18, 314. [Google Scholar] [CrossRef]
- Dong, Q.; Sanchez, M.M.; Sun, G.H.; Toutounji, M.; Dong, S.H. Tripartite Entanglement Measures of Generalized GHZ State in Uniform Acceleration. Chin. Phys. Lett. 2019, 36, 100301. [Google Scholar] [CrossRef]
- Fisher, R.A. Theory of Statistical Estimation. Proc. Camb. Philos. Soc. 1929, 22, 700, reprinted in Collected Papers of R.A. Fisher; Bennett, J.H., Ed.; Univ. of Adelaide Press: Adelaide, South Australia, 1972; pp. 15–40.. [Google Scholar] [CrossRef]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Quantum-Enhanced Measurements: Beating the Standard Quantum Limit. Science 2004, 306, 1330–1336. [Google Scholar] [CrossRef] [PubMed]
- Dowling, J. Quantum Optical Metrology-The Lowdown On High-N00N States. Contemp. Phys. 2008, 49, 125–143. [Google Scholar] [CrossRef]
- Jones, J.A.; Karlen, S.D.; Fitzsimons, J.; Ardavan, A.; Benjamin, S.C.; Briggs, G.A.D.; Morton, J.J.L. Magnetic Field Sensing Beyond the Standard Quantum Limit Using 10-SpinNOON States. Science 2009, 324, 1166–1168. [Google Scholar] [CrossRef] [PubMed]
- Simmons, S.; Jones, J.A.; Karlen, S.D.; Ardavan, A.; Morton, J.J.L. Magnetic field sensors using 13-spin cat states. Phys. Rev. A 2010, 82, 022330. [Google Scholar] [CrossRef]
- Higgins, B.L.; Berry, D.W.; Bartlett, S.D.; Wiseman, H.M.; Pryde, G.J. Entanglement-free Heisenberg-limited phase estimation. Nature 2007, 450, 393–396. [Google Scholar] [CrossRef] [PubMed]
- Dorner, U.; Smith, B.J.; Lundeen, J.S.; Wasilewski, W.; Banaszek, K.; Walmsley, I.A. Quantum phase estimation with lossy interferometers. Phys. Rev. A 2009, 80, 013825. [Google Scholar]
- Cramer, H. Mathematical Methods of Statistics; Princeton University Press: Princeton, NJ, USA, 1946. [Google Scholar]
- Dorner, U.; Demkowicz-Dobrzanski, R.; Smith, B.J.; Lundeen, J.S.; Wasilewski, W.; Banaszek, K.; Walmsley, I.A. Optimal Quantum Phase Estimation. Phys. Rev. Lett. 2009, 102, 040403. [Google Scholar] [CrossRef] [PubMed]
- Abdel-Khalek, S. Dynamics of Fisher information in Kerr medium. Int. J. Quantum Inf. 2009, 7, 1541–1548. [Google Scholar] [CrossRef]
- Joo, J.; Munro, W.J.; Spiller, T.P. Quantum Metrology with Entangled Coherent States. Phys. Rev. Lett. 2011, 107, 083601. [Google Scholar] [CrossRef]
- Rissanen, J.J. Fisher information and stochastic complexity. IEEE Trans. Inf. Theory 1996, 42, 40–47. [Google Scholar] [CrossRef]
- Braunstein, S.L.; Caves, C.M. Statistical distance and the geometry of quantum states. Phys. Rev. Lett. 1994, 72, 3439. [Google Scholar] [CrossRef]
- Alipour, S.; Mehboudi, M.; Rezakhani, A.T. Quantum metrology in open systems: Dissipative cramér-rao bound. Phys. Rev. Lett. 2014, 112, 120405. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, M.; Yang, P.; Gong, M.; Cao, Q.; Zhang, S.; Cai, J. Saturating the quantum Cramér-Rao bound and measuring the related quantum Fisher information in a nitrogen-vacancy center in diamond. arXiv 2020, arXiv:2003.08373. [Google Scholar]
- Liu, J.; Yuan, H.; Lu, X.M.; Wang, X. Quantum Fisher information matrix and multiparameter estimation. J. Phys. A Math. Theor. 2019, 53, 023001. [Google Scholar] [CrossRef]
- Helstron, C.W. Quantum Detection and Estimation Theory; Academic Press: New York, NY, USA, 1967. [Google Scholar]
- Roy, S.M.; Braunstein, S.L. Exponentially enhanced quantum metrology. Phys. Rev. Lett. 2008, 100, 220501. [Google Scholar] [CrossRef] [PubMed]
- Boixo, S.; Datta, A.; Davis, M.J.; Flammia, S.T.; Shaji, A.; Caves, C.M. Quantum metrology: Dynamics versus entanglement. Phys. Rev. Lett. 2008, 101, 040403. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Huang, Y.X.; Wang, X.; Sun, C.P. Quantum Fisher information of the Greenberger-Horne-Zeilinger state in decoherence channels. Phys. Rev. A 2011, 84, 022302. [Google Scholar] [CrossRef]
- Monras, A.; Paris, M.G. Optimal quantum estimation of loss in bosonic channels. Phys. Rev. Lett. 2007, 98, 160401. [Google Scholar] [CrossRef]
- Luo, S. Wigner-yanase skew information vs. quantum Fisher information. Proc. Am. Math. Soc. 2004, 132, 885–890. [Google Scholar] [CrossRef]
- Luo, S. Quantum Fisher information and uncertainty relations. Lett. Math. Phys. 2000, 53, 243–251. [Google Scholar] [CrossRef]
- Taddei, M.M.; Escher, B.M.; Davidovich, L.; de Matos Filho, R.L. Quantum Speed Limit for Physical Processes. Phys. Rev. Lett. 2013, 110, 050402. [Google Scholar] [CrossRef]
- Sun, Z.; Ma, J.; Lu, X.-M.; Wang, X. Fisher information in a quantum-critical environment. Phys. Rev. A 2010, 82, 022306. [Google Scholar] [CrossRef]
- Chapeau-Blondeau, F. Entanglement-assisted quantum parameter estimation from a noisy qubit pair: A Fisher information analysis. Phys. Lett. A 2017, 381, 1369–1378. [Google Scholar] [CrossRef]
- Abdel-Khalek, S.; Khalil, E.M.; Ali, S.I. Entanglement of a two-level atom papered in a finite Trio Coherent state. Laser Phys. 2008, 18, 135–143. [Google Scholar] [CrossRef]
- Abdel-Khalek, S.; Obada, A.S.F. New features of Wehrl entropy and Wehrl PD of a single-Cooper pair box placed inside a dissipative cavity. Ann. Phys. 2010, 325, 2542–2549. [Google Scholar] [CrossRef]
- Obada, A.-S.F.; Abdel-Khalek, S. Entanglement evaluation with atomic Fisher information. Physica A 2010, 389, 891–898. [Google Scholar] [CrossRef]
- Obada, A.-S.F.; Abdel-Khalek, S.; Plastino, A. Information quantifiers’s description of weak field vs. strong field dynamics for a trapped ion in a laser field. Physica A 2011, 390, 525–533. [Google Scholar] [CrossRef]
- Abdel-Khalek, S.; Berrada, K.; Obada, A.S.F. An investigation of quantum Fisher information of a single qubit system. Eur. Phys. J. D 2012, 66, 69. [Google Scholar] [CrossRef]
- Berrada, K.; Abdel-Khalek, S.; Obada, A.S.F. Quantum Fisher information for a qubit system placed inside a dissipative cavity. Phys. Lett. A 2012, 376, 1412–1416. [Google Scholar] [CrossRef]
- Li, X.-S.; Lin, D.L.; Gong, C.-D. Nonresonant interaction of a three-level atom with cavity fields. I. General formalism and level occupation probabilities. Phys. Rev. A 1987, 36, 5209–5219. [Google Scholar] [CrossRef]
- Abdel-Wahab, N.H. The general formalism for a three-level atom interacting with a two-mode cavity field. Phys. Scr. 2007, 76, 233. [Google Scholar] [CrossRef]
- Abdel-Wahab, N.H. A three-level atom interacting with a single mode cavity field: Different configurations. Phys. Scr. 2007, 76, 244. [Google Scholar] [CrossRef]
- Obada, A.-S.F.; Eied, A.A.; Abd Al-Kader, G.M. Entanglement of a general formalism-type three-level atom interacting with a non-correlated two-mode cavity field in the presence of nonlinearities. J. Phys. B 2008, 41, 195503. [Google Scholar] [CrossRef]
- Teng, J.-H.; Wang, H.-F.; Qi, L.N.; Zhang, S. Influence of Kerr medium on entanglement of Cascade-type three-level atoms and a bimodal cavity field. Int. J. Theor. Phys. 2009, 48, 2818–2825. [Google Scholar] [CrossRef]
- Mortezapoura, A.; Mahmoudib, M.; Khajehpourc, M.R.H. Atom–photon, two-mode entanglement and two-mode squeezing in the presence of cross-Kerr nonlinearity. Opt. Quantum. Electron. 2015, 47, 2311–2329. [Google Scholar] [CrossRef]
- Metwally, N.; Eleuch, H.; Obada, A.-S. Sudden death and rebirth of entanglement for different dimensional systems driven by a classical random external field. Laser Phys. Lett. 2016, 13, 105206. [Google Scholar] [CrossRef]
- Faghihia, M.J.; Tavassolya, M.K.; Hatamid, M. Dynamicsof entanglement of a three-level atom in motion interacting with two coupled modes including parametric down conversion. Physica A 2014, 407, 100–109. [Google Scholar] [CrossRef]
- Ismail, M.K.; El-Shahat, T.M. Thedampedinteraction between a single-mode cavity field with Caldirola–Kanai Hamiltonian and a three-level atom. Chin. J. Phys. 2019, 59, 273–280. [Google Scholar] [CrossRef]
- El-Wahab, N.A.; Rady, A.A.; Osman, A.N.A.; Salah, A. Influence of the gravitational field on the statistics of a three-level atom interacting with a one-mode cavity field. J. Russ. Laser Res. 2015, 36, 423–429. [Google Scholar] [CrossRef]
- Abdel-Aty, M.; Obada, A.-S.F. Engineering entanglement of a general three-level system interacting with a correlated two-mode nonlinear coherent state. Eur. Phys. J. D 2003, 23, 155–165. [Google Scholar] [CrossRef]
- Abdel-Wahab, N.H.; Salah, A. On the interaction between a time-dependent field and a two-level atom. Mod. Phys. Lett. A 2019, 34, 1950081. [Google Scholar] [CrossRef]
- Milburn, G.J. Intrinsic decoherence in quantum mechanics. Phys. Rev. A 1991, 44, 5401. [Google Scholar] [CrossRef]
- Gardiner, C.W. Quantum Noise; Springer: Berlin, Germany, 1991. [Google Scholar]
- Ghirardi, G.C.; Rimini, A.; Weber, T. Unified dynamics for microscopic and macroscopic systems. Phys. Rev. D 1986, 34, 470. [Google Scholar] [CrossRef]
- Diosi, L. Models for universal reduction of macroscopic quantum fluctuations. Phys. Rev. A 1989, 40, 1165. [Google Scholar] [CrossRef]
- Ellis, J.; Mohanty, S.; Nanopoulos, D.V. Wormholes violate quantum mechanics in SQUIDs. Phys. Lett. B 1990, 235, 305. [Google Scholar] [CrossRef]
- Anwar, S.J.; Ramzan, M.; Khan, M.K. Dynamics of entanglement and quantum Fisher information for N-level atomic system under intrinsic decoherence. Quantum Inf. Process. 2017, 16, 142. [Google Scholar] [CrossRef]
- Zheng, L.; Zhang, G.F. Intrinsic decoherence in Jaynes-Cummings model with Heisenberg exchange interaction. Eur. Phys. J. D 2017, 71, 288. [Google Scholar] [CrossRef]
- Liao, Y.Y.; Jian, S.R.; Lee, J.R. Effect of intrinsic decoherence on entanglement of three polar molecules with two-dimensional rotation. Eur. Phys. J. D 2019, 73, 47. [Google Scholar] [CrossRef]
- Obada, A.S.F.; Mohamed, A.B.A. Quantum correlations of two non-interacting ion’s internal electronic states with intrinsic decoherence. Opt. Commun. 2013, 309, 236–241. [Google Scholar] [CrossRef]
- Mohamed, A.-B. Non-local correlation and quantum discord in two atoms in the non-degenerate model. Ann. Phys. 2012, 327, 3130–3137. [Google Scholar] [CrossRef]
- Mohamed, A.B.A.; Eleuch, H. Optical tomography dynamics induced by qubit-resonator interaction under intrinsic decoherence. Sci. Rep. 2022, 12, 17162. [Google Scholar] [CrossRef]
- Mohamed, A.A.; Hessian, H.A.; Al-Duais, F.S.; Eleuch, H. Quantum coherence induced by a flux qubit coupled by a resonator coherent field through a two-photon interaction. Phys. Scr. 2021, 96, 125120. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A.; Hessian, H.A. Non-classicality in an open two-mode parametric amplifier cavity containing a qutrit system. Phys. Scr. 2021, 96, 055102. [Google Scholar] [CrossRef]
- Alliluev, S.P.; Malkin, I.A. Calculations of the Stark effect in hydrogen atoms by using the dynamical symmetry O(2, 2) × 278 O(2). Zh. Eksp. Teor. Fiz. 1974, 66, 1283–1294. [Google Scholar]
- Al Naim, A.F.; Khan, J.Y.; Khalil, E.M.; Addel-Khalek, S. Effects of Kerr medium and Stark shift parameter on Wehrl entropy and the field purity for two-photon Jaynes-Cumminges model under dispersive approximation. J. Russ. Laser. Res. 2019, 40, 20–29. [Google Scholar] [CrossRef]
- Hilal, E.M.A.; Khalil, E.M. Quantum statistical aspects of interactions between the radiation field and two entangled two-level atoms in the presence of Stark shift terms. J. Russ. Laser. Res. 2018, 39, 207–215. [Google Scholar] [CrossRef]
- Anwar, S.J.; Ramzan, M.; Usman, M.; Khan, M.K. Entanglement dynamics of three and four level atomic system under Stark effect and Kerr-like medium. Quantum Rep. 2019, 1, 23–36. [Google Scholar] [CrossRef]
- Anwar, S.J.; Ramzan, M.; Khan, M.K. Effect of Stark-and Kerr-like medium on the entanglement dynamics of two three-level atomic system. Quantum Inf. Process. 2019, 18, 192. [Google Scholar] [CrossRef]
- Anwar, S.J.; Ramzan, M.; Usman, M.; Khan, M.K. Stark and Kerr effects on the dynamics of moving N-level atomic system. J. Quantum Inf. 2019, 9, 22. [Google Scholar] [CrossRef]
- Abdel-Aty, M.; Furuichi, S.; Obada, A.F. Entanglement degree of a nonlinear multiphoton Jaynes-Cummings model. J. Opt. B Quantum Semiclass. Opt. 2002, 4, 37. [Google Scholar] [CrossRef]
- Baghshahi, H.R.; Tavassoly, M.K.; Behjat, A. Entropy squeezing and atomic inversion in the k-photon Jaynes Cummings model in the presence of the Stark shift and a Kerr medium: A full nonlinear approach. Chin. Phys. B 2014, 23, 074203. [Google Scholar] [CrossRef]
- Golkar, S.; Tavassoly, M. Dynamics and maintenance of bipartite entanglement via the Stark shift effect inside dissipative reservoirs. Laser Phys. Lett. 2018, 15, 035205. [Google Scholar] [CrossRef]
- Obada, A.F.; Abdel-Khalek, S.; Khalil, E.M.; Ali, S.I. Effects of Stark shift and decoherence terms on the dynamics of phase-space entropy of the multiphoton Jaynes Cummings model. Phys. Scr. 2012, 86, 055009. [Google Scholar] [CrossRef]
- Abdel-Khalek, S. Quantum Fisher information for moving three-level atom. Quantum Inf. Process. 2013, 12, 3761–3769. [Google Scholar] [CrossRef]
- Enaki, N.A.; Ciobanu, N.J. Quantum trapping conditions for three-level atom flying through bimodal cavity field. Mod. Opt. 2008, 55, 589–598. [Google Scholar] [CrossRef]
- Guo, J.L.; Song, H.S. Entanglement between two Tavis–Cummings atoms with phase decoherence. J. Mod. Opt. 2009, 56, 496–501. [Google Scholar] [CrossRef]
- Lu, X.; Wang, X.; Sun, C.P. Quantum Fisher information flow and non-Markovian processes of open systems. Phys. Rev. A 2010, 82, 042103. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, O.E.; Gill, R.D.; Jupp, P.E. On quantum statistical inference. J. R. Stat. Soc. B 2003, 65, 775–816. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anwar, S.J.; Ramzan, M.; Khan, M.K. Quantum Fisher Information of Three-Level Atom under the Influence of the Stark Effect and Intrinsic Dechorence. Atoms 2023, 11, 42. https://doi.org/10.3390/atoms11030042
Anwar SJ, Ramzan M, Khan MK. Quantum Fisher Information of Three-Level Atom under the Influence of the Stark Effect and Intrinsic Dechorence. Atoms. 2023; 11(3):42. https://doi.org/10.3390/atoms11030042
Chicago/Turabian StyleAnwar, S. Jamal, M. Ramzan, and M. Khalid Khan. 2023. "Quantum Fisher Information of Three-Level Atom under the Influence of the Stark Effect and Intrinsic Dechorence" Atoms 11, no. 3: 42. https://doi.org/10.3390/atoms11030042
APA StyleAnwar, S. J., Ramzan, M., & Khan, M. K. (2023). Quantum Fisher Information of Three-Level Atom under the Influence of the Stark Effect and Intrinsic Dechorence. Atoms, 11(3), 42. https://doi.org/10.3390/atoms11030042





