Abstract
The shake-off processes and charge-state fractions of Li, Li, and Li were studied following the beta decay of He in the , , and initial states. The sudden approximation was used, together with fully correlated Hylleraas wave functions and pseudostates. A projection operator method was introduced to separate the charge-state fractions in the positive energy region of overlapping continua. The results show that Li (single-ionisation) remains dominant, even in the energy range , where the formation of Li (double-ionisation) is energetically allowed. The results reduce disagreements with the experiment for the fraction of Li by nearly an order of magnitude, but substantial disagreements remain that are inconsistent with the sudden approximation widely used in other similar work.
1. Introduction
There has been a long-standing interest in the beta decay of the halo nucleus He to form Li according to the Gamow–Teller process [1,2,3]:
especially in connection with searches for new physics beyond the Standard Model [4,5,6,7]. In this context, all single beta decay processes are thought to be either of the Fermi V-type, where the beta particle (e) and the antineutrino () are coupled to form a total spin of 0 or the Gamow–Teller A-type, where e and are coupled to form a total spin of 1. The He decay process is thought to be an example of the latter. In the former case, the angular correlation coefficient between the e and the is 1, and in the latter case, it is [8]. Any deviation from these angular correlations could therefore be interpreted as a signal for new physics.
The classic experiment by Carlson et al. [1] measured the angular correlation coefficient in He decay with helium atoms prepared in the ground state. In addition, there has been an ongoing experiment [9] involving metastable helium atoms held in an MOT trap. Müller et al. recently demonstrated [10] the first precise determination of the angular correlation coefficient using He decay with a neutral trap and found results consistent with the Standard Model. The challenge in both experiments is that the cannot be detected directly, and so, its momentum vector must be deduced from the overall kinematics of the decay process, including both the particle and the recoiling Li nucleus, together with its two atomic electrons. Any additional momentum carried away by the atomic electrons must, therefore, be included in the kinematics if one or both of them are emitted in subsequent ionisation events (shake-off). Otherwise, deviations due to the electronic momentum might masquerade as a signal for new physics.
With shake-off processes included, the possible final states are, thus, Li, Li, and Li. Although there is reasonably good agreement between the theory and experiments for the Li and Li charge-state fractions, as shown in Table 1, there is a large disagreement for the small amount of Li corresponding to double-ionisation, with the theory predicting one or two orders of magnitude more than what is observed in experiments. The disagreement is equally evident for both He() [1] and He() [9] as the initial states. The table shows comparisons with both our own previous calculations based on fully correlated Hylleraas wave functions [11] and with earlier configuration interaction (CI) calculations by Wauters and Vaeck [2]. In contrast, there is excellent agreement between the theory and experiments for the charge-state fractions of Li and Li following beta decay in the one-electron case of He [3], indicating that the sudden approximation (see Section 2) universally used in past work is evidently well justified.

Table 1.
Comparison of the previous theory with experiments for the probabilities p(Li) of forming the various charge states with following the beta decay of He() or He() as the initial states. All quantities are expressed in percent (%).
This paper is organised as follows. In Section 2, we present a formulation of the problem within the sudden approximation and, in Section 3, we develop a projection operator method based on products of hydrogenic wave functions to separate the charge-state fractions in the energy region of overlapping continua for Li and Li. Perturbative corrections to the projection operators due to the electron–electron interaction are calculated and shown to be small. The results in Section 4 show that, while the projection operators substantially reduce the disagreement with the experiment, the predicted amount of Li is still larger by an order of magnitude. Possible further corrections and other applications of the projection operator method are discussed in the final Discussion Section 4. The abbreviated notations , , and are used for the ground low-lying metastable states , , and , respectively.
2. Formulation of the Problem
The kinematics of the process is as follows. As discussed previously [9,11], the emitted particle has a maximum kinetic energy of MeV with a broad energy distribution going down to nearly zero. However, in the experiment of Hong et al. [9], only those events with MeV were counted. At these energies, the particle is relativistic. From the relativistic energy–momentum equation , the maximum recoil momentum is a.u. In contrast, since the recoiling He nucleus is much more massive u), its recoil velocity of a.u. is nonrelativistic. In addition, the corresponding recoil momentum transferred to the atomic electrons is so small that it is unimportant for the purposes of the present discussion. In particular, the probability for the formation of Li can be written in the form [11]:
with so that relative to the previously calculated value . The present work, therefore, focused on the leading A term and neglected the recoil. Additional exchange effects between the particle and the atomic electrons have also been considered and found to be negligible at these energies [12,13].
With these approximations, the emitted particle can be thought of as a spherical shell of charge expanding with (nearly) the velocity of light. Past work [1,2,3,11] has always made use of the sudden approximation in which the Coulomb pulse is taken to be instantaneous and the initial helium wave function (He) is expanded over the complete set of states (Li according to
where is the recoil momentum of the Li-ion and the sum over i includes an integration over both the single- and double-electron ionisation continua to form Li and Li, respectively. The factor generates the transformation to the moving frame of reference. Recoil corrections are important for the analysis of experiments [11], but for the present study, we worked in the limit of zero recoil () since the recoil effects do not materially change the charge-state distributions, which are our main focus. The absolute squares:
are then the transition probabilities into the various final states. Although there is reasonably good agreement between the theory and experiments for the Li and Li charge-state fractions, there is a large disagreement for the small amount of Li corresponding to double-ionisation. The analysis is compounded by the fact that the Li continuum underlies the Li continuum for positive energies above the threshold for the formation of Li (see Figure 1). The two charge states must, therefore, be separated in the calculations involving the positive energy range.
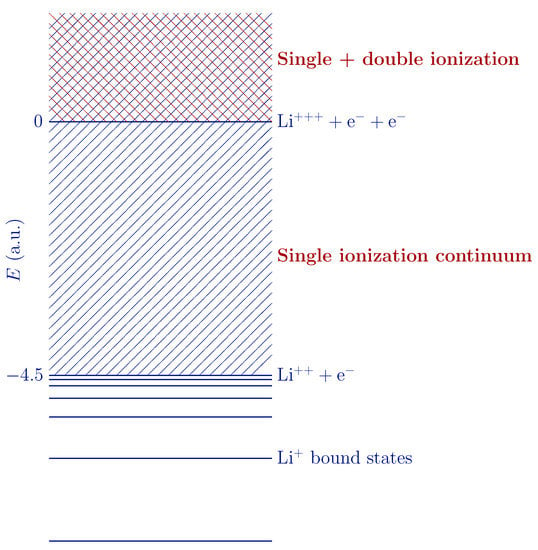
Figure 1.
Energy level diagram for Li following the beta decay. For the E > 0 region, the single-ionisation continuum underlies the double-ionisation continuum, and so, both charge states contribute to the total.
Our previous calculations of the charge-state distribution [11] in fact partitioned the possible final states by their energy range (bins), as in Figure 1, rather than the charge state, according to
where a.u. is the ground-state energy of Li, a.u., and . Bins 1 and 2 by definition consist entirely of Li and Li, respectively, but Bin 3 contains contributions from both Li and Li. The principal aim of the present work was to resolve Bin 3 into its charge-state components.
One can see from phase-space arguments that the fraction of Li is strongly suppressed near the threshold because the energy above the threshold must be equally shared between the two outgoing electrons. Otherwise, one electron will fall back to a bound state of Li, and the other will escape with all the excess energy. It is, therefore, necessary to project out of the various pseudostates satisfying E > 0 the Li component.
The problem of calculating the final-state fraction of Li to Li is closely related to the problem of calculating the ratio of photoionisation cross sections R = , on which there is a vast and rich literature for helium, ranging from many-body perturbation theory (MBPT) [14,15,16], close-coupling (cc) [17], convergent close-coupling (ccc) [18], R-matrix methods [19] with a discretisation of the continuum, and various distorted wave (DW) approximations for the final-state wave function [20,21,22,23]. The older literature up to 1996 was reviewed by Sadeghpour [24]. More recent work has applied these same methods to single- and double-photoionisation of Li, including R-matrix calculations [25,26], time-dependent close-coupling (TDCC) [27], ccc for the helium isoelectronic sequence [28], and B-spline methods [26,29]. The use of the method presented in this paper for the problem of double-photoionisation in helium is currently at a preliminary stage of investigation. This method is complementary to those mentioned above in that it uses the behaviour of the wave function as as opposed to the more common asymptotic condition as .
The present work starts with discrete variational representations of the initial and final states in terms of fully correlated wave functions in Hylleraas coordinates of the form [30,31]:
where the basis functions are defined by
The quantity represents a vector-coupled product of spherical harmonics of angular momenta and to form a state with total angular momentum L and component M. The parameter controls the size of the basis set. The basis set is “doubled” in the sense that the same combination of powers (i, j, k) occurs twice for different nonlinear parameters , and , , which characterise the asymptotic (A) and short-range (B) sectors, respectively. Diagonalisation of the Hamiltonian matrix in an orthogonalised basis set then determines a set of eigenvectors that form a pseudospectral presentation of the actual spectrum of bound and continuum states. The nonlinear parameters are determined by calculating analytically the four derivatives and and finding the zeros by Newton’s method for a particular state of interest. For the pseudostates, the parameter was adjusted to give a variational extremum for the Li charge-state fraction. The pseudostates represent a two-electron generalisation of a Coulomb Sturmian basis set for hydrogen.
The basic premise of the present work was that these fully correlated pseudostates on the right-hand-side of Equation (3) contain complete information about all possible two-electron states, including single- and double-continuum states, as well as autoionising resonances, at least in the limit of large basis sets and in the region of space near the nucleus. The reason for believing this to be true is that the same basis sets accurately satisfy a range of oscillator strength sum rules such as the Thomas–Reiche–Kuhn (TRK) sum rule [32,33]:
where for a two-electron atom, and other similar types of closure relations. Several such sum rules were tested and found to be accurately satisfied in our previous work [11], including a generalised TRK sum rule that includes the change in Coulomb potential accompanying beta decay. The use of a discrete variational representation in [11] supplemented by Stieltjes imaging techniques (a methodology on which this work directly built) allowed for accurate calculations by Goldman and Drake of the photoionisation cross section in hydrogen [34]. In fact, the same principle is contained in the assumption underlying Equation (3) that a helium wave function can be expanded in terms of a complete set of pseudostates constructed from fully correlated Hylleraas-type wave functions. The sum rules interconnect and tightly constrain the calculated charge-state fractions.
The central problem then is to construct a projection operator P and its orthogonal complement Q such that corresponds to states where both electrons have asymptotically outgoing boundary conditions and such that for states lying below the double-ionisation threshold. Our strategy was to resolve each pseudostate lying above the double-ionisation threshold at into its orthogonal component parts and , where
are the fractional probabilities for the formation of Li and Li, respectively. As usual, the projection operators have the properties and .
3. Construction of Projection Operators
Our approach was to construct projection operators for the correlated two-electron pseudostates in terms of the sums of the products of one-electron pseudostates . They were obtained by first orthogonalising and then diagonalising the unscreened hydrogenic Hamiltonian:
in a basis set of functions for a range of powers j and k such that a particular for angular momentum l has the form (for example):
for the case , where , and are linear variational parameters. Because of their shape, we call these “triangular” basis sets, as used previously in the calculation of the Bethe logarithms for hydrogen [35]. The total number of terms is if all terms in Equation (11) are kept. The triangular basis sets have two important features. First, the highest eigenvalue is pushed up by many orders of magnitude beyond what is typically achieved with a single exponential term (i.e., a “linear” basis set). For our typical values of and , the highest eigenvalue is approximately a.u., or a.u. The basis set, therefore, spans a huge range of (nonrelativistic) energy and distance scales. The ground state and first several excited states are also well represented. Second, the basis set has a remarkable degree of numerical stability, despite the huge range of distance scales covered. With quadruple precision, can be increased to around 17 or 18. As shown previously [35], the positive eigenvalues are roughly evenly spaced on a logarithmic energy scale up to very high energies. Quadruple precision was used throughout the calculations.
Assume for simplicity that is an S-state. Neglecting the electron–electron interaction, a zero-order approximation to the P projection operator can then be formed from a doubly positive energy sum over all (anti)symmetrised products of one-electron pseudostates:
where the sum over l is a sum over two-electron partial waves coupled to form an S-state and stands for a pair of integers {n,} such that both and lie in the positive energy scattering continuum. is then correspondingly defined by
where is a vector-coupled product of spherical harmonics with and . The generalisation to states of arbitrary L is straight-forward. The complementary operator is then defined by
where, for brevity, n− stands for all three combinations , , and , indicating that at least one of the two electrons is in a negative-energy-bound pseudostate.
This method of calculation is similar in spirit to that of Forrey et al. [36] for double-photoionisation of helium, except that the true Coulomb waves are here replaced by pseudostates at the same energy. As shown in Figure 2, the two agree very well out to quite large distances.
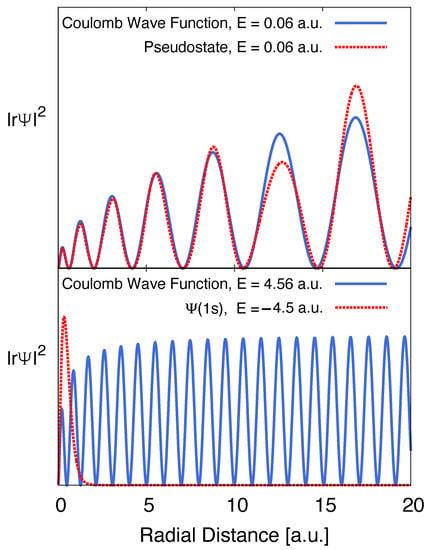
Figure 2.
Upper panel: Comparison of a one-electron pseudostate radial wave function with the corresponding exact Coulomb wave function at the same energy ( 0.06 a.u.) near the threshold. For the case of double-ionisation, both electrons have wave functions of this form. This shows that the pseudostate representation remains accurate out to reasonably large distances. Lower panel: The two one-electron states ( a.u. and a.u.) corresponding to a near-threshold single-ionisation state, demonstrating that the region nearest the nucleus is that which contributes when taking their product and forming projection operators as described in this paper.
The method is justified by the degree to which the final results converge with the basis set size, and the sum over partial waves:
is satisfied. Instead of analysing the asymptotic form of the scattering solution, as in an R-matrix calculation, the method analyses the correlated positive energy pseudostate in the region near the nucleus, where the Q operator projects out that part that has the asymptotic form of a bound state for one of the two electrons. This is then identified as the amplitude for single-ionisation and the orthogonal P component as the amplitude for double-ionisation. The contrast between the two asymptotic forms is illustrated by comparing the top and bottom panels in Figure 2.
The method must also converge with respect to inclusion of the electron–electron interaction in as a perturbation. Up to second order, the perturbed projection operator is
with
and
where the sum over the zeroth-order two-electron states {n} is understood to contain the sum over l such that the total states are formed. The perturbed wave functions are (in the finite set of pseudostates )
and
with . The (unnormalised) second-order solutions are
where, for the perturbed state ,
and p and q each take on the values + or −. Only and contribute to the positive energy projection operator P, with corresponding to virtual transitions to negative energy states and back again. The transition probability into the projected final state corresponding to Li then corresponds to the diagonal matrix elements:
The first-order correction given by
vanishes identically since the matrix elements are real and . The second-order correction consists of the diagonal matrix elements of the (0, 2) and the (1, 1) parts, as shown in Equation (18). The (0, 2) part is
The first term vanishes because it is antisymmetric under the interchange . The second and third terms can both be rewritten by the use of the identity:
to obtain the remaining diagonal part:
The remaining contribution from Equation (18) is
Interchanging the dummy indices and shows that the second term cancels the first term of Equation (27), leaving just the terms:
However, this still must be corrected so that the total wave functions are normalised to unity up to second order. The renormalisation can be accomplished by subtracting a component of the unperturbed solution from to obtain
which still satisfies the second-order perturbation equation. This contributes an additional amount:
leaving just the renormalised projection operator:
corresponding to the sum over virtual negative energy states.
It turns out that even this contribution is cancelled if one includes the counterbalancing positive energy part coming from the second-order perturbation of negative energy states. Terms from do not contribute, but the first-order cross-terms contribute:
With the change of notation , it is clear that this term cancels the one remaining term in Equation (32) for . Thus, the leading perturbative correction to P due to the electron–electron interaction is at most of third order. However, it is still of interest to calculate the
contribution (summed over positive energy pseudostates) that would still remain without this final cancellation due to the positive energy part coming from perturbed negative energy states, as discussed in the following section. The second-order contributions from only positive energy states, prior to cancellation, serves as an upper bound on the order at which third- or higher-order effects could contribute.
4. Results and Discussion
This section discusses the numerical results obtained for the transition probability coefficients P in Equation (23). The calculations are first presented to test for the convergence of the leading coefficients with respect to both controlling the projection operators and controlling the pseudospectral Hylleraas representation of the initial and final states. In addition, we examined the convergence with respect to the sum over partial waves ℓ in Equation (12) and perturbation corrections to the projection operators due to the electron–electron Coulomb interaction.
First, concerning the convergence with respect to partial waves, direct calculations were performed up to (i.e., one-electron states with were coupled to form an S-state with ) and an extrapolation performed up to . The results were found to converge relatively slowly in proportion to . As a typical example, Figure 3 shows the convergence pattern for the He() case with . The extrapolated value is shown by the intercept on the vertical axis.
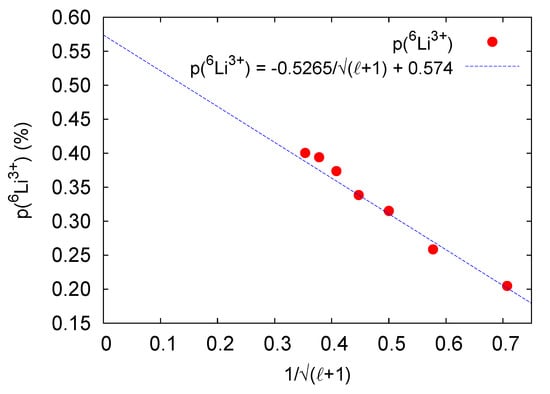
Figure 3.
An example of convergence, following the beta decay of , with respect to the number of partial waves ℓ (red dots) for the Li probability for the case .
Next, concerning the convergence with respect to and , the results are shown (as a percentage) by the top number of each pair in Table 2 and for each of the three initial atomic states. The entries along the main diagonal provide a measure of the degree of convergence and their uncertainty. Since there does not appear to be a consistent trend either up or down, we took the average of all the numbers in Table 2 with the rms statistical spread as the uncertainty. The total double-ionisation probability, prior to being subject to the projection operators of Equation (12), is the sum of overlap integrals between an optimised initial state of and a pseudospectrum representing all doubly ionised states. Although this quantity can be stated with a well-defined error, as demonstrated in [11], it does not show monotonic convergence, but rather, oscillates around a value. The reason for this is that the nonlinear parameters in Equation (6) that are used to variationally diagonalise the Hamiltonian are (necessarily) not separately optimised for each state within the pseudospectrum [37]. The actual numbers of terms in the basis sets for each are listed in Table 3.

Table 2.
Convergence table for the initial states He(1), He(2), and He(2). All entries are Li probabilities (taken in the limit of infinite partial waves, as shown in Figure 3) expressed in % shown for different sizes of both the projection operator () and Hylleraas-type pseudostate () basis sets used in Equation (23). Zeroth- and partial-second-order results from Equation (34) are at the top and bottom of each cell, respectively. The top values in the table for each state will be averaged to obtain the final Li probability.

Table 3.
Number of terms and in the basis sets. The factor 8 for accounts for the sum over partial waves up to .
Finally, concerning perturbation corrections due to the electron–electron interaction, this mixes each of the simple one-electron product pseudostates with all the others, but as shown in Equation (24), the first-order corrections cancel in pairs when summed over the complete set of states that form the projection operator. A more lengthy calculation in Section 3 shows that the second-order corrections also cancel, provided that one takes into account both the renormalisation of the perturbed wave functions so that up to second order and the counterbalancing positive energy contribution coming from the perturbed negative energy states. It is perhaps not surprising that these perturbation corrections sum to zero because the only role of the P projection operator is to enforce doubly outgoing boundary conditions via positive energy for both electrons without further energy resolution. However, it is still interesting to see the order of magnitude of the partial-second-order contributions generated by in Equation (32). The results are shown by the bottom number of each pair in Table 2. Although there is no clear convergence pattern, the magnitudes are all 2% or less of the zero-order term. One can, therefore, expect third- or higher-order contributions not included in the calculation to be smaller still. The main source of uncertainty is thus the convergence uncertainty associated with the zero-order term.
The final results are summarised in Table 4. The main conclusion is that most of the lithium-ions in the energy bin with are Li-ions plus an energetic electron, rather than Li plus two low-energy electrons. For example, for the He() case, of the calculated 1.2(1)% of the Li-ions with , 0.35(5)% are Li, and the remaining 0.85(10)% are Li. The Li fraction agrees with the 0.32% calculated by Wauters and Vaeck [2], but their total only sums to 99.85%, with no uncertainty given. For the He() case, the fractions are 0.53(7)% for Li and 1.33(7)% for Li.

Table 4.
Previous [11] and corrected Li charge-state fractions for each initial state following beta decay. All quantities expressed in percent (%).
The redistributed charge-state fractions are shown in Table 5. However, even these reduced fractions of Li-ions are still an order of magnitude or more larger than the experimental values of 0.018(15)% for the He() case and % for the He() case. The recalculated Li fraction is now also larger than the experiment, while the Li fraction remains lower than the experiment. The differences are much larger than the statistical uncertainties. It seems that the theoretical values for both Li and Li need to be lowered by about the same amount and added to Li in order to bring the theory and experiments into agreement.

Table 5.
Corrected probabilities p(Li) of forming the various charge states of Li following the beta decay of He() or He() as initial states. All quantities are expressed in percent (%).
A possible source of the discrepancy is the failure of the sudden approximation at the % level of accuracy. A more adiabatic time dependence than a step function would increase the proportion of Li at the expense of both Li and Li [38]. For this reason, the results of the sudden approximation represent an upper bound on the amount of shake-up and shake-off. However, a failure of the sudden approximation at this level would contradict the near-perfect agreement found by Couratin et al. [3] for the case of He as the initial state. Their calculation included a perturbation correction to the sudden approximation of only −0.02% (−0.0002 relative to unity) to their calculated shake-off fraction of 2.322%. The sudden approximation as currently implemented also ignored the exchange effects between the beta particle and the atomic electrons [12,13]. However, the effect of the exchange is likely to be small since the beta particle has a much higher energy than the atomic electrons, and a significantly larger effect would again contradict the good agreement for the case of He.
In summary, the present work substantially reduced the disagreement between our previous theory [11] and experiments for the Li charge-state fraction following the beta decay of both He() and He(). It also brought our results into agreement with the CI calculations of Couratin et al. [3] for the He() case. However, there remains a substantial disagreement between the theory and experiments for the charge-state fractions, which stands in sharp contrast to the overall excellent agreement found by Couratin et al. for the one-electron case of He.
Author Contributions
A.T.B. carried out the calculations that were summarised in the Results and Discussion Section. A.T.B. and G.W.F.D. co-developed the underlying theoretical techniques and co-wrote the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
Natural Science and Engineering Research Council of Canada (NSERC) and the Digital Research Alliance of Canada/Compute Ontario.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data reported in this work are available via direct contact with the corresponding author. The wave functions and matrix element FORTRAN programs used in this work are publicly available at http://drake.sharcnet.ca/wiki/index.php/Program_Notes (accessed on 26 January 2023).
Acknowledgments
Research support by the Natural Science and Engineering Research Council of Canada (NSERC), the Digital Research Alliance of Canada/Compute Ontario is gratefully acknowledged. A.T.B. is grateful for the financial support through the NSERC and Queen Elizabeth II scholarships.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Carlson, T.A.; Pleasonton, F.; Johnson, C.H. Electron Shake Off following the β− Decay of 6He. Phys. Rev. 1963, 129, 2220. [Google Scholar] [CrossRef]
- Wauters, L.; Vaeck, N. Study of the electronic rearrangement induced by nuclear transmutations: A B-spline approach applied to the β decay of 6He. Phys. Rev. C 1996, 53, 497. [Google Scholar] [CrossRef] [PubMed]
- Couratin, C.; Velten, P.; Flechard, X.; Lienard, E.; Ban, G.; Cassimi, A.; Delahaye, P.; Durand, D.; Hennecart, D.; Mauger, F.; et al. First Measurement of Pure Electron Shakeoff in the β Decay of Trapped 6He+ Ions. Phys. Rev. Lett. 2012, 108, 243201. [Google Scholar] [CrossRef] [PubMed]
- Severijns, N.; Beck, M.; Naviliat-Cuncic, O. Tests of the standard electroweak model in nuclear beta decay. Rev. Mod. Phys. 2006, 78, 991. [Google Scholar] [CrossRef]
- Naviliat-Cuncic, O. Precision correlation measurements in nuclear beta decay. Phys. Scr. 2012, T150, 014027. [Google Scholar] [CrossRef]
- Gonzalez-Alonso, M.; Naviliat-Cuncic, O.; Severijns, N. New physics searches in nuclear and neutron β decay. Prog. Particle Nucl. Phys. 2019, 104, 165. [Google Scholar] [CrossRef]
- Mukul, I.; Hass, M.; Heber, O.; Hirsh, T.Y.; Rappaport, Y.M.M.L.; Ron, G.; Shachar, Y.; Vaintraub, S. A new scheme to measure the electron-neutrino correlation – the case of 6He. arXiv 2017, arXiv:1711.08299. [Google Scholar]
- Wietfeldt, F.E.; Byrne, J.; Collett, B.; Dewey, M.S.; Jones, G.L.; Komives, A.; Laptev, A.; Nico, J.S.; Noid, G.; Stephenson, E.J.; et al. aCORN: An experiment to measure the electron–antineutrino correlation in neutron decay. Nucl. Instrum. Methods Phys. Res. A 2009, 611, 207. [Google Scholar] [CrossRef]
- Hong, R.; Leredde, A.; Bagdasarova, Y.; Fléchard, X.; García, A.; Knecht, A.; Müller, P.; Naviliat-Cuncic, O.; Pedersen, J.; Smith, E.; et al. Charge-state distribution of Li ions from the β decay of laser-trapped 6He atoms. Phys. Rev. A 2017, 96, 053411. [Google Scholar] [CrossRef]
- Müller, P.; Bagdasarova, Y.; Hong, R.; Leredde, A.; Bailey, K.G.; Fl´echard, X.; García, A.; Graner, B.; Knecht, A.; Naviliat-Cuncic, O.; et al. β-Nuclear-Recoil Correlation from 6He Decay in a Laser Trap. Phys. Rev. Lett. 2022, 129, 182502. [Google Scholar] [CrossRef]
- Schulhoff, E.E.; Drake, G.W.F. Electron emission and recoil effects following the beta decay of 6He. Phys. Rev. A 2015, 92, 050701. [Google Scholar] [CrossRef]
- Cooper, J.W.; Åberg, T. Shaking processes in β-decay. Nucl. Phys. A 1978, 298, 239. [Google Scholar] [CrossRef]
- Saenz, A.; Froelich, P. Effect of final-state interactions in allowed β decays. I. General formalism. Phys. Rev. C 1997, 56, 2132. [Google Scholar] [CrossRef]
- Carter, S.L.; Kelly, H.P. Double photoionization of helium. Phys. Rev. A 1981, 24, 170. [Google Scholar] [CrossRef]
- Sagurton, M.; Bartlett, R.J.; Samson, J.A.R.; He, Z.X.; Morgan, D. Effect of Compton scattering on the double-to-single photoionization ratio in helium. Phys. Rev. A 1995, 52, 2829. [Google Scholar] [CrossRef]
- Bergstrom, P.M.; Hino, K.I.; Macek, J.H. Two-electron ejection from helium by Compton scattering. Phys. Rev. A 1995, 51, 3044. [Google Scholar] [CrossRef]
- Tang, J.-Z.; Shimamura, I. Double photoionization of helium at low photon energies. Phys. Rev. A 1995, 52, R3413. [Google Scholar] [CrossRef]
- Kheifets, A.S.; Bray, I. Calculation of double photoionization of helium using the convergent close-coupling method. Phys. Rev. A 1996, 54, R995. [Google Scholar] [CrossRef]
- Meyer, K.W.; Greene, C.H.; Bray, I. Simplified model of electron scattering using R-matrix methods. Phys. Rev. A 1995, 52, 1334. [Google Scholar] [CrossRef]
- Proulx, D.; Shakeshaft, R. Double ionization of helium by a single photon with energy 89–140 eV. Phys. Rev. A 1993, 48, R875. [Google Scholar] [CrossRef]
- Pont, M.; Shakeshaft, R. Absolute triply differential cross sections for double photoionization of helium at 10, 20, and 52.9 eV above threshold. Phys. Rev. A 1995, 51, R2676. [Google Scholar] [CrossRef] [PubMed]
- Pont, M.; Shakeshaft, R.; Maulbetsch, F.; Briggs, J.S. Angular distributions for double photoionization of helium: Discrepancies between theory and experiment. Phys. Rev. A 1996, 53, 3671. [Google Scholar] [CrossRef] [PubMed]
- Maulbetsch, F.; Briggs, J.S. Angular distribution of electrons following double photoionization. J. Phys. B At. Mol. Opt. Phys. 1993, 26, 1679. [Google Scholar] [CrossRef]
- Sadeghpour, H. Theory of double photoionization in "two-electron" systems. Can. J. Phys. 1996, 74, 727. [Google Scholar] [CrossRef]
- McLaughlin, B.M. An R-matrix with pseudo-state approach to the single photon double ionization and excitation of the He-like Li+ ion. J. Phys. B At. Mol. Opt. Phys. 2013, 46, 075204. [Google Scholar] [CrossRef]
- McIntyre, M.W.; Scott, M.P. Photo-double-ionization of He-like and Be-like systems in excited states within an intermediate-energy R-matrix framework. Phys. Rev. A 2014, 89, 043418. [Google Scholar] [CrossRef]
- Kleiman, U.; Pindzola, M.S.; Robicheaux, F. Photoionization with excitation and double photoionization of the Li+ ground 11S state and metastable 21,3S states. Phys. Rev. A 2005, 72, 022707. [Google Scholar] [CrossRef]
- Kheifets, A.S.; Bray, I. Photoionization with excitation and double photoionization of the helium isoelectronic sequence. Phys. Rev. A 1998, 58, 4501. [Google Scholar] [CrossRef]
- Hart, H.W.v.; Feng, L. Double photoionization of excited He-like atoms. J. Phys. B At. Mol. Opt. Phys. 2001, 34, L601. [Google Scholar] [CrossRef]
- Drake, G.W.F.; Makowski, A.J. High-precision eigenvalues for the 1s2p1P and 3P states of helium. J. Opt. Soc. Am. B 1988, 5, 2207. [Google Scholar] [CrossRef]
- Drake, G.W.F.; Yan, Z.-C. Energies and relativistic corrections for the Rydberg states of helium: Variational results and asymptotic analysis. Phys. Rev. A 1992, 46, 2378. [Google Scholar] [CrossRef] [PubMed]
- Drake, G.W.F. Handbook of Atomic, Molecular, and Optical Physics; Section 11.3.1; Springer: New York, NY, USA, 2006; pp. 199–219. [Google Scholar]
- Berkowitz, J.J. Sum rules and the oscillator strength distribution in helium. Phys. B At. Mol. Opt. Phys. 1997, 30, 881. [Google Scholar] [CrossRef]
- Goldman, S.P.; Drake, G.W.F. Relativistic effects in the photoionization of hydrogenic ions. Can. J. Phys. 1983, 61, 198. [Google Scholar] [CrossRef]
- Drake, G.W.F.; Goldman, S.P. Bethe logarithms for Ps, H, and heliumlike atoms. Can. J. Phys. 1999, 77, 835. [Google Scholar] [CrossRef]
- Forrey, R.C.; Yan, Z.-C.; Sadeghpour, H.R.; Dalgarno, A. Single and double photoionization from dipole response function. Phys. Rev. Lett. 1997, 78, 3662. [Google Scholar] [CrossRef]
- Schulhoff, E.E. Excitation and Ionization of 6Li Ions following Beta-Decay of 6He. Master’s Thesis, University of Windsor, Windsor, ON, Canada, 2010. Available online: https://scholar.uwindsor.ca/etd/139/ (accessed on 10 January 2022).
- Chizma, J.; Karl, G.; Novikov, V.A. Sudden to adiabatic transition in β decay. Phys. Rev. C 1998, 58, 3674. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).