Applications of Machine Learning and Neural Networks for FT-ICR Mass Measurements with SIPT
Abstract
:1. Introduction
2. Background
2.1. Ion Motion in a Penning Trap
2.2. Fourier Transform Ion Cyclotron Resonance Technique
3. Numerical Simulation
3.1. Noise Floor Determination
3.2. Simulated Signal-to-Noise Ratio
3.3. Methods for Simulating FT-ICR Signals
| Algorithm 1: Serial method for simulating an FT-ICR time-domain signal using the ‘sum of sines’ approach. The inputs are as follows: is the number of ions in the Penning trap; f and define the ion eigenfrequency normal distribution; A and define the single-ion amplitude normal distribution; is the maximum eigenmotion phase; is the noise amplitude; , are the sample time and number of samples, respectively. The method UniformRandom (low, high, N = 1) samples N instances from a uniformly random distribution within the range defined from low (inclusive) to high (exclusive), and NormalRandom () randomly samples a Gaussian/normal distribution defined by a mean value and standard deviation . |
 |
4. Identification of Ion Signals
4.1. Dataset Construction for Signal Classifiers
4.2. Optimal Classifier Hyperparameters
4.3. Classification of Ion Signals
5. Extracting Ion Characteristics with Neural Networks
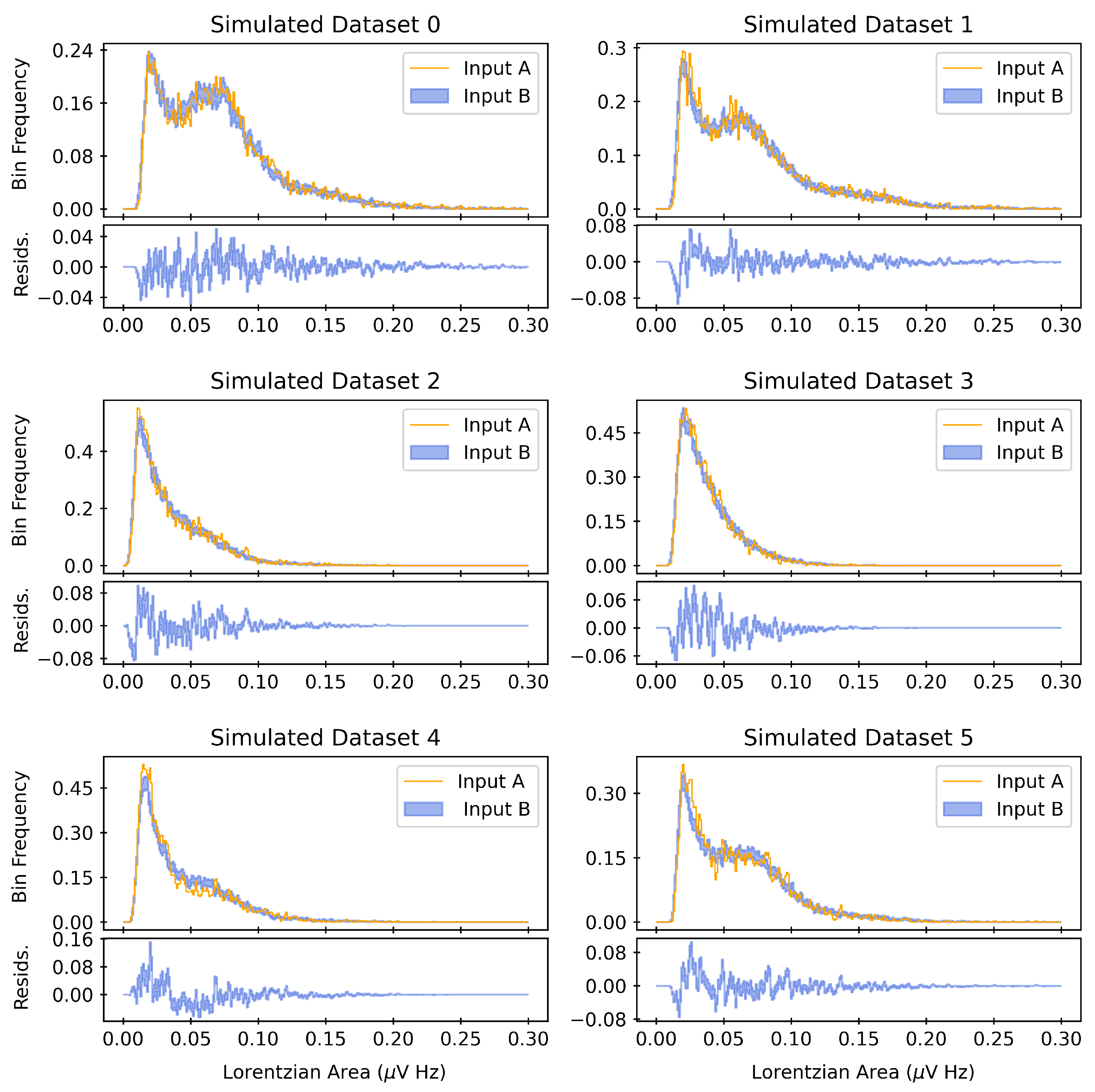
5.1. Construction of Datasets for Predicting Ion Characteristics
5.2. Network Architecture and Training
5.3. Model Uncertainty and Sensitivity Analysis
6. Applications to Experimental Data
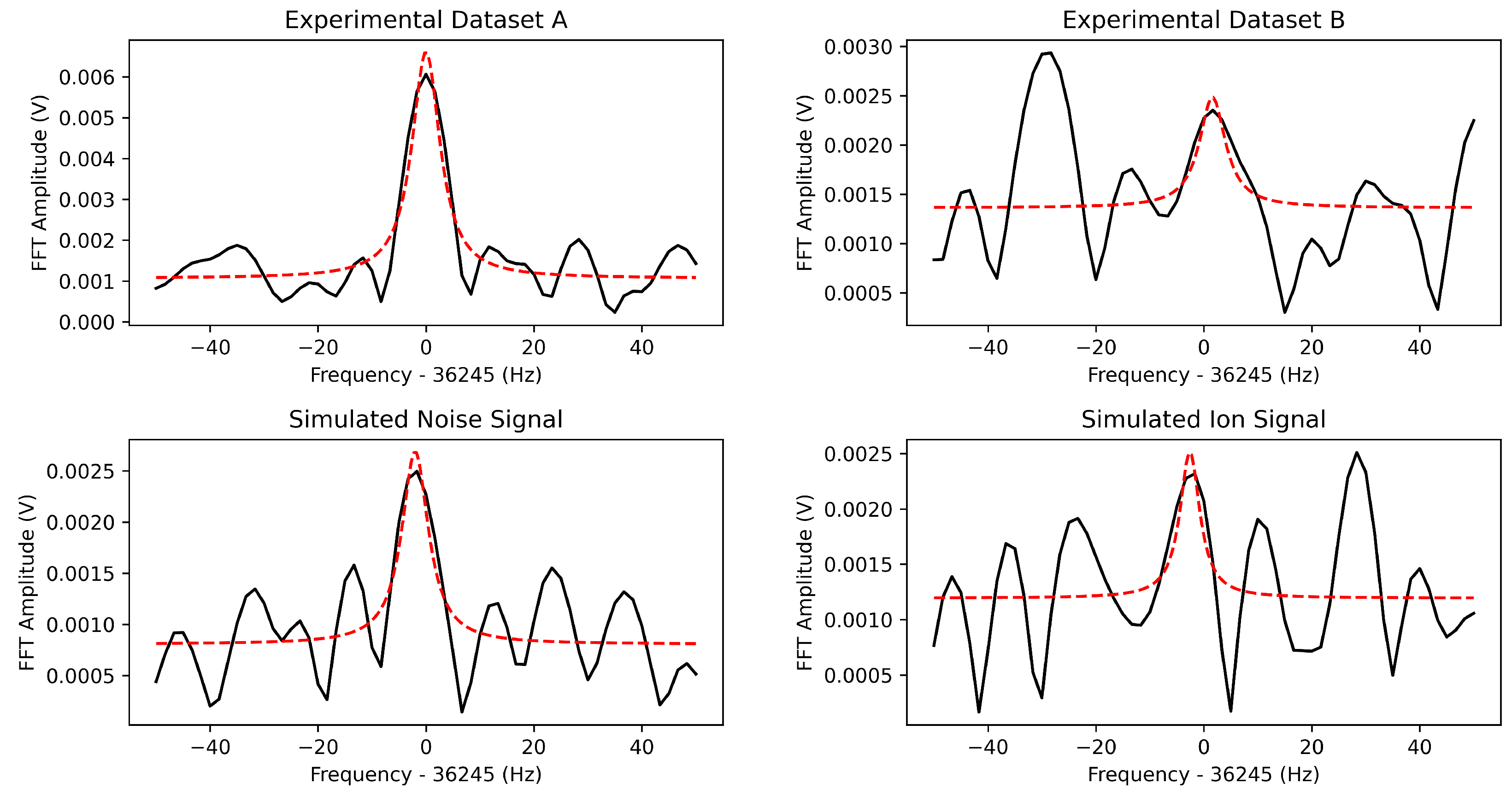
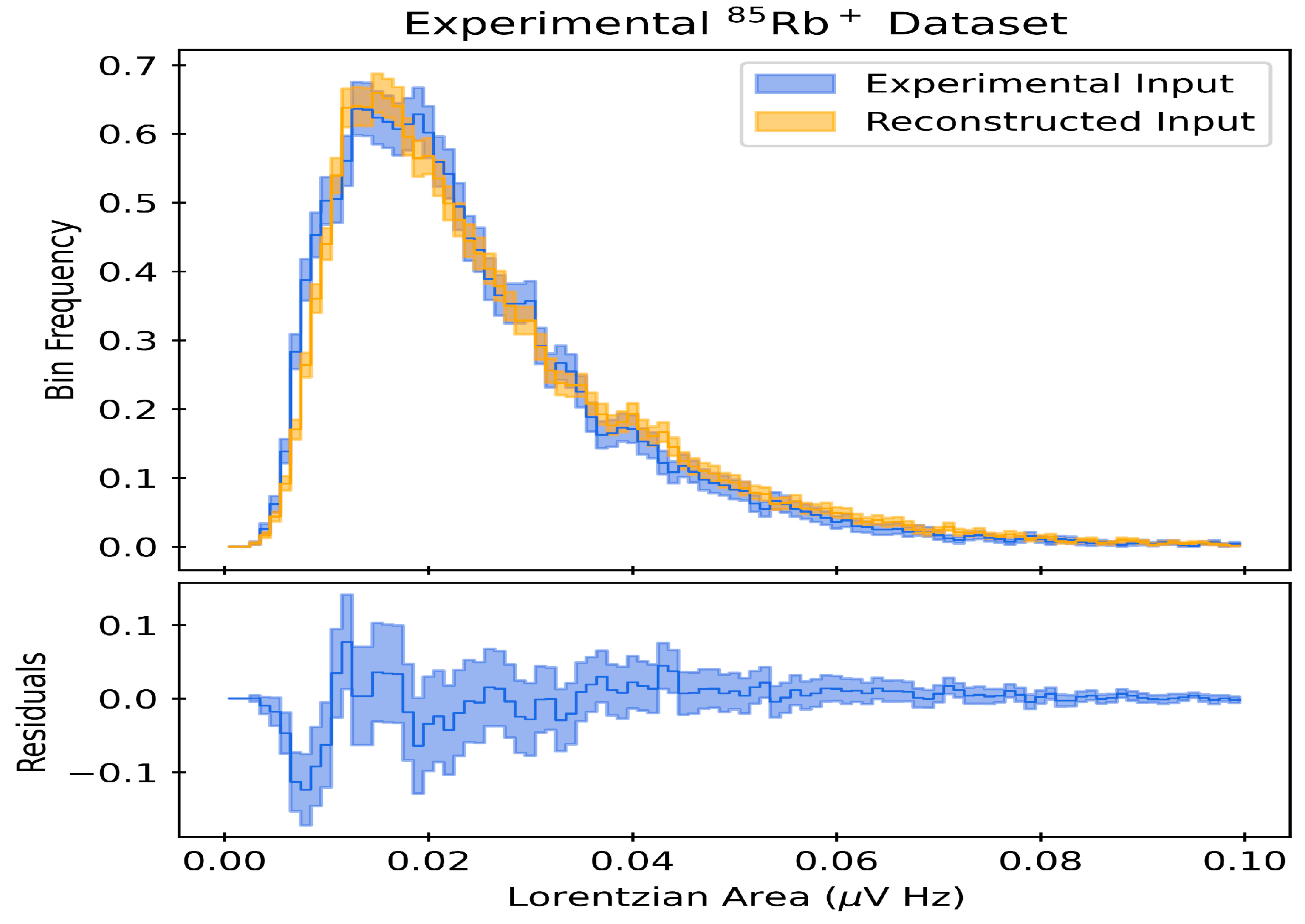
6.1. Classification of Experimental Signals
6.2. Predicted Ion Characteristics
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brown, B.A.; Richter, W.A. New “USD” Hamiltonians for the sd shell. Phys. Rev. C 2006, 74, 034315. [Google Scholar] [CrossRef]
- Schatz, H.; Ong, W. Dependence of X-ray Burst Models on Nuclear Masses. Astrophys. J. 2016, 844, 139. [Google Scholar] [CrossRef]
- Lunney, D.; Pearson, J.M.; Thibault, C. Recent trends in the determination of nuclear masses. Rev. Mod. Phys. 2003, 75, 1021–1082. [Google Scholar] [CrossRef]
- Burbidge, E.M.; Burbidge, G.R.; Fowler, W.A.; Hoyle, F. Synthesis of the Elements in Stars. Rev. Mod. Phys. 1957, 29, 547–650. [Google Scholar] [CrossRef]
- Mumpower, M.; Surman, R.; McLaughlin, G.; Aprahamian, A. The impact of individual nuclear properties on r-process nucleosynthesis. Prog. Part. Nucl. Phys. 2016, 86, 86–126. [Google Scholar] [CrossRef]
- Baumann, T.; Hausmann, M.; Sherrill, B.; Tarasov, O. Opportunities for isotope discoveries at FRIB. Nucl. Instruments Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2016, 376, 33–34. [Google Scholar] [CrossRef]
- Blaum, K. High-accuracy mass spectrometry with stored ions. Phys. Rep. 2006, 425, 1–78. [Google Scholar] [CrossRef]
- Brown, L.; Gabrielse, G. Geonium Theory: Physics of a single electron or ion in a penning trap. Rev. Mod. Phys. 1986, 58, 233. [Google Scholar] [CrossRef]
- Bollen, G.; Moore, R.; Savard, G.; Stolenzberg, H. The accuracy of heavy-ion mass measurements using time of flight-ion cyclotron resonance in a Penning trap. J. Appl. Phys. 1990, 68, 4355. [Google Scholar] [CrossRef]
- Eliseev, S.; Blaum, K.; Block, M.; Dörr, A.; Droese, C.; Eronen, T.; Goncharov, M.; Höcker, M.; Ketter, J.; Ramirez, E.M.; et al. A phase-imaging technique for cyclotron-frequency measurements. Appl. Phys. B 2014, 114, 107–128. [Google Scholar] [CrossRef]
- Haxel, O.; Jensen, J.H.D.; Suess, H.E. On the “Magic Numbers” in Nuclear Structure. Phys. Rev. 1949, 75, 1766. [Google Scholar] [CrossRef]
- Mayer, M.G. On Closed Shells in Nuclei. Phys. Rev. 1948, 74, 235–239. [Google Scholar] [CrossRef]
- Marshall, A.; Hendrickson, C.; Jackson, G. Fourier transform ion cyclotron resonance mass spectrometry: A primer. Mass Spectrom. Rev. 1998, 17, 1–35. [Google Scholar] [CrossRef]
- Kotsiantis, S.B.; Zaharakis, I.D.; Pintelas, P.E. Machine learning: A review of classification and combining techniques. Artif. Intell. Rev. 2006, 26, 159–190. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Niu, Z.; Liang, H. Nuclear mass predictions based on Bayesian neural network approach with pairing and shell effects. Phys. Lett. B 2018, 778, 48–53. [Google Scholar] [CrossRef]
- Lovell, A.E.; Mohan, A.T.; Sprouse, T.M.; Mumpower, M.R. Nuclear masses learned from a probabilistic neural network. Phys. Rev. C 2022, 106, 014305. [Google Scholar] [CrossRef]
- Dong, X.X.; An, R.; Lu, J.X.; Geng, L.S. Novel Bayesian neural network based approach for nuclear charge radii. Phys. Rev. C 2022, 105, 014308. [Google Scholar] [CrossRef]
- Jiang, W.G.; Hagen, G.; Papenbrock, T. Extrapolation of nuclear structure observables with artificial neural networks. Phys. Rev. C 2019, 100, 054326. [Google Scholar] [CrossRef]
- Du, Y. Signal Enhancement and Data Mining for Chemical and Biological Samples Using Mass Spectrometry. Ph.D. Thesis, Purdue University, Ann Arbor, MI, USA, 2015. [Google Scholar]
- Nampei, M.; Horikawa, M.; Ishizu, K.; Yamazaki, F.; Yamada, H.; Kahyo, T.; Setou, M. Unsupervised machine learning using an imaging mass spectrometry dataset automatically reassembles grey and white matter. Sci. Rep. 2019, 9, 13213. [Google Scholar] [CrossRef]
- Williams, D.K.; Kovach, A.L.; Muddiman, D.C.; Hanck, K.W. Utilizing Artificial Neural Networks in MATLAB to Achieve Parts-Per-Billion Mass Measurement Accuracy with a Fourier Transform Ion Cyclotron Resonance Mass Spectrometer. J. Am. Soc. Mass Spectrom. 2009, 20, 1303–1310. [Google Scholar] [CrossRef] [PubMed]
- Williams, D.K., Jr. Exploring Fundamental Aspects of Proteomic Measurements: Increasing Mass Measurement Accuracy, Streamlining Absolute Quantification, and Increasing Electrospray Response. Ph.D. Thesis, North Carolina State University, Ann Arbor, MI, USA, 2009. [Google Scholar]
- Boiko, D.A.; Kozlov, K.S.; Burykina, J.V.; Ilyushenkova, V.V.; Ananikov, V.P. Fully Automated Unconstrained Analysis of High-Resolution Mass Spectrometry Data with Machine Learning. J. Am. Chem. Soc. 2022, 144, 14590–14606. [Google Scholar] [CrossRef] [PubMed]
- Nesterenko, D.A.; Eronen, T.; Ge, Z.; Kankainen, A.; Vilen, M. Study of radial motion phase advance during motion excitations in a Penning trap and accuracy of JYFLTRAP mass spectrometer. Eur. Phys. J. A 2021, 57, 302. [Google Scholar] [CrossRef]
- Jeffries, J.; Barlow, S.; Dunn, G. Theory of space-charge shift of ion cyclotron resonance frequencies. Int. J. Mass Spectrom. Ion Process. 1983, 54, 169–187. [Google Scholar] [CrossRef]
- Duhamel, P.; Vetterli, M. Fast fourier transforms: A tutorial review and a state of the art. Signal Process. 1990, 19, 259–299. [Google Scholar] [CrossRef]
- Payne, T.G.; Southam, A.D.; Arvanitis, T.N.; Viant, M.R. A signal filtering method for improved quantification and noise discrimination in fourier transform ion cyclotron resonance mass spectrometry-based metabolomics data. J. Am. Soc. Mass Spectrom. 2009, 20, 1087–1095. [Google Scholar] [CrossRef]
- Chiron, L.; van Agthoven, M.A.; Kieffer, B.; Rolando, C.; Delsuc, M.A. Efficient denoising algorithms for large experimental datasets and their applications in Fourier transform ion cyclotron resonance mass spectrometry. Proc. Natl. Acad. Sci. USA 2014, 111, 1385–1390. [Google Scholar] [CrossRef]
- Kanawati, B.; Bader, T.; Wanczek, K.P.; Li, Y.; Schmitt-Kopplin, P. FT-Artifacts and Power-function Resolution Filter in Fourier Transform Mass Spectrometry. Rapid Commun. Mass Spectrom. 2017, 31, 1607–1615. [Google Scholar] [CrossRef]
- Mathur, R.; O’Connor, P.B. Artifacts in Fourier transform mass spectrometry. Rapid Commun. Mass Spectrom. RCM 2009, 23, 523–529. [Google Scholar] [CrossRef]
- Comisarow, M.B.; Marshall, A.G. Frequency-sweep fourier transform ion cyclotron resonance spectroscopy. Chem. Phys. Lett. 1974, 26, 489–490. [Google Scholar] [CrossRef]
- Kilgour, D.P.A.; Wills, R.; Qi, Y.; O’Connor, P.B. Autophaser: An Algorithm for Automated Generation of Absorption Mode Spectra for FT-ICR MS. Anal. Chem. 2013, 85, 3903–3911. [Google Scholar] [CrossRef] [PubMed]
- Brustkern, A.M.; Rempel, D.L.; Gross, M.L. An electrically compensated trap designed to eighth order for FT-ICR mass spectrometry. J. Am. Soc. Mass Spectrom. 2008, 19, 1281–1285. [Google Scholar] [CrossRef] [PubMed]
- Lincoln, D.; Baker, R.; Benjamin, A.; Bollen, G.; Redshaw, M.; Ringle, R.; Schwarz, S.; Sonea, A.; Valverde, A. Development of a high-precision Penning trap magnetometer for the LEBIT facility. Int. J. Mass Spectrom. 2015, 379, 1–8. [Google Scholar] [CrossRef]
- Hamaker, A. Mass Measurement of the Lightweight Self-Conjugate Nucleus Zirconium-80 and the Development of the Single Ion Penning Trap. Ph.D. Thesis, Michigan State University, East Lansing, MI, USA, 2021. [Google Scholar]
- Johnson, J.B. Thermal Agitation of Electricity in Conductors. Phys. Rev. 1928, 32, 97–109. [Google Scholar] [CrossRef]
- Barry, J.R.; Lee, E.A.; Messerschmitt, D.G. Digital Communication; Springer: New York, NY, USA, 2004. [Google Scholar]
- Marshall, A.G. Theoretical signal-to-noise ratio and mass resolution in Fourier transform ion cyclotron resonance mass spectrometry. Anal. Chem. 1979, 51, 1710–1714. [Google Scholar] [CrossRef]
- Dahl, D.A. Simion for the personal computer in reflection. Int. J. Mass Spectrom. 2000, 200, 3–25. [Google Scholar] [CrossRef]
- Hossin, M.; Sulaiman, M.N. A review on evaluation metrics for data classification evaluations. Int. J. Data Min. Knowl. Manag. Process. 2015, 5, 1. [Google Scholar]
- Refaeilzadeh, P.; Tang, L.; Liu, H. Cross-Validation. In Encyclopedia of Database Systems; Liu, L., Özsu, M.T., Eds.; Springer: Boston, MA, USA, 2009; pp. 532–538. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Guyon, I.; Gunn, S.; Nikravesh, M.; Zadeh, L.A. Feature Extraction: Foundations and Applications; Springer: Berlin/Heidelberg, Germany, 2008; Volume 207. [Google Scholar]
- Pechenizkiy, M. The impact of feature extraction on the performance of a classifier: kNN, Naïve Bayes and C4.5. In Proceedings of the Conference of the Canadian Society for Computational Studies of Intelligence, Victoria, BC, Canada, 9–11 May 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 268–279. [Google Scholar]
- Smith, J.O. Mathematics of the Discrete Fourier Transform (DFT): With Audio Applications; W3K Publishing, 2008. [Google Scholar]
- Diamantidis, N.; Karlis, D.; Giakoumakis, E. Unsupervised stratification of cross-validation for accuracy estimation. Artif. Intell. 2000, 116, 1–16. [Google Scholar] [CrossRef]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical Bayesian Optimization of Machine Learning Algorithms. In Proceedings of the Advances in Neural Information Processing Systems, Tahoe, NV, USA, 3–6 December 2012; Pereira, F., Burges, C., Bottou, L., Weinberger, K., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2012; Volume 25. [Google Scholar]
- Head, T.; MechCoder; Louppe, G.; Shcherbatyi, I.; Fcharras, Z.V.; cmmalone; Schröder, C.; nel215; Campos, N. scikit-optimize v0.5.2, 2018. [CrossRef]
- Svozil, D.; Kvasnicka, V.; Pospichal, J. Introduction to multi-layer feed-forward neural networks. Chemom. Intell. Lab. Syst. 1997, 39, 43–62. [Google Scholar] [CrossRef]
- Chollet, F. Keras. 2015. Available online: https://keras.io (accessed on 18 May 2022).
- Agarap, A.F. Deep Learning using Rectified Linear Units (ReLU). arXiv 2018, arXiv:1803.08375. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. Int. Conf. Learn. Represent. 2014, arXiv:1412.6980. [Google Scholar] [CrossRef]
- Gurney, K. An Introduction to Neural Networks; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Gal, Y.; Ghahramani, Z. Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 20–22 June 2016; Balcan, M.F., Weinberger, K.Q., Eds.; PMLR: New York, NY, USA, 2016; Volume 48, pp. 1050–1059. [Google Scholar]
- Yeung, D.S.; Cloete, I.; Shi, D.; wY Ng, W. Sensitivity Analysis for Neural Networks; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]




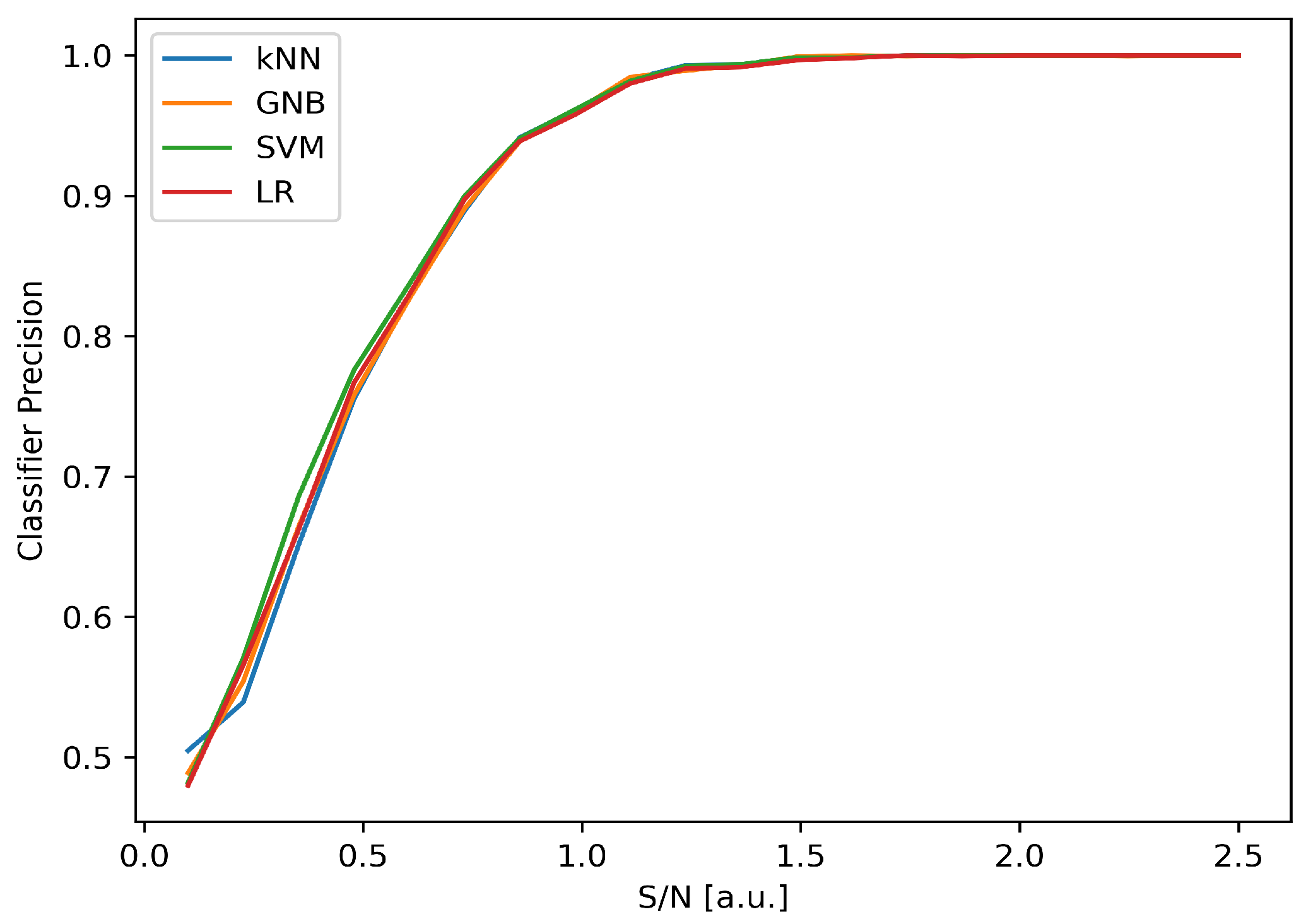
| Classifier | Parameter | Value | Precision |
|---|---|---|---|
| kNN | Algorithm | Ball Tree | 0.711 |
| Leaf Size | 46 | ||
| k Neighbors | 35 | ||
| GNB | Variable Smoothing | 0 | 0.704 |
| SVM | C | 100 | 0.715 |
| 1.895 | |||
| Degree | 8 | ||
| Kernel | rbf | ||
| LR | C | 39 | 0.735 |
| Solver | Saga | ||
| Penalty | ℓ2 |
| Sim. Dataset 0 | Sim. Dataset 1 | Sim. Dataset 2 | ||||
|---|---|---|---|---|---|---|
| True | Prediction | True | Prediction | True | Prediction | |
| μp | 0.54 | 0.54(8) | 0.37 | 0.43(8) | 0.14 | 0.18(6) |
| Asingle (mV) | 0.053 | 0.053(5) | 0.051 | 0.051(3) | 0.046 | 0.044(2) |
| σ(Asingle) (mV) | 0.000835 | 0.0017(9) | 0.00174 | 0.0023(8) | 0.000357 | 0.0024(7) |
| Voffset (μV) | 8.89 | 8.1(1.1) | 9.79 | 8.4(1.0) | 1.85 | 0.9(8) |
| (rad) | 4.85 | 4(1) | 1.91 | 1.8(1.0) | 4.47 | 3.8(9) |
| Sim. Dataset 3 | Sim. Dataset 4 | Sim. Dataset 5 | ||||
| True | Prediction | True | Prediction | True | Prediction | |
| μp | 0.36 | 0.37(7) | 0.12 | 0.18(7) | 0.29 | 0.34(8) |
| Asingle (mV) | 0.027 | 0.029(3) | 0.054 | 0.049(3) | 0.052 | 0.053(5) |
| σ(Asingle) (mV) | 0.000404 | 0.000264(12) | 0.000377 | 0.003(6) | 0.000078 | 0.00015(10) |
| Voffset (μV) | 8.66 | 7.7(9) | 4.45 | 4.0(5) | 9.73 | 8.8(1.1) |
| (rad) | 3.8 | 4.1(7) | 3.44 | 3.2(9) | 5.53 | 4.2(1.1) |
| Prediction | |
|---|---|
| 0.26(6) | |
| (mV) | 0.022(4) |
| (mV) | 0.0024(5) |
| Voffset (μV) | 2.0(7) |
| (rad) | 4.3(1.4) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Campbell, S.E.; Bollen, G.; Hamaker, A.; Kretzer, W.; Ringle, R.; Schwarz, S. Applications of Machine Learning and Neural Networks for FT-ICR Mass Measurements with SIPT. Atoms 2023, 11, 126. https://doi.org/10.3390/atoms11100126
Campbell SE, Bollen G, Hamaker A, Kretzer W, Ringle R, Schwarz S. Applications of Machine Learning and Neural Networks for FT-ICR Mass Measurements with SIPT. Atoms. 2023; 11(10):126. https://doi.org/10.3390/atoms11100126
Chicago/Turabian StyleCampbell, Scott E., Georg Bollen, Alec Hamaker, Walter Kretzer, Ryan Ringle, and Stefan Schwarz. 2023. "Applications of Machine Learning and Neural Networks for FT-ICR Mass Measurements with SIPT" Atoms 11, no. 10: 126. https://doi.org/10.3390/atoms11100126
APA StyleCampbell, S. E., Bollen, G., Hamaker, A., Kretzer, W., Ringle, R., & Schwarz, S. (2023). Applications of Machine Learning and Neural Networks for FT-ICR Mass Measurements with SIPT. Atoms, 11(10), 126. https://doi.org/10.3390/atoms11100126






