Time-Resolved Analysis of the Electron Temperature in RF Magnetron Discharges with a Pulsed Gas Injection

Abstract

Pulsed gas injection in a plasma can affect many fundamentals, including electron heating and losses. The case of an asymmetric RF magnetron plasma with a pulsed argon injection is analyzed by optical emission spectroscopy of argon 2p-to-1s transitions coupled with collisional-radiative modeling. For a fully detailed population model of argon 2p levels accounting for direct and stepwise electron-impact excitation in optically thick conditions, a rapid decrease in the electron temperature, T_e, is observed during each gas injection with the sudden pressure rise. The opposite trend, with unrealistic T_e values before and after each pulse, is observed for analysis based on simple corona models, thus emphasizing the importance of stepwise excitation processes and radiation trapping. Time-resolved electron temperature variations are directly linked to the operating parameters of the pulsed gas injection, in particular the injection frequency. Based on the complete set of data, it is shown that the instantaneous electron temperature monotonously decreases with increasing pressure, with values consistent with those expected for plasmas in which charged species are produced by electron-impact ionization of ground state argon atoms and lost by diffusion and recombination on plasma reactor walls.

1. Introduction

Pulsed matter injection is an appealing method in many plasma devices. It consists of the pulsed injection of gases, liquids, aerosols, or sprays. This can be done by gas puffing or supersonic flows [1,2], by gas or liquid valves, by ink-jet printer heads [3,4,5] or by direct liquid injection [6,7,8]. Pulsed gas injection enables to control the discharge physics. As an example, long term discharges in fusion devices can be sustained by the pulsed injection of fuel gas [9,10]. For supersonic gas injection, a significant increase in the fueling efficiency is observed due to the short injection time and the prompt cooling of the plasma edge consecutive to the massive injection of matter [9]. In RF discharges used for sputtering applications, pulsed injection of N₂ in Ne can induce a transition between two excitation mechanisms of plasma particles, from Penning reaction to electron-impact excitation [11,12]. Pulsed gas injection also enables to control the gas fluid dynamics. For example, a continuous injection of gases in a given reactor can produce an asymmetric flow and, consequently, an asymmetric distribution of the plasma parameters that pulsed plasma operation can avoid. Indeed, during the afterglow between pulses, species can efficiently diffuse in the plasma volume yielding to uniform power deposition [13]. The gas flow can also be efficiently guided to regions of interest, for example near a substrate or a target [14].

Pulsed gas injection further enables to control the plasma chemistry. First, depending on the operating conditions (gas pressure, reactor dimensions, power, etc.), it can affect the reaction kinetics involved in the plasma volume and at the plasma reactors walls [15]. For example, the production of metal-carbon clusters of higher masses is improved with the pulsed injection of He/CH₄ gas mixtures in arc discharges [16]. In addition, a pulsed injection of organosilicon precursors in an asymmetric RF plasma allows to combine plasma-enhanced chemical vapor deposition and physical vapor deposition without target poisoning [17]. Such conditions can further induce nucleation of nanoparticles in the plasma volume [18]. It is also possible to design the region of reactive species production. For example, a selective production of the precursors and deposition can be achieved by isolating spatially and temporally the injected gases from the plasma zone using a pulsed gas injection coupled with a pulsed injection of power [13,19]. In addition, many reactive precursors can be introduced in a pulsed mode. It allows to manipulate complex precursors such as liquids, metalorganic compounds diluted in solvents [20], as well as to introduce liquid dispersions of nanoparticles [8]. The latter is an attractive method for the formation of nanocomposite coatings based on at least one nanometer-sized (less than 100 nm) phase. The properties of such materials can be tailored by the chemical composition, crystal structure, and morphology of the matrix, but also by the nature, size, form, volume fraction, and distance between each nanometric inclusions (particles, filaments, tubes) [21,22]. Many studies are devoted to plasma processes with pulsed gas injection [23]. A new “hybrid” method based on a pulsed injection mode has been recently proposed [24]. It consists of a Direct Liquid Reactor-Injector (DLRI) in which nanoparticles are synthesized by mixing a liquid and a gaseous precursor prior to their injection in a pulsed mode in the plasma. The nanoparticles as well as the solvent are then injected in the plasma as a gas pulse with a duration and a frequency set by the chemical reaction kinetics.

In contrast to usual plasmas operating under constant pressure, the conception of advanced plasma processes with a pulsed gas injection inevitably implies a complex temporal dynamic associated with sudden pressure and plasma phase composition variations. Such feature can induce multiscale variations of the fundamental plasma properties, including electron density and temperature, number density of excited species, neutral gas temperature, etc. [18,25]. During nanocomposite thin film deposition using a DLRI, this can play an important role (i) on the dissociation kinetics of the matrix precursor [26], (ii) on the charging and transport dynamics of nanoparticles in the plasma [27], (iii) on the plasma-substrate interaction during thin film deposition [28], and therefore, (iv) on the physical and chemical properties of the coatings [29]. As a building block towards a better understanding of plasma processes using the DLRI, the objective of this study is to gain insights into the physics driving low-pressure RF plasmas with pulsed gas injection. Experiments are done in the specific case of a magnetron RF plasma operated in argon [30]. Optical emission spectroscopy combined with collisional-radiative modelling of Ar 2p-to-1s transitions is used to analyze the electron kinetics over a wide range of DLRI conditions.

2. Experimental Setup

2.1. Plasma Reactor and Pulsed Gas Injection

A schematic of the RF (13.56 MHz) magnetron plasma reactor used in this work is presented in Figure 1. The system consists of a 28 cm × 28 cm (diameter × height) cylindrical stainless-steel chamber with grounded walls. A two-stage pumping system ensures a residual vacuum of 10⁻⁵ Torr. Argon is fed into the reactor using an Atokit from Kemstream^® plugged on the injection ring surrounding the top electrode. The injection parameters for the set of experiments reported in this work are the opening time of the first valve before the mixing chamber (5 ms), the opening time of the outer valve leading to the injection ring (10 ms), and the offset time between the closure of the two valves (2 ms). In these experiments, the frequency of the Ar injection pulses is varied and sets sequentially at f = 0.1, 0.5 and 1 Hz. Pulsed gas injection is producing an overpressure, Δp, in the plasma chamber. Values of Δp are mainly controlled by the injection parameters and the base pressure, p₀. The latter is adjusted using a throttle valve located at the entrance of the pumping system.

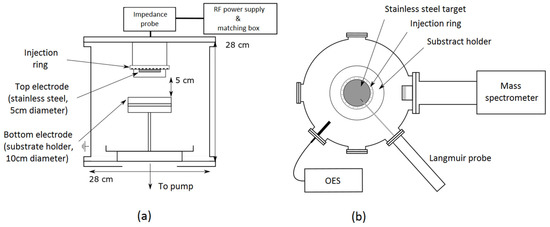
Figure 1. Overview of the experimental set up from (a) a side view and (b) a top view.

The RF power is fed to the top stainless-steel electrode (5 cm diameter), while the bottom electrode (10 cm diameter) is grounded. This results in an asymmetrical RF plasma with an inter-electrode gap of 5 cm. A matching box set between the RF power supply and the reactor is used to minimize the reflected power. For the experiments reported in this work, a nominal power of 100 W is sent to the plasma and the reflected power is oscillating with the gas pulses between 3 and 7 W.

2.2. Optical Emission Spectroscopy Measurements

As shown in Figure 1b, optical emission spectroscopy (OES) measurements are taken from a port and a collimator located on the side of the reactor. They are recorded over the 700–900 nm wavelength range with an AVANTES spectrometer (AVASpec-3648-2-USB) having a spectral resolution of ~0.16 nm (full width at half maximum). A typical spectrum depicting most of the intense Ar 2p-to-1s transitions (corrected for both background noise and apparatus spectral response) from a plasma generated at 5 mTorr and 100 W is shown in Figure 2.

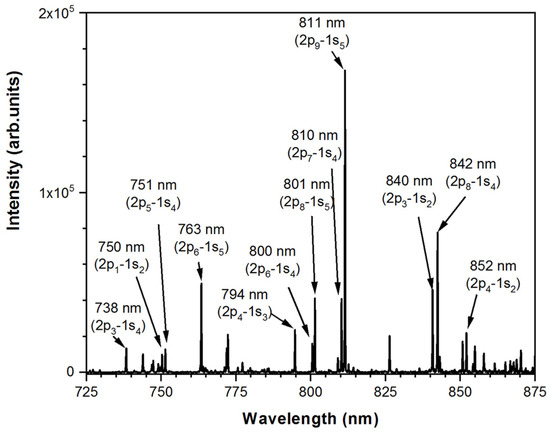
Figure 2. Typical optical emission spectrum of the argon plasma examined in this work.

For all conditions reported in this work, the measured line intensities are compared to those computed from a collisional-radiative model based on Donnelly’s trace-rare-gases optical emission spectroscopy method [31] in order to determine time-resolved electron temperature in these pulsed injection conditions. As discussed previously [18,32,33], the model is however adapted with respect to Donnelly’s work to account for radiation trapping and stepwise excitation through resonant 1s levels.

3. Results and Discussion

3.1. Influence of the Pressure Pulses

Optical emission spectra are recorded along a pulse of gas injection for an injection frequency of 0.1 Hz. Figure 3 shows the evolutions of the operating pressure (blue plot) and the Ar 811 nm emission line intensity during a period of injection (red plot) and for two conditions of base pressure set to p₀ ~5 mTorr (a) and 160 mTorr (b)—the constant pressure rise being of Δp ~70 mTorr during each cycle.

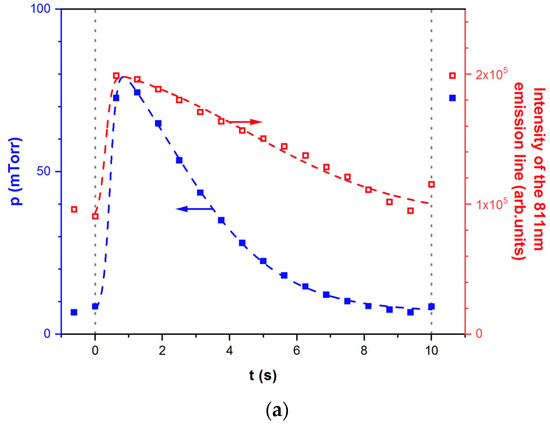
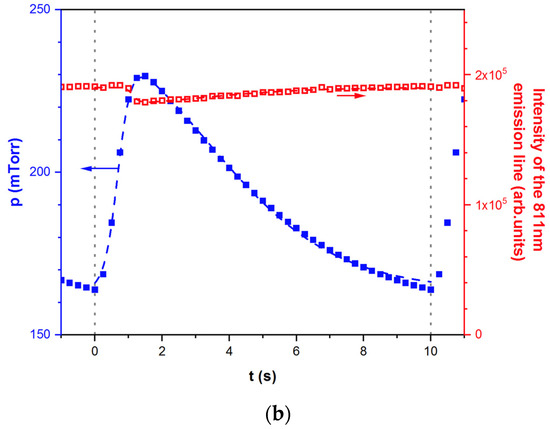
Figure 3. Comparison between the evolutions of the pressure (blue curve) and the Ar 811 nm emission line intensity (red curve) on an injection period. Injection frequency is set to 0.1 Hz corresponding to an overpressure Δp ~70 mTorr. In (a), the base pressure is set at p₀ ~5 mTorr and in (b) at p₀ ~160 mTorr.

Clearly, for both conditions presented in Figure 3, there is a synchronized evolution of the Ar 811 nm emission line intensity with the pressure pulse. In the case of the lower pressure condition, the sudden rise and slow drop in pressure led to a similar evolution of the line intensity. However, the opposite behaviour is observed at higher pressure, although the variations appear to be less pronounced than in the first condition. To understand these apparently conflicting results, it is worth looking first at the well-known equation for the measured intensity of a given emission line $I_{\lambda }$:

$$I_{\lambda }=f\left(\lambda \right)A_{ij}{n}_i{\theta }_{ij}$$

(1)

where f(λ) is the apparatus function at the wavelength λ of interest, A_ij is the Einstein coefficient for spontaneous emission of the transition, $n_i$ is the number density of the Ar emitting level, and ${\theta }_{ij}$ is the escape factor of the transition. In optically thin media (${\theta }_{ij}=1$), given that $f\left(\lambda \right)$ is measurable and that $A_{ij}$ is a known constant, the line emission intensity therefore only depends on the number density of the emitting level. In complex media such as non-equilibrium plasmas, $n_i$ cannot simply be calculated assuming a Boltzmann equilibrium (as in equilibrium plasmas), but requires a full description of its population and depopulation mechanisms through a particle balance equation. A schematic of the Ar 2p-to-1s transitions with the dominant population and depopulation mechanisms of Ar 2p states is presented in Figure 4.

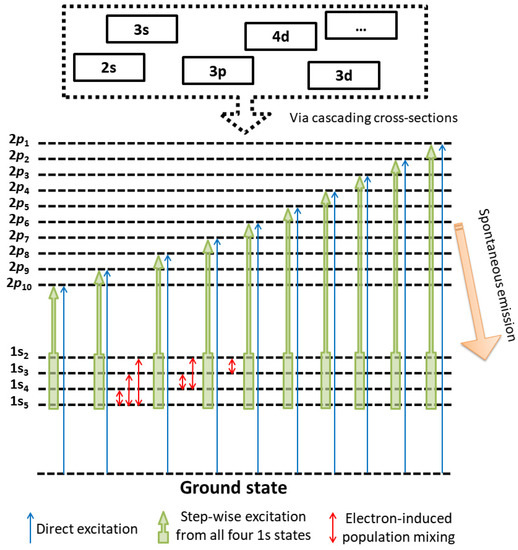
Figure 4. Schematic of the reactions considered in the CR model of argon 2p states.

As a first approximation, assuming that the Ar 2p level is mostly populated by electron impact on both ground-state argon atoms (direct excitation) and Ar 1s states (stepwise excitation via metastable and resonant levels), while only lost by spontaneous emission, the steady-state $n_i$ can be written as:

$$n_i=\frac{k_{ground-i} n_{Ar}{n}_e+k_{step-i} n_{A{r}^m}{n}_e}{{\sum }_j{A}_{ij}}$$

(2)

where k_ground-I and k_step-I are the reaction rates for direct and stepwise excitation, respectively, $n_{Ar}$ is the number density of argon atoms in the ground state level, $n_{A{r}^m}$ is the number density of argon atoms in a metastable or resonant state, $n_e$ is the electron number density, and ${\sum }_j{A}_{ij}$ is the sum of the Einstein coefficients corresponding to the allowed radiative transitions from the corresponding emitting level. Therefore, based on Equation (2), the opposing trends observed in Figure 3 can a priori be linked to changes in $n_{A{r}^m}$,$n_{Ar}$,$n_e$, T_e or a combination of all these. This readily justifies the use of a detailed collisional-radiative model for all emitting 2p states to gain further insights into the physics driving such transient plasmas.

3.2. Results from the Collisional Radiative Model and Comparison with the Experiments

The collisional radiative model used in this work is based on the resolution of the particle balance equations of all Ar 2p levels using T_e and n_e as the only adjustable parameters. More specifically, for each (T_e, n_e) pair, it calculates a theoretical spectrum by solving the ten Ar 2p balance equations (see Figure 4) and computing the resulting intensity of relevant emission lines using Equation (1). The considered population mechanisms are direct and stepwise electron impact excitation using cascading cross-sections (in order to account for the contribution of higher-energy levels [31]), while the depopulation mechanisms are radiative transitions (mitigated by radiative trapping of the lines, when applicable) and quenching reactions by collisions with neutral argon atoms (see Figure 4). It is worth mentioning that the four Ar 1s levels balance equations are also simultaneously solved to account for stepwise excitation and radiation trapping. More details can be found in [34]. Once the theoretical emission line intensities are obtained for every (T_e, n_e) pair, they are compared to the experimental (measured) ones by calculating a percentage standard deviation and the T_e and n_e values resulting in the best fit are assumed to correspond to the real plasma parameters. In order to run, the model requires input parameters such as the operating pressure and the neutral gas temperature (to calculate the number density of argon atoms in the ground state via the ideal gas law), as well as the absorption length along the line of sight of the optical emission spectroscopy measurement to account for optically thick Ar 2p-1s transitions [18,32,33].

Figure 5a shows typical percentage standard deviation plots calculated on a set of emission bands as a function of T_e for three n_e values of interest for lowest base pressure condition, p₀ ~5 mTorr. For these experimental conditions, a minimum of the percentage standard deviation is observed for an electron temperature of 2.6 eV no matter the value of the electron number density. Here, the chosen range of electron number density (10¹⁴–10¹⁶ m⁻³) is based on Langmuir probe measurements done in similar experimental conditions [30]. Figure 5b confirms the optimal agreement between the theoretical and experimental spectra as found by the CR model for T_e = 2.6 eV. Similar electron temperature values were obtained by Langmuir probes for low-pressure argon RF plasmas sustained in comparable experimental conditions (pressure, reactor dimensions) [30]. Such little influence of the electron density on the optimal T_e value observed in Figure 5a implies that the CR model is mostly independent of the electron number density over the range of experimental conditions investigated. Two physical possibilities could lead to this result: either stepwise excitation processes have no contribution on the population kinetics of the Ar 2p levels, or the stepwise processes do indeed contribute but all the other population/depopulation mechanisms also have an electron number density dependency, resulting in its vanishing from the particle balance equations of Ar 1s states. To verify which of these two hypotheses applies to the present situation, a corona model based on the work of Huddlestone et al. [35] and in which stepwise processes are neglected is also calculated.

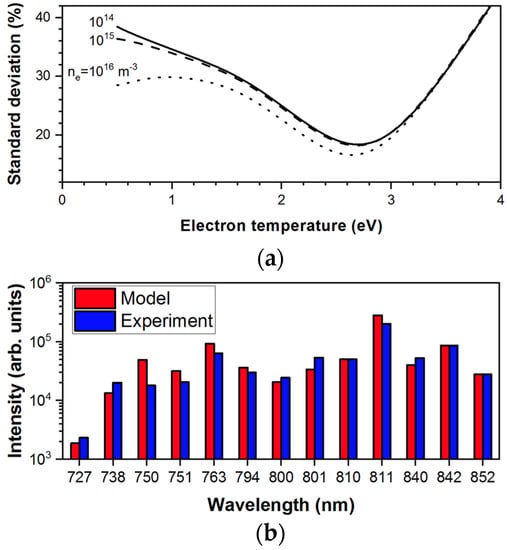
Figure 5. (a) Evolution of the percentage standard deviation as a function of the electron temperature for three electron number densities and a base pressure p₀ ~5 mTorr. (b) Agreement of the experimental and model emission line intensities for the optimal (T_e, n_e) values.

3.3. Impact of Stepwise Excitation Processes on the Study of the Electron Temperature

To determine the role of stepwise excitation processes over the range of experimental conditions examined, two separate cases were considered. First, the CR model is computed using all mechanisms that could play a role in the Ar 2p and 1s kinetics, a scenario we shall refer to as the standard CR model. Second, the same CR model is computed but all the stepwise processes are neglected, which in the end means it is considered that $n_{A{r}^m}$ = 0 and all the optical transition are optically thin. This scenario, based on the steady-state corona model, will be referred to as the Corona model. The temporal evolution of the electron temperature over the injection period is reported in Figure 6 for both scenarios. The evolution of the pressure drop is also reported.

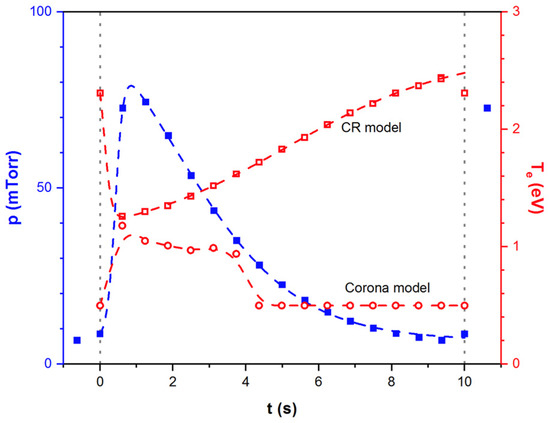
Figure 6. Comparison of the evolution of the electron temperature (red curves) and the pressure pulse (blue curve) on a normalized injection period for an injection frequency of 0.1 Hz. Electron temperatures are shown for both CR and Corona models.

In the case of the standard CR model, a decrease in T_e of about 1 eV is observed in Figure 6 concomitantly with the gas pulse, reaching a minimum of 1.4 eV and then increasing back to 2.5 eV as the pressure lowers back to its initial value. This trend agrees with the calculations of Liebermann et al. [36] as well as with the results reported by Maaloul et al. [30]. On the other hand, the opposite trend is observed in the case of the Corona model since the electron temperature rises to 1 eV and drops back to 0.5 eV as the pressure also rises and drops. More interestingly, both of the models clearly do not agree on the electron temperature at any given time of the pulse except at the close end of the pulse, where T_e (CR) is minimal and T_e (Corona) is maximal.

To verify which model better depicts the physics driving the temporal evolution of the plasma, the temporal evolution of the percentage standard deviation in both cases is analyzed; the results are shown in Figure 7a. As can be seen, the standard CR model always better describes the experimental data than the Corona model. Moreover, at the beginning of the pulse, an almost match of the electron temperature (at ~1 s) also corresponds to the time where the percentage standard deviations are equals. Therefore, even if the Corona model is less relevant to simulate the optical emission spectra, it becomes almost as accurate as the standard CR model during the gas pulse. The reason behind this similarity is due to radiation trapping, as shown in Figure 7b. Indeed, it shows the temporal evolution of the self-absorption percentage of the Ar 811 nm emission line, as calculated by the standard CR model. Self-absorption is at a minimum (~20%) directly after the beginning of the gas pulse. Since, as mentioned before, neglecting stepwise excitation processes in the Corona model implied neglecting self-absorption of argon 2p-1s transitions, it thus explains (1) why the two models almost agree when radiation trapping becomes less important, (2) why the standard CR model is systematically better at simulating the measured spectra since radiation trapping is found to be an important mechanism over an important part of the pulse cycle, and (3) why the temporal evolution of the standard deviation as well as of the electron temperature share an evolution closer to the form of the pressure pulse. Therefore, radiation trapping plays an important role in the kinetics of Ar 2p states and must imperatively be considered to obtain a correct temporal evolution of the electron temperature. Additionally, it means that processes involving Ar 1s levels do contribute to the population kinetics of the Ar 2p levels but, as mentioned before, due to all the other mechanisms also having a n_e dependency, the model is in the end independent from the electron density. Finally, a decrease in the radiation trapping with an increase in the pressure makes sense since the lower electron temperature and the additional quenching reactions by neutral argon atoms can only result in lower Ar 1s number densities and thus less self-absorption of the lines linked to 2p-to-1s transitions.

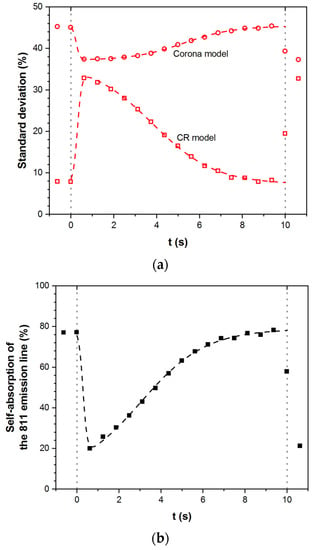
Figure 7. (a) Evolution of the percentage standard deviation over an injection period for the standard CR and Corona models (red curves). (b) Evolution of the self-absorption percentage of the Ar 811 nm emission line according to the standard CR model (black curve).

3.4. Effect of the Pulsed Gas Injection Parameters

Experiments with injection frequencies from 0.1 to 1 Hz are also carried out. For a fixed pumping valve position, the frequency reduces the overpressure from 65 to <1 mTorr when increasing the frequency (Figure 8). Spectra are analyzed in such conditions with the standard CR model. The temporal evolutions of the electron temperature are reported in Figure 8 for the four conditions. For an injection frequency of 0.1 Hz (p₀ ~160 mTorr), the electron temperature is, as in lower pressure condition (Figure 6), following the opposite trend of the pressure, but on a much smaller scale (Figure 8a). The experiment carried out with an injection frequency of 0.5Hz (p₀ ~110 mTorr) result in barely noticeable variation of the electron temperature with the pressure pulse (Figure 8b). Therefore, it can be concluded that the base pressure, p₀, more than the temporal variation, Δp, is determinant in fixing the electron temperature: this parameter being particularly sensible to temporal variations at low pressure. To verify this claim, measurements are recorded with an injection frequency of 1 Hz and two different base pressure of p₀ ~70 and 240 mTorr (Figure 8c,d). Clearly, the higher-pressure results in the lower electron temperature, confirming precedent conclusion in agreement with previous works at constant pressures [30].

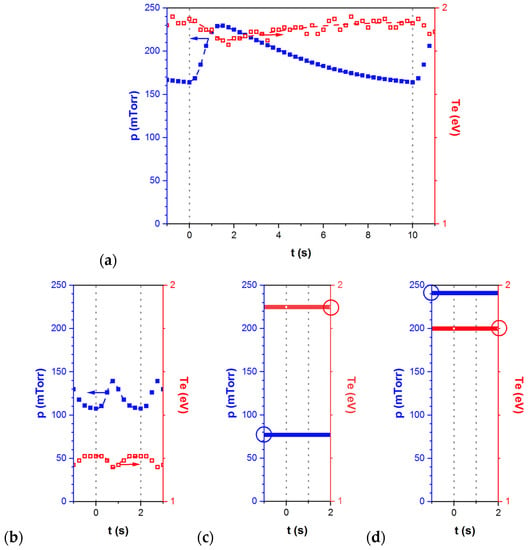
Figure 8. (a) Evolution of the pressure (blue curves) and of the electron temperature (red curves) during a pulse for (a) f = 0.1 Hz, p₀ ~160 mTorr, Δp ~70 mTorr, (b) f = 0.5 Hz, p₀ ~110 mTorr, Δp ~30 mTorr, (c) f = 1 Hz, p₀ ~70 mTorr, Δp < 1 mTorr, and (d) f = 1 Hz, p₀ ~240 mTorr, Δp < 1 mTorr.

3.5. Global Trend and Comparison with Reference Measurements

Figure 9 shows all the electron temperatures obtained from the comparison between measured and simulated (CR model) line emission intensities of Ar 2p-to-1s transitions under the different experimental conditions and reports them as a function of pressure. Clearly, a global trend emerges from this graph, which can be compared to a scaling law (curve). This scaling law is based on the resolution of the particle balance equation of charged species in which electrons and ions are mostly produced by electron-impact ionization of ground state argon atoms and lost by ambipolar diffusion and recombination on plasma reactor walls. In such model, the electron temperature becomes solely governed by the number density of ground state argon atoms (linked to the pressure via the ideal gas law) and the reactor dimensions. Here, the particle balance equation is solved for a cylindrical geometry with a length of 5 cm and a radius of 14 cm. Similar values are obtained from the heuristic global model reported in [36]. Based on this complete set of data, it is now clear that small variations of the pressure on the low-pressure side will affect more significantly the electron temperature than small variations of the pressure on the high-pressure side.

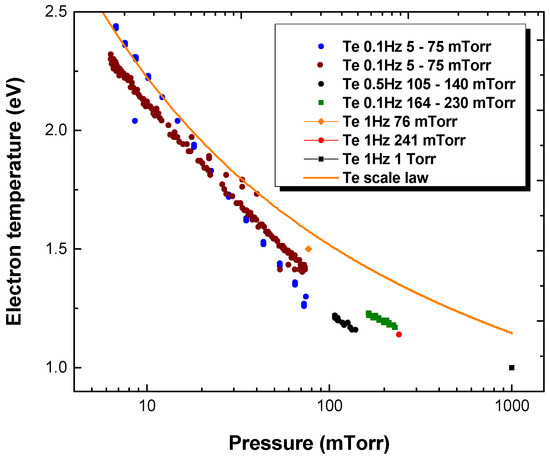
Figure 9. Evolution of the electron temperature with the pressure for the complete set of experimental conditions compared with a scale law (orange curve).

4. Conclusions and Perspectives

Optical emission spectroscopy measurement of the Ar 2p-to-1s transitions used in combination with a collisional-radiative model of the Ar 2p levels evidence that pulsed gas injections at low frequency (0.1–1 Hz) in a low-pressure capacitively coupled plasma reactor significantly affect the discharge. A decrease in the electron temperature following the pressure pulse is observed. A comparison of this result to that of a corona model highlight the importance of considering mechanisms involving Ar 1s levels, and especially radiation trapping, in the particle balance equation of Ar 2p and 1s states. Additionally, a global trend comparable to a scaling law is evidenced, linking an increase in the real-time operating pressure to a decrease in the electron temperature. Pressure variations on the low-pressure side have been observed to more importantly influence the electron temperature. This work is a first and necessary step to describe more complex plasmas in the presence of pulses of gaseous or liquid precursors with or without nanoparticles for deposition of nanocomposite coatings using the DLRI. Indeed, in such case, the role of precursors (liquid or gases) and/or nanoparticles can highly affect the plasma behavior and, especially, the electron temperature [18].