Analytical Formulas for Approximating Cross Sections of Electron Collisions with Hydrogen, Noble Gases, Alkali and Other Atoms

Abstract

This paper presents an analysis of data on the cross sections of elastic and inelastic collisions of electrons with noble gases, alkali and other atoms. For the selected sets of experimental and theoretical data, optimal analytical formulas are found, and approximation coefficients are calculated. The obtained semi-empirical formulas reproduce the values of the transport (diffusion), excitation and ionization cross sections for noble gases. Much attention is paid to the ionization cross sections of metal atoms, which are often present as an impurity in gas-discharge plasma. The approximation formulas reproduce the values of the ionization cross sections for hydrogen, metal and other elements in a wide range of energies with accurate orders of errors of the available theoretical and experimental data. For some elements with a two-hump plot of the dependence of the ionization cross section on the collision energy, it is proposed to use a two-term formula that takes into account ionization from both external and internal shells.

1. Introduction

Electron-atom cross-section data are important in a large variety of applications and fields (see for instance [1,2,3]). It is necessary to know the cross sections of electron-atomic collisions for numerical simulations of various phenomena in gas–discharge plasma by the particle method, in hydrodynamic approximation or based on the solution of the kinetic Boltzmann equation. The diffusion and drift of electrons in a gas are mainly determined by elastic collisions of electrons with atoms. The energy characteristics of a gas discharge are determined by the inelastic processes of ionization, excitation, etc. It is not our intention to give a review of the theoretical work on elastic and inelastic processes with which we compare our results. For that, we refer the reader to the review articles [4,5,6,7,8,9,10,11,12].

An exhaustive review and selection of data is contained in [1,2,3,4,5,6]. The measurement errors on the order of 1–3% given in the original works are surprisingly contrasted with each other, sometimes differing by 50%. Therefore, in the review work, only a comparative analysis of the results obtained is really possible, which shows that in the best case, the relative errors of measuring cross sections are on the order of 5–10%, and more often 20–50%, sometimes reaching 100%. Comparisons of sets of electron–neutral scattering cross sections and swarm parameters in noble gases were made in [13,14,15,16,17,18,19].

From a large number of experimental and calculated data on cross sections, we selected the data that based on the performed analysis, were recommended in these works with minor additions from later works. This made it possible to significantly expand the range of applicability of the selected analytical dependences in comparison with those given in [17].

The most convenient form of presenting of experimental and computational-theoretical data is analytical approximations of them. Analytical approximation is the most convenient and simple method of computer modeling for obtaining values at intermediate points. In addition, it allows you to analyze the accuracy of the asymptotic approximation. In [7], such approximations are selected for the cross sections of collisions of electrons with atoms of inert gases, elastic and inelastic.

2. Analytical Expression for the Transport Cross Sections in Elastic Collisions

Depending on the elastic collision cross section from the energy, three characteristic sections can be distinguished: collisions with low energy < 10 eV, collisions with medium energy and collisions with high energy > 300 eV. An approximation of the dependence of the transport cross sections for elastic collisions of electrons with atoms on the collision energy is obtained as the sum of a series of terms of the form:$(\sigma +\alpha {\epsilon }^{\delta })/(1+\beta {\epsilon }^{\gamma })$. The parameters σ, α, β, γ, δ of this approximation, which has the form of a hill, determine the magnitude of the pedestal, the steepness of the left and right slopes and the magnitude and position of the maximum. The first ionization potential I can serve as the natural scale of energy in the collision of an electron with an atom, and therefore it is convenient to shift to dimensionless energy $x=\epsilon /I$. We approximate the dependence of the cross section $\sigma (x)$ on the collision energy as the sum of the series:

$${\sigma }_{elastic}(x)={\displaystyle \sum _i\frac{{\sigma }_i+{\alpha }_i{x}^{{\delta }_i}}{1+{\beta }_i{x}^{{\gamma }_i}}}.$$

(1)

Here, the constants ${\sigma }_i$ and ${\alpha }_i$ are like the cross section. They have the dimension of the area, and the rest are dimensionless. The value of the cross section for the collision of an electron with zero energy ${\sigma }_0$ is defined by the formula ${\sigma }_0={\displaystyle \sum _i{\sigma }_i}$, which is found by solving the corresponding quantum mechanical problem.

To determine the parameters of (1), the problem of minimizing the root-mean-square deviation of the cross sections from their experimental values was solved by the standard method of coordinate descent:

$${\Delta }^2=\frac{1}{N}{\displaystyle \sum _{i=1}^N{\left[\frac{{\sigma }_{fit}(x_i)-{\sigma }_{\exp }(x_i)}{{\sigma }_{\exp }(x_i)}\right]}^2},$$

(2)

where ${\sigma }_{\exp }(x_i)$ are the measured values and ${\sigma }_{fit}(x_i)$ are the calculated cross sections in points: x_i, i = 1, …, N. Minimizing (2) instead of minimizing the simple deviation has the advantage of giving the correct statistical weight to cross sections at low- and high-impact energy. The same fitting procedure was used to evaluate excitation, ionization and elastic cross sections.

Even when using only two terms in Formula (1), a satisfactory solution to the problem of minimizing the approximation error is obtained (2% root-mean-square relative error for helium and neon and 6–9% for argon, krypton and xenon). The accuracy of the fit can be increased two to three times if three terms are used, but this makes no sense, since the errors in the input data are 10–20%.

Table 1. Values of parameters for the approximation of transport cross sections of elastic collisions of electrons with noble gas atoms.

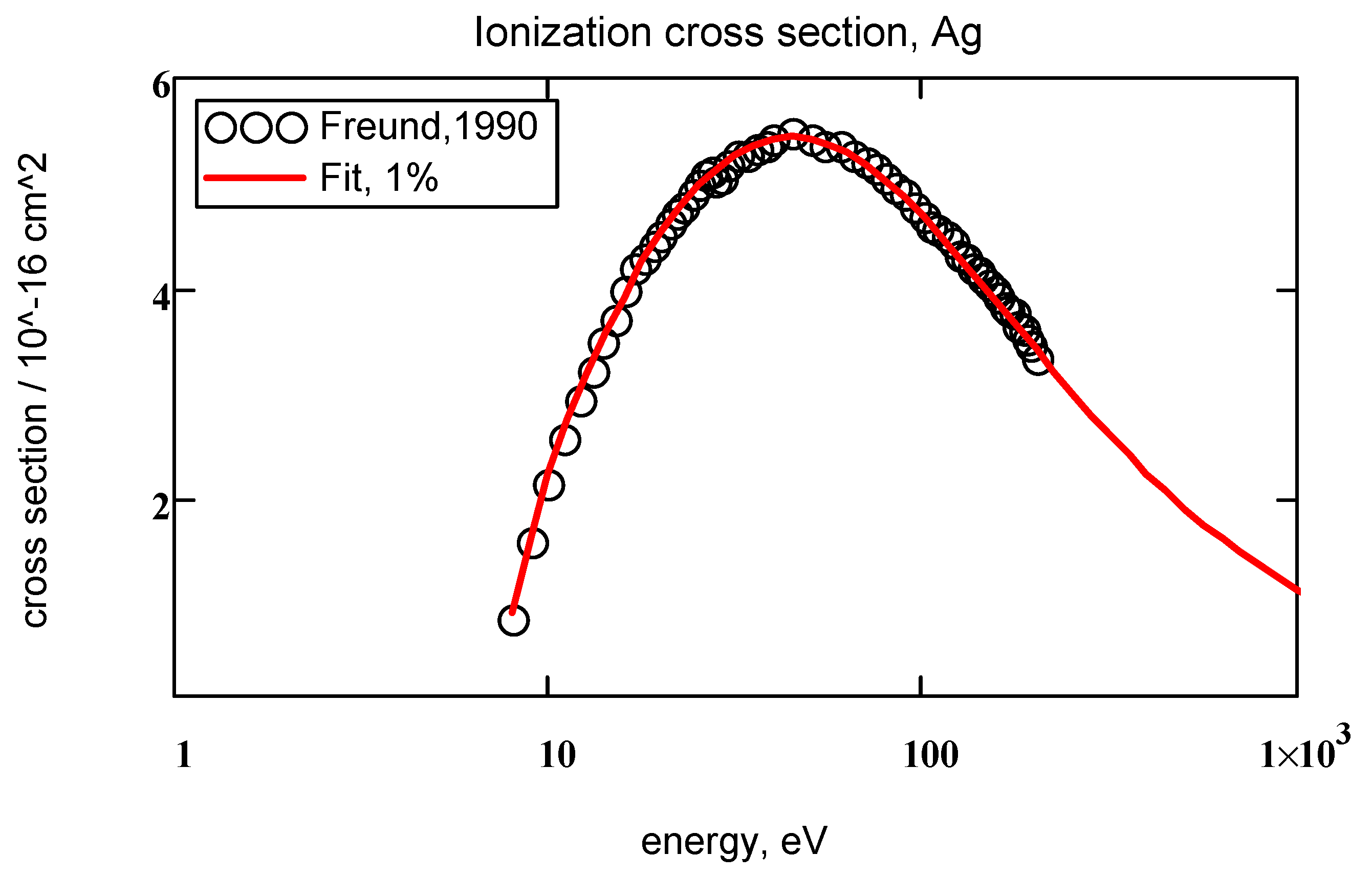
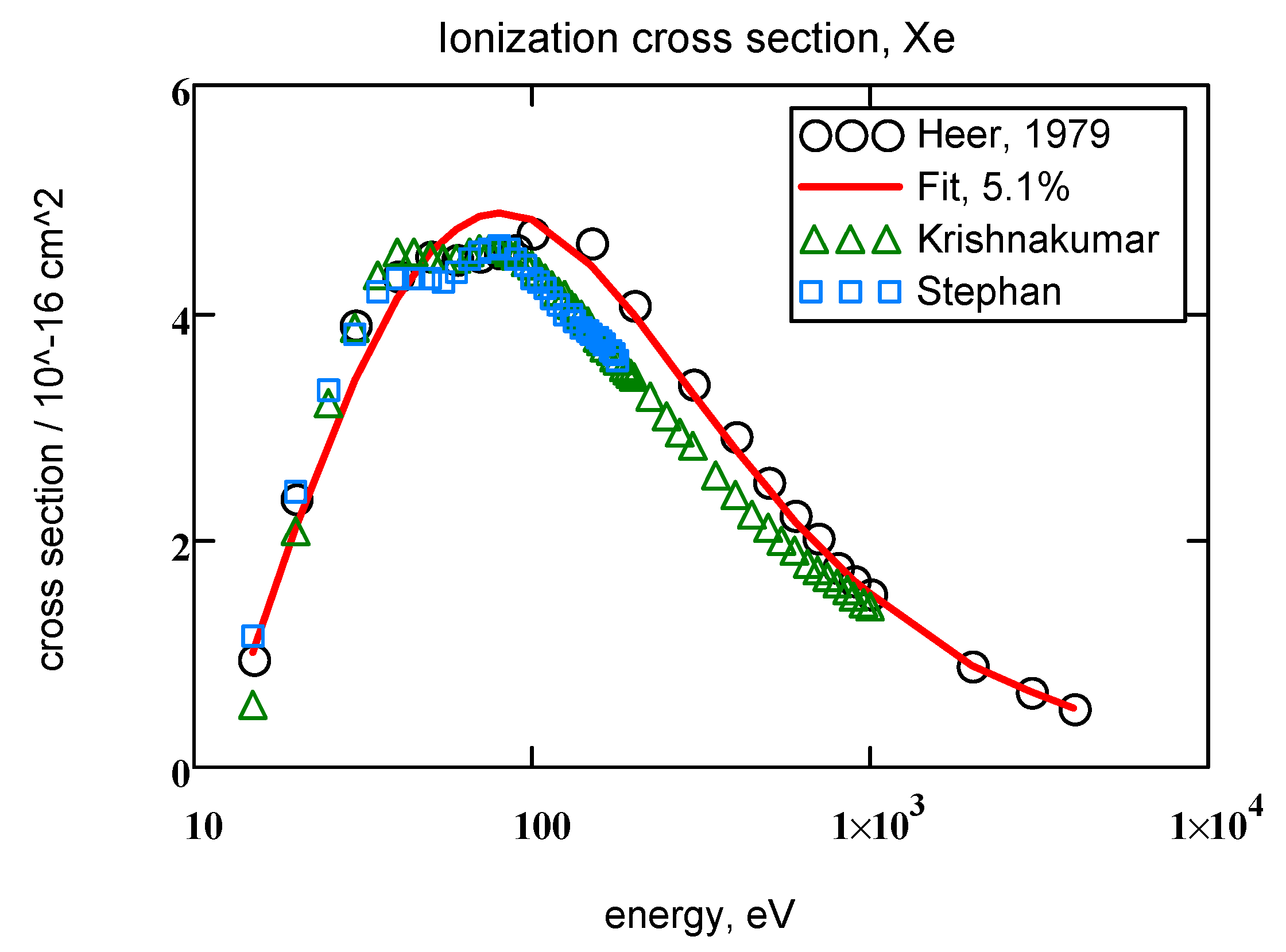
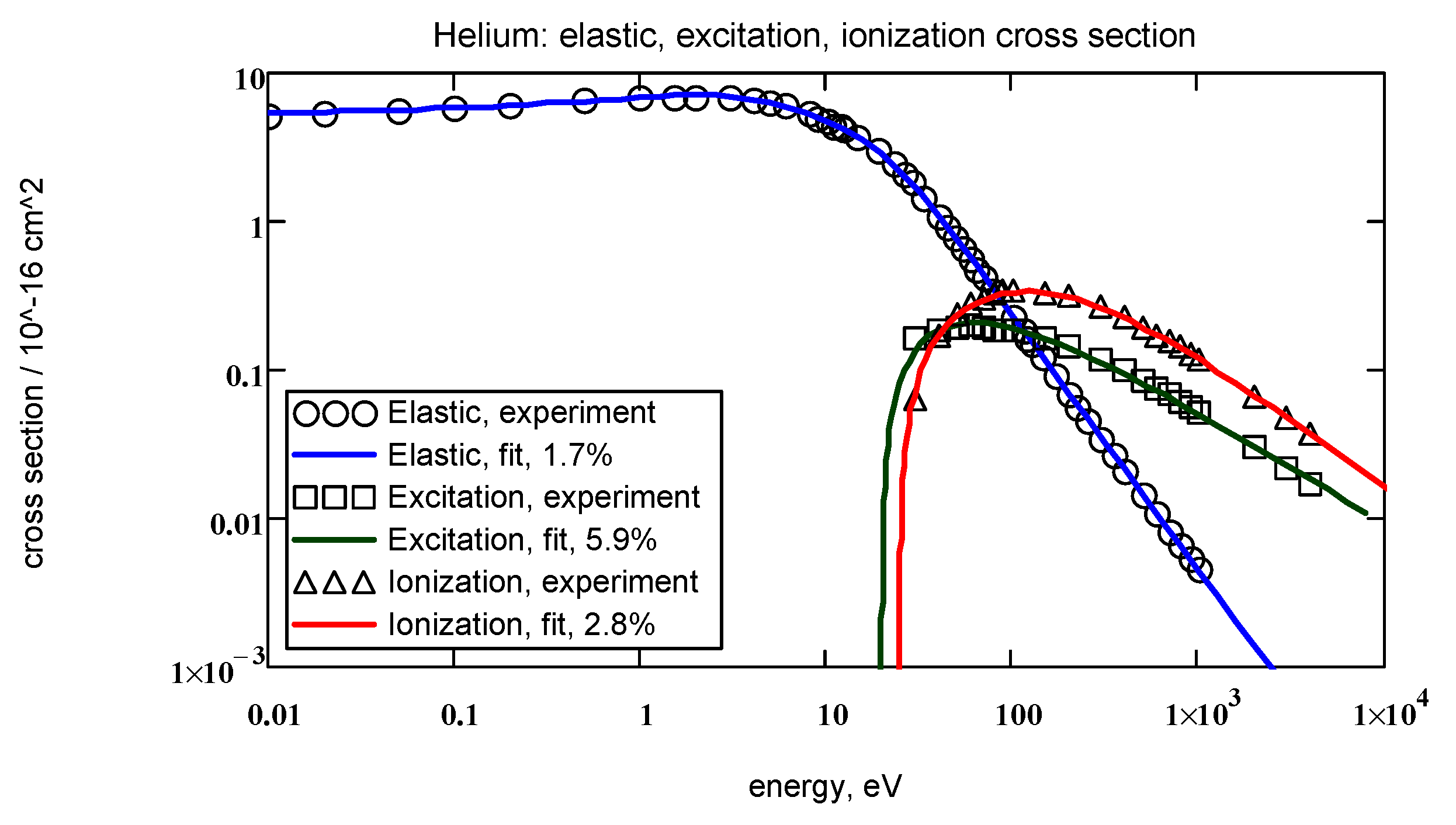
No, Symbol, I, eV	σ1 Å2	α1 Å2	β1	γ1	δ1	σ2 Å2	α2 Å2	β2	γ2	δ2	Δ, %
He, 24.584	0	7.19	3.67	2.79	1	5.16	6.09	15.0	1.91	0.41	1.7%
Ne, 21.564	0	38.7	267.	1.64	1	0.31	2.99	0.20	1.93	0.50	1.7%
Ar, 15.759	0.02	24.0	1.03	2.83	1	7.64	−65.4	1961	1.37	0.455	8.0%
Kr, 13.996	0.17	115.	9.52	3.58	1.82	40.5	−101.	1275	1.40	0.28	6.1%
Xe, 12.127	−3.1	182	10.1	2.8	1.53	136	−143.	1453	1.37	0.169	9.0%

presents the fitting coefficients of electron transport cross sections in inert gases. The collision energy is expressed in dimensionless units $x=\epsilon /I$ and the cross section in units Ų = 10⁻¹⁶ cm² = 10⁻²⁰ m².

3. Approximation of the Excitation Cross Sections for Nobles Gases Atoms

The excitation of atoms often is the main channel of energy losses. Their correct consideration is very important. In noble gases, the first levels are located rather high for the excitation cross section near the excitation threshold E₁. Sometimes, the linear approximation of the dependence of the cross section on energy is used [20]:

$${\sigma }_{excitation}(\epsilon )=C_{ex}(\epsilon -E_1),\epsilon >E_1.$$

(3)

To fit the excitation cross section, we choose the following formula [21,22]:

$${\sigma }_{excitation}(\Delta x)=\frac{\alpha \Delta x}{{(1+\beta \Delta x)}^{\gamma }},$$

(4)

where x = ε/E₁, Δx = x − 1, x > 1, $\alpha , \beta ,\gamma$—fitting constants. The maximum value of the cross section according to this formula is achieved at Δx = 1/(β (γ − 1)). We used Formula (4) earlier in [21] to approximate the excitation and ionization cross sections of noble gas atoms as well as in [23] to approximate the ionization cross sections of atoms of alkali metals, hydrogen, noble gases, some transition metals and Al, Fe, Ni, W, Au, Hg and U.

Near the threshold, Formula (4) has the same asymptotic as Formula (3). At high energies and $\gamma =2$, it agrees with the formula for the ionization cross section of a stationary electron obtained by Thomson in 1912 [24]:

$${\sigma }_{ionization}(\epsilon )=\frac{\pi e^4}{\epsilon }\left(\frac{1}{I}-\frac{1}{\epsilon }\right)\equiv 4\pi a_0^2\frac{R{y}^2(\epsilon -I)}{I{\epsilon }^2}.$$

(5)

In the high-energy region, the power-law decay of the cross section gives satisfactory agreement with the experimental and theoretical data.

The coefficients of this approximation are given in

Table 2. Parameter values for approximating the excitation cross sections of noble gases atoms.

No, Symbol	E1, eV	α, Å2	β	γ	Δ, %	${\mathit{\epsilon }}_{\mathbf{m}},$ eV	$\mathit{\sigma }$$\left({\mathit{\epsilon }}_{\mathbf{m}}\right)$ Å2
He	19.8	0.42	0.61	1.75	5.9%	63	0.21
Ne	16.619	0.20	0.34	1.85	1.9%	75	0.17
Ar	11.50	0.98	0.35	1.81	3.8%	52	0.80
Kr	9.915	1.15	0.33	1.82	2.8%	47	1.01
Xe	8.315	1.14	0.25	1.87	3.8%	47	1.28

. The collision energy is expressed in eV, and the cross section in units of Ų. Also given is the root-mean-square relative error, which for the considered gases is on the order of 2–6%. In addition, the Table 2 contains the position of the maximum cross-section and the maximum of cross-section according to the approximating formula. Note that in the experiment, it is the measurement of the maximum cross section that has the greatest accuracy.

4. Approximation of the Ionization Cross Sections by One-Term Formula

In [21,22], we already considered analytical approximations for the cross section of ionization by the electron impacts of noble gas atoms, and in [23], the analysis of the available theoretical and experimental data was carried out, and the approximation coefficients for hydrogen and some metals were found. The errors in the approximation of experimental data by the analytical dependence (4) with three fitting constants $\alpha ,\beta ,\gamma$ for noble gases and vapors of some metals lie in the range of 3–7%, which corresponds in order of magnitude to the error of the experiments themselves. For some elements, however, the error turned out to be much larger, about 10–20%. Therefore, in this paper, we propose using a four-parameter formula, which can significantly improve the accuracy of the analytical approximation:

$${\sigma }_{ionization}(\epsilon )=\frac{\alpha \Delta x^{\delta }}{{(1+\beta \Delta x)}^{{}^{\gamma }}},$$

(6)

The maximum value of the cross section according to this formula is achieved when Δx = δ/(β(γ − δ)). For δ = 1, it coincides with Formula (4).

Examples of the use of Formula (6) for approximating the ionization cross sections of inert gas atoms are given in

Table 3. Parameter values for approximating the ionization cross sections of noble gas atoms.

No, Symbol	I1, E2, eV	α, Å2	β	γ	δ	Δ, %	${\mathit{\epsilon }}_{\mathbf{m}},$ eV	$\mathit{\sigma }$$\left({\mathit{\epsilon }}_{\mathbf{m}}\right),$ Å2
2, He	24.587	0.407	0.333	2.01	1.11	0.97%	116	0.348
10, Ne	21.564, 48.47	0.454	0.229	2.22	1.33	1.2%	161	0.716
18, Ar	15.759, 29.24	3.18	0.327	1.92	1.08	2.5%	78	2.86
36, Kr	13.996, 27.51	3.74	0.302	1.86	1.07	2.7%	77	3.81
54, Xe	12.127, 23.40	3.64	0.179	1.66	0.836	5.1%	81	4.86

, and alkali metal atoms are given in

Table 4. Parameter values for approximating the ionization cross sections of H and alkali atoms.

No, Symbol	I1, E2, eV	α, Å2	β	γ	δ	Δ, %	${\mathit{\epsilon }}_{\mathbf{m}},$ eV	$\mathit{\sigma }$$\left({\mathit{\epsilon }}_{\mathbf{m}}\right),$ Å2
1, H	13.595	0.872	0.376	1.93	1.03	1.6%	55	0.63
3, Li	5.392, 58	71.9	1.28	3.65	2.84	5.6%	20	5.2
11, Na	5.139, 34	28.1	1.23	1.85	1.26	1.5%	14	6.83
19, K	4.339, 18.7	3.49	0.022	1.25	0.31	4.7%	69	5.65
37, Rb	4.176, 15.3	8.18	0.07	1.04	0.105	2.3%	11	7.7
55, Cs	3.893, 12.3	19.2	0.64	2.19	1.61	6.6%	11	4.86

.

For a number of the most commonly used substances, the data are given in

Table 5. Parameter values for approximating the ionization cross sections of various elements.

No, Symbol	I1, E2, eV	α, Å2	β	γ	δ	Δ, %	${\mathit{\epsilon }}_{\mathbf{m}},$ eV	$\left({\mathit{\epsilon }}_{\mathbf{m}}\right),$ Å2
4, Be	9.322, 115	3.82	0.439	2.16	1.09	6.9%	31	2.11
12, Mg	7.646, 54	13.6	0.713	1.87	1.0	3.1%	20	5.3
13, Al	5.986, 10.62	48.7	1.11	2.54	1.95	2.9%	24	10.1
14, Si	8.157, 13.46	16.75	0.893	1.77	1.28	2.5%	32	6.8
15, P	10.486, 16.15	18.9	0.911	4.05	3.31	4.6%	62	3.75
16, S	9.75, 20.20	66.9	1.19	5.32	4.6	3.0%	63	3.74
21, Sc	6.56, 33	66.5	1.28	3.76	3.19	7%	35	6.12
22, Ti	6.83, 38	13.4	0.456	1.58	0.71	3.1%	19	7.89
24, Cr	6.764, 48	674	1.94	4.75	4.17	4.9%	31	7.29
25, Mn	7.432, 53	219	1.75	3.75	3.19	3.8%	31	7.46
26, Fe	7.90, 59	5.34	0.129	1.29	0.35	4.6%	31	5.15
27, Co	7.86, 66	337	1.79	4.71	4.15	4.3%	41	5.43
28, Ni	7.663, 73	9.97	0.632	2.18	1.35	4.6%	27	4.36
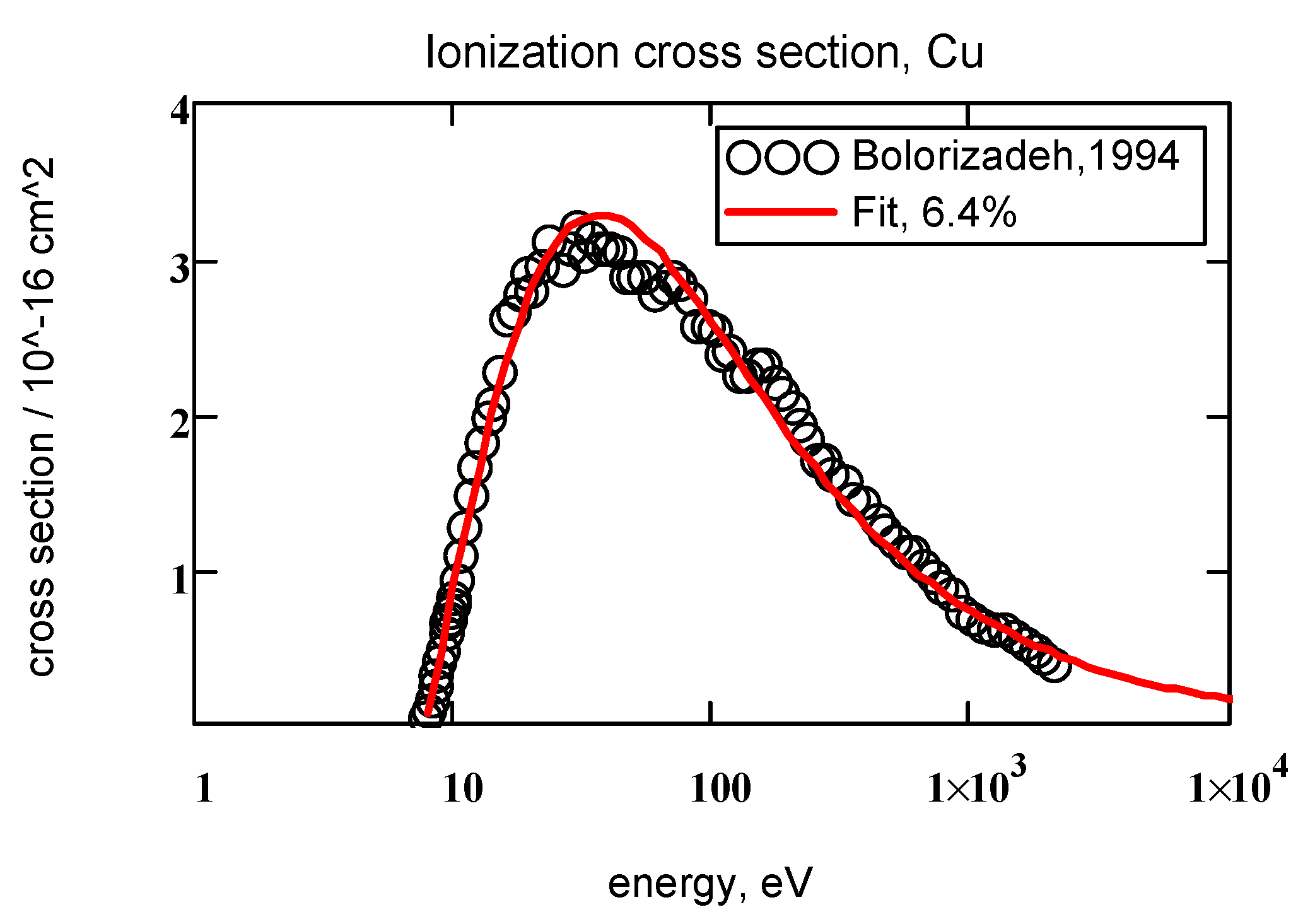
29, Cu	7.724, 80	4.45	0.469	1.78	1.13	6.4%	37	3.29
30, Zn	9.391, 91	300	1.85	4.90	4.38	3.5%	52	3.86
31, Ga	6.00, 11	163	1.5	4.53	3.98	4.1%	35	6.15
32, Ge	7.88, 14.3	6.37	0.529	2.17	1.58	6.0%	48	4.91
41, Nb	6.88, 38	422	1.81	4.14	3.56	3.9%	30	9.53
45, Rh	7.46, 53	10.5	0.745	2.46	1.96	3.4%	47	5.43
46, Pd	8.33, 57	33.2	1.23	3.91	3.46	2.0%	60	3.98
47, Ag	7.574, 63	4.52	0.141	1.434	0.59	1.0%	45	5.44
48, Cd	8.991, 71	588	2.08	4.60	4.09	3.7%	43	5.82
74, W	7.98, 41	27.6	1.00	3.86	3.31	2.1%	62	5.66
79, Au	9.223, 61	214	1.12	3.99	3.17	9.1%	41	20
80, Hg	10.434, 68	1.04	0.211	1.75	1.1	11.4	94	1.82
82, Pb	7.415, 25	7.63	0.174	1.51	0.63	3.3%	38	8.23
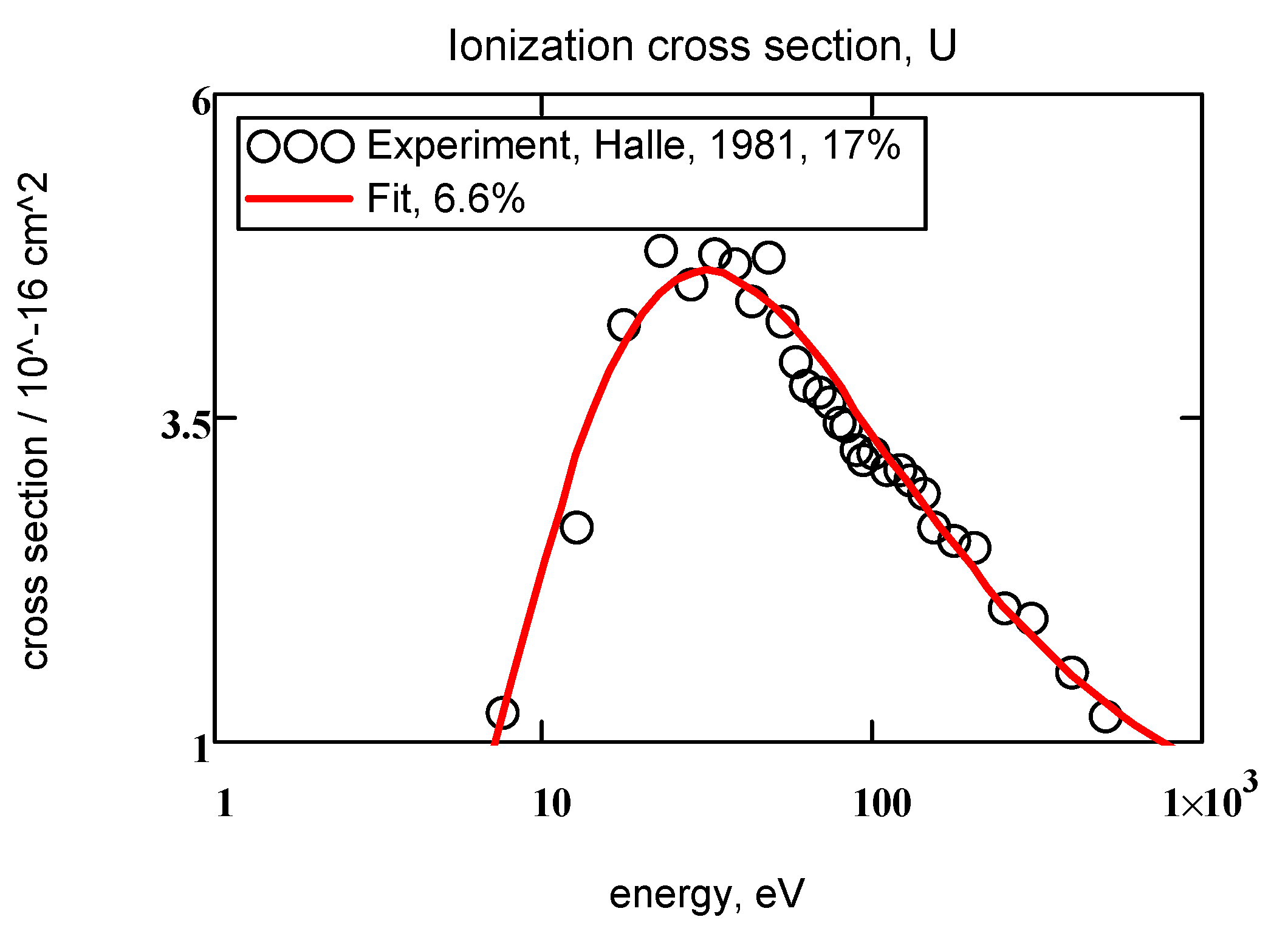
92, U	5.65, 48	4.71	0.328	1.76	1.05	6.6%	30	4.49

. For reference, Table 3, Table 4 and Table 5 also show the first ionization potential I₁ and the ionization energy from the second shell E₂ [25] (usually it is slightly larger than the second ionization potential). All tables contain the position of the maximum cross section and the maximum cross section according to the approximating formula.

The errors given in Table 3, Table 4 and Table 5 show that Formula (6) allows us to take into account the nature of the dependence for most elements with good accuracy. An example of an excellent approximation of Ag by a one-term formula is shown in Figure 1. The data on the ionization cross sections for Ag are taken from [10].

5. Approximation of the Ionization Cross Sections by Two-Term Formulas

The results of the analytical approximations of ionization cross sections given in Table 3, Table 4 and Table 5 can be recommended for use in modeling various processes in gas-discharge plasma. However, the available experimental data in some cases allow us to obtain more accurate values of the ionization cross sections. Let’s take this as an example of the ionization of Xe, Cs, Cu and U atoms. For many elements, at high collision energies (greater than the energy of knocking electrons out of the inner shells), ionization from the inner shells of the atom becomes very significant. For such elements, the curve of the cross-section is of a two-humped nature, which does not allow it to be approximated with sufficiently good accuracy using the one-term Formula (6). Therefore, in this paper, an attempt is made to account for the ionization of the atom by knocking electrons out of the inner shells. A logical way to account for this ionization channel is to use a two-term approximation (2 TA) in which the first term corresponds to ionization from the outer shell and the second term describes ionization from the second shell:

$${\sigma }_{ionization}(\epsilon )=\frac{{\alpha }_1\Delta x_1^{{\delta }_1}}{{(1+{\beta }_1\Delta x_1)}^{{\gamma }_1}}+\frac{{\alpha }_2\Delta x_2^{{\delta }_2}}{{(1+{\beta }_2\Delta x_2)}^{{\gamma }_2}},$$

(7)

where $x_1=\epsilon /I_1,\Delta x_1=x_1-1,x_1>1, x_2=\epsilon /E_2,\Delta x_2=x_2-1,x_2>1$.

For some elements with a two-hump plot of the dependence of the ionization cross section on the collision energy, we used the two-term Formula (7), which allowed us to take into account ionization from both external and internal shells. Formula (7) significantly improved the accuracy of the approximation: one and a half to two times compared with the one-term formula.

Table 6. Values of parameters for the ionization cross sections approximation of atoms of Xe, Cs, Cu, U: one−term approximation (1 TA) by Formula (6) and two−term approximation (2 TA) by Formula (7).

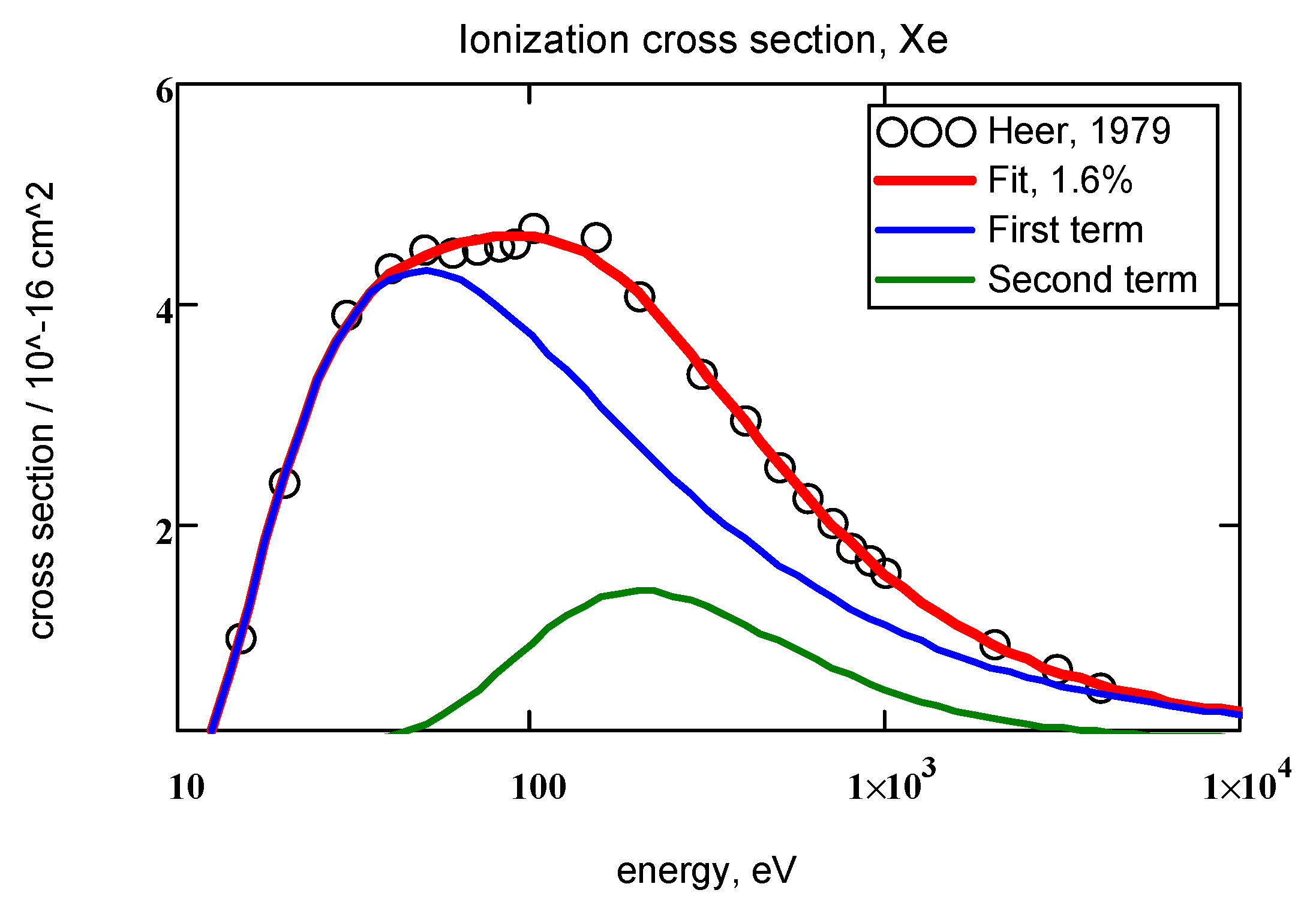
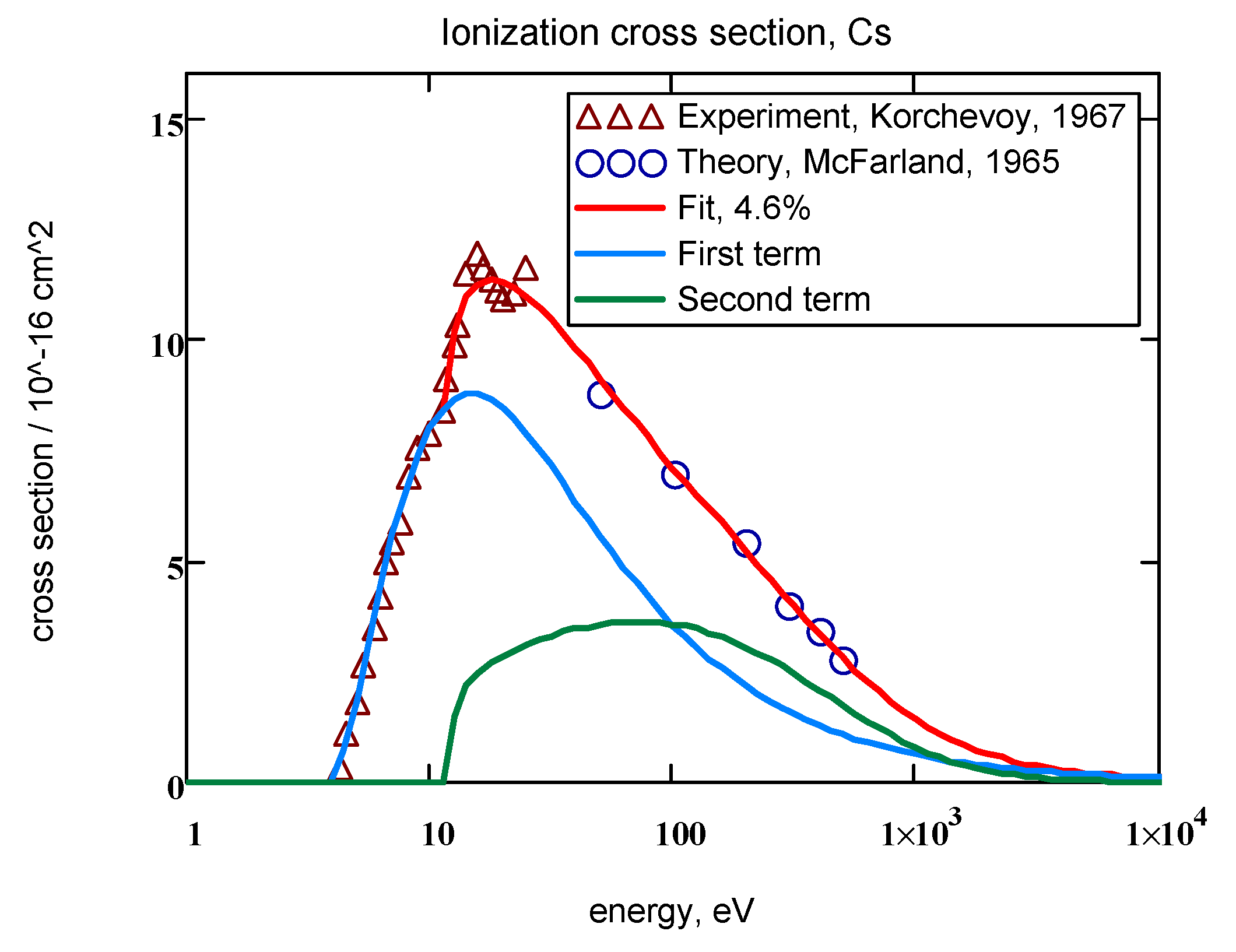
No, Symbol	I1, E2, eV	Term Index	αi, Å2	βi	γi	δi	Δ, %	Fit Terms
54, Xe	12.127, 23.40	i = 1	3.64	0.179	1.66	0.836	5.1%	1 TA
		i = 1	9.18	0.685	2.03	1.37	1.6%	2 TA
		i = 2	0.586	0.371	5.29	3.91
55, Cs	3.893, 12.3	i = 1	19.2	0.64	2.19	1.61	6.6%	1 TA
		i = 1	30.3	8.22	2.59	1.8	4.6%	2 TA
		i = 2	3.24	0.016	2.73	0.203
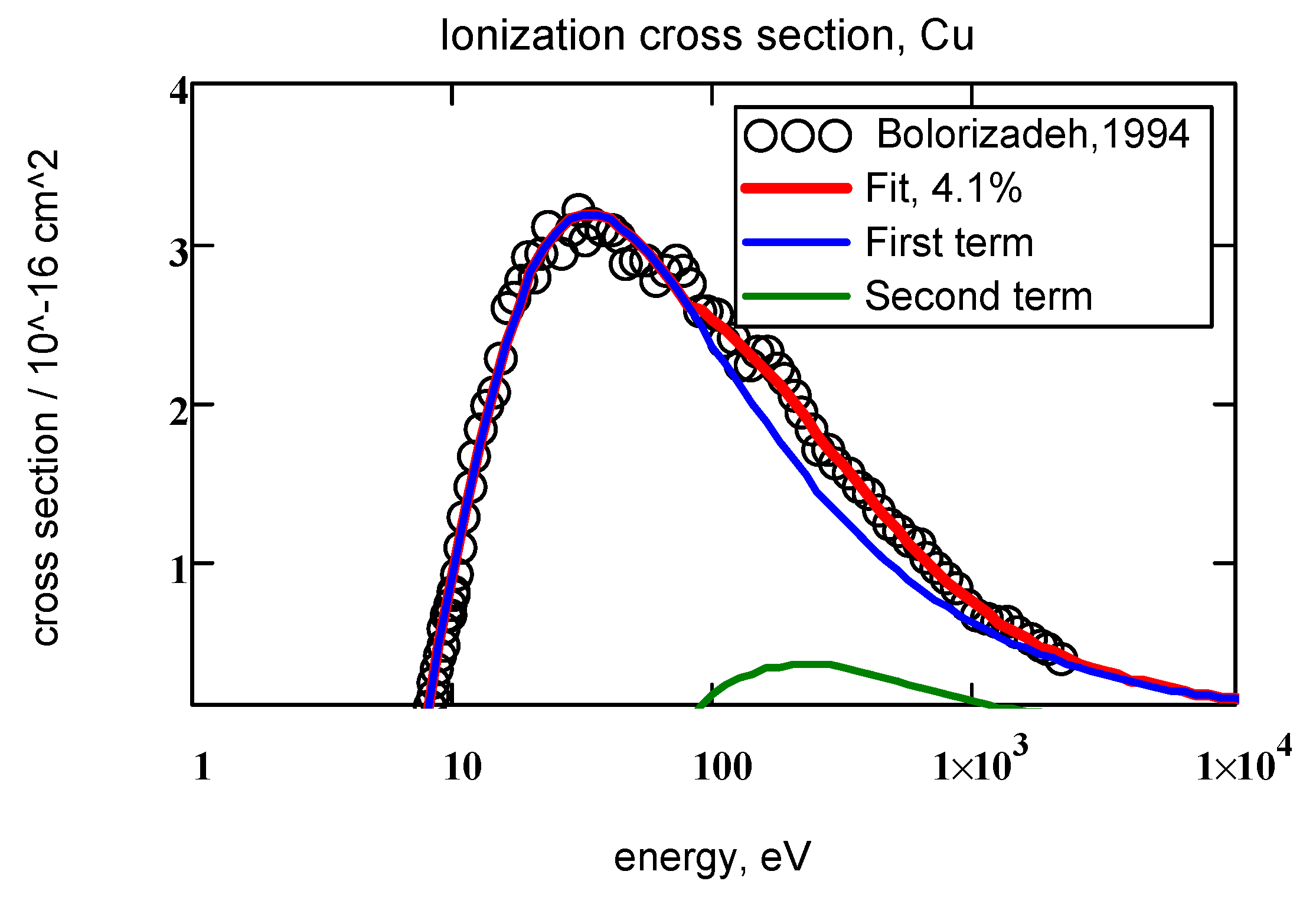
29, Cu	7.724, 80.	i = 1	4.45	0.469	1.78	1.13	6.4%	1 TA
		i = 1	5.12	0.537	1.87	1.19	4.1%	2 TA
		i = 2	0.565	0.220	2.74	0.784
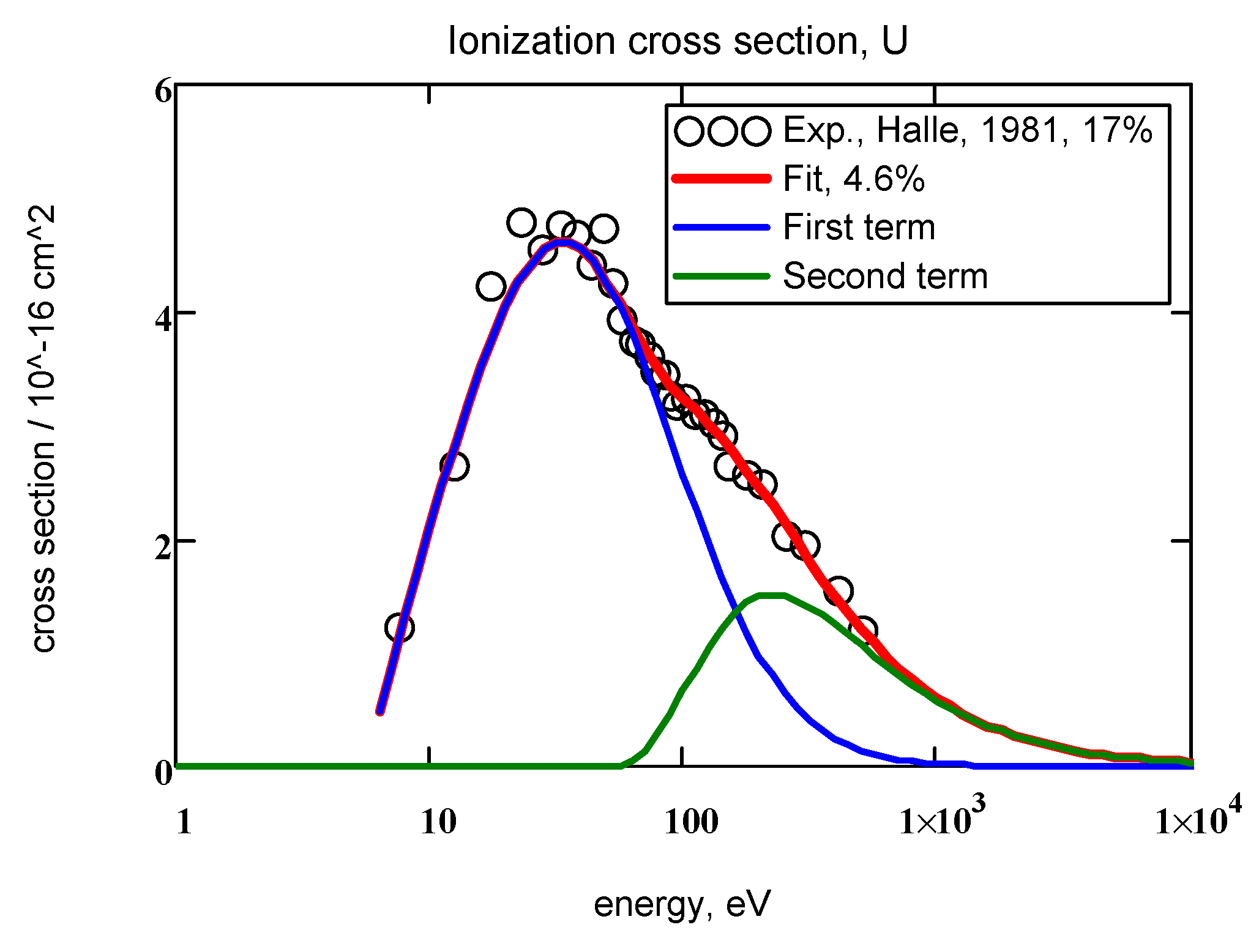
92, U	5.65, 48	i = 1	4.71	0.328	1.76	1.05	6.6%	1 TA
		i = 1	3.1	0.06	3.76	0.86	4.6%	2 TA
		i = 2	8.74	0.75	4.8	3.53

shows the values of the coefficients for Formula (7) for xenon, cesium, copper and uranium. For comparison, the errors of the one-term approximation (1 TA) Δ are also given.

The experimental data and the approximating curves for these elements are shown in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9. In all plots, the experimental values of the cross sections are shown by markers, and the solid curves are the found approximations. In addition, all figures show the values of the errors of the corresponding approximations.

Here we consider the situation in more detail using the example of xenon. The data of the ionization cross sections for Xe are taken from [18,26,27]. Experimental data [18] and the result of their approximation by a one-term formula with an accuracy of 5% are given on Figure 2. For comparison, data from [26,27] are also presented, showing that the error of experimental data is about 20%. On the other hand, all the data show the two-humped nature of the dependence of the cross section on energy, so it is more physically justified to use a two-term approximation.

The results that physically justified using a two-term approximation are shown in Figure 3, which also shows the contributions to ionization from the first and second shells. The use of two-term approximation made it possible to improve the accuracy three times.

For cesium, we combined experimental data [28] in the range of 4 eV < E < 25 eV and theoretical data [11] in the range of 50 eV < E < 500 eV and approximated them with the one-term Formula (6) and the two-term Formula (7). The results are shown in Figure 4 and Figure 5, respectively. The use of two-term approximation made it possible to reduce the error by one and a half times.

Experimental data for copper were taken from [29]. The approximation results are shown in Figure 6 and Figure 7. The use of two-term approximation made it possible to reduce the error by one and a half times.

Despite the great popularity of uranium, there are very little cross-sectional data for it, and they show a large spread. For elements for which experimental data are obtained with a large error, such as for uranium (17%) [30], the approximation dependence gives a much more acceptable result than the initial data themselves. This is clearly seen in Figure 8, where the red curve with an accuracy of 6.6% is more plausible than the randomly scattered experimental points.

The results of applying the two-term approximation are shown in Figure 9, which also shows the contributions to ionization from the first and second shells. Since the two-term approximation takes into account the actually existing different ionization channels, it can be considered a procedure for recovering data that are noisy with random errors (in [30] errors are estimated at 17%).

6. Discussion and Conclusions

Here we consider the most significant characteristics of electron-atomic collisions in the modeling of gas-discharge plasma problems. The transport cross section determines the rate of momentum loss and the rate of electron drift, the excitation cross section determines the energy costs for the excitation of atoms, and the ionization cross section from the ground state determines the frequency of the appearance of electrons and their energy spectrum [31,32,33,34].

To demonstrate the dependencies of the momentum, excitation and ionization cross section on energy the experimental data and the fitting curves are shown in Figure 10 and Figure 11 for He and Ar, respectively. On each graph, the experimental values of the cross sections are represented by markers and the found approximations by solid curves. The data for the elastic collision cross sections of He are taken from BOLSIG+. These data are from database Phelps (www.lxcat.net/PHELPS (accessed on 1 August 2021)), momentum transfer—from Crompton et al. at low energy, Hayashi at high energies). The data of the excitation and ionization cross sections for He are taken from [17]. The cross sections for elastic collision in Ar are taken from the Puech database (www.lxcat.net (accessed on 1 August 2021)), the excitation and ionization cross sections are taken from [18].

In this paper, for noble gases, the available experimental and theoretical data on the transport cross sections for electron scattering on atoms, as well as the excitation and ionization cross sections, were analyzed. Approximating formulas selected for them, and the corresponding coefficients were found. Note that in this case, the optimization problem (search for the minimum of the penalty function) is reduced to finding the minimum in a multidimensional space (three, four, eight or ten parameters), in which the penalty function has many local minima, which greatly complicates the search for approximation parameters.

In many cases, the ionization of atoms is the determining process, and it is well known that small additions of impurities to the working gas can radically affect the characteristics of the discharge. These impurities appear in the gas due to cathode sputtering, structural elements, etc. Therefore, attention is paid to the ionization of a large number of elements that are often used in technologies and in experiments and are found in nature. For some of them (xenon, cesium, coppers and uranium), approximations have been obtained that, hopefully, have better accuracy than the original data.