Ultradilute Quantum Droplets in the Presence of Higher-Order Quantum Fluctuations
Abstract
:1. Introduction
2. HFB Theory
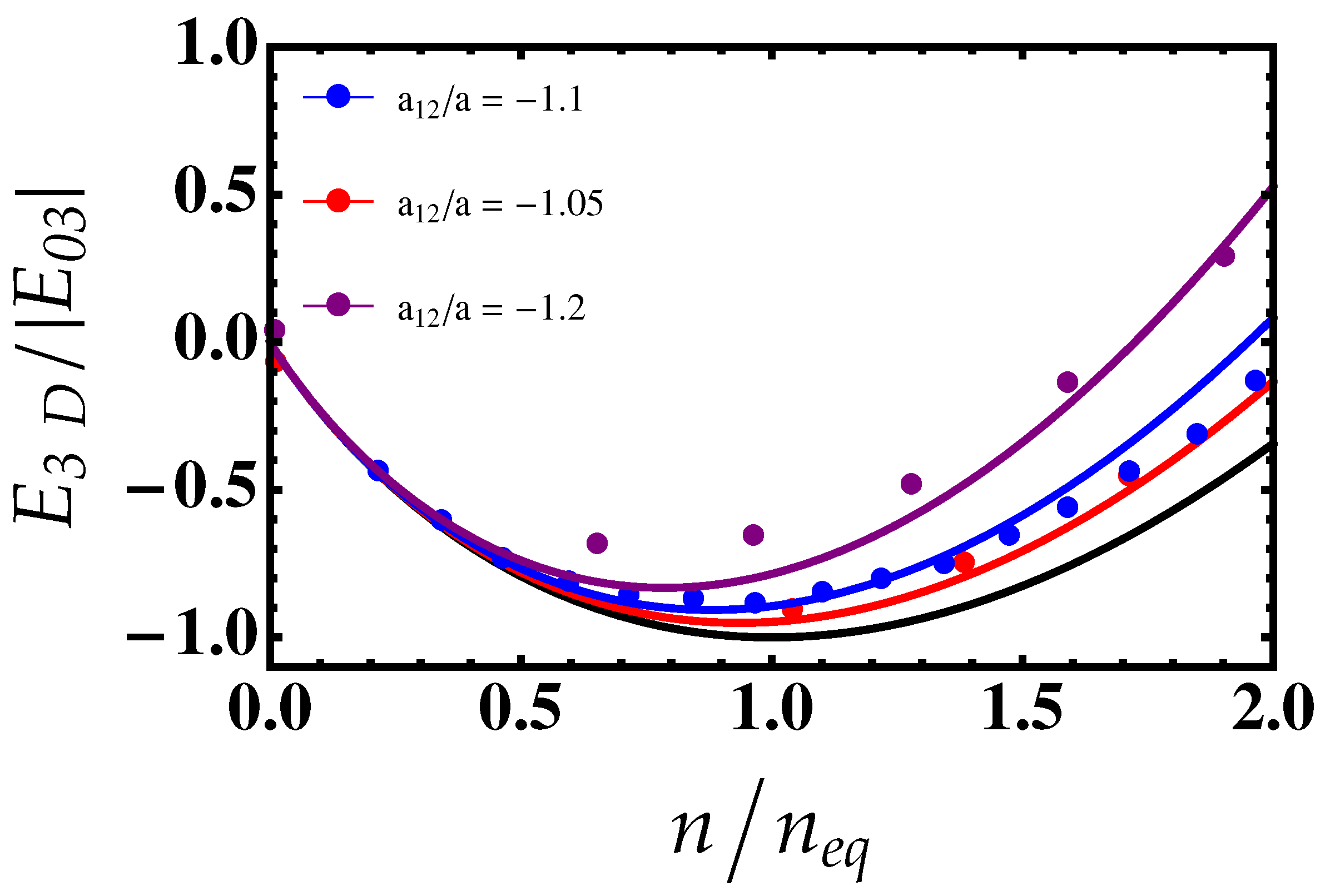
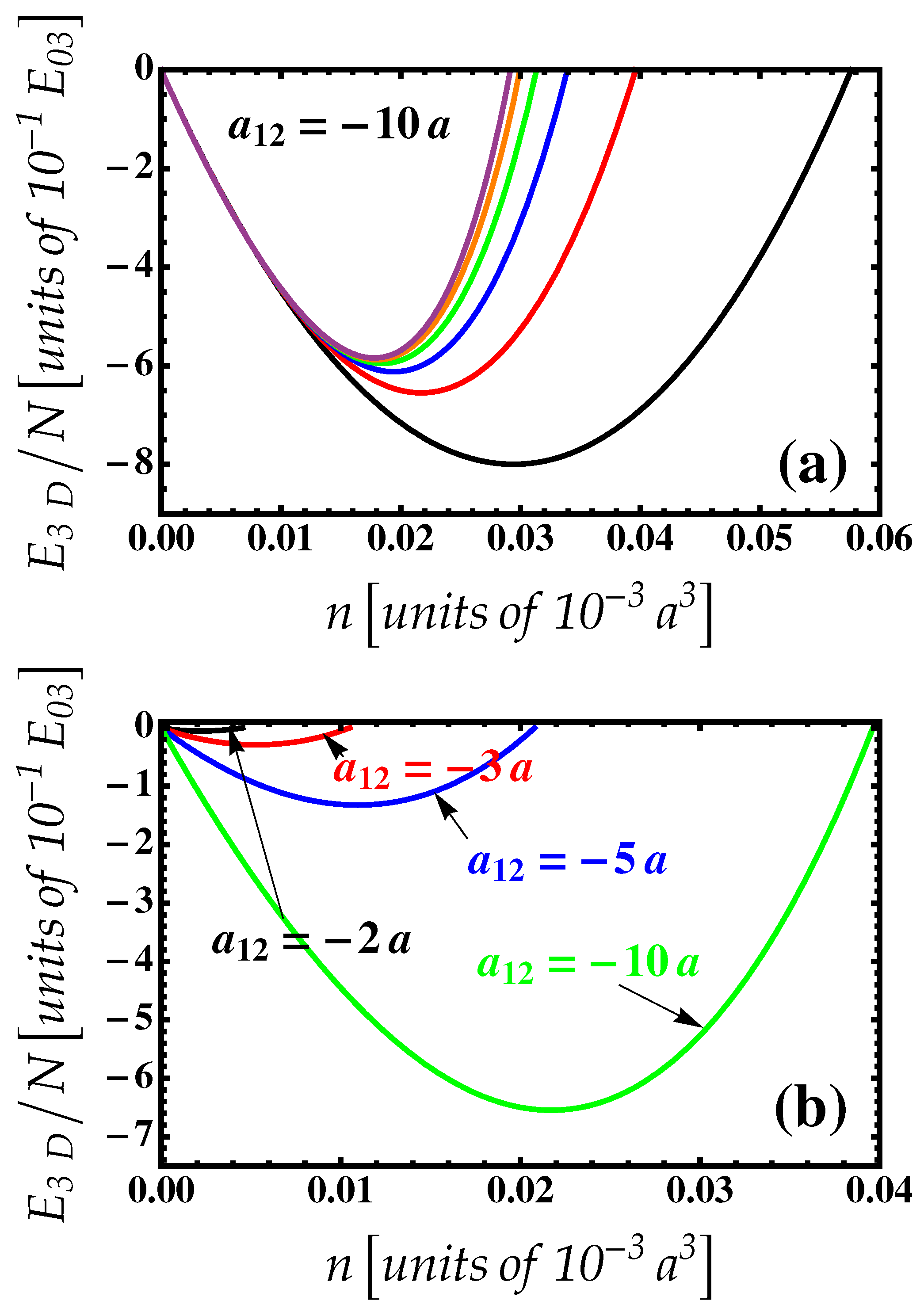
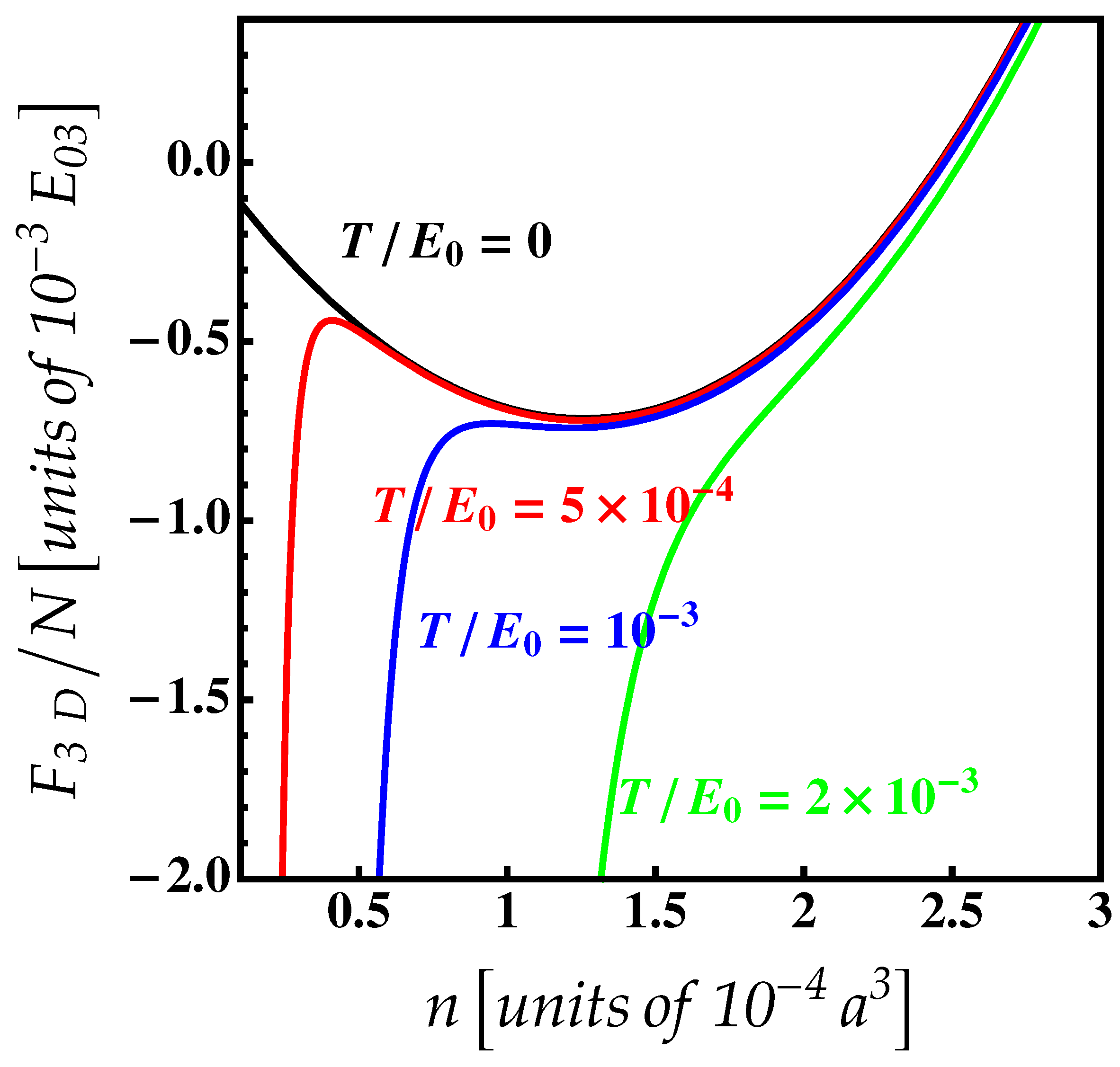
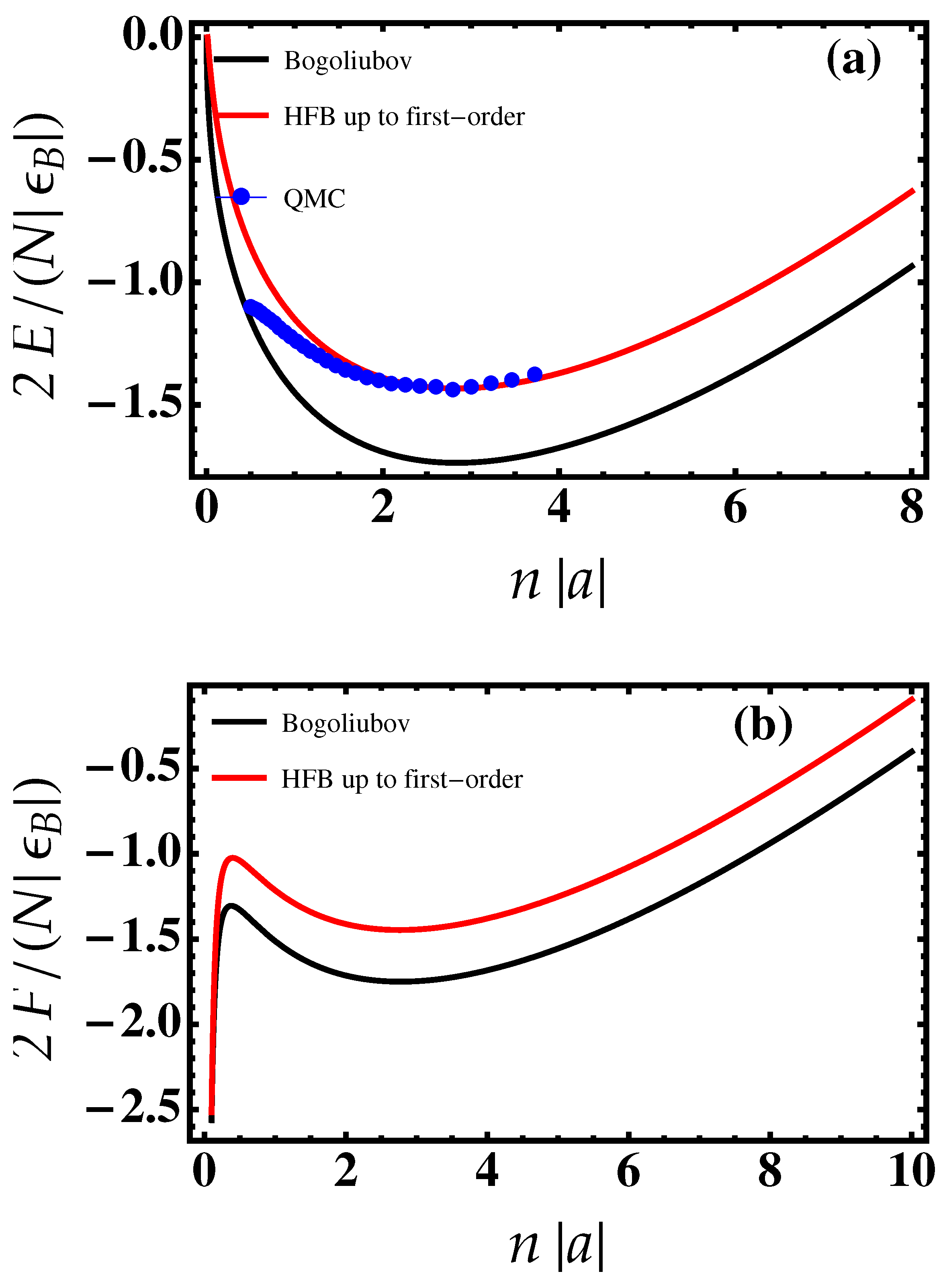
3. Three-Dimensional Droplets
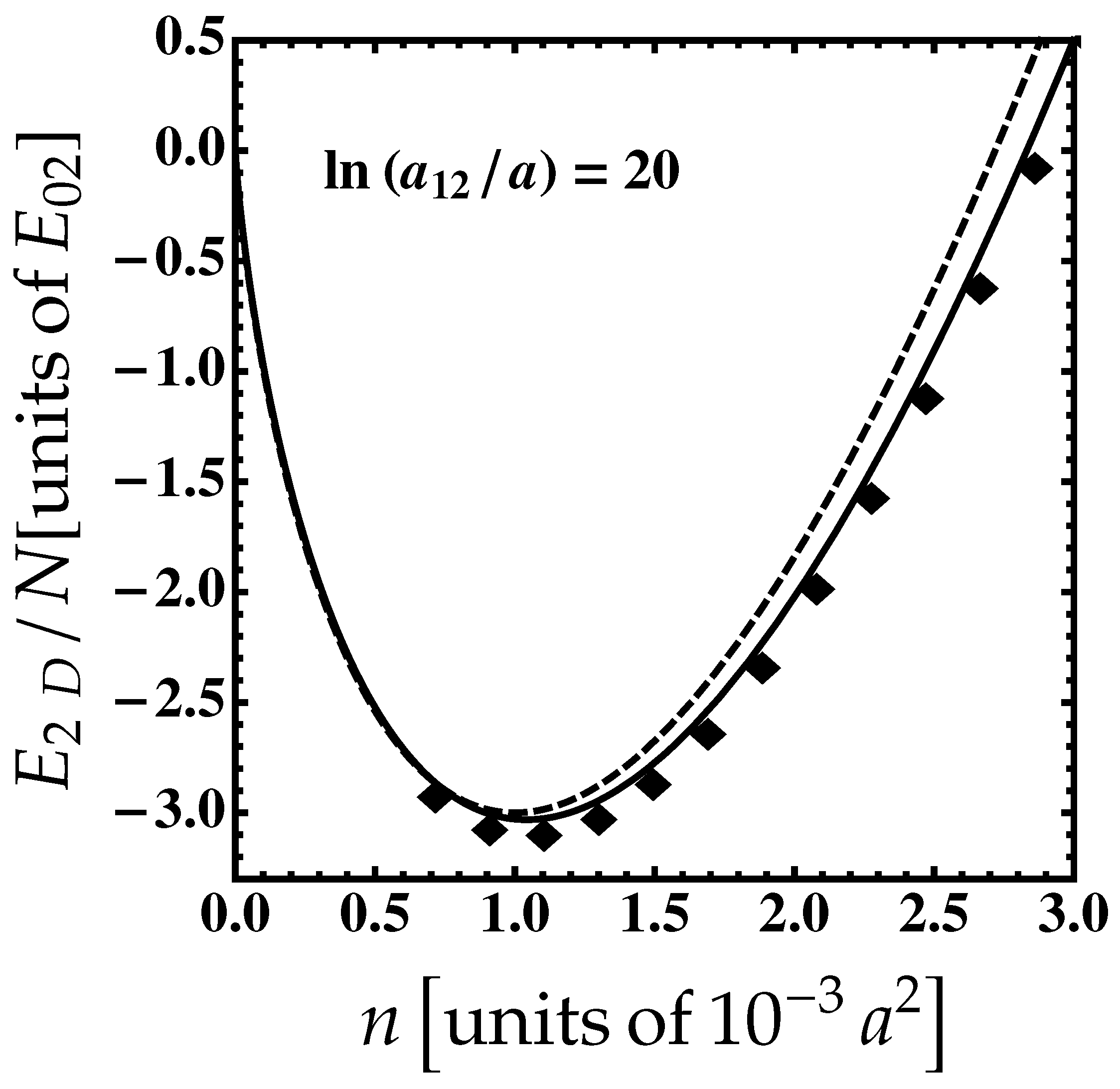
4. Two-Dimensional Droplets
5. One-Dimensional Droplets
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lee, T.D.; Huang, K.; Yang, C.N. Eigenvalues and Eigenfunctions of a Bose System of Hard Spheres and Its Low-Temperature Properties. Phys. Rev. 1957, 106, 1135. [Google Scholar] [CrossRef]
- Popov, V.N. Functional Integrals in Quantum Field Theory and Statistical Physics; D. Reidel: Dordrecht, The Netherlands, 1983. [Google Scholar]
- Pitaevskii, L.; Stringari, S. Elementary excitations in trapped Bose-Einstein condensed gases beyond the mean-field approximation. Phys. Rev. Lett. 1998, 81, 4541. [Google Scholar] [CrossRef] [Green Version]
- Braaten, E.; Pearson, J. Semiclassical corrections to the oscillation frequencies of a trapped Bose-Einstein condensate. Phys. Rev. Lett. 1999, 82, 255. [Google Scholar] [CrossRef] [Green Version]
- Astrakharchik, G.E.; Combescot, R.; Leyronas, X.; Stringari, S. Equation of state and collective frequencies of a trapped Fermi gas along the BEC-unitarity crossover. Phys. Rev. Lett. 2005, 95, 030404. [Google Scholar] [CrossRef] [Green Version]
- Boudjemâa, A. Behavior of the anomalous correlation function in a uniform two-dimensional Bose gas. Phys. Rev. A 2012, 86, 043608. [Google Scholar] [CrossRef] [Green Version]
- Lima, A.R.; Pelster, A. Beyond mean-field low-lying excitations of dipolar Bose gases. Phys. Rev. A 2012, 86, 063609. [Google Scholar] [CrossRef] [Green Version]
- Boudjemaa, A.; Shlyapnikov, G.V. Two-dimensional dipolar Bose gas with the roton-maxon excitation spectrum. Phys. Rev. A 2013, 87, 025601. [Google Scholar] [CrossRef] [Green Version]
- Boudjemâa, A. Theory of excitations of dipolar Bose—Einstein condensate at finite temperature. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 035302. [Google Scholar] [CrossRef]
- Boudjemâa, A. Properties of dipolar bosonic quantum gases at finite temperatures. J. Phys. A Math. Theor. 2016, 49, 285005. [Google Scholar] [CrossRef]
- Xu, K.; Liu, Y.; Miller, D.E.; Chin, J.; Setiawan, W.; Ketterle, W. Observation of strong quantum depletion in a gaseous Bose-Einstein condensate. Phys. Rev. Lett. 2006, 96, 180405. [Google Scholar] [CrossRef] [Green Version]
- Papp, S.B.; Pino, J.M.; Wild, R.J.; Ronen, S.; Wieman, C.E.; Jin, D.S.; Cornell, E.A. Bragg spectroscopy of a strongly interacting rb 85 bose-einstein condensate. Phys. Rev. Lett. 2008, 101, 135301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Altmeyer, A.; Riedl, S.; Kohstall, C.; Wright, M.J.; Geursen, R.; Bartenstein, M.; Chin, C.; Denschlag, J.H.; Grimm, R. Precision Measurements of Collective Oscillations in the BEC-BCS Crossover. Phys. Rev. Lett. 2007, 98, 040401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Navon, N.; Nascimbène, S.; Chevy, F.; Salomon, C. The equation of state of a low-temperature Fermi gas with tunable interactions. Science 2010, 328, 729–732. [Google Scholar] [CrossRef] [Green Version]
- Larsen, D.M. Binary mixtures of dilute bose gases with repulsive interactions at low temperature. Ann. Phys. 1963, 24, 89. [Google Scholar] [CrossRef]
- Tommasini, P.; de Passos, E.J.V.; de T. Piza, A.F.R.; Hussein, M.S. Bogoliubov theory for mutually coherent condensates. Phys. Rev. A 2003, 67, 023606. [Google Scholar] [CrossRef]
- Colson, W.B.; Fetter, A.L. Mixtures of Bose liquids at finite temperature. J. Low. Temp. Phys. 1978, 33, 231–242. [Google Scholar] [CrossRef]
- Boudjemâa, A. Quantum and thermal fluctuations in two-component Bose gases. Phys. Rev. A 2018, 97, 033627. [Google Scholar] [CrossRef] [Green Version]
- Ota, M.; Giorgini, S.; Stringari, S. Magnetic phase transition in a mixture of two interacting superfluid Bose gases at finite temperature. Phys. Rev. Lett. 2019, 123, 075301. [Google Scholar] [CrossRef] [Green Version]
- Petrov, D.S. Quantum mechanical stabilization of a collapsing Bose-Bose mixture. Phys. Rev. Lett. 2015, 115, 155302. [Google Scholar] [CrossRef] [Green Version]
- Petrov, D.S.; Astrakharchik, G.E. Ultradilute low-dimensional liquids. Phys. Rev. Lett. 2016, 117, 100401. [Google Scholar] [CrossRef] [Green Version]
- Ota, M.; Astrakharchik, G.E. Beyond Lee-Huang-Yang description of self-bound Bose mixtures. SciPost Phys. 2020, 9, 020. [Google Scholar] [CrossRef]
- Hu, H.; Wang, J.; Liu, X.-J. Microscopic pairing theory of a binary Bose mixture with interspecies attractions: Bosonic BEC-BCS crossover and ultradilute low-dimensional quantum droplets. Phys. Rev. A 2020, 102, 043301. [Google Scholar] [CrossRef]
- Guebli, N.; Boudjemâa, A. Quantum self-bound droplets in Bose-Bose mixtures: Effects of higher-order quantum and thermal fluctuations. Phys. Rev. A 2021, 104, 023310. [Google Scholar] [CrossRef]
- Boudjemâa, A. Many-body and temperature effects in two-dimensional quantum droplets in Bose-Bose mixtures. Sci. Rep. 2021, 11, 21765. [Google Scholar] [CrossRef] [PubMed]
- Kadau, H.; Schmitt, M.; Wenzel, M.; Wink, C.; Maier, T.; Ferrier-Barbut, I.; Pfau, T. Observing the Rosensweig instability of a quantum ferrofluid. Nature 2016, 530, 194–197. [Google Scholar] [CrossRef]
- Schmitt, M.; Wenzel, M.; Böttcher, F.; Ferrier-Barbut, I.; Pfau, T. Self-bound droplets of a dilute magnetic quantum liquid. Nature 2016, 539, 259–262. [Google Scholar] [CrossRef] [Green Version]
- Chomaz, L.; Baier, S.; Petter, D.; Mark, M.J.; Wächtler, F.; Santos, L.; Ferlaino, F. Quantum-fluctuation-driven crossover from a dilute Bose-Einstein condensate to a macrodroplet in a dipolar quantum fluid. Phys. Rev. X 2016, 6, 041039. [Google Scholar] [CrossRef]
- Boudjemâa, A. Fluctuations and quantum self-bound droplets in a dipolar Bose-Bose mixture. Phys. Rev. A 2018, 98, 033612. [Google Scholar] [CrossRef] [Green Version]
- Boudjemâa, A.; Guebli, N. Quantum correlations in dipolar droplets: Time-dependent Hartree-Fock-Bogoliubov theory. Phys. Rev. A 2020, 102, 023302. [Google Scholar] [CrossRef]
- Edler, D.; Mishra, C.; Wächtler, F.; Nath, R.; Sinha, S.; Santos, L. Quantum fluctuations in quasi-one-dimensional dipolar Bose-Einstein condensates. Phys. Rev. Lett. 2017, 119, 050403. [Google Scholar] [CrossRef] [Green Version]
- Boudjemâa, A. Two-dimensional quantum droplets in dipolar Bose gases. New J. Phys. 2019, 21, 093027. [Google Scholar] [CrossRef]
- Boudjemâa, A. Effects of the Lee-Huang-Yang quantum corrections on a disordered dipolar Bose gas. Eur. Phys. J. B 2019, 92, 145. [Google Scholar] [CrossRef]
- Nagler, B.; Radonjić, M.; Barbosa, S.; Koch, J.; Pelster, A.; Widera, A. Cloud shape of a molecular Bose—Einstein condensate in a disordered trap: A case study of the dirty boson problem. New J. Phys. 2020, 22, 033021. [Google Scholar] [CrossRef]
- Saito, H. Path-integral Monte Carlo study on a droplet of a dipolar Bose—Einstein condensate stabilized by quantum fluctuation. J. Phys. Soc. Jpn. 2016, 85, 053001. [Google Scholar] [CrossRef]
- Macia, A.; Sánchez-Baena, J.; Boronat, J.; Mazzanti, F. Droplets of trapped quantum dipolar bosons. Phys. Rev. Lett. 2016, 117, 205301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cikojevic, V.; Markic, L.V.; Astrakharchik, G.E.; Boronat, J. Universality in ultradilute liquid Bose-Bose mixtures. Phys. Rev. A 2019, 99, 023618. [Google Scholar] [CrossRef] [Green Version]
- Parisi, L.; Astrakharchik, G.E.; Giorgini, S. Liquid state of one-dimensional Bose mixtures: A quantum Monte Carlo study. Phys. Rev. Lett. 2019, 122, 105302. [Google Scholar] [CrossRef] [Green Version]
- Böttcher, F.; Wenzel, M.; Schmidt, J.-N.; Guo, M.; Langen, T.; Ferrier-Barbut, I.; Pfau, T.; Bombín, R.; Sánchez-Baena, J.; Boronat, J.; et al. Dilute dipolar quantum droplets beyond the extended Gross-Pitaevskii equation. Phys. Rev. Res. 2019, 1, 033088. [Google Scholar] [CrossRef] [Green Version]
- Cikojevic, V.; Markic, L.V.; Boronat, J. Finite-range effects in ultradilute quantum drops. New J. Phys. 2020, 22, 053045. [Google Scholar] [CrossRef] [Green Version]
- Cabrera, C.R.; Tanzi, L.; Sanz, J.; Naylor, B.; Thomas, P.; Cheiney, P.; Tarruell, L. Quantum liquid droplets in a mixture of Bose-Einstein condensates. Science 2018, 359, 301–304. [Google Scholar] [CrossRef] [Green Version]
- Cheiney, P.; Cabrera, C.R.; Sanz, J.; Naylor, B.; Tanzi, L.; Tarruell, L. Bright soliton to quantum droplet transition in a mixture of Bose-Einstein condensates. Phys. Rev. Lett. 2018, 120, 135301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Semeghini, G.; Ferioli, G.; Masi, L.; Mazzinghi, C.; Wolswijk, L.; Minardi, F.; Modugno, M.; Modugno, G.; Inguscio, M.; Fattori, M. Self-bound quantum droplets of atomic mixtures in free space. Phys. Rev. Lett. 2018, 120, 235301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- D’Errico, C.; Burchianti, A.; Prevedelli, M.; Salasnich, L.; Ancilotto, F.; Modugno, M.; Minardi, F.; Fort, C. Observation of quantum droplets in a heteronuclear bosonic mixture. Phys. Rev. Res. 2019, 1, 033155. [Google Scholar] [CrossRef] [Green Version]
- Hutchinson, D.A.W.; Dodd, R.J.; Burnett, K.; Morgan, S.A.; Rush, M.; Zaremba, E.; Proukakis, N.P.; Edwards, M.; Clark, C.W. Gapless mean-field theory of Bose-Einstein condensates. J. Phys. B 2000, 33, 3825. [Google Scholar] [CrossRef] [Green Version]
- Griffin, A.; Shi, H. Finite-temperature excitations in a dilute Bose-condensed gas. Phys. Rep. 1998, 304, 1–87. [Google Scholar]
- Berezinskii, V.L. Destruction of long-range order in one-dimensional and two-dimensional systems possessing a continuous symmetry group. II. Quantum systems. Sov. Phys. JETP 1972, 34, 610–616. [Google Scholar]
- Kosterlitz, J.M.; Thouless, D.J. Ordering, metastability and phase transitions in two-dimensional systems. J. Phys. C 1973, 6, 1181. [Google Scholar] [CrossRef]
- Roy, A.; Ota, M.; Recati, A.; Dalfovo, F. Finite-temperature spin dynamics of a two-dimensional Bose-Bose atomic mixture. Phys. Rev. Res. 2021, 3, 013161. [Google Scholar] [CrossRef]
- De Rosi, G.; Astrakharchik, G.E.; Stringari, S. Thermodynamic behavior of a one-dimensional Bose gas at low temperature. Phys. Rev. A 2017, 96, 013613. [Google Scholar] [CrossRef] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boudjemaa, A.; Abbas, K.; Guebli, N. Ultradilute Quantum Droplets in the Presence of Higher-Order Quantum Fluctuations. Atoms 2022, 10, 64. https://doi.org/10.3390/atoms10020064
Boudjemaa A, Abbas K, Guebli N. Ultradilute Quantum Droplets in the Presence of Higher-Order Quantum Fluctuations. Atoms. 2022; 10(2):64. https://doi.org/10.3390/atoms10020064
Chicago/Turabian StyleBoudjemaa, Abdelaali, Karima Abbas, and Nadia Guebli. 2022. "Ultradilute Quantum Droplets in the Presence of Higher-Order Quantum Fluctuations" Atoms 10, no. 2: 64. https://doi.org/10.3390/atoms10020064
APA StyleBoudjemaa, A., Abbas, K., & Guebli, N. (2022). Ultradilute Quantum Droplets in the Presence of Higher-Order Quantum Fluctuations. Atoms, 10(2), 64. https://doi.org/10.3390/atoms10020064




