Repulsive Fermi and Bose Polarons in Quantum Gases
Abstract
1. Introduction
2. Fermi and Bose Polarons
2.1. Theoretical Description
2.2. Quasiparticle Properties
2.2.1. Limit of Weak Interactions
2.2.2. Strong-Coupling Polarons
3. Experimental Probes
4. Repulsive Quasiparticle Stability
4.1. Variational Description of Attractive and Repulsive Polarons
4.2. The Case of an Infinitely Heavy Impurity
5. Beyond the Impurity Limit: Induced Interactions and Instabilities
5.1. Polaron-Polaron Induced Interactions
5.1.1. Bosonic Impurities in a Fermi Sea
5.1.2. Fermionic Impurities in a Fermi Sea
- There is no direct interaction between identical fermionic impurities (i.e., ).
- Pauli pressure dictates that impurities form their own Fermi sea, with Fermi energy . The corresponding contribution to the energy density can be sizable, and this indeed permitted a direct measurement of the effective mass of the polarons via injection RF spectroscopy in Ref. [23].
- Correspondingly, final states available to the interacting impurities are “Pauli blocked”, rather than “Bose enhanced”, so that in the numerator of Equation (28) one needs to replace by , where is now a Fermi distribution function. As a consequence, the functional derivative with respect to the distribution functions of the minority particles in Equation (29) leads to an overall sign change in the exchange interaction term for fermionic impurities, which ultimately becomes repulsive and reads:
5.1.3. Bosonic Media
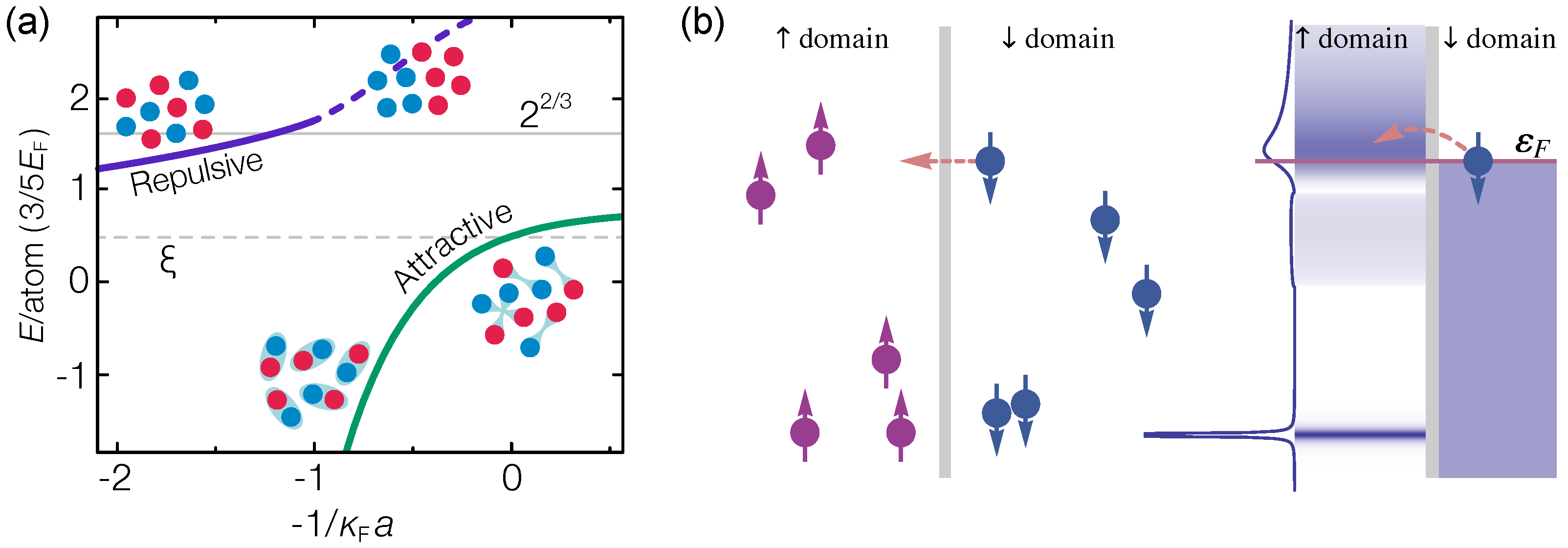
5.2. Ferromagnetic and Pairing Instabilities in Fermi–Fermi Mixtures
6. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | More generally, the s-wave scattering amplitude takes the form in terms of the two-body scattering phase shift . For a low-energy collision at relative momentum k, this may be expanded as , where a is the scattering length and is the effective range. A Feshbach resonance is classified as narrow if the effective range plays a relevant role (e.g., if in a many-body problem), while it is termed broad when this may be safely neglected. Broad resonances are accurately described by the single-channel Hamiltonian introduced in this section, while to investigate narrow resonances one needs to employ a more sophisticated two-channel model [3,61]. |
| 2 | Since the derivative of energy with respect to the Bose-Bose scattering length acts on the impurity energy, this term necessarily involves the impurity and two bosons. |
| 3 | We follow here the sign convention used in Ref. [120], but note that other sources define the Lindhard function with the opposite sign. |
References
- Mahan, G. Many-Particle Physics; Kluwer Academic/Plenum Publishers: New York, NY, USA, 2000. [Google Scholar]
- Chevy, F.; Mora, C. Ultra-cold polarized Fermi gases. Rep. Progr. Phys. 2010, 73, 112401. [Google Scholar] [CrossRef]
- Massignan, P.; Zaccanti, M.; Bruun, G.M. Polarons, dressed molecules and itinerant ferromagnetism in ultracold Fermi gases. Rep. Progr. Phys. 2014, 77, 034401. [Google Scholar] [CrossRef]
- Levinsen, J.; Parish, M.M. Strongly interacting two-dimensional Fermi gases. Annu. Rev. Cold Atoms Mol. 2015, 3, 1–75. [Google Scholar]
- Bardeen, J.; Baym, G.; Pines, D. Effective Interaction of 3He Atoms in Dilute Solutions of 3He in 4He at Low Temperatures. Phys. Rev. 1967, 156, 207–221. [Google Scholar] [CrossRef]
- Lemeshko, M.; Schmidt, R. Molecular Impurities Interacting with a Many-particle Environment: From Ultracold Gases to Helium Nanodroplets. In Cold Chemistry: Molecular Scattering and Reactivity Near Absolute Zero; Royal Society of Chemistry: London, UK, 2018; pp. 444–495. [Google Scholar] [CrossRef]
- Landau, L.D.; Pekar, S.I. Effective mass of a polaron. Zh. Eksp. Teor. Fiz. 1948, 18, 419. [Google Scholar]
- Fröhlich, H. Electrons in lattice fields. Adv. Phys. 1954, 3, 325–361. [Google Scholar] [CrossRef]
- Feynman, R.P. Slow Electrons in a Polar Crystal. Phys. Rev. 1955, 97, 660–665. [Google Scholar] [CrossRef]
- Alexandrov, A.S.; Devreese, J.T. Advances in Polaron Physics; Springer: Berlin, Germany, 2010; Volume 159. [Google Scholar]
- Klimov, V.V. Spectrum of Elementary Fermi Excitations in Quark Gluon Plasma. Sov. J. Nucl. Phys. 1981, 33, 934–935. [Google Scholar]
- Weldon, H.A. Dynamical holes in the quark-gluon plasma. Phys. Rev. D 1989, 40, 2410–2420. [Google Scholar] [CrossRef]
- Nakano, E.; Iida, K.; Horiuchi, W. Quasiparticle properties of a single α particle in cold neutron matter. Phys. Rev. C 2020, 102, 055802. [Google Scholar] [CrossRef]
- Schirotzek, A.; Wu, C.H.; Sommer, A.; Zwierlein, M.W. Observation of Fermi Polarons in a Tunable Fermi Liquid of Ultracold Atoms. Phys. Rev. Lett. 2009, 102, 230402. [Google Scholar] [CrossRef] [PubMed]
- Nascimbène, S.; Navon, N.; Jiang, K.J.; Tarruell, L.; Teichmann, M.; McKeever, J.; Chevy, F.; Salomon, C. Collective Oscillations of an Imbalanced Fermi Gas: Axial Compression Modes and Polaron Effective Mass. Phys. Rev. Lett. 2009, 103, 170402. [Google Scholar] [CrossRef] [PubMed]
- Kohstall, C.; Zaccanti, M.; Jag, M.; Trenkwalder, A.; Massignan, P.; Bruun, G.M.; Schreck, F.; Grimm, R. Metastability and coherence of repulsive polarons in a strongly interacting Fermi mixture. Nature 2012, 485, 615–618. [Google Scholar] [CrossRef] [PubMed]
- Koschorreck, M.; Pertot, D.; Vogt, E.; Fröhlich, B.; Feld, M.; Köhl, M. Attractive and repulsive Fermi polarons in two dimensions. Nature 2012, 485, 619–622. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Ong, W.; Arakelyan, I.; Thomas, J.E. Polaron-to-Polaron Transitions in the Radio-Frequency Spectrum of a Quasi-Two-Dimensional Fermi Gas. Phys. Rev. Lett. 2012, 108, 235302. [Google Scholar] [CrossRef]
- Wenz, A.N.; Zürn, G.; Murmann, S.; Brouzos, I.; Lompe, T.; Jochim, S. From Few to Many: Observing the Formation of a Fermi Sea One Atom at a Time. Science 2013, 342, 457–460. [Google Scholar] [CrossRef] [PubMed]
- Ong, W.; Cheng, C.; Arakelyan, I.; Thomas, J.E. Spin-Imbalanced Quasi-Two-Dimensional Fermi Gases. Phys. Rev. Lett. 2015, 114, 110403. [Google Scholar] [CrossRef]
- Cetina, M.; Jag, M.; Lous, R.S.; Walraven, J.T.M.; Grimm, R.; Christensen, R.S.; Bruun, G.M. Decoherence of Impurities in a Fermi Sea of Ultracold Atoms. Phys. Rev. Lett. 2015, 115, 135302. [Google Scholar] [CrossRef]
- Cetina, M.; Jag, M.; Lous, R.S.; Fritsche, I.; Walraven, J.T.M.; Grimm, R.; Levinsen, J.; Parish, M.M.; Schmidt, R.; Knap, M.; et al. Ultrafast many-body interferometry of impurities coupled to a Fermi sea. Science 2016, 354, 96–99. [Google Scholar] [CrossRef]
- Scazza, F.; Valtolina, G.; Massignan, P.; Recati, A.; Amico, A.; Burchianti, A.; Fort, C.; Inguscio, M.; Zaccanti, M.; Roati, G. Repulsive Fermi Polarons in a Resonant Mixture of Ultracold 6Li Atoms. Phys. Rev. Lett. 2017, 118, 083602. [Google Scholar] [CrossRef]
- Mukherjee, B.; Yan, Z.; Patel, P.B.; Hadzibabic, Z.; Yefsah, T.; Struck, J.; Zwierlein, M.W. Homogeneous Atomic Fermi Gases. Phys. Rev. Lett. 2017, 118, 123401. [Google Scholar] [CrossRef] [PubMed]
- Yan, Z.; Patel, P.B.; Mukherjee, B.; Fletcher, R.J.; Struck, J.; Zwierlein, M.W. Boiling a Unitary Fermi Liquid. Phys. Rev. Lett. 2019, 122, 093401. [Google Scholar] [CrossRef] [PubMed]
- Darkwah Oppong, N.; Riegger, L.; Bettermann, O.; Höfer, M.; Levinsen, J.; Parish, M.M.; Bloch, I.; Fölling, S. Observation of Coherent Multiorbital Polarons in a Two-Dimensional Fermi Gas. Phys. Rev. Lett. 2019, 122, 193604. [Google Scholar] [CrossRef]
- Ness, G.; Shkedrov, C.; Florshaim, Y.; Diessel, O.K.; von Milczewski, J.; Schmidt, R.; Sagi, Y. Observation of a Smooth Polaron-Molecule Transition in a Degenerate Fermi Gas. Phys. Rev. X 2020, 10, 041019. [Google Scholar] [CrossRef]
- Adlong, H.S.; Liu, W.E.; Scazza, F.; Zaccanti, M.; Oppong, N.D.; Fölling, S.; Parish, M.M.; Levinsen, J. Quasiparticle Lifetime of the Repulsive Fermi Polaron. Phys. Rev. Lett. 2020, 125, 133401. [Google Scholar] [CrossRef]
- Fritsche, I.; Baroni, C.; Dobler, E.; Kirilov, E.; Huang, B.; Grimm, R.; Bruun, G.M.; Massignan, P. Stability and breakdown of Fermi polarons in a strongly interacting Fermi-Bose mixture. Phys. Rev. A 2021, 103, 053314. [Google Scholar] [CrossRef]
- Sidler, M.; Back, P.; Cotlet, O.; Srivastava, A.; Fink, T.; Kroner, M.; Demler, E.; Imamoglu, A. Fermi polaron-polaritons in charge-tunable atomically thin semiconductors. Nat. Phys. 2017, 13, 255–261. [Google Scholar] [CrossRef]
- Wang, G.; Chernikov, A.; Glazov, M.M.; Heinz, T.F.; Marie, X.; Amand, T.; Urbaszek, B. Colloquium: Excitons in atomically thin transition metal dichalcogenides. Rev. Mod. Phys. 2018, 90, 021001. [Google Scholar] [CrossRef]
- Bastarrachea-Magnani, M.A.; Thomsen, J.; Camacho-Guardian, A.; Bruun, G.M. Polaritons in an Electron Gas—Quasiparticles and Landau Effective Interactions. Atoms 2021, 9, 81. [Google Scholar] [CrossRef]
- Catani, J.; Lamporesi, G.; Naik, D.; Gring, M.; Inguscio, M.; Minardi, F.; Kantian, A.; Giamarchi, T. Quantum dynamics of impurities in a one-dimensional Bose gas. Phys. Rev. A 2012, 85, 023623. [Google Scholar] [CrossRef]
- Hu, M.G.; Van de Graaff, M.J.; Kedar, D.; Corson, J.P.; Cornell, E.A.; Jin, D.S. Bose Polarons in the Strongly Interacting Regime. Phys. Rev. Lett. 2016, 117, 055301. [Google Scholar] [CrossRef] [PubMed]
- Jørgensen, N.B.; Wacker, L.; Skalmstang, K.T.; Parish, M.M.; Levinsen, J.; Christensen, R.S.; Bruun, G.M.; Arlt, J.J. Observation of Attractive and Repulsive Polarons in a Bose-Einstein Condensate. Phys. Rev. Lett. 2016, 117, 055302. [Google Scholar] [CrossRef] [PubMed]
- Yan, Z.Z.; Ni, Y.; Robens, C.; Zwierlein, M.W. Bose polarons near quantum criticality. Science 2020, 368, 190–194. [Google Scholar] [CrossRef] [PubMed]
- Skou, M.G.; Skov, T.G.; Jørgensen, N.B.; Nielsen, K.K.; Camacho-Guardian, A.; Pohl, T.; Bruun, G.M.; Arlt, J.J. Non-equilibrium quantum dynamics and formation of the Bose polaron. Nat. Phys. 2021, 17, 731–735. [Google Scholar] [CrossRef]
- Peña Ardila, L.A.; Jørgensen, N.B.; Pohl, T.; Giorgini, S.; Bruun, G.M.; Arlt, J.J. Analyzing a Bose polaron across resonant interactions. Phys. Rev. A 2019, 99, 063607. [Google Scholar] [CrossRef]
- Palzer, S.; Zipkes, C.; Sias, C.; Köhl, M. Quantum Transport through a Tonks-Girardeau Gas. Phys. Rev. Lett. 2009, 103, 150601. [Google Scholar] [CrossRef] [PubMed]
- Meinert, F.; Knap, M.; Kirilov, E.; Jag-Lauber, K.; Zvonarev, M.B.; Demler, E.; Nägerl, H.C. Bloch oscillations in the absence of a lattice. Science 2017, 356, 945–948. [Google Scholar] [CrossRef] [PubMed]
- Chin, C.; Grimm, R.; Julienne, P.; Tiesinga, E. Feshbach resonances in ultracold gases. Rev. Mod. Phys. 2010, 82, 1225–1286. [Google Scholar] [CrossRef]
- Torma, P. Physics of ultracold Fermi gases revealed by spectroscopies. Phys. Scr. 2016, 91, 043006. [Google Scholar] [CrossRef]
- Vale, C.J.; Zwierlein, M. Spectroscopic probes of quantum gases. Nat. Phys. 2021, 17, 1305–1315. [Google Scholar] [CrossRef]
- Combescot, R.; Giraud, S. Normal State of Highly Polarized Fermi Gases: Full Many-Body Treatment. Phys. Rev. Lett. 2008, 101, 050404. [Google Scholar] [CrossRef]
- Van Houcke, K.; Werner, F.; Rossi, R. High-precision numerical solution of the Fermi polaron problem and large-order behavior of its diagrammatic series. Phys. Rev. B 2020, 101, 045134. [Google Scholar] [CrossRef]
- Liu, W.E.; Levinsen, J.; Parish, M.M. Variational Approach for Impurity Dynamics at Finite Temperature. Phys. Rev. Lett. 2019, 122, 205301. [Google Scholar] [CrossRef] [PubMed]
- Parish, M.M.; Marchetti, F.M.; Lamacraft, A.; Simons, B.D. Finite-temperature phase diagram of a polarized Fermi condensate. Nat. Phys. 2007, 3, 124–128. [Google Scholar] [CrossRef]
- Stoner, E. Atomic moments in ferromagnetic metals and alloys with non-ferromagnetic elements. Philos. Mag. 1933, 15, 1018–1034. [Google Scholar] [CrossRef]
- Pilati, S.; Bertaina, G.; Giorgini, S.; Troyer, M. Itinerant Ferromagnetism of a Repulsive Atomic Fermi Gas: A Quantum Monte Carlo Study. Phys. Rev. Lett. 2010, 105, 030405. [Google Scholar] [CrossRef]
- Chang, S.Y.; Randeria, M.; Trivedi, N. Ferromagnetism in the upper branch of the Feshbach resonance and the hard-sphere Fermi gas. Proc. Nat. Acad. Sci. USA 2011, 108, 51–54. [Google Scholar] [CrossRef]
- Goulko, O.; Mishchenko, A.S.; Prokof’ev, N.; Svistunov, B. Dark continuum in the spectral function of the resonant Fermi polaron. Phys. Rev. A 2016, 94, 051605. [Google Scholar] [CrossRef]
- Goold, J.; Fogarty, T.; Lo Gullo, N.; Paternostro, M.; Busch, T. Orthogonality catastrophe as a consequence of qubit embedding in an ultracold Fermi gas. Phys. Rev. A 2011, 84, 063632. [Google Scholar] [CrossRef]
- Knap, M.; Shashi, A.; Nishida, Y.; Imambekov, A.; Abanin, D.A.; Demler, E. Time-Dependent Impurity in Ultracold Fermions: Orthogonality Catastrophe and Beyond. Phys. Rev. X 2012, 2, 041020. [Google Scholar] [CrossRef]
- Parish, M.M.; Levinsen, J. Quantum dynamics of impurities coupled to a Fermi sea. Phys. Rev. B 2016, 94, 184303. [Google Scholar] [CrossRef]
- Schmidt, R.; Knap, M.; Ivanov, D.A.; You, J.S.; Cetina, M.; Demler, E. Universal many-body response of heavy impurities coupled to a Fermi sea: A review of recent progress. Rep. Progr. Phys. 2018, 81, 024401. [Google Scholar] [CrossRef] [PubMed]
- Amico, A.; Scazza, F.; Valtolina, G.; Tavares, P.E.S.; Ketterle, W.; Inguscio, M.; Roati, G.; Zaccanti, M. Time-Resolved Observation of Competing Attractive and Repulsive Short-Range Correlations in Strongly Interacting Fermi Gases. Phys. Rev. Lett. 2018, 121, 253602. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.M.; Terças, H.; Mendonça, J.T.; Wehr, J.; Charalambous, C.; Lewenstein, M.; Garcia-March, M.A. Quantum dynamics of a Bose polaron in a d-dimensional Bose-Einstein condensate. Phys. Rev. A 2021, 103, 023303. [Google Scholar] [CrossRef]
- Seetharam, K.; Shchadilova, Y.; Grusdt, F.; Zvonarev, M.B.; Demler, E. Dynamical Quantum Cherenkov Transition of Fast Impurities in Quantum Liquids. Phys. Rev. Lett. 2021, 127, 185302. [Google Scholar] [CrossRef]
- Prokof’ev, N.; Svistunov, B. Fermi-polaron problem: Diagrammatic Monte Carlo method for divergent sign-alternating series. Phys. Rev. B 2008, 77, 020408. [Google Scholar] [CrossRef]
- Mistakidis, S.I.; Volosniev, A.G.; Barfknecht, R.E.; Fogarty, T.; Busch, T.; Foerster, A.; Schmelcher, P.; Zinner, N.T. Cold atoms in low dimensions—A laboratory for quantum dynamics. arXiv 2022, arXiv:2202.11071. [Google Scholar]
- Timmermans, E.; Tommasini, P.; Hussein, M.; Kerman, A. Feshbach resonances in atomic Bose–Einstein condensates. Phys. Rep. 1999, 315, 199–230. [Google Scholar] [CrossRef]
- Sakurai, J.J.; Tuan, S.F. Modern Quantum Mechanics; Addison-Wesley Reading: Boston, MA, USA, 1985. [Google Scholar]
- Fetter, A.L.; Walecka, J.D. Quantum Theory of Many-Particle Systems; Dover: New York, NY, USA, 2003. [Google Scholar]
- Tan, S. Energetics of a strongly correlated Fermi gas. Ann. Phys. 2008, 323, 2952–2970. [Google Scholar] [CrossRef]
- Tan, S. Large momentum part of a strongly correlated Fermi gas. Ann. Phys. 2008, 323, 2971–2986. [Google Scholar] [CrossRef]
- Braaten, E.; Platter, L. Exact Relations for a Strongly Interacting Fermi Gas from the Operator Product Expansion. Phys. Rev. Lett. 2008, 100, 205301. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.E.; Shi, Z.Y.; Levinsen, J.; Parish, M.M. Radio-Frequency Response and Contact of Impurities in a Quantum Gas. Phys. Rev. Lett. 2020, 125, 065301. [Google Scholar] [CrossRef] [PubMed]
- Massignan, P.; Pethick, C.J.; Smith, H. Static properties of positive ions in atomic Bose-Einstein condensates. Phys. Rev. A 2005, 71, 023606. [Google Scholar] [CrossRef]
- Werner, F. Virial theorems for trapped cold atoms. Phys. Rev. A 2008, 78, 025601. [Google Scholar] [CrossRef]
- Massignan, P. Polarons and dressed molecules near narrow Feshbach resonances. Europhys. Lett. 2012, 98, 10012. [Google Scholar] [CrossRef][Green Version]
- Braaten, E.; Kang, D.; Platter, L. Universal Relations for Identical Bosons from Three-Body Physics. Phys. Rev. Lett. 2011, 106, 153005. [Google Scholar] [CrossRef]
- Bishop, R. On the ground state of an impurity in a dilute fermi gas. Ann. Phys. 1973, 78, 391. [Google Scholar] [CrossRef]
- Novikov, A.; Ovchinnikov, M. A diagrammatic calculation of the energy spectrum of quantum impurity in degenerate Bose–Einstein condensate. J. Phys. Math. Theor. 2009, 42, 135301. [Google Scholar] [CrossRef]
- Christensen, R.S.; Levinsen, J.; Bruun, G.M. Quasiparticle Properties of a Mobile Impurity in a Bose-Einstein Condensate. Phys. Rev. Lett. 2015, 115, 160401. [Google Scholar] [CrossRef]
- Trefzger, C.; Castin, Y. Polaron residue and spatial structure in a Fermi gas. EPL 2013, 101, 30006. [Google Scholar] [CrossRef][Green Version]
- Casteels, W.; Wouters, M. Polaron formation in the vicinity of a narrow Feshbach resonance. Phys. Rev. A 2014, 90, 043602. [Google Scholar] [CrossRef]
- Massignan, P.; Bruun, G.M. Repulsive polarons and itinerant ferromagnetism in strongly polarized Fermi gases. EPJ D 2011, 65, 83–89. [Google Scholar] [CrossRef]
- Cui, X.; Zhai, H. Stability of a fully magnetized ferromagnetic state in repulsively interacting ultracold Fermi gases. Phys. Rev. A 2010, 81, 041602. [Google Scholar] [CrossRef]
- Tajima, H.; Uchino, S. Many Fermi polarons at nonzero temperature. New J. Phys. 2018, 20, 073048. [Google Scholar] [CrossRef]
- Mulkerin, B.C.; Liu, X.J.; Hu, H. Breakdown of the Fermi polaron description near Fermi degeneracy at unitarity. Ann. Phys. 2019, 407, 29–45. [Google Scholar] [CrossRef]
- Tajima, H.; Takahashi, J.; Mistakidis, S.I.; Nakano, E.; Iida, K. Polaron Problems in Ultracold Atoms: Role of a Fermi Sea across Different Spatial Dimensions and Quantum Fluctuations of a Bose Medium. Atoms 2021, 9, 18. [Google Scholar] [CrossRef]
- Hu, H.; Liu, X.J. Fermi polarons at finite temperature: Spectral function and rf spectroscopy. Phys. Rev. A 2022, 105, 043303. [Google Scholar] [CrossRef]
- Schmidt, R.; Enss, T. Excitation spectra and rf response near the polaron-to-molecule transition from the functional renormalization group. Phys. Rev. A 2011, 83, 063620. [Google Scholar] [CrossRef]
- Rath, S.P.; Schmidt, R. Field-theoretical study of the Bose polaron. Phys. Rev. A 2013, 88, 053632. [Google Scholar] [CrossRef]
- Guenther, N.E.; Massignan, P.; Lewenstein, M.; Bruun, G.M. Bose Polarons at Finite Temperature and Strong Coupling. Phys. Rev. Lett. 2018, 120, 050405. [Google Scholar] [CrossRef]
- Li, W.; Das Sarma, S. Variational study of polarons in Bose-Einstein condensates. Phys. Rev. A 2014, 90, 013618. [Google Scholar] [CrossRef]
- Shchadilova, Y.E.; Schmidt, R.; Grusdt, F.; Demler, E. Quantum Dynamics of Ultracold Bose Polarons. Phys. Rev. Lett. 2016, 117, 113002. [Google Scholar] [CrossRef] [PubMed]
- Field, B.; Levinsen, J.; Parish, M.M. Fate of the Bose polaron at finite temperature. Phys. Rev. A 2020, 101, 013623. [Google Scholar] [CrossRef]
- Peña Ardila, L.A.; Giorgini, S. Impurity in a Bose-Einstein condensate: Study of the attractive and repulsive branch using quantum Monte Carlo methods. Phys. Rev. A 2015, 92, 033612. [Google Scholar] [CrossRef]
- Peña Ardila, L.A.; Astrakharchik, G.E.; Giorgini, S. Strong coupling Bose polarons in a two-dimensional gas. Phys. Rev. Research 2020, 2, 023405. [Google Scholar] [CrossRef]
- Sun, M.; Zhai, H.; Cui, X. Visualizing the Efimov Correlation in Bose Polarons. Phys. Rev. Lett. 2017, 119, 013401. [Google Scholar] [CrossRef]
- Grusdt, F.; Seetharam, K.; Shchadilova, Y.; Demler, E. Strong-coupling Bose polarons out of equilibrium: Dynamical renormalization-group approach. Phys. Rev. A 2018, 97, 033612. [Google Scholar] [CrossRef]
- Isaule, F.; Morera, I.; Massignan, P.; Juliá-Díaz, B. Renormalization-group study of Bose polarons. Phys. Rev. A 2021, 104, 023317. [Google Scholar] [CrossRef]
- Punk, M.; Zwerger, W. Theory of rf-Spectroscopy of Strongly Interacting Fermions. Phys. Rev. Lett. 2007, 99, 170404. [Google Scholar] [CrossRef] [PubMed]
- Massignan, P.; Bruun, G.M.; Stoof, H.T.C. Twin peaks in rf spectra of Fermi gases at unitarity. Phys. Rev. A 2008, 77, 031601. [Google Scholar] [CrossRef]
- Scazza, F.; Hofrichter, C.; Höfer, M.; De Groot, P.C.; Bloch, I.; Fölling, S. Observation of two-orbital spin-exchange interactions with ultracold SU(N)-symmetric fermions. Nat. Phys. 2014, 10, 779. [Google Scholar] [CrossRef]
- Höfer, M.; Riegger, L.; Scazza, F.; Hofrichter, C.; Fernandes, D.R.; Parish, M.M.; Levinsen, J.; Bloch, I.; Fölling, S. Observation of an Orbital Interaction-Induced Feshbach Resonance in 173Yb. Phys. Rev. Lett. 2015, 115, 265302. [Google Scholar] [CrossRef]
- Liu, W.E.; Shi, Z.Y.; Parish, M.M.; Levinsen, J. Theory of radio-frequency spectroscopy of impurities in quantum gases. Phys. Rev. A 2020, 102, 023304. [Google Scholar] [CrossRef]
- Braaten, E.; Kang, D.; Platter, L. Short-Time Operator Product Expansion for rf Spectroscopy of a Strongly Interacting Fermi Gas. Phys. Rev. Lett. 2010, 104, 223004. [Google Scholar] [CrossRef] [PubMed]
- Guenther, N.E.; Schmidt, R.; Bruun, G.M.; Gurarie, V.; Massignan, P. Mobile impurity in a Bose-Einstein condensate and the orthogonality catastrophe. Phys. Rev. A 2021, 103, 013317. [Google Scholar] [CrossRef]
- Punk, M.; Dumitrescu, P.T.; Zwerger, W. Polaron-to-molecule transition in a strongly imbalanced Fermi gas. Phys. Rev. A 2009, 80, 053605. [Google Scholar] [CrossRef]
- Combescot, R.; Giraud, S.; Leyronas, X. Analytical theory of the dressed bound state in highly polarized Fermi gases. Europhys. Lett. 2009, 88, 60007. [Google Scholar] [CrossRef]
- Bruun, G.M.; Recati, A.; Pethick, C.J.; Smith, H.; Stringari, S. Collisional Properties of a Polarized Fermi Gas with Resonant Interactions. Phys. Rev. Lett. 2008, 100, 240406. [Google Scholar] [CrossRef]
- Trefzger, C.; Castin, Y. Impurity in a Fermi sea on a narrow Feshbach resonance: A variational study of the polaronic and dimeronic branches. Phys. Rev. A 2012, 85, 053612. [Google Scholar] [CrossRef]
- Petrov, D.S. Three-body problem in Fermi gases with short-range interparticle interaction. Phys. Rev. A 2003, 67, 010703. [Google Scholar] [CrossRef]
- Sanner, C.; Su, E.J.; Huang, W.; Keshet, A.; Gillen, J.; Ketterle, W. Correlations and Pair Formation in a Repulsively Interacting Fermi Gas. Phys. Rev. Lett. 2012, 108, 240404. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.Y.; Duda, M.; Schindewolf, A.; Bause, R.; Bloch, I.; Luo, X.Y. Suppression of Unitary Three-Body Loss in a Degenerate Bose–Fermi Mixture. Phys. Rev. Lett. 2022, 128, 153401. [Google Scholar] [CrossRef]
- Braaten, E.; Hammer, H.W. Universality in few-body systems with large scattering length. Phys. Rep. 2006, 428, 259–390. [Google Scholar] [CrossRef]
- Chevy, F. Universal phase diagram of a strongly interacting Fermi gas with unbalanced spin populations. Phys. Rev. A 2006, 74, 063628. [Google Scholar] [CrossRef]
- Combescot, R.; Recati, A.; Lobo, C.; Chevy, F. Normal State of Highly Polarized Fermi Gases: Simple Many-Body Approaches. Phys. Rev. Lett. 2007, 98, 180402. [Google Scholar] [CrossRef] [PubMed]
- Pines, D.; Noziéres, P. Theory of Quantum Liquids: Normal Fermi Liquids; Addison-Wesley: New York, NY, USA, 1966. [Google Scholar]
- Anderson, P.W. Infrared Catastrophe in Fermi Gases with Local Scattering Potentials. Phys. Rev. Lett. 1967, 18, 1049. [Google Scholar] [CrossRef]
- Drescher, M.; Salmhofer, M.; Enss, T. Quench Dynamics of the Ideal Bose Polaron at Zero and Nonzero Temperatures. Phys. Rev. A 2021, 103, 033317. [Google Scholar] [CrossRef]
- Yoshida, S.M.; Endo, S.; Levinsen, J.; Parish, M.M. Universality of an Impurity in a Bose-Einstein Condensate. Phys. Rev. X 2018, 8, 011024. [Google Scholar] [CrossRef]
- Mistakidis, S.I.; Katsimiga, G.C.; Koutentakis, G.M.; Busch, T.; Schmelcher, P. Quench Dynamics and Orthogonality Catastrophe of Bose Polarons. Phys. Rev. Lett. 2019, 122, 183001. [Google Scholar] [CrossRef]
- Levinsen, J.; Ardila, L.A.P.n.; Yoshida, S.M.; Parish, M.M. Quantum Behavior of a Heavy Impurity Strongly Coupled to a Bose Gas. Phys. Rev. Lett. 2021, 127, 033401. [Google Scholar] [CrossRef]
- Viverit, L.; Pethick, C.J.; Smith, H. Zero-temperature phase diagram of binary boson-fermion mixtures. Phys. Rev. A 2000, 61, 053605. [Google Scholar] [CrossRef]
- Yu, Z.; Zöllner, S.; Pethick, C.J. Comment on “Normal Phase of an Imbalanced Fermi Gas”. Phys. Rev. Lett. 2010, 105, 188901. [Google Scholar] [CrossRef] [PubMed]
- Yu, Z.; Pethick, C.J. Induced interactions in dilute atomic gases and liquid helium mixtures. Phys. Rev. A 2012, 85, 063616. [Google Scholar] [CrossRef]
- Pethick, C.; Smith, H. Bose–Einstein Condensation in Dilute Gases; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- DeSalvo, B.J.; Patel, K.; Cai, G.; Chin, C. Observation of fermion-mediated interactions between bosonic atoms. Nature 2019, 568, 61–64. [Google Scholar] [CrossRef] [PubMed]
- Lous, R.S.; Fritsche, I.; Jag, M.; Lehmann, F.; Kirilov, E.; Huang, B.; Grimm, R. Probing the Interface of a Phase-Separated State in a Repulsive Bose–Fermi Mixture. Phys. Rev. Lett. 2018, 120, 243403. [Google Scholar] [CrossRef] [PubMed]
- Huang, B.; Fritsche, I.; Lous, R.S.; Baroni, C.; Walraven, J.T.M.; Kirilov, E.; Grimm, R. Breathing mode of a Bose-Einstein condensate repulsively interacting with a fermionic reservoir. Phys. Rev. A 2019, 99, 041602. [Google Scholar] [CrossRef]
- Mora, C.; Chevy, F. Normal Phase of an Imbalanced Fermi Gas. Phys. Rev. Lett. 2010, 104, 230402. [Google Scholar] [CrossRef]
- Nascimbène, S.; Navon, N.; Jiang, K.J.; Chevy, F.; Salomon, C. Exploring the thermodynamics of a universal Fermi gas. Nature 2010, 463, 1057–1060. [Google Scholar] [CrossRef]
- Ho, T.L.; Zhou, Q. Obtaining the phase diagram and thermodynamic quantities of bulk systems from the densities of trapped gases. Nat. Phys. 2010, 6, 131–134. [Google Scholar] [CrossRef]
- Pilati, S.; Giorgini, S. Phase Separation in a Polarized Fermi Gas at Zero Temperature. Phys. Rev. Lett. 2008, 100, 030401. [Google Scholar] [CrossRef]
- Camacho-Guardian, A.; Bruun, G.M. Landau Effective Interaction between Quasiparticles in a Bose-Einstein Condensate. Phys. Rev. X 2018, 8, 031042. [Google Scholar] [CrossRef]
- Zwerger, W. The BCS-BEC Crossover and the Unitary Fermi Gas; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011; Volume 836. [Google Scholar]
- Ngampruetikorn, V. Low-Dimensional Fermi Gases: From Few to Many-Body Physics. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2015. [Google Scholar]
- Parish, M.M.; Adlong, H.S.; Liu, W.E.; Levinsen, J. Thermodynamic signatures of the polaron-molecule transition in a Fermi gas. Phys. Rev. A 2021, 103, 023312. [Google Scholar] [CrossRef]
- Pekker, D.; Babadi, M.; Sensarma, R.; Zinner, N.; Pollet, L.; Zwierlein, M.W.; Demler, E. Competition between Pairing and Ferromagnetic Instabilities in Ultracold Fermi Gases near Feshbach Resonances. Phys. Rev. Lett. 2011, 106, 050402. [Google Scholar] [CrossRef] [PubMed]
- Valtolina, G.; Scazza, F.; Amico, A.; Burchianti, A.; Recati, A.; Enss, T.; Inguscio, M.; Zaccanti, M.; Roati, G. Exploring the ferromagnetic behaviour of a repulsive Fermi gas through spin dynamics. Nat. Phys. 2017, 13, 704–709. [Google Scholar] [CrossRef]
- Recati, A.; Stringari, S. Spin Fluctuations, Susceptibility, and the Dipole Oscillation of a Nearly Ferromagnetic Fermi Gas. Phys. Rev. Lett. 2011, 106, 080402. [Google Scholar] [CrossRef]
- Grochowski, P.T.; Karpiuk, T.; Brewczyk, M.; Rzkażewski, K. Unified Description of Dynamics of a Repulsive Two-Component Fermi Gas. Phys. Rev. Lett. 2017, 119, 215303. [Google Scholar] [CrossRef]
- Scazza, F.; Valtolina, G.; Amico, A.; Tavares, P.E.S.; Inguscio, M.; Ketterle, W.; Roati, G.; Zaccanti, M. Exploring emergent heterogeneous phases in strongly repulsive Fermi gases. Phys. Rev. A 2020, 101, 013603. [Google Scholar] [CrossRef]
- Dagotto, E.; Burgy, J.; Moreo, A. Nanoscale phase separation in colossal magnetoresistance materials: Lessons for the cuprates? Solid State Commun. 2003, 126, 9–22. [Google Scholar] [CrossRef][Green Version]
- Dagotto, E. Complexity in Strongly Correlated Electronic Systems. Science 2005, 309, 257–262. [Google Scholar] [CrossRef]
- Petrov, D.S. Quantum Mechanical Stabilization of a Collapsing Bose-Bose Mixture. Phys. Rev. Lett. 2015, 115, 155302. [Google Scholar] [CrossRef]
- Navon, N.; Smith, R.P.; Hadzibabic, Z. Quantum gases in optical boxes. Nat. Phys. 2021, 17, 1334–1341. [Google Scholar] [CrossRef]
- Pilati, S.; Zintchenko, I.; Troyer, M. Ferromagnetism of a Repulsive Atomic Fermi Gas in an Optical Lattice: A Quantum Monte Carlo Study. Phys. Rev. Lett. 2014, 112, 015301. [Google Scholar] [CrossRef] [PubMed]
- Zintchenko, I.; Wang, L.; Troyer, M. Ferromagnetism of the repulsive atomic Fermi gas: Three-body recombination and domain formation. EPJ B 2016, 89, 180. [Google Scholar] [CrossRef]
- Conduit, G.J. Itinerant ferromagnetism in a two-dimensional atomic gas. Phys. Rev. A 2010, 82, 043604. [Google Scholar] [CrossRef]
- Cui, X.; Ho, T.L. Ground-state ferromagnetic transition in strongly repulsive one-dimensional Fermi gases. Phys. Rev. A 2014, 89, 023611. [Google Scholar] [CrossRef]
- Gross, C.; Bloch, I. Quantum simulations with ultracold atoms in optical lattices. Science 2017, 357, 995–1001. [Google Scholar] [CrossRef]
- Casalbuoni, R.; Nardulli, G. Inhomogeneous superconductivity in condensed matter and QCD. Rev. Mod. Phys. 2004, 76, 263–320. [Google Scholar] [CrossRef]
- Fukushima, K.; Hatsuda, T. The phase diagram of dense QCD. Rep. Progr. Phys. 2010, 74, 014001. [Google Scholar] [CrossRef]
- Magierski, P.; Tüzemen, B.; Wlazłowski, G. Spin-polarized droplets in the unitary Fermi gas. Phys. Rev. A 2019, 100, 033613. [Google Scholar] [CrossRef]
- Hu, H.; Wang, A.B.; Yi, S.; Liu, X.J. Fermi polaron in a one-dimensional quasiperiodic optical lattice: The simplest many-body localization challenge. Phys. Rev. A 2016, 93, 053601. [Google Scholar] [CrossRef]
- Büchler, H.P. Microscopic Derivation of Hubbard Parameters for Cold Atomic Gases. Phys. Rev. Lett. 2010, 104, 090402. [Google Scholar] [CrossRef] [PubMed]
- Ashida, Y.; Schmidt, R.; Tarruell, L.; Demler, E. Many-body interferometry of magnetic polaron dynamics. Phys. Rev. B 2018, 97, 060302. [Google Scholar] [CrossRef]
- Koepsell, J.; Vijayan, J.; Sompet, P.; Grusdt, F.; Hilker, T.A.; Demler, E.; Salomon, G.; Bloch, I.; Gross, C. Imaging magnetic polarons in the doped Fermi–Hubbard model. Nature 2019, 572, 358–362. [Google Scholar] [CrossRef]
- Ji, G.; Xu, M.; Kendrick, L.H.; Chiu, C.S.; Brüggenjürgen, J.C.; Greif, D.; Bohrdt, A.; Grusdt, F.; Demler, E.; Lebrat, M.; et al. Coupling a Mobile Hole to an Antiferromagnetic Spin Background: Transient Dynamics of a Magnetic Polaron. Phys. Rev. X 2021, 11, 021022. [Google Scholar] [CrossRef]
- Kane, C.L.; Lee, P.A.; Read, N. Motion of a single hole in a quantum antiferromagnet. Phys. Rev. B 1989, 39, 6880–6897. [Google Scholar] [CrossRef]
- Grusdt, F.; Kánasz-Nagy, M.; Bohrdt, A.; Chiu, C.S.; Ji, G.; Greiner, M.; Greif, D.; Demler, E. Parton Theory of Magnetic Polarons: Mesonic Resonances and Signatures in Dynamics. Phys. Rev. X 2018, 8, 011046. [Google Scholar] [CrossRef]
- Grusdt, F.; Bohrdt, A.; Demler, E. Microscopic spinon-chargon theory of magnetic polarons in the t-J model. Phys. Rev. B 2019, 99, 224422. [Google Scholar] [CrossRef]
- Blomquist, E.; Carlström, J. Unbiased description of magnetic polarons in a Mott insulator. Commun. Phys. 2020, 3, 172. [Google Scholar] [CrossRef]
- Nielsen, K.K.; Bastarrachea-Magnani, M.A.; Pohl, T.; Bruun, G.M. Spatial structure of magnetic polarons in strongly interacting antiferromagnets. Phys. Rev. B 2021, 104, 155136. [Google Scholar] [CrossRef]
- Lee, P.A.; Nagaosa, N.; Wen, X.G. Doping a Mott insulator: Physics of high-temperature superconductivity. Rev. Mod. Phys. 2006, 78, 17–85. [Google Scholar] [CrossRef]
- Efimkin, D.K.; MacDonald, A.H. Many-body theory of trion absorption features in two-dimensional semiconductors. Phys. Rev. B 2017, 95, 035417. [Google Scholar] [CrossRef]
- Efimkin, D.K.; MacDonald, A.H. Exciton-polarons in doped semiconductors in a strong magnetic field. Phys. Rev. B 2018, 97, 235432. [Google Scholar] [CrossRef]
- Smoleński, T.; Cotlet, O.; Popert, A.; Back, P.; Shimazaki, Y.; Knüppel, P.; Dietler, N.; Taniguchi, T.; Watanabe, K.; Kroner, M.; et al. Interaction-Induced Shubnikov–de Haas Oscillations in Optical Conductivity of Monolayer MoSe2. Phys. Rev. Lett. 2019, 123, 097403. [Google Scholar] [CrossRef] [PubMed]
- Levinsen, J.; Marchetti, F.M.; Keeling, J.; Parish, M.M. Spectroscopic Signatures of Quantum Many-Body Correlations in Polariton Microcavities. Phys. Rev. Lett. 2019, 123, 266401. [Google Scholar] [CrossRef] [PubMed]
- Cotleţ, O.; Zeytinoǧlu, S.; Sigrist, M.; Demler, E.; Imamoǧlu, A. Superconductivity and other collective phenomena in a hybrid Bose–Fermi mixture formed by a polariton condensate and an electron system in two dimensions. Phys. Rev. B 2016, 93, 054510. [Google Scholar] [CrossRef]

| Quasiparticle Property | Symbol | Relation to Self Energy |
|---|---|---|
| Energy | E | |
| Residue | Z | |
| Effective mass | ||
| Damping | Γ | |
| Contact | C | |
| Particles in dressing cloud | . |
| Fermi Polaron | Bose Polaron | |
|---|---|---|
| E | [72] | [73] |
| Z | [75] | [74] |
| [72] | [76] | |
| [28] | , if | |
| C | ||
| [77] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scazza, F.; Zaccanti, M.; Massignan, P.; Parish, M.M.; Levinsen, J. Repulsive Fermi and Bose Polarons in Quantum Gases. Atoms 2022, 10, 55. https://doi.org/10.3390/atoms10020055
Scazza F, Zaccanti M, Massignan P, Parish MM, Levinsen J. Repulsive Fermi and Bose Polarons in Quantum Gases. Atoms. 2022; 10(2):55. https://doi.org/10.3390/atoms10020055
Chicago/Turabian StyleScazza, Francesco, Matteo Zaccanti, Pietro Massignan, Meera M. Parish, and Jesper Levinsen. 2022. "Repulsive Fermi and Bose Polarons in Quantum Gases" Atoms 10, no. 2: 55. https://doi.org/10.3390/atoms10020055
APA StyleScazza, F., Zaccanti, M., Massignan, P., Parish, M. M., & Levinsen, J. (2022). Repulsive Fermi and Bose Polarons in Quantum Gases. Atoms, 10(2), 55. https://doi.org/10.3390/atoms10020055






