Ultra-Dilute Gas of Polarons in a Bose–Einstein Condensate
Abstract
1. Introduction
2. Methods
2.1. Weakly Interacting Regime
2.2. Strongly Interacting Regime
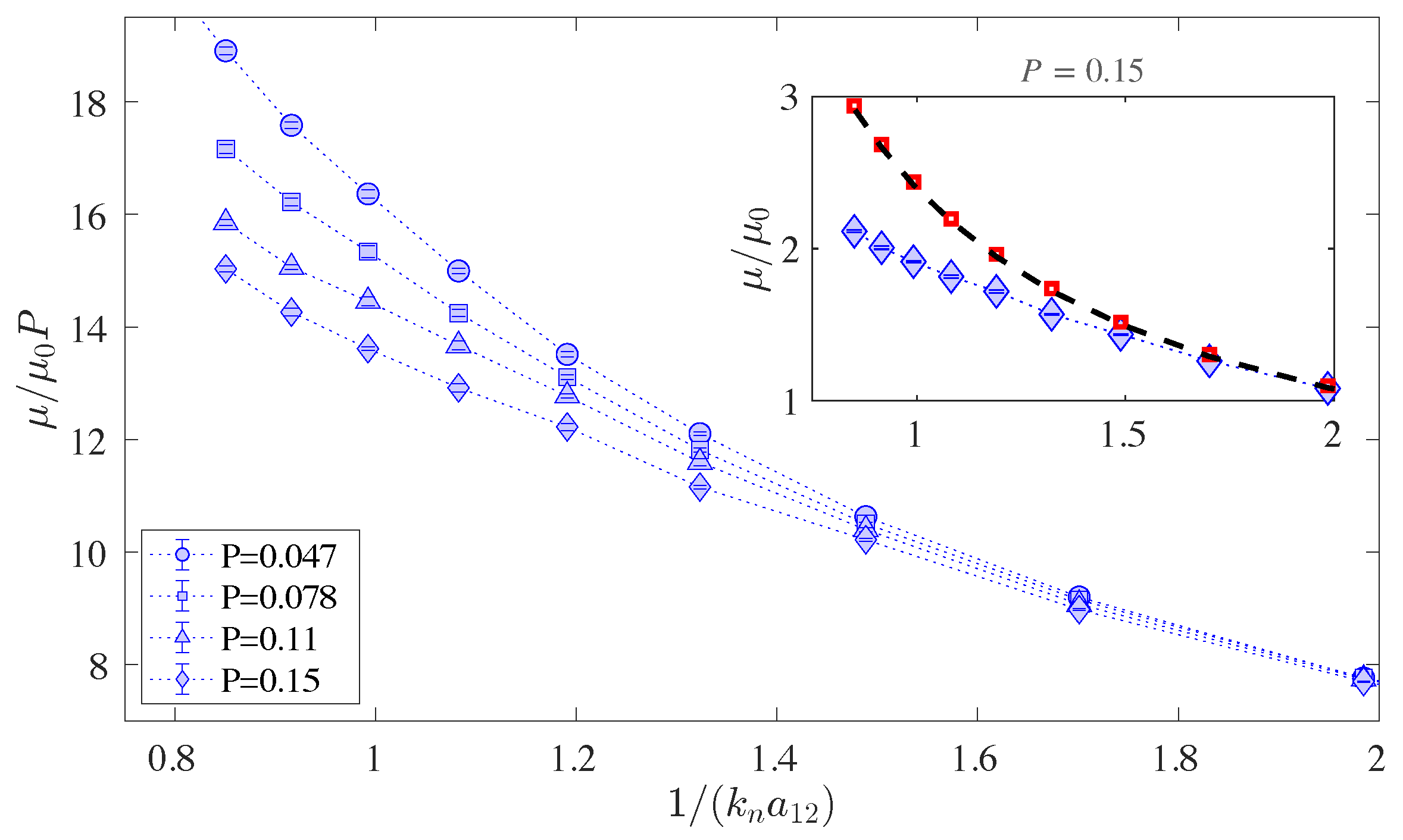
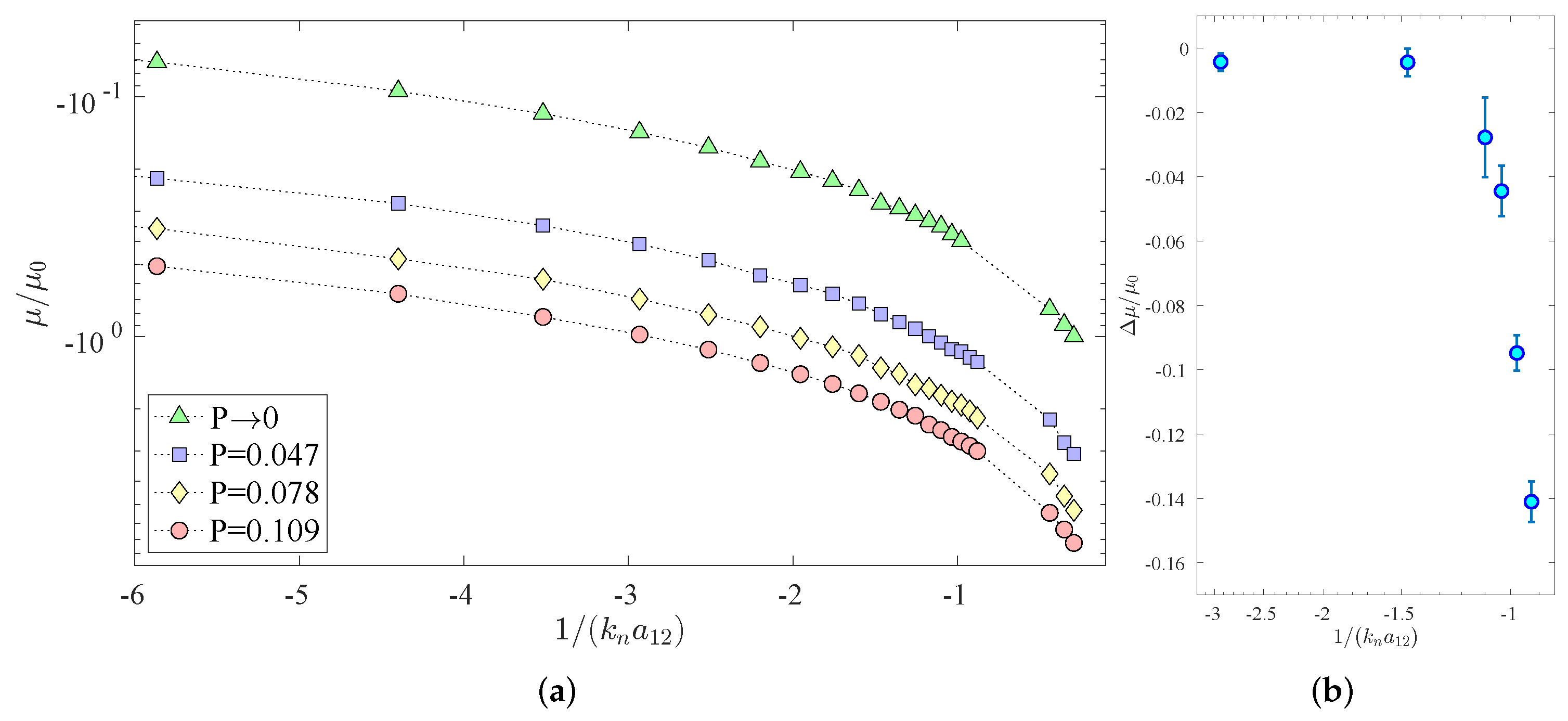
3. Results and Discussion
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References and Notes
- Landau, L.D. Über Die Bewegung der Elektronen in Kristallgitter. Phys. Z. Sowjetunion 1933, 3, 644–645. [Google Scholar]
- Landau, L.; Pekar, S. Effective mass of a polaron. J. Exp. Theor. Phys. 1948, 18, 419–423. [Google Scholar]
- Feynman, R.P. Slow Electrons in a Polar Crystal. Phys. Rev. 1955, 97, 660–665. [Google Scholar] [CrossRef]
- Devreese, J.; Peters, F. Polarons and Excitons in Polar Semiconductors and Ionic Crystals; Plenum Press: New York, NY, USA, 1984. [Google Scholar]
- Baym, G.; Pethick, C. Landau Fermi-Liquid Theory: Concepts and Applications; Wiley-VCH: New York, NY, USA, 1991. [Google Scholar]
- Camacho-Guardian, A.; Bruun, G.M. Landau Effective Interaction between Quasiparticles in a Bose-Einstein Condensate. Phys. Rev. X 2018, 8, 031042. [Google Scholar] [CrossRef]
- Schirotzek, A.; Wu, C.H.; Sommer, A.; Zwierlein, M.W. Observation of Fermi Polarons in a Tunable Fermi Liquid of Ultracold Atoms. Phys. Rev. Lett. 2009, 102, 230402. [Google Scholar] [CrossRef]
- Ngampruetikorn, V.; Levinsen, J.; Parish, M.M. Repulsive polarons in two-dimensional Fermi gases. EPL Europhys. Lett. 2012, 98, 30005. [Google Scholar] [CrossRef]
- Koschorreck, M.; Pertot, D.; Vogt, E.; Fröhlich, B.; Feld, M.; Köhl, M. Attractive and repulsive Fermi polarons in two dimensions. Nature 2012, 485, 619–622. [Google Scholar] [CrossRef]
- Kohstall, C.; Zaccanti, M.; Jag, M.; Trenkwalder, A.; Massignan, P.; Bruun, G.M.; Schreck, F.; Grimm, R. Metastability and coherence of repulsive polarons in a strongly interacting Fermi mixture. Nature 2012, 485, 615–618. [Google Scholar] [CrossRef]
- Cetina, M.; Jag, M.; Lous, R.S.; Fritsche, I.; Walraven, J.T.; Grimm, R.; Levinsen, J.; Parish, M.M.; Schmidt, R.; Knap, M.; et al. Ultrafast many-body interferometry of impurities coupled to a Fermi sea. Science 2016, 354, 96–99. [Google Scholar] [CrossRef]
- Scazza, F.; Valtolina, G.; Massignan, P.; Recati, A.; Amico, A.; Burchianti, A.; Fort, C.; Inguscio, M.; Zaccanti, M.; Roati, G. Repulsive Fermi Polarons in a Resonant Mixture of Ultracold 6Li Atoms. Phys. Rev. Lett. 2017, 118, 083602. [Google Scholar] [CrossRef]
- Sidler, M.; Back, P.; Cotlet, O.; Srivastava, A.; Fink, T.; Kroner, M.; Demler, E.; Imamoglu, A. Fermi polaron-polaritons in charge-tunable atomically thin semiconductors. Nat. Phys. 2017, 13, 255–261. [Google Scholar] [CrossRef]
- Catani, J.; Lamporesi, G.; Naik, D.; Gring, M.; Inguscio, M.; Minardi, F.; Kantian, A.; Giamarchi, T. Quantum dynamics of impurities in a one-dimensional Bose gas. Phys. Rev. A 2012, 85, 023623. [Google Scholar] [CrossRef]
- Jørgensen, N.B.; Wacker, L.; Skalmstang, K.T.; Parish, M.M.; Levinsen, J.; Christensen, R.S.; Bruun, G.M.; Arlt, J.J. Observation of Attractive and Repulsive Polarons in a Bose-Einstein Condensate. Phys. Rev. Lett. 2016, 117, 055302. [Google Scholar] [CrossRef] [PubMed]
- Hu, M.G.; Van de Graaff, M.J.; Kedar, D.; Corson, J.P.; Cornell, E.A.; Jin, D.S. Bose Polarons in the Strongly Interacting Regime. Phys. Rev. Lett. 2016, 117, 055301. [Google Scholar] [CrossRef] [PubMed]
- Yan, Z.Z.; Ni, Y.; Robens, C.; Zwierlein, M.W. Bose polarons near quantum criticality. Science 2020, 368, 190–194. [Google Scholar] [CrossRef]
- Camargo, F.; Schmidt, R.; Whalen, J.D.; Ding, R.; Woehl, G.; Yoshida, S.; Burgdörfer, J.; Dunning, F.B.; Sadeghpour, H.R.; Demler, E.; et al. Creation of Rydberg Polarons in a Bose Gas. Phys. Rev. Lett. 2018, 120, 083401. [Google Scholar] [CrossRef]
- Peña Ardila, L.A.; Jørgensen, N.B.; Pohl, T.; Giorgini, S.; Bruun, G.M.; Arlt, J.J. Analyzing a Bose polaron across resonant interactions. Phys. Rev. A 2019, 99, 063607. [Google Scholar] [CrossRef]
- Chin, C.; Grimm, R.; Julienne, P.; Tiesinga, E. Feshbach resonances in ultracold gases. Rev. Mod. Phys. 2010, 82, 1225–1286. [Google Scholar] [CrossRef]
- Bloch, I.; Dalibard, J.; Zwerger, W. Many-body physics with ultracold gases. Rev. Mod. Phys. 2008, 80, 885–964. [Google Scholar] [CrossRef]
- Tempere, J.; Casteels, W.; Oberthaler, M.K.; Knoop, S.; Timmermans, E.; Devreese, J.T. Feynman path-integral treatment of the BEC-impurity polaron. Phys. Rev. B 2009, 80, 184504. [Google Scholar] [CrossRef]
- Grusdt, F.; Demler, E. New theoretical approaches to Bose polarons. arXiv 2015, arXiv:1510.04934. [Google Scholar]
- Volosniev, A.G.; Hammer, H.W.; Zinner, N.T. Real-time dynamics of an impurity in an ideal Bose gas in a trap. Phys. Rev. A 2015, 92, 023623. [Google Scholar] [CrossRef]
- Christensen, R.S.; Levinsen, J.; Bruun, G.M. Quasiparticle Properties of a Mobile Impurity in a Bose-Einstein Condensate. Phys. Rev. Lett. 2015, 115, 160401. [Google Scholar] [CrossRef] [PubMed]
- Shchadilova, Y.E.; Schmidt, R.; Grusdt, F.; Demler, E. Quantum Dynamics of Ultracold Bose Polarons. Phys. Rev. Lett. 2016, 117, 113002. [Google Scholar] [CrossRef]
- Levinsen, J.; Parish, M.M.; Bruun, G.M. Impurity in a Bose-Einstein Condensate and the Efimov Effect. Phys. Rev. Lett. 2015, 115, 125302. [Google Scholar] [CrossRef]
- Lampo, A.; Charalambous, C.; García-March, M.A.; Lewenstein, M. Non-Markovian polaron dynamics in a trapped Bose-Einstein condensate. Phys. Rev. A 2018, 98, 063630. [Google Scholar] [CrossRef]
- Lausch, T.; Widera, A.; Fleischhauer, M. Prethermalization in the cooling dynamics of an impurity in a Bose-Einstein condensate. Phys. Rev. A 2018, 97, 023621. [Google Scholar] [CrossRef]
- Levinsen, J.; Parish, M.M.; Christensen, R.S.; Arlt, J.J.; Bruun, G.M. Finite-temperature behavior of the Bose polaron. Phys. Rev. A 2017, 96, 063622. [Google Scholar] [CrossRef]
- Nielsen, K.K.; Ardila, L.A.P.; Bruun, G.M.; Pohl, T. Critical slowdown of non-equilibrium polaron dynamics. New J. Phys. 2019, 21, 043014. [Google Scholar] [CrossRef]
- Liu, W.E.; Levinsen, J.; Parish, M.M. Variational Approach for Impurity Dynamics at Finite Temperature. Phys. Rev. Lett. 2019, 122, 205301. [Google Scholar] [CrossRef]
- Drescher, M.; Salmhofer, M.; Enss, T. Real-space dynamics of attractive and repulsive polarons in Bose-Einstein condensates. Phys. Rev. A 2019, 99, 023601. [Google Scholar] [CrossRef]
- Mistakidis, S.I.; Katsimiga, G.C.; Koutentakis, G.M.; Busch, T.; Schmelcher, P. Quench Dynamics and Orthogonality Catastrophe of Bose Polarons. Phys. Rev. Lett. 2019, 122, 183001. [Google Scholar] [CrossRef]
- Mistakidis, S.I.; Grusdt, F.; Koutentakis, G.M.; Schmelcher, P. Dissipative correlated dynamics of a moving impurity immersed in a Bose–Einstein condensate. New J. Phys. 2019, 21, 103026. [Google Scholar] [CrossRef]
- Massignan, P.; Yegovtsev, N.; Gurarie, V. Universal Aspects of a Strongly Interacting Impurity in a Dilute Bose Condensate. Phys. Rev. Lett. 2021, 126, 123403. [Google Scholar] [CrossRef] [PubMed]
- Ardila, L.A.P.; Giorgini, S. Impurity in a Bose-Einstein condensate: Study of the attractive and repulsive branch using quantum Monte Carlo methods. Phys. Rev. A 2015, 92, 033612. [Google Scholar] [CrossRef]
- Parisi, L.; Giorgini, S. Quantum Monte Carlo study of the Bose-polaron problem in a one-dimensional gas with contact interactions. Phys. Rev. A 2017, 95, 023619. [Google Scholar] [CrossRef]
- Bombín, R.; Cikojević, V.; Sánchez-Baena, J.; Boronat, J. Finite-range effects in the two-dimensional repulsive Fermi polaron. Phys. Rev. A 2021, 103, L041302. [Google Scholar] [CrossRef]
- Grusdt, F.; Astrakharchik, G.E.; Demler, E. Bose polarons in ultracold atoms in one dimension: Beyond the Fröhlich paradigm. New J. Phys. 2017, 19, 103035. [Google Scholar] [CrossRef]
- Slow impurities are defined as impurities with a momentum P≪mc where c is the speed of sound of the condensate a m is the mass of the impurity.
- Camacho-Guardian, A.; Peña Ardila, L.A.; Pohl, T.; Bruun, G.M. Bipolarons in a Bose-Einstein Condensate. Phys. Rev. Lett. 2018, 121, 013401. [Google Scholar] [CrossRef]
- Naidon, P. Two Impurities in a Bose–Einstein Condensate: From Yukawa to Efimov Attracted Polarons. J. Phys. Soc. Jpn. 2018, 87, 043002. [Google Scholar] [CrossRef]
- Will, M.; Astrakharchik, G.E.; Fleischhauer, M. Polaron Interactions and Bipolarons in One-Dimensional Bose Gases in the Strong Coupling Regime. Phys. Rev. Lett. 2021, 127, 103401. [Google Scholar] [CrossRef]
- Van Loon, S.; Casteels, W.; Tempere, J. Ground-state properties of interacting Bose polarons. Phys. Rev. A 2018, 98, 063631. [Google Scholar] [CrossRef]
- Bisset, R.N.; Ardila, L.A.P.; Santos, L. Quantum Droplets of Dipolar Mixtures. Phys. Rev. Lett. 2021, 126, 025301. [Google Scholar] [CrossRef] [PubMed]
- Petrov, D.S. Quantum Mechanical Stabilization of a Collapsing Bose-Bose Mixture. Phys. Rev. Lett. 2015, 115, 155302. [Google Scholar] [CrossRef] [PubMed]
- Ardila, L.A.P.; Giorgini, S. Bose polaron problem: Effect of mass imbalance on binding energy. Phys. Rev. A 2016, 94, 063640. [Google Scholar] [CrossRef]
- Ardila, L.A.P. Impurities in a Bose-Einstein Condensate Using Quantum Monte-Carlo Methods: Ground-State Properties. Ph.D. Thesis, University of Trento, Trento, Italy, 2015. [Google Scholar]
- Levinsen, J.; Ardila, L.A.P.; Yoshida, S.M.; Parish, M.M. Quantum Behavior of a Heavy Impurity Strongly Coupled to a Bose Gas. Phys. Rev. Lett. 2021, 127, 033401. [Google Scholar] [CrossRef]
- In trapped experiments the situation may be different since the high increase of the density to reduce the interaction energy may overcome the kinetic energy of the impuriy gas. The situation is completely analogous to attarctive particle is an harmonic potential, however in this case the trapping potential due to the deformation of the condensation sets a different scalings for the stability.
- Santamore, D.; Timmermans, E. Multi-impurity polarons in a dilute Bose–Einstein condensate. New J. Phys. 2011, 13, 103029. [Google Scholar] [CrossRef]
- Brauneis, F.; Hammer, H.W.; Lemeshko, M.; Volosniev, A.G. Impurities in a one-dimensional Bose gas: The flow equation approach. SciPost Phys. 2021, 11, 8. [Google Scholar] [CrossRef]
- Astrakharchik, G.E.; Ardila, L.A.P.; Schmidt, R.; Jachymski, K.; Negretti, A. Ionic polaron in a Bose-Einstein condensate. Commun. Phys. 2021, 4, 94. [Google Scholar] [CrossRef]
- Christensen, E.R.; Camacho-Guardian, A.; Bruun, G.M. Charged Polarons and Molecules in a Bose-Einstein Condensate. Phys. Rev. Lett. 2021, 126, 243001. [Google Scholar] [CrossRef]
- Ardila, L.A.P.n.; Astrakharchik, G.E.; Giorgini, S. Strong coupling Bose polarons in a two-dimensional gas. Phys. Rev. Res. 2020, 2, 023405. [Google Scholar] [CrossRef]
- Ospelkaus, C.; Ospelkaus, S.; Sengstock, K.; Bongs, K. Interaction-Driven Dynamics of 40K-87Rb Fermion-Boson Gas Mixtures in the Large-Particle-Number Limit. Phys. Rev. Lett. 2006, 96, 020401. [Google Scholar] [CrossRef] [PubMed]
- Ness, G.; Shkedrov, C.; Florshaim, Y.; Diessel, O.K.; von Milczewski, J.; Schmidt, R.; Sagi, Y. Observation of a Smooth Polaron-Molecule Transition in a Degenerate Fermi Gas. Phys. Rev. X 2020, 10, 041019. [Google Scholar] [CrossRef]
- Cabrera, C.R.; Tanzi, L.; Sanz, J.; Naylor, B.; Thomas, P.; Cheiney, P.; Tarruell, L. Quantum liquid droplets in a mixture of Bose-Einstein condensates. Science 2018, 359, 301–304. [Google Scholar] [CrossRef] [PubMed]
- Semeghini, G.; Ferioli, G.; Masi, L.; Mazzinghi, C.; Wolswijk, L.; Minardi, F.; Modugno, M.; Modugno, G.; Inguscio, M.; Fattori, M. Self-Bound Quantum Droplets of Atomic Mixtures in Free Space. Phys. Rev. Lett. 2018, 120, 235301. [Google Scholar] [CrossRef] [PubMed]
- Naidon, P.; Petrov, D.S. Mixed Bubbles in Bose-Bose Mixtures. Phys. Rev. Lett. 2021, 126, 115301. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ardila, L.A.P. Ultra-Dilute Gas of Polarons in a Bose–Einstein Condensate. Atoms 2022, 10, 29. https://doi.org/10.3390/atoms10010029
Ardila LAP. Ultra-Dilute Gas of Polarons in a Bose–Einstein Condensate. Atoms. 2022; 10(1):29. https://doi.org/10.3390/atoms10010029
Chicago/Turabian StyleArdila, Luis A. Peña. 2022. "Ultra-Dilute Gas of Polarons in a Bose–Einstein Condensate" Atoms 10, no. 1: 29. https://doi.org/10.3390/atoms10010029
APA StyleArdila, L. A. P. (2022). Ultra-Dilute Gas of Polarons in a Bose–Einstein Condensate. Atoms, 10(1), 29. https://doi.org/10.3390/atoms10010029





