Abstract
Since its initial development in the 1970s by Phil Burke and his collaborators, the R-matrix theory and associated computer codes have become the method of choice for the calculation of accurate data for general electron–atom/ion/molecule collision and photoionization processes. The use of a non-orthogonal set of orbitals based on B-splines, now called the B-spline R-matrix (BSR) approach, was pioneered by Zatsarinny. It has considerably extended the flexibility of the approach and improved particularly the treatment of complex many-electron atomic and ionic targets, for which accurate data are needed in many modelling applications for processes involving low-temperature plasmas. Both the original R-matrix approach and the BSR method have been extended to the interaction of short, intense electromagnetic (EM) radiation with atoms and molecules. Here, we provide an overview of the theoretical tools that were required to facilitate the extension of the theory to the time domain. As an example of a practical application, we show results for two-photon ionization of argon by intense short-pulse extreme ultraviolet radiation.
1. Introduction
The evolution of the R-matrix theory from a useful but largely phenomenological approach for the description of nuclear resonances [1,2] to an accurate computational method in atomic physics in the 1970s is primarily due to Phil Burke and his collaborators at The Queen’s University of Belfast [3,4,5,6]. The refinement of the original theory to include long-range interactions and the associated computer codes have become the method of choice for the calculation of accurate data for general electron–atom/ion/molecule collision and photoionization processes in general and cross sections in particular. These data are needed for many modeling applications for processes involving low-temperature plasmas, in addition to providing critical insights into how electrons and photons interact with atomic systems. The atomic R-matrix methods were subsequently extended to the study of electron-molecule collisions [7,8,9] and ultimately led to the now widely used UKRmol+ package [10].
A significant advance in the practical use of the R-matrix method was made by Oleg Zatsarinny who pioneered using non-orthogonal (NO) sets of orbitals for the target description and also showed that, by using a flexible radial B-spline basis, it was possible to greatly improve the accuracy of the calculated results. The B-spline R-matrix (BSR) approach [11,12] is based on an idea that had been very successfully introduced into atomic structure calculations by Charlotte Froese Fischer [13]. The NO basis enables the efficient incorporation of correlation into the atomic expansion, using individually optimized, i.e., term-dependent one-electron orbitals. The B-splines provide a very accurate description of the atomic bound and continuum orbitals, together with excellent and well-studied numerical properties. B-splines as the primitive numerical basis, together with their use to expand the non-orthogonal set of physical and pseudo-orbitals in them, provide a potent mix that may improve significantly on the standard versions of the atomic R-matrix codes.
Recently, in addition to the standard finite-difference representation of the orbitals in the well-known atomic code [14], a B-Spline version of the integral package has also been developed [15]. Similarly, the earlier UKRmol [16] implementation was also modified by incorporating a B-spline basis for the continuum functions [17], resulting in the current UKRmol+ package [10]. In the latter codes, however, the individual orbitals expanded in this basis are still assumed to be orthogonal, thereby limiting their flexibility to represent the generally existing term dependence.
This term dependence can, in principle, be represented in large configuration-interaction expansions, as done very successfully in the convergent close-coupling (CCC) [18] and R-matrix with pseudo-states (RMPS) [19] formulations. Hence, while non-orthogonal orbital sets are not an advantage per se in the general formulation of close-coupling theory, they can be highly beneficial in reducing the required size of the expansion in practical applications. Undoubtedly, they come with their own challenges, which is the main reason they tend not to be used in collision problems, where both the N-electron target and the -electron collision problem need to be handled at a comparable and consistent level of sophistication. A significant difference between atomic and molecular structure calculations and those involving scattering is that the former more commonly employ methodologies that optimize orbitals for specific states. In studying dynamical systems, where there is a strong interplay between neutral, excited, and ionic states, this is a far greater challenge.
The BSR method has been demonstrated to be capable of computing highly accurate electron-collision and photoionization amplitudes, and from them cross sections for complex atomic and ionic targets. There are now non-relativistic, semi-relativistic (Breit-Pauli), and full-relativistic (Dirac-Coulomb) versions. In some cases, the BSR predictions were shown to be more accurate than the available experimental data, and sometimes the calculations suggested problems with existing experimental data that were later corrected by newer experiments. For just one such example, see Ren et al. [20]. Another case of spectacular improvement over preceding work is the first BSR calculation for electron collisions with neon atoms [21]. Many more can be found in the Topical Review [12], and the impact of these developments on plasma applications has been substantial as well [22,23].
Around 2006–2007, it became clear that input from BSR calculations could be used to treat the interaction of intense laser radiation with complex atoms such as Ne [24] and Ar [25]. All the key ingredients were available; namely, the Hamiltonian matrix and the dipole length and/or velocity matrix elements required for the coupling of the target system to the external EM field. Since these could be “easily” extracted from the BSR code, this would provide a general ab initio and non-perturbative treatment to the problem that goes beyond quasi-one-electron or quasi-two-electron models.
The only other required ingredient is an efficient method to propagate the time-dependent wavefunction and a way to extract the information from that wavefunction when (i) the external field has died down and (ii) a possibly ejected electron has moved sufficiently far away from the target center. Schneider, Bartschat, and Guan had been working on the numerical propagation techniques using the short iterative Lanczos (SIL) method [26], and they convinced Oleg that using his BSR matrix elements would be a very useful contribution to atomic physics. The four of us combined our talents to examine the multi-photon, single-ionization of Ne and Ar, which are significantly more challenging targets than He for this process. Eventually, the method that we hereafter term TDBSR was generalized to treat two-photon, double ionization of He [27,28]. The late Cliff Noble also joined the group and was instrumental in parallelizing the codes we had developed. With the addition of Johannes Feist, we later examined the question of time delays in the photoionization of Ne [29].
The generalization of the Belfast R-matrix method to treat arbitrary time-dependent EM fields actually goes much further back to a paper written by Phil and Valerie Burke in 1997 [30]. Subsequent theoretical [31] developments led to the generation of the Time-Dependent R-matrix method (TDRM) [32], which already used a B-spline basis approach in the R-matrix inner region. Combining this with an outer region treated by the finite-difference techniques used in the HELIUM code [33] led to the first incarnation of the R-matrix with time dependence (RMT) method [34] in 2011. Since then the code has undergone extensive development, with extensions to treat arbitrary light fields [35], molecular targets [36], and the spin–orbit interaction using input from the RMATRX-I suite of codes [37], as well as improvements to the parallelization scheme [38]. It is still under active development by researchers located mostly in the UK.
Both the BSR code and the RMT suite are available from a number of sources, such as Computer Physics Communications [11,38] and designated GitHub sites [39,40]. A good place to start with these and other codes in this field is the Atomic, Molecular, and Optical Sciences (AMOS) Gateway [41].
In this contribution, we take the opportunity to examine and contrast how the TDBSR and RMT methods are structured today. Specifically, we highlight the contributions of the collaboration between Schneider at NIST and the Bartschat group at Drake University to this topic. The basic ideas are outlined in Section 2. As one representative example, we compare the TDBSR and RMT results for two-photon ionization of Ar atoms by an intense short-pulse extreme ultraviolet (XUV) laser field in Section 3. We finish in Section 4 with a summary and an outlook to suggest that a very worthwhile long-term goal is the unification or at least the interoperability of the two codes through the development of an appropriate interface.
2. Solving the TDSE via the R-Matrix Method
The first task is to solve the time-dependent Schrödinger Equation (TDSE) in the internal R-matrix region
Here is a multi-electron coordinate, with representing the space and spin coordinates of electron k and these coordinates for electron except . Furthermore, is the time-independent Hamiltonian, represents the interaction of the system with the EM field, is the Bloch operator, and contains the entire set of internal coordinates of the system. The states in Equation (1d), which are being summed over in Equation (1c), are the channel functions that are non-zero at the R-matrix boundary . Their definition depends on how asymptotically exact quantum states are constructed as the interaction between the target and the projectile approaches zero. Once that choice has been made, those parts of the wavefunction involving the internal coordinates of the target and the projectile can be coupled to form the channel functions. The coordinates as well as the angles represented by can be projected out of the calculation, thus leaving only the wavefunction in the relative coordinate r of the free electron in the asymptotic region to be determined.
Equation (1d) represents an operator that projects out from the wavefunction all the possible events that are non-zero on the R-matrix surface. Recall that solving the TDSE is an initial-value problem, and that mixes the field-free eigenstates of . In the external region, where the system fragments into two weakly interacting components, the wavefunction may be written as
After projection, it is reduced to a set of coupled, time-dependent, radial, partial differential equations:
The bold-faced notation represents matrices and vectors in the channel space. The subscript on indicates which final ionic state and which field-free partial-wave symmetry the function belongs to. Details about how one might uniquely order these functions in practice can be found, for example, in Section 5.3 of the RMT write-up [38].
The explicit inclusion of the Bloch operator in both the internal and external region is done to emphasize that it is this term that couples the two regions. Note that it is entirely independent of the specific numerical method used to solve the sets of equations in the respective regions. In the current implementation to RMT [38], a five-point finite difference (FD) is used to represent the first and second spatial derivatives.
Since the value of the logarithmic derivative to the solution of the TDSE in the inner and outer region must be the same at ,
The round brackets mean integration over all degrees of freedom save r. In a somewhat unorthodox fashion, one can replace the operation of on the right-hand side of Equation (1a) with the values of the projected external wavefunction and, similarly, on the right-hand side of Equation (3a) with the projected . Then there are additional coupling terms due to approximating the derivatives of by difference formula. At present, the formalism only treats cases where a single free electron can be explicitly in the external region. This is a restriction of the current R-matrix formalism. Removing it is a fundamental challenge.
Equations (1a) and (3a) can be elegantly rewritten using the identity
and then integrating between and t to obtain
The same can be done for Equation (3a), replacing and by and d(r,t). It is always possible to add to and subtract from any timeindependent
operator without changing the form of Equation (6). A customary and
advantageous choice is to use the value of where tm is the midpoint of
the integration interval.
The SIL or Arnoldi method is directly employed in both the inner and outer regions to evaluate the action of the matrix exponential on the vector known from the previous time step. Turning to the second term, for sufficiently short times only the part in the integral involving the Bloch operator contributes. This can be justified by noting that the term involving vanishes if the integration is performed using the midpoint rule for sufficiently small time intervals.
To evaluate the term involving the Bloch operator, the suggested procedure is to expand in a power series and then evaluate the integral between and t involving the exponential operator. It can be demonstrated that these terms may also be computed using a modification of the SIL suggested by Saad [42]. A further simplification is to use the external-region Hamiltonian rather than the internal-region Hamiltonian and the already computed outer-region vector to make that procedure even more computationally efficient. Notice that the integral involving the Bloch operator as well as the finite-difference operator contains information from points that are shared between the outer and inner regions. This requires some updating or iteration of that information at each time step.
For the remaining discussion, we assume that the time step is chosen sufficiently small that the variation of the potential with time over the step is negligible. There are prior [43] as well as ongoing investigations to explore approaches to remove the short-time approximation and hence allow larger steps in time. While a detailed discussion is beyond the scope of the present paper, preliminary results indicate that such methods are far more accurate than the short-time approximation (for the same time step) and can also be efficient if full advantage of the larger steps is taken. One interesting result that emerges from the above derivation is that the accuracy of an n-step SIL or Arnoldi propagation is second order, as follows from the midpoint formula.
Before concluding this section, some comments on the actual application of the two time-dependent R-matrix approaches are in order. The RMT grew out of a many-decades effort by Phil Burke and his collaborators to provide high-quality software for the solution of a broad class of problems in atomic and molecular physics. One should not underestimate the perseverance and dedication of all those scientists to develop the R-matrix software, which is now being used by researchers all over the world. In contrast, the BSR code was essentially due to a single individual, Oleg Zatsarinny. It was Oleg who maintained and added features to the code over a couple of decades. The Drake University/NIST effort to produce a code based on BSR to treat the interaction of EM radiation with atoms was neither planned for the long term nor was it initiated by Oleg himself. Nevertheless, Oleg was always helpful and did his best to enable the effort to move forward.
At the time, those of us interested in a TDBSR wanted to get out proof-of-principle results quickly and only later worry about questions of efficiency. The SIL had already been very successfully employed using a finite-element discrete-variable representation (FEDVR) approach in atomic He. While this approach could be generalized to systems with more than two electrons, already having at our disposal the necessary ingredients from the BSR code enabled us to quickly study systems such as Ne and Ar. The idea was simple: take the field-free Hamiltonian and dipole matrices from the time-independent BSR calculations and propagate the initial bound state (also given by BSR as the initial vector) using the SIL. No attention was paid to an internal and external region. The R-matrix box was taken to be sufficiently large, so that after the SIL propagation we could already project onto asymptotic states.
3. Example Results
Figure 1 shows one example of a comparison between the previous TDBSR [25] and new RMT calculations performed for the present paper. As expected, the agreement between the two sets of predictions is excellent, as is the agreement with the Floquet results of McKenna and van der Hart [44]. The latter, of course, are effectively a steady-state approach, i.e., the natural width of the window resonances and the effect of the intermediate state, which acts as a stepping stone, are fully resolved. In the calculations with a finite-length pulse, on the other hand, the pulse width enters as well and smears out some of the sharp structures.
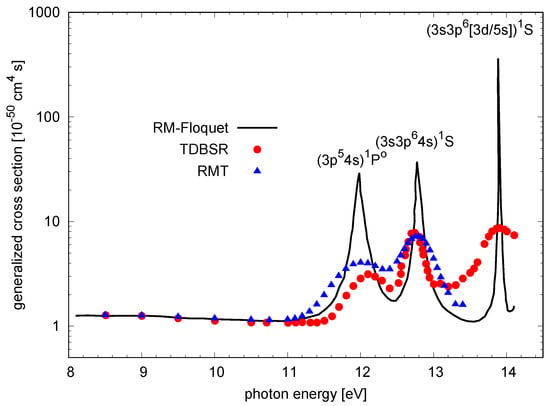
Figure 1.
Generalized cross section for two-photon ionization of Ar as a function of photon energy. A 30-cycle laser pulse with a sine-squared field envelope and a peak intensity of W/cm was used in the calculations. The Floquet results of McKenna and van der Hart [44] are compared with those from the previous TDBSR [25] and the current RMT calculations.
The remaining small disagreement between the TDBSR and the RMT results is due to the differences in the respective structure descriptions. Both the Floquet and the RMT results were obtained with the structure description developed by Burke and Taylor [45], who designed pseudo-orbitals to account for the strong term dependence of the 3s and 3p orbitals in the neutral ground state as well the coupled final ionic and states. This was particularly important to obtain accurate ionization potentials as well as the position (i.e., the excitation energy) of the intermediate state. No such special effort was devoted to this issue in the TDBSR calculations, but apparently a sufficient number of short-range orbitals were included in this case to obtain accurate results. This is definitely a topic that BSR, in principle, can handle extremely well. On the other hand, if only the bare minimum of orbitals is included, problems can arise. An example is depicted in Figure 4 of Guan et al. [24] in a similar calculation for two-photon ionization of Ne. In that very first TDBSR calculation, the ionization potential is too small, i.e., the ground state lies too high, and hence the theoretical excitation energy of the state is too small.
4. Summary and Outlook
In this contribution, we revisited some of the early work on the extension of the R-matrix (close-coupling) method, which was originally designed to accurately and efficiently treat electron and photon collisions with atoms, ions, and molecules in a steady-state scenario, to include the reaction of these targets to short-pulse intense electromagnetic radiation in a time-dependent framework. While the RMT code of the Belfast group has already been interfaced with both their atomic/ionic and molecular codes, we are currently working on interfacing the package with Oleg Zatsarinny’s suite of BSR programs. The interface will take full advantage of the BSR approach for complex targets by allowing multiple orbitals with the same nodal structure (i.e., a non-orthogonal physical basis) to describe term-dependence and correlation effects with relatively compact configuration expansions. If the success of the BSR method for the steady-case scenarios is any indication of likely future success, there is every reason to expect BSR+RMT to be another major step forward.
The authors have had significant interactions with Oleg Zatsarinny for a number of years. For details, interested readers are referred to the “Memories” contribution to this Special Issue in Oleg’s honor [46]. We hope that the BSR+RMT development will contribute to ensure Oleg’s legacy for many years to come.
Author Contributions
The project was conceived by B.I.S. who also wrote the initial draft. The RMT calculations were performed by K.R.H. and K.B. provided advice to the project, particularly regarding the presentation of the results. All authors have read and agreed to the published version of the manuscript.
Funding
B.I.S. receives support for this research from the Applied and Computational Mathematics Division of NIST. The work of K.R.H. and K.B. was supported by the United States National Science Foundation under grant Nos. PHY-1803844, OAC-1834740, PHY-2110023, and the XSEDE allocation TG-PHY-090031, and by the Texas Advanced Computing Center through the Frontera allocation PHY-20028.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| TDSE | Time-Dependent Schrödinger Equation |
| BSR | B-Spline R-Matrix |
| RMT | R-Matrix with Time Dependence |
| TDBSR | Time-Dependent B-Spline R-matrix |
| SIL | Short Iterative Lanczos |
| XUV | Extreme Ultraviolet |
References
- Lane, A.M.; Robson, D. Comprehensive Formalism for Nuclear Reaction Problems. I. Derivation of Existing Reaction Theories. Phys. Rev. 1966, 151, 774–787. [Google Scholar] [CrossRef]
- Lane, A.M. The application of Wigner’s R-matrix theory to atomic physics. J. Phys. B At. Mol. Phys. 1986, 19, 253–257. [Google Scholar] [CrossRef]
- Burke, P.G.; Hibbert, A.; Robb, W.D. Electron scattering by complex atoms. J. Phys. B At. Mol. Phys. 1971, 4, 153–161. [Google Scholar] [CrossRef]
- Berrington, K.A.; Burke, P.G.; Robb, W.D. The scattering of electrons by atomic nitrogen. J. Phys. B At. Mol. Phys. 1975, 8, 2500–2511. [Google Scholar] [CrossRef]
- Burke, P.G.; Robb, W.D. The R-Matrix Theory of Atomic Processes. Adv. At. Molec. Phys. 1976, 11, 143–214. [Google Scholar] [CrossRef]
- Burke, P.G. R-Matrix Theory of Atomic Collisions; Springer Series on Atomic, Optical, and Plasma Physics 61; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Schneider, B. R-matrix theory for electron-atom and electron-molecule collisions using analytic basis set expansions. Chem. Phys. Lett. 1975, 31, 237–241. [Google Scholar] [CrossRef]
- Schneider, B.I. R-matrix theory for electron-molecule collisions using analytic basis set expansions. II. Electron-H2 scattering in the static-exchange model. Phys. Rev. A 1975, 11, 1957. [Google Scholar] [CrossRef]
- Burke, P.G.; Mackey, I.; Shimamura, I. R-matrix theory of electron-molecule scattering. J. Phys. B At. Mol. Phys. 1977, 10, 2497–2512. [Google Scholar] [CrossRef] [Green Version]
- Mašín, Z.; Benda, J.; Gorfinkiel, J.D.; Harvey, A.G.; Tennyson, J. UKRmol+: A suite for modelling electronic processes in molecules interacting with electrons, positrons and photons using the R-matrix method. Comput. Phys. Commun. 2020, 249, 107092. [Google Scholar] [CrossRef] [Green Version]
- Zatsarinny, O. BSR: B-spline atomic R-matrix codes. Comput. Phys. Commun. 2006, 174, 273–356. [Google Scholar] [CrossRef]
- Zatsarinny, O.; Bartschat, K. The B-spline R-matrix method for atomic processes: Application to atomic structure, electron collisions and photoionization. J. Phys. B At. Mol. Opt. Phys. 2013, 46, 112001. [Google Scholar] [CrossRef]
- Froese Fischer, C.; Idrees, M. Spline algorithms for continuum functions. Comput. Phys. 1989, 3, 53–58. [Google Scholar] [CrossRef]
- Berrington, K.A.; Eissner, W.; Norrington, P.H. RMATRIX-I: Belfast Atomic R-Matrix Codes. Comput. Phys. Commun. 1995, 92, 290. [Google Scholar] [CrossRef]
- Wragg, J.; Ballance, C.; van der Hart, H. Breit–Pauli R-Matrix approach for the time-dependent investigation of ultrafast processes. Comput. Phys. Commun. 2020, 254, 107274. [Google Scholar] [CrossRef]
- Morgan, L.A.; Tennyson, J.; Gillan, C.J. The UK molecular R-matrix codes. Comput. Phys. Commun. 1998, 114, 120–128. [Google Scholar] [CrossRef]
- Meltzer, T.; Tennyson, J.; Mašín, Z.; Zammit, M.C.; Scarlett, L.H.; Fursa, D.V.; Bray, I. Benchmark calculations of electron impact electronic excitation of the hydrogen molecule. J. Phys. B At. Mol. Opt. Phys. 2020, 53, 145204. [Google Scholar] [CrossRef] [Green Version]
- Bray, I.; Fursa, D.; Kadyrov, A.; Stelbovics, A.; Kheifets, A.; Mukhamedzhanov, A. Electron- and photon-impact atomic ionisation. Phys. Rep. 2012, 520, 135–174. [Google Scholar] [CrossRef]
- Bartschat, K.; Hudson, E.T.; Scott, M.P.; Burke, P.G.; Burke, V.M. Electron-atom scattering at low and intermediate energies using a pseudo-state/ R-matrix basis. J. Phys. B At. Mol. Phys. 1996, 29, 115. [Google Scholar] [CrossRef]
- Ren, X.; Pflüger, T.; Ullrich, J.; Zatsarinny, O.; Bartschat, K.; Madison, D.H.; Dorn, A. Erratum: Low-energy electron-impact ionization of argon: Three-dimensional cross section [Phys. Rev. A 85, 032702 (2012)]. Phys. Rev. A 2015, 92, 019901. [Google Scholar] [CrossRef]
- Zatsarinny, O.; Bartschat, K. B-spline Breit-Pauli R-matrix calculations for electron collisions with neon atoms. J. Phys. B At. Mol. Opt. Phys. 2004, 37, 2173–2189. [Google Scholar] [CrossRef]
- Bartschat, K.; Kushner, M.J. Electron collisions with atoms, ions, molecules, and surfaces: Fundamental science empowering advances in technology. Proc. Nat. Acad. Sci. USA 2016, 113, 7026–7034. [Google Scholar] [CrossRef] [Green Version]
- Bartschat, K. Electron collisions—Experiment, theory, and applications. J. Phys. B At. Mol. Opt. Phys. 2018, 51, 132001. [Google Scholar] [CrossRef]
- Guan, X.; Zatsarinny, O.; Bartschat, K.; Schneider, B.I.; Feist, J.; Noble, C.J. General approach to few-cycle intense laser interactions with complex atoms. Phys. Rev. A 2007, 76, 053411. [Google Scholar] [CrossRef] [Green Version]
- Guan, X.; Noble, C.J.; Zatsarinny, O.; Bartschat, K.; Schneider, B.I. Time-dependent R-matrix calculations for multiphoton ionization of argon atoms in strong laser pulses. Phys. Rev. A 2008, 78, 053402. [Google Scholar] [CrossRef]
- Park, T.J.; Light, J.C. Unitary quantum time evolution by iterative Lanczos reduction. J. Chem. Phys. 1986, 85, 5870–5876. [Google Scholar] [CrossRef]
- Guan, X.; Bartschat, K.; Schneider, B.I. Dynamics of two-photon double ionization of helium in short intense xuv laser pulses. Phys. Rev. A 2008, 77, 043421. [Google Scholar] [CrossRef]
- Feist, J.; Nagele, S.; Pazourek, R.; Persson, E.; Schneider, B.I.; Collins, L.A.; Burgdörfer, J. Nonsequential two-photon double ionization of helium. Phys. Rev. A 2008, 77, 043420. [Google Scholar] [CrossRef] [Green Version]
- Feist, J.; Zatsarinny, O.; Nagele, S.; Pazourek, R.; Burgdörfer, J.; Guan, X.; Bartschat, K.; Schneider, B.I. Time delays for attosecond streaking in photoionization of neon. Phys. Rev. A 2014, 89, 033417. [Google Scholar] [CrossRef] [Green Version]
- Burke, P.G.; Burke, V.M. Time-dependent R-matrix theory of multiphoton processes. J. Phys. B At. Mol. Opt. Phys. 1997, 30, L383–L391. [Google Scholar] [CrossRef]
- Nikolopoulos, L.A.A.; Parker, J.S.; Taylor, K.T. Combined R-matrix eigenstate basis set and finite-difference propagation method for the time-dependent Schrödinger equation: The one-electron case. Phys. Rev. A 2008, 78, 063420. [Google Scholar] [CrossRef] [Green Version]
- Lysaght, M.A.; van der Hart, H.W.; Burke, P.G. Time-dependent R-matrix theory for ultrafast atomic processes. Phys. Rev. A 2009, 79, 053411. [Google Scholar] [CrossRef] [Green Version]
- Parker, J.S.; Doherty, B.J.S.; Taylor, K.T.; Schultz, K.D.; Blaga, C.I.; DiMauro, L.F. High-Energy Cutoff in the Spectrum of Strong-Field Nonsequential Double Ionization. Phys. Rev. Lett. 2006, 96, 133001. [Google Scholar] [CrossRef] [Green Version]
- Moore, L.; Lysaght, M.; Nikolopoulos, L.; Parker, J.; van der Hart, H.; Taylor, K. The RMT method for many-electron atomic systems in intense short-pulse laser light. J. Mod. Opt. 2011, 58, 1132–1140. [Google Scholar] [CrossRef]
- Clarke, D.D.A.; Armstrong, G.S.J.; Brown, A.C.; van der Hart, H.W. R-matrix-with-time-dependence theory for ultrafast atomic processes in arbitrary light fields. Phys. Rev. A 2018, 98, 053442. [Google Scholar] [CrossRef] [Green Version]
- Benda, J.; Gorfinkiel, J.D.; Mašín, Z.; Armstrong, G.S.J.; Brown, A.C.; Clarke, D.D.A.; van der Hart, H.W.; Wragg, J. Perturbative and nonperturbative photoionization of H2 and H2O using the molecular R-matrix-with-time method. Phys. Rev. A 2020, 102, 052826. [Google Scholar] [CrossRef]
- Wragg, J.; Clarke, D.D.A.; Armstrong, G.S.J.; Brown, A.C.; Ballance, C.P.; van der Hart, H.W. Resolving Ultrafast Spin-Orbit Dynamics in Heavy Many-Electron Atoms. Phys. Rev. Lett. 2019, 123, 163001. [Google Scholar] [CrossRef] [Green Version]
- Brown, A.C.; Armstrong, G.S.; Benda, J.; Clarke, D.D.; Wragg, J.; Hamilton, K.R.; Mašín, Z.; Gorfinkiel, J.D.; van der Hart, H.W. RMT: R-matrix with time-dependence. Solving the semi-relativistic, time-dependent Schrödinger equation for general, multielectron atoms and molecules in intense, ultrashort, arbitrarily polarized laser pulses. Comput. Phys. Commun. 2020, 250, 107062. [Google Scholar] [CrossRef] [Green Version]
- Github Repository for the B-Spline Atomic R-Matrix (BSR) Code. Available online: https://github.com/zatsaroi/BSR3 (accessed on 24 January 2022).
- Gitlab Repository for the R-Matrix with Time-Dependence (RMT) Code. Available online: https://gitlab.com/Uk-amor/RMT/rmt (accessed on 24 January 2022).
- AMOS Gateway: A Portal for Research and Education in Atomic, Molecular, and Optical Science. Available online: https://amosgateway.org/ (accessed on 20 January 2022).
- Saad, Y. Analysis of Some Krylov Subspace Approximations to the Matrix Exponential Operator. SIAM J. Num. Anal. 1992, 29, 209–228. [Google Scholar] [CrossRef]
- Ndong, M.; Tal-Ezer, H.; Kosloff, R.; Koch, C.P. A Chebychev propagator with iterative time ordering for explicitly time-dependent Hamiltonians. J. Chem. Phys. 2010, 132, 064105. [Google Scholar] [CrossRef] [Green Version]
- McKenna, C.; van der Hart, H.W. Multiphoton ionization cross sections of neon and argon. J. Phys. B At. Mol. Opt. Phys. 2003, 37, 457–470. [Google Scholar] [CrossRef]
- Burke, P.G.; Taylor, K.T. R-matrix theory of photoionization. Application to neon and argon. J. Phys. B At. Mol. Phys. 1975, 8, 2620. [Google Scholar] [CrossRef]
- Bartschat, K.; Fischer, C.F.; Grum-Grzhimailo, A.N. Oleg Zatsarinny (1953–2021): Memories by His Colleagues. Atoms 2021, 9, 109. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).