Abstract
Recently, we reported a series of global minima whose structures consist of carbon rings decorated with heavier group 14 elements. Interestingly, these structures feature planar tetracoordinate carbons (ptCs) and result from the replacement of five or six protons (H+) from the cyclopentadienyl anion (C5H5−) or the pentalene dianion (C8H62−) by three or four E2+ dications (E = Si–Pb), respectively. The silicon derivatives of these series are the Si3C5 and Si4C8 clusters. Here we show that ptC persists in some clusters with an equivalent number of C and Si atoms, i.e., Si5C5, Si8C8, and Si9C9. In all these species, the ptC is embedded in a pentagonal C5 ring and participates in a three-center, two-electron (3c-2e) Si-ptC-Si σ-bond. Furthermore, these clusters are π-aromatic species according to chemical bonding analysis and magnetic criteria.
1. Introduction
Chemists have a great interest in predicting new chemical entities with exotic non-classical structures. Planar hypercoordinate carbon (phC) atoms, i.e., molecules containing carbon atoms linked to four or more ligands in-plane, are particularly puzzling. The phCs violate the well-established rule of van’t Hoff and Le Bel (regarding the concept of tetrahedral four-coordinate carbon); thus, at the beginning, they were considered experimentally inaccessible. However, in 1968, Monkhorst evaluated, theoretically, methane stereomutation through a planar tetracoordinate carbon (ptC) transition state [1]. Two years later, Hoffmann and co-workers proposed different approaches to stabilize a ptC with the modest purpose of achieving a thermally accessible transition state for a racemization process [2]. These pioneering works inspired different studies that finally allowed the identification of viable ptC compounds [3,4,5,6,7].
In the last 50 years, significant progress has been made in synthesizing and “in silico” proposals of numerous ptC compounds [3,4,5,8,9,10,11]. Even more recently, the chemistry of the family was extended to species in which the carbon coordination number is higher than four (penta [12,13,14,15,16,17,18,19,20,21,22] and hexacoordinate [23,24,25,26]). In many of these systems, the formation of delocalized bonds plays a decisive role in their stability. For instance, the experimentally detected ptC CAl42− cluster exhibits doubly σ- and π-aromatic character [10,11].
In 2019, some of the current authors designed a series of ptC global minima composed of carbon and heavier group 14 elements (Si–Pb) [7]. These clusters were obtained by replacing five or six protons (H+) from the cyclopentadienyl anion (C5H5−) or pentalene dianion (C8H62−) by three or six E2+ dications (E = Si–Pb), respectively. In these clusters, the π-aromatic circuits of the parent aromatic hydrocarbons are preserved. The global minima structures of the clusters Si3C5, Ge3C5, Si4C8, and Ge4C8 contain one or two ptCs (see Figure 1). Chemical bonding analysis suggests that these clusters are globally π-aromatic and locally σ-aromatic, where the local aromaticity is due to the E-ptC-E 3c-2e σ-bond. It is important to note that a similar strategy has successfully allowed other aromatic hydrocarbon derivatives with ptCs [6,22,27,28].
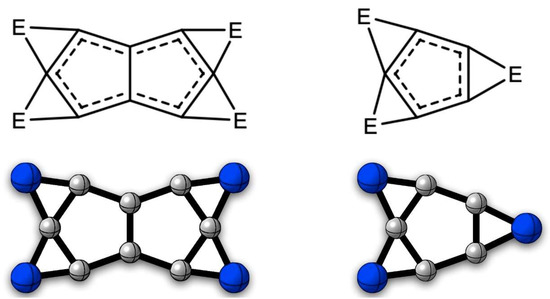
Figure 1.
E3C5 and E4C8 (E = Si–Pb) systems proposed in reference [7], when E = Si and Ge structures correspond to the global minima (see bottom of the figure).
The current work highlights that ptCs are more common than one would think in Si-C clusters. For example, in the SinCn combinations, when n = 5, 8, and 9, the global minima contain ptCs. This feature was not perceived in the works that reported these structures [29,30,31], which has motivated us to highlight it here, and analyze these species’ chemical bonding patterns. Remarkably, silicon carbide (SiC) grains are major dust components in carbon-rich stars of the asymptotic giant branch [29]; and there is evidence that combinations of carbon and silicon with suitable stoichiometries favor the formation of two-dimensional materials with the consequent hypercoordination of C and Si [32,33]. Thus, some of these clusters could be involved in these materials’ formation or fragmentation processes. On the other hand, the ptC in the studied clusters is embedded in a pentagonal C5 ring. This evidence leads us to propose that any polycyclic hydrocarbon, with pentagonal aromatic rings, can be transformed into Si-C clusters favoring the formation of ptCs.
2. Computational Details
The potential energy surface of the species Si5C5, Si8C8, and Si9C9 was explored using the AUTOMATON program [34,35]. Geometry optimizations were performed at the PBE0 [36]/def2–TZVP [37] level. Low-lying isomers were reoptimized at the PBE0–D3 [38]/def2–TZVP level, where dispersion is included in the functional, to identify possible effects on the relative energies. Vibrational frequencies were evaluated at the same level to confirm the optimized structures as true minima on their potential energy surface. These computations were performed using the Gaussian16 program [39].
We computed current densities at PBE0/def2-TZVP level using the GIMIC program [40,41], which employs the gauge-including atomic orbital (GIAO) [42] method. The calculations consider a magnetic field directed along the z-axis, i.e., perpendicular to the molecular plane. Note that the unit for current susceptibility is nA·T−1, and the results are, therefore, independent of the magnitude of the magnetic field. We prepared vector plots of the current density in a plane placed 0.5 Å above the molecular plane. In our analysis, diatropic (aromatic) and paratropic (antiaromatic) currents circle clockwise and counterclockwise, respectively. To visualize current pathways, we used Paraview 5.10.0 software [43,44]. The ring current strengths (RCS), a measure of the net current intensity around a molecular ring of interest, were obtained after considering different integration planes. The integration planes correspond to cut-off planes perpendicular to the chosen bonds of the annular moiety and extend horizontally for 3.6 Å along the ring’s plane, with 2.6 Å above and below the ring. For the integration of the current density passing through an integration plane, GIMIC uses the two-dimensional Gauss–Lobatto algorithm [41,45]. For the RCS, positive (diatropic) and negative (paratropic) signs correspond to the aromatic and anti-aromatic molecules, respectively. RCS values close to zero suggest non-aromatic character [46].
To gain insights about chemical bonding, we used different methods: Wiberg bond indices (WBI) [47], natural population analysis (NPA) [48], and the adaptive natural density partitioning (AdNDP) method [49,50]. These approaches are based on the natural bonding orbital (NBO) method and were performed at the PBE0/def2–TZVP level. The WBI and NPA were computed with the NBO 6.0 code [51], and [41] the AdNDP analysis was performed using Multiwfn 3.8 [52]. The molecular structure and AdNDP results were visualized using CYLview 2.0 [53] and VMD 1.9.3 [54], respectively.
3. Results and Discussion
Figure 2 reports the global minima structures of the clusters analyzed in this study: Si5C5, Si8C8, and Si9C9. We can confirm from our searches using the AUTOMATON program that the identified lowest energy structures are the same as those reported in references [29,30,31]. Note that the dispersion inclusion in the calculations, obtained by Grimme’s method (D3), has no significant influence on the relative energy of the lower energy isomers (see Figures S1–S3, and the Cartesian coordinates reported in Table S1). For Si5C5, the C atoms form a pentagonal ring resembling the cyclopentadienyl anion. On the other hand, for Si8C8 and Si9C9, more indene-like carbon structures are formed. Nonetheless, one Si replaces a C for the former to close the six-membered ring.
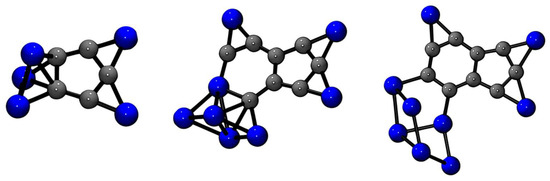
Figure 2.
Structures of the SinCn global minimum (n = 5, 8, 9) as reported in references [29,30,31] and confirmed in this work.
What about chemical bonding in these species? In general, we are interested in looking at the presence of both the 3c-2e bond of Si-ptC-Si and the π-aromatic circuit around the planar carbonaceous moiety. The NPA analysis predicts a negative partial charge distribution on the C and positive on the Si, agreeing with the differences in C/Si electronegativities. However, the most negative charges (about −0.9 ) are on the Si’s surrounding the ptC (see Figure S4). These results agree with the design model for these species, where protons are replaced by Si2+ dication.
Figure 3 shows the chemical bonding interpretation for the Si5C5 cluster according to AdNDP analysis. There are five lone pairs (one on each Si), five 2c-2e C-C σ-bonds connecting the C5 ring (similar to the cyclopentadienyl anion C5H5−). The Si’s on the plane are connected to two C’s (ptC neighbors) of the C5 ring by 2c-2e C-Si σ-bonds and participate in a 3c-2e Si-ptC-Si σ-bond. It also recovered three π-bonds distributed on the planar C5Si2 fragment, suggesting the possibility of aromaticity according to Hückel’s rule. The out-of-plane Si3 fragment shares one edge of the C5 pentagon; it exhibits three 3c-2e σ-bonds and one 2c-2e π-bond. These results show that Si5C5 retains much of the C5H5– π-aromatic features. It also exhibits the multicentric Si-ptC-Si 3c-2e σ-bond, a feature highlighted as a local aromaticity and stabilizing factor in these species [2,6,7,22]. This chemical bonding picture entirely agrees with the Wiberg bond indexes (WBI) analysis. Figure S4 shows that five C-C single bonds (with some contribution of double bonds) join the C5 ring with WBI values between 1.02 and 1.33 (higher than a single bond), the lowest being for the C-C bonded to the out-of-plane Si3 fragment. The in-plane Si-C and Si-ptC bonds have a WBI value of 1.03 and 0.51, in complete agreement with the single and multicentric bonds recovered by AdNDP analysis.
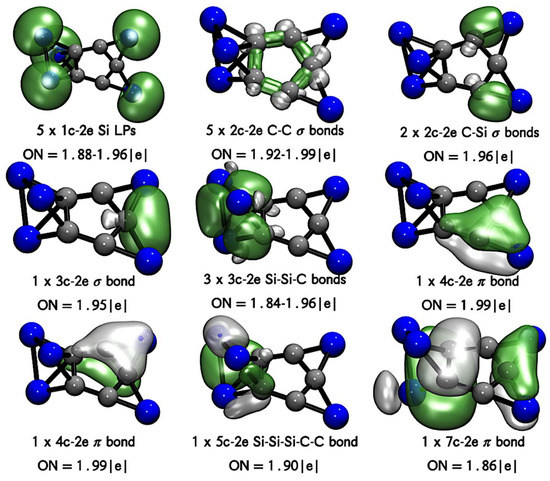
Figure 3.
AdNDP bonding pattern of cluster Si5C5. Occupation numbers (ONs) are shown.
In the case of Si8C8 and Si9C9 (Figure 4 and Figure 5), AdNDP predicts that both have a pentagonal C5 ring connected by 2c-2e C-C σ-bonds. The C5 pentagon of Si8C8 is connected to the chain -C-C-Si-C- by two neighboring vertices. Where 2c-2e σ-bonds link carbons, the Si of this chain forms multicentric bonds with the out-of-plane Si4 fragment and the neighboring C’s. In the case of Si9C9, the pentagonal ring is connected to a C4 chain, forming a bicycle analogous to the indene, where 2c-2e σ-bonds connect this bicycle. In both systems, two in-plane Si’s are coordinating the ptC (embedded in the C5 pentagon), forming part of a 3c-2e Si-ptC-Si σ-bond, in addition to 2c-2e σ-bonds with the C’s neighboring the ptC. In addition, Si9C9 has one of its Si as a bridge (single) on one side of the C6 hexagon, linked to the C’s by Si-C 2c-2e σ-bonds. All in-plane bridged silicon have a lone pair of electrons, in agreement with the design criteria for these species [2,6,7,22]. Both clusters also exhibit π-bonds, six in both cases, which could be associated with an aromatic character. Interestingly, as in Si5C5, the π orbitals are located around the SiC2 fragments (bridged silicon). This bonding feature is also in complete agreement with the initial design strategy of these systems, where it is advisable to use ligands that can receive electrons in their pz orbitals, and thus participate in the π-circuit and aromaticity when it is favored [2,6,7,22]. As with the Si5C5 cluster, the chemical bonding description provided by AdNDP is in complete agreement with the WBI analysis (see Figure S4). WBI predicts bond orders for the C-C bonds slightly higher than the single bonds (higher than 1.15). For Si8C8, the Si that closes the hexagonal ring and which is annealed to the pentagonal ring, has a bond order of 0.82 and 0.84, agreeing with the detection of multicentric bonds according to AdNDP. Besides, Si’s bridged on the hexagonal C6 ring of Si9C9 have Si-C bond orders of 0.75 and 0.81 in agreement with the detection of two S-C single bonds by AdNDP.
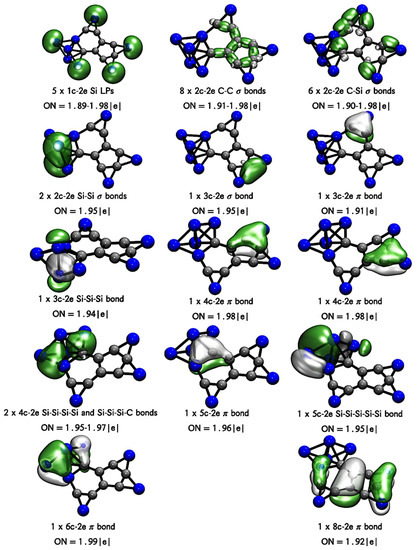
Figure 4.
AdNDP bonding pattern of cluster Si8C8. Occupation numbers (ONs) are shown.
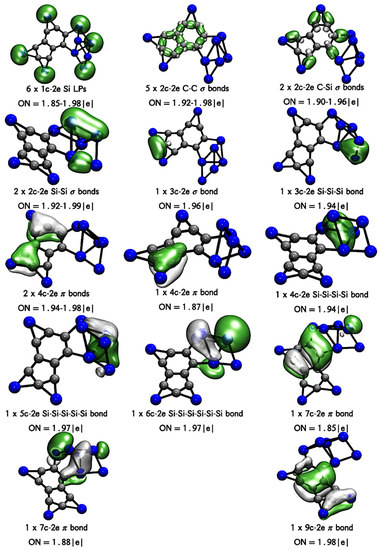
Figure 5.
AdNDP bonding pattern of cluster Si9C9. Occupation numbers (ONs) are shown.
We will now analyze the magnetic response to an external magnetic field applied perpendicular to the Cn plane. This analysis aims to identify patterns related to the (anti) aromaticity phenomenon, i.e., the presence of (diatropic) paratropic ring currents, and to evaluate their intensity (ring current strength, RCS). For reference, the ring current circuits of benzene have been analyzed at the level used in this work. As can be seen from the results (Figure S5), benzene has a paratropic ring current of medium intensity (−3.5 nA.T−1) inside the C6 ring (from σ-electrons). In addition, there is an intense diatropic ring current (15.3 nA.T−1) around the C6 ring, giving an appreciable diatropic resultant of 11.8 nA.T−1, characterizing this aromatic molecule par excellence [40,55,56,57,58].
In this study, the RCS has been evaluated using integration planes for this purpose, placed bisecting different bonds. In addition, profiles of these integration planes have been analyzed to facilitate the dissection of the different contributions: local, semi local, and global. The analysis used to identify the different ring current circuits has been performed according to the strategy initially proposed in references [46,59], which consists of establishing equations that account for the couplings of the different current flows. Note that this strategy has been used satisfactorily in our group in different recent works [60,61]. The integration planes used and the RCS values (total and partial: profiles) are reported in Figures S3–S5 in the Supplementary Material. From the results (summarized in Figure 6), we wish to highlight first the presence of a moderately intense local diatropic current around the ptC, of 4.2, 4.8, and 5.6 nAT−1, for Si5C5, Si8C8, and Si9C9, respectively. The presence of this ring current agrees with the AdNDP analysis, which detects a multicentric Si–ptC–Si σ-bond, thus providing support for the presence of a stabilizing local aromatic contribution. Next, all local C5 and C6 rings have a low-intensity inner paratropic current (between −5.4 and −1.3 nA.T−1), which would be σ in nature, analogous to that exhibited by aromatic hydrocarbons (see the case of benzene mentioned above). Si5C5 exhibits a diatropic current involving the C2-ptC-Si2 fragment, but not the entire C5 pentagon. This arises from the π-electron cloud involving the Si bridged to the C5 ring.
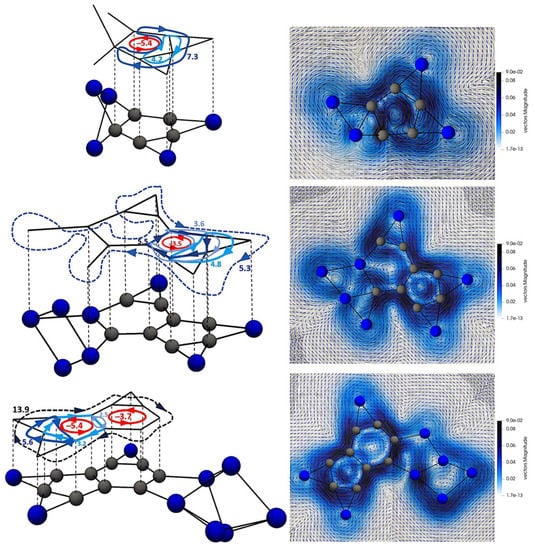
Figure 6.
Schematic representation of local and global currents for Si5C5, Si8C8 and Si9C9 (left) and, the vector plot visualization of their current densities in a plane placed 0.5 Å above the molecular plane (right). RCS values (on each ring current circuit) and the vector intensities are in nA·T−1.
Si8C8 exhibits a local current around the pentagonal C5 ring, which would result from the π bonds in this fragment. A horseshoe-shaped diatropic current circuit is also evident around the C3–ptC–C2 fragment. In addition, there is a semi-local diatropic current that does not close the SiC5 hexagonal circuit; however, it does surround the C5 ring. This is related to the delocalized π-bonds distributed throughout the system. Si9C9 exhibits a local diatropic current around the C5 ring (3.2 nA.T−1) with participation of the π-orbitals. In addition, an intense global diatropic current (13.9 nA.T−1) is evident, which is mainly delocalized around the C9 ring. To summarize (Figure 6), Si5C5, Si8C8, and Si9C9 exhibit local aromaticity (σ and π), with the participation of bridged Si and ptC and semi-local aromaticity (in the first two), and global aromaticity in the case of Si9C9, as a consequence of the π-electron cloud.
4. Conclusions
Here, we highlight that the global minima of the Si5C5, Si8C8, and Si9C9 clusters comprise a planar tetracoordinate carbon (ptC), a feature unnoticed in previous works. Chemical bonding analysis allows us to establish that Cn rings are formed, monocyclic in the case of Si5C5, and bicyclic in the other two (in the case of Si8C8, a Si atom close one of the rings). A pentagonal C5 ring is present in the latter, similar to what happens in the former. The ptC is embedded in this pentagonal ring in all cases, in which two Si form a 3c–2e Si–ptC–Si σ-bond. In addition, several delocalized π-bonds are detected. Therefore, the bonding analysis suggests the possibility of both local (σ) and semi-local or global (π) aromaticity. The latter is corroborated by the analysis of induced current density by an external magnetic field; i.e., the presence of local, semi-local, and global diatropic rings—a characteristic of aromatic compounds—is confirmed. In particular, in all cases, a local ring current is detected between the Si–ptC–Si fragment, which confirms this local aromatic σ-contribution. The other contributions would be of the π-type. These findings open up the possibility of identifying other Si–C combinations in which conditions are provided to favor the presence of ptCs; that is, to favor local, semi-local and global aromaticity in these species.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/atoms10010027/s1, Figures S1–S3: Global minimum and low-lying isomers of SinCn (n = 5, 8 and 9), their point group symmetries and spectroscopic states. Relative energies are shown in kcal.mol−1 at PBE0/def2-TZVP and PBE0-D3/def2-TZVP (in parentheses) levels, including zero-point energy (ZPE) corrections. Figure S4: Bond length in Å (black), natural charges (red), and Wiberg bond indices (blue) for (a) Si5C5, (b) Si8C8, and (c) Si9C9 global minimum at the PBE0/def2-TZVP level. Figures S5–S8: (a) Vector plot visualization of the current density of C6H6, Si5C5, Si8C8 and Si9C9 in a plane placed 0.5 Å above the molecular plane and top view of integration planes. The intensities of the diatropic currents are indicated in blue and the intensity of the paratropic currents is red. The intensity of the total current susceptibility is the sum of the paratropic and diatropic contributions. (b) Integration profiles along the integration planes of C6H6, Si5C5, Si8C8, and Si9C9. Table S1: Cartesian Coordinates of the Si5C5, Si8C8, Si9C9 global minimum calculated at the PBE0/def2-TZVP level of theory.
Author Contributions
Conceptualization, W.T., V.G., L.L.-P. and O.Y.; methodology, D.I., O.Y., J.C.C., V.G. and J.G.; software, D.I., O.Y., J.C.C. and J.G.; validation, W.T., O.Y. and V.G.; formal analysis, W.T. and L.L.-P.; investigation, W.T., L.L.-P. and O.Y.; resources, W.T. and J.G.; data curation, L.L.-P., V.G. and J.C.C.; writing—original draft preparation, W.T., L.L.-P. and V.G.; writing—review and editing, all authors.; visualization, W.T., O.Y. and V.G.; supervision, W.T.; project administration, W.T.; funding acquisition, W.T. and J.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by FONDECYT grant number 1211128.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We thank the financial support of the National Agency for Research and Development (ANID) through FONDECYT project 1211128 (W.T.) and National Agency for Research and Development (ANID)/Scholarship Program/BECAS DOCTORADO NACIONAL/2019-21190427 (D.I.). National Agency for Research and Development (ANID)/Scholarship Program/BECAS DOCTORADO NACIONAL/2020-21201177 (L.L.-P.). Powered@NLHPC: This research was partially supported by the supercomputing infrastructure of the NLHPC (ECM-02).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Monkhorst, H.J. Activation energy for interconversion of enantiomers containing an asymmetric carbon atom without breaking bonds. Chem. Commun. 1968, 18, 1111–1112. [Google Scholar] [CrossRef]
- Hoffmann, R.; Alder, R.W.; Wilcox, C.F. Planar tetracoordinate carbon. J. Am. Chem. Soc. 1970, 92, 4992–4993. [Google Scholar] [CrossRef]
- Siebert, W.; Gunale, A. Compounds containing a planar-tetracoordinate carbon atom as analogues of planar methane. Chem. Soc. Rev. 1999, 28, 367–371. [Google Scholar] [CrossRef]
- Keese, R. Carbon flatland: Planar tetracoordinate carbon and fenestranes. Chem. Rev. 2006, 106, 4787–4808. [Google Scholar] [CrossRef] [PubMed]
- Merino, G.; Méndez-Rojas, M.A.; Vela, A.; Heine, T. Recent advances in planar tetracoordinate carbon chemistry. J. Comput. Chem. 2007, 28, 362–372. [Google Scholar] [CrossRef]
- Yañez, O.; Vásquez-Espinal, A.; Pino-Rios, R.; Ferraro, F.; Pan, S.; Osorio, E.; Merino, G.; Tiznado, W. Exploiting electronic strategies to stabilize a planar tetracoordinate carbon in cyclic aromatic hydrocarbons. Chem. Commun. 2017, 53, 12112–12115. [Google Scholar] [CrossRef]
- Yañez, O.; Vásquez-Espinal, A.; Báez-Grez, R.; Rabanal-León, W.A.; Osorio, E.; Ruiz, L.; Tiznado, W. Carbon rings decorated with group 14 elements: New aromatic clusters containing planar tetracoordinate carbon. New J. Chem. 2019, 43, 6781–6785. [Google Scholar] [CrossRef]
- Erker, G. Planar-Tetracoordinate Carbon: Making Stable Anti-van′ t Hoff/LeBel Compounds. Comments Inorg. Chem. 1992, 13, 111–131. [Google Scholar] [CrossRef]
- Röttger, D.; Erker, G. Compounds Containing Planar-Tetracoordinate Carbon. Angew. Chem. Int. Ed. Engl. 1997, 36, 812–827. [Google Scholar] [CrossRef]
- Zhang, X.; Ding, Y. Computational prediction of a global planar penta-coordinate carbon structure CAl4Ga+. Comput. Theor. Chem. 2014, 1048, 18–24. [Google Scholar] [CrossRef]
- Li, X.; Zhang, H.; Wang, L.; Geske, G.D.; Boldyrev, A.I. Pentaatomic tetracoordinate planar carbon, [CAl4]2−: A new structural unit and its salt complexes. Angew. Chemie Int. Ed. 2000, 39, 3630–3632. [Google Scholar] [CrossRef]
- Wang, Z.-X.; von Ragué Schleyer, P. Construction principles of” hyparenes”: Families of molecules with planar pentacoordinate carbons. Science 2001, 292, 2465–2469. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Li, F.; Li, Y.; Chen, Z. Semi-metallic Be 5 C 2 monolayer global minimum with quasi-planar pentacoordinate carbons and negative Poisson’s ratio. Nat. Commun. 2016, 7, 11488. [Google Scholar] [CrossRef] [PubMed]
- Tiznado, W.; Leyva-Parra, L.; Diego, L.; Inostroza, D.; Yañez, O.; Pumachagua-Huertas, R.; Barroso, J.; Vásquez-Espinal, A.; Merino, G. Planar Hypercoordinate Carbons in Alkali Metal Decorated CE32-and CE22-Dianions. Chem. Eur. J. 2021, 27, 16701–16706. [Google Scholar]
- Pan, S.; Cabellos, J.L.; Orozco-Ic, M.; Chattaraj, P.K.; Zhao, L.; Merino, G. Planar pentacoordinate carbon in CGa5+ derivatives. Phys. Chem. Chem. Phys. 2018, 20, 12350–12355. [Google Scholar] [CrossRef]
- Pei, Y.; An, W.; Ito, K.; von Schleyer, P.R.; Zeng, X.C. Planar pentacoordinate carbon in CAl5+: A global minimum. J. Am. Chem. Soc. 2008, 130, 10394–10400. [Google Scholar] [CrossRef]
- Vassilev-Galindo, V.; Pan, S.; Donald, K.J.; Merino, G. Planar pentacoordinate carbons. Nat. Rev. Chem. 2018, 2, 114. [Google Scholar] [CrossRef]
- Grande-Aztatzi, R.; Cabellos, J.L.; Islas, R.; Infante, I.; Mercero, J.M.; Restrepo, A.; Merino, G. Planar pentacoordinate carbons in CBe54− derivatives. Phys. Chem. Chem. Phys. 2015, 17, 4620–4624. [Google Scholar] [CrossRef]
- Zhao, X.-F.; Bian, J.-H.; Huang, F.; Yuan, C.; Wang, Q.; Liu, P.; Li, D.; Wang, X.; Wu, Y.-B. Stabilization of beryllium-containing planar pentacoordinate carbon species through attaching hydrogen atoms. RSC Adv. 2018, 8, 36521–36526. [Google Scholar] [CrossRef]
- Jimenez-Halla, J.O.C.; Wu, Y.-B.; Wang, Z.-X.; Islas, R.; Heine, T.; Merino, G. CAl4Be and CAl3Be2−: Global minima with a planar pentacoordinate carbon atom. Chem. Commun. 2010, 46, 8776–8778. [Google Scholar] [CrossRef]
- Cui, Z.; Vassilev-Galindo, V.; Cabellos, J.L.; Osorio, E.; Orozco, M.; Pan, S.; Ding, Y.; Merino, G. Planar pentacoordinate carbon atoms embedded in a metallocene framework. Chem. Commun. 2017, 53, 138–141. [Google Scholar] [CrossRef] [PubMed]
- Yañez, O.; Báez-Grez, R.; Garza, J.; Pan, S.; Barroso, J.; Vásquez-Espinal, A.; Merino, G.; Tiznado, W. Embedding a Planar Hypercoordinate Carbon Atom into a [4n+ 2] π-System. ChemPhysChem 2020, 21, 145–148. [Google Scholar] [CrossRef]
- Wu, Y.-B.; Duan, Y.; Lu, G.; Lu, H.-G.; Yang, P.; von Rague Schleyer, P.; Merino, G.; Islas, R.; Wang, Z.-X. D3hCN3Be3+ and CO3Li3+: Viable planar hexacoordinate carbon prototypes. Phys. Chem. Chem. Phys. 2012, 14, 14760–14763. [Google Scholar] [CrossRef] [PubMed]
- Exner, K.; von Ragué Schleyer, P. Planar hexacoordinate carbon: A viable possibility. Science 2000, 290, 1937–1940. [Google Scholar] [CrossRef] [PubMed]
- Parra, L.L.; Diego, L.; Yañez, O.; Inostroza, D.; Barroso, J.; Espinal, A.V.; Merino, G.; Tiznado, W. Planar Hexacoordinate Carbons: Half Covalent, Half Ionic. Angew. Chem. Int. Ed. Engl. 2021, 60, 8700–8704. [Google Scholar] [CrossRef]
- Li, Y.; Liao, Y.; Chen, Z. Be2C monolayer with quasi-planar hexacoordinate carbons: A global minimum structure. Angew. Chemie 2014, 126, 7376–7380. [Google Scholar] [CrossRef]
- Perez, N.; Heine, T.; Barthel, R.; Seifert, G.; Vela, A.; Mendez-Rojas, M.A.; Merino, G. Planar tetracoordinate carbons in cyclic hydrocarbons. Org. Lett. 2005, 7, 1509–1512. [Google Scholar] [CrossRef]
- Perez-Peralta, N.; Sanchez, M.; Martin-Polo, J.; Islas, R.; Vela, A.; Merino, G. Planar Tetracoordinate Carbons in Cyclic Semisaturated Hydrocarbons. J. Org. Chem. 2008, 73, 7037–7044. [Google Scholar] [CrossRef]
- Gobrecht, D.; Cristallo, S.; Piersanti, L.; Bromley, S.T. Nucleation of small silicon carbide dust clusters in AGB stars. Astrophys. J. 2017, 840, 117. [Google Scholar] [CrossRef]
- Byrd, J.N.; Lutz, J.J.; Jin, Y.; Ranasinghe, D.S.; Montgomery, J.A., Jr.; Perera, A.; Duan, X.F.; Burggraf, L.W.; Sanders, B.A.; Bartlett, R.J. Predictive coupled-cluster isomer orderings for some Si n C m (m, n ≤ 12) clusters: A pragmatic comparison between DFT and complete basis limit coupled-cluster benchmarks. J. Chem. Phys. 2016, 145, 24312. [Google Scholar] [CrossRef]
- Duan, X.F.; Burggraf, L.W.; Huang, L. Searching for stable SinCn clusters: Combination of stochastic potential surface search and pseudopotential plane-wave car-parinello simulated annealing simulations. Molecules 2013, 18, 8591–8606. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Li, F.; Zhou, Z.; Chen, Z. SiC2 Silagraphene and Its One-Dimensional Derivatives: Where Planar Tetracoordinate Silicon Happens. J. Am. Chem. Soc. 2011, 133, 900–908. [Google Scholar] [CrossRef] [PubMed]
- Kilic, M.E.; Lee, K.-R. Tetrahex carbides: Two-dimensional group-IV materials for nanoelectronics and photocatalytic water splitting. Carbon N. Y. 2021, 174, 368–381. [Google Scholar] [CrossRef]
- Yañez, O.; Báez-Grez, R.; Inostroza, D.; Rabanal-León, W.A.; Pino-Rios, R.; Garza, J.; Tiznado, W. AUTOMATON: A program that combines a probabilistic cellular automata and a genetic algorithm for global minimum search of clusters and molecules. J. Chem. Theory Comput. 2019, 15, 1463–1475. [Google Scholar] [CrossRef] [PubMed]
- Yañez, O.; Inostroza, D.; Usuga-Acevedo, B.; Vásquez-Espinal, A.; Pino-Rios, R.; Tabilo-Sepulveda, M.; Garza, J.; Barroso, J.; Merino, G.; Tiznado, W. Evaluation of restricted probabilistic cellular automata on the exploration of the potential energy surface of Be6B11−. Theor. Chem. Acc. 2020, 139, 41. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revisión C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Fliegl, H.; Taubert, S.; Lehtonen, O.; Sundholm, D. The gauge including magnetically induced current method. Phys. Chem. Chem. Phys. 2011, 13, 20500–20518. [Google Scholar] [CrossRef]
- Jusélius, J.; Sundholm, D.; Gauss, J. Calculation of current densities using gauge-including atomic orbitals. J. Chem. Phys. 2004, 121, 3952–3963. [Google Scholar] [CrossRef]
- Wolinski, K.; Hinton, J.F.; Pulay, P. Efficient implementation of the gauge-independent atomic orbital method for NMR chemical shift calculations. J. Am. Chem. Soc. 1990, 112, 8251–8260. [Google Scholar] [CrossRef]
- Ahrens, J.; Geveci, B.; Law, C. Paraview: An end-user tool for large data visualization. In Visualization Handbook; Elsevier: Amsterdam, The Netherlands, 2005; ISBN 9780123875822. [Google Scholar]
- Ayachit, U. The ParaView Guide: A Parallel Visualization Application; Kitware, Inc.: New York, NY, USA, 2015; ISBN 9781930934306. [Google Scholar]
- Abramowitz, M. Handbook of Mathematical Functions, with Formulas, Graphs, and Mathematical Tables; Dover Publications, Inc.: New York, NY, USA, 1974; ISBN 0486612724. [Google Scholar]
- Sundholm, D.; Fliegl, H.; Berger, R.J.F. Calculations of magnetically induced current densities: Theory and applications. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2016, 6, 639–678. [Google Scholar] [CrossRef]
- Wiberg, K.B. Application of the pople-santry-segal CNDO method to the cyclopropylcarbinyl and cyclobutyl cation and to bicyclobutane. Tetrahedron 1968, 24, 1083–1096. [Google Scholar] [CrossRef]
- Reed, A.E.; Weinstock, R.B.; Weinhold, F. Natural population analysis. J. Chem. Phys. 1985, 83, 735–746. [Google Scholar] [CrossRef]
- Zubarev, D.Y.; Boldyrev, A.I. Developing paradigms of chemical bonding: Adaptive natural density partitioning. Phys. Chem. Chem. Phys. 2008, 10, 5207–5217. [Google Scholar] [CrossRef] [PubMed]
- Zubarev, D.Y.; Boldyrev, A.I. Revealing intuitively assessable chemical bonding patterns in organic aromatic molecules via adaptive natural density partitioning. J. Org. Chem. 2008, 73, 9251–9258. [Google Scholar] [CrossRef]
- Glendening, E.D.; Badenhoop, J.K.; Reed, A.E.; Carpenter, J.E.; Bohmann, J.A.; Morales, C.M.; Landis, C.R.; Weinhold, F. Natural Bond Orbital Analysis Program: NBO 6.0; Theoretical Chemistry Institute, University of Wisconsin: Madison, WI, USA, 2013. [Google Scholar]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Legault, C.Y. CYLview, 1.0b. Université de Sherbrooke. 2009. Available online: http://www.cylview.org (accessed on 14 January 2022).
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Lazzeretti, P. Assessment of aromaticity via molecular response properties. Phys. Chem. Chem. Phys. 2004, 6, 217–223. [Google Scholar] [CrossRef]
- Lazzeretti, P. Current density tensors. J. Chem. Phys. 2018, 148, 134109. [Google Scholar] [CrossRef]
- Lazzeretti, P.; Zanasi, R. Theoretical studies of the benzene molecule: Magnetic susceptibility and nuclear shielding constants. J. Chem. Phys. 1981, 75, 5019–5027. [Google Scholar] [CrossRef]
- Juse, J.; Sundholm, D. Ab initio determination of the induced ring current in aromatic molecules. Phys. Chem. Chem. Phys. 1999, 1, 3429–3435. [Google Scholar]
- Sundholm, D.; Berger, R.J.F.; Fliegl, H. Analysis of the magnetically induced current density of molecules consisting of annelated aromatic and antiaromatic hydrocarbon rings. Phys. Chem. Chem. Phys. 2016, 18, 15934–15942. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Inostroza, D.; García, V.; Yañez, O.; Torres-Vega, J.J.; Vásquez-Espinal, A.; Pino-Rios, R.; Báez-Grez, R.; Tiznado, W. On the NICS limitations to predict local and global current pathways in polycyclic systems. New J. Chem. 2021, 45, 8345–8351. [Google Scholar] [CrossRef]
- Torres-Vega, J.J.; Alcoba, D.R.; Oña, O.B.; Vásquez-Espinal, A.; Báez-Grez, R.; Lain, L.; Torre, A.; García, V.; Tiznado, W. Analysis of local and global aromaticity in Si3C5 and Si4C8 Clusters. Aromatic species containing planar tetracoordinate carbon. Chemistry 2021, 3, 1101–1112. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).