Abstract
Double photoionization events provide a direct evaluation of electron correlation. The recent focus on few-electron targets continues to reveal the consequences of electron correlation for targets that possess several electrons. We consider the double photoionization of the valence electrons of atomic carbon and focus on the first energetically accessible final-state symmetries that originate from coupling the active electrons in configurations, which are doubly ionized by a single photon. Comparison of this process in carbon with neon provides an analogous case for the resulting final-state symmetries within the framework where the ejected electrons are influenced by the remaining bound electrons in a frozen-core approximation. Choosing this symmetry allows for comparison with previous theoretical results for total and energy sharing cross-sections of carbon. Fully differential cross-sections for both carbon and neon are also compared.
1. Introduction
Single-photon double photoionization (DPI) from an atom or molecule has provided valuable insights into the nature of fundamental systems by serving as a direct evaluation of electron correlation and its influence on the resulting angular distributions of the outgoing two electrons. Spurred by sophisticated experimental techniques that can detect the ejected electrons in coincidence with the resulting ionic fragment(s), theoretical investigations have been undertaken for many years to study the consequences of electron correlation in simple targets. The simplest target to investigate atomic double photoionization is helium, where, for some time, good agreement between experimental and theoretical formulations has led to a virtually complete understanding of the double photoionization dynamics in this fundamental atom [1,2,3].
For other atoms, the majority of the progress towards studying double ionization has focused on helium-like systems, with several theoretical calculations exploring valence double ionization of the helium-like configurations by single photoabsorption [4,5,6,7,8,9,10,11,12,13,14,15]. As one example, several examinations [16,17,18,19] of double photoionization of the valence shell of atomic magnesium focused on pathways towards the double continuum in analyzing the experimental measurements of the triple-differential cross-section (TDCS) [16,17], which measures the angular distributions of both electrons and their energy sharing above the double ionization threshold and represents the most detailed information that can be measured in the correlated event. Determining the TDCS and analyzing the influences upon it are major goals of theory work in this field, and achieving agreement with coincidence measurements that experimentally resolve the same gives much greater insight into the details of DPI and the consequences of electron correlation.
Even if not at the level of detail examining angular distributions, double photoionization studies to measure total cross-sections of other target atoms remain an active area of research [20,21]. When considering other atomic targets in double photoionization events, particularly those that have the outgoing electrons in configurations distinct from the helium-like systems, other final-state symmetries are possible and distinct from the helium-like atoms and transitions that go into an overall final state. If we consider double photoionization of a pair of electrons, the final-state continua that are accessible by absorbing a single photon are distinguished from how the electrons are initially coupled. In the initial (bound) state, it is possible to couple these electrons into , and symmetries, of which is the lowest energy. In this case, photoabsorption selection rules lead to two possible final-state symmetries: , both with odd parity. This would be the case for the lowest energy valence double ionization of a carbon atom, which is the focus of this manuscript. Previous theoretical work for this configuration also exists [22] and allows for a comparison of the present results.
To study this valence photoionization process, one must account for the other four electrons in the core occupancy. As a starting approximation, these electrons can be held fixed in all configuration interaction (CI) expansion terms, rendering them into a “frozen-core approximation” whereby they provide a closed-shell Coulomb and exchange interaction with the outer electrons that are fully active in the CI expansion, and the action of the photon also carries these electrons into the double continuum. All that is required is the atomic orbitals of the electrons held fixed throughout, which are then placed on an underlying radial grid used to describe the active electrons. The radial profile of these atomic orbitals can be determined from a number of atomic structure packages; here, we have utilized the BSR packages of Zatsarinny and co-workers [23,24].
A brief overview of the method follows in Section 2; more detail can be found in the references that illustrate the applications in both time-independent, single-photon double ionization studies (as here) [11,13,19], as well as time-dependent frameworks [25,26,27] applied to two-photon processes. Double photoionization results from carbon are presented in Section 3 and compared with earlier MBPT calculations [22], and expanded to consider the TDCS from this initial-state symmetry that is distinct from helium-like targets. It is also interesting to consider the parallel case from a closed-shell target that can be treated equivalently in the hole states after double ionization, being similarly coupled in order to examine the consequences of the common final-state symmetry. Thus, we also present calculated results from atomic neon, where two of the valence electrons are doubly ejected into the continuum, leaving behind a double cation with the electrons coupled into configurations and thereby assuring that the outgoing (active) electrons also originated in initial-state configurations; this provides the ability to compare with the analogous ground-state process in carbon and better understand the consequences of the initial- and final-state symmetries on the resulting angular distributions.
2. Theoretical Methods
A brief overview of the description of the wave function for two active electrons in the field of the frozen-core electrons is provided below (see Ref. [19] and the references therein for more details and applications to single-photon, time-independent DPI of atoms, as well as Ref. [27] for a similar discussion of the time-dependent approach applied to two-photon absorption). We also briefly overview the calculation of the TDCS, from which integrated cross-sections can be computed. In what follows, atomic units are assumed, unless otherwise stated.
2.1. Describing the Two Active Electrons of the Atomic Target
The two-active-electron treatment applied here relies on a frozen-core approximation for the electrons that remain attached to the atomic target after double photoionization. Within this frozen-core approximation for DPI of carbon, we can thus regard the effective two-electron problem as a full CI of the valence electrons of the initial state, and throughout influenced by the presence of a (fixed) core configuration, leading to the Hamiltonian of interest for the active (outgoing) electrons:
where the interaction between the electrons to be ejected by the photoabsorption is encoded in and the influence of the remaining electrons on the fully active electrons is accounted for in the one-body operator h:
where T is the one-electron kinetic energy, is the nuclear attraction, and the terms in the sum over occupied orbitals, and , account for the direct and exchange interactions felt by the valence electrons from the and core orbitals of carbon. For each of these doubly occupied orbitals, the direct operator has the form given by
while the non-local exchange interaction operating on the orbital is given by
Thus, the effect of the doubly occupied and orbitals provides the Coulombic screening and non-local exchange interaction seen by the fully active pair of electrons for atomic carbon that are to be removed by the photon. In this case, the double ionization potential is the total energy minus the energy of the frozen-core electrons, which is also the bound-state energy of the two-active-electron Hamiltonian in Equation (1).
This is slightly modified in the case of DPI from neon that follows, in that, in addition to the (closed-shell) interactions of the and orbitals, we also add to the one-electron Hamiltonian in Equation (2), a direct interaction term representing the Coulomb screening of the remaining four valence electrons of the open-shell dication. This approximation ignores the exchange interaction of the outgoing electrons with the open-shell electrons of the target dication, which cannot be represented without introducing energy-dependent Hamiltonian terms; however, good agreement between the calculated results using this approximation (i.e., effectively ignoring exchange interactions with the open-shell electrons) still yields computed TDCS results [28] whose magnitude and angular distributions agree substantially well with experimental results for neon [29] in all final-state symmetries, as well as for argon in the configuration [30], for which state-selective DPI experimental measurements have been reported. The excellent agreement with experimental results under this approximation suggests that the key correlation to accurately account for lies between the outgoing electrons (and influenced by their initial and final state couplings) and may most significantly impact the resulting TDCS angular distributions.
In the case of either carbon or neon, the radial profiles of the atomic orbitals held fixed in the frozen-core approximation have been outputted from the BSR code [23] from a non-relativistic electronic structure calculation describing the neutral target, and numerically resolved on a radial grid that is constructed using a finite element method with discrete variable representation (FEM-DVR) [31], which gives a particularly efficient accounting for the frozen atomic orbital interactions on the fully active electrons [11]. The transformation of the underlying FEM-DVR grid basis into an atomic orbital basis (over a subset of the radial grid near the nucleus spanning the extent of the bound atomic orbitals) from the first M primitive FEM-DVR functions can be represented as a change of basis,
such that the atomic orbitals built from the underlying FEM-DVR functions , with , are precisely the atomic orbitals for the CI configurations of both active and frozen electrons throughout the problem. The key to this efficiency is the transformation of the two-electron matrix elements being diagonal in each electron’s radial coordinate arising from the underlying properties of the FEM-DVR basis, and thus the evaluation of electronic repulsion terms is never a full four-index transformation, but rather a computationally simpler two-index transformation [11]. The angular coordinates of the outgoing electrons can be efficiently described using coupled spherical harmonics , allowing for the expansion of the problem in terms of coupled radial equations as
with restrictions on the values appropriate to determine the overall configuration of the initial or final states.
2.2. Determining the Double Photoionization Amplitudes and Cross Sections
To define the cross-section data presented in Section 3 in terms of the double ionization amplitudes computed, a brief overview is provided here; more detail can be found in Ref. [11]. In the time-independent formalism we employ here, the double ionization amplitudes that describe two electrons in the continuum after photoabsorption are determined by solving a driven Schrödinger equation:
where is the total available energy that the ejected electrons share above the double ionization potential , is the photon energy, and the right-hand-side driving term of Equation (7) represents, within the dipole approximation, the action of the linearly polarized photon with polarization direction . In solving this driven equation for the scattered wave solution , we represent both the scattered and the initial state on a radial grid of atomic orbitals, which themselves are linear combinations of the underlying FEM-DVR grid (as in Equation (5)), and impose the outgoing wave boundary conditions using exterior complex scaling (ECS) [32].
From the scattered wave solution above, we can isolate the double continuum amplitudes for electrons with momenta and ,
using a surface integral formulation for each of the partial waves by integrating along a surface using testing functions that are continuum states of the individual one-body Hamiltonian h of the residual dication given in Equation (2). This renders the partial wave double ionization amplitudes into radial surface integrals along the hyper-radius arc , given by
at some appropriate hyper-radius .
From these double ionization amplitudes, the triply differential cross-sections (TDCS) can be computed (in the velocity gauge) as
with similar results differing only in the factors of and c in the length gauge. Integrating over the angular directions of the electrons ( and ) yields the single-differential cross-section (SDCS), which describes the energy sharing of the outgoing electrons for a fixed total energy above the double ionization threshold. Finally, integrating the SDCS over the possible energy sharings yields the total double ionization cross-section for a fixed photon energy :
2.3. Computational Details
The radial grid for expanding the atomic orbitals, as well as the primitive FEM-DVR grid that describes the continuum, consisted of finite element boundaries from the nucleus at and increased by bohr until , where the ECS tail consisted of two additional finite elements up to with an ECS rotation angle of . The atomic orbitals are transformed on the subset of the grid within the first four finite elements (up to ), with 18th-order DVR in each finite element throughout. Results were unchanged by increasing the DVR order or additional finite elements extending the grid. Angular convergence of the results was achieved with up to for each electron in the partial wave expansion. With these grid parameters, the double ionization potential for removing the valence electrons from the state of carbon was determined to be eV, in good agreement with tabulated atomic data results [33].
3. Results
Results for the total double photoionization cross-section of carbon have been computed and compared with the previous many-body perturbation theory (MBPT) results of Carter and Kelly [22], which, to our knowledge, are the only other results for double ionization of this atomic target. Figure 1 shows the current results (points) along with the MBPT results (lines). Both length and velocity gauge results have been computed, the difference between gauges appearing to be a small overall shift in the magnitude of the total cross-section in both the present results and the MBPT calculation. The gauge dependence largely indicates sensitivity to the exactness of the initial state, but generally good agreement in the falloff of the total DPI cross-section exists. Present results are smaller in magnitude than the MBPT calculations and appear to peak nearer to the double ionization threshold. The difference in magnitude of the cross-sections with results from Ref. [22] may lie in the previous calculation being limited to only include the lowest two angular momenta continua (), while the present results have up to and are converged to graphical accuracy with up to included for each electron.
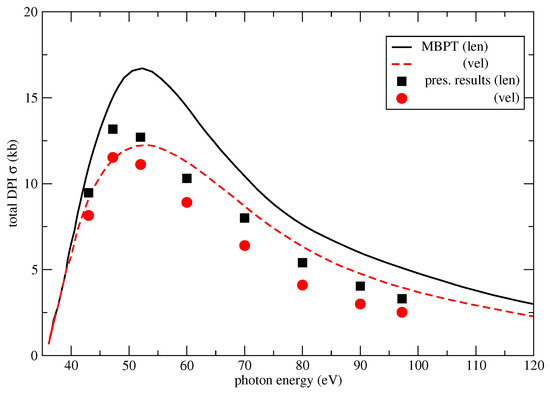
Figure 1.
Total double photoionization cross-section of the valence electrons in carbon. Lines: length (solid black) and velocity (dashed red) gauge results using MBPT from Ref. [22]; present results in length (black squares) and velocity (red circles) gauges are generally slightly smaller in magnitude. 1 kb = cm.
Figure 2 plots the single-differential cross-section (SDCS) computed for two excess photon energies; the upper panel corresponds to eV ( eV excess energy) while the lower panel shows the same at a photon energy of eV ( eV excess energy). In both cases, the length and velocity gauge results exhibit an energy sharing pattern that is familiar from the double photoionization of other atoms, where the cross-section changes from relatively flat at lower photon energies and becomes more peaked towards extreme energy sharings as the photon energy increases. Additionally plotted are the MBPT results of Ref. [22], although the authors there only provide a single partial wave component (the most significant contribution) and do not indicate the magnitude of the contribution from the continuum. In comparing with this dominant single partial wave component, though, agreement between the present results for the two gauges and with the prior MBPT calculation is reasonable and displays general trends associated with the SDCS.
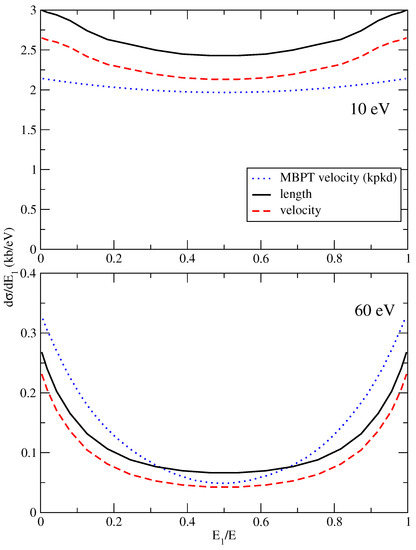
Figure 2.
Single-differential cross-section (SDCS) results from DPI of carbon at two excess energies: 10 eV (upper panel) and 60 eV (lower panel). Present results in the length (solid black line) and velocity (dashed red line) gauges are compared with the contribution of MBPT (dotted blue line) from Ref. [22]. 1 kb = cm.
We now turn our attention to the triple-differential cross-section (TDCS) and examine the co-planar geometry with the photon polarization and ejected electron directions lying in a common plane. In the following results, we focus on the velocity gauge, which has generally shown better agreement with experimentally measured angular distributions for neon and argon in this treatment [28]. Figure 3 shows the results for DPI of carbon at a photon energy of eV, leaving 10 eV of excess energy, which is shared equally between the electrons. Each panel in Figure 3 shows the cross-section as the fixed electron direction (labeled as electron 1 and indicated by the blue arrow) is changed relative to the linear polarization of the photon. Perhaps the most noteworthy aspect of these equal energy sharing cross-sections for carbon is the allowance of the electrons to go out back-to-back at equal energy sharing, in contrast to a selection rule that prohibits the same in a helium-like DPI event [34], where the event symmetry is overall for single-photon absorption.
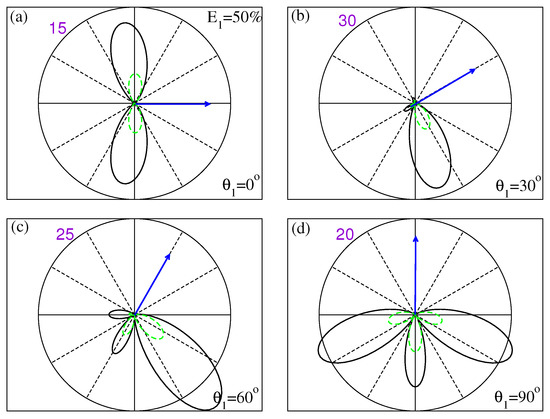
Figure 3.
Triple-differential cross-section (TDCS) results from DPI of carbon at 10 eV excess energy ( eV) and equal energy sharing (). Each panel (a–d) shows the resulting angular distribution of the second electron when the first electron direction (blue arrow) is fixed at the angle shown relative to the polarization direction (horizontal). Present results for carbon (solid black line) are shown and compared with neon results (dashed green line) for the same initial-state coupling of the outgoing electrons and at similar excess energies as a percentage of the double ionization potential ( eV for neon). The purple numbers in each panel indicate the magnitude of the cross-section (in b/(eV sr) and establishes the radius of each circle. 1 b = cm.
In addition to the carbon TDCS shown, in each panel, we also plot the absolute cross-section for DPI of neon, where the outgoing electrons are also initially coupled in a symmetry, to examine the overall consequences of the symmetry considerations that govern the angular distributions. Results for neon (dashed green curves) have been calculated such that the excess energy that the electrons carry away is the same fraction of the double ionization potential ( eV); this provides a more meaningful comparison to examine similarities between these atomic targets than comparing at the same total excess energy. Generally, the neon cross-sections are smaller in magnitude than for atomic carbon, but very similar angular distribution patterns result, indicating that the directional aspects of the double photoionization are largely determined by the overall symmetry of the transition, with being common to both atomic targets.
Finally, we examine the TDCS in a case of unequal energy sharing, as shown in Figure 4. Here, results are computed with the fixed electron (blue arrow direction) now carrying of the available excess energy. Again, the results for both carbon and neon exhibit similar angular patterns that are largely dictated by the common symmetry under single-photon absorption. The prominent lobes in the angular patterns of each target are also roughly similar in magnitude and direction to the results with equal energy sharing, with variations being seen in the relative size of secondary lobes in several of the panels being larger under unequal energy sharing.
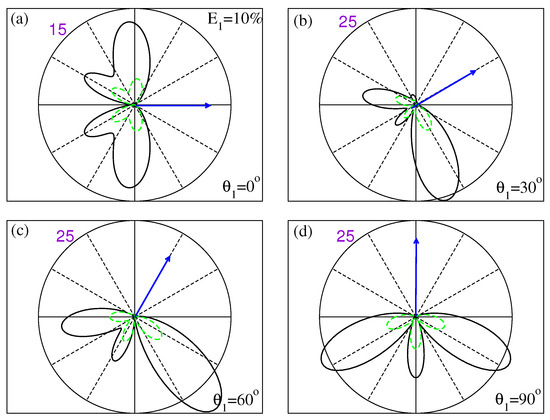
Figure 4.
TDCS results for carbon (solid black line) at 10 eV excess energy and unequal energy sharing (fixed electron is 10% of the available excess energy). Results are plotted as in Figure 3. The purple numbers in each panel (a–d) indicate the magnitude of the cross-section (in b/(eV sr), establishing the radius of each circle. 1 b = cm.
4. Conclusions
The results considered in this work illustrate the dominant impact that the initial-state coupling of the outgoing electrons possesses, along with the final-state symmetries that are accessed by dipole selection rules in single photoabsorption events may have on the resulting angular distributions of the TDCS in correlated events. Here, we have considered double ionization of the valence electrons of atomic carbon, which is noteworthy for being distinct from the helium-like systems that have been largely studied along these lines. Comparisons made to neon in the angular momentum coupling of the ejected electrons allow us to determine the features that result due to the common initial- and final-state symmetries.
Although we have here focused on the state of the valence electrons initially bound in atomic carbon in order to compare with previously published data, nothing in the method prohibits an examination of the other initial-state possibilities that arise from removing the electrons coupled in higher-energy and configurations, respectively. Completing the picture of the double ionization of atomic carbon will be the subject of future research.
Funding
This work was funded by the U.S. National Science Foundation (NSF) award PHY-1806417, and by the U.S. Department of Energy, Office of Science, Office of Workforce Development for Teachers and Scientists (WDTS) under the Visiting Faculty Program (VFP).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The author wishes to acknowledge fruitful discussions with Thomas N. Rescigno and C. William McCurdy.
Conflicts of Interest
The author declares no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DPI | Double photoionization |
| CI | Configuration interaction |
| TDCS | Triple-differential cross-section |
| SDCS | Single-differential cross-section |
| MBPT | Many-body perturbation theory |
| FEM-DVR | Finite element method discrete variable representation |
| ECS | Exterior complex scaling |
References
- Marchalant, P.J.; Bartschat, K. R matrix with pseudostates calculation for single and double ionization of helium by photon impact. Phys. Rev. A 1997, 56, R1697–R1700. [Google Scholar] [CrossRef]
- Malegat, L. (e,2e) and (γ,2e) Processes: Open and Closed Questions. Phys. Scr. 2004, 2004, 83. [Google Scholar]
- Avaldi, L.; Huetz, A. Photodouble ionization and the dynamics of electron pairs in the continuum. J. Phys. B At. Mol. Opt. Phys. 2005, 38, S861. [Google Scholar] [CrossRef]
- Kheifets, A.S.; Bray, I. Frozen-core model of the double photoionization of beryllium. Phys. Rev. A 2001, 65, 012710. [Google Scholar] [CrossRef]
- Colgan, J.; Pindzola, M. Double photoionization of beryllium. Phys. Rev. A 2002, 65, 022709. [Google Scholar] [CrossRef]
- Citrini, F.; Malegat, L.; Selles, P.; Kazansky, A.K. Direct double photoionization of the valence shell of Be. Phys. Rev. A 2003, 67, 042709. [Google Scholar] [CrossRef]
- Griffin, D.; Pindzola, M.; Ballance, C.; Colgan, J. Double photoionization of Be and Mg atoms using the R-matrix-with-pseudostates method. Phys. Rev. A 2009, 79, 023413. [Google Scholar] [CrossRef]
- Kheifets, A.S.; Bray, I. Valence-shell double photoionization of alkaline-earth-metal atoms. Phys. Rev. A 2007, 75, 042703. [Google Scholar] [CrossRef]
- Kheifets, A.S.; Bray, I.; Colgan, J.; Pindzola, M.S. Interference effects in L-shell atomic double photoionization. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 011002. [Google Scholar] [CrossRef][Green Version]
- Laulan, S.; Bachau, H. One- and two-photon double ionization of beryllium with ultrashort ultraviolet laser fields. Phys. Rev. A 2004, 69, 033408. [Google Scholar] [CrossRef]
- Yip, F.L.; McCurdy, C.W.; Rescigno, T.N. Hybrid orbital and numerical grid representation for electronic continuum processes: Double photoionization of atomic beryllium. Phys. Rev. A 2010, 81, 053407. [Google Scholar] [CrossRef]
- Yip, F.L.; McCurdy, C.W.; Rescigno, T.N. Double photoionization of excited lithium and beryllium. Phys. Rev. A 2010, 81, 063419. [Google Scholar] [CrossRef]
- Yip, F.L.; Martín, F.; McCurdy, C.W.; Rescigno, T.N. Double K-shell photoionization of atomic beryllium. Phys. Rev. A 2011, 84, 053417. [Google Scholar] [CrossRef]
- Pindzola, M.S.; Ballance, C.P.; Abdel-Naby, S.A.; Robicheaux, F.; Armstrong, G.S.J.; Colgan, J. Single and double photoionization of Be and Mg. J. Phys. B At. Mol. Opt. Phys. 2013, 46, 035201. [Google Scholar] [CrossRef]
- McIntyre, M.W.; Kinnen, A.J.; Scott, M.P. Photo-double-ionization of the He and Be isoelectronic sequences within an intermediate-energy R-matrix framework. Phys. Rev. A 2013, 88, 053413. [Google Scholar] [CrossRef]
- Sokell, E.; Bolognesi, P.; Kheifets, A.; Bray, I.; Safgren, S.; Avaldi, L. Signature of Two-Electron Interference in Angular Resolved Double Photoionization of Mg. Phys. Rev. Lett. 2013, 110, 083001. [Google Scholar] [CrossRef]
- Sokell, E.; Bolognesi, P.; Kheifets, A.; Bray, I.; Safgren, S.; Avaldi, L. Photo-double-ionization of Mg studied by electron-electron-coincidence experiments. Phys. Rev. A 2014, 89, 013413. [Google Scholar] [CrossRef]
- Abdel-Naby, S.A.; Pindzola, M.S.; Colgan, J. Differential cross section for the double photoionization of Mg. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 025204. [Google Scholar] [CrossRef]
- Yip, F.L.; Rescigno, T.N.; McCurdy, C.W. Fully differential single-photon double photoionization of atomic magnesium. Phys. Rev. A 2016, 94, 063414. [Google Scholar] [CrossRef]
- Müller, A.; Borovik, A.; Buhr, T.; Hellhund, J.; Holste, K.; Kilcoyne, A.L.D.; Klumpp, S.; Martins, M.; Ricz, S.; Viefhaus, J.; et al. Observation of a Four-Electron Auger Process in Near-K-Edge Photoionization of Singly Charged Carbon Ions. Phys. Rev. Lett. 2015, 114, 013002. [Google Scholar] [CrossRef]
- Perry-Sassmannshausen, A.; Buhr, T.; Borovik, A.; Martins, M.; Reinwardt, S.; Ricz, S.; Stock, S.O.; Trinter, F.; Müller, A.; Fritzsche, S.; et al. Multiple Photodetachment of Carbon Anions via Single and Double Core-Hole Creation. Phys. Rev. Lett. 2020, 124, 083203. [Google Scholar] [CrossRef] [PubMed]
- Carter, S.L.; Kelly, H.P. Double photoionization cross section of 3P carbon. J. Phys. B At. Mol. Phys. 1976, 9, 1887–1897. [Google Scholar] [CrossRef]
- Zatsarinny, O.; Bartschat, K. TheB-splineR-matrix method for atomic processes: Application to atomic structure, electron collisions and photoionization. J. Phys. B At. Mol. Opt. Phys. 2013, 46, 112001. [Google Scholar] [CrossRef]
- Zatsarinny, O.; Froese Fischer, C. Atomic structure calculations using MCHF and BSR. Comput. Phys. Commun. 2009, 180, 2041–2065. [Google Scholar] [CrossRef]
- Yip, F.; Palacios, A.; Rescigno, T.; McCurdy, C.; Martín, F. Time-dependent formalism of double ionization of multielectron atomic targets. Chem. Phys. 2013, 414, 112–120. [Google Scholar] [CrossRef]
- Yip, F.L.; Palacios, A.; Martín, F.; Rescigno, T.N.; McCurdy, C.W. Two-photon double ionization of atomic beryllium with ultrashort laser pulses. Phys. Rev. A 2015, 92, 053404. [Google Scholar] [CrossRef]
- Bello, R.Y.; Yip, F.L.; Rescigno, T.N.; Lucchese, R.R.; McCurdy, C.W. Two-photon double photoionization of atomic Mg by ultrashort pulses: Variation of angular distributions with pulse length. Phys. Rev. A 2020, 102, 053107. [Google Scholar] [CrossRef]
- Yip, F.L.; Rescigno, T.N.; McCurdy, C.W.; Martín, F. Fully Differential Single-Photon Double Ionization of Neon and Argon. Phys. Rev. Lett. 2013, 110, 173001. [Google Scholar] [CrossRef]
- Krässig, B.; Schaphorst, S.J.; Schwarzkopf, O.; Scherer, N.; Schmidt, V. State dependence of angular correlation patterns in double photoionization. J. Phys. B At. Mol. Opt. Phys. 1996, 29, 4255–4265. [Google Scholar] [CrossRef]
- Bolognesi, P.; Zitnik, M.; Malegat, L.; Selles, P.; Turri, G.; Coreno, M.; Camilloni, R.; Avaldi, L. Photo-double ionization of argon at 20 and 40 eV excess energy. J. Phys. B At. Mol. Opt. Phys. 2004, 37, 2285–2302. [Google Scholar] [CrossRef]
- Rescigno, T.N.; McCurdy, C.W. Numerical grid methods for quantum-mechanical scattering problems. Phys. Rev. A 2000, 62, 032706. [Google Scholar] [CrossRef]
- McCurdy, C.W.; Baertschy, M.; Rescigno, T.N. Solving the three-body Coulomb breakup problem using exterior complex scaling. J. Phys. B At. Mol. Opt. Phys. 2004, 37, R137. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database (Ver. 5.9). National Institute of Standards and Technology, Gaithersburg, MD, USA. 2021. Available online: https://physics.nist.gov/asd (accessed on 21 January 2022).
- Maulbetsch, F.; Briggs, J.S. Selection rules for transitions to two-electron continuum states. J. Phys. B At. Mol. Opt. Phys. 1995, 28, 551. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).