Abstract
The perspectives of detecting the general relativistic gravitomagnetic Lense–Thirring effect on the orbits of the Galilean moons of Jupiter induced by the angular momentum of the latter are preliminarily investigated. Numerical integrations over one century show that the expected gravitomagnetic signatures of the directly observable right ascension and declination of the satellites are as large as tens of arcseconds for Io, while for Callisto they drop to the ≃ level. Major competing effects due to the mismodeling in the zonal multipoles of the Jovian non-spherically symmetric gravity field and in the Jupiter’s spin axis should have a limited impact, especially in view of the future improvements in determining such parameters expected after the completion of the ongoing Juno mission in the next few years. On the other hand, the masses of the satellites, responsible of their mutual -body perturbations, should be known better than now. Such a task should be accomplished with the future JUICE and Clipper missions to the Jovian system. Present-day accuracy in knowing the orbits of the Jovian Galilean satellites is of the order of 10 milliarcseconds, to be likely further improved thanks to the ongoing re-reduction of old photographic plates. This suggests that, in the next future, the Lense–Thirring effect in the main Jovian system of moons might be detectable with dedicated data reductions in which the gravitomagnetic field is explicitly modeled and solved-for.
1. Introduction
The linearized equations of the weak-field and slow-motion approximation of the General Theory of Relativity (GTR) [1] formally resemble those of the Maxwellian electromagnetism giving rise to the so-called “gravitoelectromagnetic” paradigm [2,3,4,5,6,7,8,9,10,11,12,13,14]. General relativistic gravitoelectromagnetism has, actually, nothing to do with electric charges and currents, implying certain purely gravitational phenomena about orbiting test particles, precessing gyroscopes, moving clocks and atoms, and propagating electromagnetic waves [15,16,17,18,19,20,21]. In particular, matter-energy currents produce a so-called “gravitomagnetic” component of the gravitational field accounted for by the off-diagonal components of the spacetime metric tensor . To the first post-Newtonian (1pN) order, in the case of an isolated, slowly spinning body, the source of its gravitomagnetic field is its spin angular momentum which, among other things, gives rise a non-central, Lorentz-like acceleration on an orbiting test particle [22]. It induces secular precessions of the orbit of the latter [23,24,25], collectively known as Lense–Thirring (LT) effect [26,27], although it should be more correctly named as the Einstein–Thirring–Lense effect, according to recent studies [28,29,30,31].
General relativistic gravitomagnetism is believed to have a major role in observed complex processes near spinning black holes involving accretion disks and relativistic jets [5,21,32,33,34,35,36,37,38,39]. The hypothesized Penrose Process [40,41,42], the Blandford–Znajek effect [43], and superradiance [44] are due to the gravitomagnetic field of a rotating black hole as well; for a review, see, e.g., Teukolsky [45] and references. Despite the theoretically predicted large size of the gravitomagnetic effects involved, the relatively poor knowledge of the parameters characterizing such astrophysical scenarios and the related uncertainties generally prevent the designing and performing of clean and unambiguous tests of general relativity there.
In this respect, some years ago, a gravitomagnetic feature was detected in the field of the spinning Earth with the dedicated GP-B spacecraft-based mission [46] which measured the Pugh–Schiff precessions [47,48] of the axes of four gyroscopes carried onboard to an accuracy of the order of 19% [49], despite the fact that its originally expected level was about 1% [50]. Somewhat controversial attempts to measure the orbital LT precessions with the Earth’s artificial satellites of the LAGEOS type [51] and the Satellite Laser Ranging (SLR) technique [52] are currently ongoing [53,54,55]; for other proposed tests with natural and artificial bodies in the solar system, see Iorio et al. [56] and references therein. A tight binary system made of a white dwarf and a pulsar was recently used to claim a successful detection of the gravitomagnetic orbital precession of the inclination [57]; weak points of such a test were highlighted in Iorio [58]. The double pulsar PSR J0737-3039A/B [59,60] is another astrophysical laboratory of interest to attempt to measure its gravitomagnetic periastron precession in the near future [61,62].
Here, the possibility of extracting the LT signatures from long data records of accurate observations [63] of the Galilean moons of Jupiter [64] is examined. Future approved missions like Jupiter Icy Moons Explorer1 (JUICE) [65] and Clipper2 [66] should further increase the accuracy in determining their masses and orbits [67,68,69,70] which, currently, should be of the order of3 ≃; see also Arlot [63]. More precisely, the present goal is primarily pointing out that the theoretically predicted LT effect for the main Jovian satellites should fall within the measurability domain since it is much larger than the current astrometric accuracy level for them. A preliminary assessment of the major source of systematic biases is provided as well. It should be remarked that it would be incorrect to straightforwardly compare theoretical calculation of such an effect to residuals currently existing in the literature obtained without including the LT acceleration itself in the models used to produce them [71]. Actually, the LT acceleration is nowadays modeled4 in the dynamics of the Galilean moons of Jupiter (and of the Juno spacecraft as well, currently exploring the Jovian system), but, so far, no dedicated data reductions aimed to test it were performed. Furthermore, it is hoped that the present work will motivate dedicated investigations of the JUICE and Clipper teams who, hopefully, may explicitly model the Jovian gravitomagnetic field in their covariance analyses aimed at assessing the level of improvement in the ephemerides of the Galilean moons which will be achievable with such missions in connection with the proposed test.
The paper is organized as follows. In Section 2, the LT signatures of some observable quantities of Io, Europa, Ganymede, and Callisto are numerically calculated over one century and are plotted compared to time. Section 3 is devoted to the numerically integrated time series of the same observables due to the mismodeling in the multipoles of the Jovian gravity field and the uncertainties in the position in space of the spin axis of Jupiter. Section 4 deals with the mutual -body perturbations of one satellite on each other. Section 5 summarizes the findings of the paper and offers its conclusions.
2. The Lense–Thirring Signatures
Figure 1 displays the nominal centennial LT signatures of the astrometrically measurable right ascension (RA) and declination (DEC) of Io, Europa, Ganymede, and Callisto. Their LT time series and were obtained as follows. Their equations of motion, with and without the LT acceleration5 [22]
calculated with [72]
and
with [73]
for the orientation of the Jovian spin axis , were simultaneously integrated over one century in a coordinate system using rectangular Cartesian coordinates centered in the Jovian system barycenter and having the mean Earth’s equator at the reference epoch J2000 as reference plane; Equations (6) and (7) refer to it. Both the integrations shared the same initial conditions, referred to the International Celestial Reference Frame (ICRF) at some epoch and retrieved from the HORIZONS WEB interface maintained by the NASA Jet Propulsion Laboratory (JPL). Moreover, the suite of dynamical models, including for each satellite the Newtonian inverse-square law accelerations due to Jupiter and the other three moons, the Jovian gravitational multipoles up to degree , and the general relativistic Schwarschild-type gravitoelectric acceleration due to Jupiter, is the same for both the runs. For each integration, a time series was numerically computed for and . The differences and between the times series with and without the LT effect were, then, calculated and plotted compared to time.
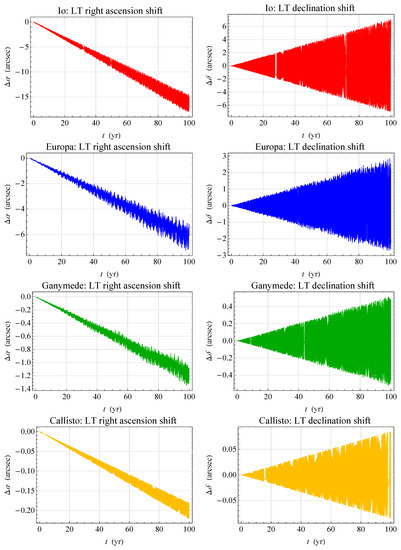
Figure 1.
Numerically produced time series of the nominal LT shifts and , in arcseconds (arcsec), of the RA and the DEC of the Galilean moons of Jupiter with respect to the ICRF.
It turns out that, for Io, the LT centennial shift on the RA looks like a negative linear trend as large as ≃ (arcsec), while the LT signal of its DEC has a peak-to-peak amplitude of ≃. The patterns of the LT signatures of Europa, Ganymede, and Callisto are the same; the sizes of the linear trends of their RA amount to approximately , and arcsec, respectively, while the peak-to-peak amplitudes of the DEC shifts are about and arcsec, respectively.
In recent years, an effort of reducing old observations using today’s accuracy has been undertaken. Indeed, at the beginning of the current century, it became possible to scan and digitize old photographic plates with modern scanners accurate to a few nanometers, and to reduce them using the new accurate catalogues of reference stars [63]. As an example, Table 15 of Arlot [63] displays the accuracy of newly digitized and re-reduced photographic plates spanning a 4 year long time interval (1986–1990) in terms of their dispersion and mean observed-minus-calculated (O-C) differences.
Over four years, the expected LT RA trend of Io reaches the arcsec level, while the peak-to-peak amplitude of its LT DEC signal is about arcsec. Such figures are to be compared with those quoted in Table 15 of Arlot [63] which, in the case of Io, are as little as () and arcsec (O-C) for the RA, and () and arcsec (O-C) for the DEC. Thus, at least in principle, a successful LT detection at about the percent level, or, perhaps, even better, might cautiously be possible by exploiting the astrometric observations of Io.
As far as Europa is concerned, its predicted LT signatures over four years are about (RA trend) and arcsec (peak-to-peak DEC amplitude), respectively. For the second Galilean moon of Jupiter, Table 15 of Arlot [63] returns () and arcsec (O-C) for the RA, and () and arcsec (O-C) for the DEC. Such errors range from some percent to about 19% of the LT effect.
Table 15 of Arlot [63] yields () and arcsec (O-C) for the RA, and () and arcsec (O-C) for the DEC of Ganymede. The predicted LT effects for the third Galilean moon of Jupiter are (RA linear trend) arcsec and arcsec (peak-to-peak DEC amplitude) over four years. In the most favorable case, the observational uncertainties are at the percent level of the LT signals, while in the worst case, they are as large as ≃40–97%.
Finally, the expected LT shifts of Callisto are arcsec (RA linear trend) arcsec and arcsec (peak-to-peak DEC amplitude) over four years. The corresponding observational errors, according to Table 15 of Arlot [63], are () and arcsec (O-C) for the RA, and () and arcsec (O-C) for the DEC. Apart from the RA O-C, which is as little as ≃2% of the LT shift, the other errors are larger than, or of the same order of magnitude of the relativistic targets.
The preliminary comparisons just presented suggest that the Jovian LT effect on the Galilean moons falls within the measurability domain to a level of accuracy which, at least for some of them, should be deemed as competitive with the GP-B experiment, which is the only currently undisputed existing test of the gravitomagnetic field. This conclusion should further strengthen as the re-reduction of the old photographic plates will go on by processing longer data records.
3. The Impact of the Zonal Harmonics of the Jovian Multipolar Gravity Field
A potentially major source of systematic error in recovering the LT effect by means of the Galilean satellites of Jupiter is represented by the accuracy with which the multipolar expansion of the classical part of the Jovian gravitational potential , accounting for its departures from spherical symmetry, will be known at the time of an actual data analysis aimed to extract the relativistic signatures of interest. In particular, both the zonal harmomic coefficients , in terms of which is parameterized, and the Jupiter’s spin axis , entering itself, need to be accurately known. The correction of degree ℓ to the gravitational potential reads
where R is the equatorial radius of the primary, and is the is the Legendre polynomial of degree ℓ whose argument is the cosine of the angle between and the position vector of the test particle.
In Figure 2, the signatures of RA and DEC due to the current level of mismodeling in up to degree are displayed. The uncertainties were retrieved from Durante et al. [73], and are based just on the first half of the currently ongoing Juno mission [74]. When all the data recorded will be available after the mission completion in the next few years, they will certainly be further improved. The time series shown were built as in Section 2 for the LT effect; in this case, for a given satellite, one run was performed with , while the other integration was made with , respectively, all the rest of the dynamical model being equal in both the runs. In particular, the orientation of the Jovian spin axis, entering explicitly the multipole-induced accelerations, was kept fixed to the same value, given by Equations (6) and (7), in both the integrations.
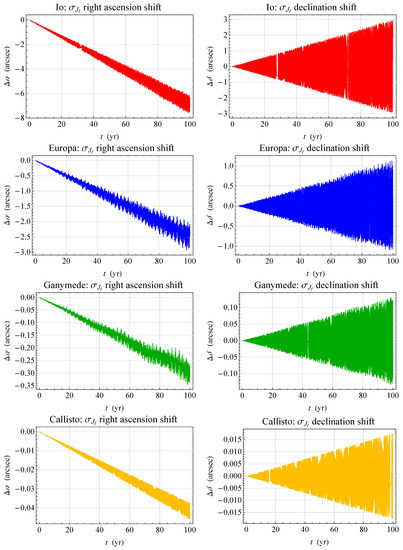
Figure 2.
Numerically produced time series of the first five mismodelled zonals shifts and , in arcseconds, of the RA and the DEC of the Galilean moons of Jupiter with respect to the ICRF. The uncertainties in the Jovian gravity field multipoles were retrieved from Durante et al. [73].
It turns out that even the current level of accuracy in knowing the Jupiter’s gravity multipoles would be adequate to yield a systematic error smaller than the LT effect. Indeed, for Io, the RA and DEC centennial signatures due to would be of the order of just ≃ (RA linear trend) and 6 arcsec (DEC peak-to-peak amplitude), i.e., ≃2.5–3 times smaller than the corresponding LT effects. For Callisto, the RA and DEC shifts due to amount to arcsec (RA linear trend) and arcsec (DEC peak-to-peak amplitude), i.e., ≃5–6 times smaller than the LT ones.
Another potential major source of systematic error for the extraction of the LT signals is represented by the impact of the uncertainty in the Jupiter’s spin axis parameterized in terms of the right ascension and declination of the Jovian pole of rotation as per Equations (3)–(5). The RA and DEC of the Jovian spin axis are currently known to the
level, as it can be inferred from Figure 3 of Durante et al. [73]. It is arguable that also the knowledge of the planet’s pole of rotation will be further improved when all the complete record of Juno’s data will be available at the end of the mission. Figure 3 shows the mismodelled RA and DEC signatures due to the planetary zonal harmonics up to degree induced by the uncertainty in according to Equations (9) and (10). For each satellite, they were obtained from the difference between two numerically integrated time series one of which calculated with and the other one with , all the rest being equal for both the runs.
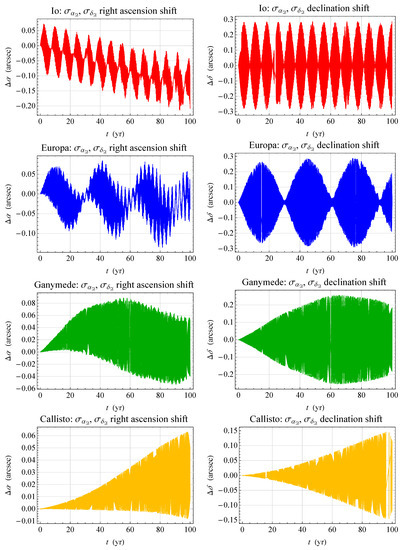
Figure 3.
Impact of the current uncertainty in the Jovian pole of rotation through the first five zonal harmonics of the gravity field on the RA and the DEC of the Galilean moons of Jupiter with respect to the ICRF; the resulting shifts and are in arcseconds. The uncertainties in are as per Equations (9) and (10).
It turns out that the current level of uncertainty in the Jupiter’s spin axis, to be improved in the ongoing future after the completion of the Juno mission, has a modest impact on the LT signature of Io. Indeed, Equations (9) and (10) induce mismodelled effects of the order of ≃0.20 arcsec (RA trend) and arcsec (peak-to-peak DEC amplitude) for Io; they are about 100 times smaller than the relativistic signals displayed in Figure 1.
Furthermore, for Europa the situation is good since the mismodelled signals are ≃10–100 times smaller than the relativistic ones in Figure 1.
The mismodelled signature of the RA of Ganymede is about one order of magnitude smaller than the corresponding relativistic ones displayed in Figure 1. For the DEC, the situation is less favorable since the impact of Equations (9) and (10) is as large as ≃60% of the LT effect.
For Callisto, the mismodelled signals due to Equations (9) and (10) are ≃0.06 arcsec (RA trend) and arcsec (peak-to-peak DEC amplitude); according to Figure 1, the corresponding nominal LT signal for the RA is ≃4 times larger, while the LT DEC one is times smaller than that due to the uncertainty in .
4. The Impact of the Newtonian -Body Mutual Perturbations
Another potentially major source of systematic bias is represented by the classical -body perturbations induced on each satellite by the Newtonian attraction of the other ones. The level of their mismodeling is set by the uncertainty with which the masses m of the Galilean satellites are known. Figure 4 shows the numerically integrated time series and of the RA and the DEC of Io, Europa, Ganymede, and Callisto due to the current errors in their masses retrieved on the Internet at https://ssd.jpl.nasa.gov/sats/phys_par/ (accessed on 20 June 2023), where the Planetary Satellite Ephemeris: JUP365 [75] is quoted as source. They were calculated by subtracting two runs differing only by the values of the masses which are set to and , respectively, all the rest being equal.
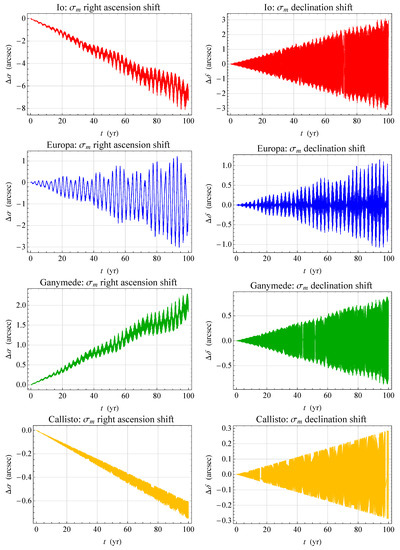
Figure 4.
Numerically produced time series of the mismodelled Newtonian body shifts and , in arcseconds, of the RA and the DEC of the Galilean moons of Jupiter with respect to the ICRF. The uncertainties in the masses of Io, Europa, Ganymede, and Callisto were retrieved from the Planetary Satellite Ephemeris: JUP365 [75], and are available on the Internet at https://ssd.jpl.nasa.gov/sats/phys_par/ (accessed on 20 June 2023).
For Io, perturbed by Europa, Ganymede, and Callisto, the RA is affected to the ≃8 arcsec level over one century, while the peak-to-peak amplitude of its DEC is 6 arcsec over the same time span. Such figures are smaller than the LT ones of Figure 1 by ≃2 times.
The mismodelled signatures of Europa amount to about 4 arcsec (RA) and 2 arcsec (DEC), which represent a significative amount of the LT ones in Figure 1.
The mismodelled shifts of Ganymede are about arcsec (RA) and 2 arcsec (DEC), which are ≃2 times larger than the LT signals displayed in Figure 1.
The mismodelled -body perturbations of the RA and DEC of Callisto are as large as arcsec and arcsec, respectively; they are about 3–4 times larger than the LT shifts in Figure 1.
Thus, improving the accuracy in the determination of the masses of the Galilean moons will be crucial for a successful test of the LT effect with the Jovian system. The situation will become more favorable when, among other things, the masses of the three outer Galilean satellites will be accurately determined by JUICE and Clipper, while the flybys of Io by Juno should allow to improve also the mass of Io. More specifically, according to Tables 1–3 of Magnanini [68], the masses of Europa, Ganymede, and Callisto should be determined by JUICE with an improvement of about 1–2 orders of magnitude with respect to the errors retrieved at https://ssd.jpl.nasa.gov/sats/phys_par/ (accessed on 20 June 2023), and used in this paper.
5. Discussion and Conclusions
The theoretically predicted LT centennial signatures of the Galilean moons of Jupiter seem to be large enough to be detectable, at least in principle, given the current level of accuracy in their astrometric measurements, of the order of ≃. Moreover, the systematic bias due to the multipolar gravity field of Jupiter appears to have a limited impact, especially in view of the likely improvements in knowing it after the completion of the ongoing Juno mission in the next few years. On the other hand, the masses of the satellites need to be improved since the mutual -body perturbations induced by one on each other are currently larger than the LT shifts, or represent a large fraction of the latter ones.
It should be recalled that if a dynamical effect of interest, such as the LT one in the present case, is not explicitly included in the models fitting the observations, the resulting post-fit residuals may not display the sought signatures to a statistically significant non-zero level because they may partly be removed in estimating the initial state vectors and other parameters of the target system [71]. Despite a general rule valid in all cases cannot be given, it might be prudently said that to (partly) avoid to be absorbed in (some of) the estimated parameters of the fit, an unmodeled dynamical feature of motion should be much larger than the observational accuracy. Be that as it may, the correct procedure consists of proceeding on a case-by-case basis producing a new series of residuals constructed by explicitly modeling the effect of interest, determining some key parameters characterizing it, and inspecting the correlations among them and the other estimated parameters [71]. To the knowledge of the present author, the gravitomagnetic field of Jupiter is currently included in the modeling of the orbits of Io, Europa, Ganymede, and Callisto, but no dedicated data reductions aimed to explicitly detect the LT precessions of such natural bodies have been performed so far.
The present study suggests that the time to successfully do it may come soon, also in view of the expected improvements in determining the orbits and the masses of Europa, Ganymede, and Callisto thanks to the forthcoming JUICE and Clipper missions. Furthermore, the orbital and physical parameters of Io should be improved by its flybys by Juno, at least to a certain extent.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
Notes
| 1 | It was launched on 14 April 2023. See the mission’s webpage https://www.esa.int/Science_Exploration/Space_Science/Juice (accessed on 20 June 2023). |
| 2 | Its launch is scheduled for October 2024. See the mission’s website https://www.jpl.nasa.gov/missions/europa-clipper (accessed on 20 June 2023). |
| 3 | R. A. Jacobson, personal communication to L. Iorio, March 2023. |
| 4 | R. A. Jacobson, private communication to L. Iorio, March 2023. |
| 5 | In Equation (1), G is the Newtonian constant of gravitation, c is the speed of light in vacuum, and and are the position and velocity vectors of the test particle with respect to the spinning central body, respectively. |
References
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; Princeton University Press: Oxford, UK, 2017. [Google Scholar]
- Cattaneo, C. General relativity: Relative standard mass, momentum, energy and gravitational field in a general system of reference. Nuovo Cim. 1958, 10, 318–337. [Google Scholar] [CrossRef]
- Thorne, K.S.; MacDonald, D.A.; Price, R.H. Black Holes: The Membrane Paradigm; Yale University Press: London, UK, 1986. [Google Scholar]
- Thorne, K.S. Black Holes: The Membrane Viewpoint. In Highlights of Modern Astrophysics: Concepts and Controversies; Shapiro, S.L., Teukolsky, S.A., Salpeter, E.E., Eds.; Wiley: New York, NY, USA, 1986; pp. 103–161. [Google Scholar]
- Thorne, K.S. Gravitomagnetism, jets in quasars, and the Stanford Gyroscope Experiment. In Near Zero: New Frontiers of Physics; Fairbank, J.D., Deaver, B.S.J., Everitt, C.W.F., Michelson, P.F., Eds.; Freeman: New York, NY, USA, 1988; pp. 573–586. [Google Scholar]
- Harris, E.G. Analogy between general relativity and electromagnetism for slowly moving particles in weak gravitational fields. Am. J. Phys. 1991, 59, 421–425. [Google Scholar] [CrossRef]
- Jantzen, R.T.; Carini, P.; Bini, D. The many faces of gravitoelectromagnetism. Ann. Phys. 1992, 215, 1–50. [Google Scholar] [CrossRef]
- Mashhoon, B. Gravitoelectromagnetism. In Reference Frames and Gravitomagnetism; Pascual-Sánchez, J.F., Floría, L., San Miguel, A., Vicente, F., Eds.; World Scientific: Singapore, 2001; pp. 121–132. [Google Scholar] [CrossRef]
- Rindler, W. Relativity: Special, General, and Cosmological; Oxford University Press: New York, NY, USA, 2001. [Google Scholar]
- Mashhoon, B. Gravitoelectromagnetism: A Brief Review. In The Measurement of Gravitomagnetism: A Challenging Enterprise; Iorio, L., Ed.; Nova Science: New York, NY, USA, 2007; pp. 29–39. [Google Scholar]
- Costa, L.F.O.; Herdeiro, C.A.R. Gravitoelectromagnetic analogy based on tidal tensors. PRD 2008, 78, 024021. [Google Scholar] [CrossRef]
- Costa, L.F.O.; Natário, J. Gravito-electromagnetic analogies. Gen. Relativ. Gravit. 2014, 46, 1792. [Google Scholar] [CrossRef]
- Costa, L.F.O.; Natário, J. Frame-Dragging: Meaning, Myths, and Misconceptions. Universe 2021, 7, 388. [Google Scholar] [CrossRef]
- Ruggiero, M.L. A Note on the Gravitoelectromagnetic Analogy. Universe 2021, 7, 451. [Google Scholar] [CrossRef]
- Braginsky, V.B.; Caves, C.M.; Thorne, K.S. Laboratory experiments to test relativistic gravity. PRD 1977, 15, 2047–2068. [Google Scholar] [CrossRef]
- Dymnikova, I.G. Reviews of Topical Problems: Motion of particles and photons in the gravitational field of a rotating body (In memory of Vladimir Afanas’evich Ruban). Sov. Phys. Usp. 1986, 29, 215–237. [Google Scholar] [CrossRef]
- Tartaglia, A. Angular-momentum effects in weak gravitational fields. Europhys. Lett. 2002, 60, 167–173. [Google Scholar] [CrossRef]
- Ruggiero, M.L.; Tartaglia, A. Gravitomagnetic effects. Nuovo Cim. B 2002, 117, 743. [Google Scholar]
- Schäfer, G. Gravitomagnetic Effects. Gen. Relativ. Gravit. 2004, 36, 2223–2235. [Google Scholar] [CrossRef]
- Schäfer, G. Gravitomagnetism in Physics and Astrophysics. Space Sci. Rev. 2009, 148, 37–52. [Google Scholar] [CrossRef]
- Stella, L.; Possenti, A. Lense-Thirring Precession in the Astrophysical Context. Space Sci. Rev. 2009, 148, 105–121. [Google Scholar] [CrossRef]
- Petit, G.; Luzum, B. IERS Conventions (2010); IERS Technical Note; Verlag des Bundesamts für Kartographie und Geodäsie: Frankfurt, Germany, 2010; Volume 36. [Google Scholar]
- Soffel, M.H. Relativity in Astrometry, Celestial Mechanics and Geodesy; Springer: Heidelberg, Germany, 1989. [Google Scholar]
- Brumberg, V.A. Essential Relativistic Celestial Mechanics; Adam Hilger: Bristol, UK, 1991. [Google Scholar]
- Soffel, M.H.; Han, W.B. Applied General Relativity; Astronomy and Astrophysics Library; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Lense, J.; Thirring, H. Über den Einfluß der Eigenrotation der Zentralkörper auf die Bewegung der Planeten und Monde nach der Einsteinschen Gravitationstheorie. Phys. Z 1918, 19, 156–163. [Google Scholar]
- Mashhoon, B.; Hehl, F.W.; Theiss, D.S. On the gravitational effects of rotating masses: The Thirring-Lense papers. Gen. Relativ. Gravit. 1984, 16, 711–750. [Google Scholar] [CrossRef]
- Pfister, H. On the history of the so-called Lense-Thirring effect. Gen. Relativ. Gravit. 2007, 39, 1735–1748. [Google Scholar] [CrossRef]
- Pfister, H. The History of the So-Called Lense-Thirring Effect. In The Eleventh Marcel Grossmann Meeting: On Recent Developments in Theoretical and Experimental General Relativity, Gravitation and Relativistic Field Theories; Kleinert, H., Jantzen, R.T., Ruffini, R., Eds.; World Scientific: Singapore, 2008; pp. 2456–2458. [Google Scholar] [CrossRef]
- Pfister, H. Editorial note to: Hans Thirring, On the formal analogy between the basic electromagnetic equations and Einstein’s gravity equations in first approximation. Gen. Relativ. Gravit. 2012, 44, 3217–3224. [Google Scholar] [CrossRef]
- Pfister, H. Gravitomagnetism: From Einstein’s 1912 Paper to the Satellites LAGEOS and Gravity Probe B. In Relativity and Gravitation; Bičák, J., Ledvinka, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; Volume 157, pp. 191–197. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Petterson, J.A. The Lense-Thirring Effect and Accretion Disks around Kerr Black Holes. Astrophys. J. Lett. 1975, 195, L65. [Google Scholar] [CrossRef]
- Rees, M.J. Relativistic jets and beams in radio galaxies. Nature 1978, 275, 516–517. [Google Scholar] [CrossRef]
- MacDonald, D.; Thorne, K.S. Black-hole electrodynamics—An absolute-space/universal-time formulation. Mon. Not. Roy. Astron. Soc. 1982, 198, 345–382. [Google Scholar] [CrossRef]
- Rees, M.J. Black Hole Models for Active Galactic Nuclei. Annu. Rev. Astron. Astr. 1984, 22, 471–506. [Google Scholar] [CrossRef]
- Armitage, P.J.; Natarajan, P. Lense-Thirring Precession of Accretion Disks around Compact Objects. Astrophys. J 1999, 525, 909–914. [Google Scholar] [CrossRef]
- Ingram, A.; Done, C.; Fragile, P.C. Low-frequency quasi-periodic oscillations spectra and Lense-Thirring precession. Mon. Not. Roy. Astron. Soc. 2009, 397, L101–L105. [Google Scholar] [CrossRef]
- Veledina, A.; Poutanen, J.; Ingram, A. A Unified Lense-Thirring Precession Model for Optical and X-Ray Quasi-periodic Oscillations in Black Hole Binaries. Astrophys. J 2013, 778, 165. [Google Scholar] [CrossRef]
- Franchini, A.; Lodato, G.; Facchini, S. Lense-Thirring precession around supermassive black holes during tidal disruption events. Mon. Not. Roy. Astron. Soc. 2016, 455, 1946–1956. [Google Scholar] [CrossRef]
- Penrose, R. “Golden Oldie”: Gravitational Collapse: The Role of General Relativity. Gen. Relativ. Gravit. 2002, 7, 1141–1165. [Google Scholar] [CrossRef]
- Penrose, R.; Floyd, R.M. Extraction of Rotational Energy from a Black Hole. Nat. Phys. Sci. 1971, 229, 177–179. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Kološ, M.; Tursunov, A. Penrose Process: Its Variants and Astrophysical Applications. Universe 2021, 7, 416. [Google Scholar] [CrossRef]
- Blandford, R.D.; Znajek, R.L. Electromagnetic extraction of energy from Kerr black holes. Mon. Not. Roy. Astron. Soc. 1977, 179, 433–456. [Google Scholar] [CrossRef]
- Zel’Dovich, Y.B. Generation of Waves by a Rotating Body. J. Exp. Theor. Phys. 1971, 14, 180. [Google Scholar]
- Teukolsky, S.A. The Kerr metric. Class. Quantum Gravity 2015, 32, 124006. [Google Scholar] [CrossRef]
- Everitt, C.W.F. The Gyroscope experiment-I: General description and analysis of gyroscope performance. In Proceedings of the International School of Physics “Enrico Fermi”; Course LVI. Experimental Gravitation; Bertotti, B., Ed.; Academic Press: New York, NY, USA; London, UK, 1974; pp. 331–360. [Google Scholar]
- Pugh, G.E. Proposal for a Satellite Test of the Coriolis Prediction of General Relativity; Research Memorandum 11; Weapons Systems Evaluation Group, The Pentagon: Washington, DC, USA, 1959. [Google Scholar]
- Schiff, L. Possible new experimental test of general relativity theory. Phys. Rev. Lett. 1960, 4, 215–217. [Google Scholar] [CrossRef]
- Everitt, C.W.F.; Debra, D.B.; Parkinson, B.W.; Turneaure, J.P.; Conklin, J.W.; Heifetz, M.I.; Keiser, G.M.; Silbergleit, A.S.; Holmes, T.; Kolodziejczak, J.; et al. Gravity Probe B: Final Results of a Space Experiment to Test General Relativity. Phys. Rev. Lett. 2011, 106, 221101. [Google Scholar] [CrossRef]
- Everitt, C.W.F.; Buchman, S.; Debra, D.B.; Keiser, G.M.; Lockhart, J.M.; Muhlfelder, B.; Parkinson, B.W.; Turneaure, J.P. Gravity Probe B: Countdown to Launch. In Gyros, Clocks, Interferometers …: Testing Relativistic Gravity in Space; Lecture Notes in Physics; Lämmerzahl, C., Everitt, C.W.F., Hehl, F.W., Eds.; Springer: Berlin, Germany, 2001; Volume 562, p. 52. [Google Scholar] [CrossRef]
- Pearlman, M.; Arnold, D.; Davis, M.; Barlier, F.; Biancale, R.; Vasiliev, V.; Ciufolini, I.; Paolozzi, A.; Pavlis, E.C.; Sośnica, K.; et al. Laser geodetic satellites: A high-accuracy scientific tool. J. Geod. 2019, 93, 2181–2194. [Google Scholar] [CrossRef]
- Coulot, D.; Deleflie, F.; Bonnefond, P.; Exertier, P.; Laurain, O.; de Saint-Jean, B. Satellite Laser Ranging. In Encyclopedia of Solid Earth Geophysics; Gupta, H.K., Ed.; Encyclopedia of Earth Sciences Series; Springer: Dordrecht, The Netherlands, 2011; pp. 1049–1055. [Google Scholar] [CrossRef]
- Ciufolini, I.; Paolozzi, A.; Koenig, R.; Pavlis, E.C.; Ries, J.; Matzner, R.; Gurzadyan, V.; Penrose, R.; Sindoni, G.; Paris, C. Fundamental Physics and General Relativity with the LARES and LAGEOS satellites. Nucl. Phys. B Proc. Suppl. 2013, 243, 180–193. [Google Scholar] [CrossRef]
- Renzetti, G. History of the attempts to measure orbital frame—Dragging with artificial satellites. Centr. Eur. J. Phys. 2013, 11, 531–544. [Google Scholar] [CrossRef]
- Iorio, L.; Ruggiero, M.L.; Corda, C. Novel considerations about the error budget of the LAGEOS-based tests of frame-dragging with GRACE geopotential models. Acta Astronaut. 2013, 91, 141–148. [Google Scholar] [CrossRef]
- Iorio, L.; Lichtenegger, H.I.M.; Ruggiero, M.L.; Corda, C. Phenomenology of the Lense-Thirring effect in the solar system. Astrophys. Space Sci. 2011, 331, 351–395. [Google Scholar] [CrossRef]
- Venkatraman Krishnan, V.; Bailes, M.; van Straten, W.; Wex, N.; Freire, P.C.C.; Keane, E.F.; Tauris, T.M.; Rosado, P.A.; Bhat, N.D.R.; Flynn, C.; et al. Lense-Thirring frame dragging induced by a fast-rotating white dwarf in a binary pulsar system. Science 2020, 367, 577–580. [Google Scholar] [CrossRef]
- Iorio, L. A comment on ’Lense-Thirring frame dragging induced by a fast-rotating white dwarf in a binary pulsar system’ by V. Venkatraman Krishnan et al. Mon. Not. Roy. Astron. Soc. 2020, 495, 2777–2785. [Google Scholar] [CrossRef]
- Burgay, M.; D’Amico, N.; Possenti, A.; Manchester, R.N.; Lyne, A.G.; Joshi, B.C.; McLaughlin, M.A.; Kramer, M.; Sarkissian, J.M.; Camilo, F.; et al. An increased estimate of the merger rate of double neutron stars from observations of a highly relativistic system. Nature 2003, 426, 531–533. [Google Scholar] [CrossRef] [PubMed]
- Lyne, A.G.; Burgay, M.; Kramer, M.; Possenti, A.; Manchester, R.N.; Camilo, F.; McLaughlin, M.A.; Lorimer, D.R.; D’Amico, N.; Joshi, B.C.; et al. A Double-Pulsar System: A Rare Laboratory for Relativistic Gravity and Plasma Physics. Science 2004, 303, 1153–1157. [Google Scholar] [CrossRef] [PubMed]
- Kehl, M.S.; Wex, N.; Kramer, M.; Liu, K. Future measurements of the Lense-Thirring effect in the Double Pulsar. In The Fourteenth Marcel Grossmann Meeting, Proceedings of the MG14 Meeting on General Relativity, Rome, Italy, 12–18 July 2015; Bianchi, M., Jantzen, R., Ruffini, R., Eds.; World Scientific: Singapore, 2017; pp. 1860–1865. [Google Scholar] [CrossRef]
- Hu, H.; Kramer, M.; Wex, N.; Champion, D.J.; Kehl, M.S. Constraining the dense matter equation-of-state with radio pulsars. Mon. Not. R. Astron. Soc. 2020, 497, 3118–3130. [Google Scholar] [CrossRef]
- Arlot, J.E. Four centuries of observations of the Galilean satellites of Jupiter: Increasing the astrometric accuracy. J. Astron. Hist. Herit. 2019, 22, 78–92. [Google Scholar]
- Schlosser, W.; Schmidt-Kaler, T.; Milone, E.F. The Galilean Moons of Jupiter. In Challenges of Astronomy: Hands-on Experiments for the Sky and Laboratory; Springer: New York, NY, USA, 1991; pp. 54–58. [Google Scholar] [CrossRef]
- Grasset, O.; Dougherty, M.K.; Coustenis, A.; Bunce, E.J.; Erd, C.; Titov, D.; Blanc, M.; Coates, A.; Drossart, P.; Fletcher, L.N.; et al. JUpiter ICy moons Explorer (JUICE): An ESA mission to orbit Ganymede and to characterise the Jupiter system. Planet. Space Sci. 2013, 78, 1–21. [Google Scholar] [CrossRef]
- Korth, H.; Pappalardo, R.; Craft, K.; Daubar, I.; Hay, H.; Howell, S.; Klima, R.; Leonard, E.; Matiella Novak, A.; Persaud, D.; et al. Europa Clipper Mission Update. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 23–27 May 2022. [Google Scholar] [CrossRef]
- Cappuccio, P.; Hickey, A.; Durante, D.; Di Benedetto, M.; Iess, L.; De Marchi, F.; Plainaki, C.; Milillo, A.; Mura, A. Ganymede’s gravity, tides and rotational state from JUICE’s 3GM experiment simulation. Planet. Space Sci. 2020, 187, 104902. [Google Scholar] [CrossRef]
- Magnanini, A. Estimation of the Ephemerides and Gravity Fields of the Galilean Moons Through Orbit Determination of the JUICE Mission. Aerotec. Missili Spaz. 2021, 100, 195–206. [Google Scholar] [CrossRef]
- Cappuccio, P.; Di Benedetto, M.; Durante, D.; Iess, L. Callisto and Europa Gravity Measurements from JUICE 3GM Experiment Simulation. Planet. Sci. J. 2022, 3, 199. [Google Scholar] [CrossRef]
- Fayolle, M.; Dirkx, D.; Lainey, V.; Gurvits, L.I.; Visser, P.N.A.M. Decoupled and coupled moons’ ephemerides estimation strategies application to the JUICE mission. Planet. Space Sci. 2022, 219, 105531. [Google Scholar] [CrossRef]
- Fienga, A.; Minazzoli, O. Testing GR and alternative theories with planetary ephemerides. arXiv 2023, arXiv:2303.01821. [Google Scholar]
- Soffel, M.; Klioner, S.A.; Petit, G.; Wolf, P.; Kopeikin, S.M.; Bretagnon, P.; Brumberg, V.A.; Capitaine, N.; Damour, T.; Fukushima, T.; et al. The IAU 2000 Resolutions for Astrometry, Celestial Mechanics, and Metrology in the Relativistic Framework: Explanatory Supplement. Astron J. 2003, 126, 2687–2706. [Google Scholar] [CrossRef]
- Durante, D.; Parisi, M.; Serra, D.; Zannoni, M.; Notaro, V.; Racioppa, P.; Buccino, D.R.; Lari, G.; Gomez Casajus, L.; Iess, L.; et al. Jupiter’s Gravity Field Halfway Through the Juno Mission. Geophys. Res. Lett. 2020, 47, e86572. [Google Scholar] [CrossRef]
- Bolton, S. The Juno Mission; Springer: Dordrecht, The Netherlands, 2018. [Google Scholar]
- Jacobson, R.A. The Orbits of the Regular Jovian Satellites and the Orientation of the Pole of Jupiter. Personal Communication to Horizons/NAIF, 2021. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).