Neutron Stars in the Context of f(
Abstract
1. Introduction
2. Gravitational Field Equations of Gravity
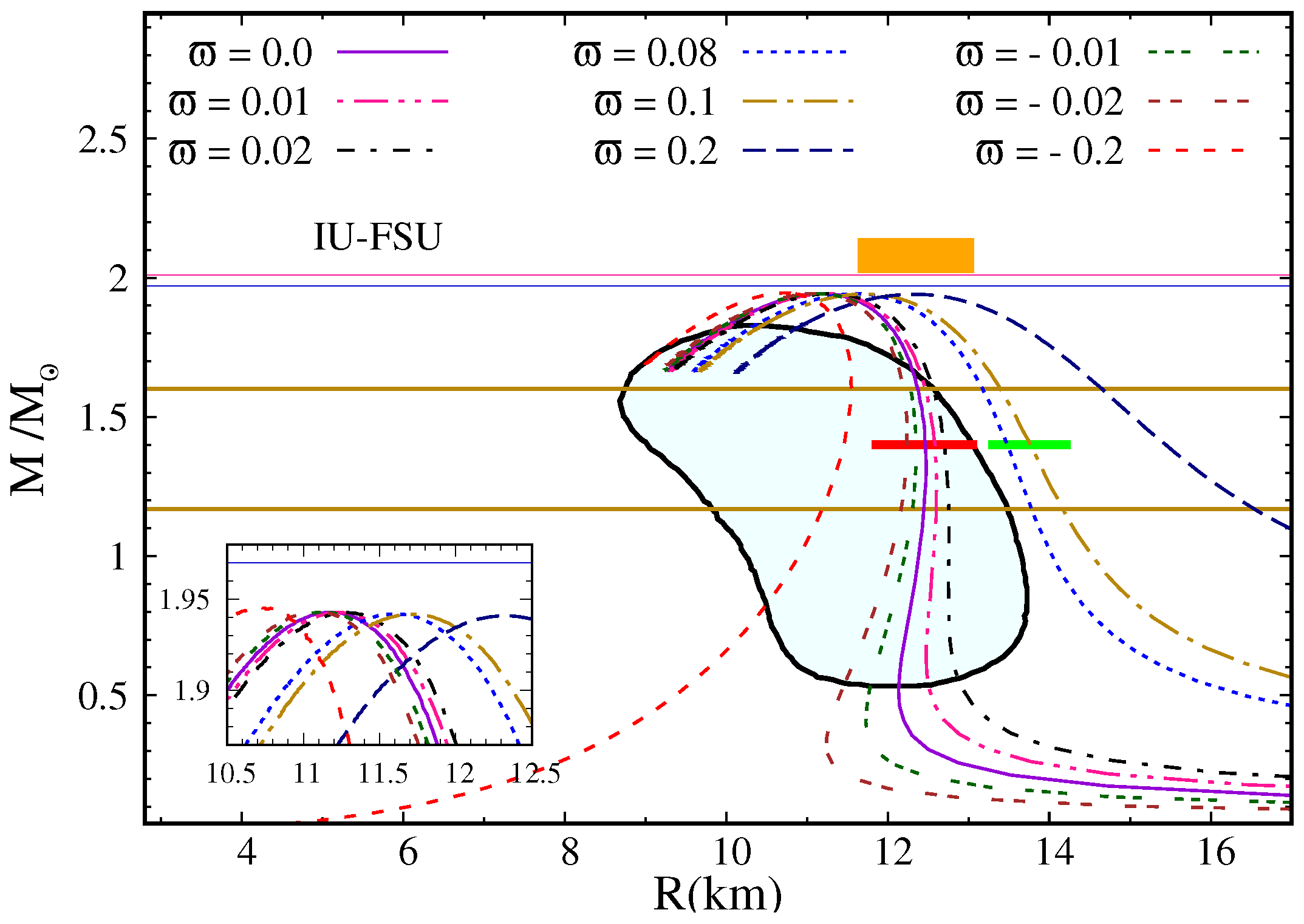
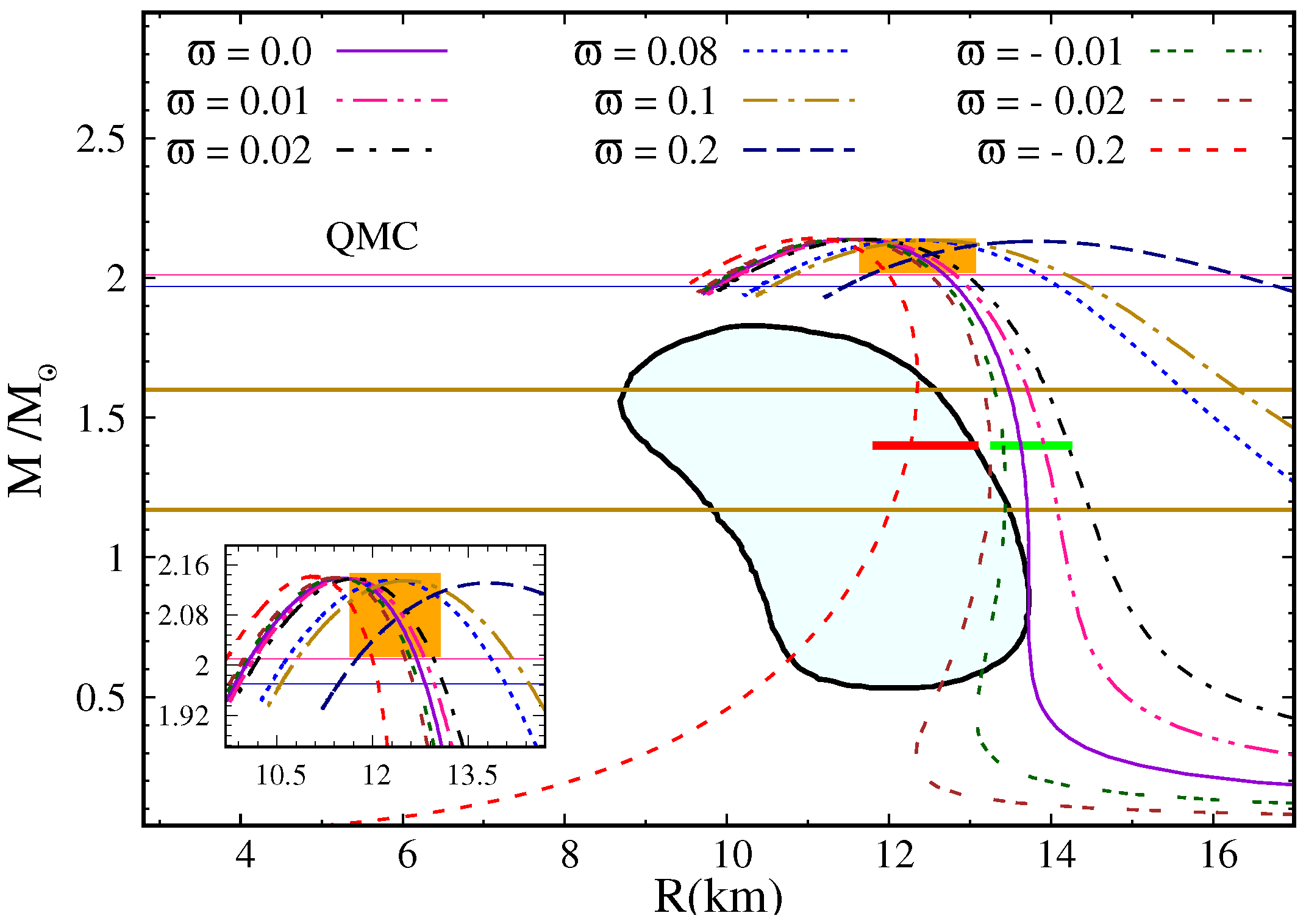
3. Stellar Structure Equations
4. Results
5. Final Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Utiyama, R.; DeWitt, B.S. Renormalization of a classical gravitational field interacting with quantized matter fields. J. Math. Phys. 1962, 3, 608–618. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Faraoni, V. f(R) Theories Of Gravity. Rev. Mod. Phys. 2010, 82, 451–497. [Google Scholar] [CrossRef]
- Rubin, V.C.; Ford, W.K., Jr. Rotation of the Andromeda nebula from a spectroscopic survey of emission regions. Astrophys. J. 1970, 159, 379. [Google Scholar] [CrossRef]
- Zwicky, F. Die rotverschiebung von extragalaktischen nebeln. Helv. Phys. Acta 1933, 6, 110–127. [Google Scholar]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 high-redshift supernovae. Astrophys. J. 1999, 517, 565. [Google Scholar] [CrossRef]
- Sahni, V. 5 dark matter and dark energy. Phys. Early Universe 2004, 653, 141–179. [Google Scholar]
- Capozziello, S.; De Laurentis, M. Extended theories of gravity. Phys. Rep. 2011, 509, 167–321. [Google Scholar] [CrossRef]
- De Felice, A.; Tsujikawa, S. f(R) theories. Living Rev. Relativ. 2010, 13, 1–161. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rep. 2011, 505, 59–144. [Google Scholar] [CrossRef]
- Lobo, F.S.N. The dark side of gravity: Modified theories of gravity. arXiv 2008, arXiv:0807.1640. [Google Scholar]
- Harada, T. Neutron stars in scalar-tensor theories of gravity and catastrophe theory. Phys. Rev. D 1998, 57, 4802. [Google Scholar] [CrossRef]
- Orellana, M.; García, F.; Pannia, F.A.T.; Romero, G.E. Structure of neutron stars in R-squared gravity. Gen. Relativ. Gravit. 2013, 45, 771–783. [Google Scholar] [CrossRef]
- Momeni, D.; Myrzakulov, R. Tolman–Oppenheimer–Volkoff equations in modified Gauss–Bonnet gravity. Int. J. Geom. Methods Mod. Phys. 2015, 12, 1550014. [Google Scholar] [CrossRef]
- Oliveira, A.; Velten, H.; Fabris, J.; Casarini, L. Neutron stars in Rastall gravity. Phys. Rev. D 2015, 92, 044020. [Google Scholar] [CrossRef]
- Hendi, S.; Bordbar, G.; Panah, B.E.; Panahiyan, S. Modified TOV in gravity’s Rainbow: Properties of neutron stars and dynamical stability conditions. J. Cosmol. Astropart. Phys. 2016, 2016, 013. [Google Scholar] [CrossRef]
- Singh, K.N.; Rahaman, F.; Banerjee, A. Einstein’s cluster mimicking compact star in the teleparallel equivalent of general relativity. Phys. Rev. D 2019, 100, 084023. [Google Scholar] [CrossRef]
- Maurya, S.K.; Tello-Ortiz, F. Charged anisotropic compact star in f(R,T) gravity: A minimal geometric deformation gravitational decoupling approach. Phys. Dark Universe 2020, 27, 100442. [Google Scholar] [CrossRef]
- Mota, C.E.; Santos, L.C.N.; Grams, G.; da Silva, F.M.; Menezes, D.P. Combined Rastall and Rainbow theories of gravity with applications to neutron stars. Phys. Rev. D 2019, 100, 024043. [Google Scholar] [CrossRef]
- Mota, C.E.; Santos, L.C.N.; da Silva, F.M.; Flores, C.V.; da Silva, T.J.N.; Menezes, D.P. Anisotropic compact stars in Rastall–Rainbow gravity. Class. Quantum Gravity 2022, 39, 085008. [Google Scholar] [CrossRef]
- da Silva, F.M.; Santos, L.C.N.; Barros, C.C. Rapidly rotating compact stars in Rastall’s gravity. Class. Quantum Gravity 2021, 38, 165011. [Google Scholar] [CrossRef]
- Cooney, A.; DeDeo, S.; Psaltis, D. Neutron stars in f(R) gravity with perturbative constraints. Phys. Rev. D 2010, 82, 064033. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M.; Farinelli, R.; Odintsov, S.D. Mass-radius relation for neutron stars in f(R) gravity. Phys. Rev. D 2016, 93, 023501. [Google Scholar] [CrossRef]
- Arapoğlu, S.; Deliduman, C.; Ekşi, K.Y. Constraints on perturbative f(R) gravity via neutron stars. J. Cosmol. Astropart. Phys. 2011, 2011, 020. [Google Scholar] [CrossRef]
- Moraes, P.H.R.S.; Arbañil, J.D.V.; Malheiro, M. Stellar equilibrium configurations of compact stars in f(R,T) theory of gravity. J. Cosmol. Astropart. Phys. 2016, 2016, 005. [Google Scholar] [CrossRef]
- Pretel, J.M.Z.; Jorás, S.E.; Reis, R.R.R.; Arbañil, J.D.V. Neutron stars in f(R,T) gravity with conserved energy-momentum tensor: Hydrostatic equilibrium and asteroseismology. J. Cosmol. Astropart. Phys. 2021, 2021, 055. [Google Scholar] [CrossRef]
- dos Santos, S.I.; Carvalho, G.A.; Moraes, P.H.R.S.; Lenzi, C.H.; Malheiro, M. A conservative energy-momentum tensor in the f(R,T) gravity and its implications for the phenomenology of neutron stars. Eur. Phys. J. Plus 2019, 134, 1–8. [Google Scholar] [CrossRef]
- Sharif, M.; Waseem, A. Anisotropic quark stars in f(R,T) gravity. Eur. Phys. J. C 2018, 78, 1–10. [Google Scholar] [CrossRef]
- Deb, D.; Ketov, S.V.; Khlopov, M.; Ray, S. Study on charged strange stars in f(R,T) gravity. J. Cosmol. Astropart. Phys. 2019, 2019, 070. [Google Scholar] [CrossRef]
- Rastall, P. Generalization of the Einstein theory. Phys. Rev. D 1972, 6, 3357. [Google Scholar] [CrossRef]
- Mota, C.E.; Santos, L.C.N.; da Silva, F.M.; Grams, G.; Lobo, I.P.; Menezes, D.P. Generalized Rastall’s gravity and its effects on compact objects. Int. J. Mod. Phys. D 2022, 31, 2250023. [Google Scholar] [CrossRef]
- Velten, H.; Caramês, T.R.P. To conserve, or not to conserve: A review of nonconservative theories of gravity. Universe 2021, 7, 38. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.N.; Otalora, G.; Saridakis, E.N. f(T,) gravity and cosmology. J. Cosmol. Astropart. Phys. 2014, 2014, 021. [Google Scholar] [CrossRef]
- Salako, I.G.; Khlopov, M.; Ray, S.; Arouko, M.; Saha, P.; Debnath, U. Study on anisotropic strange stars in f(T,T) gravity. Universe 2020, 6, 167. [Google Scholar] [CrossRef]
- Singh, V.; Singh, C. Friedmann cosmology with matter creation in modified f (R, T) gravity. Int. J. Theor. Phys. 2016, 55, 1257–1273. [Google Scholar] [CrossRef]
- Carroll, S. Spacetime and Geometry; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Fattoyev, F.J.; Horowitz, C.J.; Piekarewicz, J.; Shen, G. Relativistic effective interaction for nuclei, giant resonances, and neutron stars. Phys. Rev. C 2010, 82, 055803. [Google Scholar] [CrossRef]
- Lourenço, O.; Dutra, M.; Lenzi, C.H.; Flores, C.V.; Menezes, D.P. Consistent relativistic mean-field models constrained by GW170817. Phys. Rev. C 2019, 99, 045202. [Google Scholar] [CrossRef]
- Dutra, M.; Lourenço, O.; Menezes, D.P. Stellar properties and nuclear matter constraints. Phys. Rev. C 2016, 93, 025806. [Google Scholar] [CrossRef]
- Guichon, P.A.M. A possible quark mechanism for the saturation of nuclear matter. Phys. Lett. B 1988, 200, 235–240. [Google Scholar] [CrossRef]
- Saito, K.; Thomas, A.W. A quark-meson coupling model for nuclear and neutron matter. Phys. Lett. B 1994, 327, 9–16. [Google Scholar] [CrossRef]
- Saito, K.; Thomas, A.W. Composite nucleons in scalar and vector mean fields. Phys. Rev. C 1995, 52, 2789. [Google Scholar] [CrossRef]
- Pal, S.; Hanauske, M.; Zakout, I.; Stöcker, H.; Greiner, W. Neutron star properties in the quark-meson coupling model. Phys. Rev. C 1999, 60, 015802. [Google Scholar] [CrossRef]
- Grams, G.; Santos, A.M.; Menezes, D.P. Equation of State Grid with the Quark-Meson-Coupling Model. Braz. J. Phys. 2016, 46, 111–119. [Google Scholar] [CrossRef]
- Baym, G.; Pethick, C.; Sutherland, P. The Ground state of matter at high densities: Equation of state and stellar models. Astrophys. J. 1971, 170, 299–317. [Google Scholar] [CrossRef]
- Özel, F.; Freire, P. Masses, Radii, and the Equation of State of Neutron Stars. Annu. Rev. Astron. Astrophys. 2016, 54, 401–440. [Google Scholar] [CrossRef]
- Steiner, A.W.; Heinke, C.O.; Bogdanov, S.; Li, C.K.; Ho, W.C.; Bahramian, A.; Han, S. Constraining the mass and radius of neutron stars in globular clusters. Mon. Not. R. Astron. Soc. 2018, 476, 421–435. [Google Scholar] [CrossRef]
- Cromartie, H.T.; Fonseca, E.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Blumer, H.; Brook, P.R.; DeCesar, M.E.; Dolch, T.; Ellis, J.A.; et al. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nat. Astron. 2020, 4, 72–76. [Google Scholar] [CrossRef]
- Reed, B.T.; Fattoyev, F.J.; Horowitz, C.J.; Piekarewicz, J. Implications of PREX-2 on the equation of state of neutron-rich matter. Phys. Rev. Lett. 2021, 126, 172503. [Google Scholar] [CrossRef]
- Demorest, P.B.; Pennucci, T.; Ransom, S.M.; Roberts, M.S.E.; Hessels, J.W.T. A two-solar-mass neutron star measured using Shapiro delay. Nature 2010, 467, 1081–1083. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.C.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; Van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A massive pulsar in a compact relativistic binary. Science 2013, 340, 1233232. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mota, C.E.; Santos, L.C.N.; da Silva, F.M.; Flores, C.V.; Lobo, I.P.; Bezerra, V.B.
Neutron Stars in the Context of f(
Mota CE, Santos LCN, da Silva FM, Flores CV, Lobo IP, Bezerra VB.
Neutron Stars in the Context of f(
Mota, Clésio E., Luis C. N. Santos, Franciele M. da Silva, César V. Flores, Iarley P. Lobo, and Valdir B. Bezerra.
2023. "Neutron Stars in the Context of f(
Mota, C. E., Santos, L. C. N., da Silva, F. M., Flores, C. V., Lobo, I. P., & Bezerra, V. B.
(2023). Neutron Stars in the Context of f(






