Diagnostics of Flare Loop Parameters in Shrinkage and Ascent Stages Using Radio, X-ray, and UV Emission

Abstract

We propose the diagnostics of plasma parameters in flare loops using the data of multi-wavelength observations in both shrinkage and expansion phases of the loops. The approach of a flare loop as an equivalent electric circuit is applied. We show that depending on plasma loop parameters, the shrinkage may be accompanied by an increase in the electric current in the loop rather than a decrease. The number density, temperature, electric current, radius, loop-top altitude, and loop volume are determined for the flare events on 16 April 2002 and 24 August 2002.

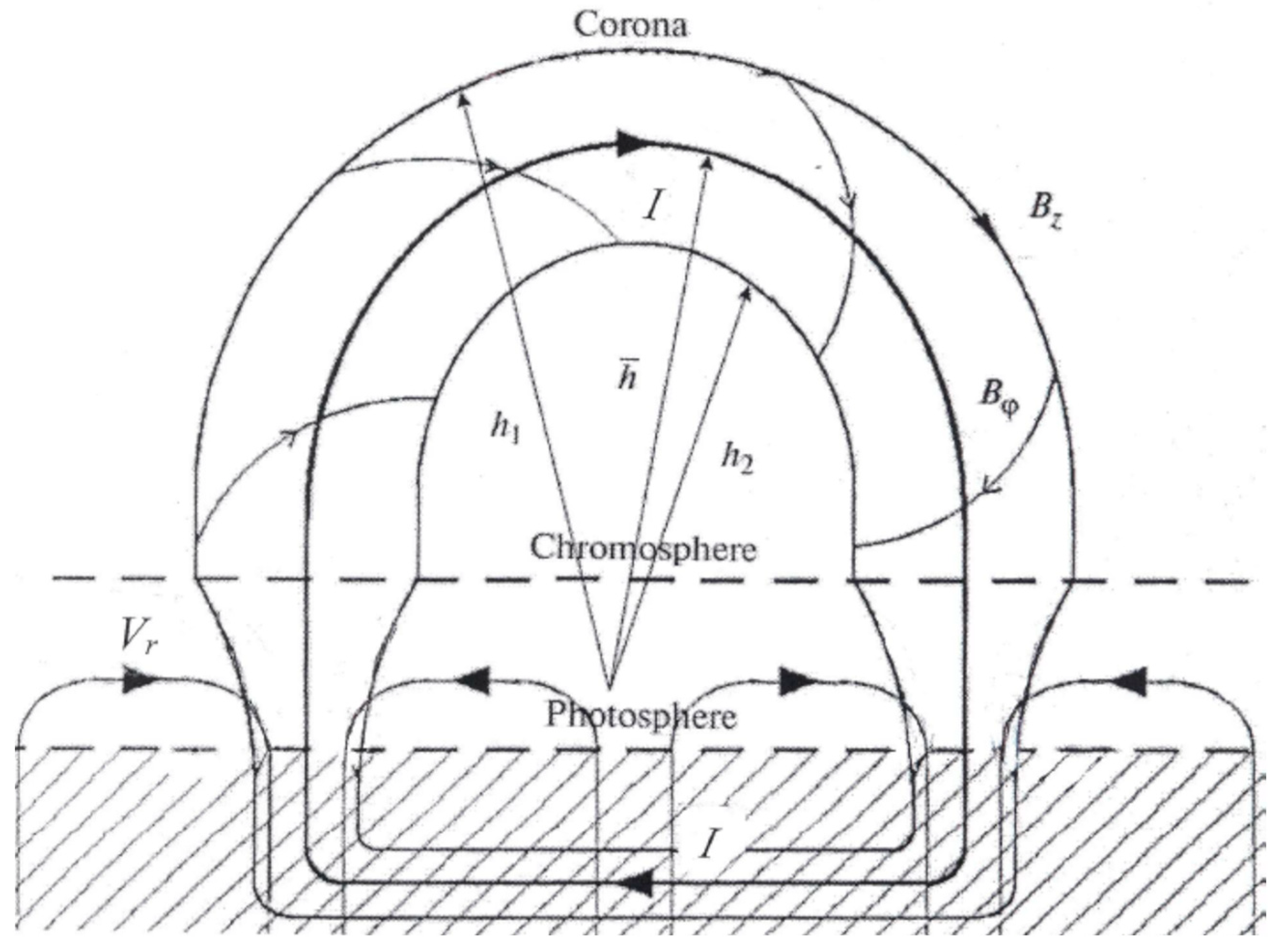
1. Introduction

The phenomenon of the shrinkage of flare loops during the impulsive phase of the flare, followed by the upward motion of the loops, was revealed in numerous observations [1,2,3,4,5,6,7]. The simulation of the shrinkage phenomenon was based mainly on magnetic reconnection, the following particular cases of which can be noted: a collapsing magnetic trap embedded in a standard 2D magnetic reconnection model [8] and the rainbow reconnection [9]. In addition, there is an alternative model of loop shrinkage based on the representation of a flare loop as an equivalent electric circuit [10,11] in which the shrinkage is induced by a slight decrease in the electric current [12].

In some flares, oscillations in UV [4] and X-ray emission [7] were observed in the course of the shrinking phase as well as in the radio emission during the altitude increase of a loop [3]. In addition, Li, and Gan [4] showed that the UV oscillations are manifested as vertical oscillations of the loop, to some extent similar to the oscillations observed by Wang and Solanki [13]. In this paper, we study the dynamics of the physical parameters of flare loops in the shrinkage and ascent phases; in so doing, we are based on the approach of the current-carrying loop as an equivalent electric (RLC) circuit. For an illustration, we present the corresponding analysis of flare loops in the flares of 16 April 2002 [4] and 24 August 2002 [3]. We will also show that the loop shrinkage can be accompanied by a decrease in the electric current [12] and its increase.

2. Loop Shrinkage in Terms of an Equivalent Electric Circuit

Consider a current-carrying magnetic loop (Figure 1), in which the electric current I flows from one loop foot point to the other through the coronal part of the loop and closes in the photosphere at a depth ${\tau }_{5000}=1$ where zero level of the solar atmosphere is located, and the conductivity is isotropic [11]. The model of the current-carrying flare loop is supported by observations (see, e.g., [14,15]). For simplicity, we present the loop as a half-circle because it follows from the radio loop observed with the Nobeyama Radio Heliograph (NoRH) at 34 GHz [3]. An electric current is generated by the electromotive force (e.m.f.) $\Xi$ located at the footpoints of the loop and arising from the interaction of photosphere convective flows with the loop magnetic field $\Xi =\frac{\left(\left|V_r\right|l_{1}I\right)}{c^2{r}_1}$ [16]. Here, $V_r$ is the radial component of the velocity of convective flow, $r_1$ $\approx$ (1–3) × ${10}^7\mathrm{cm}$ is the half-width of the loop cross-section area and $l_1\approx r_1$ is the loop length in e.m.f. region.

The forces acting on the top of the current-carrying loop can be as follows [12].

$$\frac{{\overline{B}}_z^2+{\overline{B}}_{\phi }^2}{4\pi \overline{h}}-\frac{{\overline{B}}_z^2}{4\pi \overline{h}}+\frac{2I^2}{c^2\overline{h}}\frac{1}{\pi r^{2 }} -\rho g=0$$

(1)

where $r\approx \left(h_1-h_2\right)/2$ is the radius of the loop in the coronal part, which, in accordance with the observational data, we consider to be approximately constant, $\rho =$ $m_{i}n$, $n$ is plasma number density in a loop, g = 2.74 × 10⁴ cm s⁻² is the acceleration of gravity. Here, the first term in Equation (1) means the upward pressure force of the magnetic field associated with the curvature of the magnetic field’s lines in an inhomogeneous atmosphere and refers to a unit volume. The second term is the downward magnetic tension force, the third term designates the upward Ampére force associated with the photospheric current, and the last term is the downward gravitational force.

In Equation (1), we neglected the force acting on the loop from the external magnetic field, which is possible for a typical electric current in the flaring loops, I > 10¹⁰ A, and $B_{ext}\approx 100 \mathrm{G}$ [12]. In addition, in Equation (1), the mean values of the squares of the longitudinal and azimuthal components of the magnetic field and the mean large radius of the loop are used: ${\overline{B}}_z^2,$ ${\overline{B}}_{\phi }^2,$ $\overline{h}$. Keeping in mind that ${\overline{B}}_{\phi }=2I/cr$, we can write the equilibrium condition for the loop top:

$$\frac{3I^2}{c^2\overline{h}}\frac{1}{\pi r^2}-\rho g=0$$

(2)

Hence, the average height of the loop is proportional to the square of the electric current in the loop:

$$\overline{h}\left(t\right)=\frac{3I{\left(t\right)}^2}{c^{2}gM\left(t\right)}, M\left(t\right)=\pi r^2{m}_{i}n\left(t\right)$$

(3)

where M is the flux tube mass per unit length.

Equation (3) suggests that the height of the loop top (LT) is determined by the balance of Ampére force, magnetic pressure, and gravity. As a result, the average loop height depends on the square of the electric current and the plasma number density in the loop. A similar functional relationship exists for a current-carrying filament [17]. From Equation (3), it follows that the relative change in the loop altitude in the course of the flare is determined by the formula:

$$\frac{{\overline{h}}_2-{\overline{h}}_1}{\overline{h_1}}=\frac{I_2^2}{I_1^2}\frac{n_1}{n_2}-1$$

(4)

If the flare process is not accompanied by a change in the plasma number density in the loop ($n_2=n_1)$, then a decrease in the loop height (${\overline{h}}_2<{\overline{h}}_1)$ can be caused by a decrease in the electric current:

$$\frac{\mathsf{\Delta }I}{I} \approx \frac{ 1}{2}\frac{{\overline{h}}_2-{\overline{h}}_1}{{\overline{h}}_1}$$

(5)

For example, for a flare on 24 August 2002 [3], a decrease in the loop height at the initial stage of the shrinkage under condition $n_2=n_1$ should accompanied by a decrease in the current by $\mathsf{\Delta }I/I_1$ ≈ −0.175 [12]. In reality, however, as seen from the further estimates, the decrease in the loop height can occur simultaneously with a significant increase in the plasma density inside the loop due, for example, to chromosphere evaporation. In this case, the relative change in the electric current with a change in the loop altitude is determined by the formula:

$$\frac{ I_2}{I_1}=\sqrt{\frac{{\overline{h}}_2{n}_2}{{\overline{h}}_1{n}_1}}$$

(6)

It follows that if ${\overline{h}}_2{n}_2>{\overline{h}}_1{n}_1$, then the loop shrinkage may be accompanied by an increase in the current in the loop, rather than by a decrease, i.e., the loop in the shrinkage process accompanied by chromosphere evaporation becomes quite “heavy” and, to maintain stability, the Ampère force, which depends on the magnitude of the electric current, will increase.

3. An Oscillating Loop as an Equivalent RLC Circuit

In the impulse phase of the flare on 16 April 2002 [4], the loop shrank within 5 min, which, we believe, was caused by a decrease or an increase in the electric current. During the shrinkage process, the Transition Region and Coronal Explorer (TRACE) 195 Å data indicate vertical oscillations of the loop with a period p ≈ 154 s and an amplitude of 285 km (≈2% of the loop height). Assuming that the vertical oscillations of the loop are due to the oscillations of the electric current of small amplitude, $\tilde{I}\ll I$, for which we can write the equation [11]

$$\frac{1}{c^2}L\frac{{\partial }^2\tilde{I}}{\partial t^2}+R\left(I\right)\frac{\partial \tilde{I}}{\partial t}+\frac{\tilde{I}}{C\left(I\right)}=0$$

(7)

In Equation (7), the inductance and capacitance of the loop are defined by its coronal part [16]:

$$L=2l\mathsf{\Lambda }, \mathsf{\Lambda }=\left(ln\frac{4l}{\pi r}-\frac{7}{4}\right),C\left(I\right)\approx \frac{c^4\rho S^2}{2\pi I^{2}l}$$

(8)

where $S=\pi r^2, l=\pi \overline{h}$ is the loop length. But the Cowling resistance R(I) is determined mainly by the chromosphere part of a loop due to collisions of ions with the neutral component of the plasma. The period of the electric current oscillation is [16]

$$P=\frac{2\pi }{c}\sqrt{LC\left(I\right)}={\left(2\pi \right)}^{3/2}\sqrt{\Lambda }\frac{c{r}^2\sqrt{n{m}_i}}{I}$$

(9)

The condition of in-phase oscillations of the loop (lumped RLC circuit) requires that the inverse Alfvén time $V_A/l$ be greater than the oscillation frequency of the RLC circuit, $P^{-1}=I{\left[{\left(2\pi \right)}^{3/2}c{r}^2{\left(\mathsf{\Lambda }n{m}_i\right)}^{1/2}\right]}^{-1}$ which gives $V_A/l\approx$ 2 × 10⁻² ${\mathrm{s}}^{-1}$ > $P^{-1}\approx$(0.65–0.83) × 10⁻² ${\mathrm{s}}^{-1}$, as it follows from the Section 4.

4. Dynamics of Flare Loop Parameters Inferred from Multi-Wavelength Observations

The multi-wavelength approach based on radio, X-ray, and UV observations opens up new possibilities for diagnosing the plasma parameters of flare loops during the shrinkage of the loops and their subsequent expansion. Let us apply this approach to two flares with the shrinkage phenomenon.

4.1. Loop in the Flare on 24 August 2002

The X3.1 flare on 24 August 2002 started at 00:49 UT. It was observed with Geostationary Operational Environmental Satellite (GOES-08), Reuven Ramaty High Energy Solar Spectroscopic Imager (RHESSI), NoRH at 34 GHz, and the Nobeyama Radio Polarimeter (NoRP) at 17 and 35 GHz. The loop began to shrink at 00:53 UT during the rising phase of the soft X-ray flux; the shrinkage ended at 01:02 UT. After the impulsive phase of the flare (01:02 UT), the upward motion of the loop began, and the loop expansion was interrupted at 01:09 UT. As seen in Figure 2 presented in [3], the radio image of the loop at 34 GHz (NoRH) is approximately fitted with a half-circle. From 00:53 to 01:02 UT, the loop height decreased from $2.3\times {10}^9$ cm to 1.6 $\times {10}^9 \mathrm{cm},$ i.e., by about 30%. The loop height at the ascent stage varied from h = 1.6 × 10⁹ cm at 01:02 UT to 2.45 × 10⁹ cm at 01:08 UT [3]. Oscillations of radio emission at 17 and 35 GHz began at the final stage of the loop shrinkage and ended at 01:10 UT. The oscillation period shows irregular changes at an average value of p $\approx$ 120 s. The loop half-width, according to NoRH 34 GHz data, was $r \approx 3.5\times {10}^8 \mathrm{cm}$. In further estimations, we believe that the radius r of the loop in the shrinking phase and the subsequent recovery of the loop height to its original value changed insignificantly (see, e.g., [18,19]).

Li and Gan [3] presented GOES 08 soft X-ray light curves at 0.5–4.0 Å and 1.0–8.0 Å for the flare on 24 August 2002. We use these data to determine the plasma temperature in the loop T and the plasma emission measure $EM=n^{2}V$ at various flare stages according to the method described in [20]. The temperature and measure of the emission of the loop at each stage of the evolution of the flare process depend on the ratio of the observed X-ray fluxes [20]

$$R=\frac{F_{0.5-4.8 \mathrm{\AA } }\left({\mathrm{watts} \mathrm{m}}^{-2}\right)}{F_{1.0–8.0 \mathrm{\AA }}{}_{ }\left({\mathrm{watts} \mathrm{m}}^{-2}\right)}$$

(10)

In this case, the temperature in MK and the emission measure (EM) in units of ${\mathrm{cm}}^{-3}$ are determined by the following empirical formulas:

$$T\left(R\right)MK=3.15+77.2R-164R^2+205R^3$$

(11)

$$EM\left({\mathrm{cm}}^{-3}\right)=\frac{{10}^{55}{F}_{1.0–8.0 \mathrm{\AA }}{}_{ }\left({\mathrm{watts} \mathrm{m}}^{-2}\right)}{-3.86+1.17T-1.31\times {10}^{-2}{T}^2+1.78\times {10}^{-4}{T}^3}$$

(12)

We use the emission measure to determine the plasma number density $n$ in the loop from the known volume of the loop $V={\pi }^2{r}^2\overline{h}$

$$n={\left(EM/V\right)}^{1/2}$$

(13)

The electric current in the loop I can be determined from Equation (9) for the oscillation period of the loop, assuming that the oscillations are associated with oscillations of the loop as an equivalent RLC circuit:

$$I\approx 0.9\frac{r^2\sqrt{n}}{P}$$

(14)

The results of the estimates of the shrinkage loop parameters in the course of the flare are given in

Table 1. Dynamics Loop Parameters of the Flare on 2002 August 24.

Flare Phase	$\overline{\mathit{h}}$/109 cm	R/10−2	EM/1049 cm−3	V/1027 cm3	T MK	n/1010 cm−3	I/1010 A
Flare start 00:49 UT	2.3	7.0	0.38	2.80	9.4	3.70	-
Shrink start 00:53 UT	2.3	13.3	0.78	2.80	11.0	5.28	8.6
Shrink end 01:02 UT	1.6	50.0	5.2	1.93	27.6	16.4	12.7
Oscillations 01:00–01:10 UT	2.45	31.7	22.0	2.96	17.7	27.0	15.9

.

Based on Table 1, the following preliminary conclusions can be drawn.

(i)

In the shrinking phase (00:53–01:02 UT), an increase in the plasma temperature by more than a factor of 2.5 is observed, as well as an increase in the plasma density in the loop, approximately by a factor of three. These changes in the parameters are accompanied by a relative increase in the electric current $I_2/I_1$, approximately by the factor of 1.48.

(ii)

At the stage of loop ascent (01:02–01:10 UT), accompanied by relatively small oscillations at 17 and 35 GHz, the plasma density inside the loop continues to increase approximately by a factor of 1.6, and the temperature decreases from 27.6 MK to 17.7 MK. Therefore, the above estimate of the magnitude of the electric current (14) reflects a certain average value at the stage of the loop expansion because the parameters that determine the period of oscillations: plasma density and the electric current magnitude, change during oscillations.

(iii)

The total electric current of about 10¹¹ A contained a flare loop with r = 3.5 × 10⁶ m means a current density of j ≈ 10⁻² Am⁻². This value agrees with estimates of the density of the vertical electric current found using the vector magnetograms (e.g., [21,22]). In more powerful flares, the value of j can be an order of magnitude larger.

For the loop to keep the cross-section area during the shrinkage and reverse upward movement, the condition $\beta =8\pi nkT/B^2$< 1 should be satisfied [17], where k is the Boltzmann constant, $B^2=B_{\phi }^2+B_z^2$. At the current $I=1.2\times {10}^{11}\mathrm{A}$, the value of $B_{\phi }=2I/cr\approx 70 \mathrm{G}$. At the maximum values of the density and temperature of the loop plasma (Table 1), the condition $\beta <1$ requires $B\approx B_z\approx 200 \mathrm{G}$. In flare loops, the typical value of $B_z\approx 150-400 \mathrm{G}$ [23]. The inequality $B_z>B_{\phi }$ is also necessary for the stability of the loop against MHD disturbances.

As for the role of accelerated electrons transported into a loop in the creation of electric current, we have to note that these electrons can change the total electric current in the loop during a time of loop flight (of the order of seconds), which is less than oscillation period of the loop as an RLC circuit. Moreover, this current disappears in a few bounce periods as the result of reflections of electrons from the loop magnetic mirrors.

4.2. Loop in the Flare on 16 April 2002

The second example of a loop shrinkage is in the M2.5 flare on 16 April 2002, observed by RHESSI and TRACE [4]. A specific feature of this flare is the oscillatory shrinkage during an impulsive flare phase. The TRACE 195 Å loop exhibited vertical oscillations with a period of p ≈ 154 s and an amplitude of 284 km (2% of the loop height). In this case, the loop’s height decreased from $1.4\times {10}^9$ cm to $1.15\times {10}^9$ cm. At the initial and final stages of the shrinkage, the X-ray flux, according to GOES 1.0–8.0 Å data, was, respectively $F_{1.0–8.0 \mathrm{\AA }}{}_{ }\approx 5\times {10}^{-6} \mathrm{and} 2\times {10}^{-5} {\mathrm{watts} \mathrm{m}}^{-2} (5\times {10}^{-3} \mathrm{and} 2\times {10}^{-2}\mathrm{ergs} {\mathrm{cm}}^{-2}{\mathrm{s}}^{-1}$). This flux corresponds to the loop luminosity in the soft X-ray range at the initial and final shrink stages, respectively,

$$\begin{array}{c}{L}_x=F_{1.0–8.0 \mathrm{\AA }}{}_{ }4\pi R_{S-E}^2\\ \hspace{1em}\hspace{1em}=\left(5\times {10}^{-3}-2\times {10}^{-2}\right){\mathrm{ergs} \mathrm{cm}}^{-2}{s}^{-1}4\pi {\left(1.5\times {10}^{13}\right)}^2{\mathrm{cm}}^2\hspace{1em}\hspace{1em}\approx \left(1.4-5.65\right)\times {10}^{25}{\mathrm{ergs} \mathrm{s}}^{-1}\end{array}$$

(15)

On the other hand, the luminosity of the loop is expressed by the formula [24]

$$L_x=Q\left(T\right)n^{2}V=Q\left(T\right)n^2{\pi }^2{r}^2\overline{h}$$

(16)

$$Q\left(T\right)=2\times {10}^{-27}\sqrt{T}+5\times {10}^{-25}exp\sqrt{2.8+{10}^{6}K/T} \mathrm{ergs}{ \mathrm{cm}}^3{\mathrm{s}}^{-1}$$

(17)

Assuming the probable temperature of the flare plasma $T\approx 10{ }^7\mathrm{K}$ we obtain

$$Q\left(T\right)\approx 9\times {10}^{-24}{\mathrm{ergs} \mathrm{cm}}^3{\mathrm{s}}^{-1}$$

(18)

The emission measure of the flare loop at the initial Equation (1) and final Equation (2) shrinkage phases, respectively, is equal to

$$E{M}_1=1.38\times {10}^{10}{r}^2{n}^2{ \mathrm{cm}}^{-3}, E{M}_2=1.1\times {10}^{10}{r}^2{n}^2 {\mathrm{cm}}^{-3}$$

(19)

On the other side

$$E{M}_1=\frac{L_{x1}}{Q\left(T\right)}=1.55\times {10}^{48} {\mathrm{cm}}^{-3}, E{M}_2=\frac{L_{x2}}{Q\left(T\right)}=6.2\times {10}^{48} {\mathrm{cm}}^{-3}$$

(20)

A comparison of the values (19) and (20) gives $rn\approx 1.05\times {10}^{19} {\mathrm{cm}}^{-2}$ at the initial stage of the loop shrinkage and $rn\approx 2.37\times {10}^{19}{\mathrm{cm}}^{-2}$ at the final stage. From Equations (3) and (14), the dependence of the loop radius on the altitude and period of pulsations is determined:

$$r\approx 7.4 P\sqrt{\overline{h}} \mathrm{cm}$$

(21)

Substituting the values of the period of pulsations and the height of the loop into (21), we obtain that the radius of the loop changes from $r\approx 4.2\times {10}^8$ cm to $r\approx 3.9\times {10}^8 \mathrm{cm}$, during the loop shrinkage, i.e. remains practically constant within the probable accuracy of estimates. In this case, the plasma number density changes from $n\approx 2.5\times {10}^{10 }{\mathrm{cm}}^{-3}$ to $n\approx 6.1\times {10}^{10}{ \mathrm{cm}}^{-3}$, i.e. the density changes are significant; this is likely to be associated with a certain decrease in the loop volume and chromosphere evaporation. Further, from Equation (3), the electric current magnitude is determined from the known values of $\overline{h}$, n, and r:

$$I\approx \left(1.5-1.7\right)\times {10}^{20}cgs\approx \left(5.0-5.7\right)\times {10}^{10} \mathrm{A}$$

(22)

Let us find the conditions for the plasma beta <1. Currently $I\approx 5\times {10}^{10} \mathrm{A}$ and the loop radius $r = 4\times {10}^8 \mathrm{cm}$, the value of $B_{\phi }\approx 25 \mathrm{G}$. The condition $\beta = 8\pi nkT/B^2$ < 1 at $n=6\times {10}^{10}{\mathrm{cm}}^{-3}$ and $T=10 \mathrm{MK}$ requires $B_z>46 \mathrm{G}$.

5. Conclusions

The diagnostics of plasma parameters of flare loops proposed in this paper are based on the representation of a loop as an equivalent electric circuit. This approach makes it possible to estimate, for example, the magnitude of the electric current from the observed pulsation period. Based on the considered two events with shrinkage and pulsations observed in the radio, X-ray, and UV ranges [3,4], the following conclusions can be drawn.

With a change in the size of flare loops, almost all parameters of the loop plasma change: the electric current, magnetic field, plasma density and temperature. In this case, depending on the value of $\overline{h}$n in Equation (6), the loop shrinkage can be accompanied by a decrease in the electric current [12] and its increase. In the latter case, the loop “becomes heavier” due to both a decrease in its size and the evaporation of the chromosphere plasma into the loop during the flare impulsive phase. Furthermore, since the Ampére force must increase to maintain stability, the magnitude of the electric current must also increase.

The scatter of the observational data and a small number of oscillations make it possible to estimate the loop plasma parameters, particularly the electric current, only to an order of magnitude. Nevertheless, the presented estimates give an idea of the dynamics of the parameters of flare loops as their sizes decrease and increase. As shown in this study, the loop cross-sectional radius r changes insignificantly in this case.

The self-consistent diagnostics suggested in this paper can be used to determine the plasma parameters in flare loops in other events with shrinkage and oscillations.