Abstract
In this work, the perturbed equations of motion of the infinitesimal body are constructed in the framework of the circular restricted three-body problem when the main two bodies are oblate and radiating. Under the perturbations effects of the oblateness and the radiation pressure the positions of collinear Lagrange points are evaluated, the interior and exterior first-order resonant periodic orbits are also studied. In addition, the initial positions of the periodic orbits and the size of loops have been estimated under these effects. Thus, the characteristics of periodic orbits have been studied under the combine effects of two, three and four perturbations for all the possible combinations of the perturbed parameters. The different order of resonant periodic orbits have been also analysed under the effects of Jacobi constant, mass factor, order of resonance and number of loops.
1. Introduction
In Celestial Mechanics and Astrodynamics, the three-body problem has a great importance and has numerous applications [1,2,3,4]. In [5,6,7], the authors studied the circular restricted three-body problem (CRTBP) with the perturbation impact of both the primaries in terms of oblateness and the small perturbations of coriolis and centrifugal forces. It is not precise to consider the celestial bodies as point masses without physical dimensions according to the actual cases. Rotation, as one might expect, causes deformation in the shape of objects near the equator. Oblateness describes the deviation of planets and celestial objects from spherical form caused by the rotation’s centrifugal force. Thus, there are many work for analysis of CRTBP under these perturbations [8,9,10,11,12,13,14].
In [15] the authors developed the governing equation of motion of infinitesimal body and found the locations of Lagrange points. Also, they analysed their stability by considering both the primaries as oblate bodies and sources of radiation. They also studied the periodic orbits around these points under the effect of the aforementioned perturbed forces. As a result, the vast majority of objects can be approximated as oblate spheroids. first-order resonant periodic orbits for the Saturn–Titan system are explored in [16], where Saturn’s oblateness is considered as a disruptive perturbation force. In [17] the authors investigate the stability of first-order resonant periodic orbits in the domain of the perturbed CRTBP. The effect of various parameters on geometrical properties and periodic solutions of the systems were investigated, including the mass ratio, the Jacobi constant, and the oblateness coefficient.
Periodic orbits with interior resonance of third and fourth order are analyzed in [18] within the framework of Sun–Neptune and Sun–Jupiter. In [19] the authors choose the structure in which the primaries mass are varies but the sum of their total mass always remains constant. For this scenario, they obtained the feasible region for the orbit of a satellite. The outcomes of the work used in the close binary star systems with conservative mass transfer. In [20] the authors investigated satellite orbital perturbations caused by the moon’s orbit around the Earth. The Sun–Earth–Moon bi-circular model is used to investigate the effects of this perturbation. They also investigated the effects of this perturbation on equilibrium points and the zero velocity curve.
In [21] the authors employed the RTBP in the structure of continuation fractional potential. They found thirteen equilibrium points where nine of them are collinear and other four points are noncollinear points. They also studied the zero-velocity curves and analysed the perturbation of the continuation fractional potential effect on the possible regions of the motion as well as the linear stability of all the equilibrium points are investigated. While in [22] the locations of collinear points in photogravitational ER3BP under the effect of the zonal harmonics of the smaller primary is studied with their linear stability. But the ER3BP is employed to study the halo orbits around Sun–Mars collinear points , , and when the bigger primary is a source of radiation [23]. Also in [24,25,26] the authors analysed the effects of the third body perturbation in the framework of elliptic restricted 4–body problem dynamics, where some interesting resonant periodic solutions were derived in this operative environment.
Poincaré surface section (PSS) can be used to calculate the order of resonance. In this context, the authors in [27] examined the lower order resonant periodic orbits in the structure of CRTBP, specifically order one with interior and exterior resonance, and orders of three and five with interior resonance only, using solar radiation as a perturbation force. In [28] the authors studied higher order interior resonant orbits, specifically orders seven, nine, and eleven within the framework of CRTBP considering the effect of oblateness and solar radiation perturbation. Monitoring the path of the satellite and its initial location has a great importance in Orbital Mechanics, so in [29] the authors developed a multivariate non-linear regression model to predict the initial condition of the infinitesimal body motion. They established that it can easily find the exact initial condition of an infinitesimal body’s orbit using this predicted condition.
In recent years, perturbing forces such as oblateness and radiation forces of the primaries, coriolis and centrifugal forces have been incorporated into the study of the RTBP. The main perturbations for a relatively distant Earth satellite are caused by the Earth’s oblateness, the Sun’s and Moon’s gravitational attractions. The effect of the Earth’s oblateness on satellites at a few Earth radii away is of the same order as the effect of distant bodies. This range encompasses a significant area of interest for communications satellites [30,31].
The term “cosmic radiation” refers to the radiation that reaches us from other stars. While solar radiation refers to the radiation emitted by our own Sun. The motion of an infinitesimal body caused by the mutual gravitational force of the primaries as well as radiation pressure from one or both primaries is described by photogravitational RTBP. The Sun–Planet–Satellite system can be analysed by considering the Sun as a radiating body, whereas the Star–Star–Planet system can be analysed by considering both primaries’ radiation pressure [32,33,34].
The minute pressure exerted on bodies by radiation is inversely proportional to the square of the distance between the light source and the illuminated body. Lebedev experimentally demonstrated and stated this law in 1891 [35]. Many researchers have incorporated this perturbing force, as well as other perturbing forces such as non–sphericity, atmospheric drag, and so on, into the study of RTBP. The effect of radiation force is complicated because it depends on the geometry, physical, and physicochemical properties of infinitesimal body [36]. The radiation force has a significant impact on the dynamics of the infinitesimal body [37,38,39,40,41,42,43,44].
In this work, we analyse the restricted three-body problem under the perturbation of oblateness and radiation pressure of both primaries. We derive the equation of mean motion and governing equations of motion under these perturbations. We will find numerically the solution of the perturbed motion. Interior and exterior resonant periodic orbits will be analysed under the effect of oblateness of two primaries and their radiation pressure. Effect of single, double, triple and all four perturbations and their combinations will be analysed on resonant periodic orbits. Also, effects of mass factor, Jacobi constant and number of loops on the initial position of resonant periodic orbit will analysed. Loop-size of periodic orbit under all the perturbations will be discussed. Such analysis is an innovative part of this work.
There are many known oblate stars in the Universe. For example: Altair, Achernar, Regulus, Vega, Beta Cephel, Beta Lyrae, Spica, Alpha Eridani, Bellatrix, Polaris Aa are oblate stars with different oblateness. Achernar is located in the constellation Eridanus and has several neighbouring stars that are also oblate.
- Alpha Eridani is Achernar’s closest neighbour. It is also known as “Achernar B” is an oblate star that orbit around Achernar as part of a binary system.
- Zaurak also known as Gamma Eridani is another oblate star located near Achernar.
- Rigel also known as Beta Orionis is an oblate star located in the constellation Orion which is adjacent to Eridanus [45,46].
Thus, the orbit of an infinitesimal body under the perturbation of oblateness of both primaries with radiation is important to study. Analysis of interior and exterior resonant orbits under effect of combinations of such perturbations are important to study for gaining information about such stars. Also, such analysis is rare in the literature. So, it is the focus of the study.
2. Perturbed Forces
Perturbation forces act on a body that cause a deviation from its expected or planned motion. Perturbations due to forces can be analysed mathematically using the principles of physics and engineering, such as calculus, mechanics, and dynamical systems theory. By understanding the forces acting on a system or object, engineers and scientists can predict its motion and design systems that are more resistant to perturbations. The perturbation forces are not limited to oblate or non–sphericity effects, but there are many other perturbation forces that make deviations in satellite orbits such as tidal effect. In particular, if this satellite is moving around the primary gaseous or fluid planet [47,48].
In physics, perturbations can refer to any external influence that changes the trajectory of a system or object. In the context of mechanics, perturbation forces can include external forces such as gravity, air resistance, or friction, which can affect the motion of an object. These forces may be small, but over time, they can accumulate and cause a significant deviation from the expected motion. In astronomy and celestial mechanics, the major perturbation forces come from the gravitational forces between celestial bodies, which can cause small deviations in the motion of planets, moons, and asteroids. For example, a satellite orbiting the Earth is subject to several forces, including the gravitational force from the Earth and other celestial bodies, as well as atmospheric drag and solar radiation pressure. These forces can cause small variations in the satellite’s motion over time, which can accumulate and cause the satellite to deviate from its intended orbit. These perturbations can be used to study the dynamics of the solar system and to predict the positions and motions of celestial objects.
2.1. Radiation Perturbed Forces
The radiation force exerted by a primary body on an infinitesimal body is composed of three components: radiation pressure, incident radiation doppler shift, and pointing drag. The radiation pressure is the only significant component of radiation force. The effect of incident radiation doppler shift and pointing drag on an infinitesimal body [37] is negligible. The radiation pressure force changes with the distance in the same way of gravitational attraction force . The resultant force exerted on the infinitesimal body, according to [49] is given by
where is so-called reduction mass factor, and expresses the effect of the primary’s radiation pressure on the infinitesimal body. For simplicity, this factor can be written also in the following form , where is the ratio of the radiation force to the gravitational force . The parameter is determined by the physical characteristics of both the radiating primary and the infinitesimal body and it is represented by the formula
where G is the constant of gravitation. M and L noted the mass and luminosity of the Sun respectively. In [50], the authors discovered that the luminosity of the Sun is affected by its absolute temperature. The infinitesimal body’s mass and uniform density are denoted by s and , respectively. Knowing the mass and luminosity of the Sun allows us to calculate for a given infinitesimal body for a given radius and density. If there is no perturbing force due to radiation pressure and . If then , which means . If then , which means . We use the latter case when studying photogravitational RTBP in the solar system.
2.2. Oblateness Effect
Oblateness refers to the degree to which a planet or other celestial body deviates from a perfect spherical shape. In other words, oblateness describes how flattened or bulged a planet is at its poles or equator compared to its average diameter. The oblateness of a planet is usually measured by its oblateness coefficient, which is the ratio of the difference between the equatorial and polar radii of the planet to its equatorial radius. This coefficient is typically expressed as a decimal fraction or a percentage. For example, the Earth has an oblateness coefficient of approximately , which means that its polar radius is about 21 km shorter than its equatorial radius. This slight flattening at the poles is due to the centrifugal force generated by the Earth’s rotation, which causes material to bulge outward at the equator.
Oblateness has an important effect on the dynamics of a planet’s atmosphere, the behaviour of its magnetic field, and the orbits of its moons or artificial satellites. It is also a key factor in determining the planet’s gravitational field and its potential for hosting life, as it can affect factors such as climate stability and the distribution of ocean currents.
The gravitational potential observed by the satellite can be expressed using potential theory as [2]
where G is the universal gravitational constant, and are the object’s mass and mean radius respectively, but m is mass of the infinitesimal body. While shows the satellite’s latitude, and is Legendry polynomial of degree n. Distance from the centre of the object to satellite is r and is the dimensionless zonal harmonic coefficient.
If two objects move in the same plane with constantly equal to zero, then the Equation (5) can be rewritten as
where
here n is nonnegative integer.
Substituting Equation (6) into Equation (7) with considering only the second zonal harmonic coefficient (), this means that we will consider only the coefficient (), which represent s the oblateness effect, the potential relation can be reduced to
The second term in Equation (8) represents the effect of the second zonal harmonic coefficient or oblateness effect when the two bodies are moving in the same plane. This equation can be rewritten in the following simple form [51]
where A denotes the oblateness parameter.
3. Mean Motion of Two Oblate Bodies
Now we assume that two oblate bodies of masses and are moving in circular orbit and in the same plane under their mutual gravitation forces, while the parameters and are the notation used for the oblateness coefficients of the first () and second () respectively, where the parameters of oblateness and can be evaluated by [52]
Here, , , and denotes the equatorial and polar radius of first and second primary respectively and R is the distance between primaries.
Let , be the position vectors of the two masses and with respect to the center of mass (O), and is the position vector of with respect to where as in Figure 1. Utilizing Equations (9) and (10), the potential between and m is given by
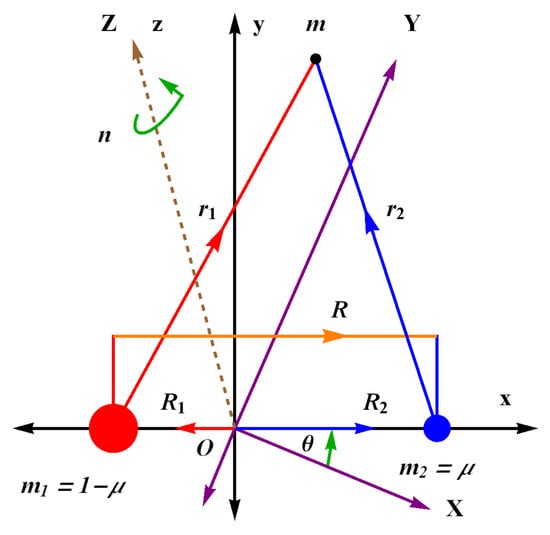
Figure 1.
Configuration of restricted three-body problem.
Then the equation of relative motion of with respect to can be written as
where
Also, the relative position vector can be defined as , where and are two orthogonal unit vectors. In polar coordinates , we can write and , where = . We also assume that the two oblate primaries are moving in circular orbit around their center of mass. Thus, mean motion n is a constant. Hence we get
It is clear that in the case of the relative motion is circular, then the relative position vector is a constant vector and from Equation (16) we can deduce that the mean motion of two bodies can be determined by
Furthermore when the separation distance between two bodies is taken as a unit distance and the sum of two masses is a unit of mass and normalized the gravitational constant to equal one, then the mean motion of Equation (17) can be reduced two the following simple formula
The above relation represents the perturbed mean motion in normalized variables between two oblate bodies, where this relation gives the perturbed mean motion by the oblateness of the first body when and the perturbed by the second body only when .
4. Model Description
We impose that , , m are the masses of two primaries and the infinitesimal bodies respectively. Also we assume that the positions of the three participating bodies in inertial sidereal frame OXYZ are given by (), () and () and in rotating reference frame Oxyz are (), () and (), where the both frames has the same origin (O) and the rotating frame is moving around z-axes with the angular velocity n. Furthermore, the Z and z axes are congruent and perpendicular to the planes of motions XY and xy, see Figure 1.
If the three participating bodies are moving in the same plane, while the both primaries are assumed to be oblate and radiating where the infinitesimal body is moving under their gravitational forces but it does not affect their motion. The equations of motion of the infinitesimal body in the inertial sidereal frame are identified by
where V is the total potential which affect the motion of the infinitesimal body. Since the primaries bodies are oblate and radiating, then from Equations (4) and (9), we get
where and are defined by
The relation between the variables in inertial frame and other variables () in the rotating frame are controlled by
Differentiate Equation (22) twice then the velocity and acceleration components are given by
And
Adopting the terminology of [1], the distance between two masses is taken as unit of distance, The unit of mass is chosen such that , the constant of gravitation G is equals one. Since with assuming that , then and . The co-ordinates of more massive and less massive primaries are and respectively. After substituting Equations (22)–(24) into Equations (19)–(21) the equations of motion of the infinitesimal body in normalized rotating reference frame are give by
where n is calculated from Equation (18), is the effective potential and defined by
while the separation distances and in rotating frame are evaluated by
Utilizing Equations (26) and (27) along with integration of system of Equation (25) the first integral of the given system is controlled by
where C is the constant of integration or called Jacobian integral. Equation (25) represent a set of differential equations which governs the spatial circular restricted three-body problem, which can be reduced to the circular planar problem when .
The system of Equation (25) is primarily transferred as a system of first order differential equations and then solved using the Runge–Kutta–Gill–fourth order integrator method. The solution set (x, y, , ) is the state vector, which gives four dimensional space. Initial position of the satellite is on the apse line which is x-axis. Thus y coordinate of initial position of satellite is zero. Also, initially satellite launching with velocity in upward direction, which is positive y-direction and initial velocity in the x-direction is zero, So . Initial positive value of obtained using Equations (26) and (28) by taking and . The values of x and can be plotted every instant the particle has and which is famous as Poincaré surface of section (PSS). Figure 2 shows the PSS for C = , = 0.00024612 and = 0.0001.
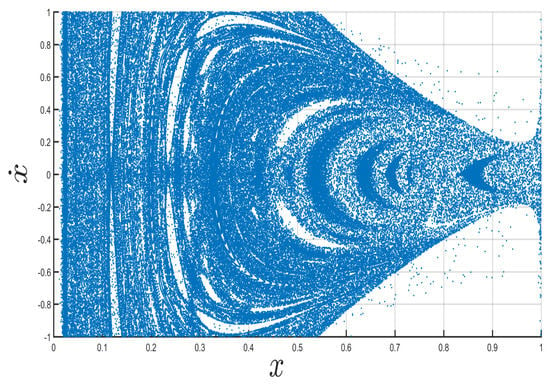
Figure 2.
Poincaré surface of section (PSS) for , = 0.00024612 and = 0.0001.
5. Computation of Collinear Lagrange Points
Lagrange points are stationary solutions of the governing equation of motion. There are five Lagrange points, three of them are called collinear and the other two are called triangular points. Collinear points are unstable points whereas triangular points are stable points. Collinear Lagrange points are located on the apse line which is x-axis of the synodic frame. These points can be determined when the components of velocity and acceleration are vanishing (i.e., ). Hence from Equation (25), , thereby we get
For collinear Lagrange points, Equation (30) gives , after substituting and into Equation (29), then the governing equation for the locations points of , and are given by
Now, we assume that the locations of the collinear points are , and with respect to the locations of , and respectively. After substantiating , and into Equation (31) with some simple calculations, the quantities , and satisfy ninth degree polynomials as in the following forms:
- Location of
- Location of
- Location of
By solving the Equations (32)–(34), we can identify the positions of the three collinear Lagrange points , and .
Table 1 display the locations of the three collinear Lagrange points , and under the different perturbation effects (oblateness and radiation effects of the first and second primaries) when the parameter of mass ratio = 0.00024612. From second raw of Table 1 it can be seen that the locations of , and are 0.95694108, 1.04382519, −1.00010257 respectively, when oblateness coefficient of the first primary is 0.0001. Value of and indicate that there is no perturbation due to radiation pressure on the more massive primary and less massive primary respectively.

Table 1.
Location of collinear Lagrange points under the effect of perturbation when = 0.000246129.
From the obtained data in Table 1, we can easily observe that the locations of all collinear points vary with the change in the values of perturbation parameters of the oblateness and radiation of both primaries. Thus, we demonstrate that these points are affected by the perturbed forces and their locations may change even if these changes are very small.
6. Resonant Periodic Orbits
Resonance is a physical phenomenon which occurs when there is a numerical relationship between frequencies or the period of the bodies. Rotational period and the orbital period of the moon is same, which generates spin–orbit resonance. This is the reason for the moon always keeps the same face towards the Earth. Numerical relationship between orbital periods of the different bodies generates orbit–orbit resonance. Such kind of resonance occur s between three major satellites of the Jupiter known as the Galilean satellites.
The orbital period of the infinitesimal body is given by . Also, from Kepler’s third law , where , , and are the orbital period and semi–major axes of the primary and infinitesimal body respectively. With the help of and , the resonance order can be found. The resonance order can also be calculated with the use of total number of island s in the PSS. If : is the resonance order of the periodic orbits. The interior resonance occurs when , otherwise it is an exterior resonance. Orbits having interior resonance with external loops and an exterior resonance with internal loops.
Figure 3 depicts 3:2 and 3:4 resonant periodic orbits with corresponding PSS when = 0.00024612, C = 2.87 and = 0. Figure 3a,b is external three–loops periodic orbit and corresponding PSS shows one island indicating first order resonance. Thus, resonance order of this periodic orbit is 3:2. Since here orbits with interior resonance. Figure 3c,d show internal three–loops periodic orbit and its corresponding PSS containing one island. Single island in the PSS indicates first order resonance. So, this periodic orbit is with 3:4 resonance order. Because, orbits with exterior resonance. Interior and exterior resonance periodic orbits are named as family–I and II respectively. Thus, Figure 3 shows first order interior and exterior resonant orbits with their corresponding PSS. Shape of the PSS of both orbits is also different, but both PSS containing single island only. Due to single island in the PSS, orbits are first order resonant orbits.
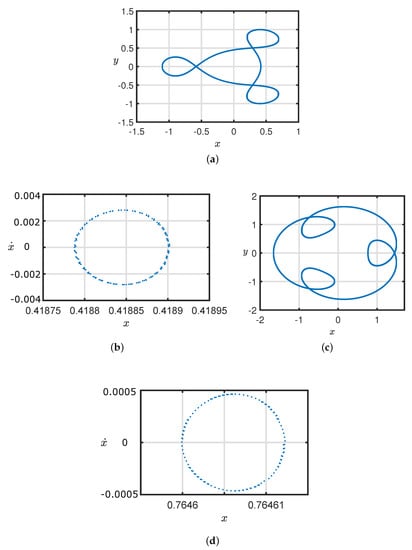
Figure 3.
First-order resonant periodic orbits with their Poincaré surface of section (PSS) for , = 0 and = 0.00024612. (a) 3:2 resonant periodic orbit; (b) PSS of 3:2 resonant periodic orbit; (c) 3:2 resonant periodic orbit; (d) PSS of 3:2 resonant periodic orbit.
7. Numerical Analysis of Periodic Orbits
The periodic orbits with order of resonance one are investigated in this section when both primaries are oblate and radiating bodies. The initial position (x) of periodic orbits is obtained using Poincaré surface of section (PSS) approach.
This study is related to analysing the effect of oblateness and radiation pressure of both primaries on the resonant periodic orbit of the infinitesimal body. To analyse the effect of each perturbation, it is necessary to keep remaining all parameter values constant. For example, to analyse the effect of oblateness coefficient of first primary () on the periodic orbit, only value of varies, remaining all parameters is constant. So we have taken single value of mass factor and Jacobi constant C during the analysis of perturbations effects.
Our objective is to analyse the effects of the individual perturbations , , , and combine effects of all mentioned perturbations on initial position and size of the loop of the of periodic orbit. This analysis includes study of interior and exterior resonant periodic orbit. During this analysis the parameters of mass factor and Jacobi constant are taken as constants. Also, this study includes analysis of these periodic orbits under the effect of the mass factor, Jacobi constant and number of loops.
The effects of single perturbations due to , , and are observed on the initial position and size of loops of periodic orbits. The initial position and size of loops of periodic orbits are also studied under the combine effects of two, three and four perturbations for all the possible combinations of perturbed parameters. The physical and geometrical properties of different orders of resonant periodic orbits are examined in relation to the Jacobi constant, mass factor, order of resonance and number of loops.
7.1. Initial Position Analysis of Periodic Orbits
The initial positions of periodic orbits is critical in determining the trajectory of a satellite in space. The majority of planets in our solar system are oblate spheroids. The astronomical dynamical systems can be analysed in terms of star-planet-satellite and star-star-satellite by considering the star as a radiating body. Because perturbations affect the initial positions of a periodic orbits [16], it is very important to analyse the initial positions of periodic orbits in the presence of various perturbations.
In this section, we looked at the initial positions of periodic orbits under the perturbation effects of the oblateness and radiation pressure of both primaries. The initial positions of 2 to 5 loops interior and 2 to 5 loops exterior first-order resonant periodic orbits are analysed under the effects of perturbations as shown in the Table 2, Table 3 and Table 4 when and . Table 2 shows the initial position of both families of periodic orbits under the effects of single perturbations , , and . In family–I, for two-loops periodic orbits with resonance order 2:1 and with the only perturbation , x is 0.25880. In family– with the same effects of perturbation, and for 2:3 resonant periodic orbits, x is 0.79910. According to Table 2, as perturbation increases from to = 0.001, the initial position of 2:1 resonant periodic orbit increases from x = 0.25880 to x = 0.26298 and for 2:3 resonant periodic orbits, it decreases from to .

Table 2.
Effects of single perturbations on initial position of first-order resonant periodic orbits for and .

Table 3.
Combine effects of two perturbations on initial position of first-order resonant periodic orbits for and .

Table 4.
Combine effects of three and four perturbations on initial position of first-order resonant periodic orbits for = 0.00024612 and C = 2.87.
Table 2 shows effect of perturbations , , and on initial position x of both families periodic orbits. It can be observed from Table 2 that for both families periodic orbits, increment in oblateness coefficient of primaries reduces the value of x and increment in the perturbations due to radiation pressure increases the value of x. Only exceptional case is observed by first and twenty-one raw of the Table 2, x of the two loops orbit increases by increment in the oblateness coefficient of bigger primary.
The initial positions of given loops of periodic orbits under the combine effect of two perturbations for all possible combinations of parameters are observed in Table 3, whereas the combine effects of three and four perturbations on x are observed in Table 4. In family–I, for two-loop periodic orbits with resonant order 2:1 and with the combine effect of , one obtains as shown in Table 3. In family– for a 2:3 resonant periodic orbit and with the same effect of perturbation, one gets . Table 3 shows that as perturbation increases from to for 2:1 resonant periodic orbit x increases from 0.25870 to 0.26210, whereas 2:3 resonant periodic orbits the value of x decrease from 0.7989 to 0.79350. According to Table 4, for 2:1 and 2:3 resonant periodic orbits under the combine effect of the three perturbations and , the values of x are 0.26351 and 0.81080 respectively.
Table 3 shows the combine effect of different combinations of the two perturbations among , , and on initial position x of both families periodic orbits. From Table 3 it can be observed that, x is major affected by , followed by , followed by and lastly by . That is highest effect on x is due to and smallest effect on x is due to . Thus, any combination of perturbation containing increase the value of x. Also, any combination of perturbation not containing but containing decrease the value of x. Combine effect of two perturbations, namely, radiation pressure of both primaries is highest in increasing the value of x. Whereas, combine effect of two perturbations, namely, oblateness coefficients of both primaries is highest in decreasing the value of x.
Similarly, Table 4 display the combine effect of different combinations of the three and four perturbations among , , and on initial position x of both families periodic orbits. It can be observed from the Table 4 that combine effect of three perturbations, namely, radiation pressure of both primaries and oblateness coefficient of first primary, is highest in increasing the value of initial position of the periodic orbits of both families. Whereas, combine effect of three perturbations, namely, oblateness coefficient of both primaries and radiation pressure of second primary is highest in decreasing the value of x.
In RTBP, the more massive primary is located at , which is very close to zero, and less massive primary is located at , which is very close to one. Figure 4 shows the effects of the radiation pressure of the more massive and less massive primaries ( and ) and the combine effects of the radiation pressure of both primaries on the initial position (x) for 2:1 resonant periodic orbits when and . In a classical case radiation pressure is . As a result, as the values of and decreases from one, the perturbation due to radiation pressure rises. According to Table 2 and Figure 4, for both families of periodic orbits, initial position x of periodic orbits shifts towards the less massive primary (i.e., values of x shift towards the one) as radiation pressure of more massive primary increases (i.e., ). As shown in Figure 4 when compared to and , has the greatest influence on x. Also, and both shift the x towards the one. As a result under the combine effects of , as perturbation increases, x shifts more towards the one.
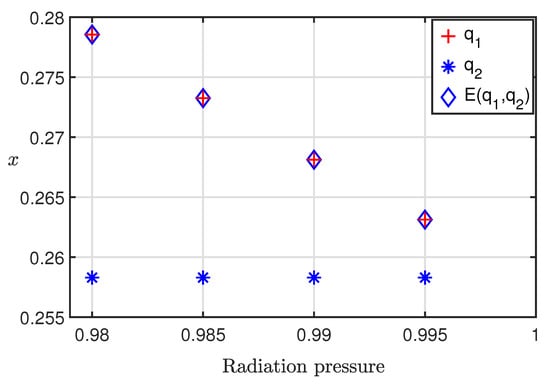
Figure 4.
Effect of radiation pressure on x of 2:1 resonant periodic orbit when = 0.00024612 and C = 2.87.
We remark that Figure 4 shows that effect of and on x is in the same direction. It increases the value of x. Thus, combine effect of two perturbations, namely, radiation pressure of both primaries is more than individual effect of radiation pressure of bigger primary or smaller primary in increasing the value of initial position of the both families periodic orbit.
Figure 5 shows the effects of oblateness of the more massive and less massive primary ( and ) and the combine effects of oblateness of both primaries on the initial position of a 3:2 resonant periodic orbit when and . According to Table 2 and Figure 5, for both families of periodic orbits, x shift towards the more massive primary (i.e., the values of x shifts towards the zero) as oblateness in terms of , and increases. Only initial position of the 2:1 resonant orbit shift towards the one as value of increases. As observed in Table 2 and Figure 5 when compared to and , has the greatest influence on x and as and both shift x in the direction of zero. Under the combine effects of , x shifts more towards the zero (i.e., near to the more massive primary) compared to single perturbations and .
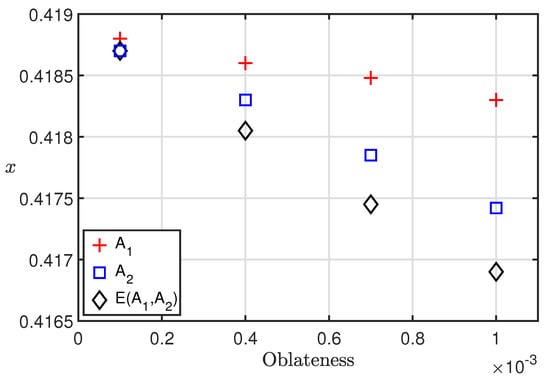
Figure 5.
Effect of oblateness on x of 3:2 resonant periodic orbit when = 0.00024612 and C = 2.87.
Thus, Figure 5 shows that effect of and on x is in the same direction. It decreases the value of x. Thus, combine effect of two perturbations, namely, oblateness coefficients of both primaries is more than individual effect of oblateness coefficient of bigger primary or smaller primary in decreasing the value of initial position of the both families periodic orbit. While Table 3 and Figure 6 show the combine effects of two perturbations due to radiation pressure and oblateness of both primaries , , and on the initial position x of periodic orbits. The preceding analysis is performed for 3:2 resonant periodic orbits when C = 2.87 and .
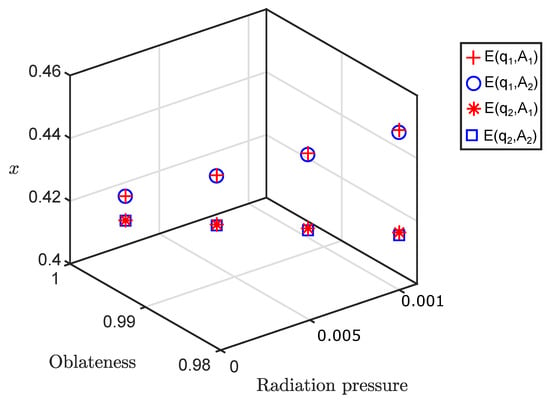
Figure 6.
Combine effect of two perturbations on x of 3:2 resonant periodic orbit when = 0.00024612 and C = 2.87.
From Table 3 and Figure 6, the following are the combine effects of radiation pressure and oblateness on x and we can deduce that
- Effect of is the largest among all the perturbations which shifts x towards the one (i.e., near to the less massive primary).
- Under the combine effects of and , x shifts towards the one.
- The next higher effect on x is due to .
- and both shift the x towards the zero (i.e., near to the more massive primary).
- Under the effects of and , x shifts towards the zero.
- has less effect than in shifting x towards zero.
- As a result, combine effects of is more compare to in shifting x towards one.
- combine effects of shift x more towards zero compared to .
Figure 6 indicates that combine effect of two perturbations, namely, radiation pressure and oblateness coefficient of bigger primary and combine effect of two perturbations namely, radiation pressure of bigger primary and oblateness coefficient of smaller primary is same which increase the value of x. Whereas, combine effect of two perturbations, namely, radiation pressure of smaller primary and oblateness coefficient of bigger primary and combine effect of two perturbations namely, radiation pressure and oblateness coefficient of smaller primary is same which decrease the value of x.
Table 4 and Figure 7 show the combine effect of three perturbations due to radiation pressure and oblateness of the more massive and less massive primary , , and on initial position x. Figure 6 indicates same for a 3:2 resonant periodic orbit when and . As a result it can be observed from Table 4 and Figure 7 that
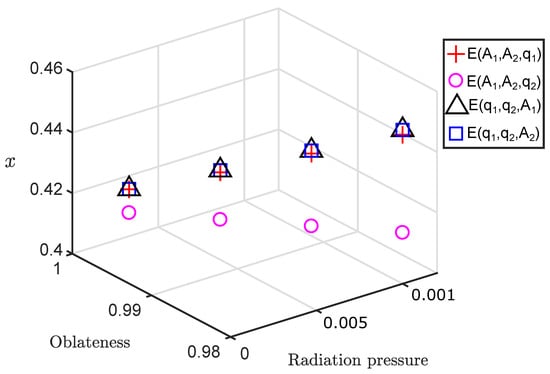
Figure 7.
Combine effects of three perturbations on x of 3:2 resonant periodic orbit when = 0.00024612 and C = 2.87.
- Effect of on x of periodic orbits from both families is significant compared to other perturbations.
- Under the combine effects of the perturbations in which is one of the perturbation parameter (i.e., , and ) initial position x of the periodic orbits shifts towards the one.
- Also, the second largest effect on x shift towards zero is due to .
- As a result, initial position x of both family orbits shifts towards the zero as perturbations rises except in the case of 2:1 orbit.
- From the second and seventeenth rows of Table 4, it can be observed that only for 2:1 resonant orbit initial position x shifts towards 1 due to increment in the perturbation .
- Effect of is much more less than effect of in shifting x towards zero.
- As a result, combine d effect of is more in shifting x towards one in comparison to and .
- Effect of is more than effect of on x.
- Increment in shifts x towards zero where as increment in shifts x towards one.
- As a result, combine effect of is more than in shifting x towards one.
- For both families of periodic orbits, under the combine increment of four perturbations , x shifts towards the one observed in Table 4.
Thus, Figure 7 indicates that combine effect of three perturbations in which is present increases the value of x. Whereas, combine effect of three perturbations in which is absent decreases the value of x.
7.2. Size Loops Analysis of Periodic Orbits
In this section, we perform the geometrical analysis of interior and exterior resonant periodic orbits under the oblateness and radiation pressure effects of both primaries. The geometrical analysis is performed in terms of size of loops for exterior resonant three loops orbits and interior, exterior resonant two loops orbits. Analysed the effects of single perturbation due to radiation pressure , and effects of on the size of loops of exterior resonant three loops orbits. The effects of single perturbation due to oblateness , and effects of are analysed on interior resonant two loops orbits. The combine effects of two and three perturbations due to oblateness and radiation pressure are analysed on exterior and interior resonant two loops orbits respectively.
Figure 8 display the effect of , and on the size of loop () of exterior resonant three loops orbits when and . Decrement in the values of and gives increment in perturbation of and . Figure 8 indicates that increment in perturbation caused by and , reduces the . Since and both reduces the , as a result the combine effects of generate the smallest of periodic orbit as seen in the Figure 8. Thus, Figure 8 indicates that effect of and reduces the size of loops. Thus, combine effect of two perturbations namely, radiation pressure of both primaries more reduces the size of the loops.
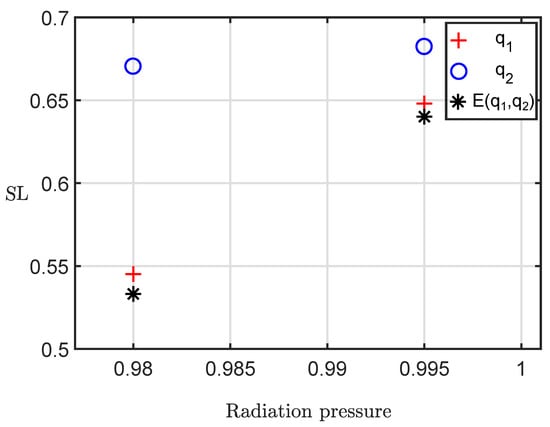
Figure 8.
Effect of radiation pressure on size of the loop for 3:4 resonant periodic orbit when and .
Figure 9 shows the effect of , and on the size of the loops () of interior resonant two loops orbits when and C = 2.87. It can be observed from the Figure 9 increment in the perturbation caused by and increases the of periodic orbits. Since and both increase the , the combine effects of give the largest of periodic orbit as seen in the Figure 9. We observe that from Figure 9 the effect of and increases the size of the loops. Thus, combine effect of two perturbations namely, oblateness coefficient of both primaries more increases the size of loops.
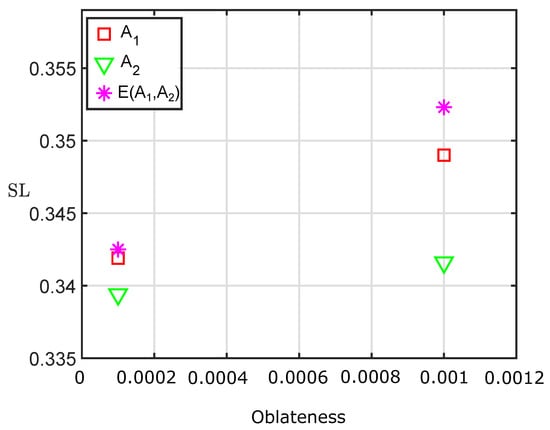
Figure 9.
Effect of oblateness on size of the loop for 2:1 resonant periodic orbit when and .
Figure 10 shows the combine effect of perturbations when is one of the perturbation on the exterior resonant two loops orbits when and . Figure 10a shows that as perturbation increases from to , the of periodic orbit decreases. Effect of is highest among all the discussed perturbations which reduces the . As a outcome under the combine effects of with all other perturbations, the periodic orbits is reduced as observed in Figure 10b–f. Thus, Figure 10 indicates that effect of single perturbation and all possible combinations of two and three perturbations in which is present reduces the size of the loops. It is remarkable observation that size of the loops is highly affected by then followed by , and lastly . Also, radiation pressure of the primary reduces the size of the loops. Whereas, oblateness coefficient of the primary increases the size of the loops.
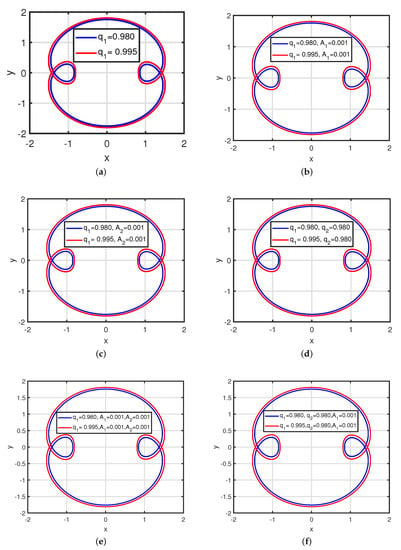
Figure 10.
Combine effect of perturbations with on size of the loop for 2:3 resonant periodic orbit when = 0.00024612 and C = 2.87. (a) Effect of ; (b) Effect of with ; (c) Effect of when ; (d) Effect of when ; (e) Effect of when ; (f) Effect of when and .
Figure 11 shows the combine effects of oblateness and on the size of loops () for a interior resonant two loops orbits when and . Increment in the values of and increases the perturbation of oblateness and decrement in the value of increase the perturbation of radiation pressure of less massive primary. Also, among , and , effect of is largest which increases the . Figure 11 indicates that as the perturbations of oblateness and increase, increases. Also, and both increase the . So, under the increment of combine effect of largest increment in can be observed in the Figure 11. We remark that the effect analysis of perturbations on holds true for all periodic orbits from both families.
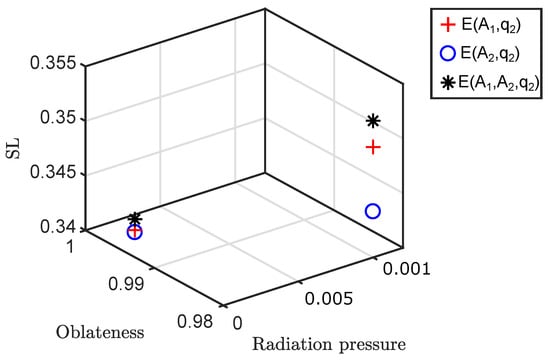
Figure 11.
Combine effect of oblateness and on size of loop for 2:1 resonant periodic orbit when = 0.00024612 and C = 2.87.
From Figure 11, we deduce that combine effect of perturbations in which is one of the perturbation on the size of the loops. Effect of is more than in increasing the size of the loops, combine effect of with increase the size of the loops more than the combine effect of with . Also, oblateness coefficient of both primaries increases the size of the loops, combine effect of oblateness coefficient of both primaries with gives more increment in the size of the loops.
Effect of perturbation on the of the periodic orbits of both families is analysed. It is observed that is highly affected by then followed by , and lastly . Thus, effect of on is minimum among all four perturbations. Also, increment in perturbation of radiation pressure of both primaries reduces whereas increment in perturbations due to oblateness of both primaries increase the .
8. Physical and Geometrical Parameters Analysis of Periodic Orbits
Performed the physical and geometrical analysis of different orders of interior and exterior resonant periodic orbits. The physical and geometrical analysis of resonant periodic orbits is performed in terms of initial condition and size of loops under the effects of Jacobi constant C, mass factor and order of resonance (). The effects of C, and are analysed for first order interior resonant two loops, third order interior resonant seven loops and first order interior resonant five loops orbits in the presence of perturbations due to oblateness and radiation pressure of both primaries.
The effect of C on x of perturbed 7:4 resonant periodic orbit when is visible in Figure 12. Effect of C is largest which shift x towards one compare to all perturbations. Thus, combine effect of C with each perturbation of , , and shifts x towards the one. Also, effect of is largest among , , , , and shifts x towards one. Thus, in the presence of and C the value of x shifts most towards one as seen in Figure 12.
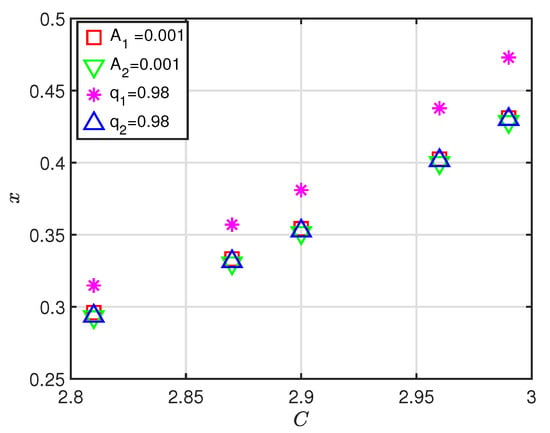
Figure 12.
Effect of C on x for 7:4 perturbed resonant periodic orbit when = 0.00024612.
Figure 12 indicates that due to increment in C, initial position x of the periodic orbit increases under the effect of all perturbations. Also, radiation pressure increase the value of x. Among radiation pressure of both primaries and oblateness coefficient of both primaries has highest effect on x. Thus, increment in C under the effect of more increase the value of x.
Figure 13 shows the effect of C with and on the of 2:1 resonant periodic orbit when . Figure 13a,b indicate effect of C in presence of and on of 2:1 resonant periodic orbit respectively. Effect of C is largest compared to all perturbations and it is reducing the of periodic orbit. Therefore, under the combine effects of C with all perturbations decreases. It is observed from Figure 13a,b as C increases from to 2.99 the of periodic orbits decreases under the effects of both and . This analysis holds true for all the loops of periodic orbits from both families.
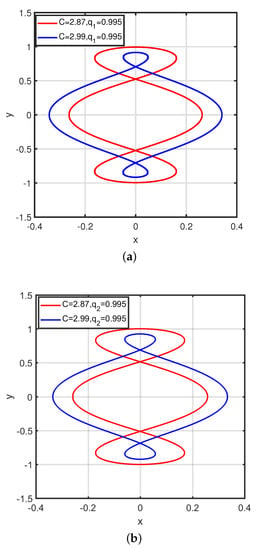
Figure 13.
Effect of C on size of loops with and for 2:1 resonant periodic orbits when = 0.00024612. (a) Effect of C when ; (b) Effect of C when .
Figure 13 display the effect of C on the size of the loops. Increment in C reduce the size of the loops. Radiation pressure of the primary also reduces the size of the loops. Effect of is more than in reducing the size of the loops. Thus, combine effect of with C reduces the size of the loops more than combine effect of with C.
Effect of mass factor on initial position and size of the loop is analysed. Figure 14 shows the effect of mass factor on x of 2:1 resonant perturbed periodic orbits when . Perturbations , , and are considered during the analysis. From Figure 14, it is observed that under the influence of each perturbation, increment in shifts x towards zero. Effect of is largest which shifts x towards zero. Also, from the perturbations , , and effect of is largest in shifting x towards zero. Thus, combine effect of and shifts x most towards zero compared to other combinations of parameters. Thereby Figure 14 indicates that increment in mass factor reduces the value of initial position x. Oblateness coefficient of the primary also reduces the x and radiation pressure increases the x. Effect of is more than in reducing the x. Under the effect of , increment in mass factor shows highest decrement in the x.
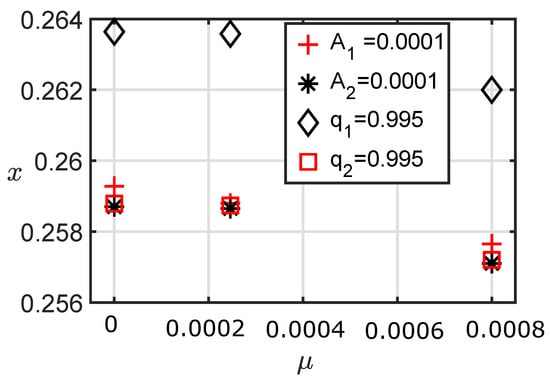
Figure 14.
Effect of on x of 2:1 resonant perturbed periodic orbit when C = 2.87.
Figure 15 display the effect of mass factor on the of a 2:1 resonant perturbed periodic orbit when . During this analysis perturbations , , , are considered. Figure 15 indicates that increment in increases the of periodic orbit under the effect of each perturbation. However, the effect of is largest on the increment of . As an output of combine effects in the presence of the largest was obtained by increment in which can be seen in Figure 15. The effect of perturbation followed by , and the smallest obtained due to perturbation with the increment of . The preceding analysis is true for all loops of periodic orbits from both families. Hence Figure 15 indicates that increment in mass factor increases the size of the loops. Oblateness coefficient also increases the size of the loops. Effect of is more than in increasing the size of the loops. Under the effect of , increment in mass factor shows larger size of the loops.
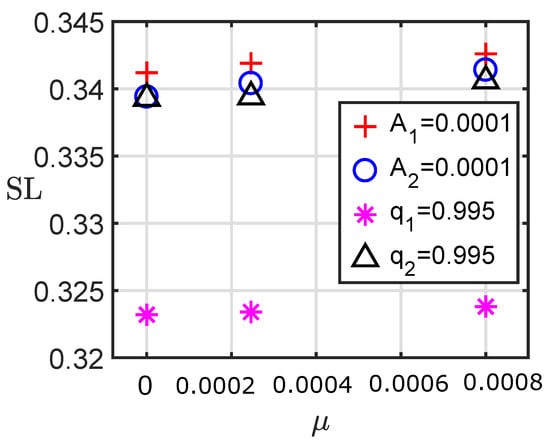
Figure 15.
Effect of on loop size of 2:1 resonant perturbed periodic orbit when C = 2.87.
Figure 16 shows the effect of resonance order () on x for five–loops interior perturbed resonance periodic orbit when and . Effect is observed in the presence of perturbations , , and . Effect of is largest which moves x towards zero. Thus, with each perturbation increment in shifts x towards zero. Figure 16 shows that as order of resonance increases from one to three, x of five–loops interior perturbed resonance periodic orbit shifts towards zero under the effects of each perturbation. Figure 16 indicates that increment in order of resonance decreases the initial position x.
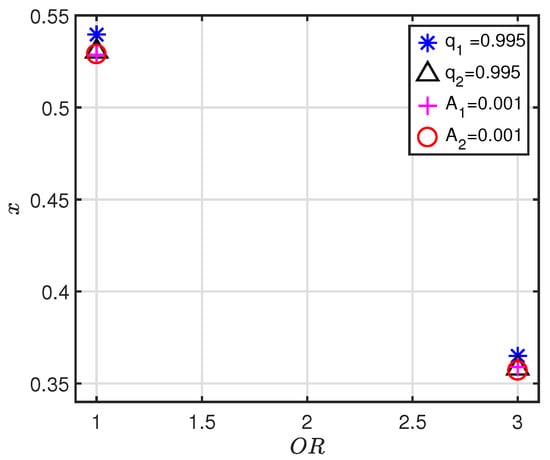
Figure 16.
Effect of resonance order on x for five–loops interior resonant perturbed periodic orbit when = 0.00024612 and C = 2.87.
Effects of resonance order on the size of the loop of interior resonant five–loops periodic orbit can be observed in Figure 17 when , and . increase the of periodic orbit. From Figure 17a,b it can be observed that as order of resonance increases from one to three, the of the perturbed periodic orbits decreases. Also, Figure 17a indicates that first order 5:4 resonant periodic orbit is symmetric about the x-axis on the left side and passes around the Lagrange point . is located at −1.00102654. Whereas Figure 17b indicates that third order 5:2 resonant periodic orbit is symmetric about the x-axis on the right side and passes around the less massive primary, which is located near to 1. Thus, Figure 17 shows that increment in order of resonance reduces the size of the loops. Symmetry of the periodic orbits also changes due to change in order of resonance.
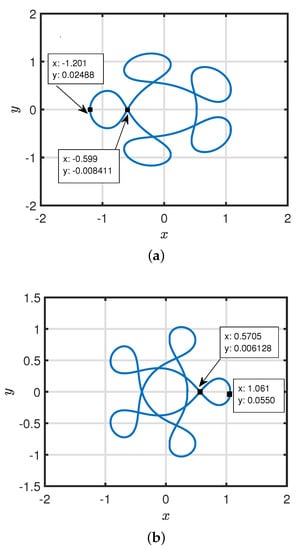
Figure 17.
Effect of resonance order on loop size of five-loops periodic orbits for C = 2.87, = 0.001 and = 0.00024612. (a) First order resonance periodic orbit at ; (b) Third order resonance periodic orbit at .
Effect of number of loops on initial position x of interior and exterior resonant perturbed periodic orbits is analysed. Interior resonant orbits have external loops and exterior resonant orbits have internal loops. Interior and exterior periodic orbits are denoted by family–I and orbits respectively.
Figure 18 shows the effects of number of loops () on x of first-order resonant perturbed periodic orbits when and . During this analysis perturbations are taken as , , and . Figure 18 indicates that as increases for family–I periodic orbits x shifts towards the one while for family– it shifts towards the zero under the effect of each perturbation. As a combine effect, in the presence of , for family–I periodic orbits, x shifts more near to the one due to the increment in compared to other perturbations. In contrast, for family– periodic orbits, in the presence of , initial position x shifts more near to zero due to the increment in compared to other perturbations. From Figure 18 we see that initial position x of family–I periodic orbits increases as number of loops increases. Whereas x of family– periodic orbit decreases with increment in the number of loops.
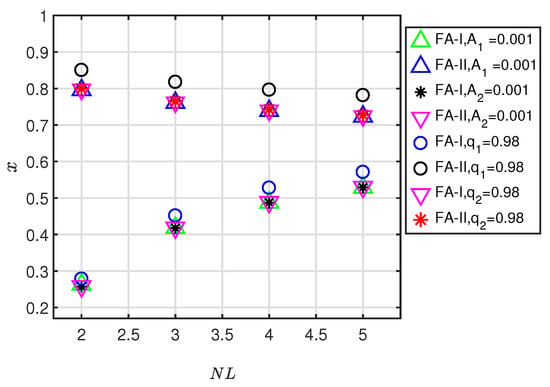
Figure 18.
Effect of number of loops () on x of first-order resonant perturbed periodic orbits when = 0.00024612 and C = 2.87.
Analysed the physical and geometrical parameters of periodic orbits under the effects of Jacobi constant C, mass factor and order of resonance. Increment in C shifting initial position x of perturbed orbit towards less massive primary. Also, Increment in C reduces the size of the loop of the periodic orbit. It is observed that increment in shifts initial position x towards more massive primary. Also, increment in is responsible for the increment in . It is analysed that as order of resonance increases the initial position of the periodic orbit shifts towards more massive primary. Also, due to increment in the order of resonance decreases.
It is important remark that during analysis of the effect of perturbations on the initial position and size of the loops, kept C and constant. Otherwise initial positions and size of the loops is combining affected by the perturbations C and . To analyze the effect of only perturbation, value of C is taken as 2.87 and . These parameter values give all loops periodic orbits in both families with all perturbations. Initial conditions of all periodic orbits can be obtained by PSS with with different perturbations. Thus, one of the PSS in which perturbation oblateness coefficient of bigger primary equals is considered in Figure 2.
9. Conclusions
The initial positions of periodic orbits play a very important role in restricted three-body problem (RTBP). In RTBP more massive primary is located at which is very near to zero and less massive primary is located at which is very near to one. The recent studies of the RTBP have included perturbing forces such as oblateness and radiation pressure of the primaries. So, it is important to study the initial positions of periodic orbits under the influence of such perturbation forces. In this work we considered both the primaries are oblate and sources of radiation. Derived the governing equations of motion in the presence of perturbation forces (oblateness and radiation pressure of both the primaries).
Also the positions of collinear Lagrange points in the presence of the aforemention perturbations calculated. In this study, interior and exterior resonant periodic orbits are analysed. Interior (exterior) resonant orbits have external (internal) loops. Interior and exterior resonant orbits are categorised as family–I and respectively. Effect of perturbations of the primaries , , and and all its combine combinations on the initial positions and size of the loop of both families periodic orbits are analysed. The physical and geometrical properties of interior and exterior resonant orbits are analysed for order of resonance, Jacobi constant C, mass factor and number of loops.
Finally, we conclude that the following analysis is preformed:
- Effect of perturbations on initial position () of periodic orbits.
- Effect of perturbations on size of the loop () of periodic orbits.
- Effect of Jacobi constant on and of perturbed periodic orbits.
- Effect of mass factor on and of perturbed periodic orbits.
- Effect of resonance order on and of perturbed periodic orbits.
- Effect of number of loops on and of perturbed periodic orbits.
Thus, final outcomes of the study are as follows:
- Degree of perturbations effects from highest to smallest on the initial position of periodic orbits are radiation pressure of bigger primary, oblateness coefficient of smaller primary, oblateness coefficient of bigger primary and radiation pressure of the smaller primary
- Radiation pressure shifts initial condition towards smaller primary. Whereas, oblateness coefficient shifts initial condition towards bigger primary.
- Size of the loops is highest affected by radiation pressure of bigger primary, followed by oblateness coefficient of bigger primary, followed by oblateness coefficient of smaller primary and then lastly by radiation pressure of the smaller primary.
- Radiation pressure reduces the size of the loops. Whereas, oblateness coefficient increases the size of the loops.
- Increment in Jacobi constance shifts initial position towards smaller primary and reduces the size of the loops.
- Increment in the mass factor shifts initial position towards bigger primary and increases the size of the loops.
- Increment in the order of resonance shifts initial position towards bigger primary and reduces the size of the loops.
- Increment in the number of loops shifts initial position of family–I periodic orbits towards smaller primary.
- Increment in the number of loops shifts initial position of family– periodic orbits towards bigger primary.
Author Contributions
Formal analysis: B.M.P., N.M.P. and E.I.A.; Investigation: B.M.P., N.M.P. and E.I.A.; Methodology: B.M.P., N.M.P. and E.I.A. Project administration: N.M.P. and E.I.A.; Software: B.M.P., N.M.P. and E.I.A.; Validation: B.M.P., N.M.P. and E.I.A.; Visualization: B.M.P., N.M.P. and E.I.A.; Writing—original draft: B.M.P., N.M.P. and E.I.A.; Writing—review & editing: B.M.P., N.M.P. and E.I.A.; Approval of the version of the manuscript to be published: B.M.P., N.M.P. and E.I.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The study does not report any data.
Acknowledgments
This work was funded by the National Research Institute of Astronomy and Geophysics (NRIAG), Helwan 11421, Cairo, Egypt. The authors, therefore, acknowledges with thanks NRIAG technical and financial support. Furthermore, the authors would like to thank the anonymous referees for all the apt suggestions and comments which improved both the quality and the clarity of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| RTBP | Restricted three-body problem |
| CRTBP | Circular restricted three-body problem |
| PSS | Poincaré surface section |
| Combine effects of and | |
| Combine effects of and | |
| Combine effects of and | |
| Combine effects of and |
| Combine effects of and | |
| Combine effects of and | |
| Combine effects of , and | |
| Combine effects of , and | |
| Combine effects of , and | |
| Combine effects of , and | |
| Combine effects of , , and |
References
- Szebehely, V.; Grebenikov, E. Theory of Orbits-The Restricted Problem of Three Bodies. Sov. Astron. 1969, 13, 364. [Google Scholar]
- Murray, C.D.; Dermott, S.F. Solar System Dynamics; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Duffy, B. Analytical Methods and Perturbation Theory for the Elliptic Restricted three-body Problem of Astrodynamics. Ph.D. Thesis, The George Washington University, Washington, DC, USA, 2012. [Google Scholar]
- Melton, R.G. Fundamentals of astrodynamics and applications. J. Guid. Control. Dyn. 1998, 21, 672. [Google Scholar] [CrossRef]
- Sharma, R.K.; Taqvi, Z.; Bhatnagar, K. Existence and stability of libration points in the restricted three-body problem when the primaries are triaxial rigid bodies. Celest. Mech. Dyn. Astron. 2001, 79, 119–133. [Google Scholar] [CrossRef]
- Singh, J. Combined effects of perturbations, radiation, and oblateness on the nonlinear stability of triangular points in the restricted three-body problem. Astrophys. Space Sci. 2011, 332, 331–339. [Google Scholar] [CrossRef]
- Selim, H.H.; Guirao, J.L.; Abouelmagd, E.I. Libration points in the restricted three-body problem: Euler angles, existence and stability. Discret. Contin. Dyn. Syst.-S 2018, 12, 703. [Google Scholar] [CrossRef]
- Hallan, P.; Rana, N. Effect of perturbations in coriolis and centrifugal forces on the location and stability of the equilibrium point in the Robe’s circular restricted three body problem. Planet. Space Sci. 2001, 49, 957–960. [Google Scholar] [CrossRef]
- Kalantonis, V.; Douskos, C.; Perdios, E. Numerical determination of homoclinic and heteroclinic orbits at collinear equilibria in the restricted three-body problem with oblateness. Celest. Mech. Dyn. Astron. 2006, 94, 135–153. [Google Scholar] [CrossRef]
- Singh, J.; Kalantonis, V.; Gyegwe, J.M.; Perdiou, A. Periodic motions around the collinear equilibrium points of the R3BP where the primary is a triaxial rigid body and the secondary is an oblate spheroid. Astrophys. J. Suppl. Ser. 2016, 227, 13. [Google Scholar] [CrossRef]
- Yousuf, S.; Kishor, R. Effects of the albedo and disc on the zero velocity curves and linear stability of equilibrium points in the generalized restricted three-body problem. Mon. Not. R. Astron. Soc. 2019, 488, 1894–1907. [Google Scholar] [CrossRef]
- Kalantonis, V.S.; Perdiou, A.E.; Perdios, E.A. On the stability of the triangular equilibrium points in the elliptic restricted three-body problem with radiation and oblateness. Math. Anal. Appl. 2019, 154, 273–286. [Google Scholar]
- Gao, F.; Wang, Y. Approximate analytical periodic solutions to the restricted three-body problem with perturbation, oblateness, radiation and varying mass. Universe 2020, 6, 110. [Google Scholar] [CrossRef]
- Gao, F.; Wang, R. Bifurcation analysis and periodic solutions of the HD 191408 system with triaxial and radiative perturbations. Universe 2020, 6, 35. [Google Scholar] [CrossRef]
- Abouelmagd, E.I. The effect of photogravitational force and oblateness in the perturbed restricted three-body problem. Astrophys. Space Sci. 2013, 346, 51–69. [Google Scholar] [CrossRef]
- Patel, B.M.; Pathak, N.M.; Abouelmagd, E.I. First-order resonant in periodic orbits. Int. J. Geom. Methods Mod. Phys. 2021, 18, 2150011. [Google Scholar] [CrossRef]
- Patel, B.M.; Pathak, N.M.; Abouelmagd, E.I. Stability analysis of first order resonant periodic orbit. Icarus 2022, 387, 115165. [Google Scholar] [CrossRef]
- Érdi, B.; Rajnai, R.; Sándor, Z.; Forgács-Dajka, E. Stability of higher order resonances in the restricted three-body problem. Celest. Mech. Dyn. Astron. 2012, 113, 95–112. [Google Scholar] [CrossRef]
- Luk’yanov, L. On the restricted circular conservative three-body problem with variable masses. Astron. Lett. 2009, 35, 349–359. [Google Scholar] [CrossRef]
- Pal, A.K.; Abouelmagd, E.I.; Kishor, R. Effect of Moon perturbation on the energy curves and equilibrium points in the Sun–Earth–Moon system. New Astron. 2021, 84, 101505. [Google Scholar] [CrossRef]
- Bairwa, L.K.; Pal, A.K.; Kumari, R.; Alhowaity, S.; Abouelmagd, E.I. Study of Lagrange Points in the Earth–Moon System with Continuation Fractional Potential. Fractal Fract. 2022, 6, 321. [Google Scholar] [CrossRef]
- Suleiman, R.; Umar, A.; Singh, J. Collinear Points in the Photogravitational ER3BP with Zonal Harmonics of the Secondary. Differ. Equ. Dyn. Syst. 2020, 28, 901–922. [Google Scholar] [CrossRef]
- Sheth, D.; Thomas, V. Halo orbits around L1, L2, and L3 in the photogravitational Sun–Mars elliptical restricted three-body problem. Astrophys. Space Sci. 2022, 367, 99. [Google Scholar] [CrossRef]
- Howell, K.C.; Spencer, D.B. Periodic orbits in the restricted four-body problem. Acta Astronaut. 1986, 13, 473–479. [Google Scholar] [CrossRef]
- Liu, C.; Gong, S. Hill stability of the satellite in the elliptic restricted four-body problem. Astrophys. Space Sci. 2018, 363, 162. [Google Scholar] [CrossRef]
- Carletta, S.; Pontani, M.; Teofilatto, P. Characterization of Low-Energy Quasiperiodic Orbits in the Elliptic Restricted 4-Body Problem with Orbital Resonance. Aerospace 2022, 9, 175. [Google Scholar] [CrossRef]
- Pathak, N.; Thomas, V.; Abouelmagd, E.I. The perturbed photogravitational restricted three-body problem: Analysis of resonant periodic orbits. Discret. Contin. Dyn. Syst.-S 2019, 12, 849. [Google Scholar] [CrossRef]
- Pathak, N.; Abouelmagd, E.I.; Thomas, V. On Higher Order Resonant Periodic Orbits in the Photo–Gravitational Planar Restricted three-body Problem with Oblateness. J. Astronaut. Sci. 2019, 66, 475–505. [Google Scholar] [CrossRef]
- Patel, B.M.; Pathak, N.M.; Abouelmagd, E.I. Nonlinear regression multivariate model for first order resonant periodic orbits and error analysis. Planet. Space Sci. 2022, 219, 105516. [Google Scholar] [CrossRef]
- Ugai, S.; Ichikawa, A. Lunar Synchronous Orbits in the Earth-Moon Circular-Restricted Three-Body Problem. J. Guid. Control. Dyn. 2010, 33, 995–1000. [Google Scholar] [CrossRef]
- Musielak, Z.E.; Quarles, B. The three-body problem. Rep. Prog. Phys. 2014, 77, 065901. [Google Scholar] [CrossRef]
- Heinrich, W.; Roesler, S.; Schraube, H. Physics of cosmic radiation fields. Radiat. Prot. Dosim. 1999, 86, 253–258. [Google Scholar] [CrossRef]
- Schuerman, D.W. The restricted three-body problem including radiation pressure. Astrophys. J. 1980, 238, 337–342. [Google Scholar] [CrossRef]
- Zotos, E.E. Fractal basins of attraction in the planar circular restricted three-body problem with oblateness and radiation pressure. Astrophys. Space Sci. 2016, 361, 181. [Google Scholar] [CrossRef]
- Dutt, P.; Sharma, R. Evolution of periodic orbits in the Sun-Mars system. J. Guid. Control. Dyn. 2011, 34, 635–644. [Google Scholar] [CrossRef]
- Poynting, J. Radiation in the solar system: Its effect on temperature and its pressure on small bodies. Mon. Not. R. Astron. Soc. 1903, 64, 1. [Google Scholar] [CrossRef]
- Radzievskii, V. The restricted problem of three bodies taking account of light pressure. Astron. Zhurnal 1950, 27, 250. [Google Scholar]
- Chernikov, Y.A. The Photogravitational Restricted Three-Body Problem. Sov. Astron. 1970, 14, 176. [Google Scholar]
- Kunitsyn, A.; Perezhogin, A. On the stability of triangular libration points of the photogravitational restricted circular three-body problem. Celest. Mech. 1978, 18, 395–408. [Google Scholar] [CrossRef]
- Schuerman, D.W. The effect of radiation pressure on the restricted three-body problem. In Symposium-International Astronomical Union; Cambridge University Press: Cambridge, UK, 1980; Volume 90, pp. 285–288. [Google Scholar]
- Markellos, V.; Perdios, E.; Papadakis, K. The stability of inner collinear equilibrium points in the photogravitational elliptic restricted problem. Astrophys. Space Sci. 1993, 199, 139–146. [Google Scholar] [CrossRef]
- Papadakis, K. Asymptotic orbits at the triangular equilibria in the photogravitational restricted three-body problem. Astrophys. Space Sci. 2006, 305, 57–66. [Google Scholar] [CrossRef]
- AbdulRaheem, A.; Singh, J. Combined effects of perturbations, radiation, and oblateness on the stability of equilibrium points in the restricted three-body problem. Astron. J. 2006, 131, 1880. [Google Scholar] [CrossRef]
- Vishnu Namboodiri, N.; Sudheer Reddy, D.; Sharma, R.K. Effect of oblateness and radiation pressure on angular frequencies at collinear points. Astrophys. Space Sci. 2008, 318, 161–168. [Google Scholar] [CrossRef]
- Proctor, R.A. Essays on Astronomy: A Series of Papers on Planets and Meteors, the Sun and Sun-Surrounding Space, Stars and Star Cloudlets; and a Dissertation on the Approaching Transits of Venus. Preceded by a Sketch of the Life and Works of Sir John Herschel; Longman’s, Green, and Company. 1872. [Google Scholar]
- Kaufmann, W.J., III. Universe, 2nd ed.; W H Freeman and Co.: USA, 1988. [Google Scholar]
- Ershkov, S.V. About tidal evolution of quasi-periodic orbits of satellites. Earth Moon Planets 2017, 120, 15–30. [Google Scholar] [CrossRef]
- Ershkov, S.; Leshchenko, D.; Abouelmagd, E.I. About influence of differential rotation in convection zone of gaseous or fluid giant planet (Uranus) onto the parameters of orbits of satellites. Eur. Phys. J. Plus 2021, 136, 1–9. [Google Scholar] [CrossRef]
- Kalvouridis, T.; Arribas, M.; Elipe, A. Parametric evolution of periodic orbits in the restricted four-body problem with radiation pressure. Planet. Space Sci. 2007, 55, 475–493. [Google Scholar] [CrossRef]
- Lukyanov, L. Family of Libration Points in the Restricted Photogravitational Three-Body Problem. Sov. Astron. 1988, 32, 215. [Google Scholar]
- Ansari, A.A.; Abouelmagd, E.I. Gravitational potential formulae between two bodies with finite dimensions. Astron. Nachrichten 2020, 341, 656–668. [Google Scholar] [CrossRef]
- McCuskey, S.W. Introduction to Celestial Mechanics; Addison-Wesley Publishinig Company: Reading, MA, USA, 1963. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).