Weak Neutrino (Antineutrino) Charged-Current Responses and Scaling for Nuclear Matter in the Relativistic Mean Field
Abstract
1. Introduction
2. General Formalism
2.1. Tensor Components Involved in the Weak Responses
2.2. Weak Nuclear Responses
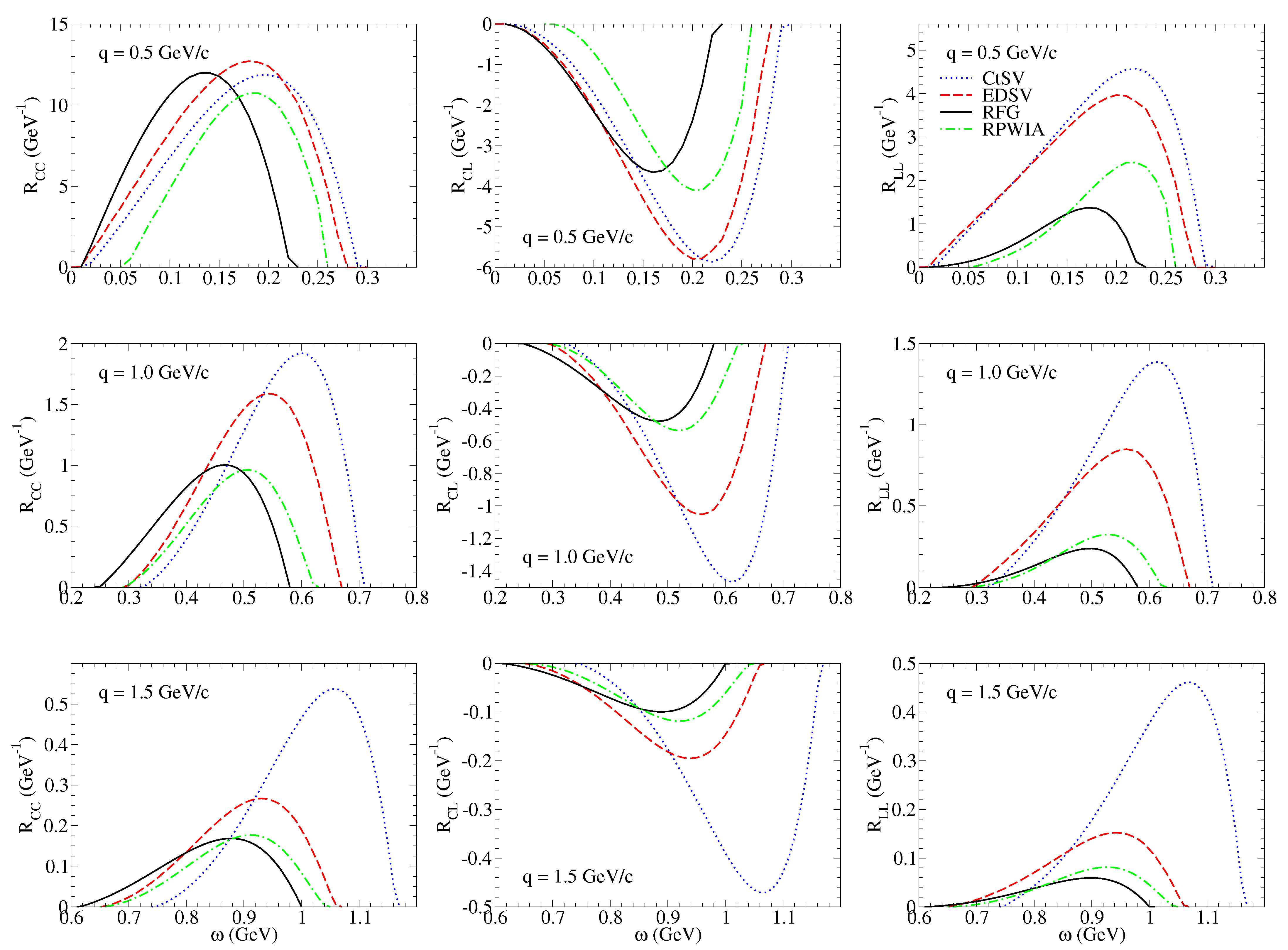
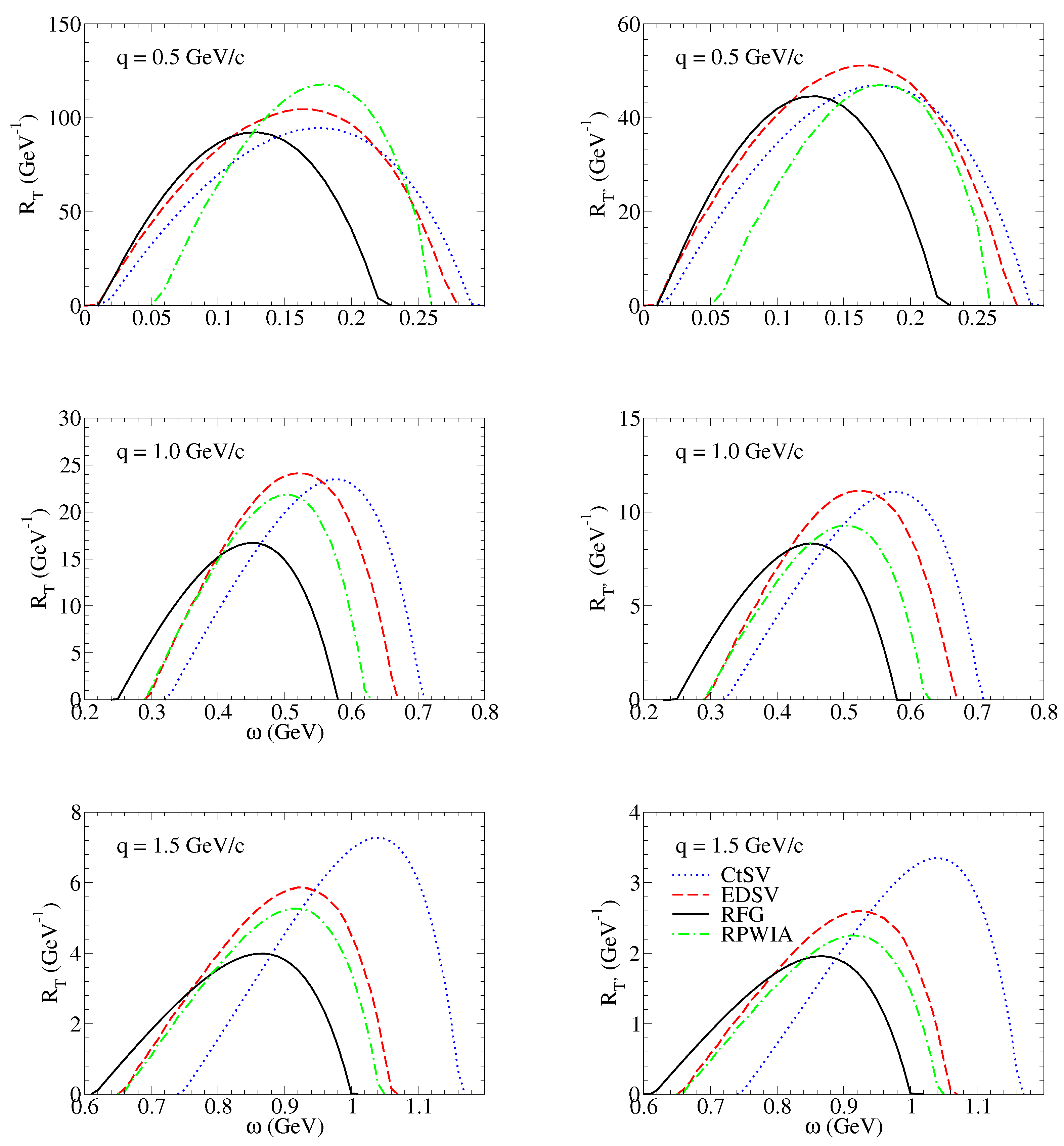
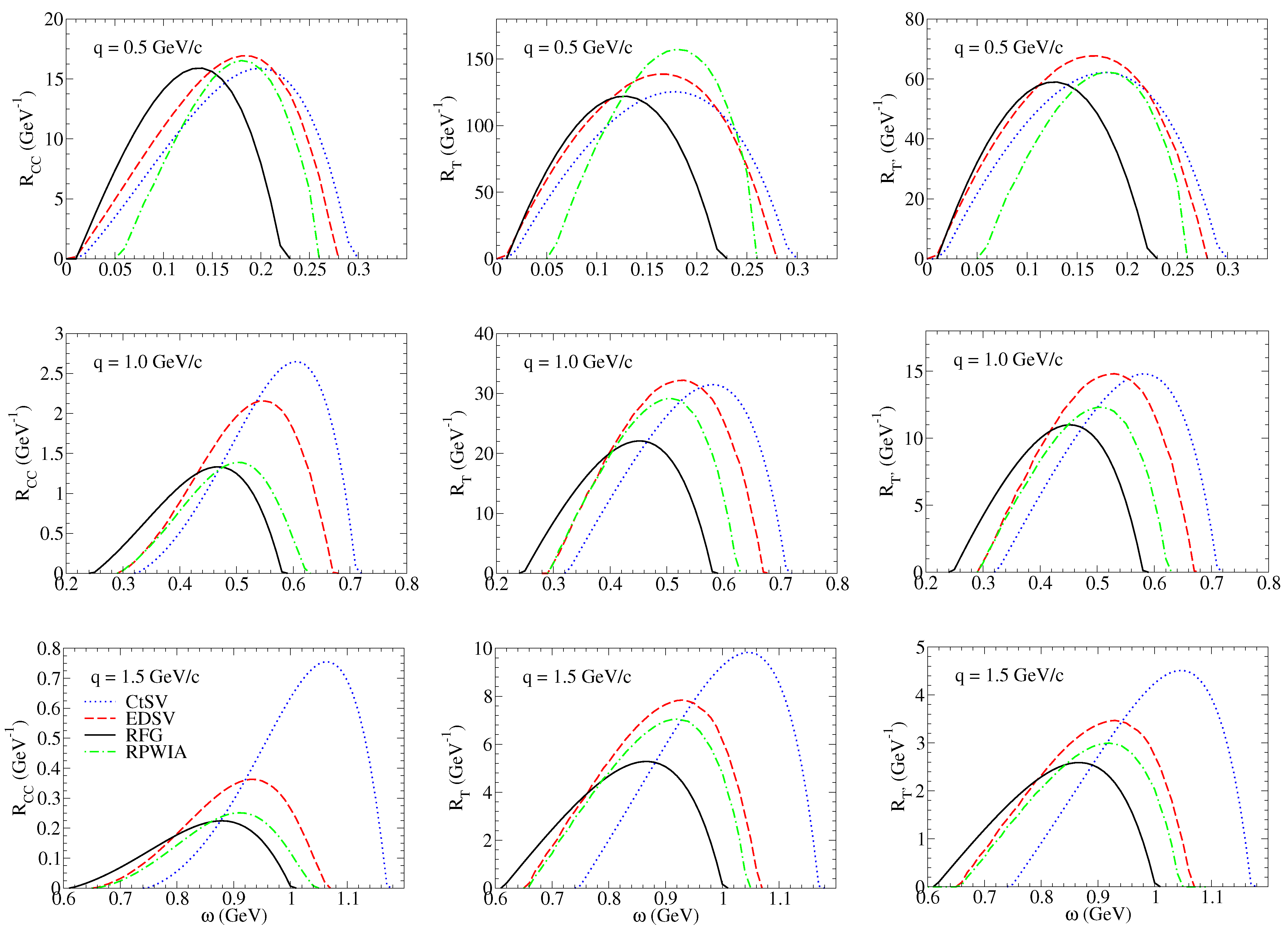
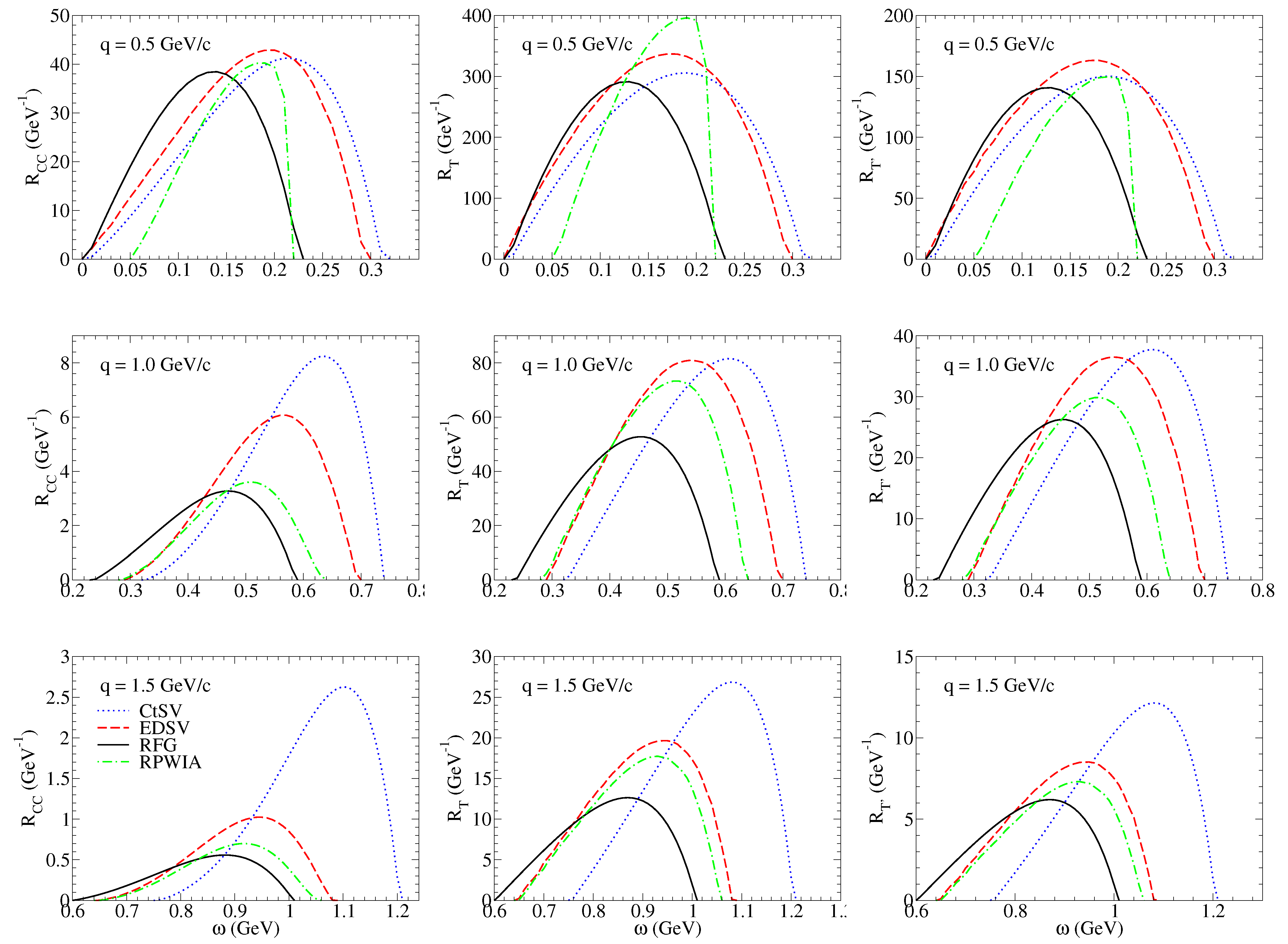
3. Discussion of Results
3.1. Nuclear Responses
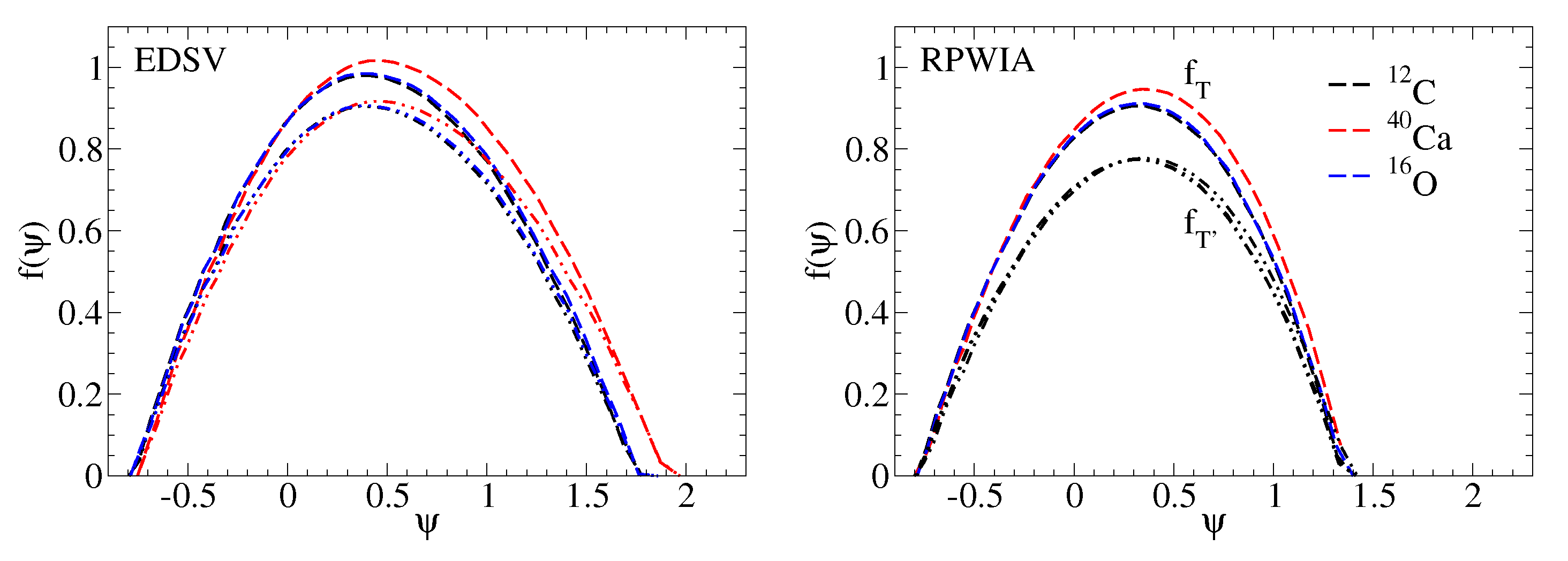
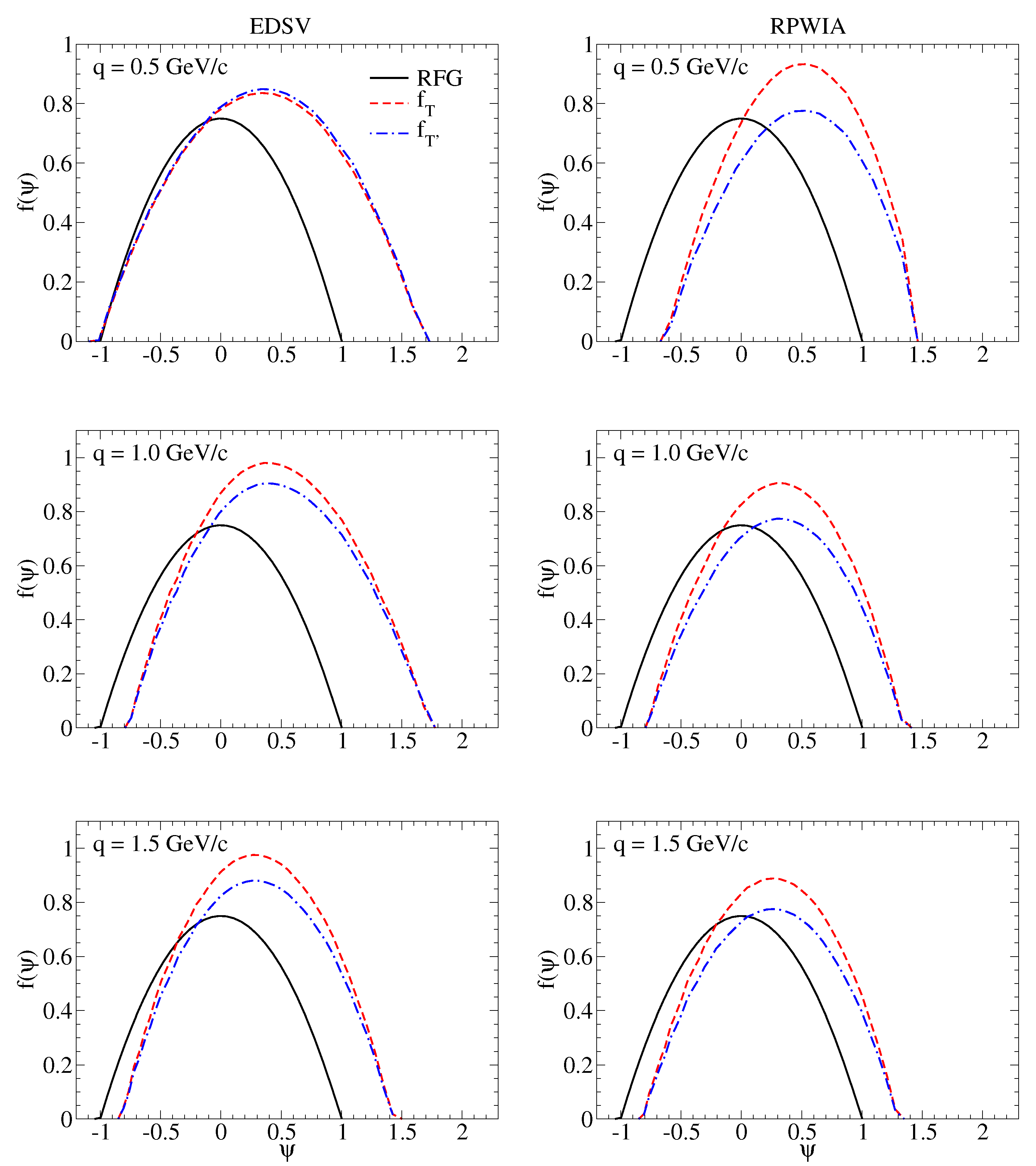
3.2. Scaling Functions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CP | Charge-Parity |
| QE | Quasielastic |
| RFG | Relativistic Fermi Gas |
| RMF | Relativistic Mean Field |
| RPWIA | Relativistic Plane Wave Impulse Approximation |
| DIS | Deep Inelastic Scattering |
| MEC | Meson Exchange Currents |
| EDSV | Energy-Dependent Scalar Vector |
| CtSV | Constant Scalar Vector |
| PCAC | Partially Conserved Axial Current |
| CC | Charge–Charge |
| CL | Charge–Longitudinal |
| LL | Longitudinal–Longitudinal |
| T | Transverse |
| T’ | Transverse interference |
| SuSAv2 | SuperScaling Approach version 2 |
| MiniBooNE | Mini Booster Neutrino Experiment |
| MINERvA | Main Injector Neutrino ExpeRiment to study v-A interactions |
| MicroBooNE | Micro Booster Neutrino Experiment |
| T2K | Tokai to Kamioka experiment |
| DUNE | Deep Underground Neutrino Experiment |
Appendix A. Single-Nucleon Tensor Tμν
References
- Alvarez-Ruso, L.; Sajjad Athar, M.; Barbaro, M.B.; Cherdack, D.; Christy, M.E.; Coloma, P.; Donnelly, T.W.; Dytman, S.; de Gouvea, A.; Hill, R.J.; et al. NuSTEC1 1Neutrino Scattering Theory Experiment Collaboration http://nustec.fnal.gov. White Paper: Status and challenges of neutrino–nucleus scattering. Prog. Part. Nucl. Phys. 2018, 100, 1–68. [Google Scholar] [CrossRef]
- Katori, T.; Martini, M. Neutrino–nucleus cross sections for oscillation experiments. J. Phys. G 2018, 45, 013001. [Google Scholar] [CrossRef]
- Acero, M.A. et al. [NOvA Collaboration] First measurement of neutrino oscillation parameters using neutrinos and antineutrinos by NOvA. Phys. Rev. Lett. 2019, 123, 151803. [Google Scholar] [CrossRef] [PubMed]
- Abe, K. et al. [The T2K Collaboration] Constraint on the matter-antimatter symmetry-violating phase in neutrino oscillations. Nature 2020, 580, 339–344. [Google Scholar] [CrossRef]
- Abe, K.; Aihara, H.; Andreopoulos, C.; Anghel, I.; Ariga, A.; Ariga, T.; Asfandiyarov, R.; Askins, M.; Back, J.J.; Ballett, P.; et al. Physics potential of a long-baseline neutrino oscillation experiment using a J-PARC neutrino beam and Hyper-Kamiokande. Prog. Theor. Exp. Phys. 2015, 2015, 053C02. [Google Scholar]
- Abed Abud, A. et al. [DUNE Collaboration] Snowmass Neutrino Frontier: DUNE Physics Summary. arXiv 2022, arXiv:2203.06100. [Google Scholar]
- Amaro, J.E.; Barbaro, M.B.; Caballero, J.A.; Donnelly, T.W.; Williamson, C.F. Meson-exchange currents and quasielastic neutrino cross sections in the superscaling approximation model. Phys. Lett. B 2011, 696, 151–155. [Google Scholar] [CrossRef]
- Megias, G.D.; Amaro, J.E.; Barbaro, M.B.; Caballero, J.A.; Donnelly, T.W. Inclusive electron scattering within the SuSAv2 meson-exchange current approach. Phys. Rev. 2016, D94, 013012. [Google Scholar] [CrossRef]
- Megias, G.D.; Barbaro, M.B.; Caballero, J.A.; Amaro, J.E.; Donnelly, T.W.; Ruiz Simo, I.; Van Orden, J.W. Neutrino-Oxygen CC0π scattering in the SuSAv2-MEC model. J. Phys. G 2019, 46, 015104. [Google Scholar] [CrossRef]
- Bodek, A.; Christy, M.E.; Coopersmith, B. Effective Spectral Function for Quasielastic Scattering on Nuclei. Nucl. Part. Phys. Proc. 2016, 273, 1705–1710. [Google Scholar] [CrossRef]
- Bodek, A.; Christy, M.E.; Coopersmith, B. Effective spectral function for quasielastic scattering on nuclei from H to Pb. AIP Conf. Proc. 2015, 1680, 020003. [Google Scholar] [CrossRef]
- Bodek, A.; Christy, M.E.; Coopersmith, B. Effective Spectral Function for Quasielastic Scattering on Nuclei. Eur. Phys. J. 2014, C74, 3091. [Google Scholar] [CrossRef]
- Kim, K.S.; Wright, L.E. y-scaling in Quasielastic Electron Scattering from Nuclei. Phys. Rev. 2007, C76, 044613. [Google Scholar] [CrossRef]
- Kim, K.S.; Wright, L.E. Quasielastic electron scattering at high energy from C-12, Fe-56, and Au-197. Phys. Rev. 2003, C67, 054604. [Google Scholar] [CrossRef]
- Giusti, C.; Meucci, A. The Relativistic Green’s Function Model for Quasielastic Neutrino-Nucleus Scattering. Nucl. Theory 2013, 32, 50–60. [Google Scholar]
- Meucci, A.; Vorabbi, M.; Giusti, C.; Pacati, F.D.; Finelli, P. Elastic and quasi-elastic electron scattering off nuclei with neutron excess. Phys. Rev. 2013, C87, 054620. [Google Scholar] [CrossRef]
- Rocco, N.; Lovato, A.; Benhar, O. Unified description of electron-nucleus scattering within the spectral function formalism. Phys. Rev. Lett. 2016, 116, 192501. [Google Scholar] [CrossRef]
- Benhar, O.; Lovato, A. Towards a unified description of the electroweak nuclear response. Int. J. Mod. Phys. 2015, E24, 1530006. [Google Scholar] [CrossRef]
- Benhar, O.; Coletti, P.; Meloni, D. Electroweak Nuclear Response in the Quasielastic Regime. Phys. Rev. Lett. 2010, 105, 132301. [Google Scholar] [CrossRef]
- Mosel, U.; Gallmeister, K. Cross sections for A(e,e′)X reactions. Phys. Rev. 2019, C99, 064605. [Google Scholar] [CrossRef]
- Amaro, J.E.; Barbaro, M.B.; Caballero, J.A.; González-Jiménez, R.; Megias, G.D.; Simo, I.R. Electron- versus neutrino-nucleus scattering. J. Phys. G Nucl. Part Phys. 2020, 47. [Google Scholar] [CrossRef]
- Alberico, W.M.; Molinari, A.; Donnelly, T.W.; Kronenberg, E.L.; Van Orden, J.W. Scaling in electron scattering from a relativistic Fermi gas. Phys. Rev. 1988, C38, 1801–1810. [Google Scholar] [CrossRef] [PubMed]
- Donnelly, T.W.; Sick, I. Superscaling in inclusive electron—Nucleus scattering. Phys. Rev. Lett. 1999, 82, 3212–3215. [Google Scholar] [CrossRef]
- Maieron, C.; Donnelly, T.W.; Sick, I. Extended superscaling of electron scattering from nuclei. Phys. Rev. 2002, C65, 025502. [Google Scholar] [CrossRef]
- Amaro, J.E.; Barbaro, M.B.; Caballero, J.A.; Donnelly, T.W.; Molinari, A.; Sick, I. Using electron scattering superscaling to predict charge-changing neutrino cross sections in nuclei. Phys. Rev. 2005, C71, 015501. [Google Scholar] [CrossRef]
- González-Jiménez, R.; Megias, G.D.; Barbaro, M.B.; Caballero, J.A.; Donnelly, T.W. Extensions of Superscaling from Relativistic Mean Field Theory: The SuSAv2 Model. Phys. Rev. 2014, C90, 035501. [Google Scholar] [CrossRef]
- Megias, G.; Amaro, J.; Barbaro, M.; Caballero, J.; Donnelly, T.; Ruiz Simo, I. Charged-current neutrino-nucleus reactions within the superscaling meson-exchange current approach. Phys. Rev. 2016, D94, 093004. [Google Scholar] [CrossRef]
- Barbaro, M.B.; Caballero, J.A.; De Pace, A.; Donnelly, T.W.; González-Jiménez, R.; Megias, G.D. Mean-field and two-body nuclear effects in inclusive electron scattering on argon, carbon, and titanium: The superscaling approach. Phys. Rev. C 2019, 99, 042501. [Google Scholar] [CrossRef]
- Donnelly, T.W.; Sick, I. Superscaling of inclusive electron scattering from nuclei. Phys. Rev. C 1999, 60, 065502. [Google Scholar] [CrossRef]
- Caballero, J.A.; Amaro, J.E.; Barbaro, M.B.; Donnelly, T.W.; Udias, J.M. Scaling and isospin effects in quasielastic lepton-nucleus scattering in the Relativistic Mean Field Approach. Phys. Lett. 2007, B653, 366–372. [Google Scholar] [CrossRef]
- González-Jiménez, R.; Barbaro, M.B.; Caballero, J.A.; Donnelly, T.W.; Jachowicz, N.; Megias, G.D.; Niewczas, K.; Nikolakopoulos, A.; Udías, J.M. Constraints in modeling the quasielastic response in inclusive lepton-nucleus scattering. Phys. Rev. C 2020, 101, 015503. [Google Scholar] [CrossRef]
- Amaro, J.E.; Barbaro, M.B.; Caballero, J.A.; Donnelly, T.W.; González-Jiménez, R.; Megias, G.D.; Ruiz Simo, I. Neutrino-nucleus scattering in the SuSA model. Eur. Phys. J. Spec. Top. 2021, 230, 4321–4338. [Google Scholar] [CrossRef]
- Megias, G.D.; Donnelly, T.W.; Moreno, O.; Williamson, C.F.; Caballero, J.A.; González-Jiménez, R.; De Pace, A.; Barbaro, M.B.; Alberico, W.M.; Nardi, M.; et al. Meson-exchange currents and quasielastic predictions for charged-current neutrino-12C scattering in the superscaling approach. Phys. Rev. D 2015, 91, 073004. [Google Scholar] [CrossRef]
- Gonzalez-Rosa, J.; Megias, G.; Caballero, J.; Barbaro, M. SuSAv2 model for inelastic neutrino-nucleus scattering. Phys. Rev. D 2022, 105, 093009. [Google Scholar] [CrossRef]
- Dolan, S.; Megias, G.D.; Bolognesi, S. Implementation of the SuSAv2-meson exchange current 1p1h and 2p2h models in GENIE and analysis of nuclear effects in T2K measurements. Phys. Rev. D 2020, 101, 033003. [Google Scholar] [CrossRef]
- Megias, G.; Barbaro, M.; Caballero, J.; Dolan, S. Analysis of the MINERvA antineutrino double-differential cross sections within the SuSAv2 model including meson-exchange currents. Phys. Rev. D 2019, 99, 113002. [Google Scholar] [CrossRef]
- Papadopoulou, A. et al. [e4υ Collaboration] Inclusive Electron Scattering And The GENIE Neutrino Event Generator. Phys. Rev. D 2021, 103, 113003. [Google Scholar] [CrossRef]
- Khachatryan, M. et al. [CLAS Collaboration & e4υ Collaboration] Electron-beam energy reconstruction for neutrino oscillation measurements. Nature 2021, 599, 565–570. [Google Scholar] [CrossRef]
- Cruz-Barrios, S.; Caballero, J.A. Analysis of quasielastic (e,e′) electromagnetic responses and scaling for nuclear matter in the relativistic mean field model. Nucl. Phys. A 2020, 994, 121667. [Google Scholar] [CrossRef]
- Galster, S.; Klein, H.; Moritz, J.; Schmidt, K.H.; Wegener, D.; Bleckwenn, J. Elastic electron-deuteron scattering and the electric neutron form factor at four-momentum transfers 5fm−2 < q2 < 14fm−2. Nucl. Phys. 1971, B32, 221–237. [Google Scholar] [CrossRef]
- Meyer, A.S.; Betancourt, M.; Gran, R.; Hill, R.J. Deuterium target data for precision neutrino-nucleus cross sections. Phys. Rev. D 2016, 93, 113015. [Google Scholar] [CrossRef]
- Gonzalez-Jimenez, R.; Caballero, J.A.; Donnelly, T.W. Parity Violation in Elastic Electron-Nucleon Scattering: Strangeness Content in the Nucleon. Phys. Rept. 2013, 524, 1–35. [Google Scholar] [CrossRef]
- Thomas, A.W.; Weise, W. The Structure of the Nucleon; Wiley-VCH Verlag GmbH: Berlin, Germany, 2001. [Google Scholar]
- Horowitz, C.J.; Piekarewicz, J. Relativistic and nuclear structure effects in parity violating quasielastic electron scattering. Phys. Rev. 1993, C47, 2924–2936. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Horowitz, C.J.; Frank, M.R. Relativistic models for quasielastic (e, e′) at large momentum transfers. Phys. Rev. 1995, C51, 792–796. [Google Scholar] [CrossRef]
- Megias, G.D.; Amaro, J.E.; Barbaro, M.B.; Caballero, J.A.; Donnelly, T.W. Neutrino and antineutrino CCQE scattering in the SuperScaling Approximation from MiniBooNE to NOMAD energies. Phys. Lett. B 2013, 725, 170–174. [Google Scholar] [CrossRef]
- Amaro, J.E.; Barbaro, M.B.; Caballero, J.A.; Donnelly, T.W.; Molinari, A. Gauge and Lorentz invariant one pion exchange currents in electron scattering from a relativistic Fermi gas. Phys. Rept. 2002, 368, 317–407. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cruz-Barrios, S.; Megias, G.D.; Caballero, J.A. Weak Neutrino (Antineutrino) Charged-Current Responses and Scaling for Nuclear Matter in the Relativistic Mean Field. Universe 2023, 9, 240. https://doi.org/10.3390/universe9050240
Cruz-Barrios S, Megias GD, Caballero JA. Weak Neutrino (Antineutrino) Charged-Current Responses and Scaling for Nuclear Matter in the Relativistic Mean Field. Universe. 2023; 9(5):240. https://doi.org/10.3390/universe9050240
Chicago/Turabian StyleCruz-Barrios, Sara, Guillermo D. Megias, and Juan A. Caballero. 2023. "Weak Neutrino (Antineutrino) Charged-Current Responses and Scaling for Nuclear Matter in the Relativistic Mean Field" Universe 9, no. 5: 240. https://doi.org/10.3390/universe9050240
APA StyleCruz-Barrios, S., Megias, G. D., & Caballero, J. A. (2023). Weak Neutrino (Antineutrino) Charged-Current Responses and Scaling for Nuclear Matter in the Relativistic Mean Field. Universe, 9(5), 240. https://doi.org/10.3390/universe9050240





