Strong Deflection Gravitational Lensing for the Photons Coupled to the Weyl Tensor in a Conformal Gravity Black Hole
Abstract
1. Introduction
2. Conformal Gravity Black Hole
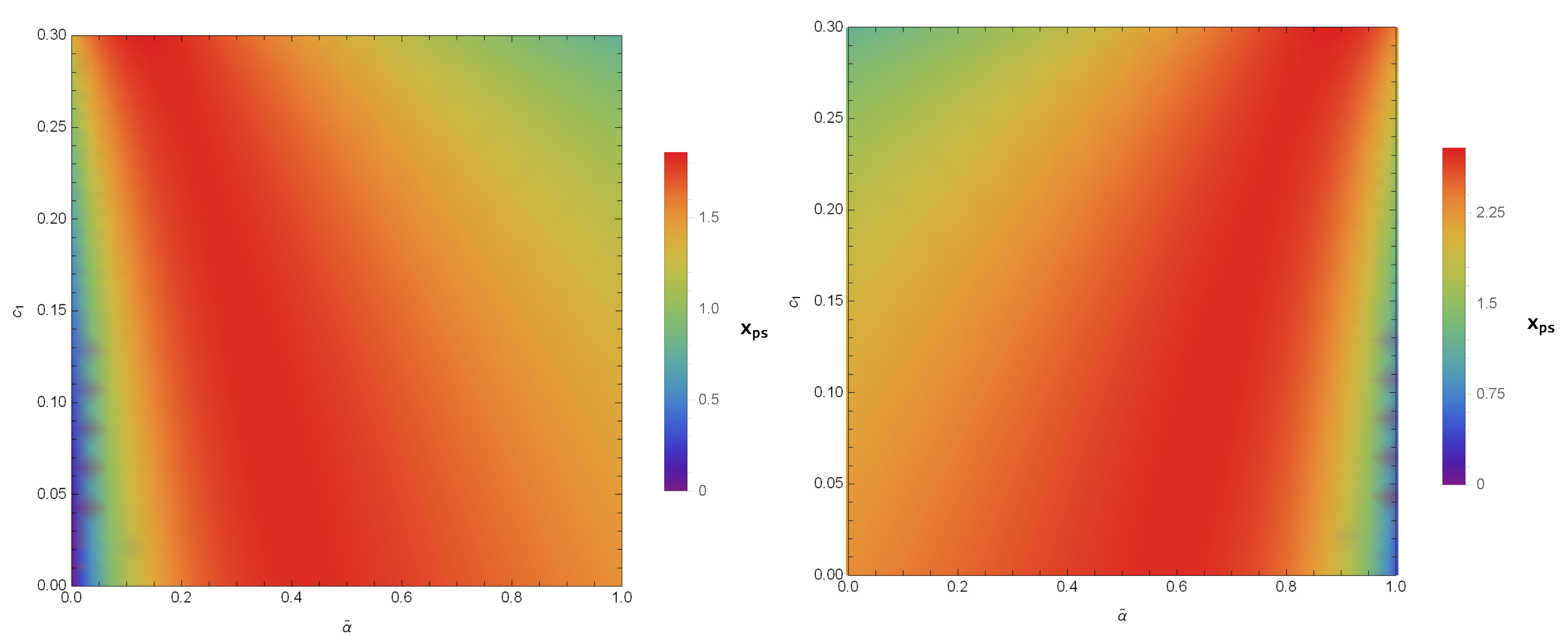
3. Equation of the Photon Sphere
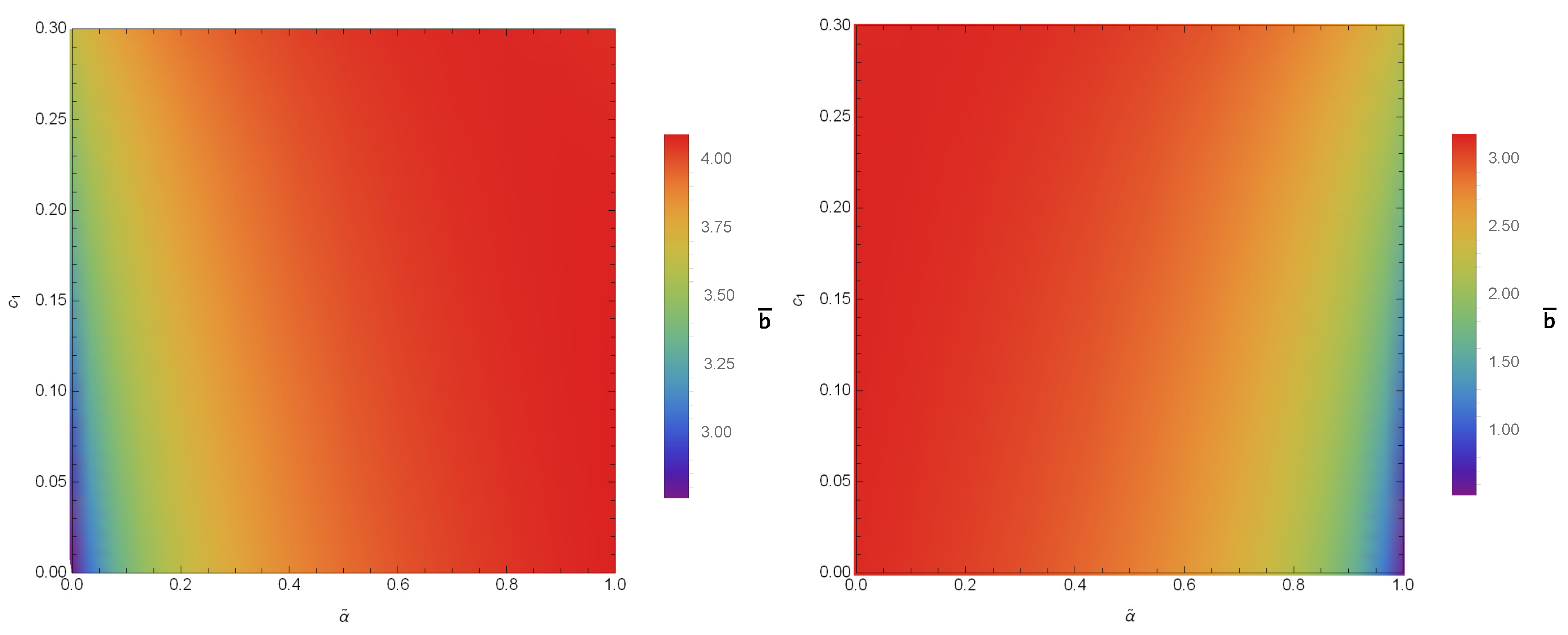
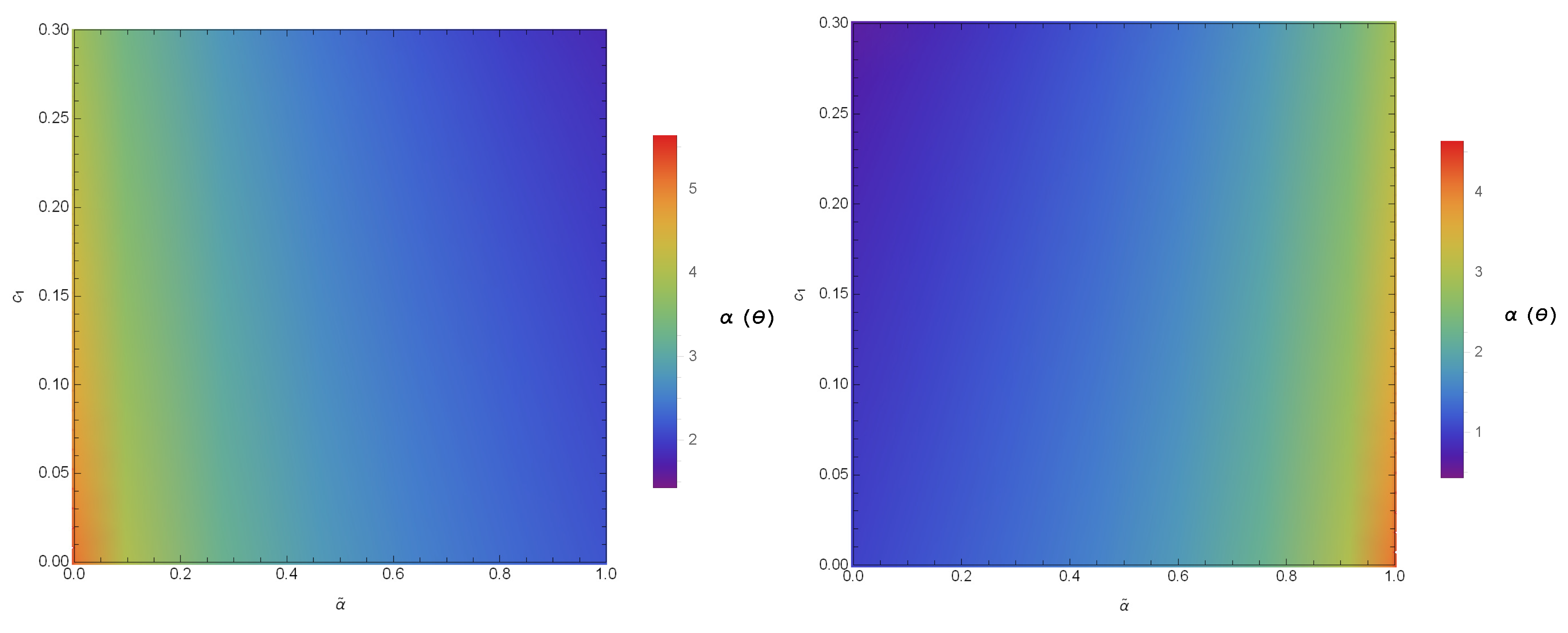
4. Strong Deflection Angle
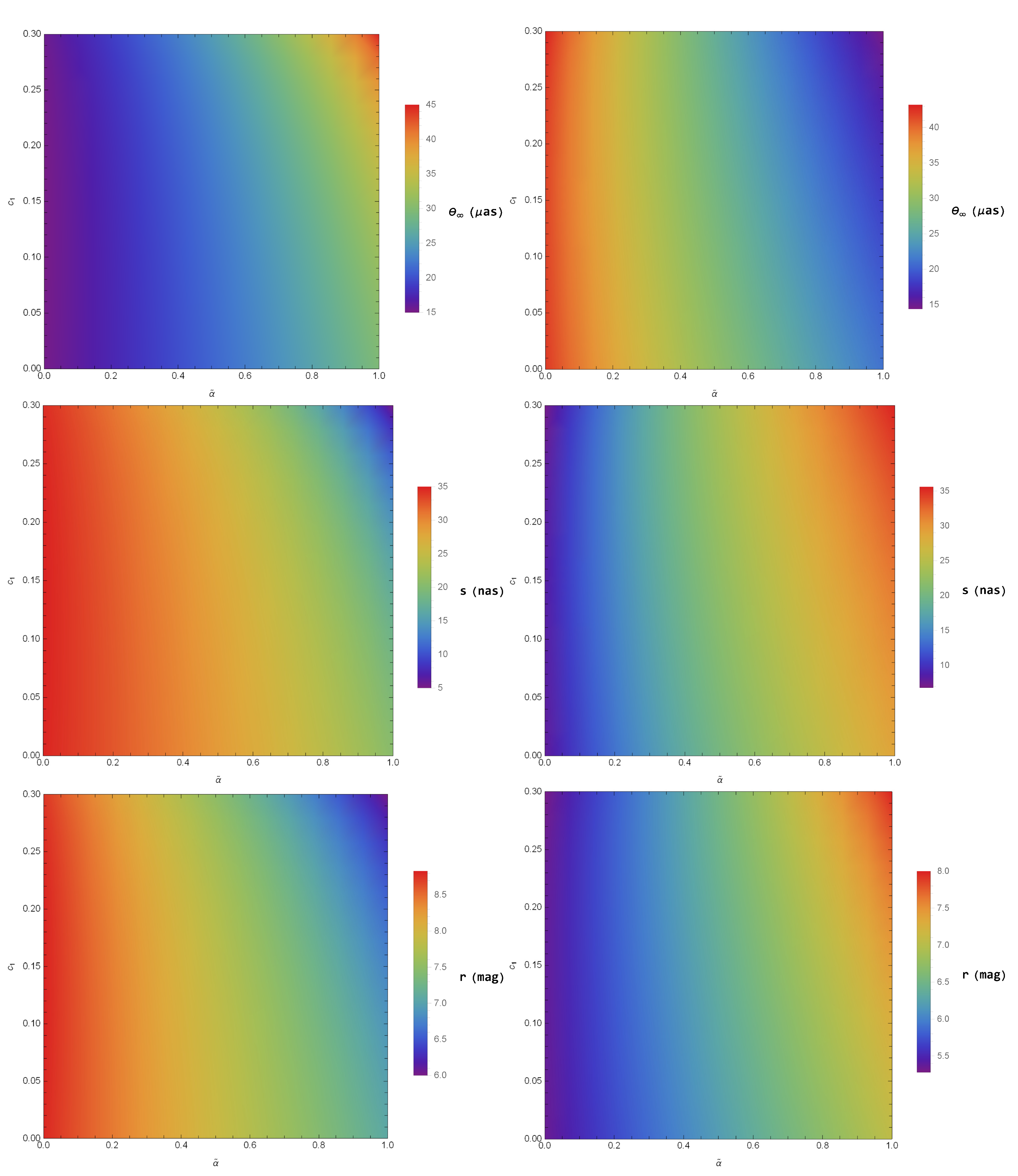
5. Strong Deflection Gravitational Lensing Observables for and
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Adler, S.L. Einstein gravity as a symmetry-breaking effect in quantum field theory. Rev. Mod. Phys. 1982, 54, 729. [Google Scholar] [CrossRef]
- Hooft, G.t. A class of elementary particle models without any adjustable real parameters. arXiv 2011, arXiv:1104.4543. [Google Scholar]
- Mannheim, P.D. Making the case for conformal gravity. Found. Phys. 2012, 42, 388. [Google Scholar] [CrossRef]
- Bergshoeff, E.; de Roo, M.; Wit, B.d. Extended conformal supergravity. Nucl. Phys. B 1981, 182, 173. [Google Scholar] [CrossRef]
- de Wit, B.; van Holten, J.W.; Proeyen, A.V. Structure of N = 2 supergravity. Nucl. Phys. B 1981, 184, 77. [Google Scholar] [CrossRef]
- Berkovits, N.; Witten, E. Conformal supergravity in twistor-string theory. J. High Energy Phys. 2004, 0408, 009. [Google Scholar] [CrossRef]
- Maldacena, J. Einstein Gravity from Conformal Gravity. arXiv 2011, arXiv:1105.5632. [Google Scholar]
- Anastasiou, G.; Olea, R. From conformal to Einstein gravity. Phys. Rev. D 2016, 94, 086008. [Google Scholar] [CrossRef]
- Mannheim, P.D. Comprehensive solution to the cosmological constant, zero-point energy, and quantum gravity problems. Gen. Rel. Grav. 2011, 43, 703. [Google Scholar] [CrossRef]
- Stelle, K.S. Renormalization of higher-derivative quantum gravity. Phys. Rev. D 1977, 16, 953. [Google Scholar] [CrossRef]
- Mannheim, P.D.; Kazanas, D. Exact vacuum solution to conformal Weyl gravity and galactic rotation curves. Astrophys. J. 1989, 342, 635. [Google Scholar] [CrossRef]
- Mannheim, P.D. Alternatives to dark matter and dark energy. Prog. Part. Nucl. Phys. 2006, 56, 340. [Google Scholar] [CrossRef]
- Mannheim, P.D.; Brien, J.G.O. Impact of a global quadratic potential on galactic rotation curves. Phys. Rev. Lett. 2011, 106, 121101. [Google Scholar] [CrossRef]
- Vagnozzi, S.; Roy, R.; Tsai, Y.D.; Visinelli, L.; Afrin, M.; Allahyari, A.; Bambhaniya, P.; Dey, D.; Ghosh, S.G.; Joshi, P.S.; et al. Horizon-scale tests of gravity theories and fundamental physics from the Event Horizon Telescope image of Sagittarius A*. arXiv 2022, arXiv:2205.07787. [Google Scholar]
- Lu, H.; Pang, Y.; Pope, C.N.; Vazquez-Poritz, J.F. AdS and Lifshitz black holes in conformal and Einstein-Weyl gravities. Phys. Rev. D 2012, 86, 044011. [Google Scholar] [CrossRef]
- Xu, W.; Zhao, L. Critical phenomena of static charged AdS black holes in conformal gravity. Phys. Lett. B 2014, 736, 214. [Google Scholar] [CrossRef]
- Xu, H.; Sun, Y.; Zhao, L. Black hole thermodynamics and heat engines in conformal gravity. Int. J. Mod. Phys. D 2017, 26, 1750151. [Google Scholar] [CrossRef]
- Xu, H.; Yung, M.H. On the thermodynamic phase structure of conformal gravity. Phys. Lett. B 2018, 783, 36. [Google Scholar] [CrossRef]
- Einstein, A. Lens-Like Action of a Star by the Deviation of Light in the Gravitational Field. Science 1936, 84, 506–507. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Darwin, C. The gravity field of a particle. Proc. R. Soc. Lond. A 1959, 249, 180. [Google Scholar]
- Virbhadra, K.S.; Ellis, G.F.R. Schwarzschild black hole lensing. Phys. Rev. D 2000, 62, 084003. [Google Scholar] [CrossRef]
- Virbhadra, K.S.; Keeton, C.R. Time delay and magnification centroid due to gravitational lensing by black holes and naked singularities. Phys. Rev. D 2008, 77, 124014. [Google Scholar] [CrossRef]
- Virbhadra, K.S. Relativistic images of Schwarzschild black hole lensing. Phys. Rev. D 2009, 79, 083004. [Google Scholar] [CrossRef]
- Frittelly, S.; Kling, T.P.; Newman, E.T. Spacetime perspective of Schwarzschild lensing. Phys. Rev. D 2000, 61, 064021. [Google Scholar] [CrossRef]
- Bozza, V.; Capozziello, S.; Lovane, G.; Scarpetta, G. Strong field limit of black hole gravitational lensing. Gen. Rel. Grav. 2001, 33, 1535. [Google Scholar] [CrossRef]
- Bozza, V. Gravitational lensing in the strong field limit. Phys. Rev. D 2002, 66, 103001. [Google Scholar] [CrossRef]
- Bozza, V. Quasiequatorial gravitational lensing by spinning black holes in the strong field limit. Phys. Rev. D 2003, 67, 103006. [Google Scholar] [CrossRef]
- Wei, S.W.; Liu, Y.X.; Fu, C.E.; Yang, K.J. Strong field limit analysis of gravitational lensing in Kerr-Taub-NUT spacetime. J. Cosmol. Astropart. Phys. 2012, 10, 053. [Google Scholar] [CrossRef]
- Wei, S.W.; Liu, Y.X. Equatorial and quasiequatorial gravitational lensingby a Kerr black hole pierced by a cosmic string. Phys. Rev. D 2012, 85, 064044. [Google Scholar] [CrossRef]
- Kraniotis, G.V. Precise analytic treatment of Kerr and Kerr-(anti) de Sitter black holes as gravitational lenses. Class. Quant. Grav. 2011, 28, 085021. [Google Scholar] [CrossRef]
- Eiroa, E.F.; Romero, G.E.; Torres, D.F. Reissner-Nordström black hole lensing. Phys. Rev. D 2002, 66, 024010. [Google Scholar] [CrossRef]
- Eiroa, E.F. Gravitational lensing by Einstein-Born-Infeld black holes. Phys. Rev. D 2006, 73, 043002. [Google Scholar] [CrossRef]
- Chen, S.B.; Jing, J.L. Strong field gravitational lensing in the deformed Hořava-Lifshitz black hole. Phys. Rev. D 2009, 80, 024036. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, S.B.; Jing, J.L. Strong gravitational lensing in a squashed Kaluza-Klein black hole spacetime. Phys. Rev. D 2010, 81, 124017. [Google Scholar] [CrossRef]
- Chen, S.B.; Jing, J.L. Geodetic precession and strong gravitational lensing in dynamical Chern–Simons-modified gravity. Class. Quantum Gravity 2010, 27, 225006. [Google Scholar] [CrossRef]
- Chen, S.B.; Liu, Y.; Jing, J.L. Strong gravitational lensing in a squashed Kaluza-Klein Godel black hole. Phys. Rev. D 2011, 83, 124019. [Google Scholar] [CrossRef]
- Ding, C.K.; Kang, S.; Chen, C.Y.; Chen, S.B.; Jing, J.L. Strong gravitational lensing in a noncommutative black-hole spacetime. Phys. Rev. D 2011, 83, 084005. [Google Scholar] [CrossRef]
- Chen, S.B.; Jing, J.L. Strong gravitational lensing by a rotating non-Kerr compact object. Phys. Rev. D 2012, 85, 124029. [Google Scholar] [CrossRef]
- Liu, C.Q.; Chen, S.B.; Jing, J.L. Strong gravitational lensing of quasi-Kerr compact object with arbitrary quadrupole moments. J. High Energy Phys. 2012, 8, 097. [Google Scholar] [CrossRef]
- Ji, L.Y.; Chen, S.B.; Jing, J.L.J. Strong gravitational lensing in a rotating Kaluza-Klein black hole with squashed horizons. J. High Energy Phys. 2014, 089. [Google Scholar] [CrossRef]
- Zhang, R.J.; Jing, J.L.; Chen, S.B. Strong gravitational lensing for black holes with scalar charge in massive gravity. Phys. Rev. D 2017, 95, 064054. [Google Scholar] [CrossRef]
- Drummond, I.T.; Hathrell, S.J. QED vacuum polarization in a background gravitational field and its effect on the velocity of photons. Phys. Rev. D 1980, 22, 343. [Google Scholar] [CrossRef]
- Turner, M.S.; Widrow, L.M. Inflation-produced, large-scale magnetic fields. Phys. Rev. D 1988, 37, 2743. [Google Scholar] [CrossRef] [PubMed]
- Ni, W.T. Equivalence Principles and Electromagnetism. Phys. Rev. Lett. 1977, 38, 301. [Google Scholar] [CrossRef]
- Ni, W.T. Equivalence principles and precision experiments. In Precision Measurements and Fundamental Constants II; Taylor, B.N., Phillips, W.D., Eds.; U.S. National Bureau of Standards Publication 617; U.S. GPO: Washington, DC, USA, 1984. [Google Scholar]
- Solanki, S.K.; Preuss, O.; Haugan, M.P.; Gandorfer, A.; Povel, H.P.; Steiner, P.; Stucki, K.; Bernasconi, P.N.; Soltau, D. Solar constraints on new couplings between electromagnetism and gravity. Phys. Rev. D 2004, 69, 062001. [Google Scholar] [CrossRef]
- Preuss, O.; Haugan, M.P.; Solanki, S.K.; Jordan, S. An astronomical search for evidence of new physics: Limits on gravity-induced birefringence from the magnetic white dwarf RE J0317-853. Phys. Rev. D 2004, 70, 067101. [Google Scholar] [CrossRef]
- Itin, Y.; Hehl, F.W. Maxwell’s field coupled nonminimally to quadratic torsion: Axion and birefringence. Phys. Rev. D 2003, 68, 127701. [Google Scholar] [CrossRef]
- Dereli, T.; Sert, O. Non-minimal ln(R)F2 couplings of electromagnetic fields to gravity: Static, spherically symmetric solutions. Eur. Phys. J. C 2011, 71, 1589. [Google Scholar] [CrossRef]
- Balakin, A.B.; Lemos, J.P.S. Non-minimal coupling for the gravitational and electromagnetic fields: A general system of equations. Class. Quantum Gravity 2005, 22, 1867. [Google Scholar] [CrossRef]
- Balakin, A.B.; Bochkarev, V.V.; Lemos, J.P.S. Nonminimal coupling for the gravitational and electromagnetic fields: Black hole solutions and solitons. Phys. Rev. D 2008, 77, 084013. [Google Scholar] [CrossRef]
- Hehl, F.W.; Obukhov, Y.N. How does the electromagnetic field couple to gravity, in particular to metric, nonmetricity, torsion, and curvature? Lect. Notes Phys. 2001, 562, 479. [Google Scholar]
- Mazzitelli, F.D.; Spedalieri, F.M. Scalar electrodynamics and primordial magnetic fields. Phys. Rev. D 1995, 52, 6694. [Google Scholar] [CrossRef]
- Lambiase, G.; Prasanna, A.R. Gauge invariant wave equations in curved space-times and primordial magnetic fields. Phys. Rev. D 2004, 70, 063502. [Google Scholar] [CrossRef]
- Raya, A.; Aguilar, J.E.M.; Bellini, M. Gravitoelectromagnetic inflation from a 5D vacuum state. Phys. Lett. B 2006, 638, 314. [Google Scholar] [CrossRef]
- Campanelli, L.; Cea, P.; Fogli, G.L.; Tedesco, L. Inflation-produced magnetic fields in RnF2 and IF2 models. Phys. Rev. D 2008, 77, 123002. [Google Scholar] [CrossRef]
- Bamba, K.; Odintsov, S.D. Inflation and late-time cosmic acceleration in non-minimal Maxwell-F(R) gravity and the generation of large-scale magnetic fields. J. Cosmol. Astropart. Phys. 2008, 0804, 024. [Google Scholar] [CrossRef]
- Kim, K.T.; Kronberg, P.P.; Dewdney, P.E.; Landecker, T.L. The Halo and Magnetic Field of the Coma Cluster of Galaxies. Astrophys. J. 1990, 355, 29. [Google Scholar] [CrossRef]
- Kim, K.T.; Tribble, P.C.; Kronberg, P.P. Detection of Excess Rotation Measure Due to Intracluster Magnetic Fields in Clusters of Galaxies. Astrophys. J. 1991, 379, 80. [Google Scholar] [CrossRef]
- Clarke, T.E.; Kronberg, P.P.; Boehringer, H. A New Radio-X-Ray Probe of Galaxy Cluster Magnetic Fields. Astrophys. J. 2001, 547, L111. [Google Scholar] [CrossRef]
- Ritz, A.; Ward, J. Weyl corrections to holographic conductivity. Phys. Rev. D 2009, 79, 066003. [Google Scholar] [CrossRef]
- Wu, J.P.; Cao, Y.; Kuang, X.M.; Li, W.J. The 3+1 holographic superconductor with Weyl corrections. Phys. Lett. B 2011, 697, 153. [Google Scholar] [CrossRef]
- Ma, D.Z.; Cao, Y.; Wu, J.P. The Stückelberg holographic superconductors with Weyl corrections. Phys. Lett. B 2011, 704, 604. [Google Scholar] [CrossRef]
- Momeni, D.; Setare, M.R. A note on holographic superconductors with Weyl corrections. Mod. Phys. Lett. A 2011, 26, 2889. [Google Scholar] [CrossRef]
- Momeni, D.; Majd, N.; Myrzakulov, R. p-Wave holographic superconductors with Weyl corrections. Europhys. Lett. 2012, 97, 61001. [Google Scholar]
- Momeni, D.; Setare, M.R.; Myrzakulov, R. Condensation of the scalar field with Stuckelberg and Weyl corrections in the background of a planar AdS-Schwarzschild black hole. Int. J. Mod. Phys. A 2012, 27, 1250128. [Google Scholar] [CrossRef]
- Roychowdhury, D. Effect of external magnetic field on holographic superconductors in presence of nonlinear corrections. Phys. Rev. D 2012, 86, 106009. [Google Scholar] [CrossRef]
- Zhao, Z.X.; Pan, Q.Y.; Jing, J.L. Holographic insulator/superconductor phase transition with Weyl corrections. Phys. Lett. B 2013, 719, 440. [Google Scholar] [CrossRef]
- Zhang, L.; Pan, Q.Y.; Jing, J.L. Holographic p-wave superconductor models with Weyl corrections. Phys. Lett. B 2015, 743, 104. [Google Scholar] [CrossRef]
- Chen, S.B.; Jing, J.L. Dynamical evolution of the electromagnetic perturbation with Weyl corrections. Phys. Rev. D 2013, 88, 064058. [Google Scholar] [CrossRef]
- Chen, S.B.; Jing, J.L. Dynamical evolution of a vector field perturbation coupled to the Einstein tensor. Phys. Rev. D 2014, 90, 124059. [Google Scholar] [CrossRef]
- Liao, H.; Chen, S.B.; Jing, J.L. Absorption cross section and Hawking radiation of the electromagnetic field with Weyl corrections. Phys. Lett. B 2014, 728, 457. [Google Scholar] [CrossRef]
- Jing, J.L.; Chen, S.B.; Pan, Q.Y. Geometric optics for a coupling model of electromagnetic and gravitational fields. Ann. Phys. 2016, 367, 219–226. [Google Scholar] [CrossRef]
- Jing, J.L.; Chen, S.B.; Pan, Q.Y.; Wang, M.J. Detect black holes using photons for coupling model of electromagnetic and gravitational fields. arXiv 2017, arXiv:1704.08794. [Google Scholar]
- Chen, S.B.; Jing, J.L. Strong gravitational lensing for the photons coupled to Weyl tensor in a Schwarzschild black hole spacetime. J. Cosmol. Astropart. Phys. 2015, 10, 002. [Google Scholar] [CrossRef]
- Cao, W.G.; Xie, Y. Weak deflection gravitational lensing for photons coupled to Weyl tensor in a Schwarzschild black hole. Eur. Phys. J. C 2018, 78, 191. [Google Scholar] [CrossRef]
- Lu, X.; Yang, F.W.; Xie, Y. Strong gravitational field time delay for photons coupled to Weyl tensor in a Schwarzschild black hole. Eur. Phys. J. C 2016, 76, 357. [Google Scholar] [CrossRef]
- Lu, X.; Xie, Y. Time delay of photons coupled to Weyl tensor in a regular phantom black hole. Eur. Phys. J. C 2020, 80, 625. [Google Scholar] [CrossRef]
- Horvath, Z.; Gergely, L.A.; Keresztes, Z.; Harko, T.; Lobo, F.S.N. Constraining Hořava-Lifshitz gravity by weak and strong gravitational lensing. Phys. Rev. D 2011, 84, 083006. [Google Scholar] [CrossRef]
- Eiroa, E.F.; Sendra, C.M. Gravitational lensing by massless braneworld black holes. Phys. Rev. D 2012, 86, 083009. [Google Scholar] [CrossRef]
- Izmailov, R.N.; Karimov, R.K.; Zhdanov, E.R.; Nandi, K.K. Modified gravity black hole lensing observables in weak and strong field of gravity. Mon. Not. Roy. Astron. Soc. 2019, 483, 3754–3761. [Google Scholar] [CrossRef]
- Gao, Y.X.; Xie, Y. Gravitational lensing by hairy black holes in Einstein-scalar-Gauss-Bonnet theories. Phys. Rev. D 2021, 103, 043008. [Google Scholar] [CrossRef]
- Cheng, X.T.; Xie, Y. Probing a black-bounce, traversable wormhole with weak deflection gravitational lensing. Phys. Rev. D 2021, 103, 064040. [Google Scholar] [CrossRef]
- Zhang, J.; Xie, Y. Gravitational lensing by a black-bounce-Reissner–Nordström spacetime. Eur. Phys. J. C 2022, 82, 471. [Google Scholar] [CrossRef]
- Kuang, X.M.; Övgün, A. Strong gravitational lensing and shadow constraint from M87* of slowly rotating Kerr-like black hole. Ann. Phys. 2022, 447, 169147. [Google Scholar] [CrossRef]
- Javed, W.; Atique, M.; Pantig, R.C.; Övgün, A. Weak Deflection Angle, Hawking Radiation and Greybody Bound of Reissner-Nordström Black Hole Corrected by Bounce Parameter. Symmetry 2023, 15, 148. [Google Scholar] [CrossRef]
- Javed, W.; Riaz, S.; Pantig, R.C.; Övgün, A. Weak gravitational lensing in dark matter and plasma mediums for wormhole-like static aether solution. Eur. Phys. J. C 2022, 82, 1057. [Google Scholar] [CrossRef]
- Javed, W.; Irshad, H.; Pantig, R.C.; Övgün, A. Weak Deflection Angle by Kalb–Ramond Traversable Wormhole in Plasma and Dark Matter Mediums. Universe 2022, 8, 599. [Google Scholar] [CrossRef]
- Pantig, R.C.; Mastrototaro, L.; Lambiase, G.; Övgün, A. Shadow, lensing, quasinormal modes, greybody bounds and neutrino propagation by dyonic ModMax black holes. Eur. Phys. J. C 2022, 82, 1155. [Google Scholar] [CrossRef]
- Pantig, R.C.; Övgün, A. Testing dynamical torsion effects on the charged black hole’s shadow, deflection angle and greybody with M87* and Sgr. A* from EHT. Ann. Phys. 2023, 448, 169197. [Google Scholar] [CrossRef]
- Uniyal, A.; Pantig, R.C.; Övgün, A. Probing a non-linear electrodynamics black hole with thin accretion disk, shadow, and deflection angle with M87* and Sgr A* from EHT. Phys. Dark Univ. 2023, 40, 101178. [Google Scholar] [CrossRef]
- Jusufi, K.; Övgün, A. Gravitational Lensing by Rotating Wormholes. Phys. Rev. D 2018, 97, 024042. [Google Scholar] [CrossRef]
- Övgün, A. Light deflection by Damour-Solodukhin wormholes and Gauss-Bonnet theorem. Phys. Rev. D 2018, 98, 044033. [Google Scholar] [CrossRef]
- Pantig, R.C.; Övgün, A. Dark matter effect on the weak deflection angle by black holes at the center of Milky Way and M87 galaxies. Eur. Phys. J. C 2022, 82, 391. [Google Scholar] [CrossRef]
- Li, G.; Deng, X.M. Classical tests of photons coupled to Weyl tensor in the Solar System. Ann. Phys. 2017, 382, 136. [Google Scholar] [CrossRef]
- Li, G.; Deng, X.M. Testing Photons Coupled to Weyl Tensor with Gravitational Time Advancement. Commun. Theor. Phys. 2018, 70, 721. [Google Scholar] [CrossRef]
- Pang, X.; Jia, J. Gravitational lensing of massive particles in Reissner–Nordström black hole spacetime. Class. Quantum Gravity 2019, 36, 065012. [Google Scholar] [CrossRef]
- Tsukamoto, N. Deflection angle in the strong deflection limit in a general asymptotically flat, static, spherically symmetric spacetime. Phys. Rev. D 2017, 95, 064035. [Google Scholar] [CrossRef]
- Zakharov, A.F.; de Paolis, F.; Ingrosso, G.; Nucita, A.A. Direct measurements of black hole charge with future astrometrical missions. Astron. Astrophys. 2005, 442, 795. [Google Scholar] [CrossRef]
- Wang, C.Y.; Shen, Y.F.; Xie, Y. Weak and strong deflection gravitational lensings by a charged Horndeski black hole. J. Cosmol. Astropart. Phys. 2019, 04, 022. [Google Scholar] [CrossRef]
- Lu, X.; Xie, Y. Weak and strong deflection gravitational lensing by a renormalization group improved Schwarzschild black hole. Eur. Phys. J. C 2019, 79, 1016. [Google Scholar] [CrossRef]
- Whisker, R. Strong gravitational lensing by braneworld black holes. Phys. Rev. D 2005, 71, 064004. [Google Scholar] [CrossRef]
- Zhao, S.S.; Xie, Y. Strong field gravitational lensing by a charged Galileon black hole. J. Cosmol. Astropart. Phys. 2016, 07, 007. [Google Scholar] [CrossRef]
- Zhao, S.S.; Xie, Y. Strong deflection gravitational lensing by a modified Hayward black hole. Eur. Phys. J. C 2017, 77, 272. [Google Scholar] [CrossRef]
- Chen, S.; Wang, S.; Huang, Y.; Jing, J.; Wang, S. Strong gravitational lensing for the photons coupled to a Weyl tensor in a Kerr black hole spacetime. Phys. Rev. D 2017, 95, 104017. [Google Scholar] [CrossRef]
- Zhang, R.; Jing, J. Strong gravitational lensing for photons coupled to Weyl tensor in a regular phantom black hole. Eur. Phys. J. C 2018, 78, 796. [Google Scholar] [CrossRef]
- Abbas, G.; Mahmood, A.; Zubair, M. Strong gravitational lensing for photon coupled to Weyl tensor in Kiselev black hole. Chin. Phys. C 2020, 44, 9. [Google Scholar] [CrossRef]
- Abbas, G.; Mahmood, A.; Zubair, M. Strong deflection gravitational lensing for photon coupled to Weyl tensor in a charged Kiselev black hole. Phys. Dark Universe 2021, 31, 100750. [Google Scholar] [CrossRef]
- Mannheim, P.D.; Kazanas, D. Current status of conformal Weyl gravity. AIP Conf. Proc. 1991, 222, 541. [Google Scholar]
- Riegert, R.J. Birkhoff’s Theorem in Conformal Gravity. Phys. Rev. Lett. 1984, 53, 315. [Google Scholar] [CrossRef]
- Klemm, D. Topological black holes in Weyl conformal gravity. Class. Quant. Grav. 1998, 15, 3195. [Google Scholar] [CrossRef]
- Hao, X.; Yung, M.-H. Black hole evaporation in conformal (Weyl) gravity. Phys. Lett. B 2019, 793, 97. [Google Scholar]
- Daniels, R.D.; Shore, G.M. “Faster than light” photons and charged black holes. Nucl. Phys. B 1994, 425, 634. [Google Scholar] [CrossRef]
- Daniels, R.D.; Shore, G.M. “Faster than light” photons and rotating black holes. Phys. Lett. B 1996, 367, 75. [Google Scholar] [CrossRef]
- Shore, G.M. Faster than light photons in gravitational fields II.: Dispersion and vacuum polarisation. Nucl.Phys. B 2002, 633, 271. [Google Scholar] [CrossRef]
- Cai, R.G. Propagation of vacuum polarized photons in topological black hole spacetimes. Nucl. Phys. B 1998, 524, 639. [Google Scholar] [CrossRef]
- Cho, H.T. “Faster than light” photons in dilaton black hole spacetimes. Phys. Rev. D 1997, 56, 6416–6424. [Google Scholar] [CrossRef]
- Lorenci, V.A.D.; Klippert, R.; Novello, M.; Salim, J.M. Light propagation in non-linear electrodynamics. Phys. Lett. B 2000, 482, 134. [Google Scholar] [CrossRef]
- Breton, N. Geodesic structure of the Born–Infeld black hole. Class. Quantum Grav. 2002, 19, 601. [Google Scholar] [CrossRef]
- Virbhadra, K.S.; Ellis, G.F.R. Gravitational lensing by naked singularities. Phys. Rev. D 2002, 65, 103004. [Google Scholar] [CrossRef]
- Claudel, C.M.; Virbhadra, K.S.; Ellis, G.F.R. The geometry of photon surfaces. J. Math. Phys. 2001, 42, 818. [Google Scholar] [CrossRef]
- Gillessen, S.; Plewa, P.M.; Eisenhauer, F.; Sari, R.; Waisberg, I.; Habibi, M.; Pfuhl, O.; George, E.; Dexter, J.; von Fellenberg, S.; et al. An Update on Monitoring Stellar Orbits in the Galactic Center. Astrophys. J. 2017, 837, 30. [Google Scholar] [CrossRef]
- The Event Horizon Telescope Collaboration; Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.-K.; Ball, D.; Baloković, M.; Barrett, J.; et al. First M87 Event Horizon Telescope Results. VI. The Shadow and Mass of the Central Black Hole. Astrophys. J. Lett. 2019, 875, L6. [Google Scholar]
- Virbhadra, K.S.; Narasimha, D.; Chitre, S.M. Role of the scalar field in gravitational lensing. Astron. Astrophys. 1998, 337, 1. [Google Scholar]
- Bozza, V.; Luca, F.D.; Scarpetta, G.; Sereno, M. Analytic Kerr black hole lensing for equatorial observers in the strong deflection limit. Phys. Rev. D 2005, 72, 083003. [Google Scholar] [CrossRef]
- Bozza, V.; Luca, F.D.; Scarpetta, G. Kerr black hole lensing for generic observers in the strong deflection limit. Phys. Rev. D 2006, 74, 063001. [Google Scholar] [CrossRef]
- The Event Horizon Telescope Collaboration; Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.-K.; Ball, D.; Baloković, M.; Barrett, J.; et al. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. Lett. 2019, 875, L1. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abbas, G.; Övgün, A.; Mahmood, A.; Zubair, M. Strong Deflection Gravitational Lensing for the Photons Coupled to the Weyl Tensor in a Conformal Gravity Black Hole. Universe 2023, 9, 130. https://doi.org/10.3390/universe9030130
Abbas G, Övgün A, Mahmood A, Zubair M. Strong Deflection Gravitational Lensing for the Photons Coupled to the Weyl Tensor in a Conformal Gravity Black Hole. Universe. 2023; 9(3):130. https://doi.org/10.3390/universe9030130
Chicago/Turabian StyleAbbas, Ghulam, Ali Övgün, Asif Mahmood, and Muhammad Zubair. 2023. "Strong Deflection Gravitational Lensing for the Photons Coupled to the Weyl Tensor in a Conformal Gravity Black Hole" Universe 9, no. 3: 130. https://doi.org/10.3390/universe9030130
APA StyleAbbas, G., Övgün, A., Mahmood, A., & Zubair, M. (2023). Strong Deflection Gravitational Lensing for the Photons Coupled to the Weyl Tensor in a Conformal Gravity Black Hole. Universe, 9(3), 130. https://doi.org/10.3390/universe9030130






