Sp(2N) Lattice Gauge Theories and Extensions of the Standard Model of Particle Physics
Abstract
1. Introduction
2. Gauge Theory and Composite Dynamics
2.1. Fields, Symmetries, and Observables
2.2. Perturbative Considerations
2.3. Low-Energy EFT
Hidden Local Symmetry
2.4. Phenomenological Applications
2.4.1. Composite Higgs
2.4.2. Top Partial Compositeness
2.4.3. Composite Dark Matter
- Gauge theories with group, coupled to families of fundamental matter, might play a central role in SIMP model building, and it is hence a priority to study them on the lattice, both in the minimal realisation and its extensions.
- In dark matter models, the mass of the lightest spin-1 composite state lies between that of the PNGBs, and about twice of it. This is to be contrasted with the CHM context, where addressing the little hierarchy problem requires a scale separation between PNGBs and heavier states. This is diametrically opposite to TC, where gauge invariance forbids fermion masses. For lattice practitioners, this observation makes the quenched calculations into a reasonable approximation of the true dynamics in the phenomenologically relevant region of parameter space.
- Many variations of the mechanism yielding the SIMP dark matter relic abundance exist, including SIMP adaptations [162] of the freeze-in mechanism [330,331,332,333,334], and more are likely to be proposed in the near future. This observation suggests to carry out broad, unprejudiced explorations of the whole parameter space. As high precision measurements are not yet a priority, feasible investigation strategies for these explorations make reasonable use of available computing resources.
- The (percolation) temperature (or Hubble parameter ) at which the phase transition ends. The phase transition starts at the critical temperature .
- The inverse duration of the transition, measured by the bubble nucleation rate computed at , defined in terms of , the 3-dimensional action of the system:
- The parameter , determining the strength of the transition, depends on , the jump at the transition in trace of the stress-energy tensor , and the enthalpy in the high-T phase:
- The bubble wall speed —the efficiency parameter (the ratio of bulk kinetic energy to vacuum energy) depends on and [335].
- The number of degrees of freedom after the phase transition.
3. Lattice Gauge Theories
3.1. Lattice Action
3.2. Simulation Strategies
3.3. Scale Setting and Topology
3.4. Measurements: Two-Point Functions, Masses, and Decay Constants
3.5. Bulk Phase Structure and Finite Volume Effects
4. Numerical Investigation I: Pure
4.1. Glueballs and String Tension
4.2. Quenched Mesons
4.3. Topology
5. Numerical Investigations II: Dynamical Fermions in Sp(4)
5.1. Fundamental Fermions
5.2. Antisymmetric and Multiple Representation Dynamical Fermions
6. Summary and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| (as) | 2-index antisymmetric (representation) |
| (A)T | (Axial-)Tensor (operator, particle) |
| (A)V | (Axial-)Vector (operator, particle) |
| BZ | Banks-Zaks |
| CB | Chimera Baryon |
| CDM | Cold Dark Matter |
| CERN | European Organisation for Nuclear Research |
| CHM | Composite Higgs Model |
| ChRMT | Chiral Random Matrix Theory |
| CoDM | Composite Dark Matter |
| (E) | Euclidean (space-time) |
| EFT | Effective Field Theory |
| ETC | Extended Technicolor |
| EW(SB) | ElectroWeak (Symmetry Breaking) |
| (f) | fundamental (representation) |
| FCNC | Flavor Changing Neutral Current |
| FV | Finite Volume |
| GIM | Glashow-Iliopoulos-Maiani (mechanism) |
| GMOR | Gell-Mann-Oakes-Renner |
| GW | Gravitational Wave |
| HB | Heat Bath |
| (R)HMC | (Rational) Hybrid Monte Carlo |
| IR | Infra-Red |
| KSRF | Kawarabayashi-Suzuki-Riazuddin-Fayyazuddin (relation) |
| HLS | Hidden Local Symmetry |
| HPC | High Performance Computing |
| LHC | Large Hadron Collider |
| LISA | Laser Interferometer Space Antenna |
| LLR | Logarithmic Linear Relaxation |
| (M) | Minkowski (space-time) |
| MC | Monte Carlo |
| MD | Molecular Dynamics |
| NDA | Naive Dimensional Analysis |
| NLO | Next-to-Leading Order |
| OR | Over-Relaxation |
| PNGB | Pseudo-Nambu–Goldstone Boson |
| PS | Pseudoscalar (operator, particle) |
| QCD | Quantum Chromodynamics |
| RG(E) | Renormalisation Group (Equation) |
| S | Scalar (operator, particle) |
| SIMP | Strongly Interacting Massive Particle |
| SM | Standard Model (of particle physics) |
| (W)TC | (Walking) Technicolor |
| TPC | Top Partial Compositeness |
| URL | Uniform Resource Locator |
| UV | Ultra-Violet |
| VEV | Vacuum Expectation Value |
| WIMP | Weakly Interacting Massive Particle |
| WZW | Wess–Zumino–Witten (interaction term) |
| (W)PT | (Wilson) Chiral Perturbation Theory |
Appendix A. Groups, Algebras and Technical Details
Appendix B. Data and Analysis Code
- A potential reader might be interested in learning how to apply one of the techniques that we have used in our work to their own research. Some technical detail might have been omitted from the published paper for presentation reasons (length or readability constraints). The reader will benefit from direct inspection of the complete procedure we followed, which can be found in the associated code release.
- A reader, who seeks to independently replicate one of our findings, might discover some tension between the results of our and their own implementation of the analysis. Direct inspection of the software we used would enable this reader to identify at what point the divergence between the two processes occurs, avoiding protracted arguments on reproducibility—see, e.g., the case described in Ref. [383].
- Lattice studies frequently generate more data than what can be feasible to fully exploit for a single group of researchers. The interested reader may perform their own, additional analysis on our data, with alternative methodologies, without the need to regenerate the data from scratch (which might require a significant investment of computer time). For example, more advanced fitting algorithms may give more detailed or precise results, or gain access to additional observables.
- Phenomenologists and other researchers who look to build on the numerical results of lattice computations may import the data from our work directly into their computational environment, without the need to resort to copying and pasting from published tables (or reading numbers off published plots). By doing so, one reduces the risk of introducing additional uncertainties, and avoids one source of potential human error.
Appendix B.1. Data Release
- Raw data, such as correlation functions and gradient flow histories, are released in their native formats as generated by the HiRep code [345,347], in accordance with the principle of “keeping raw data raw” [385]. By doing so, we reduce the chances of human error in transcription of data formats, while increasing the opportunity to detect such type of errors in a subsequent validation process.
- Reformatted raw data, obtained by taking the output files of raw data, condense the salient information in tables stored in HDF5 format [386]. Commonly available library functions can read the data in this format, so that one does not need to write a parser to interpret the bespoke formats generated by HiRep. Currently this information is generated from the raw log files as part of the analysis process.
- Metadata are collections of parameter values that identify the analysis performed. They include physical parameters, such as the lattice coupling , algorithmic ones, such as the number of trajectories between successive configurations, and analysis ones, such as the start and end of plateaux in effective mass plots. The metadata we publish are primarily those which enable the analysis.
- Final results, also presented in tabular form in the corresponding publications, are released in CSV format; they are typically compact enough that using a denser format such as HDF5 would not yield a significant benefit (in file size, for example), and the use of CSV files makes the data accessible without specialist software tools.
Appendix B.2. Analysis Code Release
- 1.
- Dependencies between steps are automatically managed. The ordering of steps is automatically decided, rather than requiring the user’s input.
- 2.
- Steps can automatically be run in parallel, with Make ensuring that no step runs before its prerequisites are complete. This allows the analysis process to scale with the available compute capacity.
- 3.
- The workflow can be interrupted partway and resumed subsequently, without the need to re-run previously completed steps.
- 4.
- Make is able to re-run only the steps of the analysis that depend on specific files, if data are updated, thereby expediting the debugging cycle.
Appendix B.3. Closing Remarks
| 1 | We borrow the terminology and nomenclature associated with mesons and baryons from QCD, when referring to the analogous composite states in new strongly coupled gauge theories. |
| 2 | In the presence of fermions transforming in different representations of the gauge group, the triangle anomaly gives mass to only one linear combination of the PNGBs associated with the breaking of the chiral symmetries acting on the different flavour species. The phenomenological implications are discussed for example in Ref. [47]. |
| 3 | |
| 4 | We denote the set of PNGBs of as , for consistency with the conventional notation of , as there are three inequivalent representations with 20 degrees of freedom, usually denoted as 20, , and [266]. |
| 5 | Although only integer values of are physically meaningful, is treated as a continuous variable. An alternative argument could be made by taking the large- (Veneziano) limit while holding fixed the continuous ratio . |
| 6 | |
| 7 | This critical condition should agree with , yet it gives rise to different results at finite order in the expansion. This critical condition reproduces the value of the critical coupling obtained from the Schwinger–Dyson analysis in the ladder approximation [296], and furthermore has a square-root singularity with respect to when the IR and UV fixed point merge [295]. |
| 8 | By preserving the whole , the model preserves custodial symmetry, suppressing new physics contributions to the T parameter [306]. |
| 9 | The important difference between CHMs and TC is that , so that can naturally be larger than the TeV scale. |
| 10 | In this work we use “reproduce” to mean “perform the same analysis on the same data and obtain the same result”, and “replicate” to mean “repeat the same or a similar analysis on freshly-obtained data and obtain compatible results”, as suggested by the Turing Way [382]. |
References
- Holland, K.; Pepe, M.; Wiese, U.J. The Deconfinement phase transition of Sp(2) and Sp(3) Yang-Mills theories in (2+1)-dimensions and (3+1)-dimensions. Nucl. Phys. B 2004, 694, 35–58. [Google Scholar] [CrossRef]
- Bennett, E.; Hong, D.K.; Lee, J.W.; Lin, C.-J.D.; Lucini, B.; Piai, M.; Vadacchino, D. Sp(4) gauge theory on the lattice: Towards SU(4)/Sp(4) composite Higgs (and beyond). J. High Energy Phys. 2018, 1803, 185. [Google Scholar] [CrossRef]
- Lee, J.W.; Bennett, E.; Hong, D.K.; Lin, C.J.D.; Lucini, B.; Piai, M.; Vadacchino, D. Progress in the lattice simulations of Sp(2N) gauge theories. PoS Lattice 2018, 2018, 192. [Google Scholar] [CrossRef]
- Bennett, E.; Hong, D.K.; Lee, J.W.; Lin, C.J.D.; Lucini, B.; Piai, M.; Vadacchino, D. Sp(4) gauge theories on the lattice: Nf = 2 dynamical fundamental fermions. J. High Energy Phys. 2019, 12, 053. [Google Scholar] [CrossRef]
- Bennett, E.; Hong, D.K.; Lee, J.W.; Lin, C.J.D.; Lucini, B.; Mesiti, M.; Piai, M.; Rantaharju, J.; Vadacchino, D. Sp(4) gauge theories on the lattice: Quenched fundamental and antisymmetric fermions. Phys. Rev. D 2020, 101, 074516. [Google Scholar] [CrossRef]
- Bennett, E.; Holligan, J.; Hong, D.K.; Lee, J.W.; Lin, C.J.D.; Lucini, B.; Piai, M.; Vadacchino, D. Color dependence of tensor and scalar glueball masses in Yang-Mills theories. Phys. Rev. D 2020, 102, 011501. [Google Scholar] [CrossRef]
- Bennett, E.; Holligan, J.; Hong, D.K.; Lee, J.W.; Lin, C.J.D.; Lucini, B.; Piai, M.; Vadacchino, D. Glueballs and strings in Sp(2N) Yang-Mills theories. Phys. Rev. D 2021, 103, 054509. [Google Scholar] [CrossRef]
- Lucini, B.; Bennett, E.; Holligan, J.; Hong, D.K.; Hsiao, H.; Lee, J.W.; Lin, C.J.D.; Mesiti, M.; Piai, M.; Vadacchino, D. Sp(4) gauge theories and beyond the standard model physics. EPJ Web Conf. 2022, 258, 08003. [Google Scholar] [CrossRef]
- Bennett, E.; Holligan, J.; Hong, D.K.; Hsiao, H.; Lee, J.W.; Lin, C.J.D.; Lucini, B.; Mesiti, M.; Piai, M.; Vadacchino, D. Progress in Sp(2N) lattice gauge theories. PoS Lattice 2022, 2021, 396. [Google Scholar] [CrossRef]
- Bennett, E.; Hong, D.K.; Hsiao, H.; Lee, J.W.; Lin, C.J.D.; Lucini, B.; Mesiti, M.; Piai, M.; Vadacchino, D. Lattice studies of the Sp(4) gauge theory with two fundamental and three antisymmetric Dirac fermions. Phys. Rev. D 2022, 106, 014501. [Google Scholar] [CrossRef]
- Bennett, E.; Hong, D.K.; Lee, J.W.; Lin, C.J.D.; Lucini, B.; Piai, M.; Vadacchino, D. Color dependence of the topological susceptibility in Yang-Mills theories. Phys. Lett. B 2022, 835, 137504. [Google Scholar] [CrossRef]
- Bennett, E.; Hong, D.K.; Lee, J.W.; Lin, C.J.D.; Lucini, B.; Piai, M.; Vadacchino, D. Sp(2N) Yang-Mills theories on the lattice: Scale setting and topology. Phys. Rev. D 2022, 106, 094503. [Google Scholar] [CrossRef]
- Bennett, E.; Hong, D.K.; Hsiao, H.; Lee, J.W.; Lin, C.J.D.; Lucini, B.; Piai, M.; Vadacchino, D. Sp(4) theories on the lattice: Dynamical antisymmetric fermions. in preparation.
- Lee, J.W.; Bennett, E.; Hong, D.K.; Hsiao, H.; Lin, C.J.D.; Lucini, B.; Piai, M.; Vadacchino, D. Spectroscopy of Sp(4) lattice gauge theory with nf = 3 antisymmetric fermions. PoS Lattice 2023, 2022, 214. [Google Scholar] [CrossRef]
- Hsiao, H.; Bennett, E.; Hong, D.K.; Lee, J.W.; Lin, C.J.D.; Lucini, B.; Piai, M.; Vadacchino, D. Spectroscopy of chimera baryons in a Sp(4) lattice gauge theory. PoS Lattice 2023, 2022, 211. [Google Scholar] [CrossRef]
- Maas, A.; Zierler, F. Strong isospin breaking in Sp(4) gauge theory. arXiv 2021, arXiv:2109.14377. [Google Scholar]
- Zierler, F.; Maas, A. Sp(4) SIMP Dark Matter on the Lattice. PoS 2021, 397, 162. [Google Scholar] [CrossRef]
- Kulkarni, S.; Maas, A.; Mee, S.; Nikolic, M.; Pradler, J.; Zierler, F. Low-energy effective description of dark Sp(4) theories. arXiv 2023, arXiv:2202.05191. [Google Scholar] [CrossRef]
- Peskin, M.E. The Alignment of the Vacuum in Theories of Technicolor. Nucl. Phys. B 1980, 175, 197–233. [Google Scholar] [CrossRef]
- Aad, G. et al. [ATLAS Collaboration] Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. B 2012, 716, 1. [Google Scholar] [CrossRef]
- Chatrchyan, S. et al. [CMS Collaboration]. Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC. Phys. Lett. B 2012, 716, 30. [Google Scholar] [CrossRef]
- Kaplan, D.B.; Georgi, H. SU(2) x U(1) Breaking by Vacuum Misalignment. Phys. Lett. B 1984, 136, 183–186. [Google Scholar] [CrossRef]
- Georgi, H.; Kaplan, D.B. Composite Higgs and Custodial SU(2). Phys. Lett. 1984, 145B, 216. [Google Scholar] [CrossRef]
- Dugan, M.J.; Georgi, H.; Kaplan, D.B. Anatomy of a Composite Higgs Model. Nucl. Phys. B 1985, 254, 299. [Google Scholar] [CrossRef]
- Panico, G.; Wulzer, A. The Composite Nambu-Goldstone Higgs. Lect. Notes Phys. 2016, 913, 1. [Google Scholar] [CrossRef]
- Witzel, O. Review on Composite Higgs Models. PoS Lattice 2019, 2018, 6. [Google Scholar] [CrossRef]
- Cacciapaglia, G.; Pica, C.; Sannino, F. Fundamental Composite Dynamics: A Review. Phys. Rep. 2020, 877, 1–70. [Google Scholar] [CrossRef]
- Ferretti, G.; Karateev, D. Fermionic UV completions of Composite Higgs models. J. High Energy Phys. 2014, 3, 77. [Google Scholar] [CrossRef]
- Ferretti, G. Gauge theories of Partial Compositeness: Scenarios for Run-II of the LHC. J. High Energy Phys. 2016, 6, 107. [Google Scholar] [CrossRef]
- Cacciapaglia, G.; Ferretti, G.; Flacke, T.; Serôdio, H. Light scalars in composite Higgs models. Front. Phys. 2019, 7, 22. [Google Scholar] [CrossRef]
- Katz, E.; Nelson, A.E.; Walker, D.G.E. The Intermediate Higgs. J. High Energy Phys. 2005, 508, 74. [Google Scholar] [CrossRef]
- Barbieri, R.; Bellazzini, B.; Rychkov, V.S.; Varagnolo, A. The Higgs boson from an extended symmetry. Phys. Rev. D 2007, 76, 115008. [Google Scholar] [CrossRef]
- Lodone, P. Vector-like quarks in a composite Higgs model. J. High Energy Phys. 2008, 812, 29. [Google Scholar] [CrossRef]
- Gripaios, B.; Pomarol, A.; Riva, F.; Serra, J. Beyond the Minimal Composite Higgs Model. J. High Energy Phys. 2009, 904, 70. [Google Scholar] [CrossRef]
- Mrazek, J.; Pomarol, A.; Rattazzi, R.; Redi, M.; Serra, J.; Wulzer, A. The Other Natural Two Higgs Doublet Model. Nucl. Phys. B 2011, 853, 1–48. [Google Scholar] [CrossRef]
- Marzocca, D.; Serone, M.; Shu, J. General Composite Higgs Models. J. High Energy Phys. 2012, 1208, 13. [Google Scholar] [CrossRef]
- Grojean, C.; Matsedonskyi, O.; Panico, G. Light top partners and precision physics. J. High Energy Phys. 2013, 1310, 160. [Google Scholar] [CrossRef]
- Cacciapaglia, G.; Sannino, F. Fundamental Composite (Goldstone) Higgs Dynamics. J. High Energy Phys. 2014, 1404, 111. [Google Scholar] [CrossRef]
- Ferretti, G. UV Completions of Partial Compositeness: The Case for a SU(4) Gauge Group. J. High Energy Phys. 2014, 6, 142. [Google Scholar] [CrossRef]
- Arbey, A.; Cacciapaglia, G.; Cai, H.; Deandrea, A.; Corre, S.L.; Sannino, F. Fundamental Composite Electroweak Dynamics: Status at the LHC. Phys. Rev. D 2017, 95, 015028. [Google Scholar] [CrossRef]
- Cacciapaglia, G.; Cai, H.; Deandrea, A.; Flacke, T.; Lee, S.J.; Parolini, A. Composite scalars at the LHC: The Higgs, the Sextet and the Octet. J. High Energy Phys. 2015, 1511, 201. [Google Scholar] [CrossRef]
- Feruglio, F.; Gavela, B.; Kanshin, K.; Machado, P.A.N.; Rigolin, S.; Saa, S. The minimal linear sigma model for the Goldstone Higgs. J. High Energy Phys. 2016, 1606, 38. [Google Scholar] [CrossRef]
- DeGrand, T.; Golterman, M.; Neil, E.T.; Shamir, Y. One-loop Chiral Perturbation Theory with two fermion representations. Phys. Rev. D 2016, 94, 025020. [Google Scholar] [CrossRef]
- Fichet, S.; Von Gersdorff, G.; Pontòn, E.; Rosenfeld, R. The Excitation of the Global Symmetry-Breaking Vacuum in Composite Higgs Models. J. High Energy Phys. 2016, 1609, 158. [Google Scholar] [CrossRef]
- Galloway, J.; Kagan, A.L.; Martin, A. A UV complete partially composite-pNGB Higgs. Phys. Rev. D 2017, 95, 035038. [Google Scholar] [CrossRef]
- Agugliaro, A.; Antipin, O.; Becciolini, D.; Curtis, S.D.; Redi, M. UV complete composite Higgs models. Phys. Rev. D 2017, 95, 035019. [Google Scholar] [CrossRef]
- Belyaev, A.; Cacciapaglia, G.; Cai, H.; Ferretti, G.; Flacke, T.; Parolini, A.; Serodio, H. Di-boson signatures as Standard Candles for Partial Compositeness. J. High Energy Phys. 2017, 1, 94. [Google Scholar] [CrossRef]
- Csaki, C.; Ma, T.; Shu, J. Maximally Symmetric Composite Higgs Models. Phys. Rev. Lett. 2017, 119, 131803. [Google Scholar] [CrossRef]
- Chala, M.; Durieux, G.; Grojean, C.; De Lima, L.; Matsedonskyi, O. Minimally extended SILH. J. High Energy Phys. 2017, 1706, 88. [Google Scholar] [CrossRef]
- Golterman, M.; Shamir, Y. Effective potential in ultraviolet completions for composite Higgs models. Phys. Rev. D 2018, 97, 095005. [Google Scholar] [CrossRef]
- Csaki, C.; Ma, T.; Shu, J. Trigonometric Parity for Composite Higgs Models. Phys. Rev. Lett. 2018, 121, 231801. [Google Scholar] [CrossRef] [PubMed]
- Alanne, T.; Franzosi, D.B.; Frandsen, M.T. A partially composite Goldstone Higgs. Phys. Rev. D 2017, 96, 095012. [Google Scholar] [CrossRef]
- Alanne, T.; Franzosi, D.B.; Frandsen, M.T.; Kristensen, M.L.A.; Meroni, A.; Rosenlyst, M. Partially composite Higgs models: Phenomenology and RG analysis. J. High Energy Phys. 2018, 1801, 51. [Google Scholar] [CrossRef]
- Sannino, F.; Stangl, P.; Straub, D.M.; Thomsen, A.E. Flavor Physics and Flavor Anomalies in Minimal Fundamental Partial Compositeness. Phys. Rev. D 2018, 97, 115046. [Google Scholar] [CrossRef]
- Alanne, T.; Bizot, N.; Cacciapaglia, G.; Sannino, F. Classification of NLO operators for composite Higgs models. Phys Rev. D 2018, 97, 075028. [Google Scholar] [CrossRef]
- Bizot, N.; Cacciapaglia, G.; Flacke, T. Common exotic decays of top partners. J. High Energy Phys. 2018, 1806, 65. [Google Scholar] [CrossRef]
- Cai, C.; Cacciapaglia, G.; Zhang, H.H. Vacuum alignment in a composite 2HDM. J. High Energy Phys. 2019, 1901, 130. [Google Scholar] [CrossRef]
- Agugliaro, A.; Cacciapaglia, G.; Deandrea, A.; Curtis, S.D. Vacuum misalignment and pattern of scalar masses in the SU(5)/SO(5) composite Higgs model. J. High Energy Phys. 2019, 1902, 89. [Google Scholar] [CrossRef]
- Cacciapaglia, G.; Ma, T.; Vatani, S.; Wu, Y. Towards a fundamental safe theory of composite Higgs and Dark Matter. Eur. Phys. J. C 2020, 80, 1088. [Google Scholar] [CrossRef]
- Gertov, H.; Nelson, A.E.; Perko, A.; Walker, D.G.E. Lattice-Friendly Gauge Completion of a Composite Higgs with Top Partners. J. High Energy Phys. 2019, 1902, 181. [Google Scholar] [CrossRef]
- Ayyar, V.; Golterman, M.F.; Hackett, D.C.; Jay, W.; Neil, E.T.; Shamir, Y.; Svetitsky, B. Radiative Contribution to the Composite-Higgs Potential in a Two-Representation Lattice Model. Phys. Rev. D 2019, 99, 094504. [Google Scholar] [CrossRef]
- Cacciapaglia, G.; Cai, H.; Deandrea, A.; Kushwaha, A. Composite Higgs and Dark Matter Model in SU(6)/SO(6). J. High Energy Phys. 2019, 1910, 35. [Google Scholar] [CrossRef]
- Franzosi, D.B.; Ferretti, G. Anomalous dimensions of potential top-partners. SciPost Phys. 2019, 7, 27. [Google Scholar] [CrossRef]
- Cacciapaglia, G.; Vatani, S.; Zhang, C. Composite Higgs Meets Planck Scale: Partial Compositeness from Partial Unification. Phys. Lett. B 2021, 815, 136177. [Google Scholar] [CrossRef]
- Cacciapaglia, G.; Deandrea, A.; Flacke, T.; Iyer, A.M. Gluon-Photon Signatures for color octet at the LHC (and beyond). J. High Energy Phys. 2020, 5, 27. [Google Scholar] [CrossRef]
- Dong, Z.Y.; Guan, C.S.; Ma, T.; Shu, J.; Xue, X. UV completed composite Higgs model with heavy composite partners. Phys. Rev. D 2021, 104, 035013. [Google Scholar] [CrossRef]
- Cacciapaglia, G.; Flacke, T.; Kunkel, M.; Porod, W. Phenomenology of unusual top partners in composite Higgs models. arXiv 2022, arXiv:2112.00019. [Google Scholar] [CrossRef]
- Banerjee, A.; Franzosi, D.B.; Ferretti, G. Modelling vector-like quarks in partial compositeness framework. arXiv 2022, arXiv:2202.00037. [Google Scholar] [CrossRef]
- Contino, R.; Nomura, Y.; Pomarol, A. Higgs as a holographic pseudoGoldstone boson. Nucl. Phys. B 2003, 671, 148–174. [Google Scholar] [CrossRef]
- Agashe, K.; Contino, R.; Pomarol, A. The Minimal composite Higgs model. Nucl. Phys. B 2005, 719, 165. [Google Scholar] [CrossRef]
- Agashe, K.; Contino, R. The Minimal composite Higgs model and electroweak precision tests. Nucl. Phys. B 2006, 742, 59–85. [Google Scholar] [CrossRef]
- Agashe, K.; Contino, R.; Rold, L.D.; Pomarol, A. A custodial symmetry for Zb. Phys. Lett. B 2006, 641, 62–66. [Google Scholar] [CrossRef]
- Contino, R.; Rold, L.D.; Pomarol, A. Light custodians in natural composite Higgs models. Phys. Rev. D 2007, 75, 055014. [Google Scholar] [CrossRef]
- Falkowski, A.; Perez-Victoria, M. Electroweak Breaking on a Soft Wall. J. High Energy Phys. 2008, 12, 107. [Google Scholar] [CrossRef]
- Contino, R. The Higgs as a Composite Nambu-Goldstone Boson. arXiv 2015. [Google Scholar] [CrossRef]
- Contino, R.; Marzocca, D.; Pappadopulo, D.; Rattazzi, R. On the effect of resonances in composite Higgs phenomenology. J. High Energy Phys. 2011, 10, 81. [Google Scholar] [CrossRef]
- Elander, D.; Fatemiabhari, A.; Piai, M. Towards composite Higgs: Minimal coset from a regular bottom-up holographic model. arXiv 2023, arXiv:2303.00541. [Google Scholar]
- Kaplan, D.B. Flavor at SSC energies: A New mechanism for dynamically generated fermion masses. Nucl. Phys. B 1991, 365, 259–278. [Google Scholar] [CrossRef]
- Grossman, Y.; Neubert, M. Neutrino masses and mixings in nonfactorizable geometry. Phys. Lett. B 2000, 474, 361–371. [Google Scholar] [CrossRef]
- Gherghetta, T.; Pomarol, A. Bulk fields and supersymmetry in a slice of AdS. Nucl. Phys. B 2000, 586, 141–162. [Google Scholar] [CrossRef]
- Chacko, Z.; Mishra, R.K. Effective Theory of a Light Dilaton. Phys. Rev. D 2013, 87, 115006. [Google Scholar] [CrossRef]
- Hietanen, A.; Lewis, R.; Pica, C.; Sannino, F. Fundamental Composite Higgs Dynamics on the Lattice: SU(2) with Two Flavors. J. High Energy Phys. 2014, 1407, 116. [Google Scholar] [CrossRef]
- Detmold, W.; McCullough, M.; Pochinsky, A. Dark nuclei. II. Nuclear spectroscopy in two-color QCD. Phys. Rev. D 2014, 90, 114506. [Google Scholar] [CrossRef]
- Arthur, R.; Drach, V.; Hansen, M.; Hietanen, A.; Pica, C.; Sannino, F. SU(2) gauge theory with two fundamental flavors: A minimal template for model building. Phys. Rev. D 2016, 94, 094507. [Google Scholar] [CrossRef]
- Arthur, R.; Drach, V.; Hietanen, A.; Pica, C.; Sannino, F. SU(2) Gauge Theory with Two Fundamental Flavours: Scalar and Pseudoscalar Spectrum. arXiv 2016, arXiv:1607.06654. [Google Scholar]
- Pica, C.; Drach, V.; Hansen, M.; Sannino, F. Composite Higgs Dynamics on the Lattice. EPJ Web Conf. 2017, 137, 10005. [Google Scholar] [CrossRef]
- Lee, J.W.; Lucini, B.; Piai, M. Symmetry restoration at high-temperature in two-color and two-flavor lattice gauge theories. J. High Energy Phys. 2017, 1704, 36. [Google Scholar] [CrossRef]
- Drach, V.; Janowski, T.; Pica, C. Update on SU(2) gauge theory with NF = 2 fundamental flavours. EPJ Web Conf. 2018, 175, 08020. [Google Scholar] [CrossRef]
- Drach, V.; Janowski, T.; Pica, C.; Prelovsek, S. Scattering of Goldstone Bosons and resonance production in a Composite Higgs model on the lattice. J. High Energy Phys. 2021, 4, 117. [Google Scholar] [CrossRef]
- Drach, V.; Fritzsch, P.; Rago, A.; Romero-López, F. Singlet channel scattering in a Composite Higgs model on the lattice. arXiv 2022, arXiv:2107.09974. [Google Scholar] [CrossRef]
- Ayyar, V.; DeGrand, T.; Golterman, M.; Hackett, D.C.; Jay, W.I.; Neil, E.T.; Shamir, Y.; Svetitsky, B. Spectroscopy of SU(4) composite Higgs theory with two distinct fermion representations. Phys. Rev. D 2018, 97, 074505. [Google Scholar] [CrossRef]
- Ayyar, V.; Degrand, T.; Hackett, D.C.; Jay, W.I.; Neil, E.T.; Shamir, Y.; Svetitsky, B. Baryon spectrum of SU(4) composite Higgs theory with two distinct fermion representations. Phys. Rev. D 2018, 97, 114505. [Google Scholar] [CrossRef]
- Ayyar, V.; DeGrand, T.; Hackett, D.C.; Jay, W.I.; Neil, E.T.; Shamir, Y.; Svetitsky, B. Finite-temperature phase structure of SU(4) gauge theory with multiple fermion representations. Phys. Rev. D 2018, 97, 114502. [Google Scholar] [CrossRef]
- Ayyar, V.; DeGrand, T.; Hackett, D.C.; Jay, W.I.; Neil, E.T.; Shamir, Y.; Svetitsky, B. Partial compositeness and baryon matrix elements on the lattice. Phys. Rev. D 2019, 99, 094502. [Google Scholar] [CrossRef]
- Cossu, G.; Debbio, L.D.; Panero, M.; Preti, D. Strong dynamics with matter in multiple representations: SU(4) gauge theory with fundamental and sextet fermions. Eur. Phys. J. C 2019, 79, 638. [Google Scholar] [CrossRef]
- Shamir, Y.; Golterman, M.; Jay, W.I.; Neil, E.T.; Svetitsky, B. S parameter from a prototype composite-Higgs model. arXiv 2021, arXiv:2110.05198. [Google Scholar]
- Debbio, L.D.; Lupo, A.; Panero, M.; Tantalo, N. Spectral reconstruction in SU(4) gauge theory with fermions in multiple representations. arXiv 2021, arXiv:2112.01158. [Google Scholar]
- Vecchi, L. A dangerous irrelevant UV-completion of the composite Higgs. J. High Energy Phys. 2017, 2, 94. [Google Scholar] [CrossRef]
- Coleman, S. Aspects of Symmetry: Selected Erice Lectures; Cambridge University Press: Cambridge, MA, USA, 1985. [Google Scholar] [CrossRef]
- Migdal, A.A.; Shifman, M.A. Dilaton Effective Lagrangian in Gluodynamics. Phys. Lett. B 1982, 114, 445. [Google Scholar] [CrossRef]
- Leung, C.N.; Love, S.T.; Bardeen, W.A. Spontaneous Symmetry Breaking in Scale Invariant Quantum Electrodynamics. Nucl. Phys. B 1986, 273, 649. [Google Scholar] [CrossRef]
- Bardeen, W.A.; Leung, C.N.; Love, S.T. The Dilaton and Chiral Symmetry Breaking. Phys. Rev. Lett. 1986, 56, 1230. [Google Scholar] [CrossRef] [PubMed]
- Yamawaki, K.; Bando, M.; Matumoto, K.I. Scale Invariant Technicolor Model and a Technidilaton. Phys. Rev. Lett. 1986, 56, 1335. [Google Scholar] [CrossRef] [PubMed]
- Goldberger, W.D.; Grinstein, B.; Skiba, W. Distinguishing the Higgs boson from the dilaton at the Large Hadron Collider. Phys. Phys. Rev. Lett. 2008, 100, 111802. [Google Scholar] [CrossRef]
- Matsuzaki, S.; Yamawaki, K. Dilaton Chiral Perturbation Theory: Determining the Mass and Decay Constant of the Technidilaton on the Lattice. Phys. Rev. Lett. 2014, 113, 082002. [Google Scholar] [CrossRef] [PubMed]
- Golterman, M.; Shamir, Y. Low-energy effective action for pions and a dilatonic meson. Phys. Rev. D 2016, 94, 054502. [Google Scholar] [CrossRef]
- Kasai, A.; Okumura, K.i.; Suzuki, H. A dilaton-pion mass relation. arXiv 2016, arXiv:1609.02264. [Google Scholar]
- Hansen, M.; Langaeble, K.; Sannino, F. Extending Chiral Perturbation Theory with an Isosinglet Scalar. Phys. Rev. D 2017, 95, 036005. [Google Scholar] [CrossRef]
- Golterman, M.; Shamir, Y. Effective pion mass term and the trace anomaly. Phys. Rev. D 2017, 95, 016003. [Google Scholar] [CrossRef]
- Appelquist, T.; Ingoldby, J.; Piai, M. Dilaton EFT Framework For Lattice Data. J. High Energy Phys. 2017, 1707, 35. [Google Scholar] [CrossRef]
- Appelquist, T.; Ingoldby, J.; Piai, M. Analysis of a Dilaton EFT for Lattice Data. J. High Energy Phys. 2018, 1803, 39. [Google Scholar] [CrossRef]
- Golterman, M.; Shamir, Y. Large-mass regime of the dilaton-pion low-energy effective theory. Phys. Rev. D 2018, 98, 056025. [Google Scholar] [CrossRef]
- Cata, O.; Muller, C. Chiral effective theories with a light scalar at one loop. Nucl. Phys. B 2020, 952, 114938. [Google Scholar] [CrossRef]
- Appelquist, T.; Ingoldby, J.; Piai, M. Dilaton potential and lattice data. Phys. Rev. D 2020, 101, 075025. [Google Scholar] [CrossRef]
- Golterman, M.; Neil, E.T.; Shamir, Y. Application of dilaton chiral perturbation theory to Nf = 8, SU(3) spectral data. Phys. Rev. D 2020, 102, 034515. [Google Scholar] [CrossRef]
- Golterman, M.; Shamir, Y. Explorations beyond dilaton chiral perturbation theory in the eight-flavor SU(3) gauge theory. Phys. Rev. D 2020, 102, 114507. [Google Scholar] [CrossRef]
- Appelquist, T.; Ingoldby, J.; Piai, M. Dilaton Effective Field Theory. Universe 2023, 9, 10. [Google Scholar] [CrossRef]
- Appelquist, T.; Ingoldby, J.; Piai, M. Nearly Conformal Composite Higgs Model. Phys. Phys. Rev. Lett. 2021, 126, 191804. [Google Scholar] [CrossRef]
- Appelquist, T.; Ingoldby, J.; Piai, M. Composite two-Higgs doublet model from dilaton effective field theory. arXiv 2022, arXiv:2205.03320. [Google Scholar] [CrossRef]
- Ma, T.; Cacciapaglia, G. Fundamental Composite 2HDM: SU(N) with 4 flavours. J. High Energy Phys. 2016, 3, 211. [Google Scholar] [CrossRef]
- Franzosi, D.B.; Cacciapaglia, G.; Deandrea, A. Sigma-assisted low scale composite Goldstone–Higgs. Eur. Phys. J. C 2020, 80, 28. [Google Scholar] [CrossRef]
- Aoki, Y. et al. [LatKMI Collaboration]. Light composite scalar in eight-flavor QCD on the lattice. Phys. Rev. D 2014, 89, 111502. [Google Scholar] [CrossRef]
- Aoki, Y. et al. [LatKMI Collaboration]. Light flavor-singlet scalars and walking signals in Nf = 8 QCD on the lattice. Phys. Rev. D 2017, 96, 014508. [Google Scholar] [CrossRef]
- Appelquist, T.; Brower, R.C.; Fleming, G.T.; Hasenfratz, A.; Jin, X.Y.; Kiskis, J.; Neil, E.T.; Osborn, J.C.; Rebbi, C.; Rinaldi, E.; et al. Strongly interacting dynamics and the search for new physics at the LHC. Phys. Rev. D 2016, 93, 114514. [Google Scholar] [CrossRef]
- Gasbarro, A.D.; Fleming, G.T. Examining the Low Energy Dynamics of Walking Gauge Theory. PoS Lattice 2017, 2016, 242. [Google Scholar] [CrossRef]
- Appelquist, T. et al. [Lattice Strong Dynamics Collaboration]. Nonperturbative investigations of SU(3) gauge theory with eight dynamical flavors. Phys. Rev. D 2019, 99, 014509. [Google Scholar] [CrossRef]
- Barnard, J.; Gherghetta, T.; Ray, T.S. UV descriptions of composite Higgs models without elementary scalars. J. High Energy Phys. 2014, 1402, 2. [Google Scholar] [CrossRef]
- Bizot, N.; Frigerio, M.; Knecht, M.; Kneur, J.L. Nonperturbative analysis of the spectrum of meson resonances in an ultraviolet-complete composite-Higgs model. Phys. Rev. D 2017, 95, 075006. [Google Scholar] [CrossRef]
- Maldacena, J.M. The Large N limit of superconformal field theories and supergravity. Int. J. Theor. Phys. 1999, 38, 1113. [Google Scholar] [CrossRef]
- Gubser, S.S.; Klebanov, I.R.; Polyakov, A.M. Gauge theory correlators from noncritical string theory. Phys. Lett. B 1998, 428, 105. [Google Scholar] [CrossRef]
- Witten, E. Anti-de Sitter space and holography. Adv. Theor. Math. Phys. 1998, 2, 253. [Google Scholar] [CrossRef]
- Aharony, O.; Gubser, S.S.; Maldacena, J.M.; Ooguri, H.; Oz, Y. Large N field theories, string theory and gravity. Phys. Rep. 2000, 323, 183. [Google Scholar] [CrossRef]
- Erdmenger, J.; Evans, N.; Porod, W.; Rigatos, K.S. Gauge/gravity dynamics for composite Higgs models and the top mass. Phys. Phys. Rev. Lett. 2021, 126, 071602. [Google Scholar] [CrossRef]
- Erdmenger, J.; Evans, N.; Porod, W.; Rigatos, K.S. Gauge/gravity dual dynamics for the strongly coupled sector of composite Higgs models. J. High Energy Phys. 2021, 2, 58. [Google Scholar] [CrossRef]
- Elander, D.; Frigerio, M.; Knecht, M.; Kneur, J.L. Holographic models of composite Higgs in the Veneziano limit. Part I. Bosonic sector. J. High Energy Phys. 2021, 3, 182. [Google Scholar] [CrossRef]
- Elander, D.; Frigerio, M.; Knecht, M.; Kneur, J.L. Holographic models of composite Higgs in the Veneziano limit: 2. Fermionic sector. arXiv 2022, arXiv:2112.14740. [Google Scholar] [CrossRef]
- Elander, D.; Piai, M. Towards top-down holographic composite Higgs: Minimal coset from maximal supergravity. J. High Energy Phys. 2022, 3, 49. [Google Scholar] [CrossRef]
- Strassler, M.J.; Zurek, K.M. Echoes of a hidden valley at hadron colliders. Phys. Lett. B 2007, 651, 374–379. [Google Scholar] [CrossRef]
- Cheung, K.; Yuan, T.C. Hidden fermion as milli-charged dark matter in Stueckelberg Z- prime model. J. High Energy Phys. 2007, 3, 120. [Google Scholar] [CrossRef]
- Hambye, T. Hidden vector dark matter. J. High Energy Phys. 2009, 1, 28. [Google Scholar] [CrossRef]
- Feng, J.L.; Kaplinghat, M.; Tu, H.; Yu, H.B. Hidden Charged Dark Matter. J. Cosmol. Astropart. Phys. 2009, 7, 4. [Google Scholar] [CrossRef]
- Cohen, T.; Phalen, D.J.; Pierce, A.; Zurek, K.M. Asymmetric Dark Matter from a GeV Hidden Sector. Phys. Rev. D 2010, 82, 056001. [Google Scholar] [CrossRef]
- Foot, R.; Vagnozzi, S. Dissipative hidden sector dark matter. Phys. Rev. D 2015, 91, 023512. [Google Scholar] [CrossRef]
- Bertone, G.; Hooper, D. History of dark matter. Rev. Mod. Phys. 2018, 90, 045002. [Google Scholar] [CrossRef]
- Nobile, E.D.; Kouvaris, C.; Sannino, F. Interfering Composite Asymmetric Dark Matter for DAMA and CoGeNT. Phys. Rev. D 2011, 84, 027301. [Google Scholar] [CrossRef]
- Hietanen, A.; Lewis, R.; Pica, C.; Sannino, F. Composite Goldstone Dark Matter: Experimental Predictions from the Lattice. J. High Energy Phys. 2014, 12, 130. [Google Scholar] [CrossRef]
- Cline, J.M.; Huang, W.; Moore, G.D. Challenges for models with composite states. Phys. Rev. D 2016, 94, 055029. [Google Scholar] [CrossRef]
- Dondi, N.A.; Sannino, F.; Smirnov, J. Thermal history of composite dark matter. Phys. Rev. D 2020, 101, 103010. [Google Scholar] [CrossRef]
- Ge, S.; Lawson, K.; Zhitnitsky, A. Axion quark nugget dark matter model: Size distribution and survival pattern. Phys. Rev. D 2019, 99, 116017. [Google Scholar] [CrossRef]
- Beylin, V.; Khlopov, M.Y.; Kuksa, V.; Volchanskiy, N. Hadronic and Hadron-Like Physics of Dark Matter. Symmetry 2019, 11, 587. [Google Scholar] [CrossRef]
- Yamanaka, N.; Iida, H.; Nakamura, A.; Wakayama, M. Dark matter scattering cross section and dynamics in dark Yang-Mills theory. Phys. Lett. B 2021, 813, 136056. [Google Scholar] [CrossRef]
- Yamanaka, N.; Iida, H.; Nakamura, A.; Wakayama, M. Glueball scattering cross section in lattice SU(2) Yang-Mills theory. Phys. Rev. D 2020, 102, 054507. [Google Scholar] [CrossRef]
- Cai, H.; Cacciapaglia, G. Singlet dark matter in the SU(6)/SO(6) composite Higgs model. Phys. Rev. D 2021, 103, 055002. [Google Scholar] [CrossRef]
- Hochberg, Y.; Kuflik, E.; Volansky, T.; Wacker, J.G. Mechanism for Thermal Relic Dark Matter of Strongly Interacting Massive Particles. Phys. Phys. Rev. Lett. 2014, 113, 171301. [Google Scholar] [CrossRef] [PubMed]
- Hochberg, Y.; Kuflik, E.; Murayama, H.; Volansky, T.; Wacker, J.G. Model for Thermal Relic Dark Matter of Strongly Interacting Massive Particles. Phys. Phys. Rev. Lett. 2015, 115, 021301. [Google Scholar] [CrossRef] [PubMed]
- Hochberg, Y.; Kuflik, E.; Murayama, H. SIMP Spectroscopy. J. High Energy Phys. 2016, 5, 90. [Google Scholar] [CrossRef]
- Berlin, A.; Blinov, N.; Gori, S.; Schuster, P.; Toro, N. Cosmology and Accelerator Tests of Strongly Interacting Dark Matter. Phys. Rev. D 2018, 97, 055033. [Google Scholar] [CrossRef]
- Bernal, N.; Chu, X.; Pradler, J. Simply split strongly interacting massive particles. Phys. Rev. D 2017, 95, 115023. [Google Scholar] [CrossRef]
- Bernal, N.; Chu, X.; Kulkarni, S.; Pradler, J. Self-interacting dark matter without prejudice. Phys. Rev. D 2020, 101, 055044. [Google Scholar] [CrossRef]
- Tsai, Y.D.; McGehee, R.; Murayama, H. Resonant Self-Interacting Dark Matter from Dark QCD. Phys. Phys. Rev. Lett. 2022, 128, 172001. [Google Scholar] [CrossRef]
- Kondo, D.; McGehee, R.; Melia, T.; Murayama, H. Linear Sigma Dark Matter. arXiv 2022, arXiv:2205.08088. [Google Scholar] [CrossRef]
- Bernal, N.; Chu, X. Z2 SIMP Dark Matter. J. Cosmol. Astropart. Phys. 2016, 1, 6. [Google Scholar] [CrossRef]
- Witten, E. Cosmic Separation of Phases. Phys. Rev. D 1984, 30, 272–285. [Google Scholar] [CrossRef]
- Kamionkowski, M.; Kosowsky, A.; Turner, M.S. Gravitational radiation from first order phase transitions. Phys. Rev. D 1994, 49, 2837–2851. [Google Scholar] [CrossRef]
- Allen, B. The Stochastic Gravity Wave Background: Sources and Detection; Atlantica: Paris, France, 1997. [Google Scholar]
- Schwaller, P. Gravitational Waves from a Dark Phase Transition. Phys. Phys. Rev. Lett. 2015, 115, 181101. [Google Scholar] [CrossRef]
- Croon, D.; Sanz, V.; White, G. Model Discrimination in Gravitational Wave spectra from Dark Phase Transitions. J. High Energy Phys. 2018, 8, 203. [Google Scholar] [CrossRef]
- Christensen, N. Stochastic Gravitational Wave Backgrounds. Rep. Prog. Phys. 2019, 82, 016903. [Google Scholar] [CrossRef]
- Seto, N.; Kawamura, S.; Nakamura, T. Possibility of direct measurement of the acceleration of the universe using 0.1-Hz band laser interferometer gravitational wave antenna in space. Phys. Phys. Rev. Lett. 2001, 87, 221103. [Google Scholar] [CrossRef]
- Kawamura, S.; Nakamura, T.; Ando, M.; Seto, N.; Tsubono, K.; Numata, K.; Takahashi, R.; Nagano, S.; Ishikawa, T.; Musha, M.; et al. The Japanese space gravitational wave antenna DECIGO. Class. Quant. Grav. 2006, 23, S125–S132. [Google Scholar] [CrossRef]
- Crowder, J.; Cornish, N.J. Beyond LISA: Exploring future gravitational wave missions. Phys. Rev. D 2005, 72, 083005. [Google Scholar] [CrossRef]
- Corbin, V.; Cornish, N.J. Detecting the cosmic gravitational wave background with the big bang observer. Class. Quant. Grav. 2006, 23, 2435–2446. [Google Scholar] [CrossRef]
- Harry, G.M.; Fritschel, P.; Shaddock, D.A.; Folkner, W.; Phinney, E.S. Laser interferometry for the big bang observer. Class. Quant. Grav. 2006, 23, 4887–4894, Erratum in Class. Quant. Grav. 2006, 23, 7361. [Google Scholar] [CrossRef]
- Hild, S.; Abernathy, M.; Acernese, F.; Amaro-Seoane, P.; Andersson, N.; Arun, K.; Barone, F.; Barr, B.; Barsuglia, M.; Beker, M.; et al. Sensitivity Studies for Third-Generation Gravitational Wave Observatories. Class. Quant. Grav. 2011, 28, 094013. [Google Scholar] [CrossRef]
- Yagi, K.; Seto, N. Detector configuration of DECIGO/BBO and identification of cosmological neutron-star binaries. Phys. Rev. D 2011, 83, 044011, Erratum in Phys. Rev. D 2017, 95, 109901. [Google Scholar] [CrossRef]
- Sathyaprakash, B.; Abernathy, M.; Acernese, F.; Ajith, P.; Allen, B.; Amaro-Seoane, P.; Andersson, N.; Aoudia, S.; Arun, K.; Astone, P.; et al. Scientific Objectives of Einstein Telescope. Class. Quant. Grav. 2012, 29, 124013, Erratum in Class. Quant. Grav. 2013, 30, 079501.. [Google Scholar] [CrossRef]
- Thrane, E.; Romano, J.D. Sensitivity curves for searches for gravitational-wave backgrounds. Phys. Rev. D 2013, 88, 124032. [Google Scholar] [CrossRef]
- Caprini, C.; Hindmarsh, M.; Huber, S.; Konstandin, T.; Kozaczuk, J.; Nardini, G.; No, J.M.; Petiteau, A.; Schwaller, P.; Servant, G.; et al. Science with the space-based interferometer eLISA. II: Gravitational waves from cosmological phase transitions. J. Cosmol. Astropart. Phys. 2016, 4, 1. [Google Scholar] [CrossRef]
- Amaro-Seoane, P. et al. [LISA] Laser Interferometer Space Antenna. arXiv 2017, arXiv:1702.00786. [Google Scholar]
- Abbott, B.P. et al. [LIGO Scientific] Exploring the Sensitivity of Next Generation Gravitational Wave Detectors. Class. Quant. Grav. 2017, 34, 044001. [Google Scholar] [CrossRef]
- Isoyama, S.; Nakano, H.; Nakamura, T. Multiband Gravitational-Wave Astronomy: Observing binary inspirals with a decihertz detector, B-DECIGO. Prog. Theor. Exp. Phys. 2018, 2018, 073E01. [Google Scholar] [CrossRef]
- Baker, J.; Bellovary, J.; Bender, P.L.; Berti, E.; Caldwell, R.; Camp, J.; Conklin, J.W.; Cornish, N.; Cutler, C.; DeRosa, R.; et al. The Laser Interferometer Space Antenna: Unveiling the Millihertz Gravitational Wave Sky. arXiv 2019, arXiv:1907.06482. [Google Scholar]
- Brdar, V.; Helmboldt, A.J.; Kubo, J. Gravitational Waves from First-Order Phase Transitions: LIGO as a Window to Unexplored Seesaw Scales. J. Cosmol. Astropart. Phys. 2019, 2, 21. [Google Scholar] [CrossRef]
- Reitze, D.; Adhikari, R.X.; Ballmer, S.; Barish, B.; Barsotti, L.; Billingsley, G.; Brown, D.A.; Chen, Y.; Coyne, D.; Eisenstein, R.; et al. Cosmic Explorer: The U.S. Contribution to Gravitational-Wave Astronomy beyond LIGO. Bull. Am. Astron. Soc. 2019, 51, 35. [Google Scholar]
- Detecting gravitational waves from cosmological phase transitions with LISA: An update. J. Cosmol. Astropart. Phys. 2020, 3, 24. [CrossRef]
- Maggiore, M.; Broeck, C.V.D.; Bartolo, N.; Belgacem, E.; Bertacca, D.; Bizouard, M.A.; Branchesi, M.; Clesse, S.; Foffa, S.; García-Bellido, J.; et al. Science Case for the Einstein Telescope. J. Cosmol. Astropart. Phys. 2020, 3, 50. [Google Scholar] [CrossRef]
- Huang, W.C.; Reichert, M.; Sannino, F.; Wang, Z.W. Testing the dark SU(N) Yang-Mills theory confined landscape: From the lattice to gravitational waves. Phys. Rev. D 2021, 104, 035005. [Google Scholar] [CrossRef]
- Halverson, J.; Long, C.; Maiti, A.; Nelson, B.; Salinas, G. Gravitational waves from dark Yang-Mills sectors. J. High Energy Phys. 2021, 5, 154. [Google Scholar] [CrossRef]
- Kang, Z.; Zhu, J.; Matsuzaki, S. Dark confinement-deconfinement phase transition: A roadmap from Polyakov loop models to gravitational waves. J. High Energy Phys. 2021, 9, 60. [Google Scholar] [CrossRef]
- Lucini, B.; Teper, M.; Wenger, U. The Deconfinement transition in SU(N) gauge theories. Phys. Lett. B 2002, 545, 197–206. [Google Scholar] [CrossRef]
- Lucini, B.; Teper, M.; Wenger, U. The High temperature phase transition in SU(N) gauge theories. J. High Energy Phys. 2004, 1, 61. [Google Scholar] [CrossRef]
- Lucini, B.; Teper, M.; Wenger, U. Properties of the deconfining phase transition in SU(N) gauge theories. J. High Energy Phys. 2005, 2, 033. [Google Scholar] [CrossRef]
- Panero, M. Thermodynamics of the QCD plasma and the large-N limit. Phys. Phys. Rev. Lett. 2009, 103, 232001. [Google Scholar] [CrossRef]
- Datta, S.; Gupta, S. Continuum Thermodynamics of the GluoNc Plasma. Phys. Rev. D 2010, 82, 114505. [Google Scholar] [CrossRef]
- Lucini, B.; Rago, A.; Rinaldi, E. SU(Nc) gauge theories at deconfinement. Phys. Lett. B 2012, 712, 279–283. [Google Scholar] [CrossRef][Green Version]
- Pepe, M. Confinement and the center of the gauge group. PoS 2006, LAT2005, 17. [Google Scholar] [CrossRef]
- Pepe, M.; Wiese, U.J. Exceptional Deconfinement in G(2) Gauge Theory. Nucl. Phys. B 2007, 768, 21–37. [Google Scholar] [CrossRef]
- Cossu, G.; D’Elia, M.; Giacomo, A.D.; Lucini, B.; Pica, C. G(2) gauge theory at finite temperature. J. High Energy Phys. 2007, 10, 100. [Google Scholar] [CrossRef]
- Bruno, M.; Caselle, M.; Panero, M.; Pellegrini, R. Exceptional thermodynamics: The equation of state of G2 gauge theory. J. High Energy Phys. 2015, 3, 57. [Google Scholar] [CrossRef]
- Appelquist, T.; Brower, R.C.; Buchoff, M.I.; Fleming, G.T.; Jin, X.Y.; Kiskis, J.; Kribs, G.D.; Neil, E.T.; Osborn, J.C.; Rebbi, C.; et al. Stealth Dark Matter: Dark scalar baryons through the Higgs portal. Phys. Rev. D 2015, 92, 075030. [Google Scholar] [CrossRef]
- Appelquist, T.; Berkowitz, E.; Brower, R.C.; Buchoff, M.I.; Fleming, G.T.; Jin, X.Y.; Kiskis, J.; Kribs, G.D.; Neil, E.T.; Osborn, J.C.; et al. Detecting Stealth Dark Matter Directly through Electromagnetic Polarizability. Phys. Phys. Rev. Lett. 2015, 115, 171803. [Google Scholar] [CrossRef]
- Brower, R.C. et al. [Lattice Strong Dynamics]. Stealth dark matter confinement transition and gravitational waves. Phys. Rev. D 2021, 103, 014505. [Google Scholar] [CrossRef]
- Borsanyi, S.; Fodor, K.R.Z.; Godzieba, D.A.; Parotto, P.; Sexty, D. Precision study of the continuum SU(3) Yang-Mills theory: How to use parallel tempering to improve on supercritical slowing down for first order phase transitions. Phys. Rev. D 2022, 105, 074513. [Google Scholar] [CrossRef]
- Langfeld, K.; Lucini, B.; Rago, A. The density of states in gauge theories. Phys. Phys. Rev. Lett. 2012, 109, 111601. [Google Scholar] [CrossRef] [PubMed]
- Langfeld, K.; Pawlowski, J.M. Two-color QCD with heavy quarks at finite densities. Phys. Rev. D 2013, 88, 071502. [Google Scholar] [CrossRef]
- Langfeld, K.; Lucini, B.; Pellegrini, R.; Rago, A. An efficient algorithm for numerical computations of continuous densities of states. Eur. Phys. J. C 2016, 76, 306. [Google Scholar] [CrossRef][Green Version]
- Cossu, G.; Lancastera, D.; Lucini, B.; Pellegrini, R.; Rago, A. Ergodic sampling of the topological charge using the density of states. Eur. Phys. J. C 2021, 81, 375. [Google Scholar] [CrossRef]
- Springer, F.; Schaich, D. Density of states for gravitational waves. PoS Lattice 2022, 2021, 43. [Google Scholar] [CrossRef]
- Mason, D.; Lucini, B.; Piai, M.; Rinaldi, E.; Vadacchino, D. The density of states method in Yang-Mills theories and first order phase transitions. EPJ Web Conf. 2022, 274, 08007. [Google Scholar] [CrossRef]
- Mason, D.; Lucini, B.; Piai, M.; Rinaldi, E.; Vadacchino, D. The density of state method for first-order phase transitions in Yang-Mills theories. PoS Lattice 2023, 2022, 216. [Google Scholar] [CrossRef]
- Springer, F. et al. [Lattice Strong Dynamics (LSD)]. Advances in using density of states for large-N Yang-Mills. PoS Lattice 2023, 2022, 223. [Google Scholar] [CrossRef]
- Brower, R.C.; Mathur, S.D.; Tan, C.I. Glueball spectrum for QCD from AdS supergravity duality. Nucl. Phys. B 2000, 587, 249–276. [Google Scholar] [CrossRef]
- Apreda, R.; Crooks, D.E.; Evans, N.J.; Petrini, M. Confinement, glueballs and strings from deformed AdS. J. High Energy Phys. 2004, 5, 65. [Google Scholar] [CrossRef][Green Version]
- Mueck, W.; Prisco, M. Glueball scattering amplitudes from holography. J. High Energy Phys. 2004, 4, 37. [Google Scholar] [CrossRef][Green Version]
- Wen, C.K.; Yang, H.X. QCD(4) glueball masses from AdS(6) black hole description. Mod. Phys. Lett. A 2005, 20, 997–1004. [Google Scholar] [CrossRef]
- Kuperstein, S.; Sonnenschein, J. Non-critical, near extremal AdS(6) background as a holographic laboratory of four dimensional YM theory. J. High Energy Phys. 2004, 11, 26. [Google Scholar] [CrossRef]
- Elander, D.; Faedo, A.F.; Hoyos, C.; Mateos, D.; Piai, M. Multiscale confining dynamics from holographic RG flows. J. High Energy Phys. 2014, 5, 3. [Google Scholar] [CrossRef]
- Athenodorou, A.; Bennett, E.; Bergner, G.; Elander, D.; Lin, C.J.D.; Lucini, B.; Piai, M. Large mass hierarchies from strongly-coupled dynamics. J. High Energy Phys. 2016, 6, 114. [Google Scholar] [CrossRef]
- Elander, D.; Piai, M.; Roughley, J. Holographic glueballs from the circle reduction of Romans supergravity. J. High Energy Phys. 2019, 2, 101. [Google Scholar] [CrossRef]
- Elander, D.; Piai, M.; Roughley, J. Probing the holographic dilaton. J. High Energy Phys. 2020, 6, 177, Erratum in J. High Energy Phys. 2020, 12, 109. [Google Scholar] [CrossRef]
- Bochicchio, M. An asymptotic solution of Large-N QCD, for the glueball and meson spectrum and the collinear S-matrix. AIP Conf. Proc. 2016, 1735, 030004. [Google Scholar] [CrossRef]
- Bochicchio, M. Glueball and meson spectrum in large-N massless QCD. arXiv 2013, arXiv:1308.2925. [Google Scholar]
- Hong, D.K.; Lee, J.W.; Lucini, B.; Piai, M.; Vadacchino, D. Casimir scaling and Yang-Mills glueballs. Phys. Lett. B 2017, 775, 89–93. [Google Scholar] [CrossRef]
- Lucini, B.; Teper, M. SU(N) gauge theories in four-dimensions: Exploring the approach to N = infinity. J. High Energy Phys. 2001, 6, 50. [Google Scholar] [CrossRef]
- Lucini, B.; Teper, M.; Wenger, U. Glueballs and k-strings in SU(N) gauge theories: Calculations with improved operators. J. High Energy Phys. 2004, 6, 12. [Google Scholar] [CrossRef]
- Lucini, B.; Rago, A.; Rinaldi, E. Glueball masses in the large N limit. J. High Energy Phys. 2010, 8, 119. [Google Scholar] [CrossRef]
- Lucini, B.; Panero, M. SU(N) gauge theories at large N. Phys. Rep. 2013, 526, 93–163. [Google Scholar] [CrossRef]
- Athenodorou, A.; Lau, R.; Teper, M. On the weak N -dependence of SO(N) and SU(N) gauge theories in 2+1 dimensions. Phys. Lett. B 2015, 749, 448–453. [Google Scholar] [CrossRef]
- Lau, R.; Teper, M. SO(N) gauge theories in 2 + 1 dimensions: Glueball spectra and confinement. J. High Energy Phys. 2017, 10, 22. [Google Scholar] [CrossRef]
- Hernández, P.; Romero-López, F. The large Nc limit of QCD on the lattice. Eur. Phys. J. A 2021, 57, 52. [Google Scholar] [CrossRef]
- Athenodorou, A.; Teper, M. SU(N) gauge theories in 3+1 dimensions: Glueball spectrum, string tensions and topology. arXiv 2021, arXiv:2106.00364. [Google Scholar] [CrossRef]
- Yamanaka, N.; Nakamura, A.; Wakayama, M. Interglueball potential in lattice SU(N) gauge theories. arXiv 2021, arXiv:2110.04521. [Google Scholar]
- Bonanno, C.; D’Elia, M.; Lucini, B.; Vadacchino, D. Towards glueball masses of large-NSU(N) pure-gauge theories without topological freezing. arXiv 2022, arXiv:2205.06190. [Google Scholar]
- Aharony, O.; Karzbrun, E. On the effective action of confining strings. J. High Energy Phys. 2009, 6, 12. [Google Scholar] [CrossRef]
- Witten, E. Current Algebra Theorems for the U(1) Goldstone Boson. Nucl. Phys. B 1979, 156, 269–283. [Google Scholar] [CrossRef]
- Veneziano, G. U(1) Without Instantons. Nucl. Phys. B 1979, 159, 213–224. [Google Scholar] [CrossRef]
- Witten, E. Theta dependence in the large N limit of four-dimensional gauge theories. Phys. Phys. Rev. Lett. 1998, 81, 2862–2865. [Google Scholar] [CrossRef]
- Vicari, E.; Panagopoulos, H. Theta dependence of SU(N) gauge theories in the presence of a topological term. Phys. Rep. 2009, 470, 93–150. [Google Scholar] [CrossRef]
- Luscher, M. Topology of Lattice Gauge Fields. Commun. Math. Phys. 1982, 85, 39. [Google Scholar] [CrossRef]
- Campostrini, M.; Giacomo, A.D.; Panagopoulos, H.; Vicari, E. Topological Charge, Renormalization and Cooling on the Lattice. Nucl. Phys. B 1990, 329, 683–697. [Google Scholar] [CrossRef]
- Debbio, L.D.; Panagopoulos, H.; Vicari, E. Theta dependence of SU(N) gauge theories. J. High Energy Phys. 2002, 8, 44. [Google Scholar] [CrossRef]
- Lucini, B.; Teper, M.; Wenger, U. Topology of SU(N) gauge theories at T =~ 0 and T =~ T(c). Nucl. Phys. B 2005, 715, 461–482. [Google Scholar] [CrossRef]
- Debbio, L.D.; Giusti, L.; Pica, C. Topological susceptibility in the SU(3) gauge theory. Phys. Phys. Rev. Lett. 2005, 94, 032003. [Google Scholar] [CrossRef]
- Luscher, M.; Palombi, F. Universality of the topological susceptibility in the SU(3) gauge theory. J. High Energy Phys. 2010, 9, 110. [Google Scholar] [CrossRef]
- Panagopoulos, H.; Vicari, E. The 4D SU(3) gauge theory with an imaginary θ term. J. High Energy Phys. 2011, 11, 119. [Google Scholar] [CrossRef]
- Bonati, C.; D’Elia, M.; Scapellato, A. θ dependence in SU(3) Yang-Mills theory from analytic continuation. Phys. Rev. D 2016, 93, 025028. [Google Scholar] [CrossRef]
- Bonati, C.; D’Elia, M.; Rossi, P.; Vicari, E. θ dependence of 4D SU(N) gauge theories in the large-N limit. Phys. Rev. D 2016, 94, 085017. [Google Scholar] [CrossRef]
- Cè, M.; Vera, M.G.; Giusti, L.; Schaefer, S. The topological susceptibility in the large-N limit of SU(N) Yang–Mills theory. Phys. Lett. B 2016, 762, 232–236. [Google Scholar] [CrossRef]
- Alexandrou, C.; Athenodorou, A.; Cichy, K.; Dromard, A.; Garcia-Ramos, E.; Jansen, K.; Wenger, U.; Zimmermann, F. Comparison of topological charge definitions in Lattice QCD. Eur. Phys. J. C 2020, 80, 424. [Google Scholar] [CrossRef]
- Bonanno, C.; Bonati, C.; D’Elia, M. Large-N SU(N) Yang-Mills theories with milder topological freezing. J. High Energy Phys. 2021, 3, 111. [Google Scholar] [CrossRef]
- Borsanyi, S.; Sexty, D. Topological susceptibility of pure gauge theory using Density of States. Phys. Lett. B 2021, 815, 136148. [Google Scholar] [CrossRef]
- Teper, M. More methods for calculating the topological charge (density) of SU(N) lattice gauge fields in 3+1 dimensions. arXiv 2022, arXiv:2202.02528. [Google Scholar]
- Bonanno, C.; D’Elia, M.; Lucini, B.; Vadacchino, D. Towards glueball masses of large-N SU(N) Yang-Mills theories without topological freezing via parallel tempering on boundary conditions. PoS Lattice 2023, 2022, 392. [Google Scholar] [CrossRef]
- Bonanno, C. Lattice determination of the topological susceptibility slope χ’ of 2d CPN-1 models at large N. Phys. Rev. D 2023, 107, 014514. [Google Scholar] [CrossRef]
- Bando, M.; Kugo, T.; Uehara, S.; Yamawaki, K.; Yanagida, T. Is rho Meson a Dynamical Gauge Boson of Hidden Local Symmetry? Phys. Rev. Lett. 1985, 54, 1215. [Google Scholar] [CrossRef] [PubMed]
- Casalbuoni, R.; Curtis, S.D.; Dominici, D.; Gatto, R. Effective Weak Interaction Theory with Possible New Vector Resonance from a Strong Higgs Sector. Phys. Lett. 1985, 155B, 95. [Google Scholar] [CrossRef]
- Bando, M.; Kugo, T.; Yamawaki, K. Nonlinear Realization and Hidden Local Symmetries. Phys. Rep. 1988, 164, 217. [Google Scholar] [CrossRef]
- Casalbuoni, R.; Curtis, S.D.; Dominici, D.; Feruglio, F.; Gatto, R. Vector and Axial Vector Bound States From a Strongly Interacting Electroweak Sector. Int. J. Mod. Phys. A 1989, 4, 1065. [Google Scholar] [CrossRef]
- Harada, M.; Yamawaki, K. Hidden local symmetry at loop: A New perspective of composite gauge boson and chiral phase transition. Phys. Rep. 2003, 381, 1. [Google Scholar] [CrossRef]
- Georgi, H. Vector Realization of Chiral Symmetry. Nucl. Phys. B 1990, 331, 311. [Google Scholar] [CrossRef]
- Appelquist, T.; da Silva, P.S.R.; Sannino, F. Enhanced global symmetries and the chiral phase transition. Phys. Rev. D 1999, 60, 116007. [Google Scholar] [CrossRef]
- Piai, M.; Pierce, A.; Wacker, J.G. Composite vector mesons from QCD to the little Higgs. arXiv 2004, arXiv:hep-ph/0405242. [Google Scholar]
- Franzosi, D.B.; Cacciapaglia, G.; Cai, H.; Deandrea, A.; Frandsen, M. Vector and Axial-vector resonances in composite models of the Higgs boson. J. High Energy Phys. 2016, 1611, 76. [Google Scholar] [CrossRef]
- Cabibbo, N.; Marinari, E. A New Method for Updating SU(N) Matrices in Computer Simulations of Gauge Theories. Phys. Lett. B 1982, 119, 387–390. [Google Scholar] [CrossRef]
- Lewis, R.; Pica, C.; Sannino, F. Light Asymmetric Dark Matter on the Lattice: SU(2) Technicolor with Two Fundamental Flavors. Phys. Rev. D 2012, 85, 014504. [Google Scholar] [CrossRef]
- Slansky, R. Group Theory for Unified Model Building. Phys. Rep. 1981, 79, 1–128. [Google Scholar] [CrossRef]
- Caswell, W.E. Asymptotic Behavior of Nonabelian Gauge Theories to Two Loop Order. Phys. Phys. Rev. Lett. 1974, 33, 244. [Google Scholar] [CrossRef]
- Banks, T.; Zaks, A. On the Phase Structure of Vector-Like Gauge Theories with Massless Fermions. Nucl. Phys. B 1982, 196, 189–204. [Google Scholar] [CrossRef]
- Chivukula, R.S. Lectures on technicolor and compositeness. arXiv 2000, arXiv:hep-ph/0011264. [Google Scholar]
- Lane, K. Two Lectures on Technicolor. arXiv 2002, arXiv:hep-ph/0202255. [Google Scholar]
- Hill, C.T.; Simmons, E.H. Strong Dynamics and Electroweak Symmetry Breaking. Phys. Rep. 2003, 381, 235–402, Erratum in Phys. Rep. 2004, 390, 553–554. [Google Scholar] [CrossRef]
- Martin, A. Predicted Signals at the LHC from Technicolor: Erice Lecture. Subnucl. Ser. 2011, 46, 135–159. [Google Scholar] [CrossRef]
- Sannino, F. Conformal Dynamics for TeV Physics and Cosmology. Acta Phys. Polon. B 2009, 40, 3533–3743. [Google Scholar]
- Piai, M. Lectures on walking technicolor, holography and gauge/gravity dualities. Adv. High Energy Phys. 2010, 2010, 464302. [Google Scholar] [CrossRef]
- Pica, C.; Sannino, F. UV and IR Zeros of Gauge Theories at The Four Loop Order and Beyond. Phys. Rev. D 2011, 83, 035013. [Google Scholar] [CrossRef]
- Baikov, P.A.; Chetyrkin, K.G.; Kühn, J.H. Five-Loop Running of the QCD coupling constant. Phys. Phys. Rev. Lett. 2017, 118, 082002. [Google Scholar] [CrossRef] [PubMed]
- Herzog, F.; Ruijl, B.; Ueda, T.; Vermaseren, J.A.M.; Vogt, A. The five-loop beta function of Yang-Mills theory with fermions. J. High Energy Phys. 2017, 2, 90. [Google Scholar] [CrossRef]
- Ryttov, T.A.; Shrock, R. Infrared Zero of β and Value of γm for an SU(3) Gauge Theory at the Five-Loop Level. Phys. Rev. D 2016, 94, 105015. [Google Scholar] [CrossRef]
- Appelquist, T.; Lane, K.D.; Mahanta, U. On the Ladder Approximation for Spontaneous Chiral Symmetry Breaking. Phys. Phys. Rev. Lett. 1988, 61, 1553. [Google Scholar] [CrossRef]
- Cohen, A.G.; Georgi, H. Walking Beyond the Rainbow. Nucl. Phys. B 1989, 314, 7–24. [Google Scholar] [CrossRef]
- Ryttov, T.A.; Sannino, F. Supersymmetry inspired QCD beta function. Phys. Rev. D 2008, 78, 065001. [Google Scholar] [CrossRef]
- Pica, C.; Sannino, F. Beta Function and Anomalous Dimensions. Phys. Rev. D 2011, 83, 116001. [Google Scholar] [CrossRef]
- Intriligator, K.A.; Seiberg, N. Lectures on supersymmetric gauge theories and electric-magnetic duality. Nucl. Phys. B Proc. Suppl. 1996, 45BC, 1–28. [Google Scholar] [CrossRef]
- Ryttov, T.A. Consistent Perturbative Fixed Point Calculations in QCD and Supersymmetric QCD. Phys. Phys. Rev. Lett. 2016, 117, 071601. [Google Scholar] [CrossRef] [PubMed]
- Ryttov, T.A.; Shrock, R. Scheme-independent calculation of γψ¯ψ,IR for an SU(3) gauge theory. Phys. Rev. D 2016, 94, 105014. [Google Scholar] [CrossRef]
- Ryttov, T.A.; Shrock, R. Scheme-Independent Series Expansions at an Infrared Zero of the Beta Function in Asymptotically Free Gauge Theories. Phys. Rev. D 2016, 94, 125005. [Google Scholar] [CrossRef]
- Ryttov, T.A.; Shrock, R. Higher-Order Scheme-Independent Calculations of Physical Quantities in the Conformal Phase of a Gauge Theory. Phys. Rev. D 2017, 95, 085012. [Google Scholar] [CrossRef]
- Ryttov, T.A.; Shrock, R. Higher-order scheme-independent series expansions of γψ¯ψ,IR and βIR′ in conformal field theories. Phys. Rev. D 2017, 95, 105004. [Google Scholar] [CrossRef]
- Ryttov, T.A.; Shrock, R. Infrared fixed point physics in SO(Nc) and Sp(Nc) gauge theories. Phys. Rev. D 2017, 96, 105015. [Google Scholar] [CrossRef]
- Gracey, J.A.; Ryttov, T.A.; Shrock, R. Scheme-Independent Calculations of Anomalous Dimensions of Baryon Operators in Conformal Field Theories. Phys. Rev. D 2018, 97, 116018. [Google Scholar] [CrossRef]
- Ryttov, T.A.; Shrock, R. Scheme-Independent Calculations of Properties at a Conformal Infrared Fixed Point in Gauge Theories with Multiple Fermion Representations. Phys. Rev. D 2018, 98, 096003. [Google Scholar] [CrossRef]
- Ryttov, T.A.; Shrock, R. Scheme-Independent Series for Anomalous Dimensions of Higher-Spin Operators at an Infrared Fixed Point in a Gauge Theory. Phys. Rev. D 2020, 101, 076018. [Google Scholar] [CrossRef]
- Kaplan, D.B.; Lee, J.W.; Son, D.T.; Stephanov, M.A. Conformality Lost. Phys. Rev. D 2009, 80, 125005. [Google Scholar] [CrossRef]
- Kim, B.S.; Hong, D.K.; Lee, J.W. Into the conformal window: Multirepresentation gauge theories. Phys. Rev. D 2020, 101, 056008. [Google Scholar] [CrossRef]
- Lee, J.W. Conformal window from conformal expansion. Phys. Rev. D 2021, 103, 076006. [Google Scholar] [CrossRef]
- Appelquist, T.; Ratnaweera, A.; Terning, J.; Wijewardhana, L.C.R. The Phase structure of an SU(N) gauge theory with N(f) flavors. Phys. Rev. D 1998, 58, 105017. [Google Scholar] [CrossRef]
- Gell-Mann, M.; Oakes, R.J.; Renner, B. Behavior of current divergences under SU(3) x SU(3). Phys. Rev. 1968, 175, 2195–2199. [Google Scholar] [CrossRef]
- Coleman, S.R.; Weinberg, E.J. Radiative Corrections as the Origin of Spontaneous Symmetry Breaking. Phys. Rev. D 1973, 7, 1888. [Google Scholar] [CrossRef]
- Einhorn, M.B.; Jones, D.R.T. The Effective potential and quadratic divergences. Phys. Rev. D 1992, 46, 5206–5208. [Google Scholar] [CrossRef]
- Weinberg, S. Implications of Dynamical Symmetry Breaking. Phys. Rev. D 1976, 19, 1277. [Google Scholar] [CrossRef]
- Susskind, L. Dynamics of Spontaneous Symmetry Breaking in the Weinberg-Salam Theory. Phys. Rev. D 1979, 20, 2619–2625. [Google Scholar] [CrossRef]
- Holdom, B. Techniodor. Phys. Lett. B 1985, 150, 301–305. [Google Scholar] [CrossRef]
- Appelquist, T.W.; Karabali, D.; Wijewardhana, L.C.R. Chiral Hierarchies and the Flavor Changing Neutral Current Problem in Technicolor. Phys. Phys. Rev. Lett. 1986, 57, 957. [Google Scholar] [CrossRef] [PubMed]
- Dimopoulos, S.; Susskind, L. Mass Without Scalars. Nucl. Phys. B 1979, 155, 237–252. [Google Scholar] [CrossRef]
- Eichten, E.; Lane, K.D. Dynamical Breaking of Weak Interaction Symmetries. Phys. Lett. B 1980, 90, 125–130. [Google Scholar] [CrossRef]
- Peskin, M.E.; Takeuchi, T. Estimation of oblique electroweak corrections. Phys. Rev. D 1992, 46, 381–409. [Google Scholar] [CrossRef]
- Barbieri, R.; Pomarol, A.; Rattazzi, R.; Strumia, A. Electroweak symmetry breaking after LEP-1 and LEP-2. Nucl. Phys. B 2004, 703, 127–146. [Google Scholar] [CrossRef]
- Appelquist, T.; Bernard, C.W. Strongly Interacting Higgs Bosons. Phys. Rev. D 1980, 22, 200. [Google Scholar] [CrossRef]
- Longhitano, A.C. Heavy Higgs Bosons in the Weinberg-Salam Model. Phys. Rev. D 1980, 22, 1166. [Google Scholar] [CrossRef]
- Longhitano, A.C. Low-Energy Impact of a Heavy Higgs Boson Sector. Nucl. Phys. B 1981, 188, 118–154. [Google Scholar] [CrossRef]
- Appelquist, T.; Wu, G.H. The Electroweak chiral Lagrangian and new precision measurements. Phys. Rev. D 1993, 48, 3235–3241. [Google Scholar] [CrossRef]
- Appelquist, T.; Wu, G.H. The Electroweak chiral Lagrangian and CP violating effects in technicolor theories. Phys. Rev. D 1995, 51, 240–250. [Google Scholar] [CrossRef]
- Glashow, S.L.; Iliopoulos, J.; Maiani, L. Weak Interactions with Lepton-Hadron Symmetry. Phys. Rev. D 1970, 2, 1285–1292. [Google Scholar] [CrossRef]
- Appelquist, T.; Terning, J. An Extended technicolor model. Phys. Rev. D 1994, 50, 2116–2126. [Google Scholar] [CrossRef] [PubMed]
- Appelquist, T.; Shrock, R. Neutrino masses in theories with dynamical electroweak symmetry breaking. Phys. Lett. B 2002, 548, 204–214. [Google Scholar] [CrossRef]
- Appelquist, T.; Shrock, R. Dynamical symmetry breaking of extended gauge symmetries. Phys. Phys. Rev. Lett. 2003, 90, 201801. [Google Scholar] [CrossRef]
- Appelquist, T.; Piai, M.; Shrock, R. Fermion masses and mixing in extended technicolor models. Phys. Rev. D 2004, 69, 015002. [Google Scholar] [CrossRef]
- Appelquist, T.; Piai, M.; Shrock, R. Lepton dipole moments in extended technicolor models. Phys. Lett. B 2004, 593, 175–180. [Google Scholar] [CrossRef][Green Version]
- Appelquist, T.; Piai, M.; Shrock, R. Quark dipole operators in extended technicolor models. Phys. Lett. B 2004, 595, 442–452. [Google Scholar] [CrossRef][Green Version]
- Appelquist, T.; Christensen, N.D.; Piai, M.; Shrock, R. Flavor-changing processes in extended technicolor. Phys. Rev. D 2004, 70, 093010. [Google Scholar] [CrossRef]
- Georgi, H. Generalized dimensional analysis. Phys. Lett. B 1993, 298, 187–189. [Google Scholar] [CrossRef]
- Leung, C.N.; Love, S.T.; Bardeen, W.A. Aspects of Dynamical Symmetry Breaking in Gauge Field Theories. Nucl. Phys. B 1989, 323, 493–512. [Google Scholar] [CrossRef]
- Luty, M.A.; Okui, T. Conformal technicolor. J. High Energy Phys. 2006, 9, 70. [Google Scholar] [CrossRef][Green Version]
- Spergel, D.N.; Steinhardt, P.J. Observational evidence for selfinteracting cold dark matter. Phys. Phys. Rev. Lett. 2000, 84, 3760–3763. [Google Scholar] [CrossRef] [PubMed]
- De Blok, W.J.G. The Core-Cusp Problem. Adv. Astron. 2010, 2010, 789293. [Google Scholar] [CrossRef]
- Boylan-Kolchin, M.; Bullock, J.S.; Kaplinghat, M. Too big to fail? The puzzling darkness of massive Milky Way subhaloes. Mon. Not. R. Astron. Soc. Lett. 2011, 415, L40. [Google Scholar] [CrossRef]
- Wess, J.; Zumino, B. Consequences of anomalous Ward identities. Phys. Lett. B 1971, 37, 95–97. [Google Scholar] [CrossRef]
- Witten, E. Global Aspects of Current Algebra. Nucl. Phys. B 1983, 223, 422–432. [Google Scholar] [CrossRef]
- Witten, E. Current Algebra, Baryons, and Quark Confinement. Nucl. Phys. B 1983, 223, 433–444. [Google Scholar] [CrossRef]
- McDonald, J. Thermally generated gauge singlet scalars as selfinteracting dark matter. Phys. Phys. Rev. Lett. 2002, 88, 091304. [Google Scholar] [CrossRef]
- Hall, L.J.; Jedamzik, K.; March-Russell, J.; West, S.M. Freeze-In Production of FIMP Dark Matter. J. High Energy Phys. 2010, 3, 80. [Google Scholar] [CrossRef]
- Yaguna, C.E. The Singlet Scalar as FIMP Dark Matter. J. High Energy Phys. 2011, 8, 60. [Google Scholar] [CrossRef]
- Campbell, R.; Godfrey, S.; Logan, H.E.; Peterson, A.D.; Poulin, A. Implications of the observation of dark matter self-interactions for singlet scalar dark matter. Phys. Rev. D 2015, 92, 055031, Erratum in Phys. Rev. D 2020, 101, 039905. [Google Scholar] [CrossRef]
- Kang, Z. View FImP miracle (by scale invariance) à la self-interaction. Phys. Lett. B 2015, 751, 201–204. [Google Scholar] [CrossRef][Green Version]
- Espinosa, J.R.; Konstandin, T.; No, J.M.; Servant, G. Energy Budget of Cosmological First-order Phase Transitions. J. Cosmol. Astropart. Phys. 2010, 6, 28. [Google Scholar] [CrossRef]
- Bigazzi, F.; Caddeo, A.; Cotrone, A.L.; Paredes, A. Fate of false vacua in holographic first-order phase transitions. J. High Energy Phys. 2020, 12, 200. [Google Scholar] [CrossRef]
- Ares, F.R.; Hindmarsh, M.; Hoyos, C.; Jokela, N. Gravitational waves from a holographic phase transition. J. High Energy Phys. 2020, 21, 100. [Google Scholar] [CrossRef]
- Bea, Y.; Casalderrey-Solana, J.; Giannakopoulos, T.; Mateos, D.; Sanchez-Garitaonandia, M.; Ao, M.Z. Bubble wall velocity from holography. Phys. Rev. D 2021, 104, L121903. [Google Scholar] [CrossRef]
- Bigazzi, F.; Caddeo, A.; Canneti, T.; Cotrone, A.L. Bubble wall velocity at strong coupling. J. High Energy Phys. 2021, 8, 90. [Google Scholar] [CrossRef]
- Henriksson, O. Black brane evaporation through D-brane bubble nucleation. Phys. Rev. D 2022, 105, L041901. [Google Scholar] [CrossRef]
- Ares, F.R.; Henriksson, O.; Hindmarsh, M.; Hoyos, C.; Jokela, N. Effective actions and bubble nucleation from holography. Phys. Rev. D 2022, 105, 066020. [Google Scholar] [CrossRef]
- Ares, F.R.; Henriksson, O.; Hindmarsh, M.; Hoyos, C.; Jokela, N. Gravitational Waves at Strong Coupling from an Effective Action. Phys. Phys. Rev. Lett. 2022, 128, 131101. [Google Scholar] [CrossRef]
- Morgante, E.; Ramberg, N.; Schwaller, P. Echo of the Dark: Gravitational Waves from Dark SU(3) Yang-Mills Theory. arXiv 2022, arXiv:2210.11821. [Google Scholar]
- Verbaarschot, J.J.M. The Spectrum of the QCD Dirac operator and chiral random matrix theory: The Threefold way. Phys. Phys. Rev. Lett. 1994, 72, 2531–2533. [Google Scholar] [CrossRef] [PubMed]
- Debbio, L.D.; Patella, A.; Pica, C. Higher representations on the lattice: Numerical simulations. SU(2) with adjoint fermions. Phys. Rev. D 2010, 81, 094503. [Google Scholar] [CrossRef]
- Available online: https://github.com/claudiopica/HiRep (accessed on 1 May 2023).
- Available online: https://github.com/sa2c/HiRep (accessed on 1 May 2023).
- Clark, M.A.; Kennedy, A.D. The RHMC algorithm for two flavors of dynamical staggered fermions. Nucl. Phys. B Proc. Suppl. 2004, 129, 850–852. [Google Scholar] [CrossRef]
- Takaishi, T.; De Forcrand, P. Testing and tuning new symplectic integrators for hybrid Monte Carlo algorithm in lattice QCD. Phys. Rev. E 2006, 73, 036706. [Google Scholar] [CrossRef]
- DeGrand, T.A.; Rossi, P. Conditioning Techniques for Dynamical Fermions. Comput. Phys. Commun. 1990, 60, 211–214. [Google Scholar] [CrossRef]
- Lüscher, M. Properties and uses of the Wilson flow in lattice QCD. J. High Energy Phys. 2010, 8, 71, Erratum in J. High Energy Phys. 2014, 3, 92. [Google Scholar] [CrossRef]
- Lüscher, M. Future applications of the Yang-Mills gradient flow in lattice QCD. PoS Lattice 2014, 2013, 16. [Google Scholar] [CrossRef]
- Luscher, M.; Weisz, P. Perturbative analysis of the gradient flow in non-abelian gauge theories. J. High Energy Phys. 2011, 2, 51. [Google Scholar] [CrossRef]
- Borsanyi, S.; Durr, S.; Fodor, Z.; Hoelbling, C.; Katz, S.D.; Krieg, S.; Kurth, T.; Lellouch, L.; Lippert, T.; McNeile, C.; et al. High-precision scale setting in lattice QCD. J. High Energy Phys. 2012, 9, 10. [Google Scholar] [CrossRef]
- Sheikholeslami, B.; Wohlert, R. Improved Continuum Limit Lattice Action for QCD with Wilson Fermions. Nucl. Phys. B 1985, 259, 572. [Google Scholar] [CrossRef]
- Hasenbusch, M.; Jansen, K. Speeding up lattice QCD simulations with clover improved Wilson fermions. Nucl. Phys. B 2003, 659, 299–320. [Google Scholar] [CrossRef]
- Luscher, M.; Schaefer, S. Lattice QCD without topology barriers. J. High Energy Phys. 2011, 7, 36. [Google Scholar] [CrossRef]
- Endres, M.G.; Brower, R.C.; Detmold, W.; Orginos, K.; Pochinsky, A.V. Multiscale Monte Carlo equilibration: Pure Yang-Mills theory. Phys. Rev. D 2015, 92, 114516. [Google Scholar] [CrossRef]
- Lüscher, M. Stochastic locality and master-field simulations of very large lattices. EPJ Web Conf. 2018, 175, 01002. [Google Scholar] [CrossRef]
- Boyle, P.A.; Juttner, A.; Kelly, C.; Kenway, R.D. Use of stochastic sources for the lattice determination of light quark physics. J. High Energy Phys. 2008, 8, 86. [Google Scholar] [CrossRef]
- Martinelli, G.; Zhang, Y.C. The Connection Between Local Operators on the Lattice and in the Continuum and Its Relation to Meson Decay Constants. Phys. Lett. B 1983, 123, 433. [Google Scholar] [CrossRef]
- Luscher, M.; Symanzik, K.; Weisz, P. Anomalies of the Free Loop Wave Equation in the WKB Approximation. Nucl. Phys. B 1980, 173, 365. [Google Scholar] [CrossRef]
- Polchinski, J.; Strominger, A. Effective string theory. Phys. Phys. Rev. Lett. 1991, 67, 1681–1684. [Google Scholar] [CrossRef]
- Luscher, M. Symmetry Breaking Aspects of the Roughening Transition in Gauge Theories. Nucl. Phys. B 1981, 180, 317–329. [Google Scholar] [CrossRef]
- Luscher, M.; Weisz, P. String excitation energies in SU(N) gauge theories beyond the free-string approximation. J. High Energy Phys. 2004, 7, 14. [Google Scholar] [CrossRef]
- Drummond, J.M. Universal subleading spectrum of effective string theory. arXiv 2004, arXiv:hep-th/0411017. [Google Scholar]
- Dass, N.D.H.; Matlock, P. Universality of correction to Luescher term in Polchinski-Strominger effective string theories. arXiv 2006, arXiv:hep-th/0606265. [Google Scholar]
- Drummond, J.M. Reply to hep-th/0606265. arXiv 2006, arXiv:hep-th/0608109. [Google Scholar]
- Dass, N.D.H.; Matlock, P. Our response to the response hep-th/0608109 by Drummond. arXiv 2006, arXiv:hep-th/0611215. [Google Scholar]
- Aharony, O.; Komargodski, Z. The Effective Theory of Long Strings. J. High Energy Phys. 2013, 5, 118. [Google Scholar] [CrossRef]
- Dubovsky, S.; Gorbenko, V. Towards a Theory of the QCD String. J. High Energy Phys. 2016, 2, 022. [Google Scholar] [CrossRef]
- Bijnens, J.; Lu, J. Technicolor and other QCD-like theories at next-to-next-to-leading order. J. High Energy Phys. 2009, 11, 116. [Google Scholar] [CrossRef]
- Athenodorou, A.; Teper, M. SU(N) gauge theories in 2+1 dimensions: Glueball spectra and k-string tensions. J. High Energy Phys. 2017, 2, 15. [Google Scholar] [CrossRef]
- Elander, D.; Faedo, A.F.; Mateos, D.; Pravos, D.; Subils, J.G. Mass spectrum of gapped, non-confining theories with multi-scale dynamics. J. High Energy Phys. 2019, 5, 175. [Google Scholar] [CrossRef]
- Leigh, R.G.; Minic, D.; Yelnikov, A. On the Glueball Spectrum of Pure Yang-Mills Theory in 2+1 Dimensions. Phys. Rev. D 2007, 76, 065018. [Google Scholar] [CrossRef]
- Rupak, G.; Shoresh, N. Chiral perturbation theory for the Wilson lattice action. Phys. Rev. D 2002, 66, 054503. [Google Scholar] [CrossRef]
- Sharpe, S.R.; Singleton, R.L., Jr. Spontaneous flavor and parity breaking with Wilson fermions. Phys. Rev. D 1998, 58, 074501. [Google Scholar] [CrossRef]
- Symanzik, K. Continuum Limit and Improved Action in Lattice Theories. 1. Principles and phi**4 Theory. Nucl. Phys. B 1983, 226, 187–204. [Google Scholar] [CrossRef]
- Luscher, M.; Sint, S.; Sommer, R.; Weisz, P. Chiral symmetry and O(a) improvement in lattice QCD. Nucl. Phys. B 1996, 478, 365–400. [Google Scholar] [CrossRef]
- Bar, O.; Golterman, M. Chiral perturbation theory for gradient flow observables. Phys. Rev. D 2014, 89, 034505, Erratum in Phys.Rev. D 2014, 89, 099905. [Google Scholar] [CrossRef]
- Jansen, K. et al. [ETM]. Meson masses and decay constants from unquenched lattice QCD. Phys. Rev. D 2009, 80, 054510. [Google Scholar] [CrossRef]
- The Turing Way Community. The Turing Way: A Handbook for Reproducible, Ethical and Collaborative Research (1.0.1); Zenodo: Geneva, Switzerland, 2021. [Google Scholar] [CrossRef]
- Smart, A.G. The war over supercooled water. Phys. Today 2018, 22. [Google Scholar] [CrossRef]
- Bennett, E.; Lenz, J. Recommendations for reproducibility in analysis of lattice data. in preparation.
- Hart, E.M.; Barmby, P.; LeBauer, D.; Michonneau, F.; Mount, S.; Mulrooney, P.; Poisot, T.; Woo, K.H.; Zimmerman, N.B.; Hollister, J.W. Ten Simple Rules for Digital Data Storage. PLoS Comput. Biol. 2016, 12, E1005097. [Google Scholar] [CrossRef] [PubMed]
- Available online: https://www.hdfgroup.org/solutions/hdf5 (accessed on 1 May 2023).
- Available online: https://www.zenodo.org (accessed on 1 May 2023).
- Rossum, G.V.; Drake, F.L. Python 3 Reference Manual; CreateSpace: Scotts Valley, CA, USA, 2009. [Google Scholar]
- Harris, C.R.; Millman, K.J.; Van Der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef] [PubMed]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Wolfram Research, Inc. Mathematica, Version 13.0; Wolfram Research, Inc.: Champaign, IL, USA, 2021. [Google Scholar]
- Available online: https://www.gnu.org/software/bash/ (accessed on 1 May 2023).
- Available online: https://www.gnu.org/software/make/ (accessed on 1 May 2023).
- Available online: https://conda.io/projects/conda/en/latest/ (accessed on 1 May 2023).
- Available online: https://github.com (accessed on 1 May 2023).
- Bennett, E. Status of reproducibility and open science in hep-lat in 2021. PoS LATTICE 2023, 2022, 337. [Google Scholar] [CrossRef]
- Athenodorou, A.; Bennett, E.; Lenz, J.; Papadopoullou, E. Open Science in Lattice Gauge Theory community. PoS Lattice 2023, 2022, 341. [Google Scholar] [CrossRef]
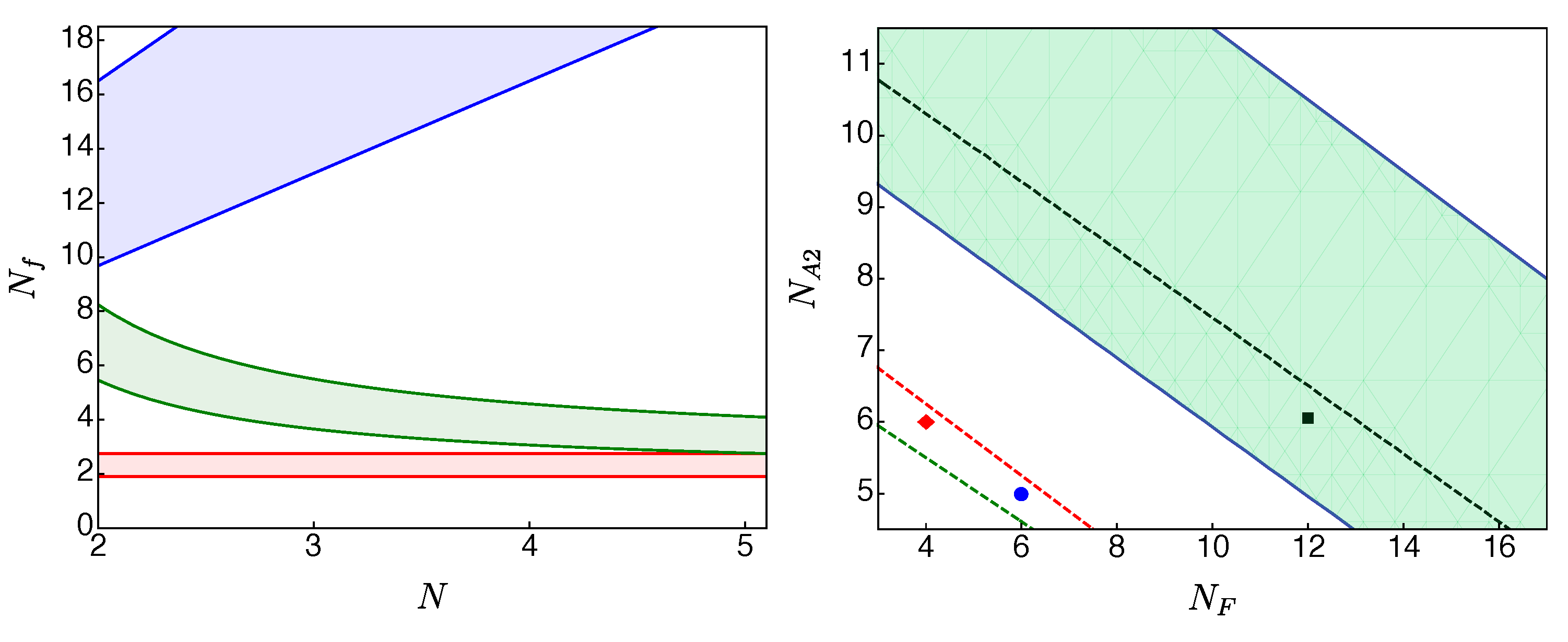
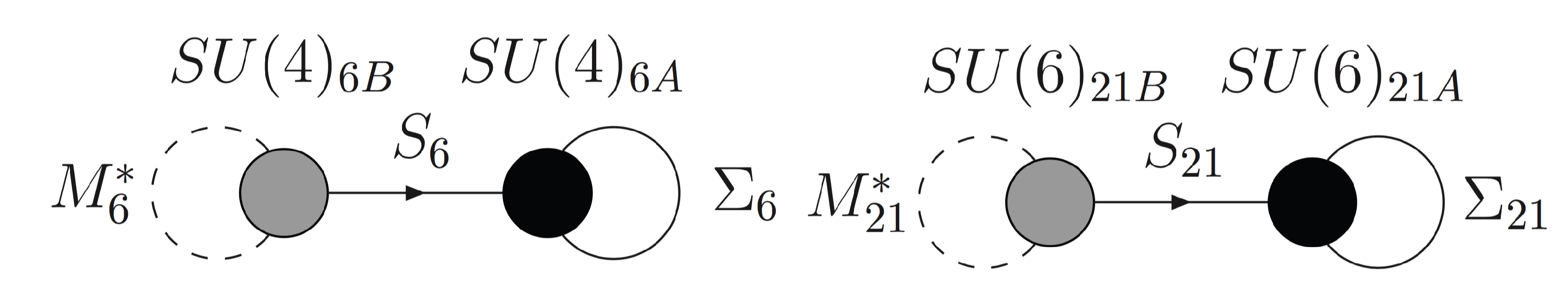



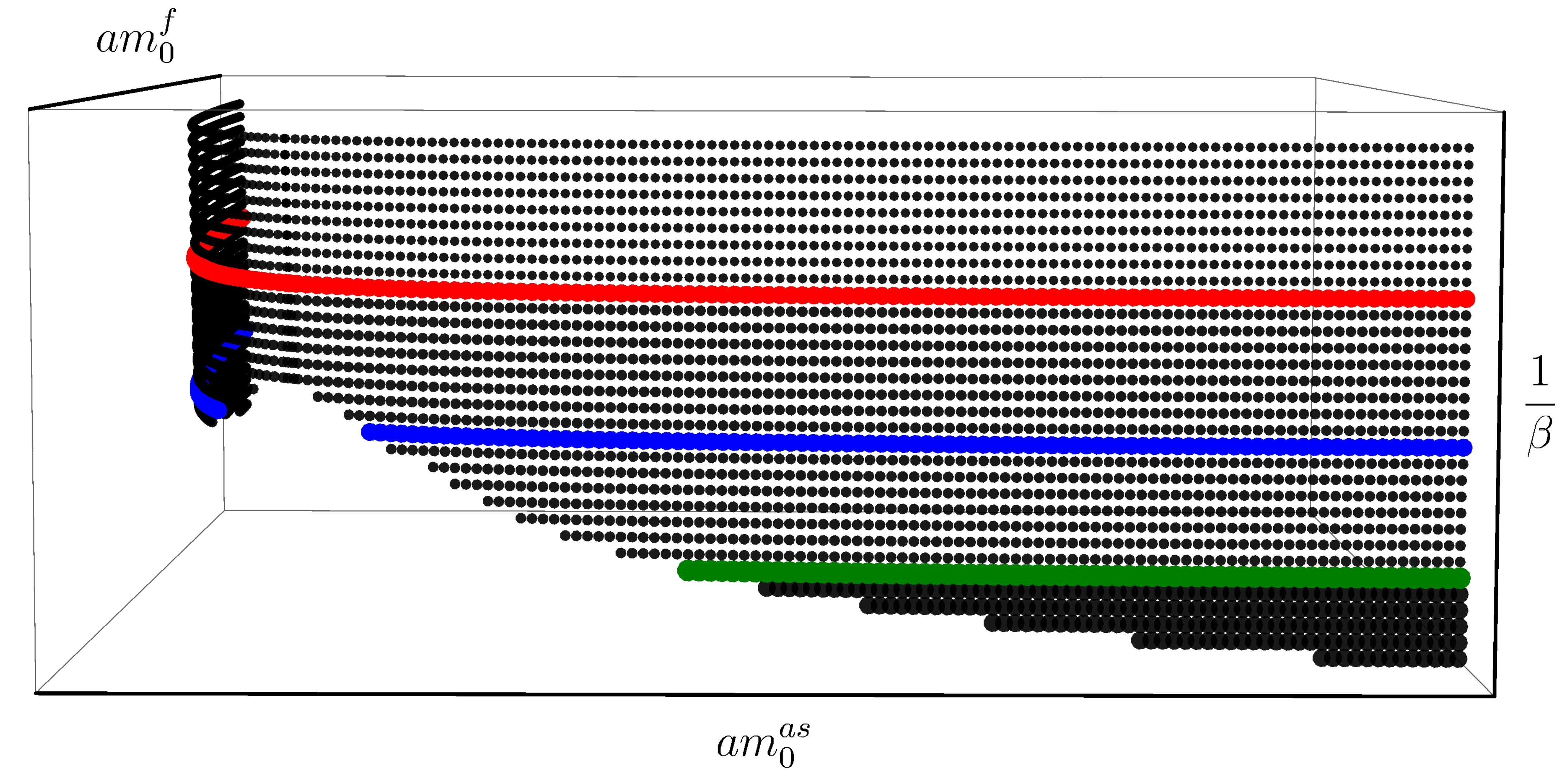
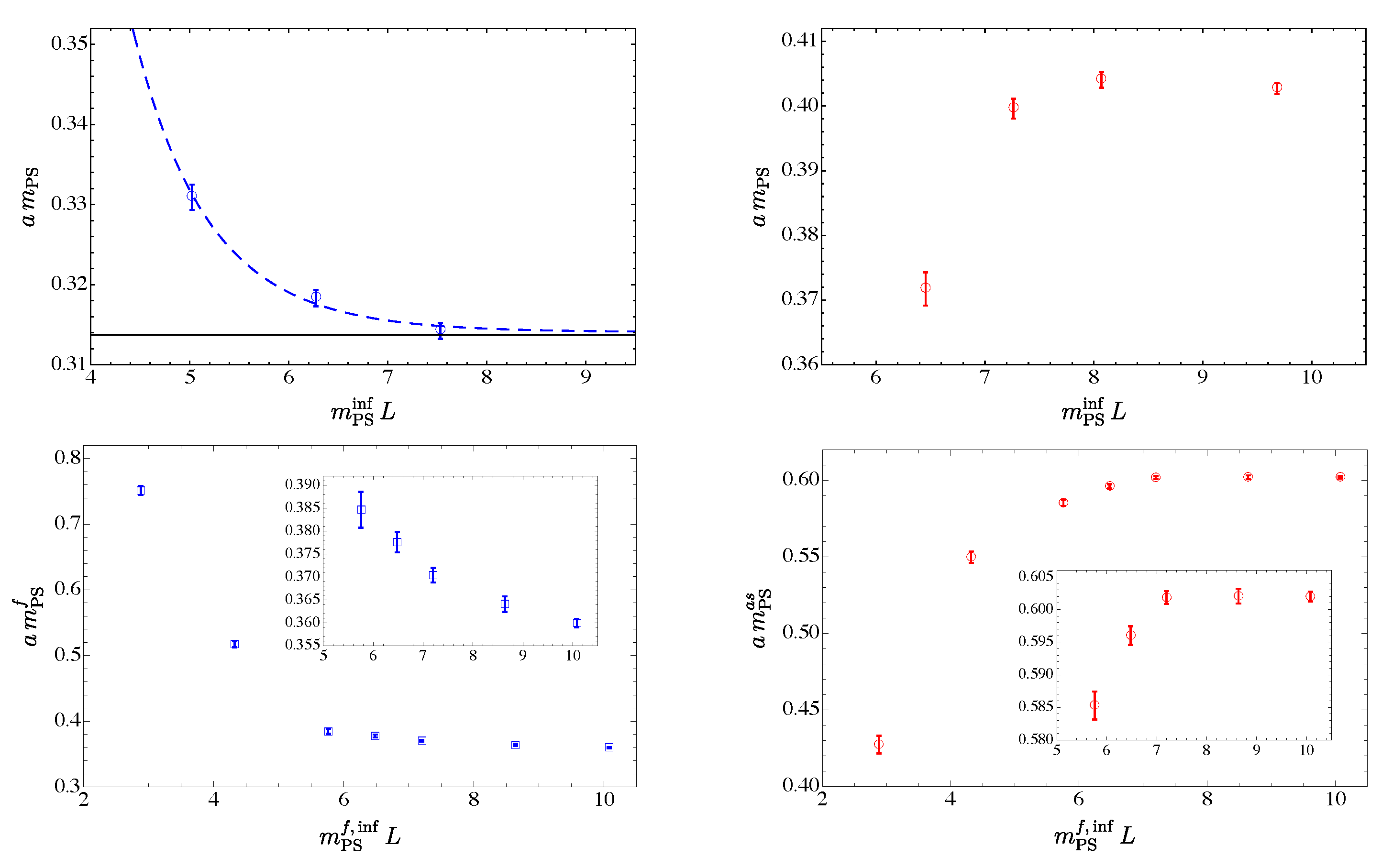
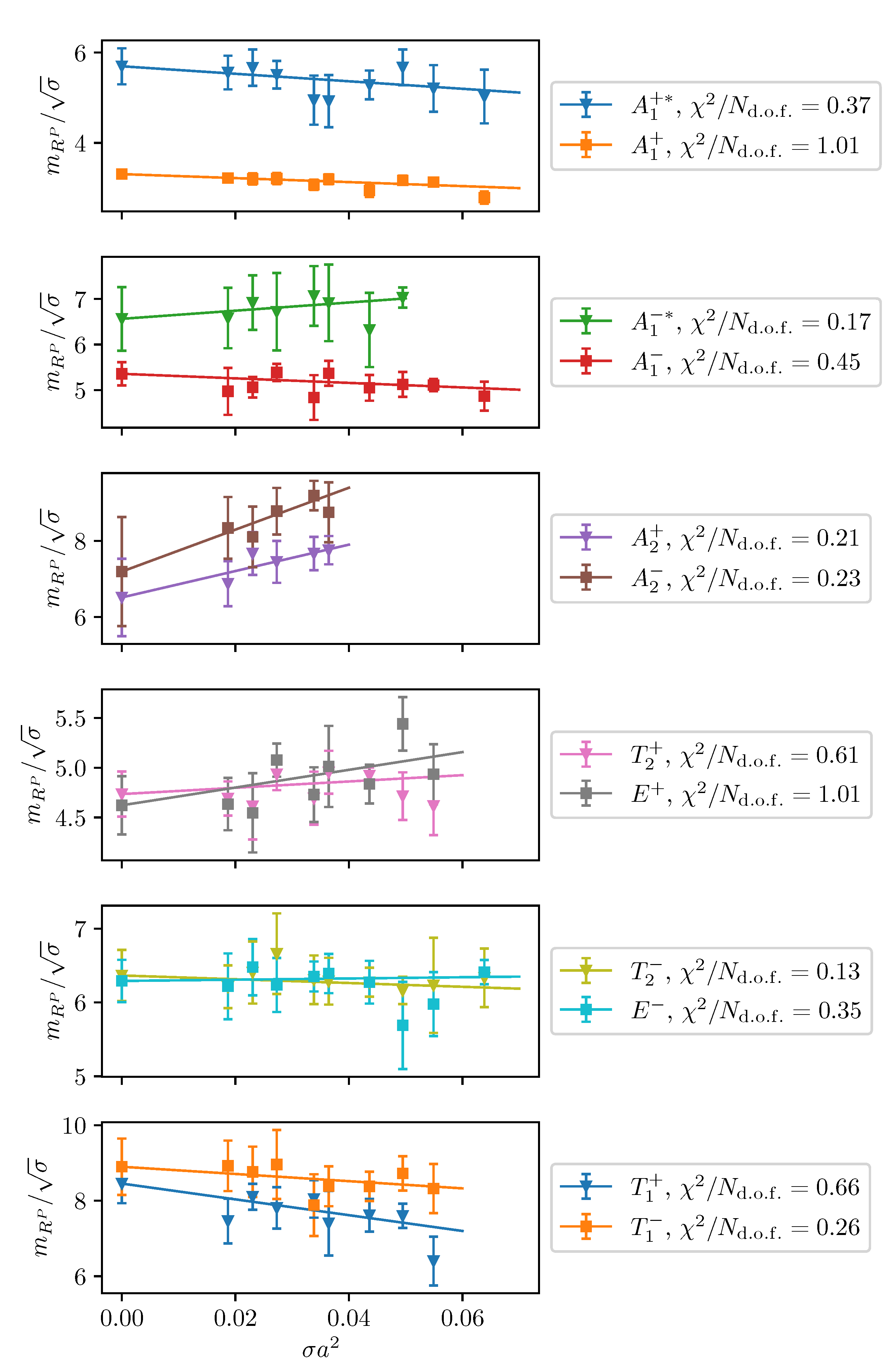
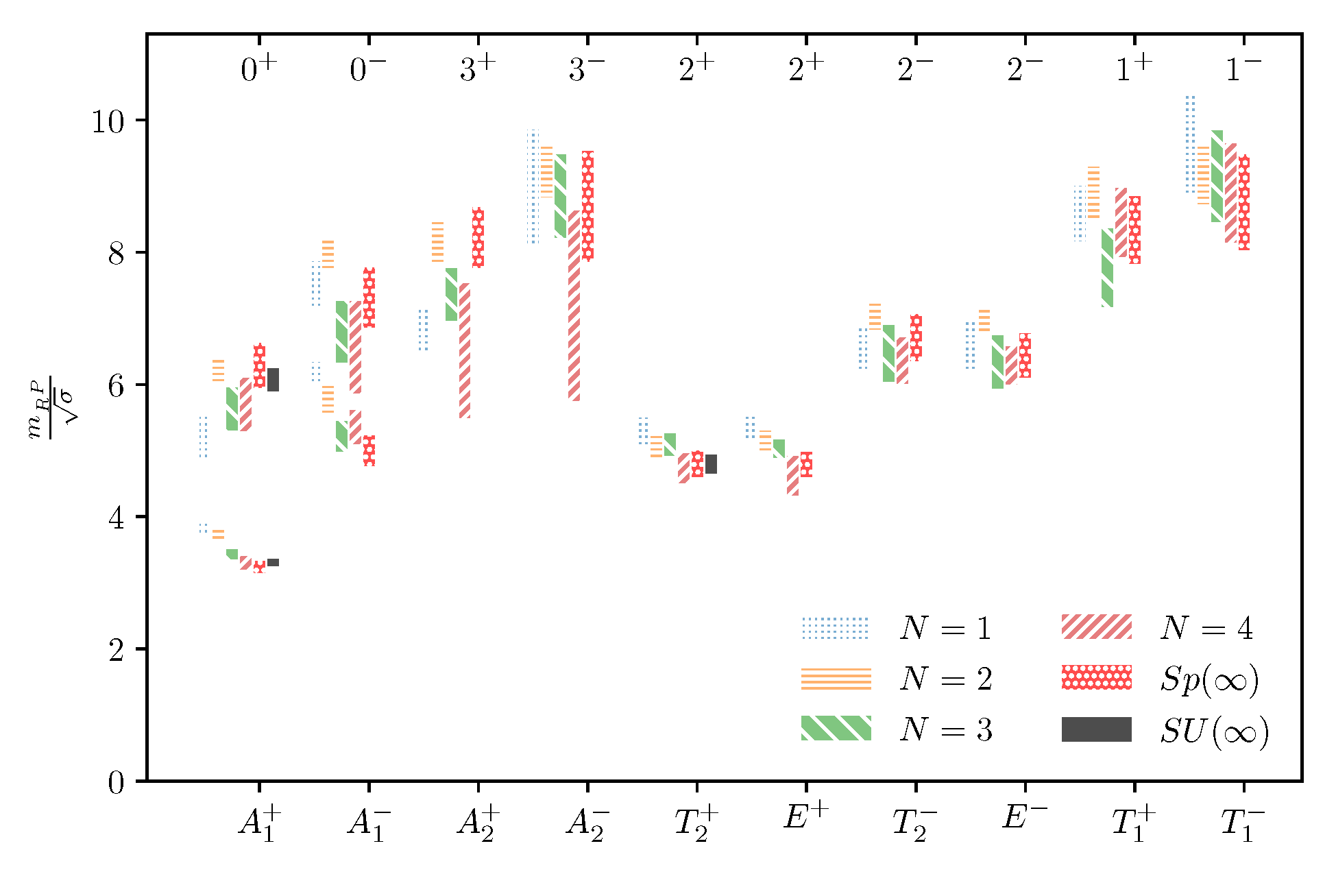
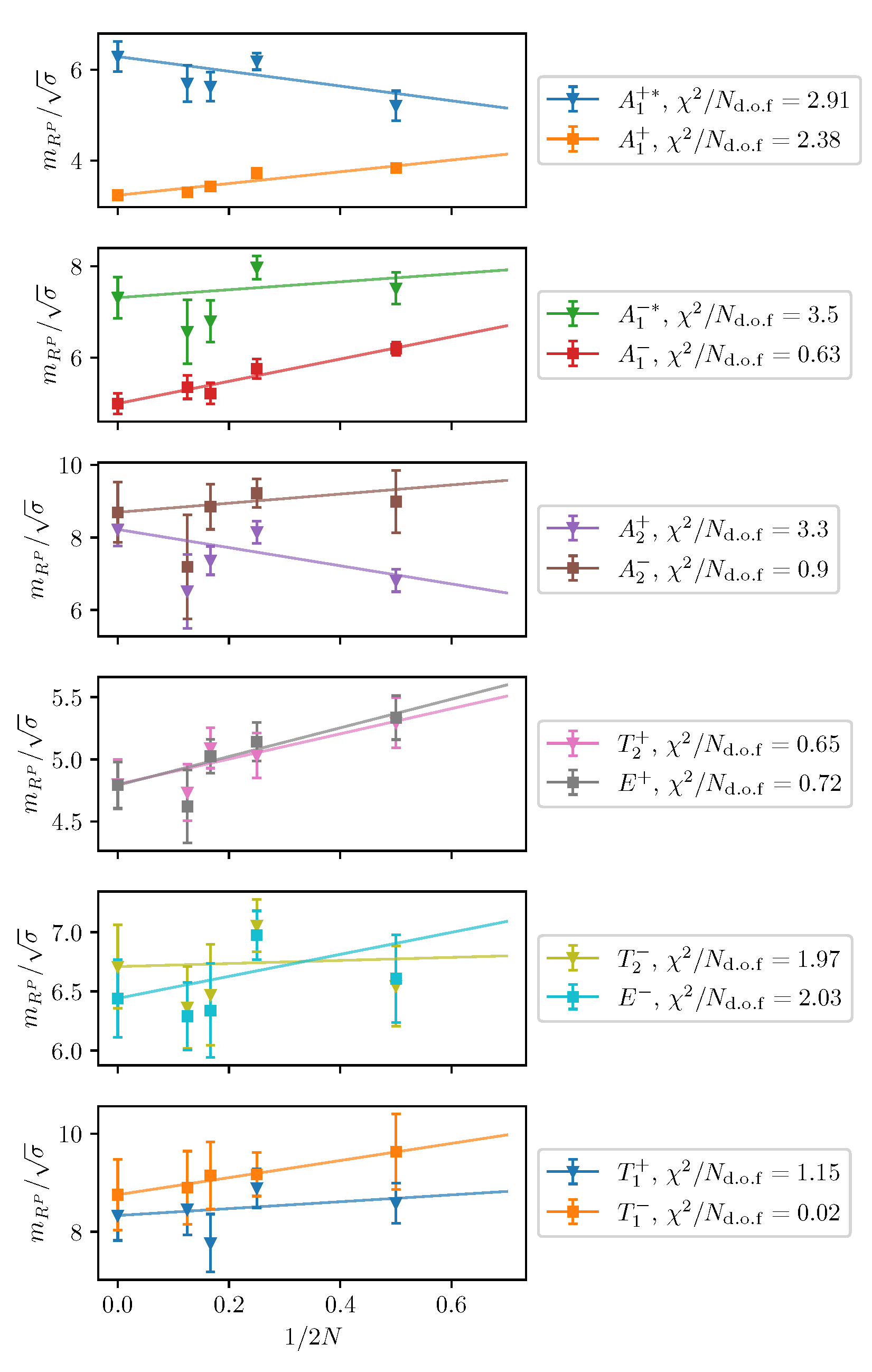
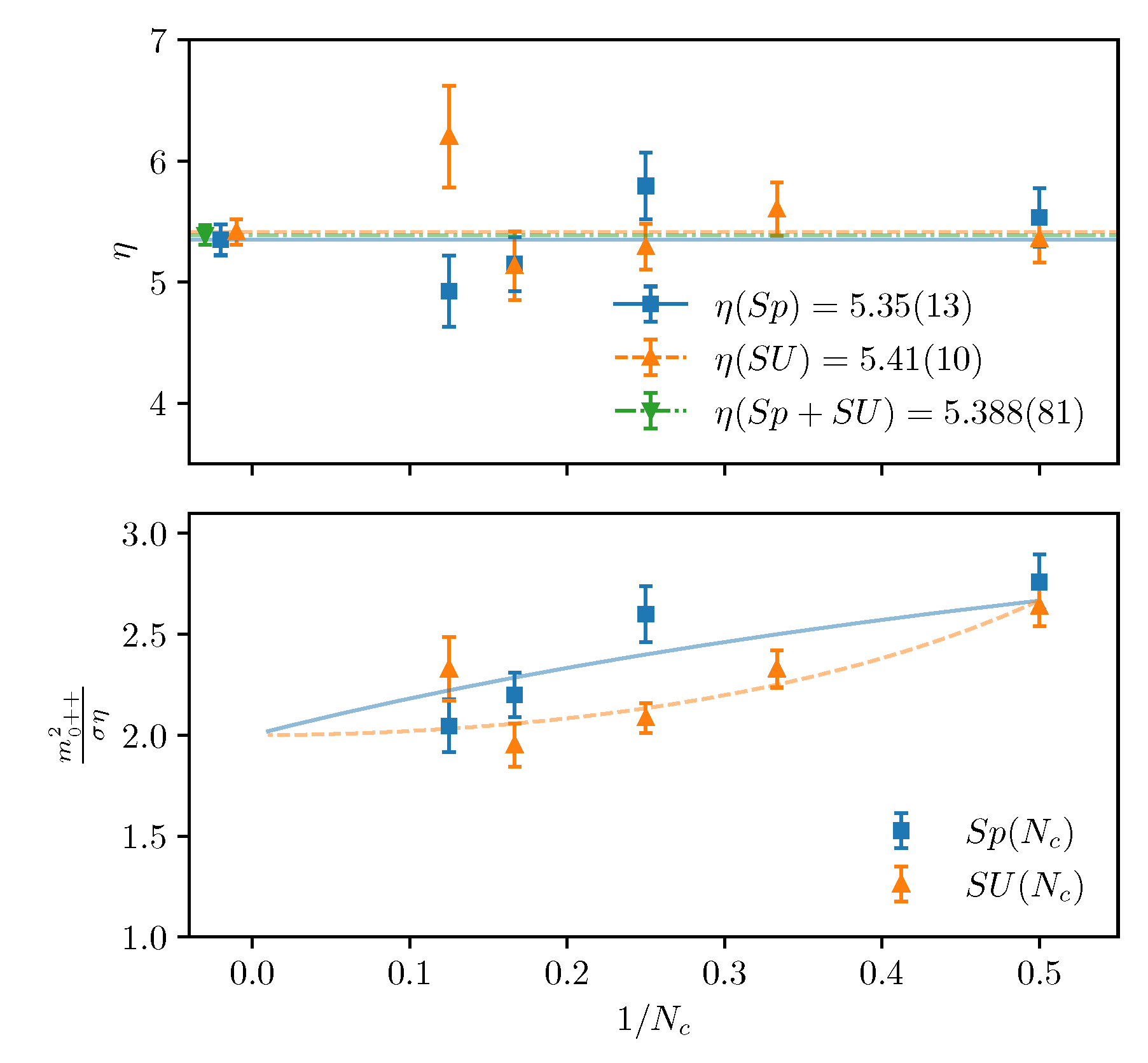
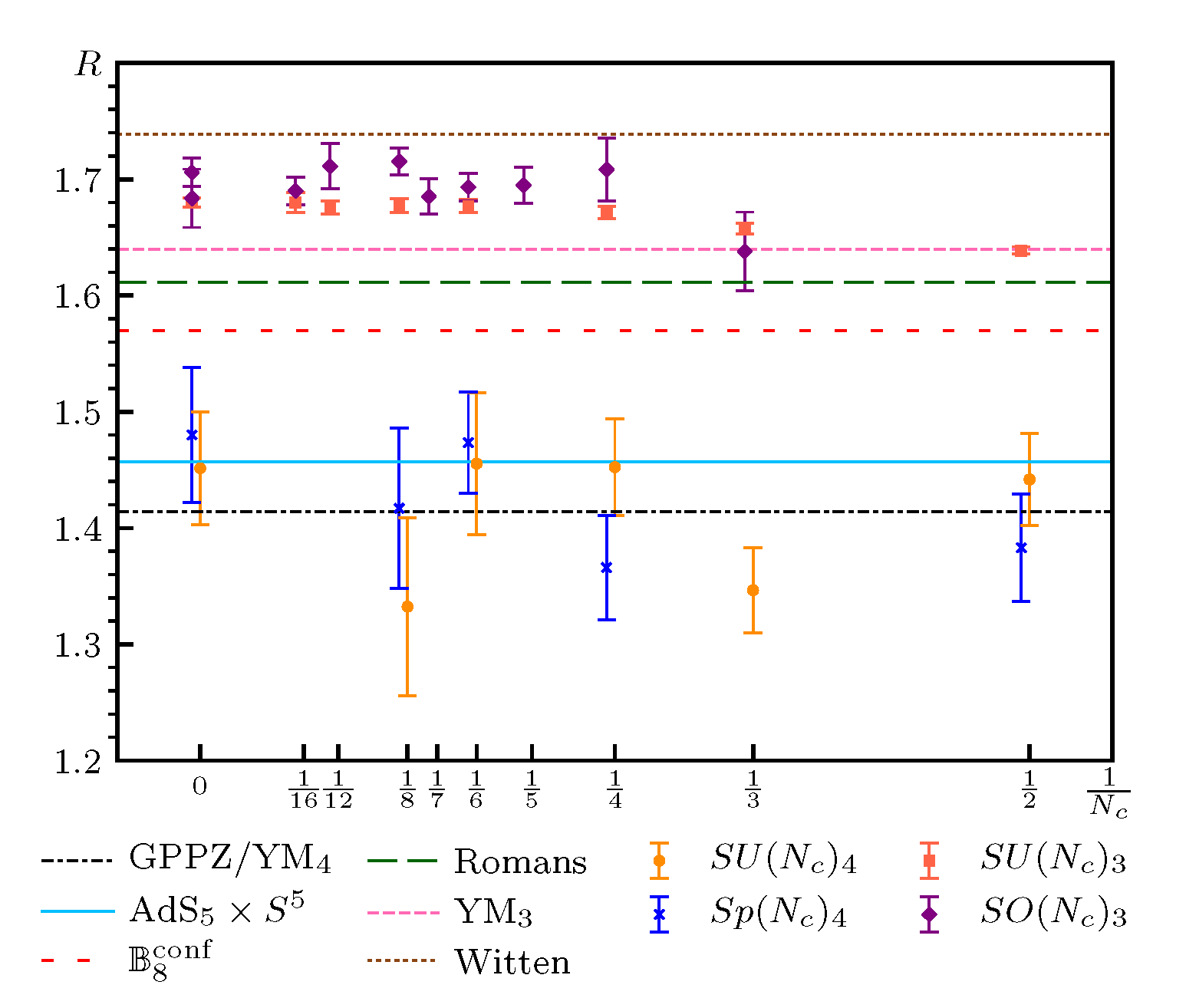
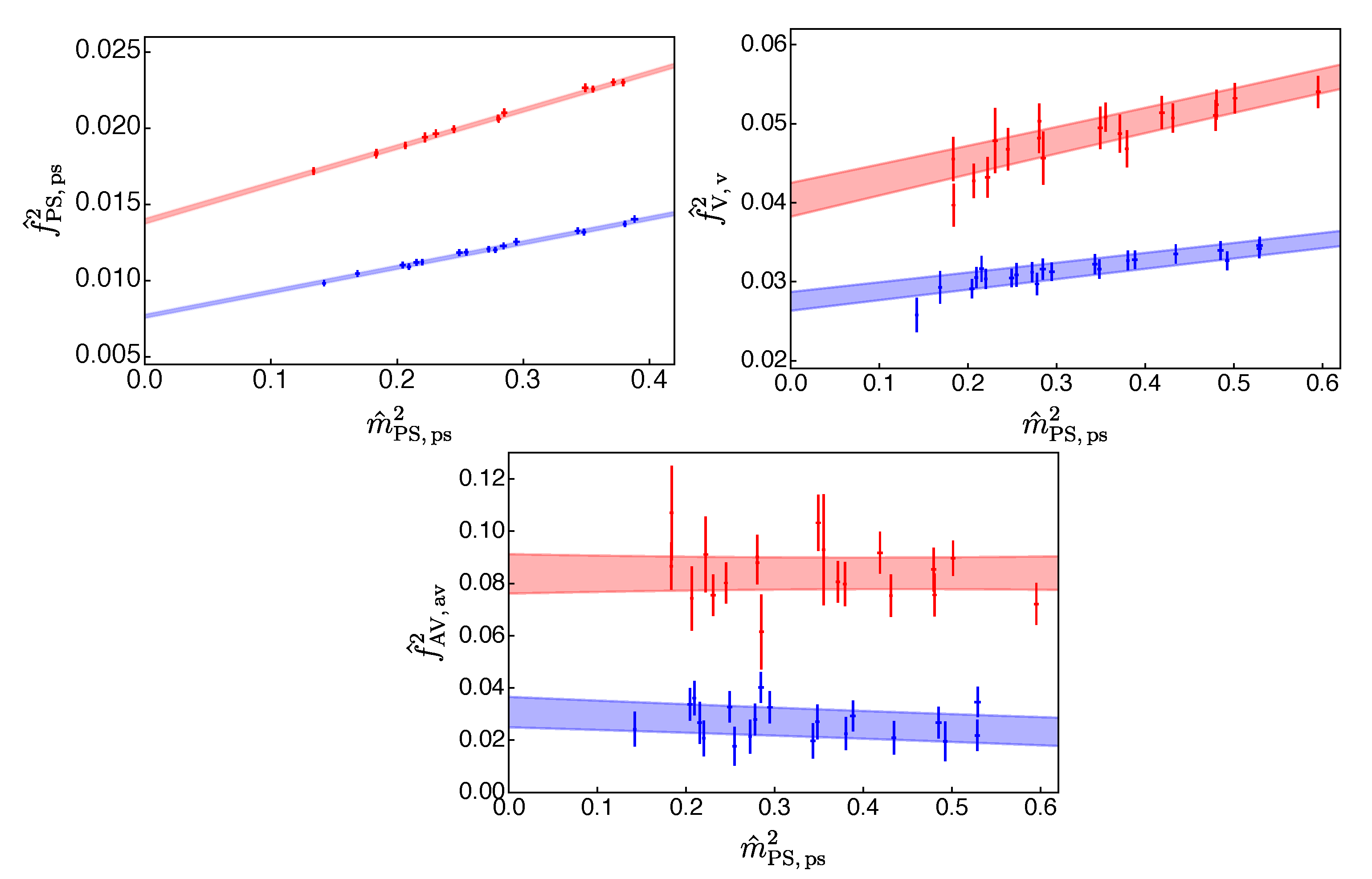

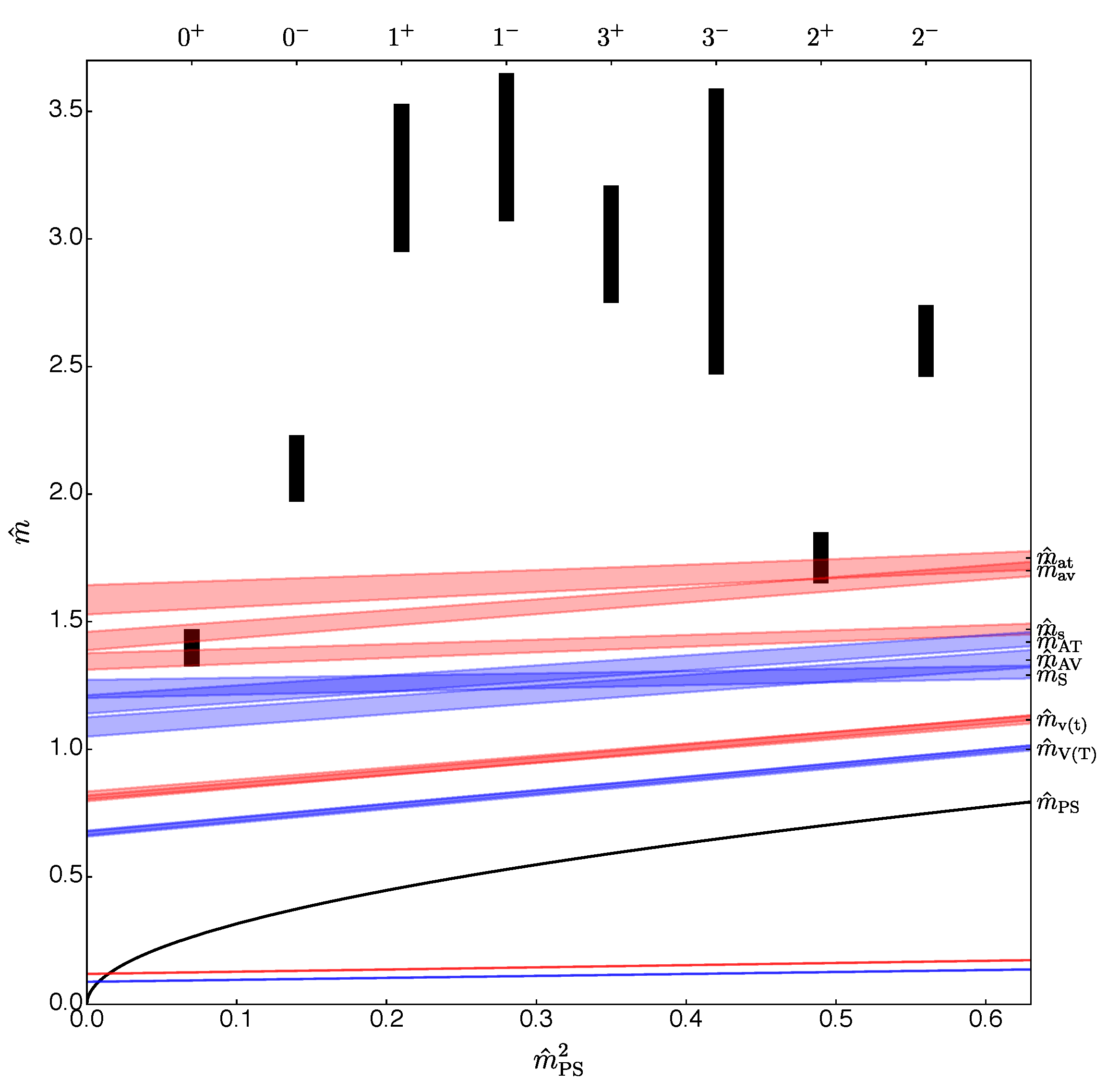

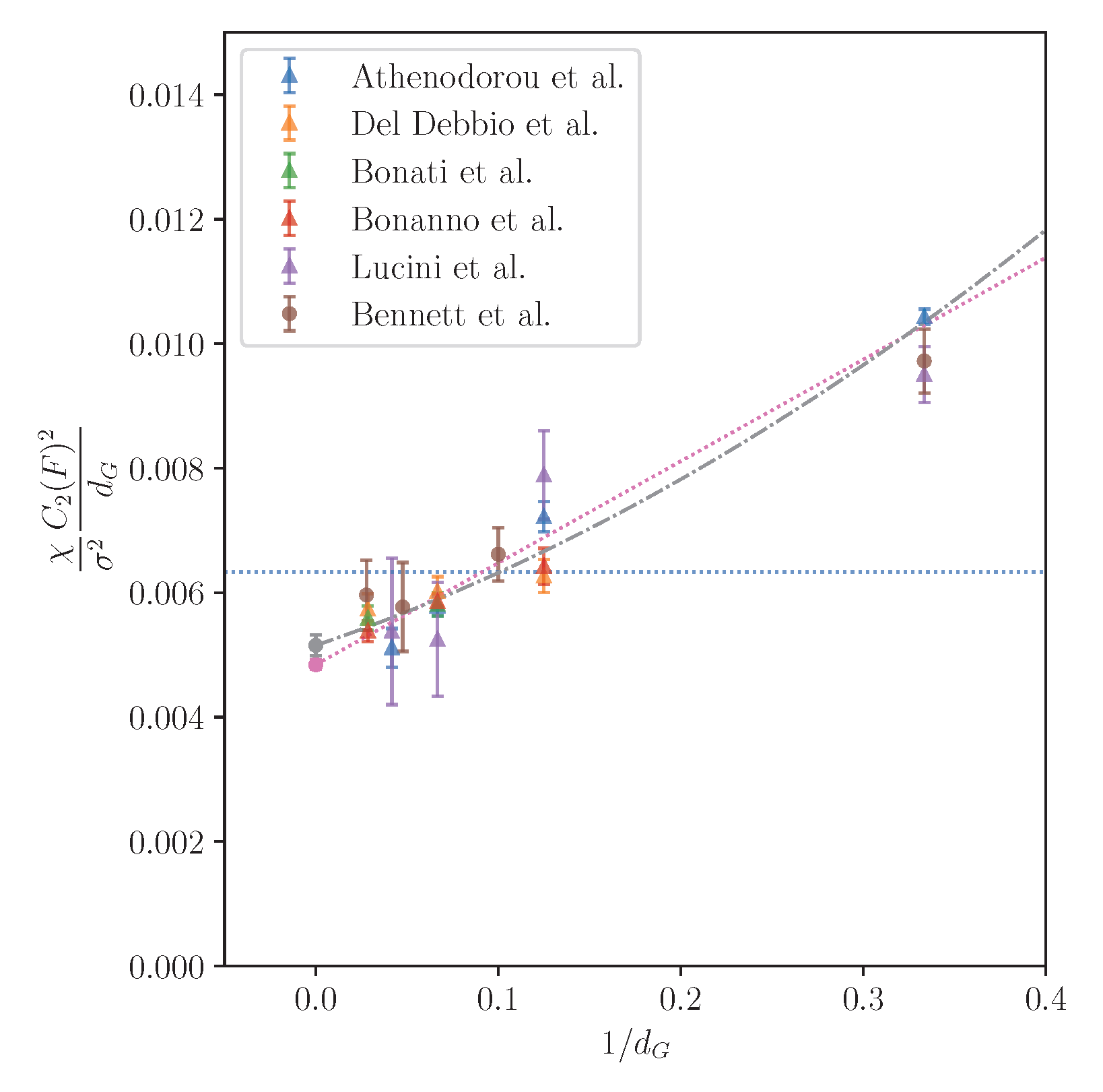
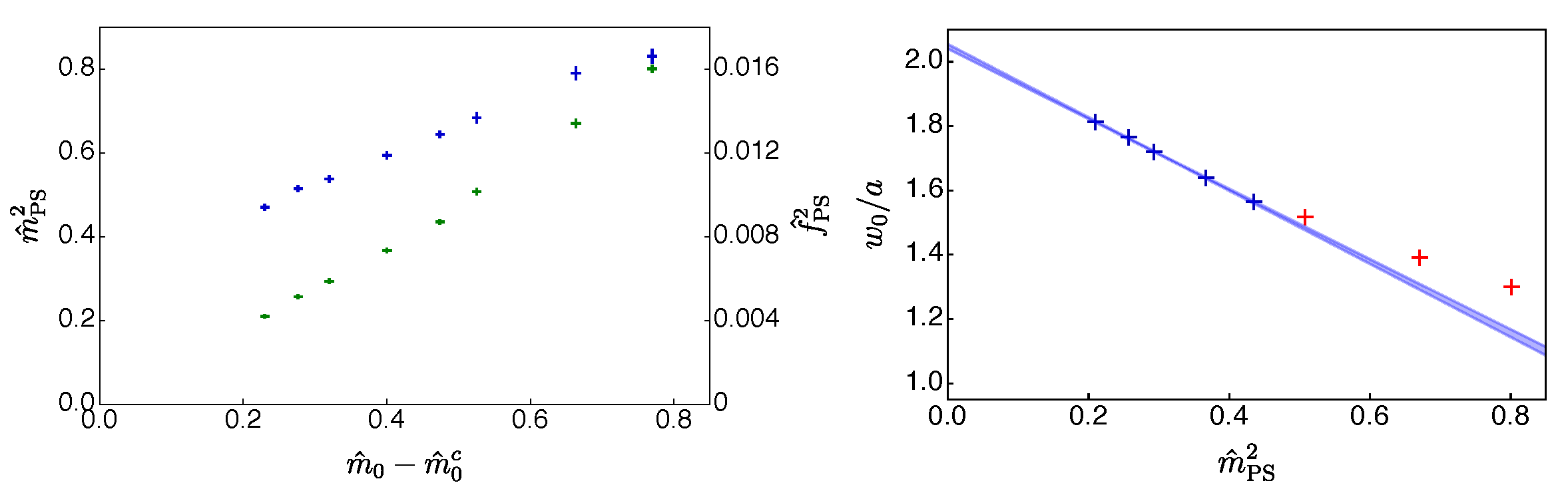
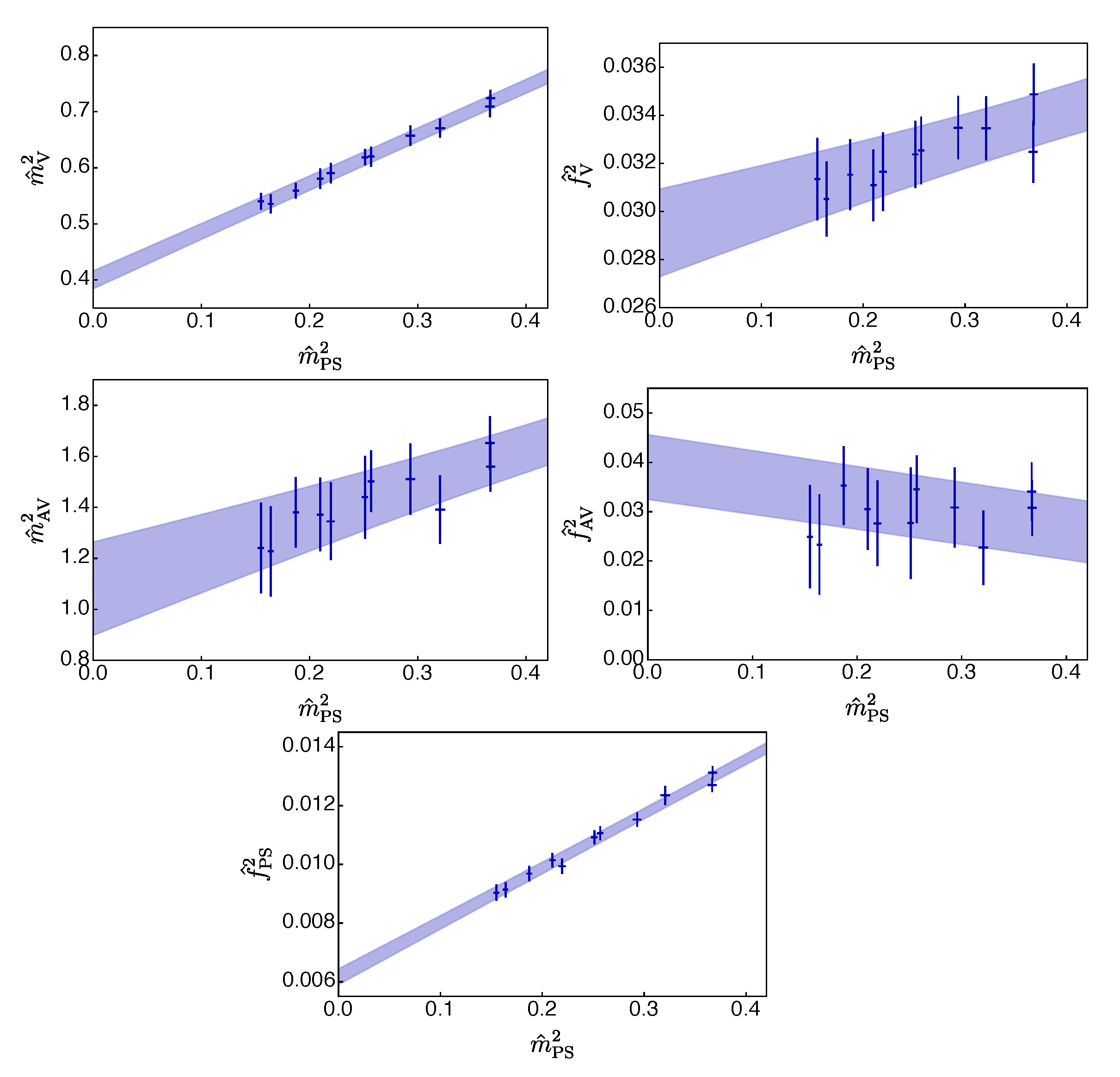

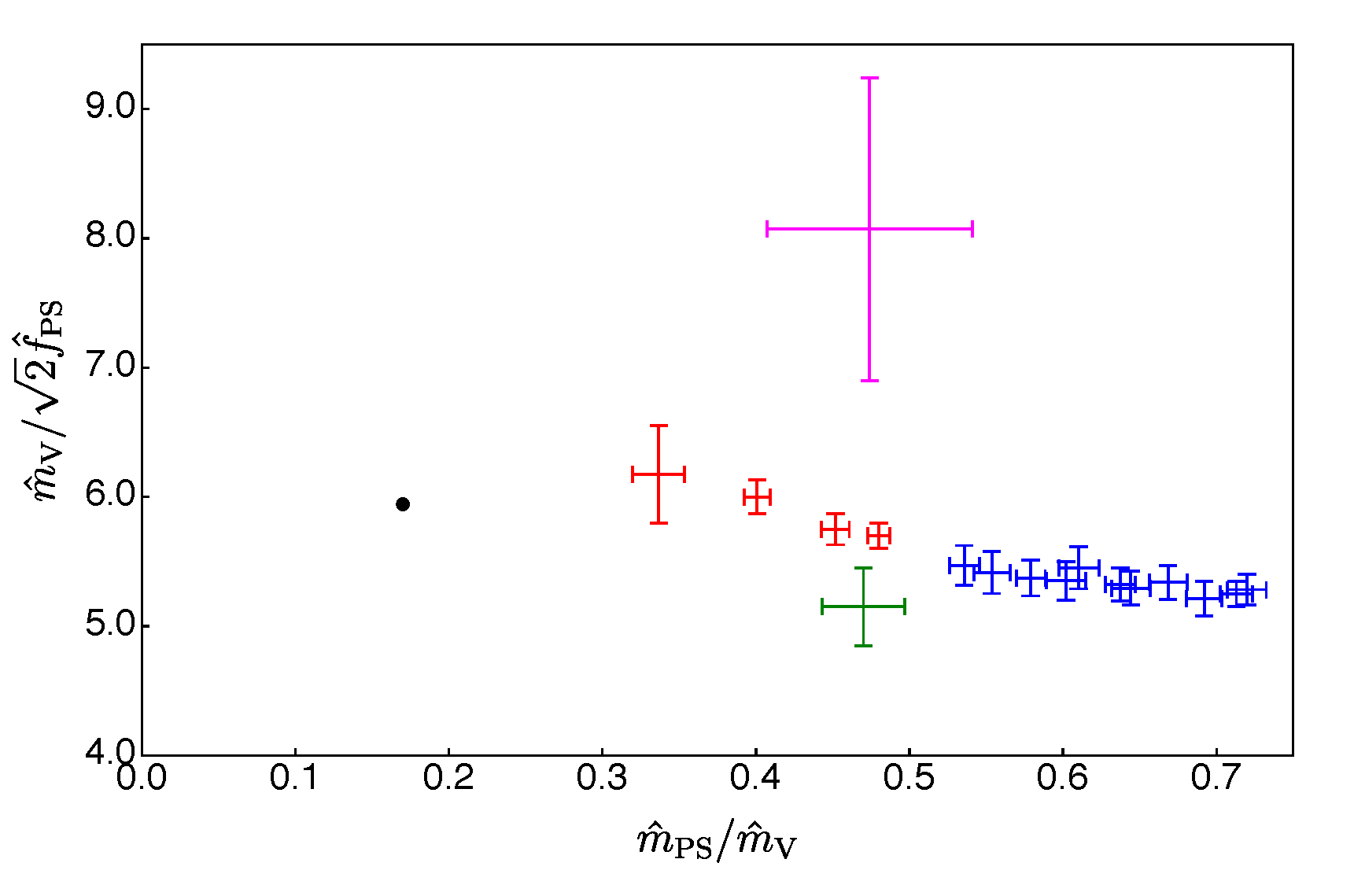
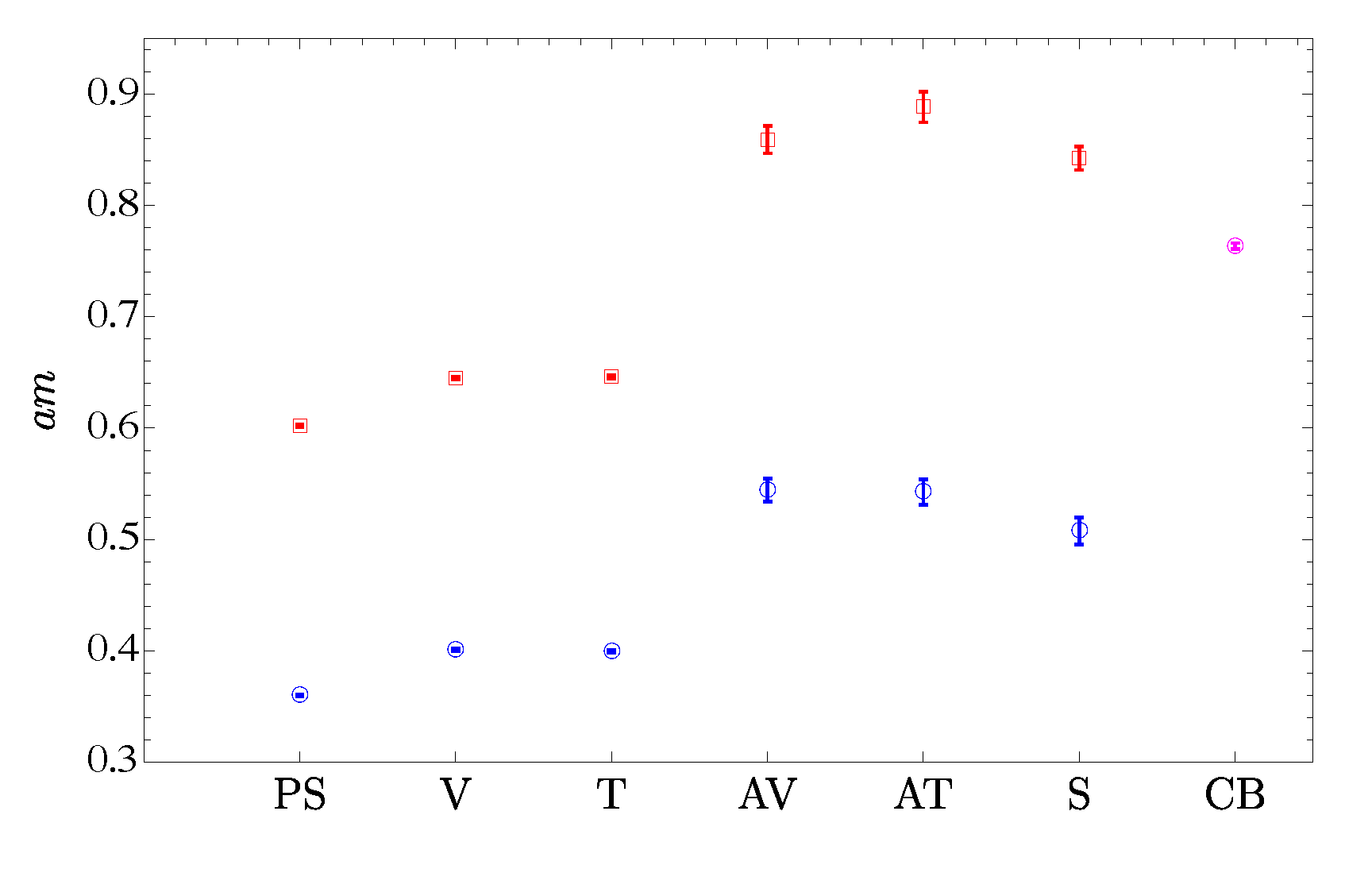
| Label M | Interpolating Operator | Mesons in QCD | |||
|---|---|---|---|---|---|
| PS | 5 | 1 | |||
| S | 5 | 1 | |||
| V | 10 | 1 | |||
| T | 10 | 1 | |||
| AV | 5 | 1 | |||
| AT | 10 | 1 | |||
| ps | 1 | ||||
| s | 1 | ||||
| v | 1 | 15 | |||
| t | 1 | 15 | |||
| av | 1 | ||||
| at | 1 | 15 |
| Label | Interpolating Operator | ||
|---|---|---|---|
| 5 | 6 | ||
| 5 | 6 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bennett, E.; Holligan, J.; Hong, D.K.; Hsiao, H.; Lee, J.-W.; Lin, C.-J.D.; Lucini, B.; Mesiti, M.; Piai, M.; Vadacchino, D. Sp(2N) Lattice Gauge Theories and Extensions of the Standard Model of Particle Physics. Universe 2023, 9, 236. https://doi.org/10.3390/universe9050236
Bennett E, Holligan J, Hong DK, Hsiao H, Lee J-W, Lin C-JD, Lucini B, Mesiti M, Piai M, Vadacchino D. Sp(2N) Lattice Gauge Theories and Extensions of the Standard Model of Particle Physics. Universe. 2023; 9(5):236. https://doi.org/10.3390/universe9050236
Chicago/Turabian StyleBennett, Ed, Jack Holligan, Deog Ki Hong, Ho Hsiao, Jong-Wan Lee, C.-J. David Lin, Biagio Lucini, Michele Mesiti, Maurizio Piai, and Davide Vadacchino. 2023. "Sp(2N) Lattice Gauge Theories and Extensions of the Standard Model of Particle Physics" Universe 9, no. 5: 236. https://doi.org/10.3390/universe9050236
APA StyleBennett, E., Holligan, J., Hong, D. K., Hsiao, H., Lee, J.-W., Lin, C.-J. D., Lucini, B., Mesiti, M., Piai, M., & Vadacchino, D. (2023). Sp(2N) Lattice Gauge Theories and Extensions of the Standard Model of Particle Physics. Universe, 9(5), 236. https://doi.org/10.3390/universe9050236







