Cosmological Neutrino N-Body Simulations of Dark Matter Halo
Abstract
1. Introduction
1.1. Neutrinos
1.2. N-Body Simulations
1.3. TianZero and TianNu
2. Numerical Methods
2.1. Parameter Preset
2.2. Code Overview
2.3. Halo Data and Parameters
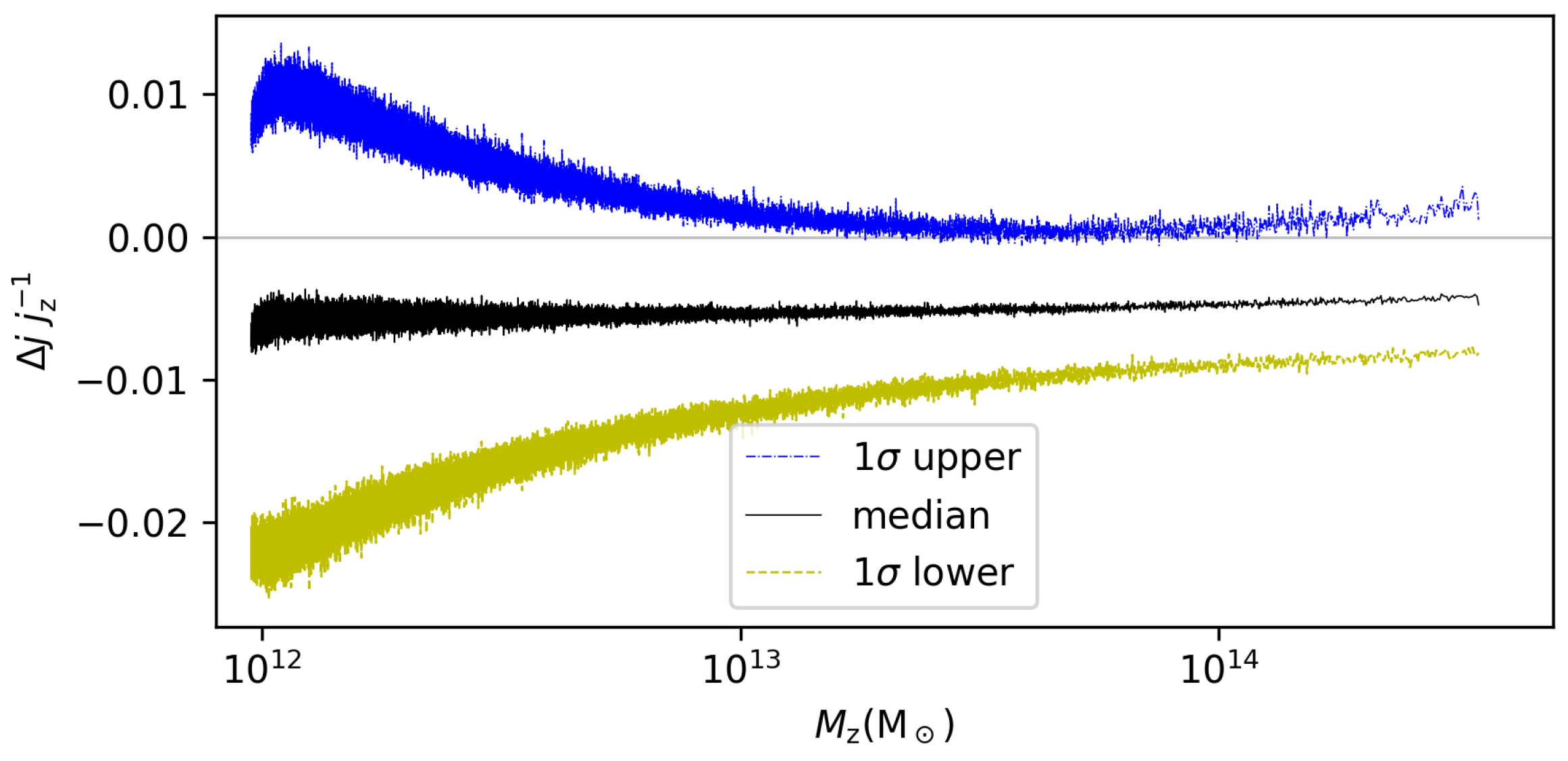
3. Data Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Arnaboldi, C.; Artusa, D.R.; Avignone, F.T.I.; Balata, M.; Bandac, I.; Barucci, M.; Beeman, J.W.; Brofferio, C.; Bucci, C.; Capelli, S.; et al. New Limit on the Neutrinoless ββ Decay of 130Te. Phys. Rev. Lett. 2005, 95, 142501. [Google Scholar] [CrossRef] [PubMed]
- Avignone, F.T.; Elliott, S.R.; Engel, J. Double Beta Decay, Majorana Neutrinos, and Neutrino Mass. Rev. Mod. Phys. 2008, 80, 481. [Google Scholar] [CrossRef]
- Azzolini, O.; Barrera, M.T.; Beeman, J.W.; Bellini, F.; Beretta, M.; Biassoni, M.; Brofferio, C.; Bucci, C.; Canonica, L.; Capelli, S.; et al. 0νββ decay: The CUPID-0 experiment. J. Phys. Conf. Ser. 2018, 1056, 012044. [Google Scholar] [CrossRef]
- Collaboration, K. KATRIN: A next generation tritium beta decay experiment with sub-eV sensitivity for the electron neutrino mass. Physics 2001, 51, 69–76. [Google Scholar]
- Thümmler, T.; Marx, R.; Weinheimer, C. Precision high voltage divider for the KATRIN experiment. New J. Phys. 2012, 11, 1911–1915. [Google Scholar] [CrossRef]
- Houdy, T.; Alborini, A.; Altenmüller, K.; Biassoni, M.; Bombelli, L.; Brunst, T.; Carminati, M.; Descher, M.; Fink, D.; Fiorini, C.; et al. Hunting keV sterile neutrinos with KATRIN: Building the first TRISTAN module. J. Phys. Conf. Ser. 2020, 1468, 012177. [Google Scholar] [CrossRef]
- Aker, M.; Altenmüller, K.; Arenz, M.; Baek, W.J.; Barrett, J.; Beglarian, A.; Behrens, J.; Berlev, A.; Besserer, U.; Blaum, K.; et al. First operation of the KATRIN experiment with tritium. Eur. Phys. J. C 2020, 80, 264. [Google Scholar] [CrossRef]
- Aker, M.; Altenmüller, K.; Beglarian, A.; Behrens, J.; Berlev, A.; Besserer, U.; Bieringer, B.; Blaum, K.; Block, F.; Bornschein, B.; et al. Analysis methods for the first KATRIN neutrino-mass measurement. Phys. Rev. D 2021, 104, 012005. [Google Scholar] [CrossRef]
- Aker, M.; Altenmüller, K.; Amsbaugh, J.F.; Arenz, M.; Babutzka, M.; Bast, J.; Bauer, S.; Bechtler, H.; Beck, M.; Beglarian, A.; et al. The design, construction, and commissioning of the KATRIN experiment. J. Instrum. 2021, 16, T08015. [Google Scholar] [CrossRef]
- Kornowski, S. Cosmic Neutrino Background. vixra 2015. viXra:1307.0048. [Google Scholar]
- Tully, C.G.; Zhang, G. Impact of Warm Dark Matter on the Cosmic Neutrino Background Anisotropies. Universe 2022, 8, 118. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al.; [Planck Collaboration] Planck 2018 results. V. CMB power spectra and likelihoods. Astron. Astrophys. 2020, 641, A5. [Google Scholar] [CrossRef]
- Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; Benabed, K.; et al.; [Planck Collaboration] Planck 2018 results. VII. Isotropy and statistics of the CMB. Astron. Astrophys. 2020, 641, A7. [Google Scholar] [CrossRef]
- Lewis, A.; Challinor, A.; Lasenby, A. Efficient Computation of CMB anisotropies in closed FRW models. Astrophys. J. 1999, 538, 473–476. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Battaner, E.; et al.; [Planck Collaboration] Planck intermediate results. XL. The Sunyaev-Zeldovich signal from the Virgo cluster. Astron. Astrophys. 2015, 596, 25–27. [Google Scholar]
- Petrakou, E.; Bravina, L.; Foka, Y.; Kabana, S. Haloscope searches for dark matter axions at the Center for Axion and Precision Physics Research. EPJ Web Conf. 2017, 164, 01012. [Google Scholar] [CrossRef]
- Millar, A.J.; Anlage, S.M.; Balafendiev, R.; Belov, P.; van Bibber, K.; Conrad, J.; Demarteau, M.; Droster, A.; Dunne, K.; Rosso, A.G.; et al. Searching for dark matter with plasma haloscopes. Phys. Rev. D 2023, 107, 055013. [Google Scholar] [CrossRef]
- Katrin, N.; et al.; [The KATRIN Collaboration] Direct neutrino-mass measurement with sub-electronvolt sensitivity. Nat. Phys. 2022, 18, 160–166. [Google Scholar] [CrossRef]
- Pompa, F.; Capozzi, F.; Mena, O.; Sorel, M. Absolute ν Mass Measurement with the DUNE Experiment. Phys. Rev. Lett. 2022, 129, 121802. [Google Scholar] [CrossRef]
- Bellini, E.; Cuesta, A.J.; Jimenez, R.; Verde, L. Constraints on deviations from ΛCDM within Horndeski gravity. J. Cosmol. Astropart. Phys. 2016, 2016, 053. [Google Scholar] [CrossRef]
- Sharov, G.S.; Myachin, V.E. Modified Equations of State for Dark Energy and Observational Limitations. Universe 2022, 8, 201. [Google Scholar] [CrossRef]
- Olive, K.A.; et al.; [Particle Data Group] Review of Particle Physics. Chin. Phys. C 2014, 38, 090001. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al.; [Planck Collaboration] Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar] [CrossRef]
- Zhu, H.M.; Pen, U.L.; Chen, X.; Inman, D.; Yu, Y. Measurement of Neutrino Masses from Relative Velocities. Phys. Rev. Lett. 2014, 113, 131301. [Google Scholar] [CrossRef]
- Harnois-Déraps, J.; Pen, U.L.; Iliev, I.T.; Merz, H.; Emberson, J.D.; Desjacques, V. High-performance P3M N-body code: CUBEP3M. Mon. Not. R. Astron. Soc. 2013, 436, 540–559. [Google Scholar] [CrossRef]
- Ali-Haïmoud, Y.; Bird, S. An efficient implementation of massive neutrinos in non-linear structure formation simulations. Mon. Not. R. Astron. Soc. 2013, 428, 3375–3389. [Google Scholar] [CrossRef]
- Nelson, D.L.; Peebles, J.; Pancotto, F. Phonetic similarity as opposed to informational structure as a determinant of word encoding. J. Exp. Psychol. 1970, 86, 117–119. [Google Scholar] [CrossRef]
- Miyoshi, K.; Kihara, T. Development of the correlation of galaxies in an expanding universe. Publ. Astron. Soc. Jpn. 1975, 27, 333–346. [Google Scholar]
- White, S.D.M. The Dynamics of Rich Clusters of Galaxies. Mon. Not. R. Astron. Soc. 1976, 177, 717–733. [Google Scholar] [CrossRef]
- Aarseth, S.J.; Turner, E.L.; Gott, J.R.I. N-body simulations of galaxy clustering. I-Initial conditions and galaxy collapse times. Astrophys. J. 1979, 228, 664–683. [Google Scholar] [CrossRef]
- Weisz, D.R.; Dolphin, A.E.; Skillman, E.D.; Holtzman, J.; Gilbert, K.M.; Dalcanton, J.J.; Williams, B.F. The Star Formation Histories of Local Group Dwarf Galaxies II. Searching For Signatures of Reionization. Astrophys. J. 2014, 789, 3733–3741. [Google Scholar] [CrossRef]
- Cheng, S.; Yu, H.R.; Inman, D.; Liao, Q.; Wu, Q.; Lin, J. CUBE—Towards an Optimal Scaling of Cosmological N-body Simulations. In Proceedings of the 2020 20th IEEE/ACM International Symposium on Cluster, Cloud and Internet Computing (CCGRID), Melbourne, VIC, Australia, 11–14 May 2020. [Google Scholar] [CrossRef]
- Yu, H.R.; Pen, U.L.; Wang, X. CUBE: An Information-optimized Parallel Cosmological N-body Algorithm. Astrophys. J. Suppl. Ser. 2018, 237, 24. [Google Scholar] [CrossRef]
- Coulton, W.R.; Villaescusa-Navarro, F.; Jamieson, D.; Baldi, M.; Jung, G.; Karagiannis, D.; Liguori, M.; Verde, L.; Wandelt, B.D. Quijote-PNG: Simulations of Primordial Non-Gaussianity and the Information Content of the Matter Field Power Spectrum and Bispectrum. Astrophys. J. 2023, 943, 64. [Google Scholar] [CrossRef]
- Hernández-Aguayo, C.; Springel, V.; Pakmor, R.; Barrera, M.; Ferlito, F.; White, S.D.M.; Hernquist, L.; Hadzhiyska, B.; Delgado, A.M.; Kannan, R.; et al. The MillenniumTNG Project: High-precision predictions for matter clustering and halo statistics. arXiv 2022, arXiv:2210.10059. [Google Scholar] [CrossRef]
- Elson, E.; Glowacki, M.; Davé, R. Measurements of the angular momentum-mass relations in the SIMBA simulation. New Ast. 2023, 99, 101964. [Google Scholar] [CrossRef]
- Costanzi, M.; Villaescusa-Navarro, F.; Viel, M.; Xia, J.; Borgani, S.; Castorina, E.; Sefusatti, E. Cosmology with massive neutrinos III: The halo mass function and an application to galaxy clusters. Physics 2013, 12, 92–101. [Google Scholar] [CrossRef]
- Inman, D.; Emberson, J.D.; Pen, U.L.; Farchi, A.; Yu, H.R.; Harnois-Déraps, J. Precision reconstruction of the dark matter-neutrino relative velocity from N-body simulations. Phys. Rev. D 2015, 92, 023502. [Google Scholar] [CrossRef]
- Blas, D.; Lesgourgues, J.; Tram, T. The Cosmic Linear Anisotropy Solving System (CLASS). Part II: Approximation schemes. J. Cosmol. Astropart. Phys. 2011, 2011, 034. [Google Scholar] [CrossRef]
- Inman, D.; Yu, H.R.; Zhu, H.M.; Emberson, J.D.; Pen, U.L.; Zhang, T.J.; Yuan, S.; Chen, X.; Xing, Z.Z. Simulating the cold dark matter-neutrino dipole with TianNu. Phys. Rev. D 2017, 95, 083518. [Google Scholar] [CrossRef]
- Qin, J.; Liang, Y.; Zhao, C.; Yu, H.R.; Liu, Y.; Zhang, T.J. The Effect of Massive Neutrinos on the Position of Cold Dark Matter Halo: Revealed via the Delaunay Triangulation Void. Astrophys. J. 2018, 862, 60. [Google Scholar] [CrossRef]
- Yu, H.R.; Emberson, J.D.; Inman, D.; Zhang, T.J.; Pen, U.L.; Harnois-Déraps, J.; Yuan, S.; Teng, H.Y.; Zhu, H.M.; Chen, X.; et al. Differential neutrino condensation onto cosmic structure. Nat. Astron. 2017, 1, 0143. [Google Scholar] [CrossRef]
- Emberson, J.D.; Yu, H.R.; Inman, D.; Zhang, T.J.; Pen, U.L.; Harnois-Déraps, J.; Yuan, S.; Teng, H.Y.; Zhu, H.M.; Chen, X.; et al. Cosmological neutrino simulations at extreme scale. Res. Astron. Astrophys. 2017, 17, 085. [Google Scholar] [CrossRef]
- Pan, Q.; Pen, U.L.; Inman, D.; Yu, H.R. Increasing the Fisher Information Content through Moving-Mesh Reconstruction. Mon. Not. R. Astron. Soc. 2017, 469, 1968–1973. [Google Scholar] [CrossRef]
- Merz, H.; Pen, U.L.; Trac, H. Towards optimal parallel PM N-body codes: PMFAST. New Ast. 2005, 10, 393–407. [Google Scholar] [CrossRef]
- Bullock, J.S.; Kolatt, T.S.; Sigad, Y.; Somerville, R.S.; Kravtsov, A.V.; Klypin, A.A.; Primack, J.R.; Dekel, A. Profiles of dark haloes: Evolution, scatter and environment. Mon. Not. R. Astron. Soc. 2001, 321, 559–575. [Google Scholar] [CrossRef]
- Liao, S.; Chen, J.; Chu, M.C. A Universal Angular Momentum Profile for Dark Matter Halos. Astrophys. J. 2017, 844, 86. [Google Scholar] [CrossRef]
- Li, J.; Obreschkow, D.; Power, C.; Lagos, C.d.P. Spin transfer from dark matter to gas during halo formation. Mon. Not. R. Astron. Soc. 2022, 515, 437–450. [Google Scholar] [CrossRef]
- Yu, H.R.; Pen, U.L.; Wang, X. Parity-odd neutrino torque detection. Phys. Rev. D 2019, 99, 123532. [Google Scholar] [CrossRef]
- Peterson, J.B.; Bandura, K.; Pen, U.L. The Hubble Sphere Hydrogen Survey. arXiv 2006. [Google Scholar] [CrossRef]
- Yoshikawa, K.; Tanaka, S.; Yoshida, N. A 400 Trillion-Grid Vlasov Simulation on Fugaku Supercomputer: Large-Scale Distribution of Cosmic Relic Neutrinos in a Six-dimensional Phase Space. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, St. Louis, MI, USA, 14–19 November 2021. [Google Scholar] [CrossRef]

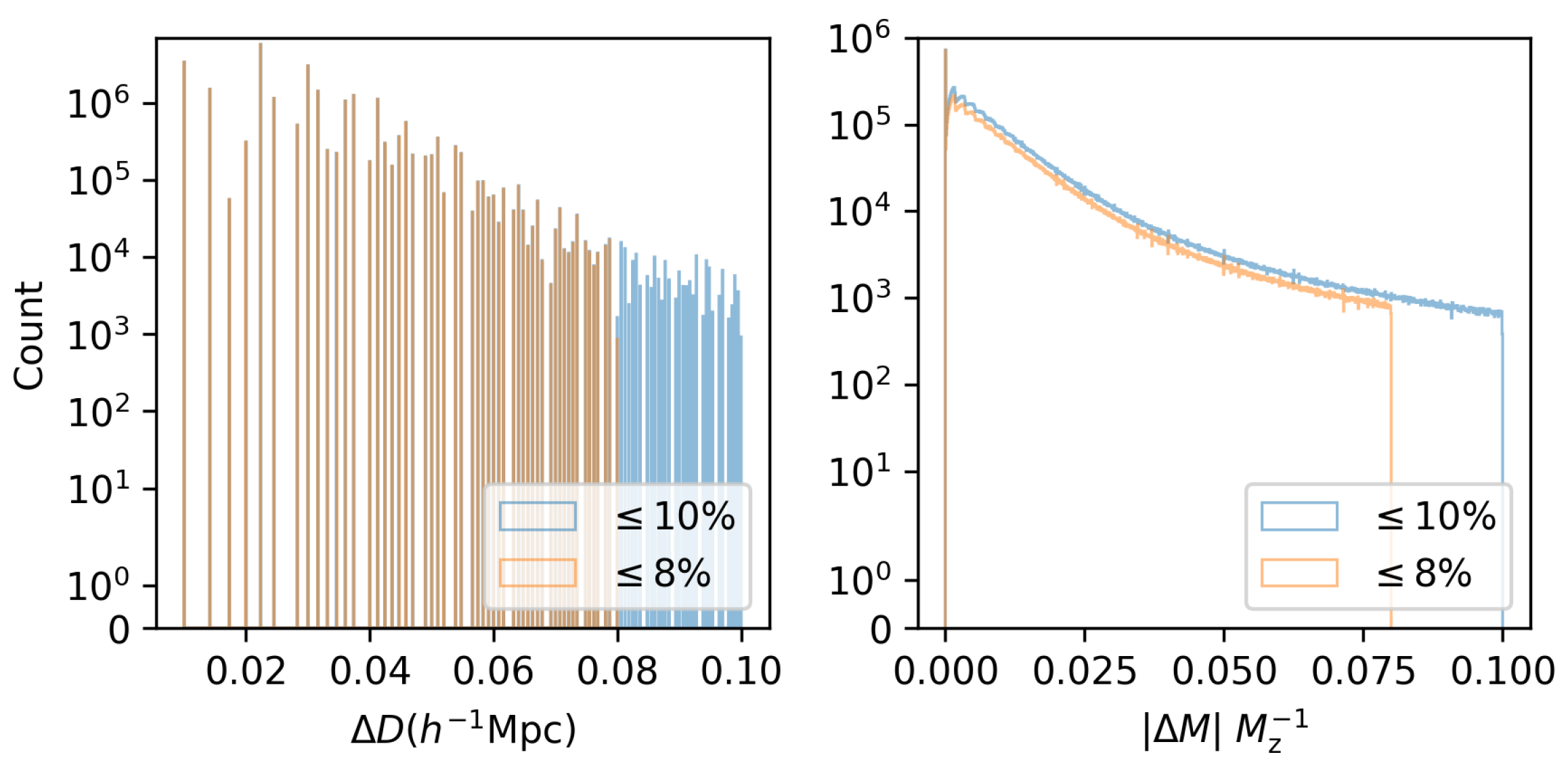
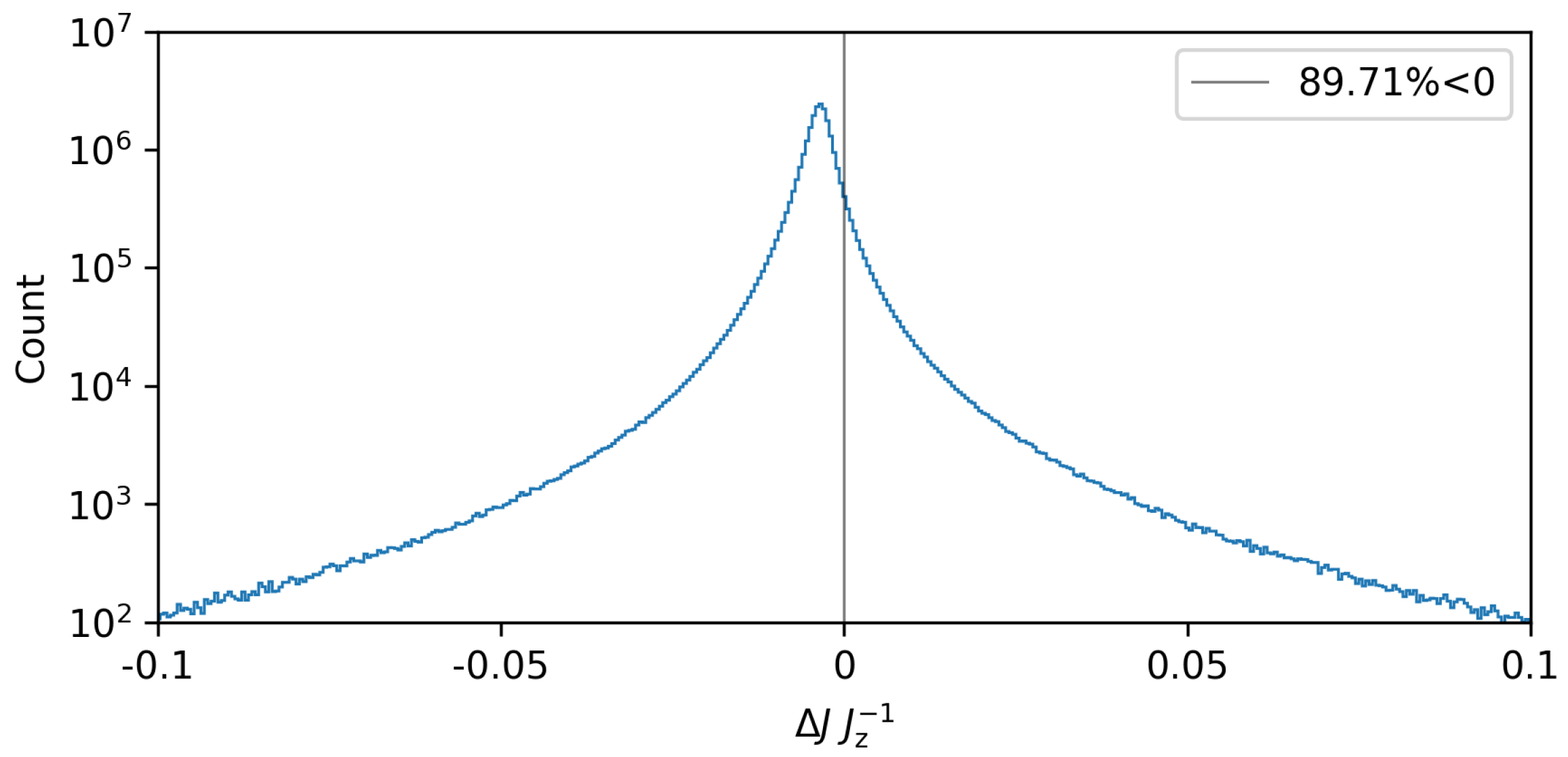
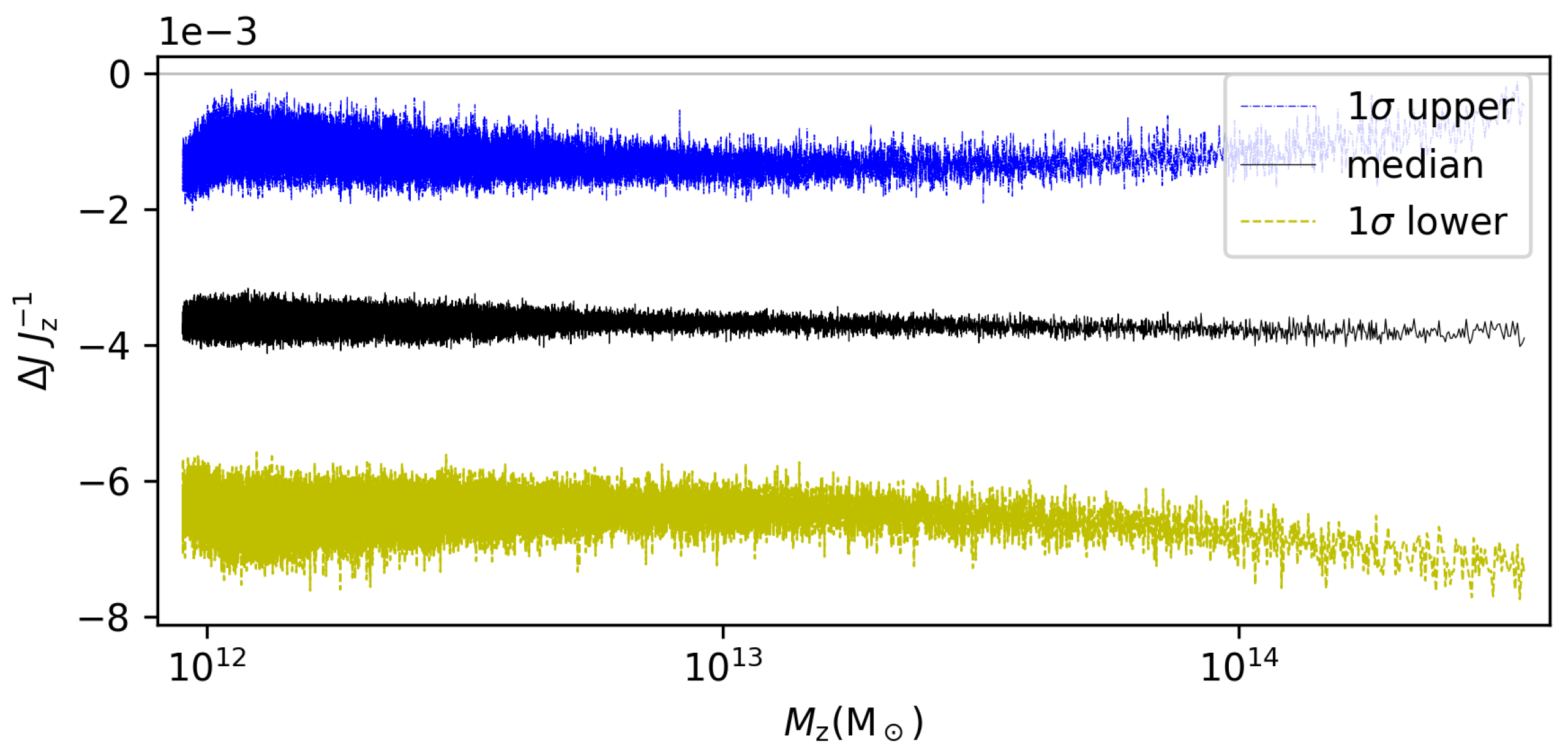
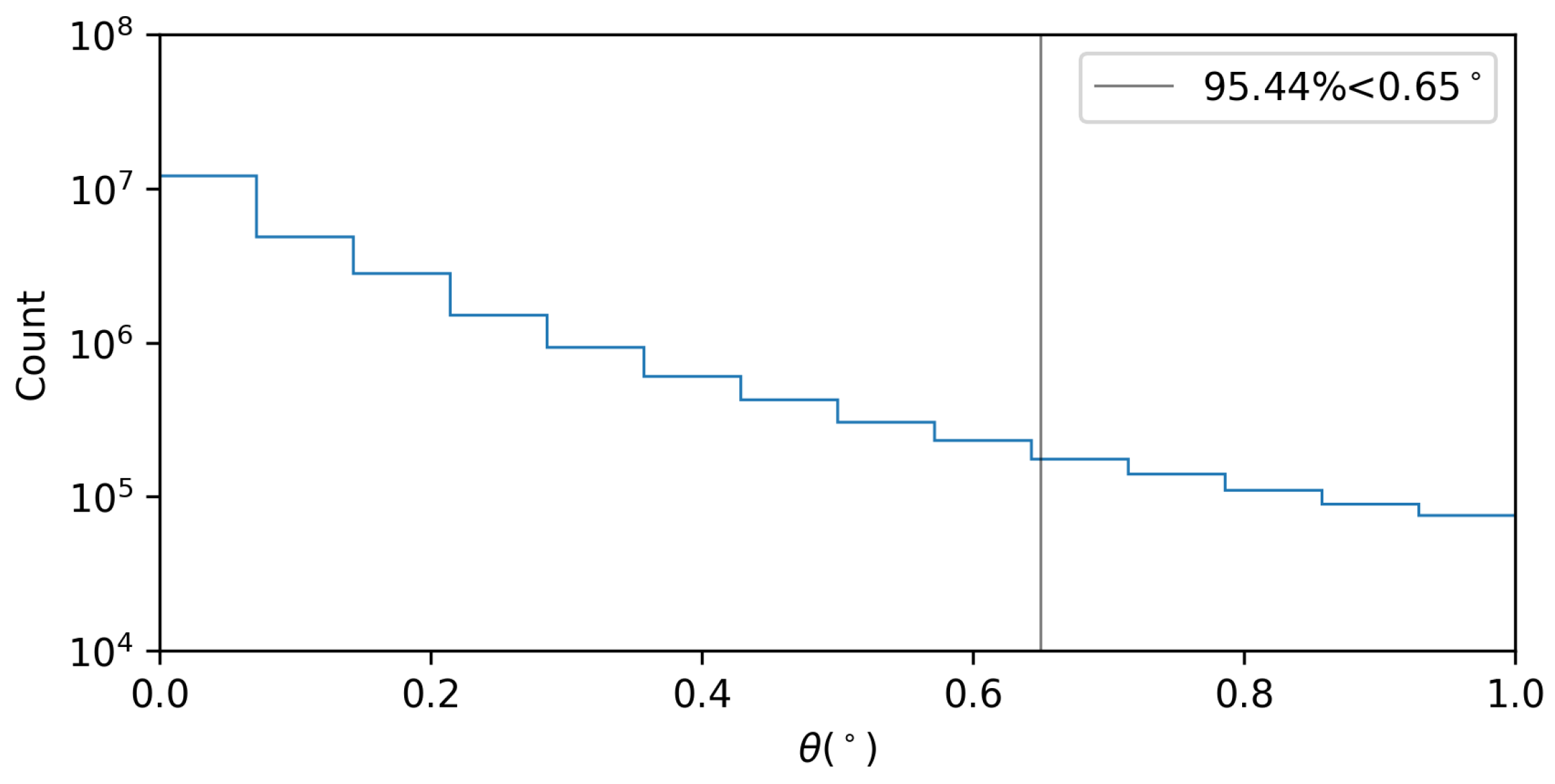
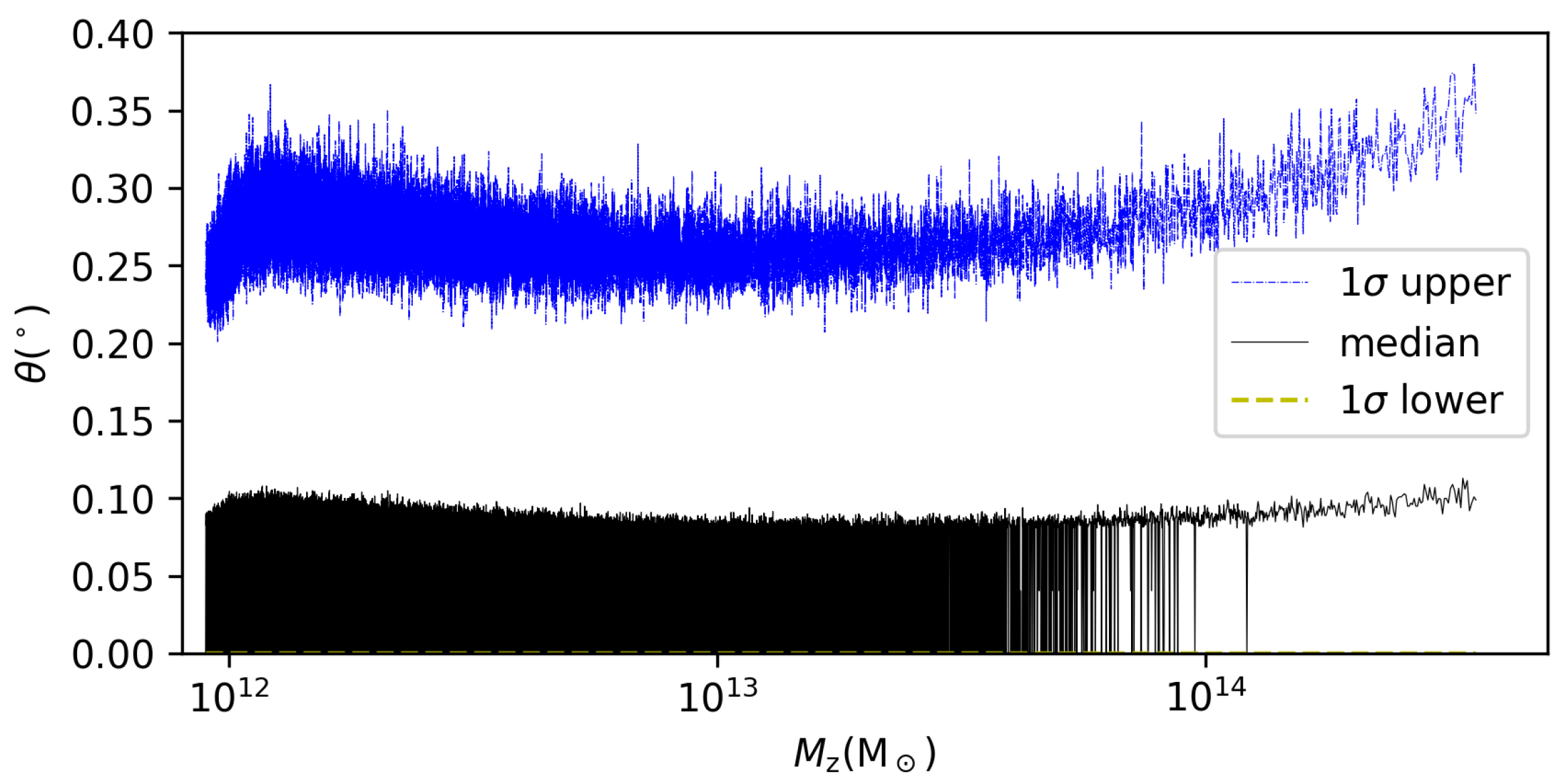
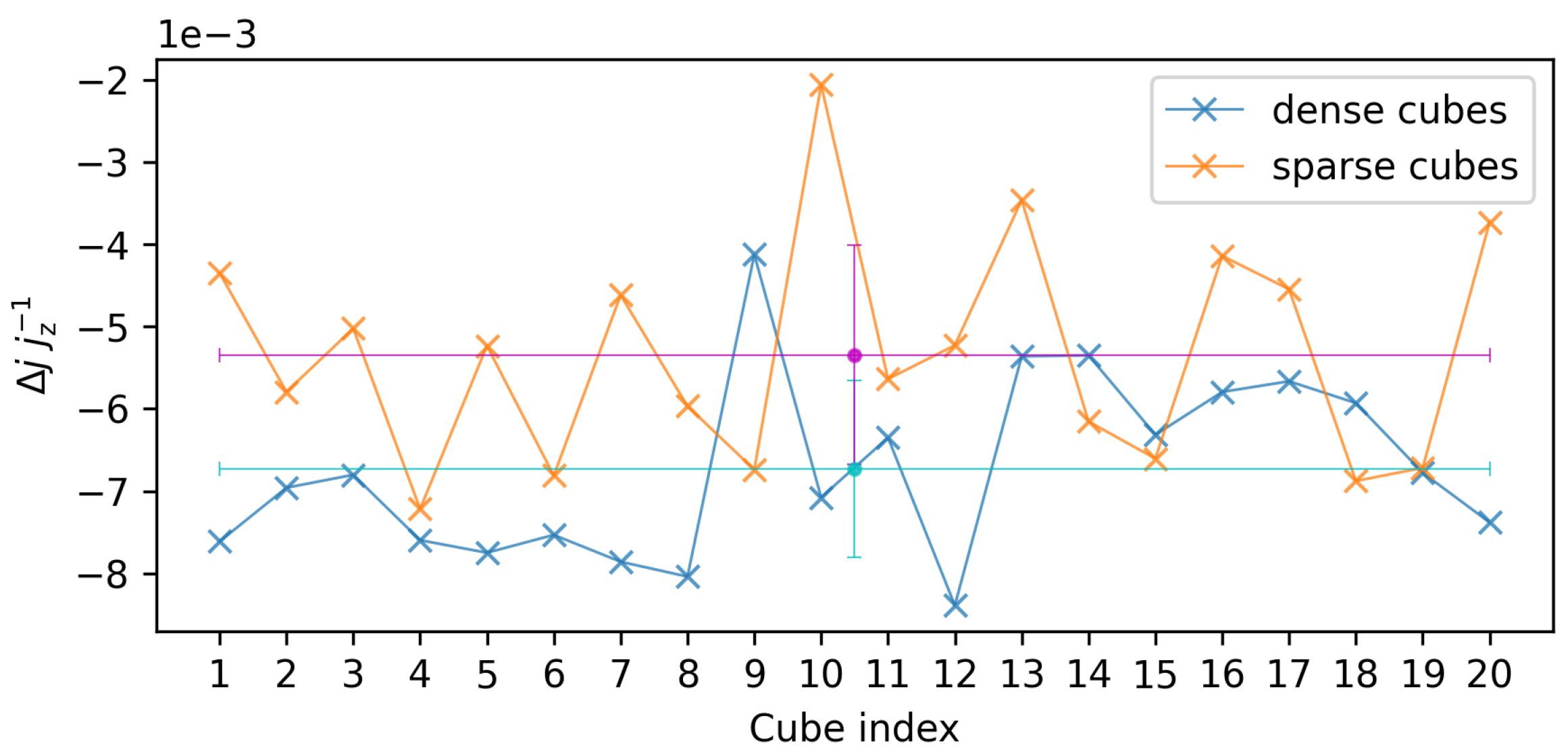
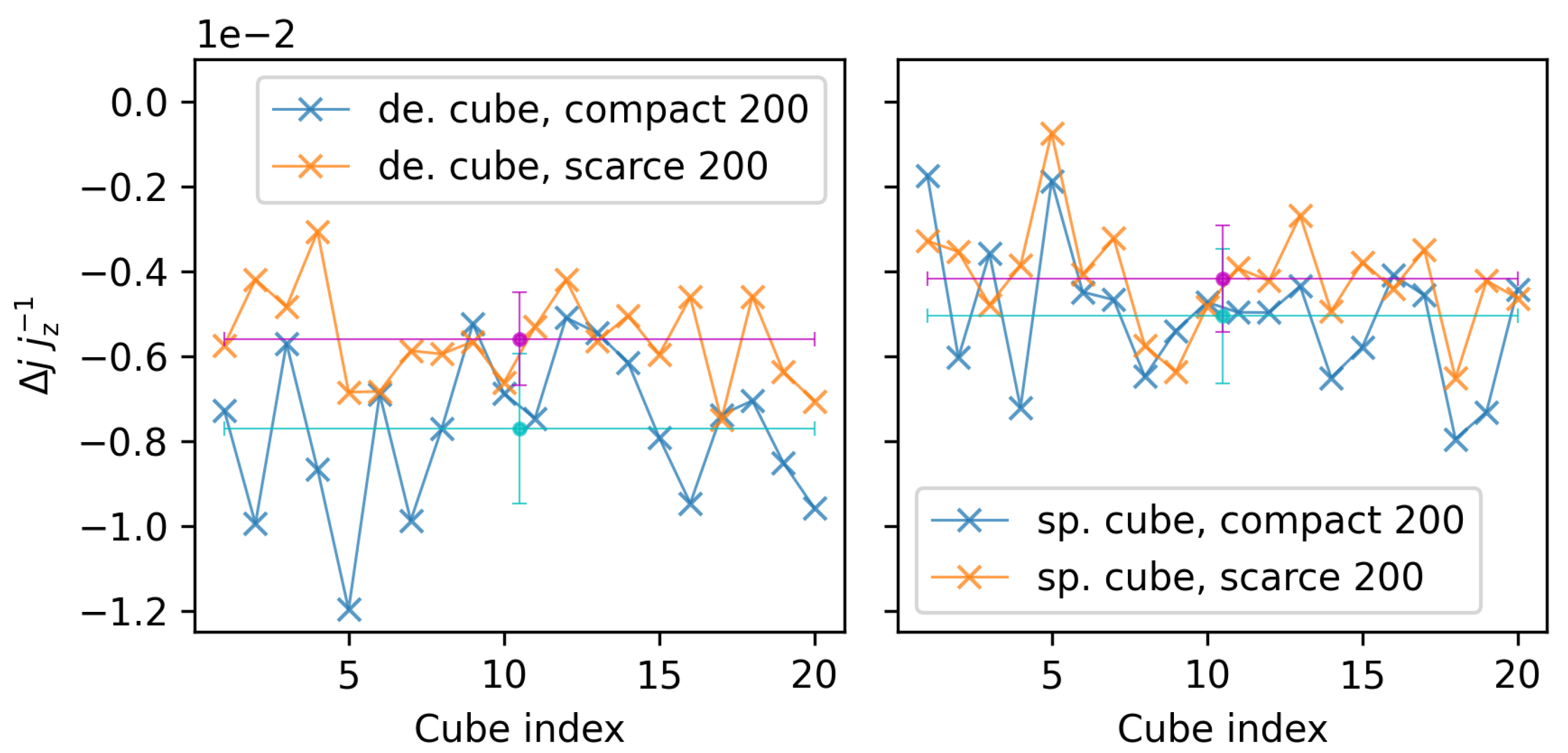
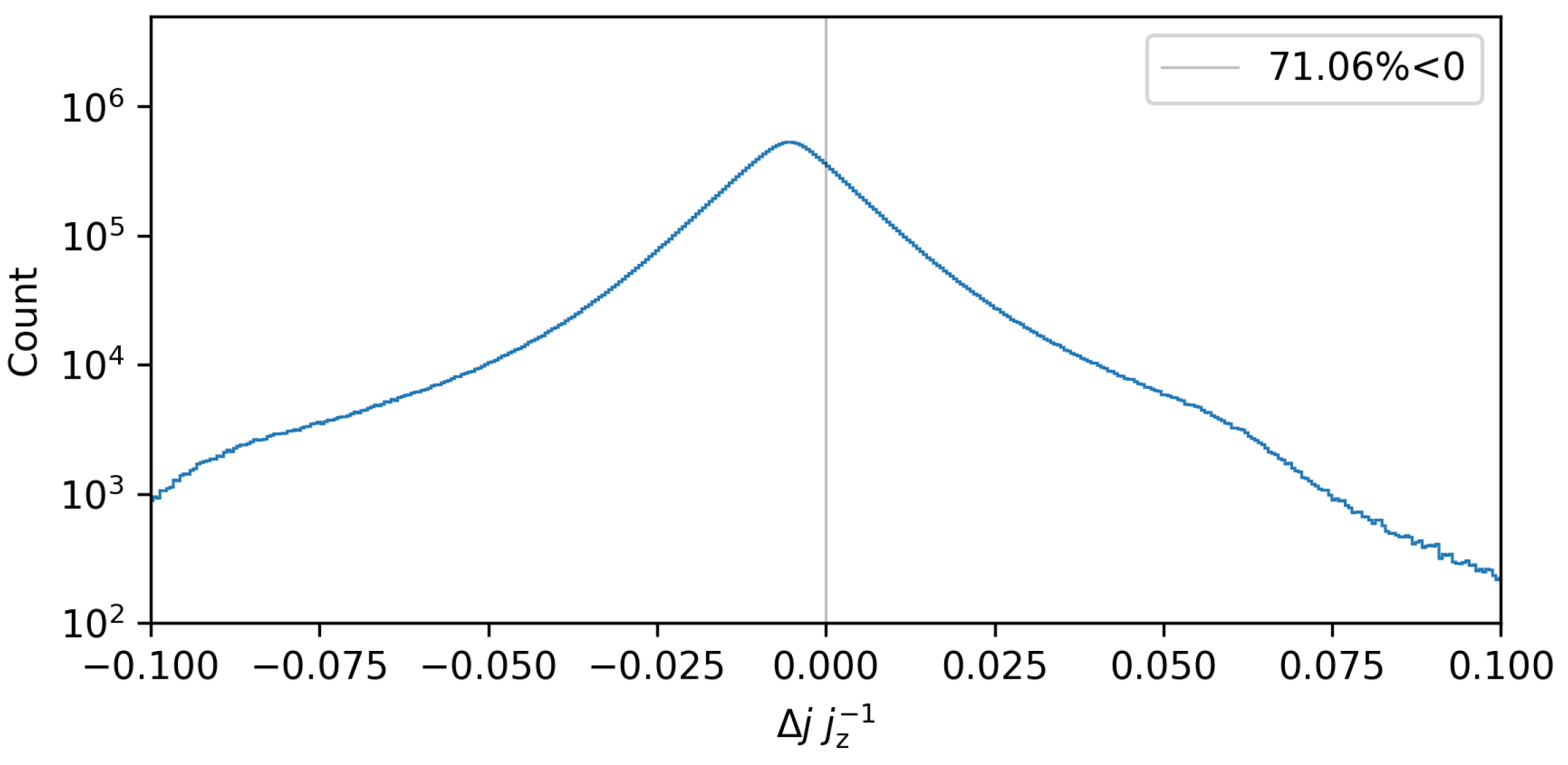
| Index | |||||||
|---|---|---|---|---|---|---|---|
| () | () | (%) | () | (%) | |||
| 1 | 3041 | 2 | 28.53 | 9.37 | −1.41% | 143.00 | −0.76% |
| 2 | 2905 | 1 | 27.91 | 9.61 | −1.32% | 166.92 | −0.70% |
| 3 | 2678 | 0 | 27.00 | 10.13 | −1.37% | 166.61 | −0.68% |
| 4 | 2888 | −1 | 26.93 | 9.33 | −1.23% | 57.83 | −0.76% |
| 5 | 2852 | 5 | 26.87 | 9.40 | −2.29% | 144.55 | −0.78% |
| 6 | 2870 | 5 | 26.22 | 9.12 | −1.27% | 165.71 | −0.75% |
| 7 | 2790 | 1 | 25.91 | 9.28 | −1.43% | 181.33 | −0.79% |
| 8 | 2936 | 2 | 25.69 | 8.74 | −1.31% | 94.63 | −0.80% |
| 9 | 2644 | 4 | 25.84 | 9.76 | −1.46% | 75.23 | −0.41% |
| 10 | 2722 | 3 | 25.67 | 9.42 | −1.26% | 147.85 | −0.71% |
| 11 | 2911 | 1 | 25.66 | 8.81 | −1.38% | 252.50 | −0.64% |
| 12 | 2623 | 6 | 25.30 | 9.62 | −1.20% | 92.09 | −0.84% |
| 13 | 2761 | 1 | 25.24 | 9.14 | −1.45% | 142.41 | −0.54% |
| 14 | 2909 | 3 | 25.18 | 8.65 | −1.33% | 287.76 | −0.53% |
| 15 | 2952 | 5 | 25.16 | 8.51 | −1.34% | 164.04 | −0.63% |
| 16 | 2790 | 5 | 24.89 | 8.91 | −1.54% | 32.12 | −0.58% |
| 17 | 2769 | 1 | 24.87 | 8.98 | −1.28% | 148.10 | −0.57% |
| 18 | 2791 | 1 | 24.82 | 8.89 | −1.35% | 84.01 | −0.59% |
| 19 | 2860 | 1 | 24.76 | 8.65 | −1.29% | 140.80 | −0.68% |
| 20 | 2864 | 4 | 24.70 | 8.61 | −1.30% | 121.08 | −0.74% |
| Index | |||||||
|---|---|---|---|---|---|---|---|
| () | () | (%) | () | (%) | |||
| 1 | 743 | −1 | 3.13 | 4.22 | −1.40% | 77.77 | −0.46% |
| 2 | 726 | 0 | 3.25 | 4.47 | −1.40% | 148.00 | −0.58% |
| 3 | 839 | −1 | 3.28 | 3.92 | −1.43% | 40.74 | −0.50% |
| 4 | 855 | 0 | 3.40 | 3.98 | −1.25% | 99.81 | −0.72% |
| 5 | 858 | −4 | 3.44 | 4.03 | −0.55% | 27.99 | −0.52% |
| 6 | 828 | −1 | 3.53 | 4.27 | −1.14% | 147.53 | −0.68% |
| 7 | 831 | −1 | 3.57 | 4.30 | −1.41% | 32.64 | −0.46% |
| 8 | 875 | 0 | 3.59 | 4.10 | −1.45% | 113.56 | −0.60% |
| 9 | 803 | 1 | 3.63 | 4.51 | −1.19% | 180.72 | −0.67% |
| 10 | 813 | −1 | 3.63 | 4.47 | −1.67% | 95.40 | −0.21% |
| 11 | 759 | −1 | 3.68 | 4.86 | −1.51% | 151.03 | −0.56% |
| 12 | 868 | 0 | 3.83 | 4.41 | −1.33% | 149.97 | −0.52% |
| 13 | 822 | −1 | 3.85 | 4.70 | −1.44% | 40.90 | −0.35% |
| 14 | 912 | 0 | 3.89 | 4.26 | −1.21% | 141.78 | −0.61% |
| 15 | 910 | −1 | 3.97 | 4.37 | −0.003% | 87.19 | −0.66% |
| 16 | 858 | −2 | 4.05 | 4.73 | −1.37% | 150.18 | −0.41% |
| 17 | 1096 | 0 | 4.12 | 3.76 | −1.23% | 67.54 | −0.45% |
| 18 | 856 | 0 | 4.15 | 4.85 | −1.25% | 64.36 | −0.69% |
| 19 | 923 | −1 | 4.18 | 4.54 | −1.21% | 150.18 | −0.67% |
| 20 | 917 | 0 | 4.19 | 4.57 | −1.30% | 115.81 | −0.37% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Lu, C.-Z.; Li, J.; Liu, S.; Zhang, T.-J.; Zhang, T. Cosmological Neutrino N-Body Simulations of Dark Matter Halo. Universe 2023, 9, 237. https://doi.org/10.3390/universe9050237
Chen Y, Lu C-Z, Li J, Liu S, Zhang T-J, Zhang T. Cosmological Neutrino N-Body Simulations of Dark Matter Halo. Universe. 2023; 9(5):237. https://doi.org/10.3390/universe9050237
Chicago/Turabian StyleChen, Yu, Chang-Zhi Lu, Juan Li, Siqi Liu, Tong-Jie Zhang, and Tingting Zhang. 2023. "Cosmological Neutrino N-Body Simulations of Dark Matter Halo" Universe 9, no. 5: 237. https://doi.org/10.3390/universe9050237
APA StyleChen, Y., Lu, C.-Z., Li, J., Liu, S., Zhang, T.-J., & Zhang, T. (2023). Cosmological Neutrino N-Body Simulations of Dark Matter Halo. Universe, 9(5), 237. https://doi.org/10.3390/universe9050237







