Elimination of QCD Renormalization Scale and Scheme Ambiguities
Abstract
1. Introduction
2. A Mini-Review of the PMC Scale-Setting Method
3. Applications
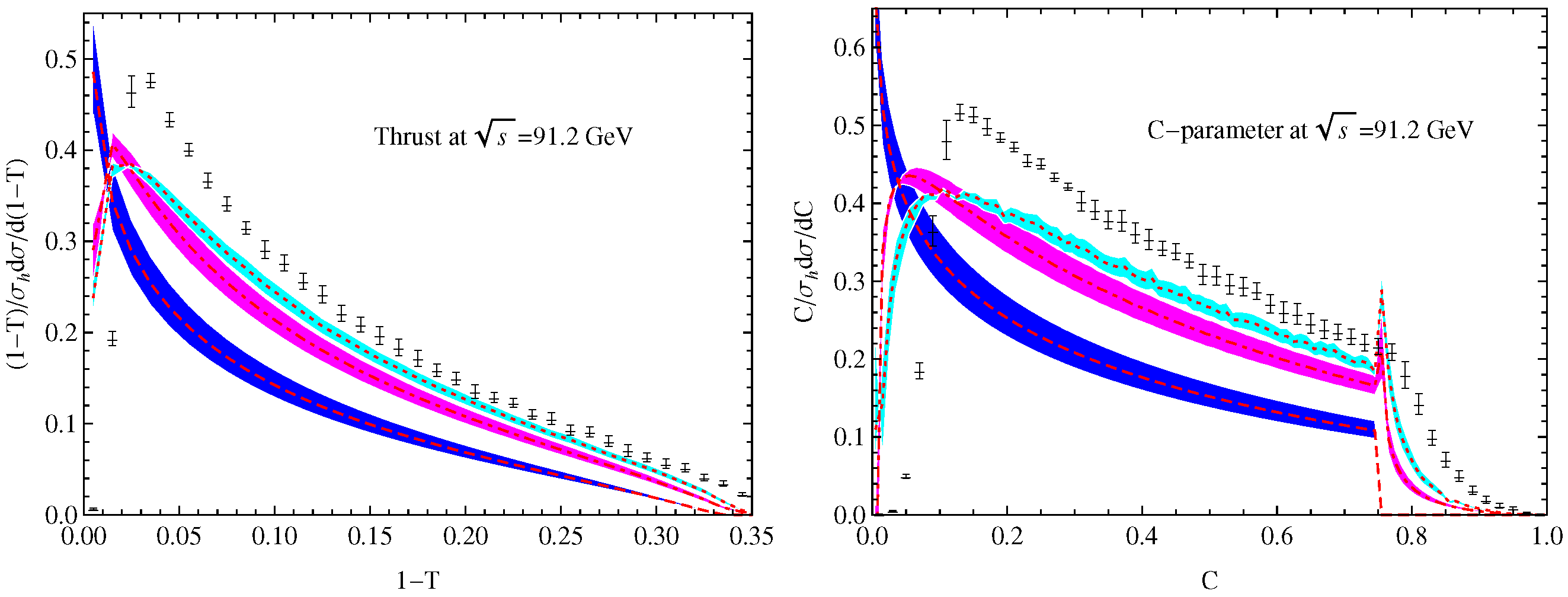
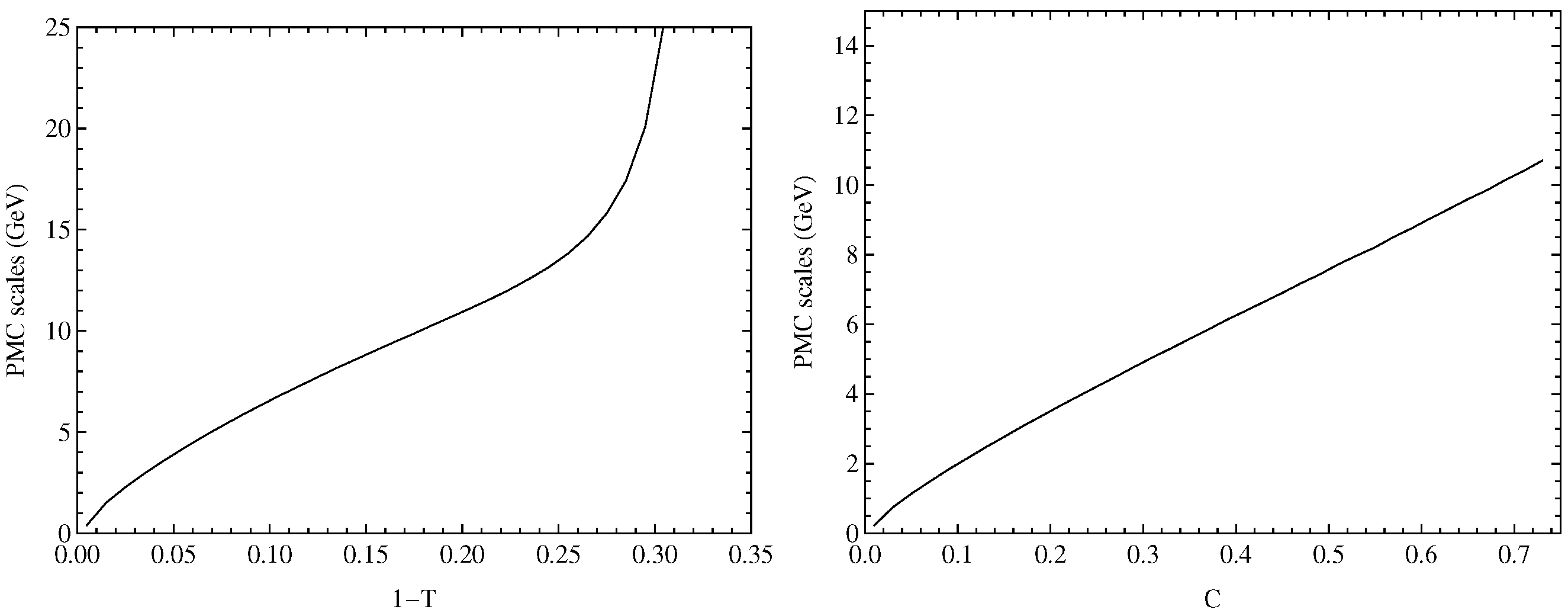
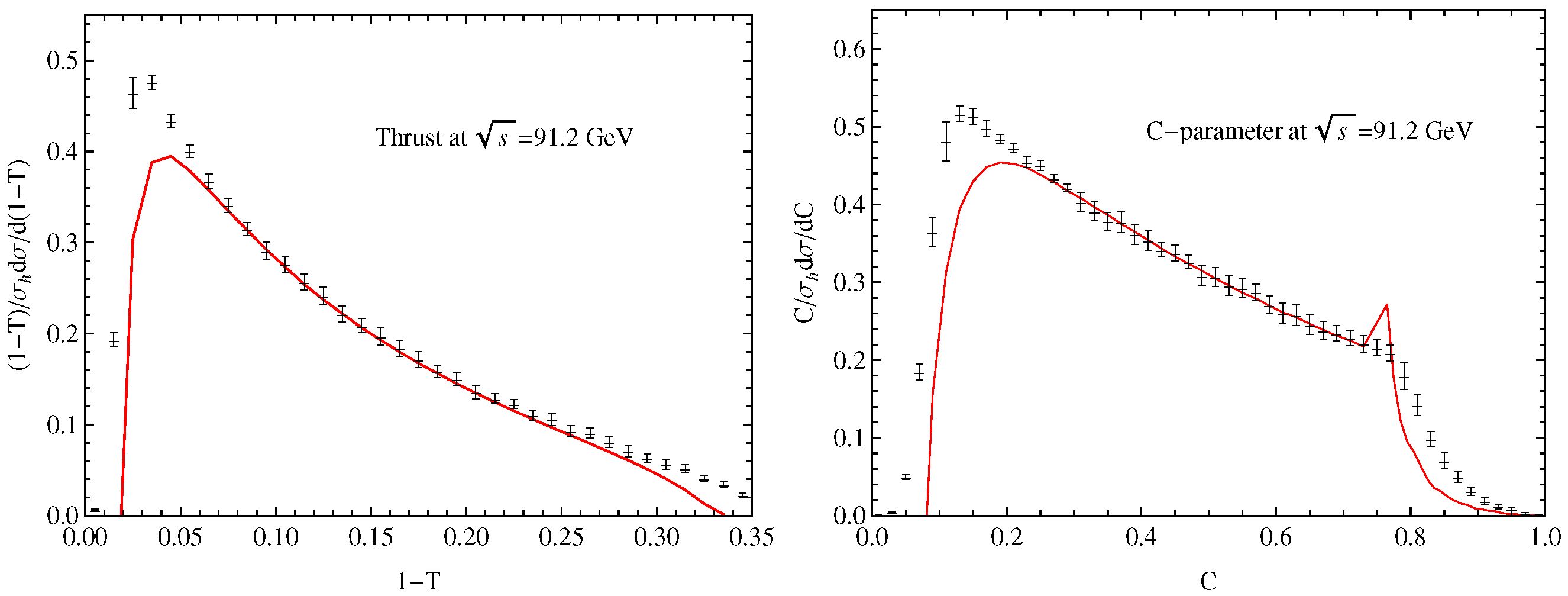
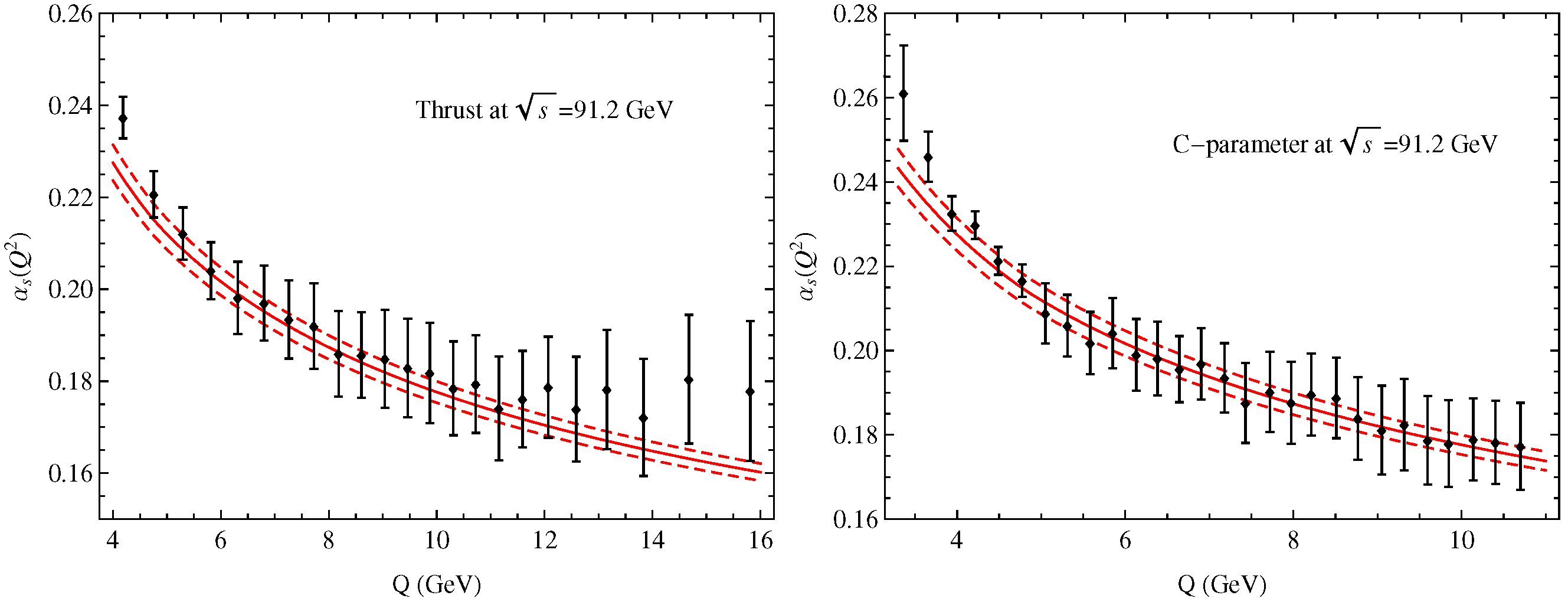
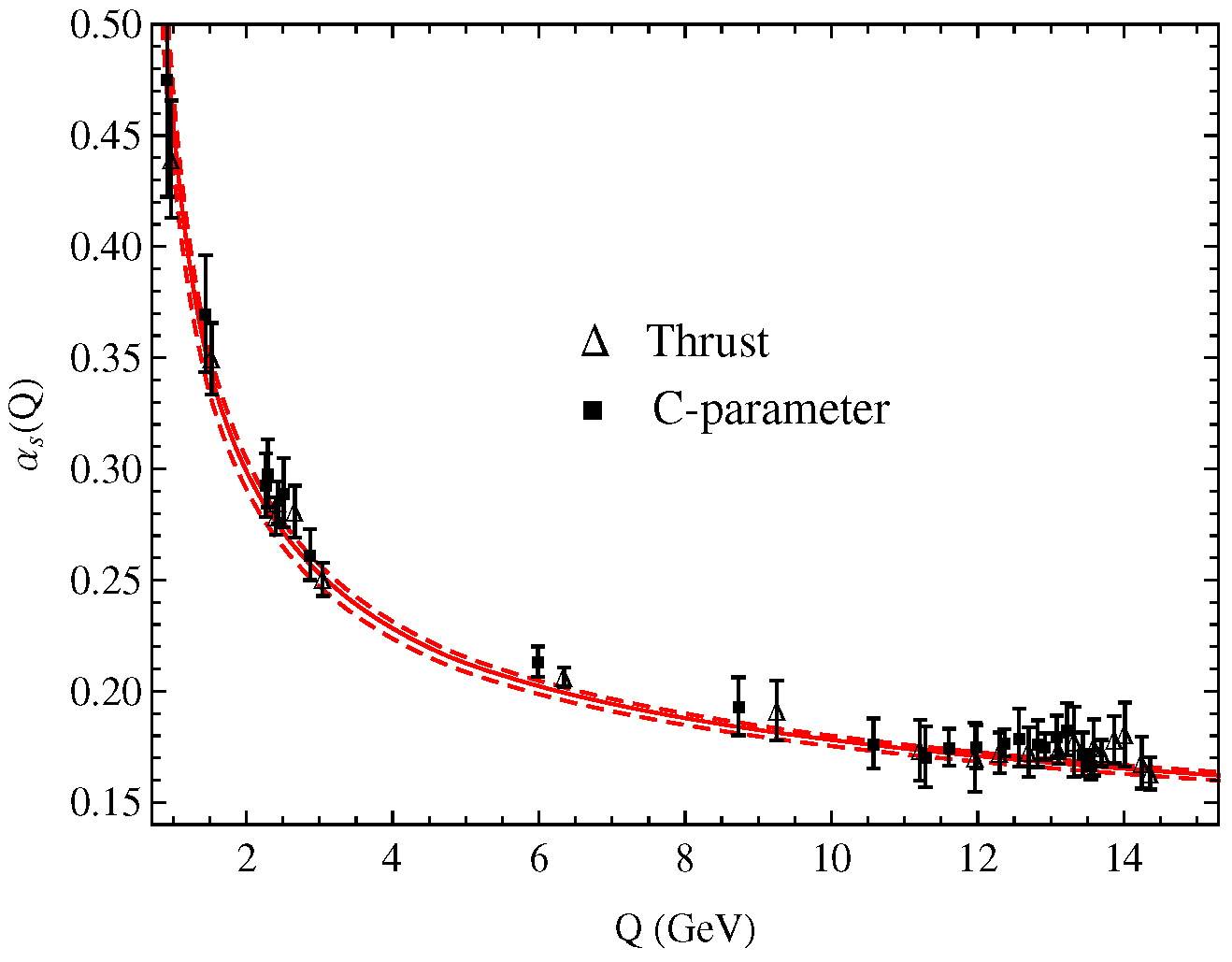
3.1. New Analyses of Event Shape Observables in Annihilation
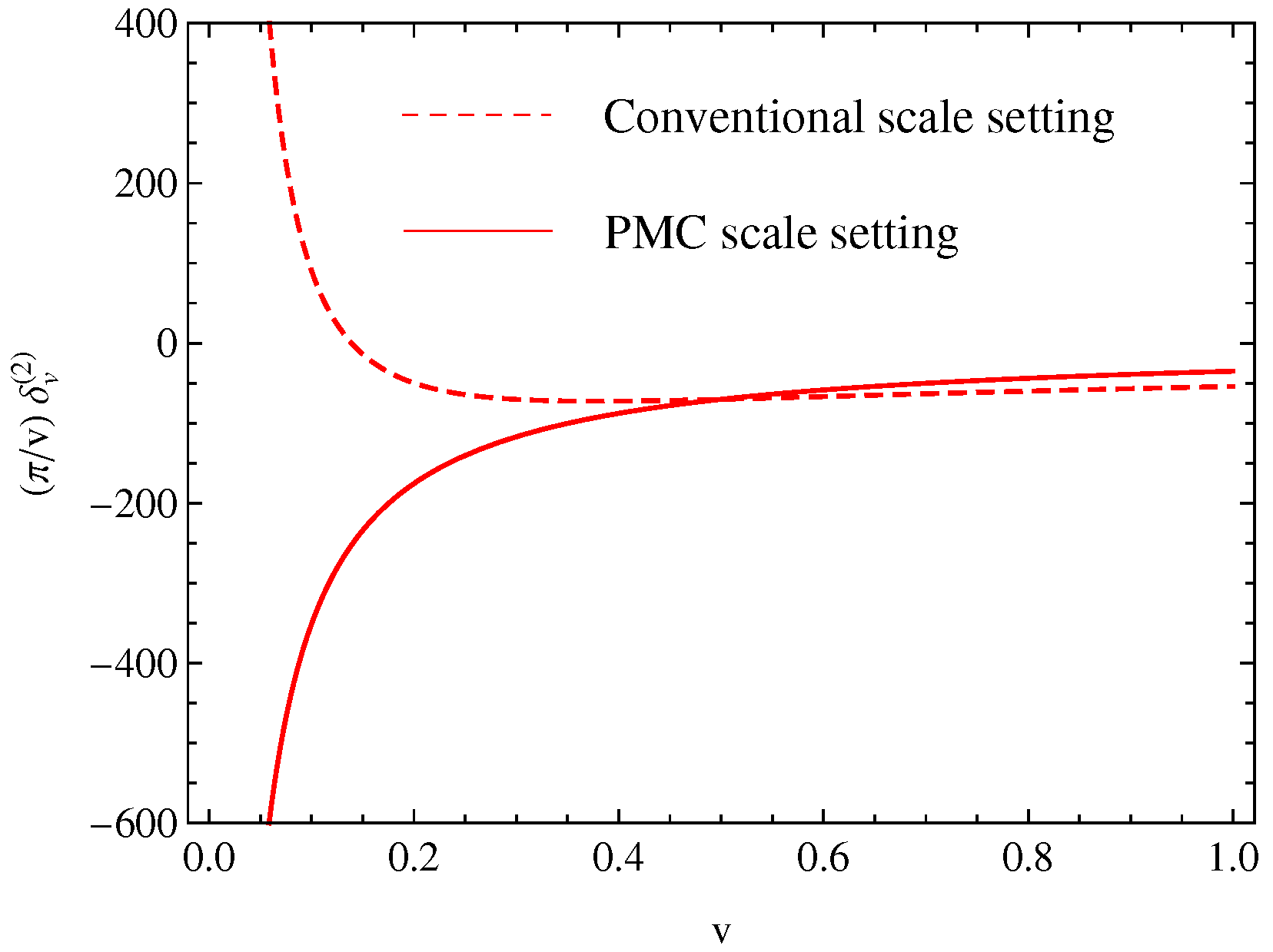
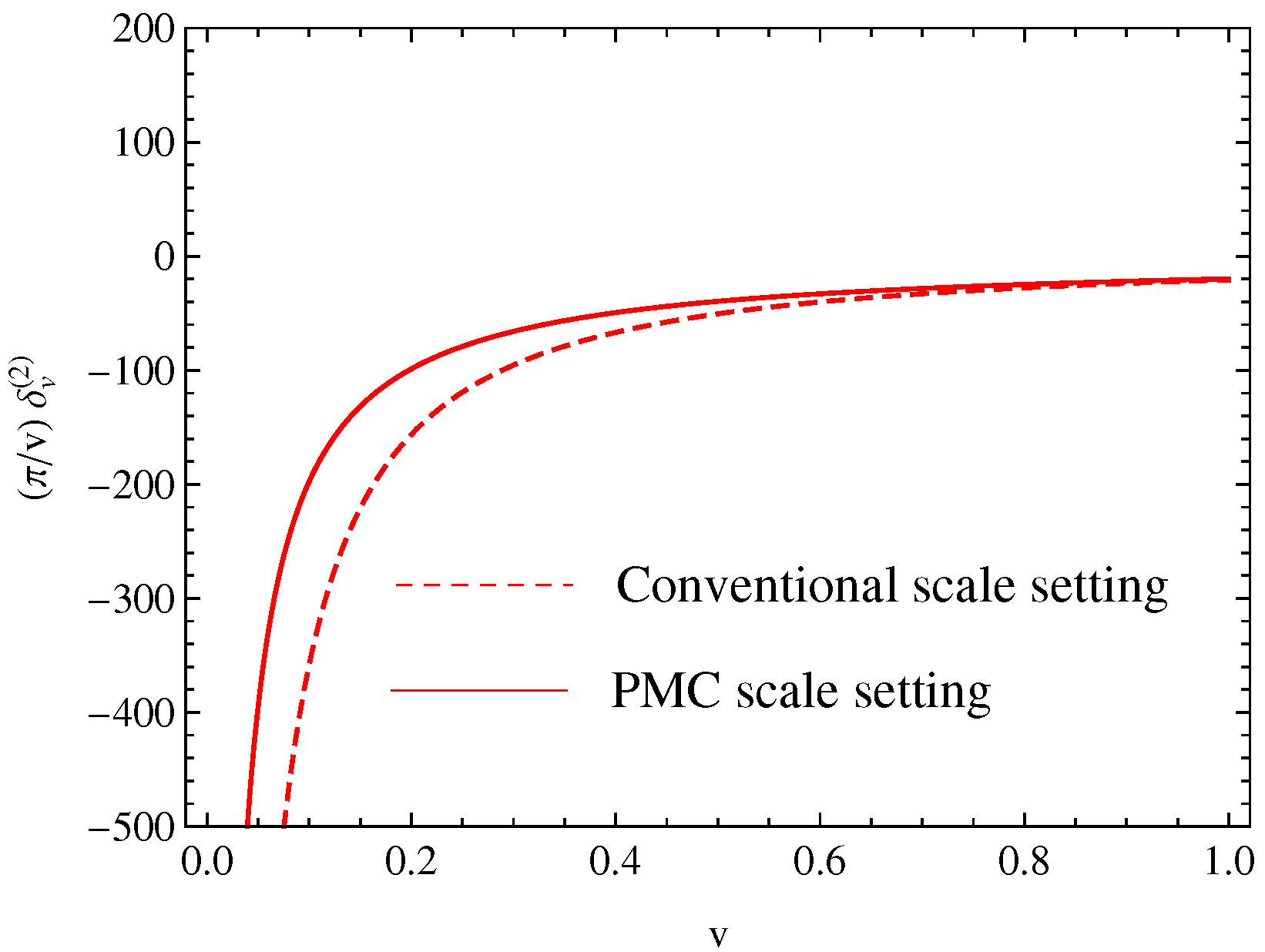
3.2. Heavy Quark Pair Production in Annihilation near the Threshold Region
3.3. TReanalysis of the Top-Quark Decay at Next-To-Next-To-Leading Order
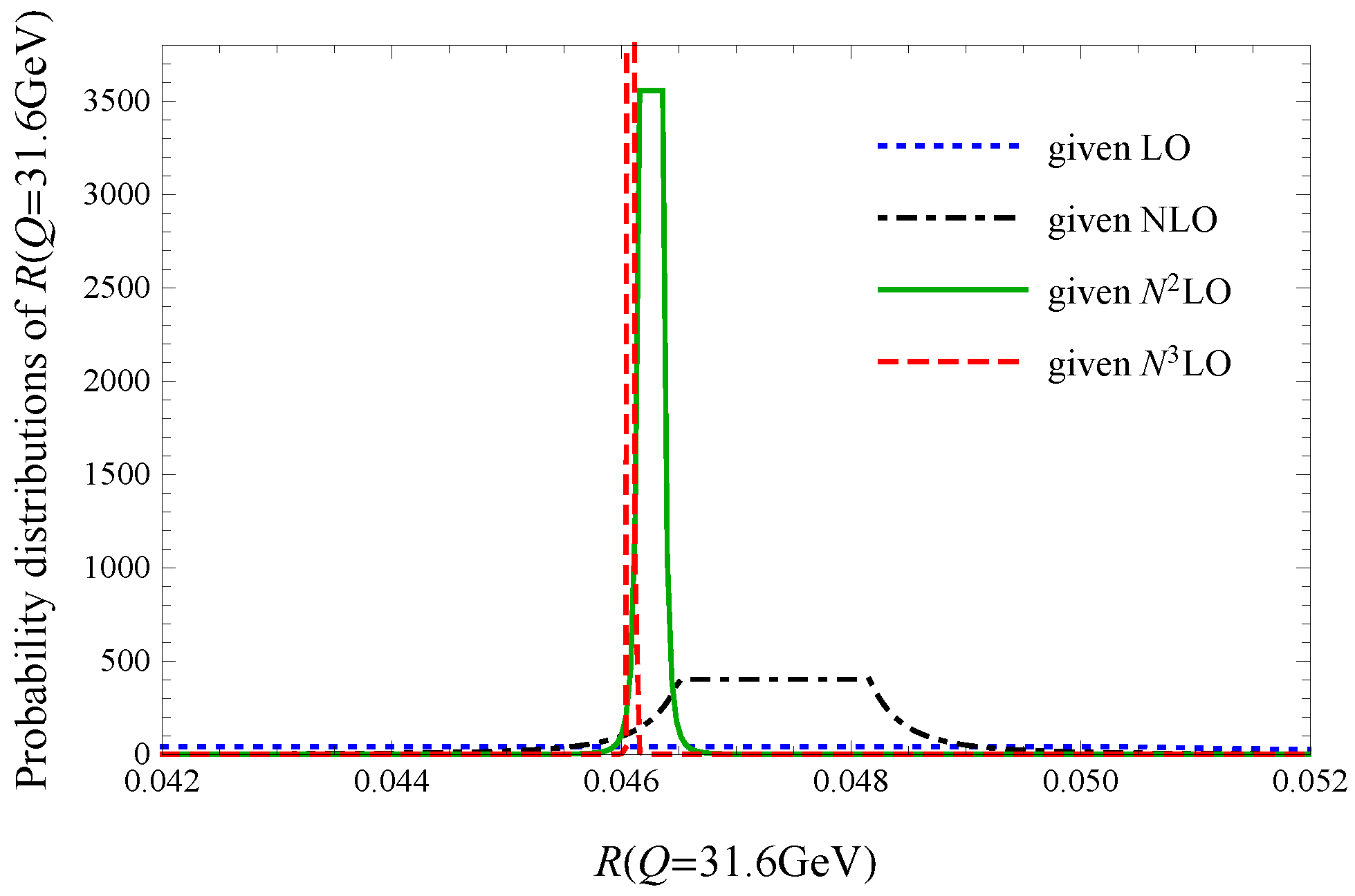
3.4. An Estimate of the Contributions from Uncalculated Higher-Order Terms
3.4.1. Applying PAA to Evaluate the UHO Contributions
3.4.2. Applying BA to Evaluate the UHO Contributions
4. Summary
Funding
Conflicts of Interest
| 1 | One may also use a credible interval (CI) to compare with experimental data in the same confidence level, or use CI for a more conservative estimation. |
References
- Politzer, H.D. Reliable Perturbative Results for Strong Interactions? Phys. Rev. Lett. 1973, 30, 1346. [Google Scholar] [CrossRef]
- Gross, D.J.; Wilczek, F. Ultraviolet Behavior of Nonabelian Gauge Theories. Phys. Rev. Lett. 1973, 30, 1343. [Google Scholar] [CrossRef]
- Beneke, M. Renormalons. Phys. Rept. 1999, 317, 1. [Google Scholar] [CrossRef]
- Gell-Mann, M.; Low, F.E. Quantum electrodynamics at small distances. Phys. Rev. 1954, 95, 1300. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Huet, P. Aspects of SU(N(c)) gauge theories in the limit of small number of colors. Phys. Lett. B 1998, 417, 145. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Lepage, G.P.; Mackenzie, P.B. On the Elimination of Scale Ambiguities in Perturbative Quantum Chromodynamics. Phys. Rev. D 1983, 28, 228. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Wu, X.G. Scale Setting Using the Extended Renormalization Group and the Principle of Maximum Conformality: The QCD Coupling Constant at Four Loops. Phys. Rev. D 2012, 85, 034038. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Wu, X.G. Eliminating the Renormalization Scale Ambiguity for Top-Pair Production Using the Principle of Maximum Conformality. Phys. Rev. Lett. 2012, 109, 042002. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Giustino, L.D. Setting the Renormalization Scale in QCD: The Principle of Maximum Conformality. Phys. Rev. D 2012, 86, 085026. [Google Scholar] [CrossRef]
- Mojaza, M.; Brodsky, S.J.; Wu, X.G. Systematic All-Orders Method to Eliminate Renormalization-Scale and Scheme Ambiguities in Perturbative QCD. Phys. Rev. Lett. 2013, 110, 192001. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Mojaza, M.; Wu, X.G. Systematic Scale-Setting to All Orders: The Principle of Maximum Conformality and Commensurate Scale Relations. Phys. Rev. D 2014, 89, 014027. [Google Scholar] [CrossRef]
- Wu, X.G.; Brodsky, S.J.; Mojaza, M. The Renormalization Scale-Setting Problem in QCD. Prog. Part. Nucl. Phys. 2013, 72, 44. [Google Scholar] [CrossRef]
- Wu, X.G.; Ma, Y.; Wang, S.Q.; Fu, H.B.; Ma, H.H.; Brodsky, S.J.; Mojaza, M. Renormalization Group Invariance and Optimal QCD Renormalization Scale-Setting. Rept. Prog. Phys. 2015, 78, 126201. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.G.; Shen, J.M.; Du, B.L.; Huang, X.D.; Wang, S.Q.; Brodsky, S.J. The QCD renormalization group equation and the elimination of fixed-order scheme-and-scale ambiguities using the principle of maximum conformality. Prog. Part. Nucl. Phys. 2019, 108, 103706. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Wu, X.G. Self-Consistency Requirements of the Renormalization Group for Setting the Renormalization Scale. Phys. Rev. D 2012, 86, 054018. [Google Scholar] [CrossRef]
- Shen, J.M.; Wu, X.G.; Du, B.L.; Brodsky, S.J. Novel All-Orders Single-Scale Approach to QCD Renormalization Scale-Setting. Phys. Rev. D 2017, 95, 094006. [Google Scholar] [CrossRef]
- Giustino, L.D.; Brodsky, S.J.; Wang, S.Q.; Wu, X.G. Infinite-order scale-setting using the principle of maximum conformality: A remarkably efficient method for eliminating renormalization scale ambiguities for perturbative QCD. Phys. Rev. D 2020, 102, 014015. [Google Scholar] [CrossRef]
- Yan, J.; Wu, Z.F.; Shen, J.M.; Wu, X.G. Precise perturbative predictions from fixed-order calculations. J. Phys. G 2023, 50, 045001. [Google Scholar] [CrossRef]
- Bi, H.Y.; Wu, X.G.; Ma, Y.; Ma, H.H.; Brodsky, S.J.; Mojaza, M. Degeneracy Relations in QCD and the Equivalence of Two Systematic All-Orders Methods for Setting the Renormalization Scale. Phys. Lett. B 2015, 748, 13. [Google Scholar] [CrossRef]
- Zheng, X.C.; Wu, X.G.; Wang, S.Q.; Shen, J.M.; Zhang, Q.L. Reanalysis of the BFKL Pomeron at the next-to-leading logarithmic accuracy. J. High Energy Phys. 2013, 117, 1310. [Google Scholar] [CrossRef]
- Deur, A.; Shen, J.M.; Wu, X.G.; Brodsky, S.J.; de Teramond, G.F. Implications of the Principle of Maximum Conformality for the QCD Strong Coupling. Phys. Lett. B 2017, 98, 773. [Google Scholar] [CrossRef]
- Yu, Q.; Zhou, H.; Huang, X.D.; Shen, J.M.; Wu, X.G. Novel and self-consistency analysis of the QCD running coupling αs(Q) in both the perturbative and nonperturbative domains. Chin. Phys. Lett. 2022, 39, 071201. [Google Scholar] [CrossRef]
- Wu, X.G.; Wang, S.Q.; Brodsky, S.J. Importance of proper renormalization scale-setting for QCD testing at colliders. Front. Phys. (Beijing) 2016, 11, 111201. [Google Scholar] [CrossRef]
- Meng, R.Q.; Wang, S.Q.; Sun, T.; Luo, C.Q.; Shen, J.M.; Wu, X.G. QCD improved top-quark decay at next-to-next-to-leading order. Eur. Phys. J. C 2023, 83, 59. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Fadin, V.S.; Kim, V.T.; Lipatov, L.N.; Pivovarov, G.B. The QCD pomeron with optimal renormalization. JETP Lett. 1999, 70, 155. [Google Scholar] [CrossRef]
- Hentschinski, M.; Vera, A.S.; Salas, C. Hard to Soft Pomeron Transition in Small-x Deep Inelastic Scattering Data Using Optimal Renormalization. Phys. Rev. Lett. 2013, 110, 041601. [Google Scholar] [CrossRef] [PubMed]
- Caporale, F.; Ivanov, D.Y.; Murdaca, B.; Papa, A. Brodsky-Lepage-Mackenzie optimal renormalization scale setting for semihard processes. Phys. Rev. D 2015, 91, 114009. [Google Scholar] [CrossRef]
- Wang, S.Q.; Luo, C.Q.; Wu, X.G.; Shen, J.M.; Giustino, L.D. New analyses of event shape observables in electron-positron annihilation and the determination of αs running behavior in perturbative domain. J. High Energy Phys. 2022, 9, 137. [Google Scholar] [CrossRef]
- Wang, S.Q.; Wu, X.G.; Shen, J.M.; Han, H.Y.; Ma, Y. QCD improved electroweak parameter ρ. Phys. Rev. D 2014, 89, 116001. [Google Scholar] [CrossRef]
- Yu, Q.; Zhou, H.; Yan, J.; Huang, X.D.; Wu, X.G. A new analysis of the pQCD contributions to the electroweak parameter ρ using the single-scale approach of principle of maximum conformality. Phys. Lett. B 2021, 820, 136574. [Google Scholar] [CrossRef]
- Shen, J.M.; Wu, X.G.; Ma, H.H.; Bi, H.Y.; Wang, S.Q. Renormalization group improved pQCD prediction for Υ(1S) leptonic decay. J. High Energy Phys. 2015, 1506, 169. [Google Scholar] [CrossRef]
- Huang, X.D.; Wu, X.G.; Zeng, J.; Yu, Q.; Shen, J.M. The Υ(1S) leptonic decay using the principle of maximum conformality. Eur. Phys. J. C 2019, 79, 650. [Google Scholar] [CrossRef]
- Wang, S.Q.; Wu, X.G.; Zheng, X.C.; Shen, J.M.; Zhang, Q.L. J/ψ+χcJ Production at the B Factories under the Principle of Maximum Conformality. Nucl. Phys. B 2013, 876, 731. [Google Scholar] [CrossRef]
- Sun, Z.; Wu, X.G.; Ma, Y.; Brodsky, S.J. Exclusive production of J/ψ+ηc at the B factories Belle and Babar using the principle of maximum conformality. Phys. Rev. D 2018, 98, 094001. [Google Scholar] [CrossRef]
- Yu, H.M.; Sang, W.L.; Huang, X.D.; Zeng, J.; Wu, X.G.; Brodsky, S.J. Scale-fixed predictions for γ+ηc production in electron-positron collisions at NNLO in perturbative QCD. J. High Energy Phys. 2021, 1, 131. [Google Scholar] [CrossRef]
- Qiao, C.F.; Zhu, R.L.; Wu, X.G.; Brodsky, S.J. A possible solution to the B->PIPI puzzle using the principle of maximum conformality. Phys. Lett. B 2015, 748, 422. [Google Scholar] [CrossRef]
- Wang, S.Q.; Wu, X.G.; Sang, W.L.; Brodsky, S.J. Solution to the γγ*→ηc puzzle using the principle of maximum conformality. Phys. Rev. D 2018, 97, 094034. [Google Scholar] [CrossRef]
- Zyla, P.A. et al. [Particle Data Group] Review of Particle Physics. Prog. Theor. Exp. Phys. 2020, 2020, 083C01. [Google Scholar] [CrossRef]
- Heister, A. et al. [ALEPH Collaboration] Studies of QCD at e+e- centre-of-mass energies between 91 GeV and 209 GeV. Eur. Phys. J. C 2004, 35, 457. [Google Scholar] [CrossRef]
- Abdallah, J. et al. [DELPHI Collaboration] A Study of the energy evolution of event shape distributions and their means with the DELPHI detector at LEP. Eur. Phys. J. C 2003, 29, 285. [Google Scholar] [CrossRef]
- Abbiendi, G. et al. [OPAL Collaboration] Measurement of event shape distributions and moments in e+e-→ hadrons at 91-209 GeV and a determination of αs. Eur. Phys. J. C 2005, 40, 287. [Google Scholar] [CrossRef]
- Achard, P. et al. [L3 Collaboration] Studies of hadronic event structure in e+e- annihilation from 30 to 209 GeV with the L3 detector. Phys. Rept. 2004, 399, 71. [Google Scholar] [CrossRef]
- Abe, K. et al. [SLD Collaboration] Measurement of αs(MZ2) from hadronic event observables at the Z0 resonance. Phys. Rev. D 1995, 51, 962. [Google Scholar] [CrossRef]
- Ridder, A.G.; Gehrmann, T.; Glover, E.W.N.; Heinrich, G. Second-order QCD corrections to the thrust distribution. Phys. Rev. Lett. 2007, 99, 132002. [Google Scholar] [CrossRef]
- Ridder, A.G.; Gehrmann, T.; Glover, E.W.N.; Heinrich, G. NNLO corrections to event shapes in e+e- annihilation. J. High Energy Phys. 2007, 0712, 094. [Google Scholar] [CrossRef]
- Ridder, A.G.; Gehrmann, T.; Glover, E.W.N.; Heinrich, G. EERAD3: Event shapes and jet rates in electron-positron annihilation at order αs3. Comput. Phys. Commun. 2014, 185, 3331. [Google Scholar] [CrossRef]
- Weinzierl, S. NNLO corrections to 3-jet observables in electron-positron annihilation. Phys. Rev. Lett. 2008, 101, 162001. [Google Scholar] [CrossRef]
- Weinzierl, S. Event shapes and jet rates in electron-positron annihilation at NNLO. J. High Energy Phys. 2009, 0906, 041. [Google Scholar] [CrossRef]
- Duca, V.D.; Duhr, C.; Kardos, A.; Somogyi, G.; Trócsányi, Z. Three-Jet Production in Electron-Positron Collisions at Next-to-Next-to-Leading Order Accuracy. Phys. Rev. Lett. 2016, 117, 152004. [Google Scholar] [CrossRef]
- Duca, V.D.; Duhr, C.; Kardos, A.; Somogyi, G.; Szór, Z.; Trxoxcsányi, Z.; Tulipxaxnt, Z. Jet production in the CoLoRFulNNLO method: Event shapes in electron-positron collisions. Phys. Rev. D 2016, 94, 074019. [Google Scholar] [CrossRef]
- Wang, S.Q.; Brodsky, S.J.; Wu, X.G.; Shen, J.M.; Giustino, L.D. Novel method for the precise determination of the QCD running coupling from event shape distributions in electron-positron annihilation. Phys. Rev. D 2019, 100, 094010. [Google Scholar] [CrossRef]
- Brandt, S.; Peyrou, C.; Sosnowski, R.; Wroblewski, A. The Principal axis of jets. An Attempt to analyze high-energy collisions as two-body processes. Phys. Lett. 1964, 12, 57. [Google Scholar] [CrossRef]
- Farhi, E. A QCD Test for Jets. Phys. Rev. Lett. 1977, 39, 1587. [Google Scholar] [CrossRef]
- Parisi, G. Super Inclusive Cross-Sections. Phys. Lett. B 1978, 74, 65. [Google Scholar] [CrossRef]
- Donoghue, J.F.; Low, F.E.; Pi, S.Y. Tensor Analysis of Hadronic Jets in Quantum Chromodynamics. Phys. Rev. D 1979, 20, 2759. [Google Scholar] [CrossRef]
- Ridder, A.G.; Gehrmann, T.; Glover, E.W.N.; Heinrich, G. NNLO moments of event shapes in e+e- annihilation. J. High Energy Phys. 2009, 0905, 106. [Google Scholar] [CrossRef]
- Weinzierl, S. Moments of event shapes in electron-positron annihilation at NNLO. Phys. Rev. D 2009, 80, 094018. [Google Scholar] [CrossRef]
- Pahl, C.J. CERN-THESIS-2007-188. Available online: http://cds.cern.ch/record/2284229 (accessed on 13 April 2023).
- Czarnecki, A.; Melnikov, K. Two loop QCD corrections to the heavy quark pair production cross-section in e+e- annihilation near the threshold. Phys. Rev. Lett. 1998, 80, 2531. [Google Scholar] [CrossRef]
- Beneke, M.; Signer, A.; Smirnov, V.A. Two loop correction to the leptonic decay of quarkonium. Phys. Rev. Lett. 1998, 80, 2535. [Google Scholar] [CrossRef]
- Bernreuther, W.; Bonciani, R.; Gehrmann, T.; Heinesch, R.; Leineweber, T.; Mastrolia, P.; Remiddi, E. Two-Parton Contribution to the Heavy-Quark Forward-Backward Asymmetry in NNLO QCD. Nucl. Phys. B 2006, 750, 83. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Hoang, A.H.; Kuhn, J.H.; Teubner, T. Angular distributions of massive quarks and leptons close to threshold. Phys. Lett. B 1995, 359, 355. [Google Scholar] [CrossRef]
- Appelquist, T.; Dine, M.; Muzinich, I.J. The Static Potential in Quantum Chromodynamics. Phys. Lett. 1977, 69B, 231. [Google Scholar] [CrossRef]
- Fischler, W. Quark-anti-Quark Potential in QCD. Nucl. Phys. B 1977, 129, 157. [Google Scholar] [CrossRef]
- Peter, M. The Static quark-antiquark potential in QCD to three loops. Phys. Rev. Lett. 1997, 78, 602. [Google Scholar] [CrossRef]
- Schroder, Y. The Static potential in QCD to two loops. Phys. Lett. B 1999, 447, 321. [Google Scholar] [CrossRef]
- Smirnov, A.V.; Smirnov, V.A.; Steinhauser, M. Fermionic contributions to the three-loop static potential. Phys. Lett. B 2008, 668, 293. [Google Scholar] [CrossRef]
- Smirnov, A.V.; Smirnov, V.A.; Steinhauser, M. Three-loop static potential. Phys. Rev. Lett. 2010, 104, 112002. [Google Scholar] [CrossRef] [PubMed]
- Anzai, C.; Kiyo, Y.; Sumino, Y. Static QCD potential at three-loop order. Phys. Rev. Lett. 2010, 104, 112003. [Google Scholar] [CrossRef]
- Kataev, A.L.; Molokoedov, V.S. Fourth-order QCD renormalization group quantities in the V scheme and the relation of the β function to the Gell-Mann–Low function in QED. Phys. Rev. D 2015, 92, 054008. [Google Scholar] [CrossRef]
- Kataev, A.L.; Molokoedov, V.S. The generalized Crewther relation and V-scheme: Analytic O(αs4) results in QCD and QED. arXiv 2023, arXiv:2302.03443. [Google Scholar]
- Wang, S.Q.; Brodsky, S.J.; Wu, X.G.; Giustino, L.D.; Shen, J.M. Renormalization scale setting for heavy quark pair production in e+e- annihilation near the threshold region. Phys. Rev. D 2020, 102, 014005. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Lu, H.J. Commensurate scale relations in quantum chromodynamics. Phys. Rev. D 1995, 51, 3652. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.J.; Brodsky, S.J. Relating physical observables in QCD without scale-scheme ambiguity. Phys. Rev. D 1993, 48, 3310. [Google Scholar] [CrossRef]
- Hoang, A.H.; Kuhn, J.H.; Teubner, T. Radiation of light fermions in heavy fermion production. Nucl. Phys. B 1995, 452, 173. [Google Scholar] [CrossRef]
- Hoang, A.H. Two loop corrections to the electromagnetic vertex for energies close to threshold. Phys. Rev. D 1997, 56, 7276. [Google Scholar] [CrossRef]
- Czarnecki, A.; Melnikov, K. Two loop QCD corrections to top quark width. Nucl. Phys. B 1999, 544, 520. [Google Scholar] [CrossRef]
- Chetyrkin, K.G.; Harlander, R.; Seidensticker, T.; Steinhauser, M. Second order QCD corrections to t→W+b. Phys. Rev. D 1999, 60, 114015. [Google Scholar] [CrossRef]
- Blokland, I.R.; Czarnecki, A.; Slusarczyk, M.; Tkachov, F. Heavy to light decays with a two loop accuracy. Phys. Rev. Lett. 2004, 93, 062001. [Google Scholar] [CrossRef]
- Blokland, I.R.; Czarnecki, A.; Slusarczyk, M.; Tkachov, F. Next-to-next-to-leading order calculations for heavy-to-light decays. Phys. Rev. D 2005, 71, 054004. [Google Scholar] [CrossRef]
- Gao, J.; Li, C.S.; Zhu, H.X. Top Quark Decay at Next-to-Next-to Leading Order in QCD. Phys. Rev. Lett. 2013, 110, 042001. [Google Scholar] [CrossRef]
- Brucherseifer, M.; Caola, F.; Melnikov, K. O(αs2) corrections to fully-differential top quark decays. J. High Energy Phys. 2013, 4, 059. [Google Scholar] [CrossRef]
- Khachatryan, V. et al. [CMS] Measurement of the ratio B(t→Wb)/B(t→Wq) in pp collisions at s = 8 TeV. Phys. Lett. B 2014, 736, 33–57. [Google Scholar] [CrossRef]
- Basdevant, J.L. The Pade approximation and its physical applications. Fortsch. Phys. 1972, 20, 283. [Google Scholar] [CrossRef]
- Samuel, M.A.; Li, G.; Steinfelds, E. Estimating perturbative coefficients in quantum field theory using Pade approximants. Phys. Lett. B 1994, 323, 188. [Google Scholar] [CrossRef]
- Samuel, M.A.; Ellis, J.R.; Karliner, M. Comparison of the Pade approximation approach to perturbative QCD calculations. Phys. Rev. Lett. 1995, 74, 4380. [Google Scholar] [CrossRef] [PubMed]
- Cacciari, M.; Houdeau, N. Meaningful characterisation of perturbative theoretical uncertainties. J. High Energy Phys. 2011, 9, 39. [Google Scholar] [CrossRef]
- Bagnaschi, E.; Cacciari, M.; Guffanti, A.; Jenniches, L. An extensive survey of the estimation of uncertainties from missing higher orders in perturbative calculations. J. High Energy Phys. 2015, 2, 133. [Google Scholar] [CrossRef]
- Bonvini, M. Probabilistic definition of the perturbative theoretical uncertainty from missing higher orders. Eur. Phys. J. C 2020, 80, 989. [Google Scholar] [CrossRef]
- Duhr, C.; Huss, A.; Mazeliauskas, A.; Szafron, R. An analysis of Bayesian estimates for missing higher orders in perturbative calculations. J. High Energy Phys. 2021, 9, 122. [Google Scholar] [CrossRef]
- Gardi, E. Why Pade approximants reduce the renormalization scale dependence in QFT? Phys. Rev. D 1997, 56, 68. [Google Scholar] [CrossRef]
- Cvetic, G. Improvement of the approach of diagonal Pade approximants for perturbative series in gauge theories. Phys. Rev. D 1998, 57, R3209. [Google Scholar] [CrossRef]
- Du, B.L.; Wu, X.G.; Shen, J.M.; Brodsky, S.J. Extending the Predictive Power of Perturbative QCD. Eur. Phys. J. C 2019, 79, 182. [Google Scholar] [CrossRef]
- Shen, J.M.; Zhou, Z.J.; Wang, S.Q.; Yan, J.; Wu, Z.F.; Wu, X.G.; Brodsky, S.J. Extending the Predictive Power of Perturbative QCD Using the Principle of Maximum Conformality and Bayesian Analysis. arXiv 2022, arXiv:2209.03546. [Google Scholar]

| Scale | |||||
|---|---|---|---|---|---|
| 1.4806 | −0.1394 | −0.0234 | 1.3179 | ||
| Conv. | 1.4806 | −0.1261 | −0.0306 | 1.3239 | |
| 1.4806 | −0.1161 | −0.0357 | 1.3288 | ||
| PMC | 1.4806 | −0.1892 | 0.0207 | 1.3122 |
| 172.5 | −0.0038 | −0.0221 | 0.0249 | 1.3112 | |
| 173.5 | −0.0039 | −0.0225 | 0.0255 | 1.3383 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.-Q.; Brodsky, S.J.; Wu, X.-G.; Shen, J.-M.; Di Giustino, L. Elimination of QCD Renormalization Scale and Scheme Ambiguities. Universe 2023, 9, 193. https://doi.org/10.3390/universe9040193
Wang S-Q, Brodsky SJ, Wu X-G, Shen J-M, Di Giustino L. Elimination of QCD Renormalization Scale and Scheme Ambiguities. Universe. 2023; 9(4):193. https://doi.org/10.3390/universe9040193
Chicago/Turabian StyleWang, Sheng-Quan, Stanley J. Brodsky, Xing-Gang Wu, Jian-Ming Shen, and Leonardo Di Giustino. 2023. "Elimination of QCD Renormalization Scale and Scheme Ambiguities" Universe 9, no. 4: 193. https://doi.org/10.3390/universe9040193
APA StyleWang, S.-Q., Brodsky, S. J., Wu, X.-G., Shen, J.-M., & Di Giustino, L. (2023). Elimination of QCD Renormalization Scale and Scheme Ambiguities. Universe, 9(4), 193. https://doi.org/10.3390/universe9040193







