Abstract
Astrophysical plasma ejections (jets) are formed and powered by black holes that accrete material from their companion star in binary systems. Black hole X-ray binary systems constitute potential powerful galactic and extragalactic neutrino and gamma-ray sources. After being accelerated to highly relativistic velocities and subjected to various energy-consuming interactions, the lepto-hadronic content of the jets produces secondary particles such as pions and muons that decay to gamma-ray photons and neutrinos heading towards the Earth. In this work, we employ a jet emission model in order to predict the neutrino and gamma-ray integral fluxes emanating from some of the most investigated and prominent stellar black hole X-ray binary systems in the Milky Way, such as GRO J1655-40, Cygnus X-1, SS 433, and GRS 1915+105. For the sake of comparison, we also include an extragalactic system, namely, LMC X-1, located in the Large Magellanic Cloud. For the case of gamma-ray emissions, we also include absorption effects due to X-ray emission from the accretion disk and the black hole corona, as well as ultraviolet (UV) emission from the binary system’s companion star.
1. Introduction
Stellar-mass black holes accrete material from their companion star, forming black hole X-ray binary systems (BHXRBs). As matter falls toward the black hole, it does not follow straight trajectories into it, but instead, it forms an accretion disk. These disks give rise to astrophysical jets coming from the vicinity of the compact object [1]. The jets are potential multimessenger emitters of radio emissions, X-rays, gamma-rays, and high-energy neutrinos [2,3]. Such emissions may arrive at Earth-bound telescopes, relevant space stations, and other terrestrial detectors and provide valuable astrophysical information concerning the formation and acceleration mechanisms of the jets [4,5,6,7,8,9,10,11].
There is little observational data on high-energy gamma-ray and neutrino emissions from X-ray binary systems (XRBs). The most promising system is Cygnus X-1 regarding the detection of emitted gamma-rays. Specifically, Fermi-LAT detected emission in the 0.06–20 GeV range [12] and in the 0.04–60 GeV range during the system’s hard and intermediate states [13]. An upper limit of (>200 cm−2 s−1, for very high energy (VHE) gamma-ray emissions, was estimated by the MAGIC telescope [14]. Emission related to the jet interaction with the interstellar medium was observed from SS 433 by HAWC [15]. For VHE gamma-rays, only upper limits, such as cm−2 s−1, were established by MAGIC and HEGRA [16,17,18]. Similarly, there was no detection of VHE emissions from LMC X-1, GRS 1915+105, and GRO J1655-40, only less energetic outbursts [19,20]. Upper limits for the emitted integral flux from GRS 1915+105 were set as cm−2 s−1, (>410 cm−2 s−1, and (>1101 cm−2 s−1 [21,22,23].
Neutrinos have not been detected yet from any X-ray binary system [24,25,26] despite discussions and theoretical predictions [3,27]. Recently, 90% confidence level (CL) upper flux limits (ULs) were estimated from a periodic emission search of 7.5-year IceCube data [28]. Those involve GeV cm−2 s−1 for Cygnus X-1, GeV cm−2 s−1 for SS 433, and GeV cm−2 s−1 for GRS 1915+105. Concerning SS 433, the time-integrated upper flux limit was also calculated as GeV cm−2 s−1 [28]. The above upper limits were estimated for power law spectra with index and flux normalization at 1 TeV.
There have been many attempts towards modeling the relativistic jets and acquiring predictions over their emission output, including neutrinos and gamma-rays. Jet modeling is often associated with different high-energy emission mechanisms depending on whether leptons or hadrons carry the majority of the jet power. In the first case, the prevalent emission mechanisms involve leptons emitting synchrotron radiation or engaging in inverse Compton interactions with photons from the system’s environment (i.e., accretion disk, corona, companion star) [29,30,31]. Very high energy gamma-rays and neutrinos can be produced primarily through hadronic processes involving relativistic proton interactions with lower-energy protons or photons generated inside or outside the jet [32,33,34,35].
In this work, we aim to estimate the high-energy gamma-ray and neutrino fluxes emitted and directed towards the Earth from those systems. One of our goals is to offer possible explanations for the lack of relevant observations. For that purpose, we adopt a hadronic one-zone jet model to make reliable predictions about the neutrino and gamma-ray fluxes that are expected to reach the Earth from some of the most researched and observed X-ray binaries in our galaxy, including Cygnus X-1, GRS 1915+105, GRO J1655-40, SS 433, etc. Our focus is primarily on the hadronic processes that produce neutrinos via secondary particle decays. We consider steady-state particle transport equations in order to calculate their respective energy distributions [35,36]. They also produce gamma-rays, mainly originating from the decay of neutral pions and eta particles with energies exceeding those achieved due to purely leptonic mechanisms such as Compton up-scattering and synchrotron radiation emission [31].
One possible explanation for the lack of gamma-ray detection is the pair production via photon annihilation, which is frequent in the binary system’s environment. It often involves highly energetic jet photons and higher-wavelength thermal photons emitted by the extremely hot and optically thick accretion disk or the system’s companion star [37,38]. Non-thermal coronal emission also contributes to a lesser extent. The effect of all these interactions, leading to severe photon absorption, is also included in our calculations related to the expected gamma-ray differential and integral fluxes.
The rest of the article is organized as follows. In Section 2, we present the particle and photon emission model. Then, in Section 3, we discuss the primary sources of lower-energy photons that cause substantial jet-photon absorption. In Section 4, we discuss some multidimensional simulated results for several black hole X-ray binaries. Finally, in Section 5, we summarize this work’s main results and discuss the next generation of investigations.
2. Model Calculations for the Astrophysical Outflows from X-ray Binaries
The energy spectra associated with those systems follow a power law energy dependence often modified by an exponential cutoff at high energies. With the appropriate choice of parameters, such as the lepton-to-hadron ratio, the jet’s bulk velocity, the jet’s opening angle, etc., the above jet models explain sufficiently the observed distributions in the energy range 1.2 GeV ≤ E ≤ 10 TeV.
In previous works, we assumed purely hadronic jets focusing on multiple independent acceleration zones [39], or we studied primarily the lepton-induced mechanisms investigating the dependence on the jet parameterization [40]. In both cases, priority was given only to the multi-wavelength photon emission from X-ray binary systems and not the production of neutrinos, which is included in this work.
In the following subsection, we briefly summarize the model’s main features, which describe multimessenger emission generated through the collisions of thermal protons with non-thermal ones within the jet.
2.1. p-p Collision Mechanism Inside the Jets
The collision of non-thermal protons with cold ones inside the hadronic jets (p-p collision mechanism) produces high-energy charged particles (pions , kaons , muons , etc.) and neutral particles (, , , particles, etc.). The non-thermal protons are initially accelerated to relativistic energies through shock-induced mechanisms within a conical jet zonal region.
The secondary charged pions then decay to charged leptons (muons ) as well as neutrinos and anti-neutrinos:
We mention that neutral pions (), -particles, etc., decay, producing gamma-rays according to the reactions
In the context of this work, we consider that neutrinos are generated only from charged-pion decays (for neutrinos coming from kaon decays, the reader is referred, e.g., to Ref. [41]) and subsequently from charged muon decays [42]. Moreover, the gamma-rays are produced from the decays of neutral pions and eta particles. Typically, high-energy neutrinos are always accompanied by gamma-rays.
We assume that some of the protons inside the jet carry half of the relativistic jet power, , where is the hadron-to-lepton ratio of the jet’s content, denotes the relativistic-to-slow particle ratio (including both hadrons and leptons), and the total kinetic luminosity of the jet. The relativistic particles acquire high velocities through consistent acceleration due to shock waves [43] with an efficiency given by another model parameter, namely, . The acceleration occurs within the length of the jet, starting from distance from the black hole up to .
2.2. Neutrino and Gamma-Ray Production in the Jet Frame
The mathematical formulation describing the production rate and the cooling mechanisms of the relativistic protons and the secondary particles is based on the general transport equation [35,36,44]. In order to avoid unnecessary and complex calculations that often contribute negligibly, we use a simplified form that is given by [35,36]
where denotes the particle energy distribution and is the particle production rate (in units of GeV−1 cm−3 s−1). The energy-loss rate is given by . In addition, the time scale, which corresponds to the reduction in the particle density inside the jet, is given by . The particle escape rate from the jet’s frame is .
The energy distribution is given by the solution to the above transport equation:
where is the maximum energy achieved through the combination of the acceleration and cooling mechanisms.
The transport equation describes the energy distribution of the particles within a defined jet region due to external or internal interactions or changes regarding the radius of the jet along the z-axis. Particle decays and interactions with the jet’s magnetic field lines (i.e., synchrotron emission) are prevalent in shaping the final distributions.
Moreover, the corresponding differential equation is not homogeneous, as it employs the production rate that depends on the collision frequency and the respective cross-section, leading to different particle production. Starting from the distribution of the relativistic protons, their injection rate, given in the jet co-moving reference frame, is written as
where c is the speed of light and z is the distance from the compact object along the jet axis. is the Lorentz factor corresponding to the jet bulk velocity, . The jet’s angle to the line of sight is symbolized by i. The injection rate depends primarily on the normalization constant , that depends on the power carried by the jet particles and the maximum energy gained through particle acceleration. The latter is heavily dependent on the relative rate between the energy gain and cooling of protons. Furthermore, the charged pion injection rate depends on the inelastic cross-section for proton–proton collisions and the density of cold protons inside the jet, . Hence, it is given by
where and is the maximum proton energy within the jet acceleration zone. Here, the proton energy distribution is employed along with the inelastic p-p collision cross-section, . In the latter integral, denotes the pion mean number produced per p-p collision, as described in [45].
Subsequently, we can calculate the neutrino emissivity by making use of the step function as follows:
where , and s). Evidently, denotes the pion energy distribution. As mentioned, gamma-rays are products of neutral pion decays, thus the respective neutral pion production rate is required:
The inelasticity of the p-p collision is and the mean number of neutral pions produced per collision is . Also, the proton energy is given by . Finally, the gamma-ray emissivity due to neutral pion decay is written as
where . In addition, the gamma-ray spectrum per p-p collision, , is incorporated [45].
In order to calculate the time-independent emissivities of gamma-rays and neutrinos, one needs, first, to calculate the distributions and for protons and pions, respectively, that constitute the solutions to the coupled transport equations. Details on this matter have been addressed in our previous works and the reader is referred to Refs. [39,46] and references therein.
It is worth noting that in the above equations some additional terms may appear, corresponding to the rates of some other processes, such as inverse Compton scattering (ICS), pion–muon () scattering, etc. These may contribute negatively to the final emission to some degree.
3. Photon Annihilation in the X-ray Binary Environment
A substantial portion of the emitted radiation is annihilated by photons of lower energy originating from the accretion disk of the XRB, the secondary stellar component, and the surrounding plasma of the black hole corona. More specifically, the accretion disk emits mainly in the soft X-ray range of the spectrum, while the corona contributes to the hard X-ray counterpart. Even less energetic photons that can absorb very high energy gamma-rays in the TeV regime emanate from the companion star as black body radiation that peaks at UV frequencies.
The calculation of the optical depth accounts for all the possible interactions of a single photon, emitted from a jet zone at distance z, with photons coming from the donor star’s direction, the accretion disk, and the corona. Furthermore, the optical depth integrates over the distance covered by the jet photon, which depends on the angle between the directions of the two interacting photons and the angle to the line of sight. We assume an isotropic emission only for the corona while the jet photon is still inside its spherical region.
The lower-energy photon densities of the accretion disk, stellar emission, and black hole corona, contributing mainly to gamma-ray absorption, are given by the expressions [37,38]
In the latter equations, the dimensionless parameter is employed, where T corresponds to the disk’s radius-dependent temperature profile or the stellar effective surface temperature. denotes the total stellar luminosity and represents the distance from the companion star. The details for the optical depth calculation corresponding to the stellar thermal emission can be found in [37].
We assume a spherical corona of radius , where is the gravitational radius. Similar values are associated with the hard state of jet activity [47]. Then, a power law distribution with an exponential cutoff at keV describes the respective emitted spectrum. The spectral index is taken as . In Equation (13), A denotes a normalization constant and is the distance from the compact object.
The implemented accretion disk model in the present work fits the classic Shakura–Sunyaev type for an Eddington accretion limit. Hence, the disk is assumed to be a geometrically thin and optically thick powerful X-ray source, as described in [48]. It is often assumed that the inner disk radius begins at the last stable orbit (i.e., ) for a non-spinning black hole, which is equal to . We adopt the same assumption for all the studied XRB systems. We calculate the outer boundary of the disk through Eggleton’s formula [49] for a donor star that fills 90% of its Roche lobe, which holds for most cases. It is usually on the order of cm.
Moreover, a thorough geometrical analysis of the disk, utilized in the optical depth calculations, is conducted in Ref. [38]. In that work, gamma-ray absorption from the disk and the corona was investigated and applied to Cygnus X-3. However, the accretion disk size employed was relatively small (i.e., cm), which led to a significant underestimation of the optical depth compared to our results.
The dependence of the jet gamma-ray photon absorption on the disk’s geometry and radiative efficiency is better illustrated in Refs. [39,40]. In those works, we conducted similar calculations which are, in the present work, extended by applications on two additional X-ray binaries, namely, GRO J1655-40 and LMC X-1. This time, we also consider an exponential cutoff for the corona emission. In addition, we extend the energy range of our calculations to 0.1 GeV in order to study the impact of absorption on the emitted spectrum for energies that present a greater chance of detection.
It should be mentioned that the phenomenon of disk truncation during the spectral phase transition of the system is possible [50]. That would lead to a substantial decrease in photon absorption, as discussed in [40]. Nonetheless, for the time being, we adopt the conditions that allow maximum photon absorption in order to set minimum integral flux limits and thoroughly explore the impact of photon annihilation on the expected gamma-ray spectrum. In addition, disk irradiation effects [51] could be considered, but they are not expected to have a substantial impact on the lower-energy regime of the gamma-ray spectrum. Similar effects will be investigated thoroughly in future works.
Our jet model parameterization is presented in Table 1. A critical aspect that enters the calculations of the disk emission optical depth is the mass accretion rate . Although it varies, depending on the XRB, in most cases, we assume values near the Eddington limit (see Table 1). Some notable exceptions include the super-Eddington accretion cases, including SS 433 [52]. In this study, we adopt Eddington mass accretion rates for all the XRB cases to avoid extreme temperatures in the innermost disk region. These correspond to higher accretion rates that are not described by the adopted disk model. This compensates, in a way, for the disk truncation phenomenon that would otherwise extend the inner disk boundary to a greater radius, corresponding to lower temperatures.

Table 1.
Constant parameters employed for the jet model in this work.
In Table 2, we tabulate some of the most well-studied examples of X-ray binary systems with a compact object widely considered to be a black hole. We also list their distance from Earth d, the compact object and companion stellar masses and , and the jet’s bulk velocity , along with the donor star’s luminosity and effective surface temperature . The latter fits the corresponding stellar types that were mentioned in the literature review. We selected to apply our model to these XRB examples due to the variety of their characteristics, which allows for a thorough comparison of the expected neutrino and gamma-ray fluxes.

Table 2.
X-ray binary (XRB) parameters used in the calculations.
4. Results
In Figure 1, we plot the calculated ratio of final-to-initial gamma-ray intensity due to pair production. Even without considering an Eddington mass accretion rate [52], SS 443 still shows the largest gamma-ray photon annihilation, both due to its accretion disk (left panel) and its donor star (right panel). The angle to the line of sight of this system, combined with a fairly luminous companion star, plays an important role in obtaining these results. This is not the case, however, for GRS 1915+105. For the rest of the studied systems, the situation is intermediate.
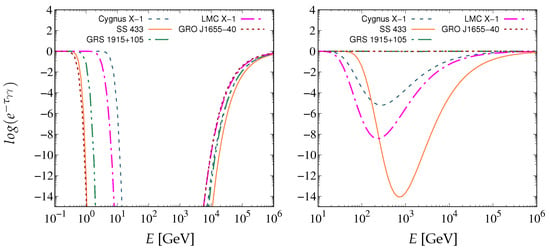
Figure 1.
The predicted absorption due to the thermal emission from the accretion disk (left panel) and the donor star (right panel) is estimated for the XRB systems of Table 2.
The contribution of the coronal emission to the jet gamma-ray photon annihilation is more than four orders of magnitude smaller than that of the accretion disk and the donor star. The fact that we consider the acceleration zone outside the corona boundary diminishes further the gamma-ray photon interactions with the corona non-thermal photons.
In Figure 2, we demonstrate the intrinsic muon neutrino and gamma-ray differential fluxes produced inside the jets of the BHXRBs listed in Table 2. The top-left panel demonstrates the neutrino flux produced by decaying pions not subjected to cooling mechanisms, such as synchrotron emission and p-π collisions inside the jet. On the other hand, the top-right graph illustrates the reduced neutrino flux, which is produced from pions after they have lost part of their initial energy. As shown in Figure 2 (top panels), the neutrino differential flux gap between Cygnus X-1, SS 443, and the rest of the XRBs is mainly attributed to the substantial jet confinement of Cygnus X-1 and SS 433.
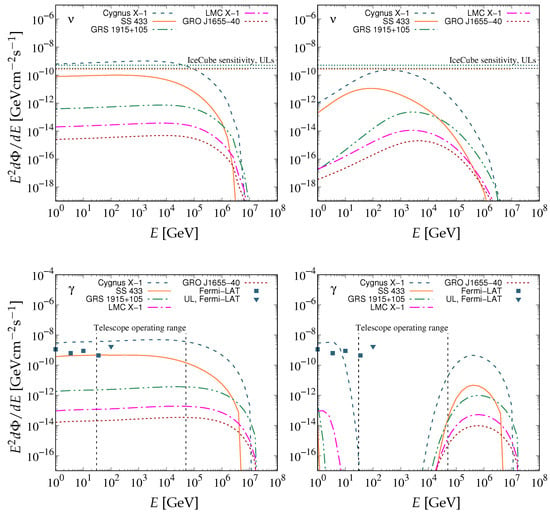
Figure 2.
The estimated differential fluxes for neutrinos without pion cooling (top-left panel), neutrinos after pion cooling (top-right panel), and gamma-rays (bottom-left panel) are presented. The bottom-right panel depicts the differential fluxes for gamma-rays after photon annihilation with photons emitted by the accretion disk, the donor star, and the corona. The black dotted line corresponds to the IceCube sensitivity [26], while the rest of the colored horizontal lines correspond to the upper limits for the XRBs of the same color [28]. The gamma-ray flux is compared to measurements and upper limits from Fermi-LAT [13].
Particle cooling plays a prominent role in shaping the final energy distributions that could lead to detectable neutrino fluxes. In Figure 2, the neutrino distribution peaks at 0.1–10 TeV for all XRBs and drops abruptly for lower energies due to intense cooling of the respective high-energy decaying pions. The jets of Cygnus X-1 and GRS 1915+105 are less effective in cooling down the accelerated particles. This leads to an extension of the neutrino energy range (i.e., higher-energy neutrinos are produced in those systems) and a steeper drop in the lower-energy neutrino density compared to the rest of the studied XRBs.
In the top panels of Figure 2, we compare the predicted neutrino flux with the IceCube sensitivity for a point-like source with an spectrum at 100 TeV based on 8 years of data for comparison [26]. We also plot the 90% confidence level upper limits for Cygnus X-1 ( GeV cm−2 s−1), SS 433 ( GeV cm−2 s−1), and GRS 1915+105 ( GeV cm−2 s−1) for an spectrum at 1 TeV based on the 7.5-year IceCube data [28]. The sensitivity depends on the declination. However, the respective deviation is smaller than the y-axis scale in Figure 2. The value employed corresponds to . It is clear that, according to our estimations, the neutrino output for the majority of the studied systems is out of reach even for the most advanced detectors in operation. Nonetheless, Cygnus X-1 exhibits promising prospects for future high-energy neutrino detection.
The gamma-ray differential fluxes before and after considering photon absorption effects are presented in the bottom panels of Figure 2. The unabsorbed spectra resemble the respective neutrino ones (without pion cooling), albeit slightly increased. The photon inflow gap between 100 GeV and 1 TeV essentially coincides with the energy range of most operating telescopes in that regime, such as MAGIC, H.E.S.S, and VERITAS, justifying the lack of relevant observations. These results agree with measurements and upper limits from Fermi-LAT in the 1–100 GeV range for Cygnus X-1 in its hard state [13]. The spectrum between 0.1–10 GeV could be fitted by a power law with a spectral index near . The emission above 10 GeV, including the one measured at 35 GeV, could be produced in a higher part of the jet, where photon absorption is much less prominent.
The factors defining the expected particle or photon flux per unit of energy are (i) the mass of the black hole, (ii) the distance from the Earth, and (iii) the assumed jet opening angle. The latter is sometimes uncertain, so a maximum angle limit based on observations is employed.
The integral fluxes before and after absorption for the studied XRBs are listed in Table 3 for two different threshold energies, (i) MeV and (ii) GeV, for gamma-rays, and one threshold energy, GeV, for neutrinos. In addition, the 99% CL upper limits for GRS 1915+105 [73] from H.E.S.S collaboration, and SS 433 [18] (MAGIC collaboration), and the 95% CL upper limit for Cygnus X-1 [14] (MAGIC collaboration), are listed in Table 3 for comparison.

Table 3.
The predicted XRB neutrino and gamma-ray integral fluxes that are emitted before and after photon absorption occurs. Also, the upper limits from MAGIC [14,18] and H.E.S.S [73] are listed.
On the other hand, the results in Table 3 indicate marginal detection probabilities, at least for Cygnus X-1, SS 433, and GRS 1915+105, if we ignore the pair production taking place in the vicinity of these systems. However, the drop in high-frequency photon flux due to absorption is enormous in all the above systems. This holds even for Cygnus X-1, which demonstrates a substantially higher flux of photons beyond 10 GeV thanks to its relative inclination compared to the Earth. We should point out that the predicted gamma-ray integral fluxes consist of particles with energies greater than 100 GeV, while the upper limits refer to higher energy thresholds. Nevertheless, this does not affect any XRB due to the photon inflow gap between 100 GeV and 1 TeV, as seen in Figure 2 (bottom-right panel).
In Figure 3, we present the neutrino and gamma-ray integral fluxes for various values of the half-opening angle, , to better demonstrate the impact of the jet’s confinement on the emitted integral fluxes. A substantial flux increase, corresponding to a more compact and confined jet, is obtained with . This is due to the considerable increase in the p-p collision rate with smaller opening angles. This positively affects the secondary particle production rate, leading to higher neutrino and gamma-ray fluxes. Furthermore, the results in Figure 3 showcase the emitted flux discrepancies between some of the most well-studied XRBs without accounting for the dependence on the jet radius, since it is the same for all systems. The jet’s half-opening angle is not a well-constrained quantity in most modeling cases.
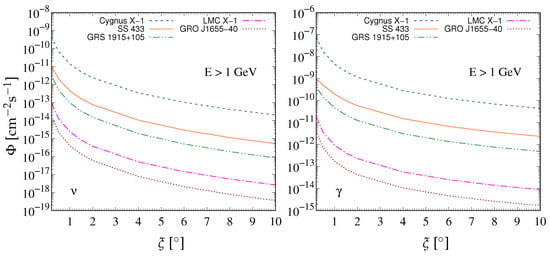
Figure 3.
The integral flux dependence on the jet’s half-opening angle is demonstrated for neutrinos (left panel) and gamma-rays (right panel) from the black hole X-ray binaries of Table 2.
The jets have been modeled in a similar way in previous works [35,74]. The differences lie in the main physical assumptions about the geometry, the content of the jet, and the focus on the gamma-ray absorption that occurs in the proximity of the binary system, mainly due to the accretion disk thermal emission.
Specifically, various XRBs have already been modeled before, such as Cygnus X-1 [75], SS 433 [36], and GRS 1915+105 [76]. Our predictions for Cygnus X-1 show an increased contribution of the p-p mechanism to the VHE gamma-ray flux compared to [75]. This could be partially attributed to the difference in the power law spectral index (p = 1.7 instead of 2) which makes the produced flux comparable to the Fermi-LAT measurements. However, in our case, the emitted spectrum is heavily attenuated after 20 GeV due to disk-induced absorption. In the case of SS 433, we employ a similar model to [36]. The differences lie in the parameterization. We estimate neutrino and gamma-ray intensities that are lower by one or two orders of magnitude in comparison. It should be pointed out that some XRB parameters have been re-evaluated since then [55].
In most modeling cases, the focus is on X-ray and lower gamma-ray emissions, which are not heavily affected by absorption. In other studies, the modeling is based on a single system. In our case, the same hadronic model for various XRBs is employed in order to demonstrate the high-energy flux deviation between them based on their characteristics (i.e., the masses of the components, distance from Earth, inclination, etc.). The lack of relevant observations could be justified by our results combined with the upper limits and sensitivities of some of the most advanced telescopes and detectors in operation. For the case of gamma-rays, photon absorption is crucial in its role in decreasing the probabilities of VHE emission detection.
In addition, little attention is given to the GRO J1655-40 and LMC X-1 systems due to the lack of relevant observations. We model the jets of these XRBs with the purpose of drawing conclusions regarding the potential detection of high-energy neutrinos and gamma-rays. We confirm the comparably very low expected integral fluxes. That is justified for the case of LMC X-1 due to its distance from the Earth and the present day sensitivity of the available detectors. In the case of GRO J1655-40, the results are attributed to the combination of the system’s high inclination, the jet’s relatively large half-opening angle, and the low black hole mass.
In closing, the emission from the accretion disk and the donor star is large enough to substantially increase the pion production through interactions with the jet relativistic protons (p- mechanism). However, there would also be a significant increase in the cooling of the proton distribution. We plan to investigate thoroughly the total impact of p- interactions on the neutrino and gamma-ray intensities in the near future.
5. Summary and Outlook
Material outflows in stellar-mass black hole binaries involving accretion disks are usually ejected perpendicular to the accretion disk’s surface, forming strongly collimated jets. These jets are usually treated magnetohydrodynamically, assuming various reliable emission models. Considering that the jet’s material is lepto-hadronic (i.e., ), secondary neutral and charged particles are generated via inelastic collisions of relativistic protons with the cold ones (p-p interaction mechanism). The charged pion decays lead to high-energy electron-neutrinos () and muon-neutrinos (), while the neutral pion decays lead to gamma-ray emission. The produced neutrinos ( and ) and gamma-rays may reach space-based and Earth-based telescopes.
In this work, we modeled the astrophysical jets of the galactic XRBs, GRS 1915+105, GRO J1655-40, Cygnus X-1, SS 433, and the extragalactic LMC X-1. We computed the emissions of very high energy gamma-ray and neutrino fluxes from these binary systems and compared them to the present day detector sensitivities as well as the established upper limits. Our investigation includes the photon absorption via pair production that occurs due to the thermal emission of (i) the accretion disk and (ii) the stellar component, in addition to the coronal non-thermal emission.
Our findings show small possibilities of neutrino detection for all studied XRBs, except Cygnus X-1 in the 0.1–1 TeV range. Particle cooling inside the jet frame has a significant negative impact on the emitted neutrino flux, especially for energies below 100 GeV. Concerning gamma-rays, the differential fluxes reaching the Earth are strongly affected by absorption effects, mainly in the 100 GeV < < 10 TeV range, where most gamma-ray telescopes operate. This could explain the lack of high-energy gamma-ray detection from XRBs.
The most significant high-energy emission activity is exhibited by the SS 433 and Cygnus X-1 binaries, which may keep attracting research interest around the physics of the jets as well as the particle acceleration and high-energy photon emission. Gamma-rays with GeV could be emitted from jet regions far from the black hole, where photon annihilation efficiency appears to be considerably reduced.
Among the studied XRBs, GRO J1655-40 and LMC X-1 show little promise for future high-energy detection. The reason is a combination of the binary inclination, the opening angle of the jet, the black hole mass, and the distance from the Earth. An increase in the jet half-opening angle above 1° (possibly related to the weakening of the magnetic field lines) could lead to a drop of even two orders of magnitude regarding the neutrino integral flux and one order of magnitude for the gamma-ray flux beyond 1 GeV. Nonetheless, additional mechanisms, such as the p- interactions of relativistic protons with synchrotron emission or photons from the disk and the donor star, could substantially increase the jet’s high-energy emission output. This will be one of our main focal points in future studies.
In the near future, more accurate measurements of gamma-ray and neutrino fluxes are expected by the coming observatories (CTA telescope array, etc.), which can verify or disprove our assumptions on these significant emission sources. From the perspective of neutrino detection, adding more years of data from the continuous operation of IceCube will improve the research prospects concerning galactic sources of cosmic neutrinos. Furthermore, the next-generation detection telescope IceCube-Gen2 is expected to measure the properties of cosmic neutrino sources with unprecedented accuracy and increased energy range.
Author Contributions
Conceptualization, O.K. and T.P.; methodology, T.P.; software, T.P.; validation, O.K., T.P. and T.K.; formal analysis, T.P.; investigation, O.K. and T.P.; resources, T.K.; data curation, O.K.; writing—original draft preparation, T.P.; writing—review and editing, O.K.; visualization, T.P.; supervision, T.K.; project administration, T.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work is financially supported by: “The Association for Advancement of Research on Open Problems in Nuclear Physics and Particle Physics (OPRA Association)”, Tel Aviv, Israel.
Data Availability Statement
The datasets generated during and/or analyzed in the present study are available upon request from the corresponding author.
Acknowledgments
This paper is dedicated to Sabin Stoica on the occasion of his 70th birthday. It aims to recognize his many contributions in Nuclear and Astro-Particle physics.
Conflicts of Interest
Author O. Kosmas was employed by the company Conigital LTD. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Blandford, R.D.; Znajek, R.L. Electromagnetic extraction of energy from Kerr black holes. Mon. Not. R. Astron. Soc. 1977, 179, 433–456. [Google Scholar] [CrossRef]
- Aharonian, F.; Akhperjanian, A.G.; Aye, K.M.; Bazer-Bachi, A.R.; Beilicke, M.; Benbow, W.; Berge, D.; Berghaus, P.; Bernlohr, K.; Boisson, C.; et al. Discovery of Very High Energy Gamma Rays Associated with an X-ray Binary. Science 2005. [Google Scholar] [CrossRef] [PubMed]
- Aharonian, F.; Anchordoqui, L.; Khangulyan, D.; Montaruli, T. Microquasar LS 5039: A TeV gamma-ray emitter and a potential TeV neutrino source. J. Phys. Conf. Ser. 2006, 39, 408. [Google Scholar] [CrossRef]
- Aartsen, M.G. et al. [The IceCube Collaboration] Searches for Sterile Neutrinos with the IceCube Detector. Phys. Rev. Lett. 2016, 117, 071801. [Google Scholar] [CrossRef] [PubMed]
- Aartsen, M.G. et al. [The IceCube Collaboration] All-sky Search for Time-integrated Neutrino Emission from Astrophysical Sources with 7 yr of IceCube Data. Astrophys. J. 2017, 835, 151. [Google Scholar] [CrossRef]
- Adrian-Martinez, S.; Ageron, M.; Aharonian, F.; Aiello, S.; Albert, A.; Ameli, F.; Anassontzis, E.; Andre, M.; Androulakis, G.; Anghinolfi, M.; et al. Letter of intent for KM3NeT 2.0. J. Phys. G Nucl. Part. Phys. 2016, 43, 084001. [Google Scholar] [CrossRef]
- Albert, A.; André, M.; Anghinolfi, M.; Anton, G.; Ardid, M.; Aubert, J.J.; Aublin, J.; Baret, B.; Basa, S.; Belhorma, B.; et al. ANTARES and IceCube Combined Search for Neutrino Point-like and Extended Sources in the Southern Sky. Astrophys. J. 2020, 892, 92. [Google Scholar] [CrossRef]
- Albert, A.; André, M.; Anghinolfi, M.; Anton, G.; Ardid, M.; Aubert, J.J.; Avgitas, T.; Baret, B.; Barrios-Martí, J.; Basa, S.; et al. First all-flavor neutrino pointlike source search with the ANTARES neutrino telescope. Phys. Rev. D 2017, 96, 082001. [Google Scholar] [CrossRef]
- Atwood, W.B.; Abdo, A.A.; Ackermann, M.; Althouse, W.; Anderson, B.; Axelsson, M.; Baldini, L.; Ballet, J.; Band, D.L.; Barbiellini, G.; et al. The large area telescope on the Fermi gamma-ray space telescope mission. Astrophys. J. 2009, 697, 1071. [Google Scholar] [CrossRef]
- Aleksić, J.; Ansoldi, S.; Antonelli, L.A.; Antoranz, P.; Babic, A.; Bangale, P.; Barceló, M.; Barrio, J.A.; González, J.B.; Bednarek, W.; et al. The major upgrade of the MAGIC telescopes, Part I: The hardware improvements and the commissioning of the system. Astropart. Phys. 2016, 72, 61–75. [Google Scholar] [CrossRef]
- Acharya B.S. et al. [Cherenkov Telescope Array Consortium] Science with the Cherenkov Telescope Array; World Scientific Publishing Co. Pte Ltd.: Singapore, 2019. [Google Scholar] [CrossRef]
- Zanin, R.; Fernández-Barral, A.; de Oña Wilhelmi, E.; Aharonian, F.; Blanch, O.; Bosch-Ramon, V.; Galindo, D. Gamma rays detected from Cygnus with likely jet origin. Astron. Astrophys. 2016, 596, A55. [Google Scholar] [CrossRef]
- Zdziarski, A.A.; Malyshev, D.; Chernyakova, M.; Pooley, G.G. High-energy gamma-rays from Cyg X-1. Mon. Not. R. Astron. Soc. 2017, 471, 3657–3667. [Google Scholar] [CrossRef]
- Ahnen, M.L.; Ansoldi, S.; Antonelli, L.A.; Arcaro, C.; Babić, A.; Banerjee, B.; Bangale, P.; de Almeida, U.B.; Barrio, J.A.; González, J.B.; et al. Search for very high-energy gamma-ray emission from the microquasar Cygnus X-1 with the MAGIC telescopes. Mon. Not. R. Astron. Soc. 2017, 472, 3474–3485. [Google Scholar] [CrossRef]
- Abeysekara, A.U.; Albert, A. Very-high-energy particle acceleration powered by the jets of the microquasar SS 433. Nature 2018, 562, 82–85. [Google Scholar] [CrossRef]
- Aharonian, F.; Akhperjanian, A.; Beilicke, M.; Bernlöhr, K.; Börst, H.G.; Bojahr, H.; Bolz, O.; Coarasa, T.; Contreras, J.; Cortina, J.; et al. TeV gamma-ray observations of SS-433 and a survey of the surrounding field with the HEGRA IACT-System. Astron. Astrophys. 2005, 439, 635–643. [Google Scholar] [CrossRef][Green Version]
- Saito, T.Y.; Zanin, R.; Bordas, P.; Bosch-Ramon, V.; Jogler, T.; Paredes, J.M.; Ribo, M.; Rissi, M.; Rico, J.; Torres, D.F. Microquasar observations with the MAGIC telescope. arXiv 2009, arXiv:0907.1017. [Google Scholar] [CrossRef]
- Ahnen, M.L. et al. [MAGIC Collaboration] Constraints on particle acceleration in SS433/W50 from MAGIC and H.E.S.S. observations. Astron. Astrophys. 2018, 612, A14. [Google Scholar] [CrossRef]
- Zhang, S.N.; Ebisawa, K.; Sunyaev, R.; Ueda, Y.; Harmon, B.A.; Sazonov, S.; Fishman, G.J.; Inoue, H.; Paciesas, W.S.; Takahash, T. Broadband High-Energy Observations of the Superluminal Jet Source GRO J1655–40 during an Outburst. Astrophys. J. 1997, 479, 381. [Google Scholar] [CrossRef]
- Kroeger, R.A.; Strickman, M.S.; Grove, J.E.; Kaaret, P.; Ford, E.; Harmon, B.A.; McConnell, M. Gamma-Ray Observations of GRO J1655-40. Astron. Astrophys. Suppl. Ser. 1996, 120, C117. [Google Scholar]
- Bodaghee, A.; Tomsick, J.A.; Pottschmidt, K.; Rodriguez, J.; Wilms, J.; Pooley, G.G. Gamma-ray observations of the microquasars cygnus X-1, CYGNUS X-3, GRS 1915+105, and GX 339-4 with the FERMI large area telescope. Astrophys. J. 2013, 775, 98. [Google Scholar] [CrossRef]
- Szostek, A.; Dubus, G.; Brun, F.; de Naurois, M. VHE gamma-ray observations of the microquasar GRS 1915+105. arXiv 2009, arXiv:0907.3034. [Google Scholar] [CrossRef]
- Schüssler, F.; Bordas, P.; Chadwick, P.M.; Dickinson, H.; Ernenwein, J.P. Simultaneous H.E.S.S. and RXTE observations of the microquasars GRS 1915+105, Circinus X-1 and V4641 Sgr. arXiv 2015, arXiv:1509.03039. [Google Scholar] [CrossRef]
- Aartsen, M.G.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Altmann, D.; Anderson, T.; Archinger, M.; Arguelles, C.; et al. Searches for time-dependent neutrino sources with icecube data from 2008 to 2012. Astrophys. J. 2015, 807, 46. [Google Scholar] [CrossRef]
- Albert, A.; André, M.; Anton, G.; Ardid, M.; Aubert, J.J.; Avgitas, T.; Baret, B.; Barrios-Martí, J.; Basa, S.; Bertin, V.; et al. Time-dependent search for neutrino emission from X-ray binaries with the ANTARES telescope. J. Cosmol. Astropart. Phys. 2017, 2017, 019. [Google Scholar] [CrossRef]
- Aartsen, M.G. et al. [The IceCube Collaboration] Search for steady point-like sources in the astrophysical muon neutrino flux with 8 years of IceCube data. Eur. Phys. J. C 2019, 79, 234. [Google Scholar] [CrossRef]
- Reynoso, M.M.; Carulli, A.M. On the possibilities of high-energy neutrino production in the jets of microquasar SS433 in light of new observational data. Astropart. Phys. 2019, 109, 25–32. [Google Scholar] [CrossRef]
- Abbasi, R.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Alameddine, J.M.; Alves, A.A.; Amin, N.M.; Andeen, K.; et al. Search for High-energy Neutrino Emission from Galactic X-ray Binaries with IceCube. Astrophys. J. Lett. 2022, 930, L24. [Google Scholar] [CrossRef]
- Aharonian, F.; Atoyan, A. Gamma rays from galactic sources with relativistic jets. New Astron. Rev. 1998, 42, 579–584. [Google Scholar] [CrossRef]
- Markoff, S.; Falcke, H.; Fender, R. A jet model for the broadband spectrum of XTE J1118+480 - Synchrotron emission from radio to X-rays in the Low/Hard spectral state. Astron. Astrophys. 2001, 372, L25–L28. [Google Scholar] [CrossRef]
- Bosch-Ramon, V.; Romero, G.E.; Paredes, J.M. A broadband leptonic model for gamma-ray emitting microquasars. Astron. Astrophys. 2006, 447, 263–276. [Google Scholar] [CrossRef]
- Levinson, A.; Waxman, E. Probing Microquasars with TeV Neutrinos. Phys. Rev. Lett. 2001, 87, 171101. [Google Scholar] [CrossRef] [PubMed]
- Romero, G.E.; Torres, D.F.; Kaufman Bernadó, M.M.; Mirabel, I.F. Hadronic gamma-ray emission from windy microquasars. Astron. Astrophys. 2003, 410, L1–L4. [Google Scholar] [CrossRef]
- Bednarek, W. TeV Neutrinos from Microquasars in Compact Massive Binaries. Astrophys. J. 2005, 631, 466. [Google Scholar] [CrossRef][Green Version]
- Reynoso, M.M.; Romero, G.E. Magnetic field effects on neutrino production in microquasars. Astron. Astrophys. 2009, 493, 1–11. [Google Scholar] [CrossRef]
- Reynoso, M.M.; Romero, G.E.; Christiansen, H.R. Production of gamma rays and neutrinos in the dark jets of the microquasar SS433. Mon. Not. R. Astron. Soc. 2008, 387, 1745–1754. [Google Scholar] [CrossRef][Green Version]
- Böttcher, M.; Dermer, C.D. Photon-Photon Absorption of Very High Energy Gamma Rays from Microquasars: Application to LS 5039. Astrophys. J. 2005, 634, L81–L84. [Google Scholar] [CrossRef]
- Cerutti, B.; Dubus, G.; Malzac, J.; Szostek, A.; Belmont, R.; Zdziarski, A.A.; Henri, G. Absorption of high-energy gamma rays in Cygnus X-3. Astron. Astrophys. 2011, 529, A120. [Google Scholar] [CrossRef][Green Version]
- Papavasileiou, T.V.; Kosmas, O.T.; Sinatkas, I. Prediction of gamma-ray emission from Cygnus X-1, SS 433, and GRS 1915+105 after absorption. Astron. Astrophys. 2023, in press. [Google Scholar] [CrossRef]
- Papavasileiou, T.; Kosmas, O.; Sinatkas, I. Studying the Spectral Energy Distributions Emanating from Regular Galactic XRBs. Universe 2023, 9, 312. [Google Scholar] [CrossRef]
- Lipari, P.; Lusignoli, M.; Meloni, D. Flavor composition and energy spectrum of astrophysical neutrinos. Phys. Rev. D 2007, 75, 123005. [Google Scholar] [CrossRef]
- Papadopoulos, D.A.; Kosmas, O.T.; Ganatsios, S. Modeling Particle Transport in Astrophysical Outflows and Simulations of Associated Emissions from Hadronic Microquasar Jets. Adv. High Energy Phys. 2022, 2022, 8146675. [Google Scholar] [CrossRef]
- Gallant, Y.A.; Achterberg, A. Ultra-high-energy cosmic ray acceleration by relativistic blast waves. Mon. Not. R. Astron. Soc. 1999, 305, L6–L10. [Google Scholar] [CrossRef]
- Vieyro, F.L.; Romero, G.E. Particle transport in magnetized media around black holes and associated radiation. Astron. Astrophys. 2012, 542, A7. [Google Scholar] [CrossRef]
- Kelner, S.R.; Aharonian, F.A.; Bugayov, V.V. Energy spectra of gamma rays, electrons, and neutrinos produced at proton-proton interactions in the very high energy regime. Phys. Rev. D 2006, 74, 034018. [Google Scholar] [CrossRef]
- Papavasileiou, T.; Kosmas, O.; Sinatkas, I. Simulations of Neutrino and Gamma-Ray Production from Relativistic Black-Hole Microquasar Jets. Galaxies 2021, 9, 67. [Google Scholar] [CrossRef]
- García, F.; Karpouzas, K.; Méndez, M.; Zhang, L.; Zhang, Y.; Belloni, T.; Altamirano, D. The evolving properties of the corona of GRS 1915+105: A spectral-timing perspective through variable-Comptonization modelling. Mon. Not. R. Astron. Soc. 2022, 513, 4196–4207. [Google Scholar] [CrossRef]
- Shakura, N.I.; Sunyaev, R.A. Black holes in binary systems. Observational appearance. Astron. Astrophys. 1973, 24, 337–355. [Google Scholar]
- Eggleton, P.P. Aproximations to the radii of Roche lobes. Astrophys. J. 1983, 268, 368–369. [Google Scholar] [CrossRef]
- Done, C.; Gierliński, M.; Kubota, A. Modelling the behaviour of accretion flows in X-ray binaries. Astron. Astrophys. Rev. 2007, 15, 1–66. [Google Scholar] [CrossRef]
- Maitra, D.; Markoff, S.; Brocksopp, C.; Noble, M.; Nowak, M.; Wilms, J. Constraining jet/disc geometry and radiative processes in stellar black holes XTE J1118+480 and GX 339-4. Mon. Not. R. Astron. Soc. 2009, 398, 1638–1650. [Google Scholar] [CrossRef][Green Version]
- Fabrika, S. The jets and supercritical accretion disk in SS433. Astrophys. Space Phys. Rev. 2004, 12, 1–152. [Google Scholar]
- Stuchlík, Z.; Kološ, M. Controversy of the gro J1655-40 black hole mass and spin estimates and its possible solutions. Astrophys. J. 2016, 825, 13. [Google Scholar] [CrossRef]
- Reid, M.J.; McClintock, J.E.; Steiner, J.F.; Steeghs, D.; Remillard, R.A.; Dhawan, V.; Narayan, R. A parallax distance to the microquasar GRS 1915+ 105 and a revised estimate of its black hole mass. Astrophys. J. 2014, 796, 2. [Google Scholar] [CrossRef]
- Miller-Jones, J.C.A.; Bahramian, A.; Orosz, J.A.; Mandel, I.; Gou, L.; Maccarone, T.J.; Neijssel, C.J.; Zhao, X.; Ziółkowski, J.; Reid, M.J.; et al. Cygnus X-1 contains a 21–solar mass black hole—Implications for massive star winds. Science Science 2021, 371, 1046–1049. [Google Scholar] [CrossRef] [PubMed]
- Bowler, M.G. SS 433: Two robust determinations fix the mass ratio. Astron. Astrophys. 2018, 619, L4. [Google Scholar] [CrossRef]
- Orosz, J.A.; Steeghs, D.; McClintock, J.E.; Torres, M.A.P.; Bochkov, I.; Gou, L.; Narayan, R.; Blaschak, M.; Levine, A.M.; Remillard, R.A.; et al. A new dynamical model for the black hole binary LMC X-1. Astrophys. J. 2009, 697, 573–591. [Google Scholar] [CrossRef]
- Beer, M.E.; Podsiadlowski, P. The quiescent light curve and the evolutionary state of GRO J1655-40. Mon. Not. R. Astron. Soc. 2002, 331, 351–360. [Google Scholar] [CrossRef]
- Hjellming, R.M.; Rupen, M.P. Episodic ejection of relativistic jets by the X-ray transient GRO J1655-40. Nature 1995, 375, 464–468. [Google Scholar] [CrossRef]
- Romney, J.D.; Schilizzi, R.T.; Fejes, I.; Spencer, R.E. The Inner Beams of SS 433. Astrophys. J. 1987, 321, 822. [Google Scholar] [CrossRef]
- Bailyn, C.D.; Orosz, J.A.; McClintock, J.E.; Remillard, R.A. Dynamical evidence for a black hole in the eclipsing X-ray nova GRO J1655-40. Nature 1995, 378, 157–159. [Google Scholar] [CrossRef]
- Steeghs, D.; McClintock, J.E.; Parsons, S.G.; Reid, M.J.; Littlefair, S.; Dhillon, V.S. THE NOT-SO-MASSIVE BLACK HOLE IN THE MICROQUASAR GRS1915+105. Astrophys. J. 2013, 768, 185. [Google Scholar] [CrossRef]
- Brocksopp, C.; Fender, R.P.; Larionov, V.; Lyuty, V.M.; Tarasov, A.E.; Pooley, G.G.; Paciesas, W.S.; Roche, P. Orbital, precessional and flaring variability of Cygnus X-1. Mon. Not. R. Astron. Soc. 1999, 309, 1063–1073. [Google Scholar] [CrossRef]
- Cherepashchuk, A.M.; Belinski, A.A.; Dodin, A.V.; Postnov, K.A. Discovery of orbital eccentricity and evidence for orbital period increase of SS433. Mon. Not. R. Astron. Soc. Let 2021, 507, L19–L23. [Google Scholar] [CrossRef]
- Saikia, P.; Russell, D.M.; Bramich, D.M.; Miller-Jones, J.C.A.; Baglio, M.C.; Degenaar, N. Lorentz Factors of Compact Jets in Black Hole X-ray Binaries. Astrophys. J. 2019, 887, 21. [Google Scholar] [CrossRef]
- Koljonen, K.I.I.; Hovatta, T. ALMA/NICER observations of GRS 1915+105 indicate a return to a hard state. Astron. Astrophys. 2021, 647, A173. [Google Scholar] [CrossRef]
- Zdziarski, A.A.; Egron, E. What are the Composition and Power of the Jet in Cyg X-1? Astrophys. J. Lett. 2022, 935, L4. [Google Scholar] [CrossRef]
- Punsly, B.; Rodriguez, J. A temporal analysis indicates a mildly relativistic compact jet in GRS 1915+105. Astrophys. J. 2016, 823, 54. [Google Scholar] [CrossRef]
- Tetarenko, A.J.; Casella, P.; Miller-Jones, J.C.A.; Sivakoff, G.R.; Tetarenko, B.E.; Maccarone, T.J.; Gandhi, P.; Eikenberry, S. Radio frequency timing analysis of the compact jet in the black hole X-ray binary Cygnus X-1. Mon. Not. R. Astron. Soc. 2019, 484, 2987–3003. [Google Scholar] [CrossRef]
- Miller-Jones, J.C.A.; Fender, R.P.; Nakar, E. Opening angles, Lorentz factors and confinement of X-ray binary jets. Mon. Not. R. Astron. Soc. 2006, 367, 1432–1440. [Google Scholar] [CrossRef]
- Stirling, A.; Spencer, R.; de La Force, C.; Garrett, M.; Fender, R.; Ogley, R. A relativistic jet from Cygnus X-1 in the low/hard X-ray state. Mon. Not. R. Astron. Soc. 2001, 327, 1273–1278. [Google Scholar] [CrossRef]
- Cherepashchuk, A.M.; Sunyaev, R.A.; Fabrika, S.N.; Postnov, K.A.; Molkov, S.V.; Barsukova, E.A.; Antokhina, E.A.; Irsmambetova, T.R.; Panchenko, I.E.; Seifina, E.V.; et al. INTEGRAL observations of SS433: Results of a coordinated campaign. Astron. Astrophys. 2005, 437, 561–573. [Google Scholar] [CrossRef]
- Abdalla, H.; Abramowski, A.; Aharonian, F.; Benkhali, F.A.; Akhperjanian, A.G.; Angüner, E.O.; Arrieta, M.; Aubert, P.; Backes, M.; Balzer, A.; et al. A search for very high-energy flares from the microquasars GRS 1915+105, Circinus X-1, and V4641 Sgr using contemporaneous H.E.S.S. and RXTE observations. Astron. Astrophys. 2018, 612, A10. [Google Scholar] [CrossRef]
- Romero, G.E.; Okazaki, A.T.; Orellana, M.; Owocki, S.P. Accretion vs. colliding wind models for the gamma-ray binary LS I +61 303: An assessment. Astron. Astrophys. 2007, 474, 15–22. [Google Scholar] [CrossRef]
- Kantzas, D.; Markoff, S.; Beuchert, T.; Lucchini, M.; Chhotray, A.; Ceccobello, C.; Tetarenko, A.J.; Miller-Jones, J.C.A.; Bremer, M.; Garcia, J.A.; et al. A new lepto-hadronic model applied to the first simultaneous multiwavelength data set for Cygnus X–1. Mon. Not. R. Astron. Soc. 2020, 500, 2112–2126. [Google Scholar] [CrossRef]
- Punsly, B. Models of the compact jet in GRS 1915+105. Mon. Not. R. Astron. Soc. 2011, 418, 2736–2743. [Google Scholar] [CrossRef][Green Version]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).