Torsion at Different Scales: From Materials to the Universe
Abstract
1. Introduction
2. Properties of Torsion
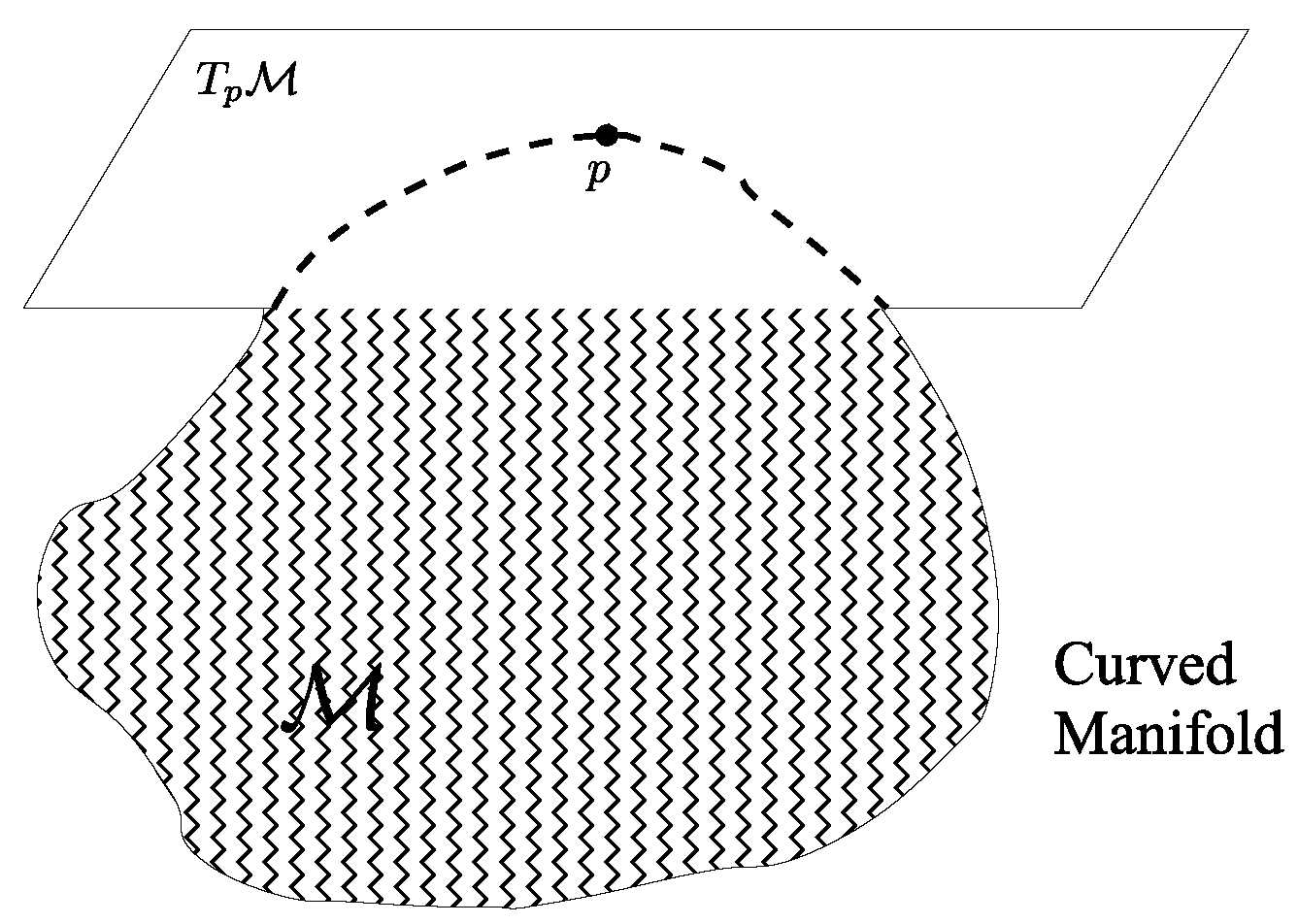
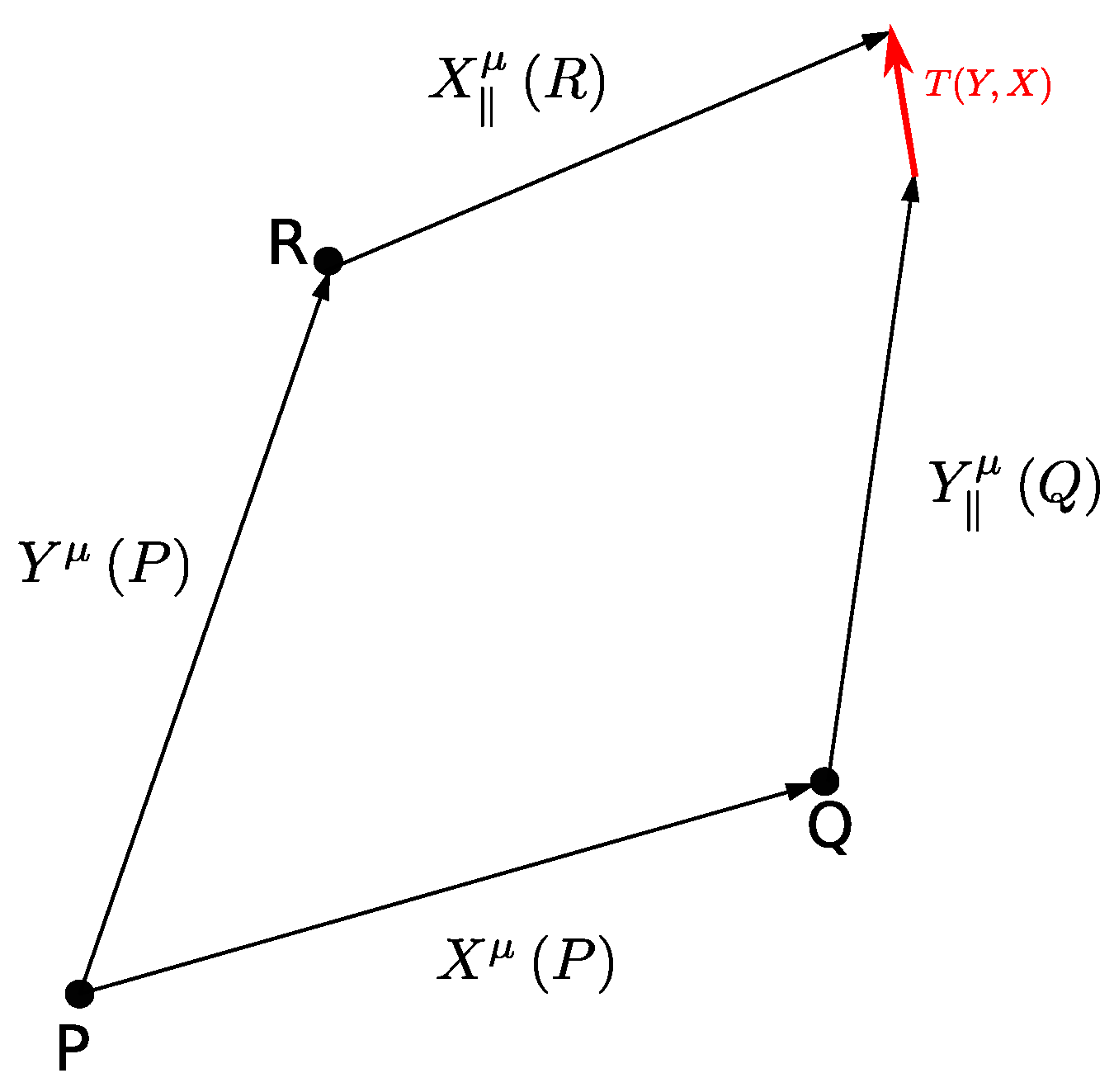
2.1. Geometric Interpretation
2.2. Gravitational Dynamics in Presence of Torsion
3. (Quantum) Torsion, Axions and Anomalies in Einstein–Cartan Quantum Electrodynamics
4. Ambiguities in the Einstein–Cartan Theory —The Barbero–Immirzi Parameter
4.1. Holst Actions for Fermions and Topological Invariants
4.2. Barbero–Immirzi Parameter as an Axion Field
- (i)
- The consistency of (55), given that now the BI parameter being a pseudoscalar field, reinstates the validity of the first of the Equation (55), since the product of its right-hand side is now parity even, and thus transforms as a vector, in agreement with the nature of the left-hand side of the equation.
- (ii)
- Additional terms of interaction of the fermions with the derivative of the BI field :with being the axial current (34) andthe vector current.
- (iii)
- Interaction terms of fermions with non-derivative terms:with being the diffeomorphic covariant derivative, expressed in terms of the torsion-free Christoffel connection, which is the result of [36], as expected, because this term contains non derivative terms of the BI.
5. Torsion on Graphene
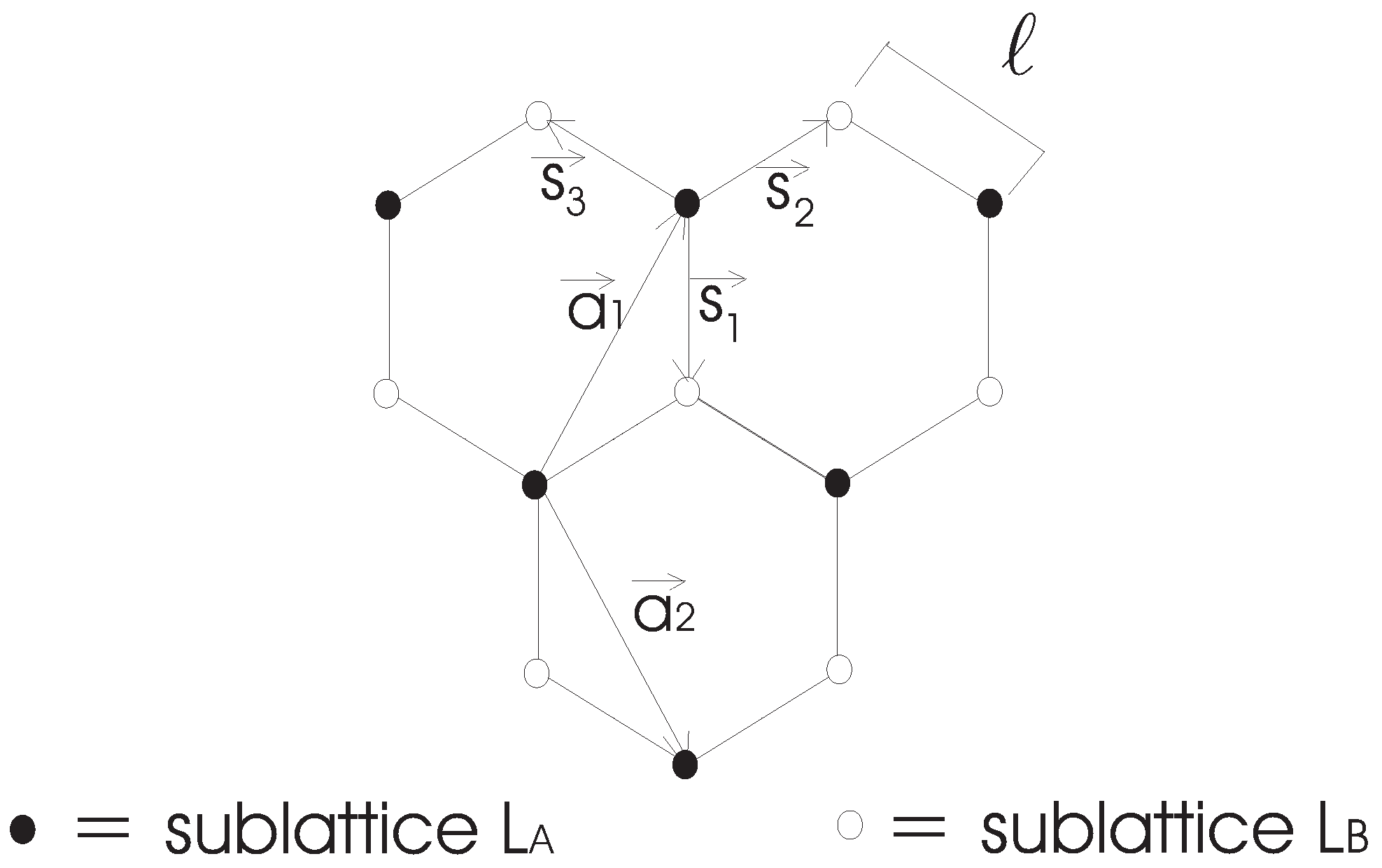
5.1. Torsion as Continuous Limit of Dislocations
- (i)
- a time-directed screw dislocation (only possible if the crystal has a time direction)or
- (ii)
- an edge dislocation “felt” by an integration along a spacetime circuit (only possible if we can actually go around a loop in time), e.g,This last scenario is depicted in Figure 6.
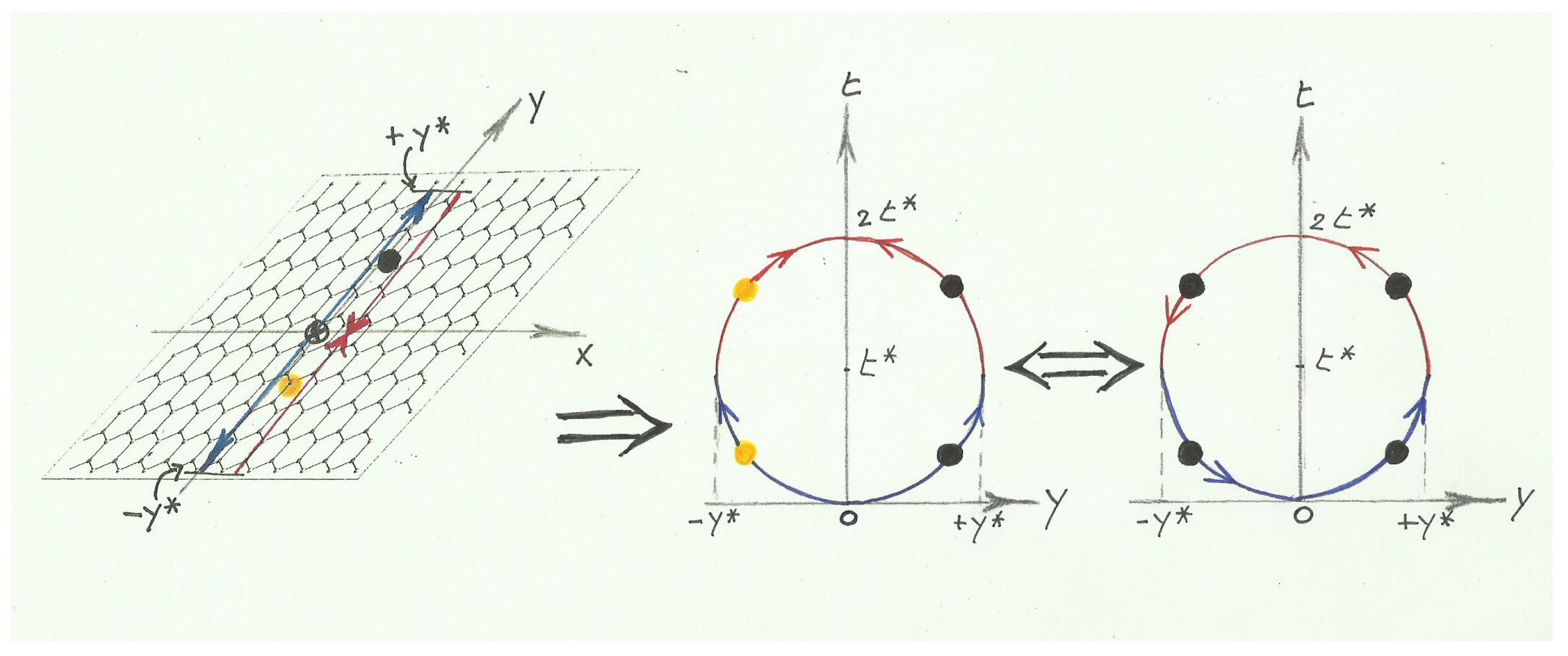
5.2. Time-Loops in Graphene
5.3. Towards Spotting Torsion in a Lab
- (i)
- the particle-hole pair required for the time-loop to be excited by an external electromagnetic field, and
- (ii)
- that what we shall call holonomy—a proper disclination or torsion—provides the non-closure of the loop in the proper direction.
5.4. On the Continuum Description of the Two Inequivalent Dirac Points
6. Torsion in Standard Local Supersymmetry
7. Torsion in Unconventional Supersymmetry
8. Torsion in Cosmology
8.1. Quantum Torsion in String-Inspired Cosmologies and the Universe Dark Sector
8.2. Comments on Other Contorted Cosmological Models with a Spin
9. Concluding Remarks: Other Observational Effects of Torsion
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | Although the contorted geometry formalism can be generic and valid in -dimensional spacetime, nonetheless for the sake of concreteness, in this work we shall present the analysis for , and, in the case of graphene, for . |
| 2 | |
| 3 | |
| 4 | For a recent study of the massive case, where the focus is on neutrino mixing and oscillations, see [11]. |
| 5 | In the original formulation of Barbero and Immirzi, the BI parameter is , but this is not important for our purposes. |
| 6 | Indeed, by applying the decomposition (23) onto (57), prior to imposing (59), we obtain the following extra contribution in the effective action, as compared to the terms discussed previously in the case [37]:
|
| 7 | It is possible to include in the description next-to-near neighbour contributions, while keeping a modified Dirac structure [53]. In fact, such modifications allow for the reproduction of scenarios related to generalised uncertainty principles both for commuting coordinates [54] and noncommuting coordinates [55]. |
| 8 | Actually, there are six such points, but the only two shown above are inequivalent under lattice discrete symmetry. |
| 9 | A deep study of how curvature and torsion emerge in a geometrical approach to quantum gravity, along the lines of how classical elastic-theory emerges from QED, can be found in [58], see also [59]. In those papers, the authors elaborate on a model of quantum gravity inspired by graphene, but independent from it [60,61], see also [62,63]. A review can be found in [48] |
| 10 | This is due to the reducible, rather than irreducible, representation of the Lorentz group we use |
| 11 | The Goldstino is a Majorana spin 1/2 fermion which plays the role of the Goldstone-type fermionic mode arising from the spontaneous breaking of global SUSY. To incorporate the relevant dynamics into the dynamically-broken SUGRA scenario, one adds to the SUGRA Lagrangian (104) the terms
|
| 12 | It is possible to add a central extension generator and its corresponding one-form coefficient b [106]. However, we shall not consider this extension in the present work. |
| 13 | Here, we omitted the wedge notation for the exterior product. For instance, stands for the three-form . |
| 14 | The case is the globally anti-De Sitter space, while the other cases are conical singularities [109]. |
| 15 | We note for completeness that, by exploiting local field redefinition ambiguities [6,137,138,139], which do not affect the perturbative scattering amplitudes, one may extend the above conclusion to the fourth order in derivatives, that is, to the effective low-energy action, which includes quadratic curvature terms. |
| 16 | |
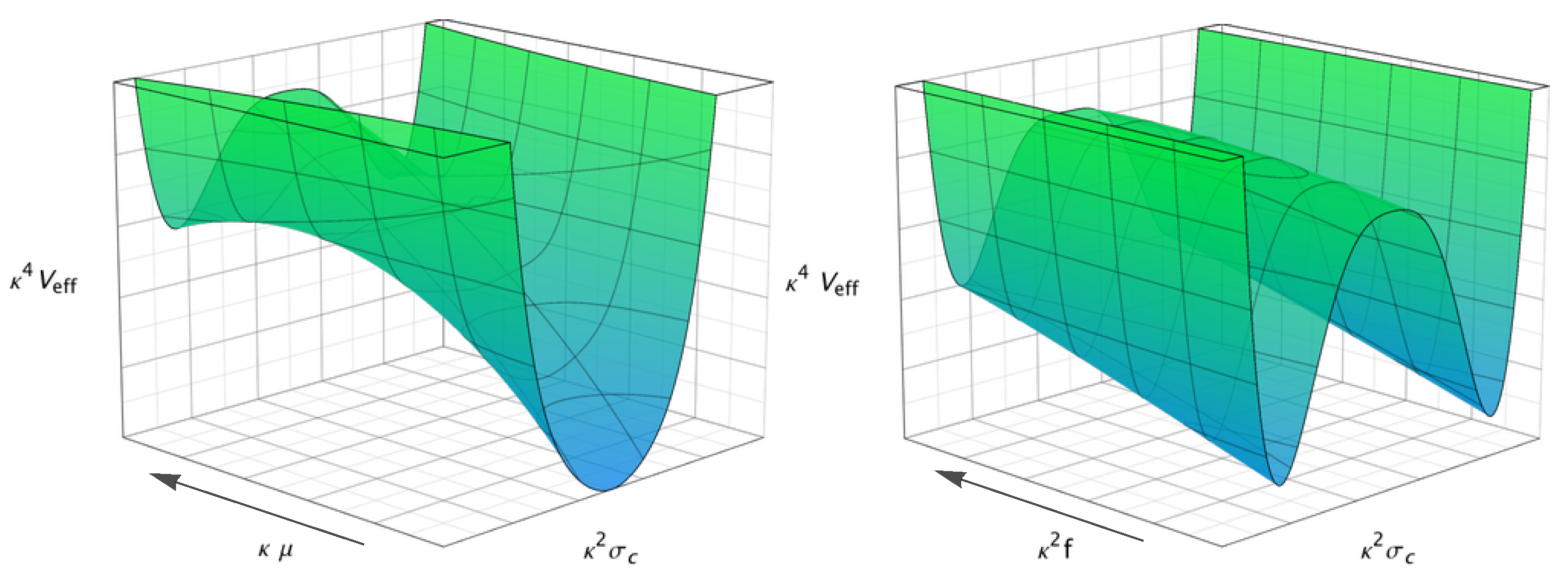
| 17 | To ensure homogeneity and isotropy conditions, the authors of [135] assumed the existence of a stiff-axion-b-dominated era (i.e., with equation of state ) that succeeds a first hill-top inflation [103] (cf. Figure 9), which is the result of dynamical breaking of local SUSY (SUGRA) right after the Big Bang, that is assumed to characterise the superstring inspired theories. This breaking is achieved by a condensation of the gravitino (supersymmetric partner of gravitons) as a result of the existence of attractive channels in the four-gravitino interactions that characterise the SUGRA Lagrangian due to fermionic torsion [99,100], as discussed in Section 6. As argued in [135,136], unstable domain walls (DW) are formed as a result of the gravitino condensate double well potential (Figure 8), whose degeneracy can be lifted by percolation effects [147]. The non-spherical collapse of such DW leads to primordial GW, which then condense leading to (133). |
References
- Cartan, E. Riemannian Geometry in an Orthogonal Frame; World Scientific: Singapore, 2001. [Google Scholar]
- Hehl, F.W.; Von Der Heyde, P.; Kerlick, G.D.; Nester, J.M. General Relativity with Spin and Torsion: Foundations and Prospects. Rev. Mod. Phys. 1976, 48, 393–416. [Google Scholar] [CrossRef]
- Shapiro, I.L. Physical aspects of the space-time torsion. Phys. Rep. 2002, 357, 113. [Google Scholar] [CrossRef]
- Eguchi, T.; Gilkey, P.B.; Hanson, A.J. Gravitation, Gauge Theories and Differential Geometry. Phys. Rep. 1980, 66, 213. [Google Scholar] [CrossRef]
- Nakahara, M. Geometry, Topology and Physics; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Duncan, M.J.; Kaloper, N.; Olive, K.A. Axion hair and dynamical torsion from anomalies. Nucl. Phys. B 1992, 387, 215–235. [Google Scholar] [CrossRef]
- Santaló, L.A. Vectores y Tensores con sus Aplicaciones; Editorial Universitaria de Buenos Aires: Buenos Aires, Argentina, 1973. [Google Scholar]
- Hehl, F.W.; Obukhov, Y.N. Elie Cartan’s torsion in geometry and in field theory, an essay. Ann. Fond. Broglie 2007, 32, 157. [Google Scholar]
- Iorio, A.; Pais, P. Time-loops to spot torsion on bidimensional Dirac materials with dislocations. In Proceedings of the Spacetime, Matter, Quantum Mechanics, Castiglioncello, Italy, 19–23 September 2022. [Google Scholar]
- Capozziello, S.; Lambiase, G.; Stornaiolo, C. Geometric classification of the torsion tensor in space-time. Ann. Phys. 2001, 10, 713–727. [Google Scholar] [CrossRef]
- Capolupo, A.; Maria, G.D.; Monda, S.; Quaranta, A.; Serao, R. Quantum Field Theory of neutrino mixing in spacetimes with torsion. arXiv 2023, arXiv:2310.09309. [Google Scholar]
- Adler, S.L. Axial-Vector Vertex in Spinor Electrodynamics. Phys. Rev. 1969, 177, 2426–2438. [Google Scholar] [CrossRef]
- Bell, J.S.; Jackiw, R. A PCAC puzzle: π0→γγ in the σ-model. Il Nuovo C. A (1965–1970) 1969, 60, 47–61. [Google Scholar] [CrossRef]
- Bardeen, W.A.; Zumino, B. Consistent and Covariant Anomalies in Gauge and Gravitational Theories. Nucl. Phys. B 1984, 244, 421–453. [Google Scholar] [CrossRef]
- Zumino, B.; Wu, Y.S.; Zee, A. Chiral Anomalies, Higher Dimensions, and Differential Geometry. Nucl. Phys. B 1984, 239, 477–507. [Google Scholar] [CrossRef]
- Fujikawa, K. Comment on Chiral and Conformal Anomalies. Phys. Rev. Lett. 1980, 44, 1733. [Google Scholar] [CrossRef]
- Alvarez-Gaume, L.; Witten, E. Gravitational Anomalies. Nucl. Phys. B 1984, 234, 269. [Google Scholar] [CrossRef]
- Hull, C.M. Anomalies, Ambiguities and Superstrings. Phys. Lett. B 1986, 167, 51–55. [Google Scholar] [CrossRef]
- Mavromatos, N.E. A Note on the Atiyah-singer Index Theorem for Manifolds With Totally Antisymmetric H Torsion. J. Phys. A 1988, 21, 2279. [Google Scholar] [CrossRef]
- Kim, J.E.; Carosi, G. Axions and the Strong CP Problem. Rev. Mod. Phys. 2010, 82, 557–602, Erratum in Rev. Mod. Phys. 2019, 91, 049902. [Google Scholar] [CrossRef]
- Jackiw, R.; Pi, S.Y. Chern–Simons modification of general relativity. Phys. Rev. D 2003, 68, 104012. [Google Scholar] [CrossRef]
- Guralnik, G.; Iorio, A.; Jackiw, R.; Pi, S.Y. Dimensionally reduced gravitational Chern–Simons term and its kink. Ann. Phys. 2003, 308, 222–236. [Google Scholar] [CrossRef]
- Alexander, S.; Yunes, N. Chern–Simons Modified General Relativity. Phys. Rep. 2009, 480, 1–55. [Google Scholar] [CrossRef]
- Mavromatos, N.E. Geometrical origins of the universe dark sector: String-inspired torsion and anomalies as seeds for inflation and dark matter. Phil. Trans. A Math. Phys. Eng. Sci. 2022, 380, 20210188. [Google Scholar] [CrossRef]
- Ashtekar, A.; Lewandowski, J. Background independent quantum gravity: A Status report. Class. Quantum Gravity 2004, 21, R53. [Google Scholar] [CrossRef]
- Rovelli, C. Quantum Gravity; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar] [CrossRef]
- Immirzi, G. Real and complex connections for canonical gravity. Class. Quantum Gravity 1997, 14, L177–L181. [Google Scholar] [CrossRef]
- Immirzi, G. Quantum gravity and Regge calculus. Nucl. Phys. B Proc. Suppl. 1997, 57, 65–72. [Google Scholar] [CrossRef]
- Holst, S. Barbero’s Hamiltonian derived from a generalised Hilbert-Palatini action. Phys. Rev. D 1996, 53, 5966–5969. [Google Scholar] [CrossRef]
- Barbero, G.J.F. Real Ashtekar variables for Lorentzian signature space times. Phys. Rev. D 1995, 51, 5507–5510. [Google Scholar] [CrossRef]
- Barbero, G.J.F. Reality conditions and Ashtekar variables: A Different perspective. Phys. Rev. D 1995, 51, 5498–5506. [Google Scholar] [CrossRef]
- Ashtekar, A. New Variables for Classical and Quantum Gravity. Phys. Rev. Lett. 1986, 57, 2244–2247. [Google Scholar] [CrossRef] [PubMed]
- Ashtekar, A. New Hamiltonian Formulation of General Relativity. Phys. Rev. D 1987, 36, 1587–1602. [Google Scholar] [CrossRef]
- Ashtekar, A.; Romano, J.D.; Tate, R.S. New Variables for Gravity: Inclusion of Matter. Phys. Rev. D 1989, 40, 2572. [Google Scholar] [CrossRef]
- Perez, A.; Rovelli, C. Physical effects of the Immirzi parameter. Phys. Rev. D 2006, 73, 044013. [Google Scholar] [CrossRef]
- Freidel, L.; Minic, D.; Takeuchi, T. Quantum gravity, torsion, parity violation and all that. Phys. Rev. D 2005, 72, 104002. [Google Scholar] [CrossRef]
- Mercuri, S. Fermions in Ashtekar-Barbero connections formalism for arbitrary values of the Immirzi parameter. Phys. Rev. D 2006, 73, 084016. [Google Scholar] [CrossRef]
- Calcagni, G.; Mercuri, S. The Barbero–Immirzi field in canonical formalism of pure gravity. Phys. Rev. D 2009, 79, 084004. [Google Scholar] [CrossRef]
- Nieh, H.T.; Yan, M.L. An Identity in Riemann–Cartan Geometry. J. Math. Phys. 1982, 23, 373. [Google Scholar] [CrossRef]
- Kaul, R.K. Holst Actions for Supergravity Theories. Phys. Rev. D 2008, 77, 045030. [Google Scholar] [CrossRef]
- Mavromatos, N.E. Torsion in String-Inspired Cosmologies and the Universe Dark Sector. Universe 2021, 7, 480. [Google Scholar] [CrossRef]
- Castellani, L.; D’Auria, R.; Fre, P. Supergravity and Superstrings: A Geometric Perspective. Vol. 1: Mathematical Foundations; World Scientific: Singapore, 1991. [Google Scholar]
- Tsuda, M. generalised Lagrangian of N = 1 supergravity and its canonical constraints with the real Ashtekar variable. Phys. Rev. D 2000, 61, 024025. [Google Scholar] [CrossRef]
- Taveras, V.; Yunes, N. The Barbero–Immirzi Parameter as a Scalar Field: K-Inflation from Loop Quantum Gravity? Phys. Rev. D 2008, 78, 064070. [Google Scholar] [CrossRef]
- Torres-Gomez, A.; Krasnov, K. Remarks on Barbero–Immirzi parameter as a field. Phys. Rev. D 2009, 79, 104014. [Google Scholar] [CrossRef]
- Iorio, A. Weyl-gauge symmetry of graphene. Ann. Phys. 2011, 326, 1334–1353. [Google Scholar] [CrossRef]
- Iorio, A. Curved Spacetimes and Curved Graphene: A status report of the Weyl-symmetry approach. Int. J. Mod. Phys. D 2015, 24, 1530013. [Google Scholar] [CrossRef]
- Acquaviva, G.; Iorio, A.; Pais, P.; Smaldone, L. Hunting Quantum Gravity with Analogs: The case of graphene. Universe 2022, 8, 455. [Google Scholar] [CrossRef]
- Wallace, P.R. The Band Theory of Graphite. Phys. Rev. 1947, 71, 622–634. [Google Scholar] [CrossRef]
- Semenoff, G.W. Condensed-Matter Simulation of a Three-Dimensional Anomaly. Phys. Rev. Lett. 1984, 53, 2449–2452. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Iorio, A.; Lambiase, G. Quantum field theory in curved graphene spacetimes, Lobachevsky geometry, Weyl symmetry, Hawking effect, and all that. Phys. Rev. D 2014, 90, 025006. [Google Scholar] [CrossRef]
- Iorio, A.; Pais, P.; Elmashad, I.A.; Ali, A.F.; Faizal, M.; Abou-Salem, L.I. generalised Dirac structure beyond the linear regime in graphene. Int. J. Mod. Phys. 2018, D27, 1850080. [Google Scholar] [CrossRef]
- Iorio, A.; Ivetić, B.; Mignemi, S.; Pais, P. Three “layers” of graphene monolayer and their analog generalised uncertainty principles. Phys. Rev. D 2022, 106, 116011. [Google Scholar] [CrossRef]
- Iorio, A.; Ivetić, B.; Pais, P. Turning graphene into a lab for noncommutativity. arXiv 2023, arXiv:2306.17196. [Google Scholar]
- Wehling, T.; Black-Schaffer, A.; Balatsky, A. Dirac materials. Adv. Phys. 2014, 63, 1–76. [Google Scholar] [CrossRef]
- Ruggiero, M.L.; Tartaglia, A. Einstein–Cartan theory as a theory of defects in space-time. Am. J. Phys. 2003, 71, 1303–1313. [Google Scholar] [CrossRef]
- Iorio, A.; Smaldone, L. Quantum black holes as classical space factories. Int. J. Mod. Phys. D 2023, 32, 2350063. [Google Scholar] [CrossRef]
- Iorio, A.; Smaldone, L. Classical space from quantum condensates. J. Phys. Conf. Ser. 2023, 2533, 012030. [Google Scholar] [CrossRef]
- Acquaviva, G.; Iorio, A.; Scholtz, M. On the implications of the Bekenstein bound for black hole evaporation. Ann. Phys. 2017, 387, 317–333. [Google Scholar] [CrossRef]
- Acquaviva, G.; Iorio, A.; Smaldone, L. Bekenstein bound from the Pauli principle. Phys. Rev. D 2020, 102, 106002. [Google Scholar] [CrossRef]
- Acquaviva, G.; Iorio, A.; Scholtz, M. Quasiparticle picture from the Bekenstein bound. PoS 2017, CORFU2017, 206. [Google Scholar] [CrossRef][Green Version]
- Acquaviva, G.; Iorio, A.; Smaldone, L. Bekenstein bound from the Pauli principle: A brief introduction. PoS 2021, ICHEP2020, 681. [Google Scholar] [CrossRef]
- Kleinert, H. Gauge Fields in Condensed Matter; World Scientific: Singapore, 1989. [Google Scholar] [CrossRef]
- Katanaev, M.; Volovich, I. Theory of defects in solids and three-dimensional gravity. Ann. Phys. 1992, 216, 1–28. [Google Scholar] [CrossRef]
- Iorio, A.; Pais, P. (Anti-)de Sitter, Poincaré, Super symmetries, and the two Dirac points of graphene. Ann. Phys. 2018, 398, 265–286. [Google Scholar] [CrossRef]
- Katanaev, M.O. Geometric theory of defects. Phys. Usp. 2005, 48, 675–701. [Google Scholar] [CrossRef]
- Lazar, M. A Nonsingular solution of the edge dislocation in the gauge theory of dislocations. J. Phys. A 2003, 36, 1415. [Google Scholar] [CrossRef]
- Ciappina, M.F.; Iorio, A.; Pais, P.; Zampeli, A. Torsion in quantum field theory through time-loops on Dirac materials. Phys. Rev. D 2020, 101, 036021. [Google Scholar] [CrossRef]
- de Juan, F.; Cortijo, A.; Vozmediano, M.A.H. Dislocations and torsion in graphene and related systems. Nucl. Phys. B 2010, 828, 625. [Google Scholar] [CrossRef]
- Vozmediano, M.A.H.; Katsnelson, M.I.; Guinea, F. Gauge fields in graphene. Phys. Rep. 2010, 496, 109. [Google Scholar] [CrossRef]
- Amorim, B.; Cortijo, A.; de Juan, F.; Grushin, A.G.; Guinea, F.; Gutiérrez-Rubio, A.; Ochoa, H.; Parente, V.; Roldán, R.; San-Jose, P.; et al. Novel effects of strains in graphene and other two dimensional materials. Phys. Rep. 2016, 617, 1. [Google Scholar] [CrossRef]
- Wilczek, F. Quantum Time Crystals. Phys. Rev. Lett. 2012, 109, 160401. [Google Scholar] [CrossRef]
- Shapere, A.; Wilczek, F. Classical Time Crystals. Phys. Rev. Lett. 2012, 109, 160402. [Google Scholar] [CrossRef]
- Li, T.; Gong, Z.X.; Yin, Z.Q.; Quan, H.T.; Yin, X.; Zhang, P.; Duan, L.M.; Zhang, X. Space-Time Crystals of Trapped Ions. Phys. Rev. Lett. 2012, 109, 163001. [Google Scholar] [CrossRef] [PubMed]
- Smits, J.; Liao, L.; Stoof, H.T.C.; van der Straten, P. Observation of a Space-Time Crystal in a Superfluid Quantum Gas. Phys. Rev. Lett. 2018, 121, 185301. [Google Scholar] [CrossRef] [PubMed]
- Loll, R. Discrete approaches to quantum gravity in four-dimensions. Living Rev. Rel. 1998, 1, 13. [Google Scholar] [CrossRef]
- Heide, C.; Higuchi, T.; Weber, H.B.; Hommelhoff, P. Coherent Electron Trajectory Control in Graphene. Phys. Rev. Lett. 2018, 121, 207401. [Google Scholar] [CrossRef]
- Higuchi, T.; Heide, C.; Ullmann, K.; Weber, H.B.; Hommelhoff, P. Light-field-driven currents in graphene. Nature 2017, 550, 224. [Google Scholar] [CrossRef]
- Marino, E.C. Quantum electrodynamics of particles on a plane and the Chern–Simons theory. Nucl. Phys. B 1993, 408, 551. [Google Scholar] [CrossRef]
- Gorbar, E.V.; Gusynin, V.P.; Miransky, V.A. Dynamical chiral symmetry breaking on a brane in reduced QED. Phys. Rev. D 2001, 64, 105028. [Google Scholar] [CrossRef]
- Dudal, D.; Mizher, A.J.; Pais, P. Remarks on the Chern–Simons photon term in the QED description of graphene. Phys. Rev. D 2018, 98, 065008. [Google Scholar] [CrossRef]
- Dudal, D.; Mizher, A.J.; Pais, P. Exact quantum scale invariance of three-dimensional reduced QED theories. Phys. Rev. D 2019, 99, 045017. [Google Scholar] [CrossRef]
- Iorio, A.; Pais, P. Revisiting the gauge fields of strained graphene. Phys. Rev. D 2015, 92, 125005. [Google Scholar] [CrossRef]
- Andrianopoli, L.; Cerchiai, B.L.; D’Auria, R.; Gallerati, A.; Noris, R.; Trigiante, M.; Zanelli, J. -extended D = 4 supergravity, unconventional SUSY and graphene. J. High Energy Phys. 2020, 1, 084. [Google Scholar] [CrossRef]
- Peskin, M.E.; Schroeder, D.V. An Introduction to Quantum Field Theory; Addison-Wesley: Reading, PA, USA, 1995. [Google Scholar]
- Kruchinin, S.Y.; Krausz, F.; Yakovlev, V.S. Colloquium: Strong-field phenomena in periodic systems. Rev. Mod. Phys. 2018, 90, 021002. [Google Scholar] [CrossRef]
- Castro Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar] [CrossRef]
- Gusynin, V.P.; Sharapov, S.G.; Carbotte, J.P. AC conductivity of graphene: From light-binding model to 2 + 1-dimensional quantum electrodynamics. Int. J. Mod. Phys. B 2007, 21, 4611–4658. [Google Scholar] [CrossRef]
- Gonzalez, J.; Guinea, F.; Vozmediano, M.A.H. The Electronic spectrum of fullerenes from the Dirac equation. Nucl. Phys. B 1993, 406, 771. [Google Scholar] [CrossRef]
- Yazyev, O.V.; Chen, Y.P. Polycrystalline graphene and other two-dimensional materials. Nat. Nanotechnol. 2014, 9, 755–767. [Google Scholar] [CrossRef]
- Yazyev, O.V.; Louie, S.G. Topological defects in graphene: Dislocations and grain boundaries. Phys. Rev. B 2010, 81, 195420. [Google Scholar] [CrossRef]
- Hirth, J.; Lothe, J. Theory of Dislocations; McGraw-Hill Series in Electrical Engineering: Electronics and Electronic Circuits; McGraw-Hill: New York, NY, USA, 1967. [Google Scholar]
- Zhang, X.; Xu, Z.; Yuan, Q.; Xin, J.; Ding, F. The favourable large misorientation angle grain boundaries in graphene. Nanoscale 2015, 7, 20082–20088. [Google Scholar] [CrossRef] [PubMed]
- Freedman, D.Z.; van Nieuwenhuizen, P.; Ferrara, S. Progress Toward a Theory of Supergravity. Phys. Rev. D 1976, 13, 3214–3218. [Google Scholar] [CrossRef]
- Ferrara, S.; van Nieuwenhuizen, P. Simplifications of Einstein Supergravity. Phys. Rev. D 1979, 20, 2079. [Google Scholar] [CrossRef]
- Van Nieuwenhuizen, P. Supergravity. Phys. Rep. 1981, 68, 189–398. [Google Scholar] [CrossRef]
- Nilles, H.P. Supersymmetry, Supergravity and Particle Physics. Phys. Rep. 1984, 110, 1–162. [Google Scholar] [CrossRef]
- Alexandre, J.; Houston, N.; Mavromatos, N.E. Dynamical Supergravity Breaking via the Super-Higgs Effect Revisited. Phys. Rev. D 2013, 88, 125017. [Google Scholar] [CrossRef]
- Alexandre, J.; Houston, N.; Mavromatos, N.E. Inflation via Gravitino Condensation in Dynamically Broken Supergravity. Int. J. Mod. Phys. D 2015, 24, 1541004. [Google Scholar] [CrossRef]
- Deser, S.; Zumino, B. Broken Supersymmetry and Supergravity. Phys. Rev. Lett. 1977, 38, 1433–1436. [Google Scholar] [CrossRef]
- Volkov, D.V.; Akulov, V.P. Possible universal neutrino interaction. JETP Lett. 1972, 16, 438–440. [Google Scholar]
- Ellis, J.; Mavromatos, N.E. Inflation induced by gravitino condensation in supergravity. Phys. Rev. D 2013, 88, 085029. [Google Scholar] [CrossRef]
- Alvarez, P.D.; Valenzuela, M.; Zanelli, J. Supersymmetry of a different kind. J. High Energy Phys. 2012, 1204, 058. [Google Scholar] [CrossRef]
- Guevara, A.; Pais, P.; Zanelli, J. Dynamical Contents of Unconventional Supersymmetry. J. High Energy Phys. 2016, 08, 085. [Google Scholar] [CrossRef]
- Alvarez, P.D.; Pais, P.; Rodríguez, E.; Salgado-Rebolledo, P.; Zanelli, J. Supersymmetric 3D model for gravity with SU(2) gauge symmetry, mass generation and effective cosmological constant. Class. Quantum Gravity 2015, 32, 175014. [Google Scholar] [CrossRef]
- Bañados, M.; Teitelboim, C.; Zanelli, J. Black hole in three-dimensional spacetime. Phys. Rev. Lett. 1992, 69, 1849–1851. [Google Scholar] [CrossRef]
- Alvarez, P.D.; Pais, P.; Rodríguez, E.; Salgado-Rebolledo, P.; Zanelli, J. The BTZ black hole as a Lorentz-flat geometry. Phys. Lett. B 2014, 738, 134–135. [Google Scholar] [CrossRef]
- Miskovic, O.; Zanelli, J. On the negative spectrum of the 2 + 1 black hole. Phys. Rev. D 2009, 79, 105011. [Google Scholar] [CrossRef]
- Iorio, A.; Lambiase, G.; Pais, P.; Scardigli, F. generalised uncertainty principle in three-dimensional gravity and the BTZ black hole. Phys. Rev. D 2020, 101, 105002. [Google Scholar] [CrossRef]
- Iorio, A.; Pais, P. generalised uncertainty principle in graphene. J. Phys. Conf. Ser. 2019, 1275, 012061. [Google Scholar] [CrossRef]
- Iorio, A.; Lambiase, G. The Hawking–Unruh phenomenon on graphene. Phys. Lett. 2012, B716, 334–337. [Google Scholar] [CrossRef]
- Aghanim, N. et al. [Planck Collaboration] Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6, Erratum in Astron. Astrophys. 2021, 652, C4. [Google Scholar] [CrossRef]
- Verde, L.; Treu, T.; Riess, A.G. Tensions between the Early and the Late Universe. Nat. Astron. 2019, 3, 891. [Google Scholar] [CrossRef]
- Perivolaropoulos, L.; Skara, F. Challenges for ΛCDM: An update. New Astron. Rev. 2022, 95, 101659. [Google Scholar] [CrossRef]
- Abdalla, E.; Abellán, G.F.; Aboubrahim, A.; Agnello, A.; Akarsu, Ö.; Akrami, Y.; Alestas, G.; Aloni, D.; Amendola, L.; Anchordoqui, L.A.; et al. Cosmology intertwined: A review of the particle physics, astrophysics, and cosmology associated with the cosmological tensions and anomalies. J. High Energy Astrophys. 2022, 34, 49–211. [Google Scholar] [CrossRef]
- Freedman, W.L. Cosmology at a Crossroads. Nat. Astron. 2017, 1, 0121. [Google Scholar] [CrossRef]
- Green, M.B.; Schwarz, J.H.; Witten, E. Superstring Theory Vol. 1: 25th Anniversary Edition; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar] [CrossRef]
- Green, M.B.; Schwarz, J.H.; Witten, E. Superstring Theory Vol. 2: 25th Anniversary Edition; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar] [CrossRef]
- Polchinski, J. String Theory. Vol. 2: Superstring Theory and Beyond; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar] [CrossRef]
- Hellerman, S.; Kaloper, N.; Susskind, L. String theory and quintessence. J. High Energy Phys. 2001, 06, 003. [Google Scholar] [CrossRef]
- Fischler, W.; Kashani-Poor, A.; McNees, R.; Paban, S. The Acceleration of the universe, a challenge for string theory. J. High Energy Phys. 2001, 07, 003. [Google Scholar] [CrossRef]
- Palti, E. The Swampland: Introduction and Review. Fortsch. Phys. 2019, 67, 1900037. [Google Scholar] [CrossRef]
- Palti, E. The swampland and string theory. Contemp. Phys. 2022, 62, 165–179. [Google Scholar] [CrossRef]
- Obied, G.; Ooguri, H.; Spodyneiko, L.; Vafa, C. De Sitter Space and the Swampland. arXiv 2018, arXiv:1806.08362. [Google Scholar]
- Agrawal, P.; Obied, G.; Steinhardt, P.J.; Vafa, C. On the Cosmological Implications of the String Swampland. Phys. Lett. B 2018, 784, 271–276. [Google Scholar] [CrossRef]
- Garg, S.K.; Krishnan, C. Bounds on Slow Roll and the de Sitter Swampland. J. High Energy Phys. 2019, 11, 075. [Google Scholar] [CrossRef]
- Ooguri, H.; Palti, E.; Shiu, G.; Vafa, C. Distance and de Sitter Conjectures on the Swampland. Phys. Lett. B 2019, 788, 180–184. [Google Scholar] [CrossRef]
- Mohayaee, R.; Rameez, M.; Sarkar, S. Do supernovae indicate an accelerating universe? Eur. Phys. J. Spec. Top. 2021, 230, 2067–2076. [Google Scholar] [CrossRef]
- Secrest, N.J.; von Hausegger, S.; Rameez, M.; Mohayaee, R.; Sarkar, S. A Challenge to the Standard Cosmological Model. Astrophys. J. Lett. 2022, 937, L31. [Google Scholar] [CrossRef]
- Di Valentino, E.; Mena, O.; Pan, S.; Visinelli, L.; Yang, W.; Melchiorri, A.; Mota, D.F.; Riess, A.G.; Silk, J. In the realm of the Hubble tension—A review of solutions. Class. Quantum Gravity 2021, 38, 153001. [Google Scholar] [CrossRef]
- Mavromatos, N.E. Anomalies, the Dark Universe and Matter-Antimatter asymmetry. In Proceedings of the DICE 2022: Spacetime, Matter, Quantum Mechanics, Castiglioncello, Italy, 19–23 September 2022. [Google Scholar]
- Basilakos, S.; Mavromatos, N.E.; Solà Peracaula, J. Gravitational and Chiral Anomalies in the Running Vacuum Universe and Matter-Antimatter Asymmetry. Phys. Rev. D 2020, 101, 045001. [Google Scholar] [CrossRef]
- Basilakos, S.; Mavromatos, N.E.; Solà Peracaula, J. Quantum Anomalies in String-Inspired Running Vacuum Universe: Inflation and Axion Dark Matter. Phys. Lett. B 2020, 803, 135342. [Google Scholar] [CrossRef]
- Mavromatos, N.E.; Solà Peracaula, J. Stringy-running-vacuum-model inflation: From primordial gravitational waves and stiff axion matter to dynamical dark energy. Eur. Phys. J. Spec. Top. 2021, 230, 2077–2110. [Google Scholar] [CrossRef]
- Mavromatos, N.E.; Solà Peracaula, J. Inflationary physics and trans-Planckian conjecture in the stringy running vacuum model: From the phantom vacuum to the true vacuum. Eur. Phys. J. Plus 2021, 136, 1152. [Google Scholar] [CrossRef]
- Gross, D.J.; Sloan, J.H. The Quartic Effective Action for the Heterotic String. Nucl. Phys. B 1987, 291, 41–89. [Google Scholar] [CrossRef]
- Metsaev, R.R.; Tseytlin, A.A. Order alpha-prime (Two Loop) Equivalence of the String Equations of Motion and the Sigma Model Weyl Invariance Conditions: Dependence on the Dilaton and the Antisymmetric Tensor. Nucl. Phys. B 1987, 293, 385–419. [Google Scholar] [CrossRef]
- Bento, M.C.; Mavromatos, N.E. Ambiguities in the Low-energy Effective Actions of String Theories With the Inclusion of Antisymmetric Tensor and Dilaton Fields. Phys. Lett. B 1987, 190, 105–109. [Google Scholar] [CrossRef]
- Green, M.B.; Schwarz, J.H. Anomaly Cancellation in Supersymmetric D = 10 Gauge Theory and Superstring Theory. Phys. Lett. B 1984, 149, 117–122. [Google Scholar] [CrossRef]
- Svrcek, P.; Witten, E. Axions in String Theory. J. High Energy Phys. 2006, 6, 051. [Google Scholar] [CrossRef]
- Arvanitaki, A.; Dimopoulos, S.; Dubovsky, S.; Kaloper, N.; March-Russell, J. String Axiverse. Phys. Rev. D 2010, 81, 123530. [Google Scholar] [CrossRef]
- Marsh, D.J.E. Axion Cosmology. Phys. Rep. 2016, 643, 1–79. [Google Scholar] [CrossRef]
- Alexander, S.H.S.; Peskin, M.E.; Sheikh-Jabbari, M.M. Leptogenesis from gravity waves in models of inflation. Phys. Rev. Lett. 2006, 96, 081301. [Google Scholar] [CrossRef]
- Lyth, D.H.; Quimbay, C.; Rodriguez, Y. Leptogenesis and tensor polarisation from a gravitational Chern–Simons term. J. High Energy Phys. 2005, 3, 016. [Google Scholar] [CrossRef]
- Mavromatos, N.E. Lorentz Symmetry Violation in String-Inspired Effective Modified Gravity Theories. In Proceedings of the 740. WE-Heraeus-Seminar: Experimental Tests and Signatures of Modified and Quantum Gravity Workshop, Bad Honnef, Germany, 1–5 February 2023. [Google Scholar]
- Lalak, Z.; Lola, S.; Ovrut, B.A.; Ross, G.G. Large scale structure from biased nonequilibrium phase transitions: Percolation theory picture. Nucl. Phys. B 1995, 434, 675–696. [Google Scholar] [CrossRef]
- Shapiro, I.L.; Sola, J. Scaling behavior of the cosmological constant: Interface between quantum field theory and cosmology. J. High Energy Phys. 2002, 2, 006. [Google Scholar] [CrossRef]
- Shapiro, I.L.; Sola, J. On the possible running of the cosmological ‘constant’. Phys. Lett. B 2009, 682, 105–113. [Google Scholar] [CrossRef]
- Shapiro, I.L.; Sola, J. Cosmological constant, renormalisation group and Planck scale physics. Nucl. Phys. B Proc. Suppl. 2004, 127, 71–76. [Google Scholar] [CrossRef]
- Perico, E.L.D.; Lima, J.A.S.; Basilakos, S.; Sola, J. Complete Cosmic History with a dynamical Λ = Λ(H) term. Phys. Rev. D 2013, 88, 063531. [Google Scholar] [CrossRef]
- Lima, J.A.S.; Basilakos, S.; Sola, J. Expansion History with Decaying Vacuum: A Complete Cosmological Scenario. Mon. Not. R. Astron. Soc. 2013, 431, 923–929. [Google Scholar] [CrossRef]
- Sola Peracaula, J. The cosmological constant problem and running vacuum in the expanding universe. Phil. Trans. R. Soc. Lond. A 2022, 380, 20210182. [Google Scholar] [CrossRef]
- Kanti, P.; Mavromatos, N.E.; Rizos, J.; Tamvakis, K.; Winstanley, E. Dilatonic black holes in higher curvature string gravity. Phys. Rev. D 1996, 54, 5049–5058. [Google Scholar] [CrossRef]
- Moreno-Pulido, C.; Sola, J. Running vacuum in quantum field theory in curved spacetime: Renormalizing ρvac without ∼m4 terms. Eur. Phys. J. C 2020, 80, 692. [Google Scholar] [CrossRef]
- Moreno-Pulido, C.; Sola Peracaula, J. Renormalizing the vacuum energy in cosmological spacetime: Implications for the cosmological constant problem. Eur. Phys. J. C 2022, 82, 551. [Google Scholar] [CrossRef]
- Moreno-Pulido, C.; Sola Peracaula, J. Equation of state of the running vacuum. Eur. Phys. J. C 2022, 82, 1137. [Google Scholar] [CrossRef]
- Moreno-Pulido, C.; Sola Peracaula, J.; Cheraghchi, S. Running vacuum in QFT in FLRW spacetime: The dynamics of ρvac(H) from the quantized matter fields. Eur. Phys. J. C 2023, 83, 637. [Google Scholar] [CrossRef]
- Bossingham, T.; Mavromatos, N.E.; Sarkar, S. Leptogenesis from Heavy Right-Handed Neutrinos in CPT Violating Backgrounds. Eur. Phys. J. C 2018, 78, 113. [Google Scholar] [CrossRef] [PubMed]
- Bossingham, T.; Mavromatos, N.E.; Sarkar, S. The role of temperature dependent string-inspired CPT violating backgrounds in leptogenesis and the chiral magnetic effect. Eur. Phys. J. C 2019, 79, 50. [Google Scholar] [CrossRef] [PubMed]
- Mavromatos, N.E.; Sarkar, S. Curvature and thermal corrections in tree-level CPT-Violating Leptogenesis. Eur. Phys. J. C 2020, 80, 558. [Google Scholar] [CrossRef]
- Kostelecky, V.A.; Russell, N. Data Tables for Lorentz and CPT Violation. Rev. Mod. Phys. 2011, 83, 11–31. [Google Scholar] [CrossRef]
- Capanelli, C.; Jenks, L.; Kolb, E.W.; McDonough, E. Cosmological Implications of Kalb–Ramond-Like-Particles. arXiv 2023, arXiv:2309.02485. [Google Scholar]
- Popławski, N.J. Cosmology with torsion: An alternative to cosmic inflation. Phys. Lett. B 2010, 694, 181–185, Erratum in Phys. Lett. B 2011, 701, 672–672. [Google Scholar] [CrossRef]
- Poplawski, N.J. Cosmological constant from quarks and torsion. Ann. Phys. 2011, 523, 291–295. [Google Scholar] [CrossRef]
- Magueijo, J.; Zlosnik, T.G.; Kibble, T.W.B. Cosmology with a spin. Phys. Rev. D 2013, 87, 063504. [Google Scholar] [CrossRef]
- Poplawski, N.J. Nonsingular, big-bounce cosmology from spinor-torsion coupling. Phys. Rev. D 2012, 85, 107502. [Google Scholar] [CrossRef]
- Giacosa, F.; Hofmann, R.; Neubert, M. A model for the very early Universe. J. High Energy Phys. 2008, 02, 077. [Google Scholar] [CrossRef]
- Kostelecky, V.A.; Russell, N.; Tasson, J. New Constraints on Torsion from Lorentz Violation. Phys. Rev. Lett. 2008, 100, 111102. [Google Scholar] [CrossRef] [PubMed]
- Bolejko, K.; Cinus, M.; Roukema, B.F. Cosmological signatures of torsion and how to distinguish torsion from the dark sector. Phys. Rev. D 2020, 101, 104046. [Google Scholar] [CrossRef]
- Aluri, P.K.; Cea, P.; Chingangbam, P.; Chu, M.; Clowes, R.G.; Hutsemékers, D.; Kochappan, J.P.; Lopez, A.M.; Liu, L.; Martens, N.C.M.; et al. Is the observable Universe consistent with the cosmological principle? Class. Quantum Gravity 2023, 40, 094001. [Google Scholar] [CrossRef]
- Gómez-Valent, A.; Mavromatos, N.E.; Solà Peracaula, J. Stringy Running Vacuum Model and current Tensions in Cosmology. arXiv 2023, arXiv:2305.15774. [Google Scholar] [CrossRef]
- Garcia de Andrade, L.C. Torsion bounds from CP violation alpha(2)-dynamo in axion-photon cosmic plasma. Mod. Phys. Lett. A 2011, 26, 2863–2868. [Google Scholar] [CrossRef]
- Campanelli, L.; Giannotti, M. Magnetic helicity generation from the cosmic axion field. Phys. Rev. D 2005, 72, 123001. [Google Scholar] [CrossRef]
- Cai, Y.F.; Capozziello, S.; De Laurentis, M.; Saridakis, E.N. f(T) teleparallel gravity and cosmology. Rep. Prog. Phys. 2016, 79, 106901. [Google Scholar] [CrossRef] [PubMed]
- D’Ambrosio, F.; Fell, S.D.B.; Heisenberg, L.; Kuhn, S. Black holes in f(Q) gravity. Phys. Rev. D 2022, 105, 024042. [Google Scholar] [CrossRef]
- Fernández, N.; Pujol, P.; Solís, M.; Vargas, T. Revisiting the electronic properties of disclinated graphene sheets. Eur. Phys. J. B 2023, 96, 68. [Google Scholar] [CrossRef]
- Nissinen, J.; Volovik, G.E. On thermal Nieh–Yan anomaly in topological Weyl materials. JETP Lett. 2019, 110, 789–792. [Google Scholar] [CrossRef]
- Nissinen, J.; Volovik, G.E. Thermal Nieh–Yan anomaly in Weyl superfluids. Phys. Rev. Res. 2020, 2, 033269. [Google Scholar] [CrossRef]
- Bombacigno, F.; Cianfrani, F.; Montani, G. Big-Bounce cosmology in the presence of Immirzi field. Phys. Rev. D 2016, 94, 064021. [Google Scholar] [CrossRef]
- Bombacigno, F.; Montani, G. Big bounce cosmology for Palatini R2 gravity with a Nieh–Yan term. Eur. Phys. J. C 2019, 79, 405. [Google Scholar] [CrossRef]
- Bombacigno, F.; Boudet, S.; Montani, G. generalised Ashtekar variables for Palatini f() models. Nucl. Phys. B 2021, 963, 115281. [Google Scholar] [CrossRef]
- Boudet, S.; Bombacigno, F.; Montani, G.; Rinaldi, M. Superentropic black hole with Immirzi hair. Phys. Rev. D 2021, 103, 084034. [Google Scholar] [CrossRef]
- Bombacigno, F.; Boudet, S.; Olmo, G.J.; Montani, G. Big bounce and future time singularity resolution in Bianchi I cosmologies: The projective invariant Nieh–Yan case. Phys. Rev. D 2021, 103, 124031. [Google Scholar] [CrossRef]
- Elizalde, E.; Odintsov, S.D.; Paul, T.; Sáez-Chillón Gómez, D. Inflationary universe in F(R) gravity with antisymmetric tensor fields and their suppression during its evolution. Phys. Rev. D 2019, 99, 063506. [Google Scholar] [CrossRef]
- Paul, T.; Banerjee, N. Cosmological quantum entanglement: A possible testbed for the existence of Kalb–Ramond field. Class. Quantum Gravity 2020, 37, 135013. [Google Scholar] [CrossRef]
- Paul, T. Antisymmetric tensor fields in modified gravity: A summary. Symmetry 2020, 12, 1573. [Google Scholar] [CrossRef]
- Paul, T.; SenGupta, S. Dynamical suppression of spacetime torsion. Eur. Phys. J. C 2019, 79, 591. [Google Scholar] [CrossRef]
- Das, A.; Paul, T.; Sengupta, S. Invisibility of antisymmetric tensor fields in the light of F(R) gravity. Phys. Rev. D 2018, 98, 104002. [Google Scholar] [CrossRef]
- Nascimento, J.R.; Petrov, A.Y.; Porfírio, P.J. Induced gravitational topological term and the Einstein–Cartan modified theory. Phys. Rev. D 2022, 105, 044053. [Google Scholar] [CrossRef]
- Battista, E.; De Falco, V. First post-Newtonian generation of gravitational waves in Einstein–Cartan theory. Phys. Rev. D 2021, 104, 084067. [Google Scholar] [CrossRef]
- Battista, E.; De Falco, V. Gravitational waves at the first post-Newtonian order with the Weyssenhoff fluid in Einstein–Cartan theory. Eur. Phys. J. C 2022, 82, 628. [Google Scholar] [CrossRef] [PubMed]
- Battista, E.; De Falco, V. First post-Newtonian N-body problem in Einstein–Cartan theory with the Weyssenhoff fluid: Equations of motion. Eur. Phys. J. C 2022, 82, 782. [Google Scholar] [CrossRef]
- De Falco, V.; Battista, E.; Antoniadis, J. Analytical coordinate time at first post-Newtonian order. Europhys. Lett. 2023, 141, 29002. [Google Scholar] [CrossRef]
- Battista, E.; De Falco, V.; Usseglio, D. First post-Newtonian N-body problem in Einstein–Cartan theory with the Weyssenhoff fluid: Lagrangian and first integrals. Eur. Phys. J. C 2023, 83, 112. [Google Scholar] [CrossRef]
- De Falco, V.; Battista, E. Analytical results for binary dynamics at the first post-Newtonian order in Einstein–Cartan theory with the Weyssenhoff fluid. Phys. Rev. D 2023, 108, 064032. [Google Scholar] [CrossRef]
- Mondal, V.; Chakraborty, S. Lorentzian quantum cosmology with torsion. arXiv 2023, arXiv:2305.01690. [Google Scholar]
- Chakraborty, S.; Dey, R. Noether Current, Black Hole Entropy and Spacetime Torsion. Phys. Lett. B 2018, 786, 432–441. [Google Scholar] [CrossRef]
- Banerjee, R.; Chakraborty, S.; Mukherjee, P. Late-time acceleration driven by shift-symmetric Galileon in the presence of torsion. Phys. Rev. D 2018, 98, 083506. [Google Scholar] [CrossRef]
- Sharma, M.K.; Sur, S. Growth of matter perturbations in an interacting dark energy scenario emerging from metric-scalar-torsion couplings. Phys. Sci. Forum 2021, 2, 51. [Google Scholar]
- Boos, J.; Hehl, F.W. Gravity-induced four-fermion contact interaction implies gravitational intermediate W and Z type gauge bosons. Int. J. Theor. Phys. 2017, 56, 751–756. [Google Scholar] [CrossRef]
- Gialamas, I.D.; Veermäe, H. Electroweak vacuum decay in metric-affine gravity. Phys. Lett. B 2023, 844, 138109. [Google Scholar] [CrossRef]
- Pal, K.; Pal, K.; Sarkar, T. Conformal Fisher information metric with torsion. J. Phys. A 2023, 56, 335001. [Google Scholar] [CrossRef]
- Gallegos, A.D.; Gürsoy, U.; Yarom, A. Hydrodynamics of spin currents. SciPost Phys. 2021, 11, 041. [Google Scholar] [CrossRef]
- Adamczyk, L. et al. [The STAR Collaboration] Global Λ hyperon polarisation in nuclear collisions: Evidence for the most vortical fluid. Nature 2017, 548, 62–65. [Google Scholar] [CrossRef]
- Adam, J. et al. [STAR Collaboration] Global polarisation of Λ hyperons in Au+Au collisions at = 200 GeV. Phys. Rev. C 2018, 98, 014910. [Google Scholar] [CrossRef]
- Takahashi, R. Spin hydrodynamic generation. Nat. Phys. 2015, 12, 52. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mavromatos, N.E.; Pais, P.; Iorio, A. Torsion at Different Scales: From Materials to the Universe. Universe 2023, 9, 516. https://doi.org/10.3390/universe9120516
Mavromatos NE, Pais P, Iorio A. Torsion at Different Scales: From Materials to the Universe. Universe. 2023; 9(12):516. https://doi.org/10.3390/universe9120516
Chicago/Turabian StyleMavromatos, Nick E., Pablo Pais, and Alfredo Iorio. 2023. "Torsion at Different Scales: From Materials to the Universe" Universe 9, no. 12: 516. https://doi.org/10.3390/universe9120516
APA StyleMavromatos, N. E., Pais, P., & Iorio, A. (2023). Torsion at Different Scales: From Materials to the Universe. Universe, 9(12), 516. https://doi.org/10.3390/universe9120516








