Abstract
In this overview, we discuss the (Schwartz) distributional stress–energy quadrupole and show it is a source of gravitational waves. We provide an explicit formula for the metric of linearised gravity in the case of a background Minkowski spacetime. We compare and contrast the two different representations for quadrupoles taken by Dixon and Ellis, present the formula for the dynamics of the quadrupole moments, and determine the number of free components. We review other approaches to the dynamics of quadrupoles, comparing our results.
1. Introduction and Summary
Gravitational waves (GWs) offer a unique window into the most energetic events in the cosmos, such as colliding black holes, neutron stars and interactions in the early universe. The recent rise in gravitational wave astronomy highlighted the need for better models of gravitational wave sources. Due to the large distances involved from the source, it is reasonable to make the approximation that the size of gravitational wave sources are significantly smaller than this distance. One may use an approximation where the source is considered point-like, but with additional structure contained in the moments. These moments can be represented as Schwartz distributional [1] (e.g., –function) stress–energy tensors , over the worldline of a chosen centre of the source. By imposing symmetry, , and the divergence-free condition, , one obtains ordinary differential equations (ODEs) for the moments. These ODEs are given in Equations (7)–(10) and (20)–(23), below. By solving these, one may predict the gravitational waves that the system will produce [2,3]. The distributional source approximation has several advantages. Solving a system of ODEs is much easier to solve than a system of partial differential equations (PDEs). In addition, there is an algebraic formula for the gravitational waves in terms of the components, given below in (30). Another advantage is that, in principle, one can use this formula to directly measure the components of the multipole. This would require significant improvement in the sensitivity of gravitational wave detection, as one would need to measure the individual components of the gravitational wave perturbation tensor, and how they change when one changed the detectors’ position in space. In contrast, for a continuous stress–energy source, one can only measure the integrated contributions. These measured moments may provide physical insights into the source of the gravitational waves, especially when there is no model, or competing models for the dynamics of the source. This would then provide a direct comparison to the quadrupole, or higher multipole, model.
In the case of the monopole, the divergence-free condition implies that the point source undergoes geodesic motion, whereas for the dipole, this condition implies the Mathisson–Papapetrou–Tulczyjew–Dixon equations. The quadrupole is particularly interesting, as it is the quadrupole terms which give rise to gravitational waves. However, for the quadrupole, there are 60 moments (after imposing symmetries) but only 40 ODEs [2,3]. This implies that one requires additional ODEs or algebraic equations to determine the remaining 20 free components. We call additional equations constitutive relations, because they will depend on the underlying material which we are approximating with the quadrupole. One would expect “dust” to have different constitutive relations from a neutron star, or two orbiting neutron stars. To date, there are no models at all for these constitutive relations, although in [2], a suggestion is made. The freedom in the componets corresponds to the idea that a blob of matter can spread out and then recombine without breaking any conservation laws; see Figure 1. The divergencelessness of the stress–energy tensor, Equation (6), below, is not affected by certain internal dynamics of the multipole, as these internal dynamics are completely determined by the free components.
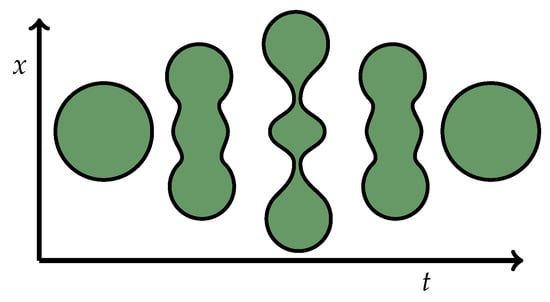
Figure 1.
Schematic of a blob of matter which separates and then recombines. These internal dynamics can take place without affecting the divergencelessness of the stress–energy tensor. This is a freedom of the moments of the stress–energy tensor.
A similar situation, which requires constitutive relations, occurs when the worldline of the source is not specified. This is called the Pole–Dipole problem [4,5,6,7,8,9,10,11,12]. In this case, the Mathisson–Papapetrou–Tulczyjew–Dixon equations, which are the only equations arising from the divergencelessness of the stress–energy tensor, are insufficient to determine both the dynamics of the worldline and the dynamics of the dipole moments. In this work, by contrast, we assume the worldline is specified, and hence the Mathisson–Papapetrou–Tulczyjew–Dixon equations completely specify the dynamics of the dipole.
Quadrupoles, and general multipoles, are abstract geometric objects, but it is useful to represent them using coordinates. There are two representations, the Dixon representation [13,14,15,16,17] and the Ellis representation [18], which are defined below. Both these representations consist of components defined only over a worldline, which is usually a path within, or close to, the extended body. The components correspond to the moments of the extended body. However, in order to calculate the moments, all the stress–energy tensors at the same “time” must be transported to the same point on the worldline, such that one can integrate them. This gives rise to two choices that one must make. The first is to decide which points in the extended object are at the same “time”. The other choice is how to transport the tensors. Dixon and Ellis make two different choices; this corresponds to how the multipoles are represented.
For the spatial timeslice, Dixon chose the orthogonal hypersurface. For a point on the worldline, take all the geodesics which emanate from this point and are orthogonal to the worldline. Then, use parallel transport to transport the tensors on this timeslice, along the geodesics, to the worldline to be integrated [15]. These choices give rise to the Dixon representation. However, this representation is a little more general since one does not have to choose the tangent to the worldline to define the orthogonal hypersurface. Instead, one can use another arbitrary 4–vector along the worldline. This vector is called the Dixon vector ; see Figure 2. In this case, one chooses all the geodesics which are orthogonal to . There are cases where using a Dixon vector which is not the 4–velocity of the worldline would be advantageous. One example is when there is a global timelike Killing vector, such as when considering matter near a black hole. Another is when considering ultra-relativistic particles expanded around a lightlike worldline, in which case the orthogonal hypersurfaces would not be transverse to the worldline.
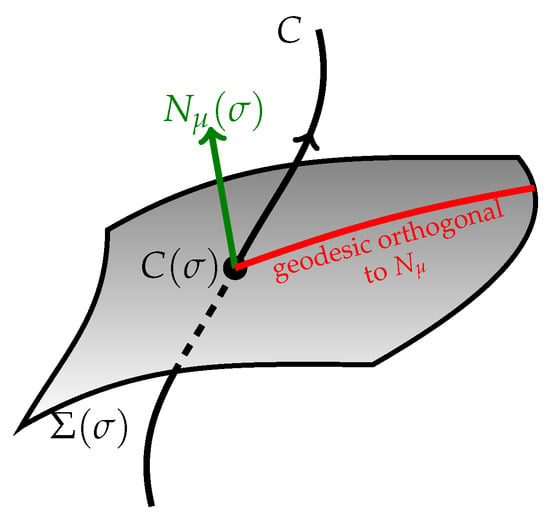
Figure 2.
On the worldline C, the Dixon vector defines the orthogonal hypersurface .
There are many advantages to using the Dixon representation. One, the components are tensor fields along the worldline. Two, these components are unique, in that given a particular quadrupole, there is a formula for the corresponding components. This is distinct from the Ellis representation. Three, the quadrupole is written as a sum of the monopole, dipole and quadrupole terms and there is no freedom in this splitting. This monopole can be used to define the mass of the quadrupole, but in general, this mass is not conserved. The disadvantage is that there is a non-tensorial dependency of the components on the Dixon vector. Furthermore, this change of Dixon vector will mix the various orders so that the quadrupole will contribute to the dipole and visa-versa. In fact an explicit formula for that transformation of the components, arising from changing the Dixon vector, is not currently known.
For the Ellis representation, one simply chooses a coordinate system and then transports the vectors using Lie-transport with respect to this coordinate system. This results in taking the components of the tensors, with respect to this coordinate system, and simply integrating these values. Since no timeslice is chosen, the corresponding components are not unique (they possess a gauge-like freedom). Although the transformation of the components is given below, it is not tensorial. Indeed, for the quadrupole, it involves second derivatives and integrals of the coordinate transformations. In addition, there is no formula for the monopole and dipole terms of the quadrupole. From a mathematical point of view, an advantage is that this representation does not require an additional structure, such as the connection, on the manifold. Thus, it can be generalised to manifolds, such as phase spaces [19], which do not possess a connection.
For the Ellis representation, the situation can be improved if one chooses a coordinate system which is adapted to the worldline. In this case, the timelike coordinate defines the timeslices and one uses Lie-transport with respect to spatial coordinates. In addition, the components are unique and one can separate out the monopole, dipole and quadrupole terms. However, this split is dependent on the coordinate system.
In both representations, the dipole can be written consistently with the Mathisson–Papapetrou–Tulczyjew–Dixon equations. Also, in both representations, one can formulate a regular tensor field whose moments, up to k, are the components of the distribution. If all the moments are known, and satisfy Carleman’s conditions, then one can reconstitute the original distribution. As stated, both Ellis and Dixon are representations of an abstract geometric object, which can be formulated in a coordinate-free way, employing the de Rham pushforward [2,20].
2. Existing Literature on the Derivation of the Dynamics of the Quadrupole Moments
As stated in the introduction, the dynamics of the components of the dipole are given by the Mathisson–Papapetrou–Tulczyjew–Dixon equation. Thus, given the worldline and the initial values for the moments, they completely specify the moments. One may expect that the same would happen for the components of the quadrupole, and there have been several attempts, particularly by Dixon, to specify these ordinary differential equations for these moments. In his work, Dixon [16,17] makes two conjectures for the dynamics of the components of a quadrupole.
In [15] (7.34)–(7.37), Dixon postulates simple rotational dynamics. Here, he introduces a connection [15] (7.18), defined by
where is described as the body’s dynamical velocity, and . He writes as . Using this connection, we can formulate a rotation tensor ; [15] (7.34) where,
From this, the dynamical equation for a non-rotating quadrupole is given by [15] (7.36)
As an alternative, Dixon also posits a non-dynamical equation based on symmetry [16] (4.11).
We observe in Section 6 below, that neither of these approaches correspond to the divergence-free condition (6). Thus, they are not the generalisation of the Mathisson–Papapetrou–Tulczyjew–Dixon equations for the quadrupole.
In [4], Steinhoff and Puetzfeld obtain the equations of motion of an extended test body in the framework of Einstein’s theory of gravitation. The equations of motion were derived via Tulczyjew’s multipolar approximation method, up to the quadrupole order. The canonical form of the energy-momentum density was explicitly constructed. The set of gravitational multipolar moments and the corresponding equations of motion were compared to alternative multipolar approximation schemes. They introduced the classification of two different types of equations, named “constraint” and “evolution”. The same type of pattern of equations replicates at each multipolar order. More than two equations of the evolution-type are not to be expected in the context of Tulczyjew’s approximation scheme. Moreover, in Tulczyjew’s method, which is used in [4], the orthogonal decomposition of the moments is employed to facilitate the derivation of the canonical form. In particular, higher-order moments are recursively transferred to lower differential orders in the canonical form. For the quadrupole system, they take a similar approach to ours and we conjecture that our results (7)–(10) are equivalent to theirs. However, since they have used a different decomposition, it would require significant work to establish a direct comparison.
3. The Dixon and Ellis Representation of Quadrupole
Let be a spacetime with metric and the Levi–Civita1 connection with Christoffel symbol . Here, Greek indices run and Latin indices . Let , where , is the worldline of the source2 with worldline components , where parameterises the worldline. At this point, we do not assume that the parameter is the proper time. Let the tangent vector be . Here, we consider stress–energy tensors , which are non-zero only on the worldline , where it has Dirac–-like properties. Such stress–energy tensors are called distributional tensors.
3.1. The Dixon Representation of Quadrupoles
The Dixon vector defines the orthogonal hypersurface; see Figure 2. The quadrupole stress–energy tensor (density), written using the Dixon representation [17], requires one to choose a Dixon vector, . This is an arbitrary vector field along the worldline, which satisfies .
The Dixon representation of the stress–energy quadrupole tensor is given by
where the components , and have symmetry properties and . They also have the orthogonality condition with respect to the Dixon vector, and . The components are essentially the moments of the distribution. If we think of the distributional as representing an extended body, then we can think of it as extending into the orthogonal hyperspace given in Figure 2. This is the hyperspace in which we need to integrate to obtain the moments. This notion can be precise in terms of squeezing a regular distribution of mass down to a worldline, which is provided in Section 5, below. This squeezing also enables a direct comparison between the components and the moments of a regular stress–energy tensor. The components are only defined on the worldline and transform as tensors. We observe from (4) that a quadrupole is a sum of a monopole term, a dipole term and a pure quadrupole term.
Since is a tensor distribution, this allows us to apply the covariant derivative to a test tensor , giving,
If was expressed in another way such that one could calculate the integrals on the left-hand side of (5), but the components were unknown; then, by a judicious choice of test tensors , one can calculate the components on the right-hand side of (5). Such a scenario could be if was provided using the Ellis representation below, or in a Dixon representation but with respect to another Dixon vector . For this reason, we say that the components in the Dixon representation are unique.
The use of the test tensor also enables us to derive the dynamical equations for the components. Imposing the symmetry and divergence-free conditions,
yields the subsequent tensor equations for the components
together with the constraint
and the round brackets on the indices correspond to the total symmetric component, i.e., . Thus, we have dynamical equations for the internal moments of the quadrupole. By counting the number of equations and the number of unknown components, we observe that there are 20 free components. Hence, the system is under-determined. There are many possible motions of the moments that are consistent with the vanishing of the stress–energy tensor. An example is depicted in Figure 1. This freedom requires additional equations called constitutive relations. It is a goal of current research to derive the constitutive relations for a variety of physically interesting scenarios such as dust and orbiting masses. Such constitutive relations must, of course, be consistent with the component Equations (7)–(10).
The proof of (7)–(10) is very involved and detailed in [3]. Here, we summarise the steps. We first prove it in Dixon-adapted coordinates. We take the divergence of and express this as
where
It is then necessary to manipulate , and by acting on a test form . The key is to manipulate the terms to act on , where is the tangent to the geodesics which define the surface , as such terms give rise to unique components which can be extracted. We can then generalise these results to arbitrary coordinate systems, using the tensor nature of the components.
3.2. The Ellis Representation of Quadrupoles
The Ellis representation of a quadrupole uses partial derivatives instead of covariant derivatives. It is given by
When acting on the test tensor , one has
As in [1], under a change of coordinate to , we have a complex transformation involving derivatives and integrals
where is given by
and
Proof.
The Ellis representation is simplified when written in terms of an adapted coordinate system. In these coordinates, is the time coordinate, while are the transverse spatial coordinates. In this coordinate system , , . Thus, (13) becomes
From Equation (18), one can identify the monopole, dipole and pure quadrupole terms. However, this splitting is coordinate-dependent, and changing the coordinates will mix these terms.
The relationship between the components and is given by
One can now write down the differential and algebraic equations on the components arising from the divergencelessness conditions (6), as established below.
together with the algebraic equation
4. Distributional Quadrupole Sources of Gravitational Waves
Einstein’s equations
are non-linear. Recall that the distributional stress–energy tensor is an approximation to a regular stress–energy tensor, for which (24) can be directly applied. In linear theories like electromagnetism, one often uses distributional sources. For example, an arbitrary moving point charge yields the Liénard–Wiechard fields. For a distributional matter, the stress–energy tensor can be written as (4), (13) or (18). However, solutions of the Einstein Equation (24) will diverge along the worldline C, and the meaning of Equation (24) requires interpretation. Indeed, according to Geroch [21],
“There have been attempts to introduce into general relativity sources to represent gravitating point particles, i.e., sources concentrated on one-dimensional surfaces in space-time. One goal of this work was to find equations of motion for such point particles. To this end, there was introduced a class of metrics, specified by their behavior on approaching a singular worldline, to describe the near-field of such a particle. It now appears, however, that the metrics in this class may not be physically realistic, for one expects that such a concentration of matter would result in collapse through a horizon, and that inside this horizon there will be further structure. Indeed, it now seems likely that there is in general relativity no mathematical framework whatever for matter sources concentrated on one-dimensional surfaces in space-time.”
There have been several attempts to have a non-linear theory of distributions, the most successful being Colombeau, the algebra of generalised functions [22]. An alternative approach is to consider a set of regular stress–energy tensors , for which (24) is valid. Dixon [16] uses an exponential map, to connect points off the worldline to points on the worldline, to identify the distributional stress–energy with the regular tensor. Geroch and Weatherall [23] consider an infinite set of regular stress–energy tensors fulfilling the dominant energy condition. They find a sequence which tends to the monopole stress–energy tensor. This is similar to use of squeezed tensors we consider in Section 5, below.
Since we are primarily interested in sources of gravitational waves, we imply solve the linearlised Einstein’s equations. Expanding the gravitational metric, is a pertubation about a background , where is the small perturbation parameter and is the perturbation term, and inserting the expansion into the Einstein Equation (24), one has
Hence, the background metric satisfies . The linearised equations are then given by
In the case when the background metric is the Minkowski metric , then (26) becomes [24]
where , , and we have employed the Lorenz gauge, also called the de Donder gauge, (). We can provide in terms of an integral over the retarded Green’s functions:
Let us choose a one-parameter family of regular stress–energy tensors , where is the parameter. Let these tensors tend to the distributional tensor in the limit . An example of such a one-parameter family is provided in Section 5. Then, the gravitational waves arising from are the limit of the gravitational waves emanating from , i.e.,
Let be provided by the right-hand side of (4); then, we have an explicit formula for on a flat background (28). Both the retarded Green’s function, and hence (29) and the distribution , are coordinate independent objects. Thus, the corresponding field is a tensor. However, in order to express in terms of components, it is necessary either to use the Dixon representation and choose or use the Ellis representation and choose adapted coordinate systems. We will choose Cartesian coordinates and set to be timelike and parallel. Thus, the components are constant. In this case, we have an explicit expression given by
where is the retarded time, , , and .
5. Squeezed Tensors
To interpret the components as integrals over spatial coordinates, i.e., moments, one can use squeezed tensors. In this section, we use the Ellis representation in adapted coordinates, Equation (18). We construct a one-parameter family of regular stress–energy tensor densities, labelled by . Starting with a regular stress–energy tensor , where , let
In the weak limit, as , tends to be a distributional stress–energy tensor .
We assume that has compact support in the transverse planes, i.e., for each , there is a function such that
This ensures that all the moments are finite.
We, thus, obtain
where
In [3], it is shown that the same squeezed forms can be achieved using the Dixon representation. Here, the integrals are over the hyperspace orthogonal to the Dixon vector, as shown in Figure 2.
6. Comparison of Dixon’s Equations for the Moments, with Those Presented Here
In order to compare Dixon’s equations for the moment with ours, it is necessary to relate the components. In [17] (10.17), we see the term when we expand the right-hand side. To understand this, we use, in turn [17] (10.9), [17] (10.6), [16] (4.5), [16] (7.4) to give
since from [17] (10.17) . Here, the moments fulfil the symmetry conditions [17] (10.3), and orthogonality condition [17] (10.4). Thus, the first term in the last expression corresponds to the right-hand side of (5) if we set . However, the orthogonality condition does not completely correspond. Thus, we can identify , and . Using [17] (1.37) and [14] (2.4), we can write . Since this, by default, has the symmetries of the Riemann curvature tensor, it has 20 independent components. Most of these symmetries are necessitated because it is contracted with the Riemann curvature tensor [17] (1.28) and (1.29). However, the 20 free components presented in this work do not correspond to 20 independent components of the quadrupole moment .
The main dissimilarity is the necessity of the divergenceless condition. In [17], this is realised by putting the divergence operator into the argument of I, as observed in the term in [17] (10.16). As stated by comment (vii) in [17] (p. 109), this does not yield any additional algebraic or differential equations for the . It solely impacts the dynamics of the dipole [17] (1.28) and (1.29). Contrarily, in our approach, we obtain the ODEs and free components of the or , by applying the divergence operator directly to the distribution. Therefore, a non-rotating quadrupole would not fulfill (7)–(10) and therefore does not correspond to a divergenceless stress–energy tensor.
Dixon’s alternative approach, [16] Equation (4.11), becomes, in our language
7. Concluding Remarks
In this overview, we have discussed the distributional stress–energy quadrupole as a source of gravitational waves, and have provided an explicit form for the perturbation to the metric. We have compared and contrasted the Dixon representation and the Ellis representation for quadrupoles. We have elucidated how distributional stress–energy quadrupoles act as sources of gravitational waves. We have determined the number of free components for a stress–energy quadrupole. We have provided and analysed the mathematical machinery requisite for the Dixon and Ellis representations. There are a number of interesting ideas that follow from this review. As a future development, it would be instructive to investigate different constitutive relations. To date, the only constitutive relations prescribed are for a simple dust model [2]. Natural choices will be to look at a general dust model and orbiting masses. It would be useful to have a formula for the transformation in Dixon components when changes. This would then confirm that the equation for gravitational waves is indeed independent of the choice of .
Author Contributions
Conceptualization, J.G. and S.T.; methodology, J.G. and S.T.; formal analysis, J.G. and S.T.; investigation, J.G. and S.T.; writing—original draft preparation, J.G. and S.T.; writing—review and editing, J.G. and S.T.; project administration, J.G.; funding acquisition, J.G.; All authors have read and agreed to the published version of the manuscript.
Funding
J.G. is grateful for the support provided by STFC (the Cockcroft Institute ST/V001612/1). S.T. would like to thank the Faculty of Science and Technology, Lancaster University for their support.
Acknowledgments
We would like to thank Finlay Gunneberg, Alex Warwick, and Willow Sparks for helping to prepare this manuscript and suggesting some references.
Conflicts of Interest
The authors declare no conflict of interest.
Notes
| 1 | It transpires that in most of our calculations in this review, the metric is immaterial and an arbitrary linear connection may be employed. |
| 2 | Even using proper time in Minkowski space, one cannot surmise that , since it is possible to accelerate to lightlike infinity in the finite proper time. |
References
- Gratus, J.; Banaszek, T. The correct and unusual coordinate transformation rules for electromagnetic quadrupoles. Proc. R. Soc. Lond. A 2018, 474, 20170652. [Google Scholar] [CrossRef] [PubMed]
- Gratus, J.; Pinto, P.; Talaganis, S. The distributional stress-energy quadrupole. Class. Quant. Grav. 2021, 38, 035011. [Google Scholar] [CrossRef]
- Gratus, J.; Talaganis, S. The tensorial representation of the distributional stress-energy quadrupole and its dynamics. Class. Quant. Grav. 2023, 40, 085012. [Google Scholar] [CrossRef]
- Steinhoff, J.; Puetzfeld, D. Multipolar equations of motion for extended test bodies in General Relativity. Phys. Rev. D 2010, 81, 044019. [Google Scholar] [CrossRef]
- Steinhoff, J.; Puetzfeld, D. Influence of internal structure on the motion of test bodies in extreme mass ratio situations. Phys. Rev. D 2012, 86, 044033. [Google Scholar] [CrossRef]
- Mathisson, M. Neue mechanik materieller systemes. Acta Phys. Polon. 1937, 6, 163–200. [Google Scholar]
- Frenkel, J. Die Elektrodynamik des rotierenden Elektrons. Z. Phys. 1926, 37, 243–262. [Google Scholar] [CrossRef]
- Pirani, F.A.E. On the physical significance of the Riemann tensor. Acta Phys. Polon. 1956, 15, 389–405. [Google Scholar]
- Semerak, O. Spinning test particles in a Kerr field. I. Mon. Not. R. Astron. Soc. 1999, 308, 863–875. [Google Scholar] [CrossRef]
- Kyrian, K.; Semerak, O. Spinning test particles in a Kerr field. II. Mon. Not. R. Astron. Soc. 2007, 382, 1922–1932. [Google Scholar] [CrossRef]
- Rüdiger, R.; Penrose, R. Conserved quantities of spinning test particles in general relativity. I. Proc. R. Soc. Lond. A 1981, 375, 185–193. [Google Scholar]
- Rüdiger, R.; Penrose, R. Conserved quantities of spinning test particles in general relativity. II. Proc. R. Soc. Lond. A 1983, 385, 229–239. [Google Scholar]
- Dixon, W.G. A covariant multipole formalism for extended test bodies in general relativity. Il Nuovo Cimento (1955–1965) 1964, 34, 317–339. [Google Scholar] [CrossRef]
- Dixon, W.G. Description of Extended Bodies by Multipole Moments in Special Relativity. J. Math. Phys. 1967, 8, 1591–1605. [Google Scholar] [CrossRef]
- Dixon, W.G. Dynamics of extended bodies in general relativity. I. Momentum and angular momentum. Proc. R. Soc. Lond. A 1970, 314, 499–527. [Google Scholar]
- Dixon, W.G. Dynamics of extended bodies in general relativity. II. Moments of the charge-current vector. Proc. R. Soc. Lond. A 1970, 319, 509–547. [Google Scholar]
- Dixon, W.G. Dynamics of extended bodies in general relativity III. Equations of motion. Philosophical Transactions of the Royal Society of London. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1974, 277, 59–119. [Google Scholar]
- Ellis, J.R. Motion of a classical particle with spin. Math. Proc. Camb. Philos. Soc. 1975, 78, 145–156. [Google Scholar] [CrossRef]
- Warwick, A.; Gratus, J. Moment tracking and their coordinate transformations for macroparticles with an application to plasmas around black hole. arXiv 2023, arXiv:2308.01276. [Google Scholar] [CrossRef]
- de Rham, G. Differentiable Manifolds: Forms, Currents, Harmonic Forms. Grundlehren Der Mathematischen Wissenschaften; Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar]
- Geroch, R.P.; Traschen, J.H. Strings and other distributional sources in general relativity. Phys. Rev. D 1987, 36, 1017. [Google Scholar] [CrossRef]
- Steinbauer, R.; Vickers, J.A. The use of generalized functions and distributions in general relativity. Class. Quantum Gravity 2006, 23, R91–R114. [Google Scholar] [CrossRef]
- Geroch, R.; Weatherall, J.O. The Motion of Small Bodies in Space-time. Commun. Math. Phys. 2018, 364, 607–634. [Google Scholar] [CrossRef]
- Flanagan, E.E.; Hughes, S.A. The Basics of gravitational wave theory. New J. Phys. 2005, 7, 204. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).