Abstract
General relativity and its Newtonian weak field limit are not sufficient to explain the observed phenomenology in the Universe, from the formation of large-scale structures to the dynamics of galaxies, with the only presence of baryonic matter. The most investigated cosmological model, the CDM, accounts for the majority of observations by introducing two dark components, dark energy and dark matter, which represent ∼95% of the mass-energy budget of the Universe. Nevertheless, the CDM model faces important challenges on the scale of galaxies. For example, some very tight relations between the properties of dark and baryonic matters in disk galaxies, such as the baryonic Tully–Fisher relation (BTFR), the mass discrepancy–acceleration relation (MDAR), and the radial acceleration relation (RAR), which see the emergence of the acceleration scale m s, cannot be intuitively explained by the CDM paradigm, where cosmic structures form through a stochastic merging process. An even more outstanding coincidence is due to the fact that the acceleration scale , emerging from galaxy dynamics, also seems to be related to the cosmological constant . Another challenge is provided by dwarf galaxies, which are darker than what is expected in their innermost regions. These pieces of evidence can be more naturally explained, or sometimes even predicted, by modified theories of gravity, that do not introduce any dark fluid. I illustrate possible solutions to these problems with the modified theory of gravity MOND, which departs from Newtonian gravity for accelerations smaller than , and with Refracted Gravity, a novel classical theory of gravity introduced in 2016, where the modification of the law of gravity is instead regulated by a density scale.
1. Introduction
If we assume the validity of standard gravity, that is, General Relativity (GR), and the presence of ordinary (baryonic) matter alone, we cannot explain the observations from the largest to the smallest scales of the Universe. The cosmic microwave background (CMB) radiation [1], the dynamics and the large-scale distribution of the cosmic structure [2,3], the gravitational lensing, with particular reference to the Bullet Cluster [4,5,6], the dynamics of galaxy clusters [7], and the flat trend of the rotation curves of disk galaxies [8,9,10] all show a mass discrepancy of ∼80–90%. Moreover, the Hubble diagram of Ia Supernovae [11,12] proved the expansion of the Universe to be accelerated, which is not what we expect from the attractive nature of the gravity force. This probably represents the most important open question in modern cosmology and it launches several lines of research.
With the only presence of baryonic matter, GR cannot justify ∼95% of the components of the Universe. The most investigated solution is provided by the cold dark matter (CDM) cosmological model, which assumes the validity of GR and introduces two dark components besides baryonic matter to explain this missing ∼95%.
The first dark component is an exotic fluid with negative pressure called dark energy (DE), which causes the accelerated expansion of the Universe and explains ∼70% of its mass-energy budget. The DE can be identified with the cosmological constant , present in the Einstein equations. The second dark component is an invisible form of matter with a nonbaryonic nature, the dark matter (DM), which interacts with baryonic matter only gravitationally and explains ∼25% of the mass-energy budget of the Universe. To account for the observed bottom-up formation scenario of cosmic structures, DM has also to be “cold”, i.e., nonrelativistic at the epoch of decoupling from radiation.
The CDM model can account for almost all the mentioned pieces of evidence. Yet, it presents some issues, both on cosmological and small scales. Three of the most puzzling challenges on large scales are the cosmological constant problem [13,14], the coincidence problem [15], and the tensions between the cosmological parameters inferred from the late and the early Universe [1,16,17]. However, the most important problems of the CDM paradigm are observed on the scale of galaxies. The cusp/core, missing satellites, too-big-to-fail, and planes of satellite galaxies problems are among the most investigated (see [18,19] for a review).
Among the small-scale problems, particularly relevant is also the presence of very tight scaling relations between the properties of dark and baryonic matters in galaxies. These are the baryonic Tully–Fisher relation (BTFR) [20], the mass discrepancy–acceleration relation (MDAR) [21], and the radial acceleration relation (RAR) [22], whose scatter is consistent with the observational errors. In a CDM context, it is not trivial to explain why quantities related to DM, which represents ∼90% of the galaxy mass, are so tightly regulated by baryonic matter, which only represents ∼10% of the galaxy mass. Moreover, these pieces of evidence are not intuitively explained in a Universe where the formation of structures occurs hierarchically through a stochastic merging process dominated by DM.
An even more noteworthy coincidence, which might be difficult to interpret in CDM, is the emergence of an acceleration scale, m s, from the three relations. This acceleration scale, expressed in natural units, can also be written as , which is even more puzzling since it seems to suggest that DM and DE phenomenologies are regulated by the same acceleration scale [23]. This is even less intuitive in CDM.
At last, another issue on the galaxy scale is provided by the complex dynamics of some categories of systems. The relative contributions of the stellar disk, made of baryonic matter, and of the DM halo to the overall rotation curves of disk galaxies are degenerate to each other, a problem known as the “disk-halo conspiracy” [24,25]. Many pieces of evidence suggest the “maximum-disk hypothesis” [25,26,27,28,29,30], where the disk maximally contributes to the inner part of the rotation curve. However, this assumption is only valid for high surface brightness (HSB) galaxies, whose rotation curves are steeply rising in their central regions and are described with a cuspy DM density profile. Instead, dwarf, low surface brightness (LSB), and dwarf spheroidal (dSph) galaxies are DM-dominated even in their innermost regions and, thus, their rotation curves, slowly rising in their central part and modelled with a cored DM density profile, cannot be described by a maximum-disk model [31,32]. These categories of galaxies represent one of the best pieces of evidence of the mass-discrepancy problem on the scale of galaxies since they are among the darkest galaxies in the Universe, e.g., [33], and they give rise to the cusp/core problem. Intriguingly, there are systems with similar baryonic masses but completely different dynamics. They are globular clusters (GCs), which seem to be nearly DM-free [34,35,36,37,38,39,40].
Some of these problems are more intuitively explained, rather than with the CDM paradigm, with a modification of the law of gravity with respect to standard gravity, without introducing any dark component. According to the theory modified Newtonian dynamics (MOND) [41,42,43], the law of gravity departs from the Newtonian one when the acceleration goes below . This theory not only reproduces but actually predicted some pieces of evidence on the galaxy scale, such as the three mentioned scaling relations and the difference between the dynamics of HSB and LSB galaxies.
Another theory of modified gravity, more recently introduced, is refracted gravity (RG) [44], a classical theory where the modification of the law of gravity is regulated by the value of the local mass density, rather than of the acceleration. RG has shown some encouraging results in describing the dynamics of galaxies of different shapes, such as disk [45] and elliptical E0 galaxies with nearly spherical morphology [46]. In RG, the shape of the gravitational field lines depends on the morphology of the system: they are refracted towards the mid-plane of flattened systems and they remain radial for spherical systems, which might intuitively explain the different dynamics of dwarf galaxies (more flattened) and globular clusters (nearly spherical). Moreover, the relativistic formulation of RG [47] belongs to the class of scalar-tensor theories and introduces a single scalar field that explains the phenomenology of both DM and DE. The covariant RG provides a natural explanation for the relation, suggesting a unification of the two dark sectors.
In this review, we present more intuitive explanations, with the theories MOND and RG, for the three scaling relations, for the emergence of the same acceleration scale from these relations and from the DE sector, and for the different dynamics of LSB, dwarf, and dSph galaxies and of GCs. The outline of the paper develops as follows. In Section 2, we detail the BTFR, the MDAR, and the RAR (Section 2.1) and we explain the different interpretations of these relations in a CDM framework (Section 2.2). Section 3 describes the formulation of MOND and RG theories (Section 3.1) and the interpretation of the three scaling relations with these theories (Section 3.2). Section 4 illustrates how the acceleration scale and the – relation emerge in Newtonian, MOND, and RG theories. Section 5 describes the different dynamical properties of LSB, dwarf, and dSph galaxies and of GCs and how they can be modelled or interpreted in Newtonian, MOND, and RG gravities. Section 6 concludes the paper.
2. The Baryonic Scaling Relations
The mass discrepancy on the galaxy scale can be neatly quantified by three relations that tightly correlate the properties of dark and baryonic matters in galaxies: the BTFR, the MDAR, and the RAR.
2.1. Description of the Three Relations
The BTFR [20] (Figure 1) correlates the total baryonic mass, , and the asymptotic value of the flat part of the rotation curve of galaxies, , according to the relation, e.g., [48]:
where the normalisation A and the slope b are free parameters. In the BTFR, each point corresponds to one galaxy. McGaugh [48] fits the (,) data points from 47 gas-rich galaxies with Equation (1), adopting different techniques. The normalisations resulting from these fits are in agreement with each other and the slopes are consistent with 4. In the BTFR, the acceleration scale emerges from its normalisation. Setting the slope to 4, McGaugh [48] found the normalisation M km s, comparable to the expression . For mass-to-light ratios in the 3.6 m band M/L, the BTFR intrinsic scatter is minimised to ∼0.10 dex [49]. The residuals of the measured BTFR from the model (Equation (1)) do not correlate with galaxy properties, such as the radius or the surface brightness [50].

Figure 1.
The baryonic Tully–Fisher relation (BTFR) built for a subsample of 123 galaxies from the SPARC catalogue [51]. is the total galaxy baryonic mass, accounting for the stars and the gas, and is the mean circular velocity along the flat region of the rotation curve. The black solid line represents the linear fit to the data with the relation . denotes the intrinsic scatter of the BTFR, expressed in dex. The galaxies are colour-coded according to the gas fraction to the total baryonic mass. The figure is re-adapted from Figure 2 in [52].
Two local, rather than global, scaling relations related to the BTFR are the MDAR and the RAR [53]. The MDAR [21] anti-correlates, at each distance R from the galaxy centre, the Newtonian acceleration generated by the baryons distribution, , and the squared ratio , where V and are the total and the baryons-only velocities (Figure 2, top panel). If we assume spherical symmetry, the ratio coincides with the mass discrepancy, , where M and are the masses of the entire galaxy and of its baryonic component. The MDAR can be modelled by the following relation, e.g., [54]:
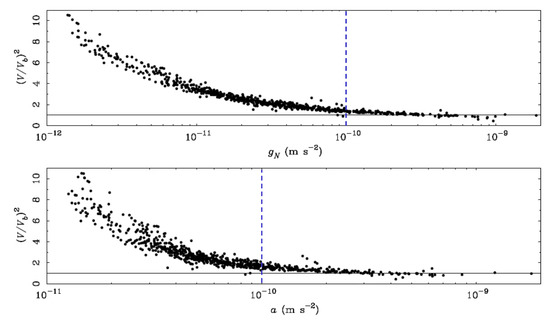
Figure 2.
The mass discrepancy–acceleration relation (MDAR) represented as the squared ratio between the total (V) and the baryonic () velocities as a function of the Newtonian acceleration due to baryonic matter, (top panel) and the total acceleration a (bottom panel). We can clearly see that the mass discrepancy is observed from accelerations smaller than m s (indicated in the figure as a vertical blue dashed line, for reference). The relation shows a slightly larger scatter than the relation. The black dots represent hundreds of individual resolved data points belonging to the rotation curves of about one hundred spiral galaxies. The black solid line , showing the no mass discrepancy case, is illustrated as a reference in both panels. The figure is re-adapted from Figure 10 in [23].
As long as the acceleration is , the mass discrepancy maintains around 1. Instead, when goes below , the mass discrepancy starts to increase. The intrinsic scatter in both the MDAR and the BTFR is minimised by the same mass-to-light ratio, consistent with the estimates from stellar population synthesis (SPS) models [21]. In fact, the MDAR can also be expressed as a relation between the mass discrepancy and (Figure 2, bottom panel), that is, the total observed acceleration, which presents a slightly larger scatter than the relation with [23]. This relation can be reproduced by replacing with in Equation (2).
A slightly different perspective with respect to the MDAR is provided by the RAR [55] (Figure 3), which links the centripetal acceleration inferred from the observed rotation curve , , with the Newtonian acceleration due to the baryons alone, [22]. The data in the (,) plane of the RAR present an even tighter relation with respect to the data in the (,) plane of the MDAR. Moreover, the (,) plane presents an advantage compared to the (,) plane, since the and quantities and their corresponding uncertainties are completely independent from each other [56].

Figure 3.
The radial acceleration relation (RAR) built from Spitzer photometry and accurate rotation curves (SPARC) galaxies. For each galaxy, a mass-to-light ratio in the 3.6 m band for the disk and the bulge equal to 0.5 and 0.7 M/L, respectively, is adopted. The black solid line represents the fit to the data with Equation (3) and the black dashed line is the relation, for reference. The only best-fit parameter, , is highlighted in the top-left corner of the panel and it is 1 consistent with the acceleration scale . The histogram and the bottom panel show the distribution of the residuals of the observed RAR from Equation (3), and its standard deviation , which quantifies the RAR observed scatter, is shown in the top-left corner of the panel. The figure is re-adapted from Figure 2 in [57].
McGaugh and coauthors [22] fitted the (,) data from 153 edge-on disk galaxies belonging to Spitzer photometry and accurate rotation curves (SPARC) catalogue [51] with the relation:
where the only free parameter m s is 1 consistent with . The errors of m s and of m s represent the random and the systematic contributions to the uncertainty, respectively. In particular, the random error represents the 1 confidence interval and the systematic error represents the 20% normalisation uncertainty due to the fact that the mass-to-light ratios of the disks and the bulges of the galaxies are kept fixed across the SPARC sample.
Assuming a disk and a bulge mass-to-light ratio of 0.5 and 0.7 M/L, respectively, which are reasonable values in the 3.6 m band, the RAR of SPARC galaxies is retrieved with an observed scatter of 0.13 dex [22]. This value closely coincides with the scatter of 0.12 dex due to the observational errors of the measured rotation curves, distances, and galaxy inclinations, and to the possible variation of the mass-to-light ratio among galaxies, which leaves little room for intrinsic scatter [22,53].
Li and collaborators [56] wanted to test whether the RAR was followed by the individual galaxies in the SPARC sample. They fitted Equation (3) to the observed RAR of the individual SPARC galaxies, finding a RAR with a smaller scatter of [0.054–0.057] dex, both by fixing to and by leaving it free to vary. Since, differently from [22], they estimated the mass-to-light ratios and marginalised over the errors on the galaxy distances and inclinations from the RAR of the single SPARC galaxies, the obtained scatter might be assimilated to the intrinsic one, rather than to the observed one.
The three relations cover a baryonic mass range of six orders of magnitude, from , correspondent to the most massive HSB spiral galaxies, to , correspondent to the dwarf and the LSB galaxies. However, the observed scatter of the RAR might increase from 0.13 dex to 0.24 dex for small due to dwarf and LSB galaxies with slowly-rising rotation curves [58], which requires further investigation.
The works of McGaugh et al. and of Kroupa et al. [59,60] might demonstrate a fundamental origin for the acceleration scale , and, thus, for the RAR, since they show a consistency of among different galaxies. The work of Li et al. [56] might suggest the same result, since fitting Equation (3) to the RAR of the individual SPARC galaxies by leaving free to vary does neither improve the nor reduce the obtained scatter with respect to the fits in which is fixed to m s. However, several works question this result. For example, Rodrigues et al. [61] estimated the parameter with Bayesian inference from 193 individual galaxies from SPARC [51] and THINGS [62,63] samples, rejecting the consistency of among the galaxies at the 10 level. The discrepancy reduces but does not disappear by removing some approximations, becoming equal to 5 [64]. The work of Zhou et al. [65] leads to a similar result. If this is the case, it would represent an important challenge for MOND (see Section 3.2). A debate about the existence or the absence of a universal is presented in [66]. Another study sees the emergence of an acceleration scale consistent with , besides from the BTFR, built from rotationally-supported galaxies, from the baryonic Faber–Jackson relation built from pressure-supported galaxies, such as elliptical galaxies and GCs, and from the baryonic Faber–Jackson relation built from galaxy clusters ([67] and references). The fact that the same acceleration scale also emerges from the dynamics of galaxy clusters, which are different from galaxies both in terms of scale and evolutionary histories, might pose an even more severe issue for CDM.
2.2. Interpretation of the Three Relations in Newtonian Gravity
The CDM paradigm does not provide a natural explanation for these three relations. Indeed, these relations correlate quantities related to the dynamics of a galaxy to its baryonic content, which is counterintuitive in a universe where the dynamics of structures is dominated by DM. The pieces of evidence that are most difficult to interpret are the small scatter, in agreement with observational uncertainties, and the lack of correlations of the residuals between the observed and the modelled relations with the galaxy properties. This phenomenology indicates a quite precise fine-tuning between dark and baryonic matter in galaxies. Moreover, the MDAR and the RAR pose a more serious issue for CDM compared to the BTFR due to their local, rather than global, nature.
The three relations resulting from semi-analytical models of galaxy formation and DM-only cosmological simulations in CDM do not completely agree with the observational data. The predicted minimum scatter of the BTFR is larger than the observed one (0.17 dex vs 0.10 dex) [68,69] and the simulated BTFR slope b is equal to 3, 8 discrepant from the value , fitted by McGaugh and coauthors [20] from the observed BTFR. However, some successful explanations for the three relations remaining within the CDM paradigm exist, even if with some issues.
Ludlow et al. [70] demonstrated that a set of galaxies resulting from the EAGLE suite of CDM hydrodynamical simulations, run with the same initial conditions but with different stellar and active galactic nuclei (AGN) feedback processes for the baryonic component, follow a RAR-like relation, independently from the considered feedback. Different feedback models make simulated galaxies moving along the RAR and not perpendicular to it, which produces a small RAR scatter dex. However, the parameter fitted with Equation (3) from the galaxies simulated in [70] results in a 70 inconsistency with m s. Moreover, measurement errors are not included in the simulated galaxies and the obtained result about the scatter should be further investigated [56]. The same consideration can be drawn for the scatter of 0.06 dex of the RAR obtained from the 32 galaxies resulting from the MUGS2 “zoom-in” hydrodynamic simulations in CDM [71]. On the other hand, Stone and Courteau [72] found that the intrinsic scatter of the stellar RAR, where only stellar mass is considered to compute the baryonic acceleration, is of dex, in agreement, despite being slightly larger, with CDM predictions. They obtained this result from PROBES, a catalogue made of more than 2500 spiral galaxies taken from six deep imaging and spectroscopic surveys. Yet, neglecting gas masses might affect the obtained result. In fact, the question of the RAR raises further complications since for small , namely for dwarf and LSB galaxies, its scatter increases [58] (see Section 2.1), and the RAR built from some galaxy samples different from SPARC shows some correlations between its residuals and certain galaxy properties [45,73].
Some hydrodynamical simulations, which are simulations that include the presence of baryons, can reproduce the slope of the BTFR [74,75]. Yet, the small scatter of the BTFR can only be explained with a quite precise balance between star formation efficiency and stellar feedback processes [48,49].
With the semi-empirical model proposed by Di Cintio and Lelli [69], the shape and the scatter of the MDAR are reproduced but this does not simultaneously account for the small scatter of ∼0.10 dex of the BTFR, which instead results in 0.17 dex.
Mayer et al. [54] used the Magneticum hydrodynamical simulation, which provides a large and representative sample of galaxies covering a large range of masses and a variety of morphologies, from to , to see whether the baryonic scaling relations (BTFR, MDAR, and RAR) were reproduced in a CDM context. The resulting BTFR, built for galaxies at different redshifts in the range of , has a slope more consistent with 3, rather than with 4, as in the observed BTFR. The MDAR and the RAR built from simulated Magneticum galaxies at redshift reproduce the observed relations (Equations (2) and (3)) with a fitted acceleration scale consistent with m s and a scatter in agreement with the observations from the SPARC sample. However, the simulated MDAR and RAR show a positive correlation between the total baryonic mass and the mass discrepancy which is not observed in SPARC data. Other CDM hydrodynamical simulations of single galaxies might indicate that the baryonic scaling relations naturally emerge in this framework as well [76,77].
It is important to note that many small-scale problems of CDM, such as too large bulges in disk galaxies, the cusp/core problem, and the too-big-to-fail problem, have been, at least partially, solved by introducing baryonic feedback mechanisms, such as outflows due to AGN and Supernovae, and, therefore, it is not so unlikely to suppose that galaxy dynamics is regulated by baryonic physics [54].
3. MOND and RG
A totally different scenario for the three scaling relations is provided by theories of modified gravity that do not imply the presence of DM. Without DM, the fine-tuning issue between the properties of dark and baryonic matters disappears. A modified gravity theory that not only describes but even predicted these scaling relations is MOND. Another theory of modified gravity that seems to account for these relations is RG. In the following subsections, I present the formulation of these two theories of gravity and how they reproduce the mentioned scaling relations.
3.1. Summary of Theories Formulation
3.1.1. MOND
In 1983, Milgrom [41,42,43] formulated MOND, a theory of gravity that mimics the effect of DM with a boost of the gravitational field compared to the Newtonian one in low-acceleration environments. MOND is a general paradigm that assumes spacetime scale-invariance when the acceleration is . Specifically, the acceleration a presents the following asymptotic values:
where is the Newtonian acceleration.
The MOND paradigm is obtained by modifying either gravity, e.g., [78] or inertia [79], where the modified-inertia version [79] was less developed. In the first nonrelativistic modified gravity version of MOND [78], the following Poisson equation was defined:
where the interpolating function , monotonic in its argument, has these two asymptotic behaviours:
For , the Newtonian Poisson equation is retrieved:
and for , we observe a boost of the gravitational field over the Newtonian one. In this regime, whereas the Newtonian field is , the MOND field is , deviating from the Newtonian inverse square law and reproducing the flat trend of the rotation curves without the presence of DM.
The MOND paradigm was also defined with other modified gravity formulations, such as QUMOND [80], where the MONDian behaviour of the gravitational field is obtained with the Poisson equation:
where is Newtonian gravitational potential. A possible form of the interpolating function is given by the “simple -function” (Equation (50) with in [23]):
with y being equal to .
3.1.2. Refracted Gravity
RG is a novel theory of modified gravity inspired by the behaviour of electrodynamics in matter that does not resort to DM [44]. RG was formulated in a nonrelativistic way by [44] and its gravitational potential obeys the modified Poisson equation:
where the gravitational permittivity mimics the DM phenomenology.
Whereas in MOND the modification of the law of gravity is regulated by an acceleration scale, in RG it is regulated by a mass density scale. The gravitational permittivity is a monotonic increasing function of the local mass density , it depends on three universal free parameters, and it presents the following asymptotic limits in the high and low-density regimes:
where the permittivity of vacuum and the critical density are two of the three free parameters of the theory.
As in MOND for , for , Equation (10) reduces to the Newtonian Poisson equation (7). When , the RG field is boosted compared to the Newtonian one thanks to the value of .
RG predicts a different behaviour for the gravitational field in the low-density environments of spherical and flattened systems. In the external regions of spherical systems, where , the gravitational field does not deviate from the inverse square law, i.e., , as in the Newtonian case, but it is boosted with respect to the Newtonian field by the inverse of the gravitational permittivity, as obtained by integrating Equation (10):
where is the system mass within the spherical radius r.
Whereas for spherical systems we still observe a Newtonian trend, in the outskirts of flattened systems the field lines are refracted toward the mid-plane of the object. This can be seen by expanding the left-hand side of Equation (10):
where the term “”, different from zero in nonspherical systems, is responsible for the focussing of the field lines. In nonspherical configurations, we thus observe an analogy with electrodynamics in matter: the gravitational field lines behave like electric field lines when they cross a dielectric medium with a nonuniform permittivity, changing both in direction and in magnitude.
This redirection effect in the low-density regions of flattened systems yields the trend for the RG gravitational field [44], where is the Newtonian field. In this regime, the RG field deviates from the Newtonian inverse square law and is subject to a boost that in Newtonian gravity is obtained with the presence of DM. This limit also coincides with the MOND asymptotic behaviour for (see Equation (4)) and it suggests that the ability of MOND in describing galaxy dynamics is shared by RG, as demonstrated in [45]. According to Equation (13), the flatter the system, the larger the boost of the gravitational field, and, thus, the larger the mass discrepancy, as interpreted in Newtonian theory. Figure 4 summarises the analogies and the differences between Newtonian (top panels) and RG (bottom panels) gravitational fields for flat (left panels) and spherical (right panels) systems.
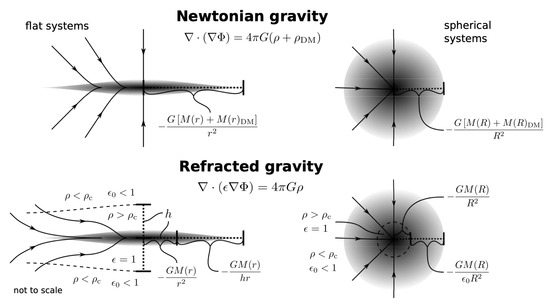
Figure 4.
Comparison between the behaviour of Newtonian (top panels) and refracted gravity (RG) (bottom panels) gravitational fields for flat (left panels) and spherical (right panels) systems. The figure is taken from Figure 16 in [44].
The behaviour of the RG gravitational field in the low-density regime is comparable to the behaviour of the MOND gravitational field in the low-acceleration regime only for nonspherical configurations. In the low-acceleration regions of spherical systems, MOND field is , as in the low-acceleration regions of flattened systems, whereas, in the low-density regions of spherical systems, the R-dependence of RG field remains Newtonian. Moreover, RG and MOND fields also present a difference for flattened systems. As we can see in the left panels of Figure 4, the refraction effect of the RG field lines in a flattened object already begins where the local density is still above and, in that region, the RG field already begins to be boosted compared to Newtonian one. Instead, MOND modification with respect to the Newtonian field only appears in regions where .
In all the analyses of galaxy dynamics performed with RG [44,45,46], the following smooth step function of the gravitational permittivity was adopted:
where the power index Q is the third free parameter of the theory and it regulates the transition speed between Newtonian and RG regimes (the larger its value the steeper the transition).
Being that the modification of the law of gravity is dependent on a scalar quantity, the mass density of baryonic matter1, it was possible to build a covariant formulation of RG [47] without the challenges encountered in defining a relativistic extension of MOND [78,81,82,83,84]. On the other hand, a modification of the law of gravity that is dependent on a density scale might appear not so intuitive, given that the majority of the pieces of evidence on galaxy scale rather see the emergence of an acceleration scale, , below which a departure from Newtonian gravity is observed. However, the acceleration scale also seems to appear in RG, from the weak field limit (WFL) of covariant refracted gravity (CRG). This point will be better addressed in Section 4 and Section 6.
3.2. Interpretation of the Three Scaling Relations in MOND and RG
The fact that the acceleration scale emerges from the three scaling relations seems to identify MOND as the most natural solution to explain them. MOND not only reproduces but actually predicted the three relations with a zero intrinsic scatter many years before they were observed, besides other pieces of evidence on the galaxy scale. It is the only theory of gravity that has this peculiar feature. Already in its first formulation of 1983 [42], Milgrom concludes that “The relation should hold exactly”, where is the asymptotic flat velocity of the rotation curve, M is the total baryonic mass of the galaxy (the total mass in MOND), and the mentioned equation coincides with the BTFR (Equation (1)). The acceleration scale is set by its normalisation. Later observations confirmed this prediction (see Section 2.1). In his first works of 1983, Milgrom calculated in several independent ways the value of [42], which turned out to be consistent with the value observed years after from the scaling relations. Moreover, Milgrom predicted that the BTFR does not depend on the galaxy type or on any other galaxy property [42], in agreement with the future observations.
The condition on the acceleration , where the departure from Newtonian dynamics begins to be observed, can be translated in a condition on the surface mass density, , where [23]. This implies a relation between the mass discrepancy in galaxies and the acceleration due to baryons, which is observed to hold from HSB to LSB galaxies with a very narrow intrinsic scatter and no dependency on galaxy properties [23].
Concerning the RAR, MOND predicted this relation with a null intrinsic scatter only for the modified inertia version of MOND and for circular orbits [79]. For the modified gravity versions of MOND, the RAR is recovered with zero intrinsic scatter only for spherical systems, whereas, for other systems morphologies, it is retrieved with a very small intrinsic scatter, in agreement with the observations [53,78,85].
A work of Eriksen et al. [86] seems to challenge MOND in modelling the RAR. Specifically, MOND might present a “cusp/core like” issue, different from the classical cusp/core problem of CDM. This issue is particularly relevant for the modified inertia version of MOND. Moreover, by fitting the RAR relation (Equation (3)), in both modified gravity and modified inertia versions of MOND, from the observational data of SPARC galaxies, the best fit acceleration scale might result inconsistent among different galaxies.
Matsakos and Diaferio [44] demonstrated that RG reproduces both the BTFR and the MDAR. In Section 3.1.2, I showed that the asymptotic limit for the gravitational field in low-density environments of nonspherical systems is , as in MOND, in the low-acceleration regime. In fact, Matsakos and Diaferio [44] write this asymptotic limit as:
where b is an acceleration scale that can be expressed as:
and is the height from the disk plane where the condition is reached. In a simplified formulation for RG (SRG), whose conclusions can be extended to a more generic RG framework, the volume within the disk planes and is where the redirection effect of the field lines occurs.
In the low-density regime, the condition on the gravitational field given by Equation (15) can be translated in a condition on the rotation velocity:
being . Inverting the above equation,
we obtain the BTFR (Equation (1)) with the correct slope. To make the normalisation of Equation (18) in agreement with the normalisation of the observed BTFR, the acceleration b has to coincide with , which sets a condition on the planes that depends on the galaxy baryonic mass.
Matsakos and Diaferio [44] plotted the points from real data [87] (black dots in Figure 5) and from some disk galaxy models of star- and gas-dominated disk galaxies, with typical values of the central surface mass density, , and of the disk scale-length, (open circles and squares in Figure 5). Both sets of points follow relation (18) (black solid line in Figure 5).
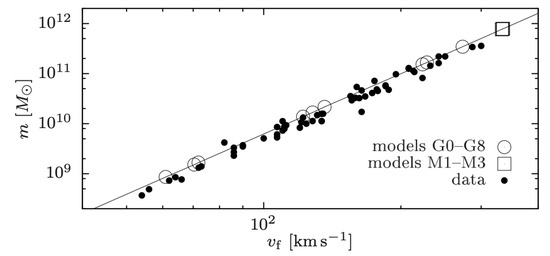
Figure 5.
The BTFR built in RG using Equation (18) (black solid line) and from the observational data of [87] (black dots) and some models of star- and gas-dominated disk galaxies (open circles and squares). The RG BTFR properly describes both the data and the model points. The figure is re-adapted from Figure 9 in [44].
RG also recovers the MDAR of the galaxies (Figure 6). Matsakos and Diaferio [44] plotted the squared ratio between the rotation velocity predicted by the SRG framework and the Newtonian theory ( and in Figure 6) against the Newtonian and the SRG accelerations ( and in Figure 6) for the same models used to build the BTFR and for a set of point masses having M, with , settling between two parallel planes with . The models are plotted together with a set of data points, taken from [21,23], and they properly reproduce the data, both in the and in the planes. The gas-rich galaxies models (where the gas represents more than 20% of the total baryonic mass) have a smaller and they distribute in the leftmost part of the MDAR, in agreement with MOND prediction according to which a larger mass discrepancy is observed when . On the contrary, the star-rich galaxies curves distribute on the rightmost part of the MDAR.

Figure 6.
The MDAR built in RG as the squared ratio between the SRG and the Newtonian speeds, and , respectively, as a function of the Newtonian (top panel) and the SRG (bottom panel) accelerations, and , respectively, for the same set of models represented as open circles and squares in Figure 5 (black solid lines) and for a set of point masses having M, with (black dotted lines). The solid and dotted lines appear almost indistinguishable in the (,) and (,) planes. The gas-rich galaxies models appear in the leftmost part of the plots, indicating that they are always in the “mass discrepancy regime”. The curves are plotted together with observational measurements from [21,23] (black dots), showing that they properly reproduce the data. The black dashed line , showing the no mass discrepancy case, and the blue dashed lines m s and m s are illustrated as a reference in both panels. The figure is re-adapted from Figure 10 in [44].
Cesare et al. [45] built the RAR of 30 galaxies from the DiskMass Survey (DMS) [88], adopting the general RG framework and the QUMOND formulation of MOND (blue and green solid lines in Figure 7). They modelled with RG, at the same time, the rotation curve and the vertical velocity dispersion profile of each DMS galaxy, obtaining mass-to-light ratios consistent with SPS models, disk scale heights in agreement with the observations of edge-on galaxies, and RG parameters consistent among the different galaxies, suggesting their universality. To build the RG acceleration, they numerically solved the RG Poisson equation (Equation (10)), adopting the mass-to-light ratios, the disk-scale heights, and the three RG parameters estimated from the kinematic profiles of each DMS galaxy. To compute the QUMOND acceleration, they numerically solved the QUMOND Poisson equation (Equation (8)) with the same mass-to-light ratios and disk scale heights found in RG, since they are fully in agreement with the parameters found by Angus et al. [89] by performing the same analysis of the dynamics of DMS galaxies in QUMOND. The Newtonian acceleration, , was calculated by solving the Newtonian Poisson equation (Equation (7)) with the same mass-to-light ratios used to compute the RG and QUMOND accelerations, being in agreement with SPS models, and with disk-scale heights derived from the scale relation between the disk-scale lengths and heights:
estimated from 60 edge-on late-type galaxies [45,90].
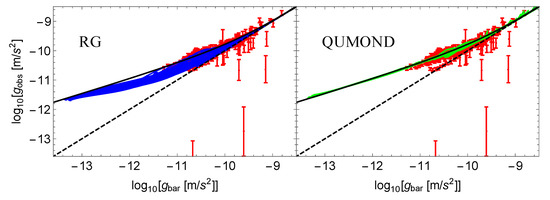
Figure 7.
The RAR built in RG (left panel, blue solid lines) and in QUMOND (right panel, green solid lines) for DMS galaxies. The RG and QUMOND models are superimposed onto the observed RAR of DMS galaxies (red dots with error bars). Equation (3) (black solid line) and the line (black dashed line) are shown as a reference. The figure is taken from Figure 11 in [45]. Credit: Cesare V., Diaferio A., Matsakos T., and Angus G., A&A, 637, A70, 2020, reproduced with permission © ESO.
RG properly reproduces the asymptotic limits of the observed RAR (Equation (3), black solid line in Figure 7) but it tends to underestimate relation (3) at low , even if it generally interpolates the observational data (red dots with error bars in Figure 7). Instead, QUMOND reproduces the RAR with the correct shape. This can be interpreted by the fact that RG might attribute more luminous mass than QUMOND.
A more serious problem for RG is that the RAR presents a too large intrinsic scatter (0.11 dex, whereas the possible intrinsic scatter of the RAR found by Li et al. [56] for SPARC galaxies is 0.057 dex) and some correlations between the residuals from Equation (3) and certain galaxy properties, in disagreement with the observations [22,53]. However, this question has to be further deepened by building the RAR in RG for a larger sample of disk galaxies with more accurate rotation curves, such as SPARC, before concluding that this is due to an issue of RG theory. Indeed, the RAR of DMS data also shows some correlations between the residuals and some galaxy properties, which might not be observed in the SPARC sample and suggests that the DMS could not be the most suitable sample where to investigate the RAR.
In contrast, the RAR curves computed in QUMOND, very neatly distribute around Equation (3) with an intrinsic scatter of 0.017 dex. This is consistent with expectations, since QUMOND is a modified gravity version of MOND, and, thus, it does not provide a RAR with zero intrinsic scatter for nonspherical systems as disk galaxies [78]. Moreover, QUMOND RAR also presents correlations between its residuals and some galaxy properties, again in agreement with the fact that, in this case, the scatter of the RAR is not equal to zero and which might further suggest that the DMS sample was not the most suitable to investigate the RAR.
4. Possible Interpretations for an Intriguing Acceleration Scale
If the observed DM-baryons scaling relations might appear not so intuitive in the CDM context, a piece of evidence even more difficult to interpret in this framework is the emergence of an acceleration scale, , from the three relations. However, this acceleration scale seems to be retrieved in the CDM model as well, for example, from the MDAR and the RAR built from the simulated galaxies in the Magneticum simulation at [54]. These relations were fitted with Equations (2) and (3), obtaining an consistent with m s [54] (see Section 2.2). Mayer et al. [54] also found that Magneticum galaxies followed a MDAR (Equation (2)) and a RAR (Equation (3)) relation at higher redshifts but with a fitted substantially different. Specifically, decreases for decreasing redshift, that is, in the more recent Universe. This trend means that the mass discrepancy decreases, and, thus, galaxies become more baryons-dominated, as cosmic time advances, and this can be explained by the progressive cooling of the gas during time.
Mayer et al. [54] tried to assess whether the relation observed in simulated Magneticum galaxies is consistent or not with MOND predictions, which is not trivial since MOND is not formulated as a relativistic theory. Milgrom [41] pointed out that , which might suggest that the redshift dependence of is similar to the one of the Hubble parameter . This would imply the following relation:
where the fraction of baryonic matter and of the cosmological constant with respect to the total mass-energy budget of the Universe are put equal to and , following [91], and is the value of the acceleration scale m s observed today. However, this relation is too steep compared to the relation observed in Magneticum simulation and it also seems to disagree with observational data. More realistic predictions of the relation in MOND might be provided by relativistic theories that have MOND as a limiting case in a nonrelativistic regime, such as tensor-vector-scalar gravity (TeVeS) [92] and covariant emergent gravity (CEG) [93]. TeVeS might suggest that varies on timescales larger than the Hubble time, even if, according to [91], this change is also possible on cosmological timescales. Anyway, the relation predicted by TeVeS is not consistent with the one observed in [54] from Magneticum galaxies. CEG predicts an relation dependent on the variation of the size of the cosmological horizon [94]. However, the redshift dependence of this relation is smaller than the one observed from the galaxies in the MUGS2 simulated sample in CDM [71].
An even more striking coincidence is given by the near equality between emerging from the local universe, that is, from galactic dynamics, and from cosmology. Given the two acceleration cosmological parameters [95]:
and
where and are the present values of the Hubble parameter and of the cosmological constant, the following equivalence subsists:
This arises an outstanding coincidence that needs careful investigation since is assumed to be constant across cosmic time and is the value at the present epoch of the Hubble parameter, , that varies across cosmic time.
Some interpretations of the relation in the MOND context were provided by [23,95,96,97]. In the most recent work among these, Milgrom [95] re-wrote Equation (23) in terms of length or mass, introducing the “MOND length”, , and the “MOND mass”, :
and
where is the Hubble radius, is the de Sitter radius related to , and and are the total mass of the Universe enclosed within and , respectively.
Equation (23) emerges in some particular effective-field, relativistic extensions of MOND, where MOND is retrieved in their WFL. In these MOND relativistic formulations, an additional Lagrangian term,
is added to the GR Einstein–Hilbert (EH) Lagrangian density:
where R is the Riemann curvature scalar. In Equation (26), l is a length constant, needed to provide the Lagrangian with the correct dimension, is a dimensionless function, and Q has the dimension of a length and it is built from the first space-time derivatives of the gravitational degrees of freedom [95]. Some examples of MOND relativistic extensions where a Lagrangian-like term as Equation (26) is included are the MOND adaptations of the Einstein–Aether theories [98], bimetric MOND (BIMOND) [99], bimetric massive gravity [100], and the noncovariant theory presented in [101].
If we include the cosmological constant term in the EH Lagrangian, Equation (27) becomes:
Therefore, we can see from Equation (26) that any constant term added to , which has to be of the order of unity due to naturalness, can be identified with a cosmological constant term of this kind:
that, combined with Equation (24), gives the -cosmology coincidence given by Equations (22) and (23) [95]. It is important to point out that this result is not obtained by adding a cosmological constant term, , “ad-hoc” to the Lagrangian, verifying a posteriori that , but by the presence of the two l-terms in the Lagrangian (26), appearing inside and outside for dimensional reasons and playing different roles. This suggests that the two l-terms derive from the same underlying physics, whereas a constant added “ad-hoc” might have suggested a different physical origin.
Milgrom [95] also suggested that the -cosmology connection can also emerge from a scenario in which the Universe is seen as a sphere-like submanifold, that is a brane, of radius or , embedded in a space-time with higher dimension [102]. The dynamics of the submanifold is the one we observe, that is the MOND one, and it emerges from the dynamics of the higher dimension space-time. In fact, the acceleration scale is seen as an emergent acceleration constant in a brane scenario. Further details can be found in [102].
In RG, where the transition between Newtonian and modified gravity regimes is regulated by a density scale , rather than by an acceleration scale , the -cosmology relation might appear harder to interpret. However, Sanna et al. [47] recently formulated a covariant extension of RG, where seems to emerge from the WFL of the theory and the - coincidence might be explained.
CRG is a scalar-tensor theory that introduces a single scalar field , nonminimally coupled to the metric, that mimics both the DM effect on galaxy scale and the DE effect on cosmic scale, namely, the accelerated expansion of the Universe. Therefore, CRG belongs to the restricted class of modified gravity models that invoke a unified dark sector, that is, that attribute the phenomenologies of DM and DE to a single cause.
CRG is derived from a general scalar-tensor action:
(see [47] for the explanation of the symbols). In CRG, the general differentiable function of the scalar field is:
and the potential has a self-interaction form:
where is a constant parameter. With the definitions adopted for and , the CRG equations below are obtained:
and
CRG is based on a chameleon screening mechanism, e.g., [103], that is, in regions where the Newtonian WFL holds, the extra degree of freedom of the scalar field mediates a fifth force which can be detected, whereas, in high-density regions, this degree of freedom is screened. This behaviour is also what we expect from the RG gravitational permittivity , which, therefore, might be related to .
The WFL of CRG holds the following equation:
which reduces to RG Poisson equation (10) if the scalar field is twice the permittivity, . This is an important result since it confirms that the scalar field is associated with the phenomenology mimicked by the gravitational permittivity, that is of DM on galaxy scale. Instead, the Newtonian Poisson equation is recovered for a constant scalar field .
Calculating the CRG gravitational field in the WFL from Equation (35) for a spherical source with density , monotonically decreasing with r, immersed in a homogeneous background with constant density , Sanna et al. [47] found that an acceleration scale can be set. At large distances from the source, the scalar and the gravitational fields, and , are linked by the relation:
where is . The acceleration scale:
is set from Equation (36). In regions where , the gravitational field has a similar r-dependence as the gravitational field calculated close to the source, that is, the Newtonian field. Instead, for , it departs from the Newtonian one. From this result, the acceleration recalls since it demarcates Newtonian from modified gravity regimes. Solving the CRG field equations for a homogeneous and isotropic universe with flat curvature, Sanna et al. [47] found that , and, thus, plays the role of the cosmological constant in CDM. In the limit obtained at large distances from the source,
Equation (37) becomes:
Using the observed value of at the present epoch, Equation (39) holds m s, fully in agreement with the value of , and it also provides the relation , which is the observed -cosmology connection.
The difference between and consists in the fact that, whereas is a constant independent of the gravitational field source, , depends on the source, given Equation (37), even if for large distances from the source this dependence drops since . Future investigations have to verify whether by repeating the calculations for a generic case and not for a specific source, the connection between and continues to hold in a real Universe.
Given the connection between and the cosmological constant , it can be concluded that the scalar field is also responsible for the accelerated expansion of the Universe, that is for the DE phenomenology, besides the DM phenomenology on galaxy scale, given its connection to the gravitational permittivity . The fact that the DM and the DE effects are described by a single scalar field might provide an advantage for CRG since the idea of a unified dark sector is theoretically justified. The relation itself represents one possible piece of evidence for the unification of the dark sector. Moreover, Martin Kunz claims that gravity can only probe the total energy-momentum tensor of the Universe, implying a degeneracy between the dark components, which further goes in this direction [104,105].
CRG is not the only theory that provides a single explanation for the DM and DE phenomenologies. Among the other theories that invoke a unified dark sector we can mention: (I) Conformal gravity [106,107,108]; (II) the models of Martin Kunz [104,105]; (III) the quartessence model [109,110,111] (known also as Unified Dark Matter or Unified Dark Energy), which includes the generalised Chaplygin gas [112,113,114], the K-essence [115,116], the fast transition models [117,118], and other models that assume the presence of condensates [119,120,121]; (IV) theories, e.g., [122]; (V) mimetic gravity [123]; (VI) a class of models where the cosmic acceleration emerges from the interactions between DM and baryons [124]; (VII) the unified superfluid dark sector [111]; (VIII) the fuzzy dark fluid [125].
Among these models, Conformal gravity is one of the first to invoke the unified dark sector, even if it might present some problems in modelling the rotation curves of galaxies and the gravitational lensing effects [108]. Two recent and novel models invoking the unified dark sector are the unified superfluid dark sector [111] and the fuzzy dark fluid [125]. In the unified superfluid dark sector, the Universe is dominated by a unique DM superfluid made of axion-like particles, with two energy states having an energy gap smaller than that can interact with each other. These interactions at the microscopic level change the macroscopic behaviour of the fluid, producing an accelerated expansion of the Universe that mimics DE. Besides the effect of DE, this fluid can also mimic the galaxy phenomenology due to DM without facing some problems encountered by others of these models, such as superluminal sound speeds or the need for a UV completion.
In the fuzzy dark fluid model, besides the behaviours of DM and DE, a single scalar field also mimics the behaviour of inflation, by assuming a nonminimal coupling to the gravitational field, a Mexican hat-shape potential, and a spontaneous symmetry breaking before the inflationary period. This peculiar feature of a unique description of the DM, DE, and inflation phenomenologies is also shared by mimetic gravity [123].
5. Dwarf Galaxies and Globular Clusters
The flatness of the rotation curves of disk galaxies and the three scaling relations, BTFR, MDAR, and RAR, observed on the galaxy scale, are only some of the predictions of MOND. MOND predicted additional pieces of evidence about galactic dynamics before they were observed. Among them, the dynamics of LSB galaxies is worth mentioning.
As already mentioned in the Introduction (Section 1), HSB disk galaxies are dominated by stellar mass in their central regions, where their rotation curves are steeply rising toward their asymptotic values. Instead, the dynamics of LSB galaxies, generally dwarf and dSph galaxies, is observed to be different. Their rotation curves are slowly rising toward their flat region and they appear to be DM-dominated even in their innermost regions. Therefore, the maximum-disk hypothesis cannot be applied as for HSB galaxies [31,32]. Specifically, dwarf galaxies are among the known darkest galaxies observed: they have an inner velocity dispersion km s, an order of magnitude larger than the velocity dispersion km s expected for systems having the same luminosity and scale radius (∼100 pc) at equilibrium [33]. Their luminosity varies in the range ∼[, ] L [126,127] but their velocity dispersions are similar, which might indicate that they are dominated by a similar DM distribution [19,128].
This different shape of the rotation curves of HSB and LSB galaxies reflects in one of the small-scale issues of the CDM model, the cusp/core problem. Indeed, steeply-rising rotation curves can be modelled by a Navarro Frenk White (NFW) DM density profile [129,130], cuspy in its innermost part and predicted by collisionless N-body simulations, whereas slowly-rising rotation curves can only be reproduced by a cored DM density profile, which might be accounted for in CDM only introducing baryonic feedback and tidal effects [131].
The different dynamic properties of these two categories of galaxies were instead predicted by MOND some years before they were observed [42]. Milgrom [42] predicted that dwarf galaxies would have shown strong deviations from standard gravity and in particular that when the velocity dispersion data of dwarf galaxies had been available, these galaxies would have presented a mass discrepancy equal to 10 or larger, depending on their distance from the Milky Way, when modelled in standard gravity.
As already anticipated in Section 3.2, the MOND acceleration scale can be translated on a surface mass density scale [23,42]. Small surface mass densities also indicate small surface brightnesses and Milgrom predicted that LSB galaxies would have shown stronger effects of the modification of the law of gravity with respect to the Newtonian one. The effect of gravity modification already appears in the innermost radii of these galaxies. Milgrom [42] predicted that a transition radius between the standard and the modified gravity regimes, dependent on the local value of the rotation velocity V, would have been set when the equality occurs. In particular, where , the local mass-to-light ratio of the galaxy should not indicate the presence of a hidden mass, and where starts to go below , the local should begin to rapidly increase. The smaller the average surface brightness of the galaxy, the smaller the in units of the galaxy scale length . A similar result was also found by [44] for RG (see the top panel of Figure 10 of [44]). Moreover, Milgrom [42] also predicted a correlation between the average surface mass density or surface brightness and the steepness of the rotation curve in reaching its asymptotic limit, which states that galaxies with small surface densities show a slowly-rising rotation curve and vice-versa, as observed by successive measurements.
A possible challenge for MOND on galaxy scale is instead provided by the internal dynamics of GCs, which have baryonic masses similar to the ones of LSB galaxies, settling in the outermost regions of the Milky Way. In those regions, the background acceleration is much smaller than and the external field effect is negligible. Therefore, we expect that their stellar velocity dispersion profiles present a MONDian behaviour but this is not the case. Newtonian theory without the presence of a DM halo can better fit these kinematic profiles than MOND, whose predicted velocity dispersions can exceed the Newtonian ones also by a factor of ∼3 [34,35,36,37,38,39,40]. Relevant examples for this result are provided by the GCs NGC 2419, Palomar 14, and Palomar 4 [35,36,38,39,40]. Yet, this tension between MOND predictions and measurements might not indicate an issue of the theory but it might be due to inaccurate data or approximate modelling.
Concerning the former case, inaccurate data can derive from low-resolution spectroscopy and from errors on GCs distances larger than 10% of their values (e.g., [37]). The Gaia mission, which provides the parallaxes of the stars from which to derive their distances, accurate at the arcsec level, might represent a turning point in this sense [132]. Concerning the latter case, most of the adopted models assume spherical symmetry, absence of rotation, and orbital isotropy. Whereas the first two assumptions can be justified by observations, orbital anisotropies in GCs are predicted by N-body simulations [133] and including strong radial anisotropies in the modelling can reconcile MOND expectations with the observed velocity dispersions. Further studies with high-precision measurements, which allow us to neatly disentangle the effect of a strong radial anisotropy and the adopted theory of gravity, need to be performed [37]. Moreover, the question might be even harder to understand, since some theories of formation and evolution of GCs predict the presence of DM in these objects and its observational evidence is debated [134,135,136].
Instead, RG theory provides a more natural solution for the different dynamic properties of LSB, dwarf, and dSph galaxies and GCs. As anticipated in Section 3.1.2, RG predicts a different shape for the gravitational field lines in flat and spherical systems. Specifically, whereas in spherical systems the gravitational field lines always maintain a radial direction following the Newtonian trend and become enhanced compared to the Newtonian field in the external regions of the systems, where the density goes below the critical value , in nonspherical configurations we observe a refraction of the field lines toward the equatorial plane of the object and the deviations from Newtonian gravity already begin to appear in regions where . In particular, the flatter the system the stronger the redirection effect of the field lines and the larger the mass discrepancy if interpreted in a Newtonian framework. This can intuitively explain the diverse dynamic behaviour of LSB, dwarf, and dSph galaxies and GCs, the former generally having a flatter shape and the latter a more spherical one [44].
This RG prediction is also in agreement with a claimed positive correlation between the elliptical galaxies’ ellipticities and their DM content [137,138]. As mentioned in Section 1 and Section 3.2, Cesare et al. [45,46] demonstrated that RG can model the dynamics of flat (30 disk galaxies from the DMS) and spherical (three E0 galaxies from the SLUGGS survey) systems. The modelling of the two classes of systems is obtained with statistically consistent parameters, showing that the gravitational permittivity is independent of the shape of the considered system. To perform a more robust test of the theory, Cesare et al. [45] estimated the three RG parameters both from each individual DMS galaxy, simultaneously modelling its rotation curve and vertical velocity dispersion profile, and from the kinematic profiles of the entire DMS sample considered at the same time. The two sets of values are consistent within 2. The average Q and derived from the simultaneous modelling of the velocity dispersions of the stars and the blue and red GCs in each E0 galaxy are consistent within 1 with the Q and averaged from the values obtained from each DMS galaxy, whereas the parameters are still in agreement within 3. The average Q and from the E0 galaxies are also consistent, within 3, with the unique combination of Q and derived from the entire DMS sample. Instead, the tension increases to 14.8 for the parameter. However, this does not necessarily indicate an issue for RG. This might be due to the approximate procedure with which the single combination of RG parameters is estimated from the entire DMS sample, which results in error bars of the parameter that are much smaller than the error bars of the average of DMS galaxies. Moreover, it might be due to incorrect modelling of the dynamics of elliptical galaxies, which are treated as isolated systems without net rotation, or to a wrong assumption for the gravitational permittivity functional form [46]. A review of both the works about disk and elliptical galaxies in RG is presented in [139].
6. Discussion and Conclusions
The most investigated cosmological model is CDM, which assumes the validity of GR and the inclusion of two dark components, DE and DM, besides baryonic matter, which only represents the ∼5% of the mass-energy budget of the Universe. The CDM paradigm reconciles with the majority of the observations, from the largest to the smallest scales. However, the results of the detection, through direct, indirect, or collider experiments, of the most investigated DM candidate, the weakly interacting massive particles (WIMPs), are still under debate [140]. Moreover, the nature of DE is still unknown. Future experiments, such as Euclid, might shed light on its nature.
Furthermore, the CDM model presents some issues, both on large and on small scales. Particularly relevant are the problems observed on the galaxy scale, such as some remarkable coincidences that can hardly be explained by the stochastic merging process of structure formation predicted by CDM, unless precise fine-tuning between DM and baryonic processes is invoked. Among these coincidences, three scaling relations between dark and baryonic matters in galaxies, the BTFR, the MDAR, and the RAR, that neatly quantify the mass discrepancy on galaxy scale, are observed and they see the appearance of the acceleration scale m s. The results of Mayer et al. [54] from the galaxies in the Magneticum simulation can reproduce in CDM the emergence of this acceleration scale at redshift . They also predicted an evolution of with redshift, where decreases with increasing redshift, which still has to be confirmed. Intriguingly, the acceleration scale presents another coincidence, being its value consistent with the combination of some cosmological parameters: . In particular, the relation links a quantity observed on galaxy scale and the parameter that regulates the Universe accelerated expansion, which suggests a unification of the two dark sectors and connects the physics on small and large scales. This is even less intuitive to interpret in a CDM framework.
On the other hand, MOND theory not only reproduces but even predicted, with either a small or a null intrinsic scatter, these three relations, assuming a modification of the law of gravity for accelerations smaller than . The value of was estimated by Milgrom [42] in several independent ways before it emerged from observations and it turned out to be consistent with the value of observed some years later from the DM-baryons scaling relations. MOND predicted other pieces of evidence on the galaxy scale, such as the fact that LSB galaxies appear “darker” and with more slowly-rising rotation curves than HSB galaxies. However, it presents some issues in describing the dynamics of GCs residing in the Milky Way outskirts, which present a Newtonian behaviour even if the background acceleration is below . MOND also reproduces the relation, as presented in several studies [23,95,96,97].
A more recent theory of modified gravity, RG, formulated in a nonrelativistic way by Matsakos and Diaferio in 2016 [44], might shed further light on galaxy dynamics. RG has already presented some encouraging results on galaxy scale, reproducing the dynamics of both flat and spherical systems with a consistent set of RG parameters [45,46,139], the BTFR, and the MDAR of real and simulated galaxies. It also models the RAR of DMS galaxies, even if with some issues, which requires further investigations to assess whether these problems are due to the chosen galaxy sample or to RG theory. RG predicts a different shape for the gravitational field lines in spherical and nonspherical systems. Specifically, the field lines remain radial in spherical systems and become increasingly refracted toward the equatorial plane of increasingly flat systems. The refraction of the field lines produces a boost of the gravitational field that mimics the presence of a DM halo in Newtonian gravity. This means that an increasingly flat system is increasingly DM-dominated, if interpreted in the Newtonian context. With this feature, RG naturally due to the different dynamic properties of LSB galaxies and GCs to their diverse shape, the former generally being flatter and the latter nearly spherical. This system morphology–mass discrepancy relation predicted by RG is also consistent with the possible ellipticity–total M/L correlation of elliptical galaxies estimated by Deur [137,138].
Despite the promising results shown by different theories, we are still far from the answer for a final scenario of the cosmological model. Given the emergence of from several pieces of evidence on galaxy scale, MOND might seem the most intuitive solution. However, it presents several issues on a larger scale. For example, it can reduce but not eliminate all the mass discrepancy in galaxy clusters [141,142,143]. Moreover, the building of a covariant version of MOND seems to appear challenging. Some attempts at formulating this relativistic extension failed to describe the features of gravitational lenses, provided superluminal speeds, or were not in agreement with the post-Newtonian tests of General Relativity [78,81,82]. A relativistic extension of MOND is TeVeS [92], which solved some of these problems but was unable to reproduce cosmological pieces of evidence, such as the CMB or the matter power spectra [83,84]. However, further studies about covariant MOND are still ongoing and some recent results might look promising [144,145].
RG might provide an alternative solution. Despite being based on a density scale-dependent modification of the law of gravity, which is not what observations might suggest, a covariant formulation of RG, CRG, seems to be promising, given the results of [47] that also show that the acceleration scale might emerge from the WFL of the theory. In particular, building a relativistic extension of RG was possible since the modification of the law of gravity depends on a scalar quantity, in this case the density, whereas for MOND it depends on a vector quantity, namely, the acceleration. CRG describes the DM and DE phenomenologies with a single scalar field, suggesting a unified dark sector, and retrieves the relation, which is a remarkable result.
However, further studies have to be performed to validate RG. A more accurate study of elliptical galaxies, removing the assumptions adopted in [46] and considering a larger sample with different ellipticities and extended kinematic profiles (e.g., SLUGGS [146] and ePN.S [147] surveys), have to be made to better assess if RG can reproduce the dynamics of these systems. The fact that RG can account for the different dynamics of dwarf galaxies and GCs is only a hypothesis that should be tested on real samples, such as the dwarf galaxies surrounding the Milky Way, e.g., [148] and belonging to the LITTLE THINGS survey [149], and the GCs settling in the Milky Way outskirts, in particular NGC 2419, Palomar 14, and Palomar 4, e.g., [35,36,39,40]. Moreover, RG should be tested on larger scales, to verify whether it can describe the dynamics of galaxy clusters. Some preliminary encouraging results in this sense were obtained by Matsakos and Diaferio [44] but these studies have to be extended to larger samples (e.g., CIRS and HeCS [150,151]) and with less approximate modelling. At last, the studies on cosmological scales have to be completed with CRG.
MOND and RG are only two possible theories of modified gravity but many other theories that might provide a solution for small- and large-scale problems have been built. Another theory that is worth mentioning is scalar-vector-tensor gravity (SVTG), better known as modified gravity (MOG) [152]. Whereas the modification of the law of gravity in MOND and RG depends on an acceleration and on a density scale, respectively, in MOG it depends on a length scale. MOG is a theory of gravity built in a covariant way that introduces a scalar, a tensor, and a massive vector field, whose contributions are added to the classical EH action. MOG assumes that the gravitational constant G, the coupling constant and the mass of the vector field, and the cosmological constant are dynamical scalar fields which vary with space and time [152].
MOG has two progenitor theories, nonsymmetric gravity theory (NGT) [153] and metric-skew-tensor gravity (MSTG) theory [154], which produce the same modified acceleration law as MOG for weak gravitational fields. NGT, MSTG, and MOG presented several encouraging results on different scales. They can reproduce solar system and terrestrial gravitational tests, the observations of the binary pulsar PSR 1913+16 [155], the rotation curves of both HSB and LSB galaxies and the BTFR [154,155,156], the dynamics of an elliptical galaxy [155], the velocity dispersion of Milky Way (MW) satellite galaxies [157], the internal velocity dispersion profiles of GCs [158], the cluster lensing [154], the mass profiles of galaxy clusters derived from X-ray emitting gas [159] and their thermal profiles [156], the Bullet cluster [160], and several cosmological observations, such as the CMB temperature anisotropy, the galaxy power spectrum, and the supernova luminosity-distance measurements [156,161,162,163]. A more recent work seems to demonstrate that MOG is able to reproduce also the RAR of 153 spiral galaxies from SPARC sample [164].
The dynamics of GCs, of galaxy clusters, and of systems at sufficiently large distances from their centres provide an important test to distinguish among MOG, MOND, and RG. MOG reproduces the internal velocity dispersions of GCs around the MW, independently from their distance from the Galaxy centre, consistently with Newtonian expectations. This is not the case for MOND, which predicts a MONDian behaviour for the dynamics of GCs sufficiently distant from the MW centre, such that the background acceleration goes below . However, observations suggest a Newtonian behaviour also for these GCs, where MOND predictions may exceed the measured velocity dispersions also by a factor of ∼3, e.g., [35]. Moreover, as already specified, whereas MOG can reproduce the masses of galaxy clusters, and also RG is likely to do this, MOND can only retrieve them with an additional DM component.
To distinguish among MOG, MOND, and CRG, it would be ideal to have the kinematic data of different systems at large distances from their centres. Indeed, at these distances, MOG predicts a Newtonian keplerian trend of the rotation velocity, i.e., , consistent with the results of [165] and with the gravitational lensing results of [166]. However, this trend is not predicted by MOND and RG (see Section 3).
Both MOG and RG, also with its covariant extension CRG, reproduce pieces of evidence on different scales. However, some fundamental features distinguish MOG from CRG. Whereas MOG introduces a scalar, a tensor, and a vector fields, CRG only includes a single scalar field. Moreover, whereas the CRG scalar field is responsible for both the DM and the DE phenomenologies, MOG attributes the two dark sectors to two different causes and it introduces a cosmological constant, dependent on space and time, to mimic DE effect. Concerning the relation, whereas CRG retrieves it as a consequence, MOG imposes it [155] to constrain some MOG parameters (, , and ). Several works, e.g., [155,156], demonstrate that MOG can model different pieces of evidence with a minimal number or with no free parameters. The results of Cesare et al. [45,46] show that a universal combination of RG free parameters might exist. Additional studies have to be performed to verify if the phenomenology at several scales in the Universe can be modelled with this unique combination of RG free parameters. Generally, further tests have to assess which of the three theories of modified gravity, MOND, RG, or MOG, better describe the pieces of evidence on different scales.
To conclude, the correct cosmological model might, at last, be CDM and further baryonic processes might still be discovered to properly reconcile the theory with all the observed coincidences on the galaxy scale.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
I sincerely thank the four referees whose suggestions and corrections improved my review. Part of this work is the result of my Ph. D. activity at the Physics Department of the University of Turin (2017–2021). I sincerely thank all the people that helped me during my Ph. D., in particular Antonaldo Diaferio, who supervised my Ph. D. activity.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AGN | Active Galactic Nuclei |
| BIMOND | bimetric MOND |
| BTFR | baryonic Tully–Fisher relation |
| CEG | Covariant Emergent Gravity |
| CMB | cosmic microwave background |
| CRG | covariant refracted gravity |
| DE | dark energy |
| DM | dark matter |
| DMS | DiskMass Survey |
| dSph | dwarf spheroidal |
| EH | Einstein-Hilbert |
| GCs | globular clusters |
| GR | General Relativity |
| HSB | high surface brightness |
| CDM | cold dark matter |
| LSB | low surface brightness |
| MDAR | mass discrepancy–acceleration relation |
| MOG | MOdified Gravity |
| MOND | MOdified Newtonian Dynamics |
| MW | Milky Way |
| NFW | Navarro Frenk White |
| RAR | radial acceleration relation |
| RG | Refracted Gravity |
| SPARC | Spitzer Photometry and Accurate Rotation Curves |
| SPS | stellar population synthesis |
| SRG | simplified refracted gravity |
| SVTG | Scalar-Vector-Tensor gravity |
| TeVeS | Tensor Vector Scalar gravity |
| WFL | weak field limit |
| WIMPs | weakly interacting massive particles |
Note
| 1 | In fact, the gravitational sources depend on other scalar quantities besides the mass density, such as their total mechanical and thermodynamical energy or their entropy. Yet, these quantities depend in turn on the mass density and, thus, adopting a gravitational permittivity also dependent on these quantities would be likely to produce a phenomenology comparable to the one obtained with the simple dependence on the mass density alone [44,45]. |
References
- Aghanim, N. et al. [Planck Collaboration] Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar] [CrossRef]
- Davis, M.; Efstathiou, G.; Frenk, C.S.; White, S.D.M. The evolution of large-scale structure in a universe dominated by cold dark matter. Astrophys. J. 1985, 292, 371–394. [Google Scholar] [CrossRef]
- Springel, V.; Frenk, C.S.; White, S.D.M. The large-scale structure of the Universe. Nature 2006, 440, 1137–1144. [Google Scholar] [CrossRef] [PubMed]
- Markevitch, M. Chandra Observation of the Most Interesting Cluster in the Universe. In The X-ray Universe 2005; Wilson, A., Ed.; ESA Special Publication: Washington, DC, USA, 2006; Volume 604, p. 723. [Google Scholar]
- Clowe, D.; Bradač, M.; Gonzalez, A.H.; Markevitch, M.; Randall, S.W.; Jones, C.; Zaritsky, D. A Direct Empirical Proof of the Existence of Dark Matter. Astrophys. J. 2006, 648, L109–L113. [Google Scholar] [CrossRef]
- Paraficz, D.; Kneib, J.P.; Richard, J.; Morandi, A.; Limousin, M.; Jullo, E.; Martinez, J. The Bullet cluster at its best: Weighing stars, gas, and dark matter. Astron. Astrophys. 2016, 594, A121. [Google Scholar] [CrossRef]
- Zwicky, F. Die Rotverschiebung von extragalaktischen Nebeln. Helv. Phys. Acta 1933, 6, 110–127. [Google Scholar]
- Rubin, V.C.; Ford, W.K., Jr. Rotation of the Andromeda Nebula from a Spectroscopic Survey of Emission Regions. Astrophys. J. 1970, 159, 379. [Google Scholar] [CrossRef]
- Bosma, A. The Distribution and Kinematics of Neutral Hydrogen in Spiral Galaxies of Various Morphological Types. Ph.D. Thesis, Rijksuniversiteit te Groningen, Groningen, The Netherlands, 1978. [Google Scholar]
- Sanders, R.H. Mass discrepancies in galaxies: Dark matter and alternatives. Astron. Astrophys. Rev. 1990, 2, 1–28. [Google Scholar] [CrossRef]
- Kirshner, R. Measuring the Universe with Supernovae. In Proceedings of the APS Meeting Abstracts, Vancouver, BC, Canada, 16–19 October 1996; p. F4.01. [Google Scholar]
- Peebles, P.J.; Ratra, B. The cosmological constant and dark energy. Rev. Mod. Phys. 2003, 75, 559–606. [Google Scholar] [CrossRef]
- Weinberg, S. The cosmological constant problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Luo, M.J. The cosmological constant problem and re-interpretation of time. Nucl. Phys. B 2014, 884, 344–356. [Google Scholar] [CrossRef]
- Velten, H.E.S.; vom Marttens, R.F.; Zimdahl, W. Aspects of the cosmological “coincidence problem”. Eur. Phys. J. C 2014, 74, 3160. [Google Scholar] [CrossRef]
- Fleury, P.; Dupuy, H.; Uzan, J.P. Can All Cosmological Observations Be Accurately Interpreted with a Unique Geometry? Phys. Rev. Lett. 2013, 111, 091302. [Google Scholar] [CrossRef] [PubMed]
- Douspis, M.; Salvati, L.; Aghanim, N. On the tension between Large Scale Structures and Cosmic Microwave Background. arXiv 2019, arXiv:1901.05289. [Google Scholar]
- Del Popolo, A.; Le Delliou, M. Small Scale Problems of the ΛCDM Model: A Short Review. Galaxies 2017, 5, 17. [Google Scholar] [CrossRef]
- de Martino, I.; Chakrabarty, S.S.; Cesare, V.; Gallo, A.; Ostorero, L.; Diaferio, A. Dark Matters on the Scale of Galaxies. Universe 2020, 6, 107. [Google Scholar] [CrossRef]
- McGaugh, S.S.; Schombert, J.M.; Bothun, G.D.; de Blok, W.J.G. The Baryonic Tully-Fisher Relation. Astrophys. J. 2000, 533, L99–L102. [Google Scholar] [CrossRef] [PubMed]
- McGaugh, S.S. The Mass Discrepancy-Acceleration Relation: Disk Mass and the Dark Matter Distribution. Astrophys. J. 2004, 609, 652–666. [Google Scholar] [CrossRef]
- McGaugh, S.S.; Lelli, F.; Schombert, J.M. Radial Acceleration Relation in Rotationally Supported Galaxies. Phys. Rev. Lett. 2016, 117, 201101. [Google Scholar] [CrossRef]
- Famaey, B.; McGaugh, S.S. Modified Newtonian Dynamics (MOND): Observational Phenomenology and Relativistic Extensions. Living Rev. Relativ. 2012, 15, 10. [Google Scholar] [CrossRef]
- van Albada, T.S.; Bahcall, J.N.; Begeman, K.; Sancisi, R. Distribution of dark matter in the spiral galaxy NGC 3198. Astrophys. J. 1985, 295, 305–313. [Google Scholar] [CrossRef]
- van Albada, T.S.; Sancisi, R. Dark Matter in Spiral Galaxies. Philos. Trans. R. Soc. Lond. Ser. A 1986, 320, 447–464. [Google Scholar] [CrossRef]
- Sackett, P.D. Does the Milky Way Have a Maximal Disk? Astrophys. J. 1997, 483, 103–110. [Google Scholar] [CrossRef]
- Courteau, S.; Rix, H.W. Maximal Disks and the Tully-Fisher Relation. Astrophys. J. 1999, 513, 561–571. [Google Scholar] [CrossRef]
- Bissantz, N.; Gerhard, O. Spiral arms, bar shape and bulge microlensing in the Milky Way. Mon. Not. R. Astron. Soc. 2002, 330, 591–608. [Google Scholar] [CrossRef]
- Sellwood, J.A.; Debattista, V.P. Re-interpretation of “Bar slowdown and the distribution of dark matter in barred galaxies” by Athanassoula. arXiv 2014, arXiv:1410.0834. [Google Scholar]
- McGaugh, S.S.; Schombert, J.M. Weighing Galaxy Disks With the Baryonic Tully-Fisher Relation. Astrophys. J. 2015, 802, 18. [Google Scholar] [CrossRef]
- Strigari, L.E.; Bullock, J.S.; Kaplinghat, M.; Simon, J.D.; Geha, M.; Willman, B.; Walker, M.G. A common mass scale for satellite galaxies of the Milky Way. Nature 2008, 454, 1096–1097. [Google Scholar] [CrossRef]
- Di Paolo, C.; Salucci, P.; Erkurt, A. The universal rotation curve of low surface brightness galaxies—IV. The interrelation between dark and luminous matter. Mon. Not. R. Astron. Soc. 2019, 490, 5451–5477. [Google Scholar] [CrossRef]
- Mateo, M.L. Dwarf Galaxies of the Local Group. Ann. Rev. Astron. Astrophys. 1998, 36, 435–506. [Google Scholar] [CrossRef]
- Baumgardt, H.; Grebel, E.K.; Kroupa, P. Using distant globular clusters as a test for gravitational theories. Mon. Not. R. Astron. Soc. 2005, 359, L1–L4. [Google Scholar] [CrossRef]
- Jordi, K.; Grebel, E.K.; Hilker, M.; Baumgardt, H.; Frank, M.; Kroupa, P.; Haghi, H.; Côté, P.; Djorgovski, S.G. Testing Fundamental Physics with Distant Star Clusters: Analysis of Observational Data on Palomar 14. Astron. J. 2009, 137, 4586–4596. [Google Scholar] [CrossRef]
- Baumgardt, H.; Côté, P.; Hilker, M.; Rejkuba, M.; Mieske, S.; Djorgovski, S.G.; Stetson, P. The velocity dispersion and mass-to-light ratio of the remote halo globular cluster NGC2419. Mon. Not. R. Astron. Soc. 2009, 396, 2051–2060. [Google Scholar] [CrossRef]
- Sollima, A.; Nipoti, C. Globular clusters in modified Newtonian dynamics: Velocity dispersion profiles from self-consistent models. Mon. Not. R. Astron. Soc. 2010, 401, 131–142. [Google Scholar] [CrossRef]
- Ibata, R.; Sollima, A.; Nipoti, C.; Bellazzini, M.; Chapman, S.C.; Dalessandro, E. The Globular Cluster NGC 2419: A Crucible for Theories of Gravity. Astrophys. J. 2011, 738, 186. [Google Scholar] [CrossRef]
- Ibata, R.; Sollima, A.; Nipoti, C.; Bellazzini, M.; Chapman, S.C.; Dalessandro, E. Polytropic Model Fits to the Globular Cluster NGC 2419 in Modified Newtonian Dynamics. Astrophys. J. 2011, 743, 43. [Google Scholar] [CrossRef]
- Frank, M.J.; Hilker, M.; Baumgardt, H.; Côté, P.; Grebel, E.K.; Haghi, H.; Küpper, A.H.W.; Djorgovski, S.G. The velocity dispersion and mass function of the outer halo globular cluster Palomar 4. Mon. Not. R. Astron. Soc. 2012, 423, 2917–2932. [Google Scholar] [CrossRef]
- Milgrom, M. A modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis. Astrophys. J. 1983, 270, 365–370. [Google Scholar] [CrossRef]
- Milgrom, M. A modification of the Newtonian dynamics—Implications for galaxies. Astrophys. J. 1983, 270, 371–383. [Google Scholar] [CrossRef]
- Milgrom, M. A modification of the newtonian dynamics: Implications for galaxy systems. Astrophys. J. 1983, 270, 384–389. [Google Scholar] [CrossRef]
- Matsakos, T.; Diaferio, A. Dynamics of galaxies and clusters in refracted gravity. arXiv 2016, arXiv:1603.04943. [Google Scholar]
- Cesare, V.; Diaferio, A.; Matsakos, T.; Angus, G. Dynamics of DiskMass Survey galaxies in refracted gravity. Astron. Astrophys. 2020, 637, A70. [Google Scholar] [CrossRef]
- Cesare, V.; Diaferio, A.; Matsakos, T. The dynamics of three nearby E0 galaxies in refracted gravity. Astron. Astrophys. 2022, 657, A133. [Google Scholar] [CrossRef]
- Sanna, A.P.; Matsakos, T.; Diaferio, A. Covariant Formulation of refracted gravity. arXiv 2021, arXiv:2109.11217. [Google Scholar]
- McGaugh, S.S. The Baryonic Tully-Fisher Relation of Gas-rich Galaxies as a Test of ΛCDM and MOND. Astron. J. 2012, 143, 40. [Google Scholar] [CrossRef]
- Lelli, F.; McGaugh, S.S.; Schombert, J.M. The Small Scatter of the Baryonic Tully-Fisher Relation. Astrophys. J. 2016, 816, L14. [Google Scholar] [CrossRef]
- Desmond, H.; Wechsler, R.H. The Tully-Fisher and mass-size relations from halo abundance matching. Mon. Not. R. Astron. Soc. 2015, 454, 322–343. [Google Scholar] [CrossRef]
- Lelli, F.; McGaugh, S.S.; Schombert, J.M. SPARC: Mass Models for 175 Disk Galaxies with Spitzer Photometry and Accurate Rotation Curves. Astron. J. 2016, 152, 157. [Google Scholar] [CrossRef]
- Lelli, F.; McGaugh, S.S.; Schombert, J.M.; Desmond, H.; Katz, H. The baryonic Tully-Fisher relation for different velocity definitions and implications for galaxy angular momentum. Mon. Not. R. Astron. Soc. 2019, 484, 3267–3278. [Google Scholar] [CrossRef]
- Lelli, F.; McGaugh, S.S.; Schombert, J.M.; Pawlowski, M.S. One Law to Rule Them All: The Radial Acceleration Relation of Galaxies. Astrophys. J. 2017, 836, 152. [Google Scholar] [CrossRef]
- Mayer, A.C.; Teklu, A.F.; Dolag, K.; Remus, R.S. ΛCDM with baryons versus MOND: The time evolution of the universal acceleration scale in the Magneticum simulations. Mon. Not. R. Astron. Soc. 2023, 518, 257–269. [Google Scholar] [CrossRef]
- Milgrom, M. MOND impact on and of the recently updated mass-discrepancy-acceleration relation. arXiv 2016, arXiv:1609.06642. [Google Scholar]
- Li, P.; Lelli, F.; McGaugh, S.; Schombert, J. Fitting the radial acceleration relation to individual SPARC galaxies. Astron. Astrophys. 2018, 615, A3. [Google Scholar] [CrossRef]
- Ghari, A.; Haghi, H.; Zonoozi, A.H. The radial acceleration relation and dark baryons in MOND. Mon. Not. R. Astron. Soc. 2019, 487, 2148–2165. [Google Scholar] [CrossRef]
- Santos-Santos, I.M.E.; Navarro, J.F.; Robertson, A.; Benítez-Llambay, A.; Oman, K.A.; Lovell, M.R.; Frenk, C.S.; Ludlow, A.D.; Fattahi, A.; Ritz, A. Baryonic clues to the puzzling diversity of dwarf galaxy rotation curves. Mon. Not. R. Astron. Soc. 2020, 495, 58–77. [Google Scholar] [CrossRef]
- McGaugh, S.S.; Li, P.; Lelli, F.; Schombert, J.M. Presence of a fundamental acceleration scale in galaxies. Nat. Astron. 2018, 2, 924. [Google Scholar] [CrossRef]
- Kroupa, P.; Banik, I.; Haghi, H.; Zonoozi, A.H.; Dabringhausen, J.; Javanmardi, B.; Müller, O.; Wu, X.; Zhao, H. A common Milgromian acceleration scale in nature. Nat. Astron. 2018, 2, 925–926. [Google Scholar] [CrossRef]
- Rodrigues, D.C.; Marra, V.; del Popolo, A.; Davari, Z. Absence of a fundamental acceleration scale in galaxies. Nat. Astron. 2018, 2, 668–672. [Google Scholar] [CrossRef]
- Walter, F.; Brinks, E.; de Blok, W.J.G.; Bigiel, F.; Kennicutt, R.C., Jr.; Thornley, M.D.; Leroy, A. THINGS: The H I Nearby Galaxy Survey. Astron. J. 2008, 136, 2563–2647. [Google Scholar] [CrossRef]
- de Blok, W.J.G.; Walter, F.; Brinks, E.; Trachternach, C.; Oh, S.H.; Kennicutt, R.C.J. High-Resolution Rotation Curves and Galaxy Mass Models from THINGS. Astron. J. 2008, 136, 2648–2719. [Google Scholar] [CrossRef]
- Marra, V.; Rodrigues, D.C.; de Almeida, Á.O.F. A fundamental test for MOND. Mon. Not. R. Astron. Soc. 2020, 494, 2875–2885. [Google Scholar] [CrossRef]
- Zhou, Y.; Del Popolo, A.; Chang, Z. On the absence of a universal surface density, and a maximum Newtonian acceleration in dark matter haloes: Consequences for MOND. Phys. Dark Universe 2020, 28, 100468. [Google Scholar] [CrossRef]
- Rodrigues, D.C.; Marra, V.; Del Popolo, A.; Davari, Z. Reply to ‘Presence of a fundamental acceleration scale in galaxies’ and ‘A common Milgromian acceleration scale in nature’. Nat. Astron. 2018, 2, 927–929. [Google Scholar] [CrossRef]
- Edmonds, D.; Minic, D.; Takeuchi, T. Presence of a Fundamental Acceleration Scale in Galaxy Clusters. arXiv 2020, arXiv:2009.12915. [Google Scholar]
- Dutton, A.A. The baryonic Tully-Fisher relation and galactic outflows. Mon. Not. R. Astron. Soc. 2012, 424, 3123–3128. [Google Scholar] [CrossRef]
- Di Cintio, A.; Lelli, F. The mass discrepancy acceleration relation in a ΛCDM context. Mon. Not. R. Astron. Soc. 2016, 456, L127–L131. [Google Scholar] [CrossRef]
- Ludlow, A.D.; Benítez-Llambay, A.; Schaller, M.; Theuns, T.; Frenk, C.S.; Bower, R.; Schaye, J.; Crain, R.A.; Navarro, J.F.; Fattahi, A.; et al. Mass-Discrepancy Acceleration Relation: A Natural Outcome of Galaxy Formation in Cold Dark Matter Halos. Phys. Rev. Lett. 2017, 118, 161103. [Google Scholar] [CrossRef]
- Keller, B.W.; Wadsley, J.W. ΛCDM is Consistent with SPARC Radial Acceleration Relation. Astrophys. J. 2017, 835, L17. [Google Scholar] [CrossRef]
- Stone, C.; Courteau, S. The Intrinsic Scatter of the Radial Acceleration Relation. Astrophys. J. 2019, 882, 6. [Google Scholar] [CrossRef]
- Di Paolo, C.; Salucci, P.; Fontaine, J.P. The Radial Acceleration Relation (RAR): Crucial Cases of Dwarf Disks and Low-surface-brightness Galaxies. Astrophys. J. 2019, 873, 106. [Google Scholar] [CrossRef]
- Ferrero, I.; Navarro, J.F.; Abadi, M.G.; Sales, L.V.; Bower, R.G.; Crain, R.A.; Frenk, C.S.; Schaller, M.; Schaye, J.; Theuns, T. Size matters: Abundance matching, galaxy sizes, and the Tully-Fisher relation in EAGLE. Mon. Not. R. Astron. Soc. 2017, 464, 4736–4746. [Google Scholar] [CrossRef]
- Ferrero, I.; Abadi, M.G. Redshift evolution of Tully-Fisher relation. In Formation and Evolution of Galaxy Outskirts; Gil de Paz, A., Knapen, J.H., Lee, J.C., Eds.; Cambridge University Press: Cambridge, UK, 2017; Volume 321, p. 126. [Google Scholar] [CrossRef]
- Navarro, J.F.; Benítez-Llambay, A.; Fattahi, A.; Frenk, C.S.; Ludlow, A.D.; Oman, K.A.; Schaller, M.; Theuns, T. The origin of the mass discrepancy-acceleration relation in ΛCDM. Mon. Not. R. Astron. Soc. 2017, 471, 1841–1848. [Google Scholar] [CrossRef]
- Dutton, A.A.; Macciò, A.V.; Obreja, A.; Buck, T. NIHAO-XVIII. Origin of the MOND phenomenology of galactic rotation curves in a ΛCDM universe. Mon. Not. R. Astron. Soc. 2019, 485, 1886–1899. [Google Scholar] [CrossRef]
- Bekenstein, J.; Milgrom, M. Does the missing mass problem signal the breakdown of Newtonian gravity? Astrophys. J. 1984, 286, 7–14. [Google Scholar] [CrossRef]
- Milgrom, M. Dynamics with a Nonstandard Inertia-Acceleration Relation: An Alternative to Dark Matter in Galactic Systems. Ann. Phys. 1994, 229, 384–415. [Google Scholar] [CrossRef]
- Milgrom, M. Quasi-linear formulation of MOND. Mon. Not. R. Astron. Soc. 2010, 403, 886–895. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Phase coupling gravitation: Symmetries and gauge fields. Phys. Lett. B 1988, 202, 497–500. [Google Scholar] [CrossRef]
- Sanders, R.H. Phase coupling gravity and astronomical mass discrepancies. Mon. Not. R. Astron. Soc. 1988, 235, 105–121. [Google Scholar] [CrossRef]
- Skordis, C. TOPICAL REVIEW: The tensor-vector-scalar theory and its cosmology. Class. Quantum Gravity 2009, 26, 143001. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Tensor-vector-scalar-modified gravity: From small scale to cosmology. Philos. Trans. R. Soc. Lond. Ser. A 2011, 369, 5003–5017. [Google Scholar] [CrossRef]
- Brada, R.; Milgrom, M. Exact solutions and approximations of MOND fields of disc galaxies. Mon. Not. R. Astron. Soc. 1995, 276, 453–459. [Google Scholar] [CrossRef]
- Eriksen, M.H.; Frandsen, M.T.; From, M.H. A Cusp-Core like challenge for Modified Newtonian Dynamics. arXiv 2019, arXiv:1906.07823. [Google Scholar] [CrossRef]
- McGaugh, S.S. The Baryonic Tully-Fisher Relation of Galaxies with Extended Rotation Curves and the Stellar Mass of Rotating Galaxies. Astrophys. J. 2005, 632, 859–871. [Google Scholar] [CrossRef]
- Bershady, M.A.; Verheijen, M.A.W.; Swaters, R.A.; Andersen, D.R.; Westfall, K.B.; Martinsson, T. The DiskMass Survey. I. Overview. Astrophys. J. 2010, 716, 198–233. [Google Scholar] [CrossRef]
- Angus, G.W.; Gentile, G.; Swaters, R.; Famaey, B.; Diaferio, A.; McGaugh, S.S.; Heyden, K.J.v.d. Mass models of disc galaxies from the DiskMass Survey in modified Newtonian dynamics. Mon. Not. R. Astron. Soc. 2015, 451, 3551–3580. [Google Scholar] [CrossRef]
- Bershady, M.A.; Verheijen, M.A.W.; Westfall, K.B.; Andersen, D.R.; Swaters, R.A.; Martinsson, T. The DiskMass Survey. II. Error Budget. Astrophys. J. 2010, 716, 234–268. [Google Scholar] [CrossRef]
- Bekenstein, J.D.; Sagi, E. Do Newton’s G and Milgrom’s a0 vary with cosmological epoch? Phys. Rev. D 2008, 77, 103512. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Relativistic gravitation theory for the modified Newtonian dynamics paradigm. Phys. Rev. D 2004, 70, 083509. [Google Scholar] [CrossRef]
- Hossenfelder, S. Covariant version of Verlinde’s emergent gravity. Phys. Rev. D 2017, 95, 124018. [Google Scholar] [CrossRef]
- Hossenfelder, S.; Mistele, T. The redshift-dependence of radial acceleration: Modified gravity versus particle dark matter. Int. J. Mod. Phys. D 2018, 27, 1847010. [Google Scholar] [CrossRef]
- Milgrom, M. The a0—Cosmology connection in MOND. arXiv 2020, arXiv:2001.09729. [Google Scholar]
- Milgrom, M. Alternatives to Dark Matter. Comments Astrophys. 1989, 13, 215. [Google Scholar]
- Milgrom, M. The modified dynamics as a vacuum effect. Phys. Lett. A 1999, 253, 273–279. [Google Scholar] [CrossRef]
- Zlosnik, T.G.; Ferreira, P.G.; Starkman, G.D. Modifying gravity with the aether: An alternative to dark matter. Phys. Rev. D 2007, 75, 044017. [Google Scholar] [CrossRef]
- Milgrom, M. Bimetric MOND gravity. Phys. Rev. D 2009, 80, 123536. [Google Scholar] [CrossRef]
- Blanchet, L.; Heisenberg, L. Dipolar dark matter as an effective field theory. Phys. Rev. D 2017, 96, 083512. [Google Scholar] [CrossRef]
- Milgrom, M. Noncovariance at low accelerations as a route to MOND. Phys. Rev. D 2019, 100, 084039. [Google Scholar] [CrossRef]
- Milgrom, M. MOND from a Brane-World Picture; World Scientific Publishing: Singapore, 2020. [Google Scholar] [CrossRef]
- Khoury, J.; Weltman, A. Chameleon cosmology. Phys. Rev. D 2004, 69, 044026. [Google Scholar] [CrossRef]
- Kunz, M.; Liddle, A.R.; Parkinson, D.; Gao, C. Constraining the dark fluid. Phys. Rev. D 2009, 80, 083533. [Google Scholar] [CrossRef]
- Kunz, M. Degeneracy between the dark components resulting from the fact that gravity only measures the total energy-momentum tensor. Phys. Rev. D 2009, 80, 123001. [Google Scholar] [CrossRef]
- Mannheim, P.D.; Kazanas, D. Exact Vacuum Solution to Conformal Weyl Gravity and Galactic Rotation Curves. Astrophys. J. 1989, 342, 635. [Google Scholar] [CrossRef]
- Nesbet, R. Conformal Gravity: Dark Matter and Dark Energy. Entropy 2013, 15, 162–176. [Google Scholar] [CrossRef]
- Campigotto, M.C.; Diaferio, A.; Fatibene, L. Conformal gravity: Light deflection revisited and the galactic rotation curve failure. Class. Quantum Gravity 2019, 36, 245014. [Google Scholar] [CrossRef]
- Makler, M.; de Oliveira, S.Q.; Waga, I. Constraints on the generalized Chaplygin gas from supernovae observations. Phys. Lett. B 2003, 555, 1–6. [Google Scholar] [CrossRef]
- Brandenberger, R.; Cuzinatto, R.R.; Fröhlich, J.; Namba, R. New scalar field quartessence. J. Cosmol. Astropart. Phys. 2019, 2019, 043. [Google Scholar] [CrossRef]
- Ferreira, E.G.M.; Franzmann, G.; Khoury, J.; Brandenberger, R. Unified superfluid dark sector. J. Cosmol. Astropart. Phys. 2019, 2019, 027. [Google Scholar] [CrossRef]
- Bento, M.C.; Bertolami, O.; Sen, A.A. Generalized Chaplygin gas, accelerated expansion, and dark-energy-matter unification. Phys. Rev. D 2002, 66, 043507. [Google Scholar] [CrossRef]
- Carturan, D.; Finelli, F. Cosmological effects of a class of fluid dark energy models. Phys. Rev. D 2003, 68, 103501. [Google Scholar] [CrossRef]
- Sandvik, H.B.; Tegmark, M.; Zaldarriaga, M.; Waga, I. The end of unified dark matter? Phys. Rev. D 2004, 69, 123524. [Google Scholar] [CrossRef]
- Scherrer, R.J. Purely Kinetic k Essence as Unified Dark Matter. Phys. Rev. Lett. 2004, 93, 011301. [Google Scholar] [CrossRef]
- Giannakis, D.; Hu, W. Challenges for the kinetic unified dark matter model. Phys. Rev. D 2005, 72, 063502. [Google Scholar] [CrossRef]
- Bruni, M.; Lazkoz, R.; Rozas-Fernández, A. Phenomenological models for unified dark matter with fast transition. Mon. Not. R. Astron. Soc. 2013, 431, 2907–2916. [Google Scholar] [CrossRef]
- Leanizbarrutia, I.; Rozas-Fernández, A.; Tereno, I. Cosmological constraints on a unified dark matter-energy scalar field model with fast transition. Phys. Rev. D 2017, 96, 023503. [Google Scholar] [CrossRef]
- Cadoni, M.; Casadio, R.; Giusti, A.; Mück, W.; Tuveri, M. Effective fluid description of the dark universe. Phys. Lett. B 2018, 776, 242–248. [Google Scholar] [CrossRef]
- Cadoni, M.; Casadio, R.; Giusti, A.; Tuveri, M. Emergence of a dark force in corpuscular gravity. Phys. Rev. D 2018, 97, 044047. [Google Scholar] [CrossRef]
- Alexander, S.; Biswas, T.; Calcagni, G. Cosmological Bardeen-Cooper-Schrieffer condensate as dark energy. Phys. Rev. D 2010, 81, 043511. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Faraoni, V. f(R) theories of gravity. Rev. Mod. Phys. 2010, 82, 451–497. [Google Scholar] [CrossRef]
- Sebastiani, L.; Vagnozzi, S.; Myrzakulov, R. Mimetic gravity: A review of recent developments and applications to cosmology and astrophysics. arXiv 2016, arXiv:1612.08661. [Google Scholar] [CrossRef]
- Berezhiani, L.; Khoury, J.; Wang, J. Universe without dark energy: Cosmic acceleration from dark matter-baryon interactions. Phys. Rev. D 2017, 95, 123530. [Google Scholar] [CrossRef]
- Arbey, A.; Coupechoux, J.F. Unifying dark matter, dark energy and inflation with a fuzzy dark fluid. J. Cosmol. Astropart. Phys. 2021, 2021, 033. [Google Scholar] [CrossRef]
- McConnachie, A.W. The Observed Properties of Dwarf Galaxies in and around the Local Group. Astron. J. 2012, 144, 4. [Google Scholar] [CrossRef]
- Javanmardi, B.; Martinez-Delgado, D.; Kroupa, P.; Henkel, C.; Crawford, K.; Teuwen, K.; Gabany, R.J.; Hanson, M.; Chonis, T.S.; Neyer, F. DGSAT: Dwarf Galaxy Survey with Amateur Telescopes. I. Discovery of low surface brightness systems around nearby spiral galaxies. Astron. Astrophys. 2016, 588, A89. [Google Scholar] [CrossRef]
- Mateo, M.; Olszewski, E.W.; Pryor, C.; Welch, D.L.; Fischer, P. The Carina Dwarf Spheroidal Galaxy: How Dark is it? Astron. J. 1993, 105, 510. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. The Structure of Cold Dark Matter Halos. Astrophys. J. 1996, 462, 563. [Google Scholar] [CrossRef]
- Dubinski, J.; Carlberg, R.G. The Structure of Cold Dark Matter Halos. Astrophys. J. 1991, 378, 496. [Google Scholar] [CrossRef]
- Torrealba, G.; Belokurov, V.; Koposov, S.E.; Li, T.S.; Walker, M.G.; Sanders, J.L.; Geringer-Sameth, A.; Zucker, D.B.; Kuehn, K.; Evans, N.W.; et al. The hidden giant: Discovery of an enormous Galactic dwarf satellite in Gaia DR2. Mon. Not. R. Astron. Soc. 2019, 488, 2743–2766. [Google Scholar] [CrossRef]
- Helmi, A. et al. [Gaia Collaboration] Gaia Data Release 2. Kinematics of globular clusters and dwarf galaxies around the Milky Way. Astron. Astrophys. 2018, 616, A12. [Google Scholar] [CrossRef]
- Giersz, M. Monte Carlo simulations of star clusters—III. A million-body star cluster. Mon. Not. R. Astron. Soc. 2006, 371, 484–494. [Google Scholar] [CrossRef]
- Mashchenko, S.; Sills, A. Globular Clusters with Dark Matter Halos. I. Initial Relaxation. Astrophys. J. 2005, 619, 243–257. [Google Scholar] [CrossRef]
- Moore, B. Constraints on the Global Mass-to-Light Ratios and on the Extent of Dark Matter Halos in Globular Clusters and Dwarf Spheroidals. Astrophys. J. 1996, 461, L13. [Google Scholar] [CrossRef]
- Forbes, D.A.; Lasky, P.; Graham, A.W.; Spitler, L. Uniting old stellar systems: From globular clusters to giant ellipticals. Mon. Not. R. Astron. Soc. 2008, 389, 1924–1936. [Google Scholar] [CrossRef]
- Deur, A. A relation between the dark mass of elliptical galaxies and their shape. Mon. Not. R. Astron. Soc. 2014, 438, 1535–1551. [Google Scholar] [CrossRef]
- Deur, A. A correlation between the dark content of elliptical galaxies and their ellipticity. arXiv 2020, arXiv:2010.06692. [Google Scholar]
- Cesare, V. Dynamics of Disk and Elliptical Galaxies in Refracted Gravity. Phys. Sci. Forum 2021, 2, 9292. [Google Scholar] [CrossRef]
- Tanabashi, M.; Hagiwara, K.; Hikasa, K.; Nakamura, K.; Sumino, Y.; Takahashi, F.; Tanaka, J.; Agashe, K.; Aielli, G.; Amsler, C.; et al. Review of Particle Physics*. Phys. Rev. D 2018, 98, 030001. [Google Scholar] [CrossRef]
- Sanders, R.H. The Virial Discrepancy in Clusters of Galaxies in the Context of Modified Newtonian Dynamics. Astrophys. J. 1999, 512, L23–L26. [Google Scholar] [CrossRef]
- Sanders, R.H. Clusters of galaxies with modified Newtonian dynamics. Mon. Not. R. Astron. Soc. 2003, 342, 901–908. [Google Scholar] [CrossRef]
- Hodson, A.O.; Zhao, H. Generalizing MOND to explain the missing mass in galaxy clusters. Astron. Astrophys. 2017, 598, A127. [Google Scholar] [CrossRef]
- Hernandez, X.; Sussman, R.A.; Nasser, L. Approaching the Dark Sector through a bounding curvature criterion. Mon. Not. R. Astron. Soc. 2019, 483, 147–151. [Google Scholar] [CrossRef]
- Skordis, C.; Złośnik, T. New Relativistic Theory for Modified Newtonian Dynamics. Phys. Rev. Lett. 2021, 127, 161302. [Google Scholar] [CrossRef]
- Forbes, D.A.; Alabi, A.; Brodie, J.P.; Romanowsky, A.J.; Strader, J.; Foster, C.; Usher, C.; Spitler, L.; Bellstedt, S.; Pastorello, N.; et al. The SLUGGS Survey: A Catalog of Over 4000 Globular Cluster Radial Velocities in 27 Nearby Early-type Galaxies. Astron. J. 2017, 153, 114. [Google Scholar] [CrossRef]
- Pulsoni, C.; Gerhard, O.; Arnaboldi, M.; Coccato, L.; Longobardi, A.; Napolitano, N.R.; Moylan, E.; Narayan, C.; Gupta, V.; Burkert, A.; et al. The extended Planetary Nebula Spectrograph (ePN.S) early-type galaxy survey: The kinematic diversity of stellar halos and the relation between halo transition scale and stellar mass. Astron. Astrophys. 2018, 618, A94. [Google Scholar] [CrossRef]
- Salucci, P.; Wilkinson, M.I.; Walker, M.G.; Gilmore, G.F.; Grebel, E.K.; Koch, A.; Frigerio Martins, C.; Wyse, R.F.G. Dwarf spheroidal galaxy kinematics and spiral galaxy scaling laws. Mon. Not. R. Astron. Soc. 2012, 420, 2034–2041. [Google Scholar] [CrossRef]
- Oh, S.H.; Hunter, D.A.; Brinks, E.; Elmegreen, B.G.; Schruba, A.; Walter, F.; Rupen, M.P.; Young, L.M.; Simpson, C.E.; Johnson, M.C.; et al. High-resolution Mass Models of Dwarf Galaxies from LITTLE THINGS. Astron. J. 2015, 149, 180. [Google Scholar] [CrossRef]
- Rines, K.; Diaferio, A. CIRS: Cluster Infall Regions in the Sloan Digital Sky Survey. I. Infall Patterns and Mass Profiles. Astron. J. 2006, 132, 1275–1297. [Google Scholar] [CrossRef]
- Rines, K.; Geller, M.J.; Diaferio, A.; Kurtz, M.J. Measuring the Ultimate Halo Mass of Galaxy Clusters: Redshifts and Mass Profiles from the Hectospec Cluster Survey (HeCS). Astrophys. J. 2013, 767, 15. [Google Scholar] [CrossRef]
- Moffat, J.W. Scalar tensor vector gravity theory. J. Cosmol. Astropart. Phys. 2006, 2006, 004. [Google Scholar] [CrossRef]
- Moffat, J.W. A new nonsymmetric gravitational theory. Phys. Lett. B 1995, 355, 447–452. [Google Scholar] [CrossRef]
- Moffat, J.W. Gravitational theory, galaxy rotation curves and cosmology without dark matter. J. Cosmol. Astropart. Phys. 2005, 2005, 003. [Google Scholar] [CrossRef]
- Brownstein, J.R.; Moffat, J.W. Galaxy Rotation Curves without Nonbaryonic Dark Matter. Astrophys. J. 2006, 636, 721–741. [Google Scholar] [CrossRef]
- Moffat, J.W.; Toth, V.T. Fundamental parameter-free solutions in modified gravity. Class. Quantum Gravity 2009, 26, 085002. [Google Scholar] [CrossRef]
- Moffat, J.W.; Toth, V.T. Testing modified gravity with motion of satellites around galaxies. arXiv 2007, arXiv:0708.1264. [Google Scholar]
- Moffat, J.W.; Toth, V.T. Testing Modified Gravity with Globular Cluster Velocity Dispersions. Astrophys. J. 2008, 680, 1158–1161. [Google Scholar] [CrossRef]
- Brownstein, J.R.; Moffat, J.W. Galaxy cluster masses without non-baryonic dark matter. Mon. Not. R. Astron. Soc. 2006, 367, 527–540. [Google Scholar] [CrossRef]
- Brownstein, J.R.; Moffat, J.W. The Bullet Cluster 1E0657-558 evidence shows modified gravity in the absence of dark matter. Mon. Not. R. Astron. Soc. 2007, 382, 29–47. [Google Scholar] [CrossRef]
- Moffat, J.W. A Modified Gravity and its Consequences for the Solar System, Astrophysics and Cosmology. Int. J. Mod. Phys. D 2007, 16, 2075–2090. [Google Scholar] [CrossRef]
- Moffat, J.W.; Toth, V.T. Modified Gravity: Cosmology without dark matter or Einstein’s cosmological constant. arXiv 2007, arXiv:0710.0364. [Google Scholar]
- Moffat, J.W.; Toth, V.T. Modified Gravity and the origin of inertia. Mon. Not. R. Astron. Soc. 2009, 395, L25–L28. [Google Scholar] [CrossRef]
- Moffat, J.W. Acceleration in Modified Gravity (MOG) and the Mass-Discrepancy Baryonic Relation. arXiv 2016, arXiv:1610.06909. [Google Scholar]
- Prada, F.; Vitvitska, M.; Klypin, A.; Holtzman, J.A.; Schlegel, D.J.; Grebel, E.K.; Rix, H.W.; Brinkmann, J.; McKay, T.A.; Csabai, I. Observing the Dark Matter Density Profile of Isolated Galaxies. Astrophys. J. 2003, 598, 260–271. [Google Scholar] [CrossRef]
- Sheldon, E.S.; Johnston, D.E.; Frieman, J.A.; Scranton, R.; McKay, T.A.; Connolly, A.J.; Budavári, T.; Zehavi, I.; Bahcall, N.A.; Brinkmann, J.; et al. The Galaxy-Mass Correlation Function Measured from Weak Lensing in the Sloan Digital Sky Survey. Astron. J. 2004, 127, 2544–2564. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).