Novel Exact Solution for the Bidirectional Sixth-Order Sawada–Kotera Equation

Abstract

In this paper, we take the bidirectional sixth-order Sawada–Kotera equation as an instance and use a new limit approach to generate a multiple-pole solution and the degenerate of the breather wave from the N-order soliton solution. We show not only the substitution method, but also the specific mathematical expression of the double-pole, triple-pole, and the degenerate breather solution after the substitution. Meanwhile, we give the dynamic images and trajectories of the different multiple-pole solution. Moreover, we also acquire the interaction between two double-pole solutions and different nonlinear superposition solutions.

1. Introduction

With the continuous development of science and technology, as well as scientific research tools, the importance of nonlinear phenomena in nature is gradually increasing [1]. The different forms of solutions are the most interesting points in the study of partial differential equations [2]. Particularly for multiple-pole solutions, which consist of groups of weakly bound solitons with similar velocity and amplitude [3]. In fact, most researchers have used the inverse scattering method and Darboux transformation method to acquire the multiple-pole solution [4,5,6,7]. The Darboux transformation method has formed a mature theoretical system [8,9]. Some productive systems are cumbersome to calculate using the inverse scattering method. For Equation (1), there will be a fifth-order differential operator in the solving process [10]. To the best of our knowledge, relatively few papers have studied this solution using the bilinear method; this method allows the calculation steps to be simplified. In this paper, we take the bidirectional sixth-order Sawada–Kotera equation as an instance and use a new limit approach to generate a multiple-pole solution and the degenerate of the breather wave from the N-order soliton solution.

The bidirectional sixth-order Sawada–Kotera equation has the following form:

$$5u_{tt}+5u_{xxxt}-15u_x{u}_{xt}-15u_{xx}{u}_t-45{\left(u_x\right)}^2{u}_{xx}+15u_{xx}{u}_{xxx}+15u_x{u}_{xxx}-u_{xxxxxx}=0,$$

(1)

which is a sixth-order nonlinear equation (KdV6) that was derived from the fifth-order Sawada–Kotera equation [11]. The Sawada–Kotera model is a well-known equation that due to the gravitational force and conformal field theory, preserved the current of the Liouville sample. Equation (1) is better for certain physical environments because it permits us to describe waves that spread in opposite orientations [12]. Equation (1) passes the Painlevé analysis test [13] and its integrability is discussed in [14].

For Equation (1), Hu et al presented a Lax pair and Bäcklund transformation forms [15]. Huber found new exact solutions using the homogeneous balance method [16]. Kupershmidt found an auto-Bäcklund transformation for it using the method of truncated singular expansion [14]. Wazwaz derived multiple soliton solutions and multiple singular soliton solutions using the Cole–Hopf transformation [11]. Li et al constructed vector fields and the optimal system using the Lie symmetry analysis approach and derived a periodic wave solution with detailed analysis [13]. Yin et al presented its multiple kink solutions [17].

The structure of the paper is as follows. In Section 2, N-soliton solutions of Equation (1) is given directly by Hirota bilinear method. In Section 3, based on N-soliton solutions and new limit-approach constraints, we obtain the double-pole, triple-pole and quadruple-pole solution. In Section 4, the interaction between two double-pole solutions is constructed by changing the constraints. Meanwhile, we also acquire the degenerate solution of a second-order breather solution with module resonance conditions. We observed the different superposition solutions using MAPLE. Section 5 contains our conclusions.

2. $\mathbf{N}$-Soliton Solution

The Hirota bilinear method is a well-known method for solving the soliton solution of nonlinear equations [18]. Using logarithmic transformation

$$u=2{\left(\ln f\right)}_x,$$

(2)

Equation (1) can be transformed into the bilinear form

$$(5D_t^2+5D_x^3{D}_t-D_x^6)(f·f)=0,$$

(3)

where $D_x,D_t$ are defined by

$$D_x^m{D}_t^n(f·g)={(\frac{\partial }{\partial x_1}-\frac{\partial }{\partial x_2})}^m{(\frac{\partial }{\partial t_1}-\frac{\partial }{\partial t_2})}^n(f(x_1,t_1)·g(x_2,t_2)){|}_{x_1=x_2,t_1=t_2}.$$

(4)

So Equation (3) is equivalent to

$$\begin{array}{cc}\hfill 5f{f}_{2t}-5f_t^2-f{f}_{6x}& +6f_x{f}_{5x}-15f_{2x}{f}_{4x}+10f_{3x}^2\hfill \\ \hfill & +5f_{xxxt}f-5f_{3x}{f}_t-15f_{xxt}{f}_x+15f_{2x}{f}_{xt}=0.\hfill \end{array}$$

Then, based on the above form, the f can be directly obtained as

$$f=f_N=\sum _{\mu =0,1}^{}\exp \left(\sum _{j=1}^N{\mu }_j{\theta }_j+\sum _{j<s}^N{\mu }_j{\mu }_s{A}_{js}\right),$$

(5)

where

$${\theta }_j=k_{j}x+{\omega }_{j}t+{\eta }_j^{\left(0\right)},{\omega }_j=\left(-\frac{1}{2}\pm \frac{3\sqrt{5}}{10}\right)k_j^3,$$

(6)

$$e^{A_{js}}=\frac{\left(2k_j^2-(1\pm \sqrt{5})k_j{k}_s+2k_s^2\right){\left(k_j-k_s\right)}^2}{\left(2k_j^2+(1\pm \sqrt{5})k_j{k}_s+2k_s^2\right){\left(k_j+k_s\right)}^2}.$$

Here, $k_j,{\eta }_j^{\left(0\right)}(j=1,2,\cdots ,N)$ are arbitrary complex constants,${\displaystyle \sum _{\mu =0,1}}$ is all possible combinations of ${\mu }_j=0,1$. We depict the 3D plot, density plot and contour plot of a single-soliton and two-soliton solution. Figure 1 is presented by taking parameters $k_1=2,k_2=3,{\eta }_1^{\left(0\right)}={\eta }_2^{\left(0\right)}=0$ in Equation (1). All lines in Figure 1c are parallel, and the slope is constant as ${\displaystyle \frac{5-3\sqrt{5}}{10}{k}_1^2}$ when $\left|t\right|\to \infty$. Two different slopes (red and yellow line) in Figure 1f are ${\displaystyle \frac{5-3\sqrt{5}}{10}{k}_1^2}$ and ${\displaystyle 5-\frac{5-3\sqrt{5}}{10}{k}_2^2}$ when $\left|t\right|\to \infty$.

In our previous research [19], we found that two solitons will transform to resonance Y-type soliton if we take suitable $k_1,k_2$ in accordance with $\{\exp \left(A_{12}\right)=0,k_1\ne k_2\}$. Equation (6) demonstrates that there is no resonance in this model. In fact, for the vast majority of (1 + 1)-dimensional evolution equations, it is hardly possible to find two solitons that merge into one at some point.

3. Multiple-Pole Solutions

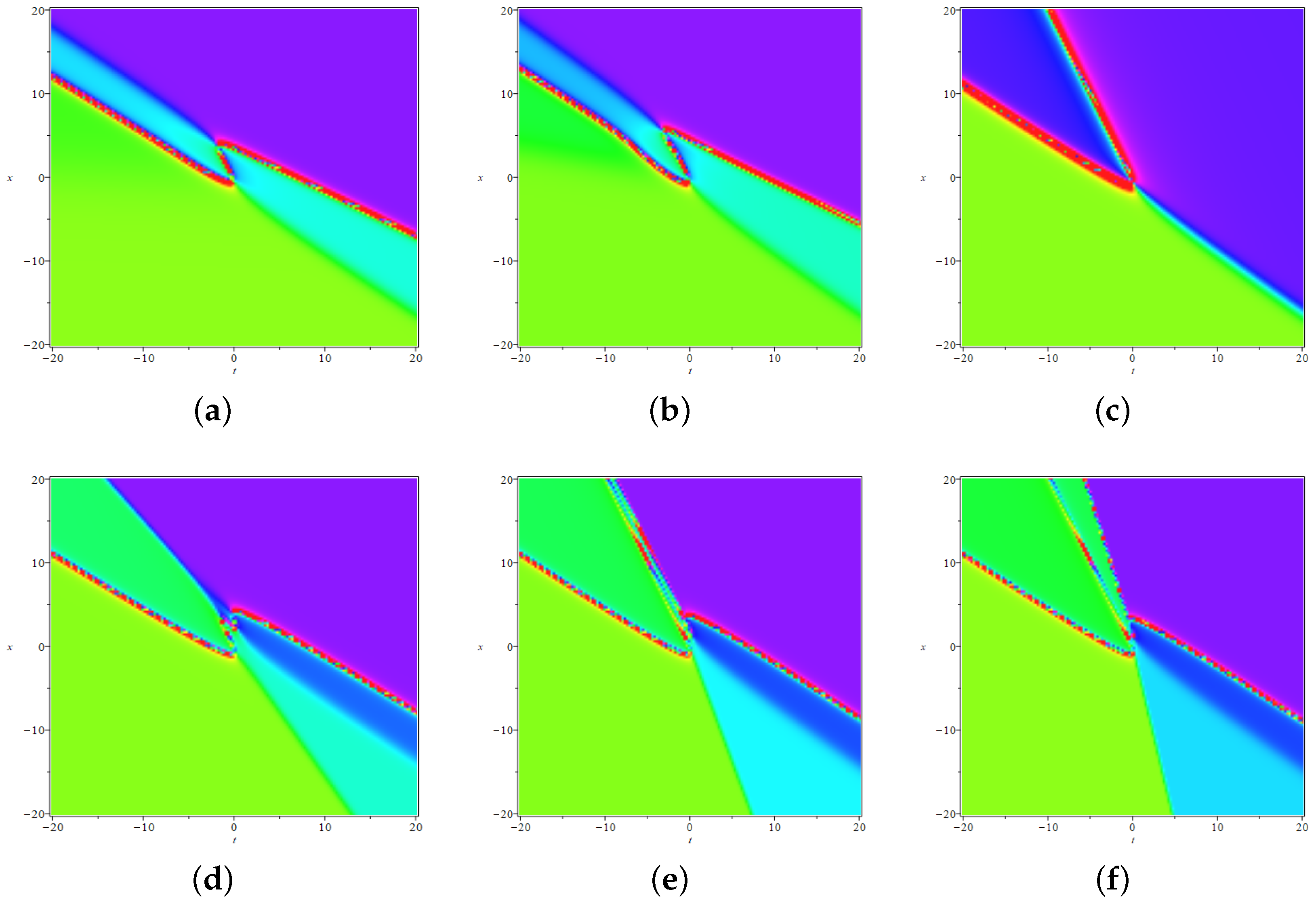
3.1. Double-Pole Solution

Let

$$N=2,k_2=k_1+ϵ,{\eta }_1^{\left(0\right)}={\chi }_1^{\left(0\right)}+\ln \left(-\frac{\beta }{ϵ}\right),{\eta }_2^{\left(0\right)}={\chi }_1^{\left(0\right)}+\ln \left(\frac{\beta }{ϵ}\right)$$

(7)

in Equation (5), then the second-order soliton solution will be degenerated to a double-pole solution $u_2$ when $ϵ\to 0$, and this degenerated solution has the following form

$$u_2=2{\left(\ln f\right)}_x,f=1+\beta {\partial }_{k_1}\left(e^{{\displaystyle {\chi }_1}}\right)-D_{11}{\beta }^2{e}^{{\displaystyle 2{\chi }_1}},$$

(8)

with

$${\chi }_j=k_{j}x+{\omega }_{j}t+{\chi }_j^{\left(0\right)},D_{js}=\left\{\begin{array}{cc}{\displaystyle \frac{2\sqrt{5}-5}{20k_1^2},}\hfill & j=s,\hfill \\ {\displaystyle \frac{{(k_1-k_2)}^2((\sqrt{5}-3)k_1^2+(\sqrt{5}-1)k_1{k}_2+(\sqrt{5}-3)k_2^2)}{{(k_1+k_2)}^2((\sqrt{5}-3)k_1^2-(\sqrt{5}-1)k_1{k}_2+(\sqrt{5}-3)k_2^2)},}\hfill & j\ne s,\hfill \end{array}\right.$$

and $k_j,{\chi }_j^{\left(0\right)},\beta (j=1,2)$ are all real parameters.

The parameter $\beta$ in Equation (7) not only affects the initial position of the solution, but also controls the perturbation direction of the degenerated solution. It is well known that the bright multiple-pole solution which is derivative with respect to x has a maximum point [20]. Similarly, the dark multiple-pole solution has a minimum point [21]. In this system, Figure 2 visually depicts two different types, $\beta >0$ and $\beta <0$. Choosing $\left\{\beta =4\sqrt{5+2\sqrt{5}},k_1=\pm 2\right\}$, we obtain a bright double-pole solution in Figure 2a. If $\left\{\beta =-4\sqrt{5+2\sqrt{5}},k_1=\pm 2\right\}$, the dark double-pole solution is depicted in Figure 2d. Moreover, if we take $\beta =\pm 2\sqrt{5+2\sqrt{5}}{k}_1$, two different trajectory equations in Figure 2b,e are symmetrical about the origin when $\left|t\right|\to \infty$. Their specific expressions are as follows:

$$x=\frac{5-3\sqrt{5}}{10}{k}_1^{2}t\pm \frac{\ln \left(18(5-\sqrt{5})k_1^6{t}^2\right)-\ln 5}{2k_1}.$$

(9)

According to Equation (9), we can deduce that the velocity of $u_2$ while in motion is not constant, but varies with time. This conclusion is also graphically illustrated in Figure 2.

3.2. Triple-Pole Solution

Let

$$\begin{array}{cc}\hfill N=3,& k_2=k_1+ϵ,k_3=k_1+2ϵ,{\eta }_1^{\left(0\right)}={\chi }_1^{\left(0\right)}+\ln \left(\frac{\beta }{{ϵ}^2}\right),\hfill \\ \hfill & {\eta }_2^{\left(0\right)}={\chi }_1^{\left(0\right)}+\ln \left(-\frac{2\beta }{{ϵ}^2}\right),{\eta }_3^{\left(0\right)}={\chi }_1^{\left(0\right)}+\ln \left(\frac{\beta }{{ϵ}^2}\right),\hfill \end{array}$$

(10)

then the third-order soliton solution will be degenerated to a triple-pole solution $u_3$ when $ϵ\to 0$, and this solution is expressed as

$$u_3=2{(lnf)}_x,$$

(11)

where

$$\begin{array}{cc}\hfill f=1& +\beta {\partial }_{k_1}^2\left(e^{{\displaystyle {\chi }_1}}\right)-{\beta }^2\left[{\displaystyle D_{11}\left(2{\left({\partial }_{k_1}{\chi }_1\right)}^2-2{\partial }_{k_1}^2{\chi }_1\right)+2\left({\partial }_{k_1}{D}_{11}\right)\left({\partial }_{k_1}{\chi }_1\right)+\frac{1}{2}{\partial }_{k_1}^2{D}_{11}}\right]e^{{\displaystyle 2{\chi }_1}}\hfill \\ \hfill & -8{\beta }^3{D}_{11}^3{e}^{{\displaystyle 3{\chi }_1}}.\hfill \end{array}$$

(12)

Here, $k_1,{\chi }_1^{\left(0\right)}$ are arbitrary real parameters.

Resemble the conclusion of the degenerate solution $u_2$, the degenerate solution of the third-order soliton has bright and dark solutions with different parameters. Likewise, $\beta >0$ or $\beta <0$ is a significant impact factor. Figure 3 portrays the bright triple-pole solution in Figure 3a, with the dark one in Figure 3c. Moreover, we let parameters $\left\{\beta =\pm \left(4\sqrt{5}+10\right)k_1^2,{\chi }_1^{\left(0\right)}=0\right\}$ in order to have the center of the solution in Equation (11) at the origin and the trajectory symmetric about the $(0,0)$ when $\left|t\right|\to \infty$. For each particular $k_1$, the mathematical expressions for the three trajectories in Figure 3b,d at infinity are

$$\begin{array}{cc}\hfill & x=\frac{5-3\sqrt{5}}{10}{k}_1^{2}t\pm \frac{\ln \left(162(3-\sqrt{5})k_1^{12}{t}^4\right)-\ln 5}{2k_1},\hfill \\ \hfill & x=\frac{5-3\sqrt{5}}{10}{k}_1^{2}t+\frac{1}{k_1}\ln \frac{10k_1^2(21\sqrt{5}-47)}{\beta (199\sqrt{5}-445)}.\hfill \end{array}$$

(13)

When $\beta =\pm \left(4\sqrt{5}+10\right)k_1^2$, the second formula in Equation (13), i.e., the middle trajectory, will simplify to ${\displaystyle x=\frac{5-3\sqrt{5}}{10}{k}_1^{2}t}$. In addition, $u_3$ at infinity distance can be approximated as a nonlinear superposition of three solutions; one has constant velocity, and the other two solutions have ever-changing speed. It follows that Equation (13) supports the above conclusion.

3.3. Quadruple-Pole Solution

For $N=4$, ensure that

$$\begin{array}{cc}\hfill & k_2=k_1+ϵ,k_3=k_1+2ϵ,k_4=k_1+3ϵ,{\eta }_1^{\left(0\right)}={\chi }_1^{\left(0\right)}+\ln \left(-\frac{\beta }{{ϵ}^3}\right),\hfill \\ \hfill & {\eta }_2^{\left(0\right)}={\chi }_1^{\left(0\right)}+\ln \left(\frac{3\beta }{{ϵ}^3}\right),{\eta }_3^{\left(0\right)}={\chi }_1^{\left(0\right)}+\ln \left(-\frac{3\beta }{{ϵ}^3}\right),{\eta }_4^{\left(0\right)}={\chi }_1^{\left(0\right)}+\ln \left(\frac{\beta }{{ϵ}^3}\right).\hfill \end{array}$$

(14)

When $ϵ\to 0$, we obtain the exact expression of quadruple-pole solution $u_4=2{(lnf)}_x$ after a very cumbersome calculation.

$$f=1+\beta {\partial }_{k_1}^3\left(e^{{\displaystyle {\chi }_1}}\right)+P{e}^{{\displaystyle 2{\chi }_1}}+Q{e}^{{\displaystyle 3{\chi }_1}}+1296{\beta }^4{D}_{11}^6{e}^{{\displaystyle 4{\chi }_1}}$$

(15)

where

$$\begin{array}{cc}\hfill P=3{\beta }^2[& {\displaystyle -\frac{1}{16}\left({\partial }_{k_1}^4{D}_{11}\right)-\frac{1}{2}\left({\displaystyle {\partial }_{k_1}{\chi }_1}\right)\left({\partial }_{k_1}^3{D}_{11}\right)-\frac{3}{2}{\left({\displaystyle {\partial }_{k_1}{\chi }_1}\right)}^2\left({\partial }_{k_1}^2{D}_{11}\right)+({\partial }_{k_1}^3{\chi }_1}\hfill \\ \hfill & -2{\left({\displaystyle {\partial }_{k_1}{\chi }_1}\right)}^3)\left({\partial }_{k_1}{D}_{11}\right)+\left(2\left({\displaystyle {\partial }_{k_1}{\chi }_1}\right)\left({\displaystyle {\partial }_{k_1}^3{\chi }_1}\right)-3{\left({\displaystyle {\partial }_{k_1}^2{\chi }_1}\right)}^2-{\left({\displaystyle {\partial }_{k_1}{\chi }_1}\right)}^4\right)D_{11}],\hfill \end{array}$$

$$\begin{array}{cc}\hfill Q=-18{\beta }^3[& {\displaystyle \left(4{\partial }_{k_1}^3{\chi }_1-6\left({\displaystyle {\partial }_{k_1}{\chi }_1}\right)\left({\displaystyle {\partial }_{k_1}^2{\chi }_1}\right)\right)D_{11}^3+(6\left({\partial }_{k_1}{D}_{11}\right){\left({\displaystyle {\partial }_{k_1}{\chi }_1}\right)}^2-6\left({\partial }_{k_1}{D}_{11}\right)\left({\displaystyle {\partial }_{k_1}^2{\chi }_1}\right)}\hfill \\ \hfill & -\left({\partial }_{k_1}^3{D}_{11}\right))D_{11}^2+\left(6{\left({\partial }_{k_1}{D}_{11}\right)}^2\left({\displaystyle {\partial }_{k_1}{\chi }_1}\right)+3\left({\partial }_{k_1}{D}_{11}\right)\left({\partial }_{k_1}^2{D}_{11}\right)\right)D_{11}],\hfill \end{array}$$

and $k_1,{\chi }_1^{\left(0\right)}$ are arbitrary real parameters, $D_{11}$ fulfils Equation (8).

With ${\displaystyle \beta =\pm \frac{4}{3}{(5+2\sqrt{5})}^{\frac{3}{2}}{k}_1^3}$, we give bright ($\beta >0$) and dark ($\beta <0$) quadruple-pole solutions in Figure 4. Each solution has a protruding part and a collapsing part, with the protruding part of the light solution in the same position as the collapsing part of the dark solution, and vice versa. It follows that two types of solutions have exactly the same trajectory at infinity and are symmetric about the origin. The four trajectories in Figure 4b,d are

$$\begin{array}{cc}\hfill & x=\frac{5-3\sqrt{5}}{10}{k}_1^{2}t\pm \frac{\ln \left(9(5-\sqrt{5})k_1^6{t}^2\right)-\ln 10}{2k_1},\hfill \\ \hfill & x=\frac{5-3\sqrt{5}}{10}{k}_1^{2}t\pm \frac{\ln \left(1296(5-2\sqrt{5})k_1^{18}{t}^6\right)-2\ln 5}{2k_1}.\hfill \end{array}$$

(16)

4. Interaction between Multiple-Pole Solutions

As we all know, the interaction between solitons causes phase shifts, so interaction between double-pole solutions also causes phase shifts. Actually, based on Equation (7), let

$$\begin{array}{cc}\hfill N=2n,& k_2=k_1+ϵ,k_4=k_3+ϵ,\cdots ,k_{2n}=k_1+(2n-1)ϵ,\hfill \\ \hfill & {\eta }_1^{\left(0\right)}={\chi }_1^{\left(0\right)}+\ln \left(-\frac{\beta }{ϵ}\right),{\eta }_2^{\left(0\right)}={\chi }_1^{\left(0\right)}+\ln \left(\frac{\beta }{ϵ}\right),\cdots ,\hfill \\ \hfill & {\eta }_{2n-1}^{\left(0\right)}={\chi }_{2n-1}^{\left(0\right)}+\ln \left(-\frac{\beta }{ϵ}\right),{\eta }_{2n}^{\left(0\right)}={\chi }_{2n-1}^{\left(0\right)}+\ln \left(\frac{\beta }{ϵ}\right),\hfill \end{array}$$

(17)

then a $2n$-order soliton solution will be degenerated to the interaction between n double-pole solutions when $ϵ\to 0$, $k_j,{\chi }_j^{\left(0\right)}$ are consistent with the above constraints.

For $n=1$, apparently, we can acquire a double-pole soliton as shown in Equation (8).

For $n=2$, the expression of the interaction between two double-pole solutions $u_{2-2}$ is

$$u_{2-2}=2ln{\left(f\right)}_x,$$

(18)

$$\begin{array}{cc}\hfill f=1& +\beta {\partial }_{k_1}\left(e^{{\displaystyle {\chi }_1}}\right)+\beta {\partial }_{k_3}\left(e^{{\displaystyle {\chi }_3}}\right)-{\beta }^2{D}_{11}{e}^{{\displaystyle 2{\chi }_1}}-{\beta }^2{D}_{33}{e}^{{\displaystyle 2{\chi }_3}}+{\beta }^2\left({\partial }_{k_1}{\partial }_{k_3}{D}_{13}\right)e^{{\displaystyle {\chi }_1+{\chi }_3}}\hfill \\ \hfill & -{\beta }^3{D}_{13}{D}_{11}\left(D_{13}\left({\partial }_{k_3}{\chi }_3\right)+2{\partial }_{k_3}{D}_{13}\right)e^{{\displaystyle 2{\chi }_1+{\chi }_3}}\hfill \\ \hfill & {\displaystyle -{\beta }^3{D}_{13}{D}_{33}\left(D_{13}\left({\partial }_{k_1}{\chi }_1\right)+2{\partial }_{k_1}{D}_{13}\right)e^{{\displaystyle {\chi }_1+2{\chi }_3}}+{\beta }^4{D}_{11}{D}_{13}^4{D}_{33}{e}^{{\displaystyle 2({\chi }_1+{\chi }_3)}}.}\hfill \end{array}$$

(19)

Taking parameters $k_1=\frac{3}{5},k_3=\frac{13}{10},{\chi }_1^{\left(0\right)}={\chi }_3^{\left(0\right)}=0$, the solution defined by Equation (18) is shown in Figure 5. To show the dynamic behavior more clearly, unlike Equation (8), we choose ${\displaystyle {\omega }_j=-\frac{5+3\sqrt{5}}{10}{k}_j^3}$. Comparing the two cases (${\displaystyle \beta =\pm \frac{1}{10}}$) in Figure 5, we find that the positive or negative of $\beta$ only affects the direction of the perturbation, not the orientation of where the solution lies. Based on the conclusion of Equation (8) and the method of analyzing the interaction solution mentioned in [22], we have promotional conclusions about trajectories in Figure 5b,d. To facilitate further study of this by other scholars, we likewise give the mathematical expressions of the trajectory of $u_{2-2}$ when $\left|t\right|\to \infty$.

The trajectory corresponding to $k_1$:

$$\begin{array}{cc}\hfill & x=\frac{(3\sqrt{5}+5)}{10}{k}_1^{2}t\pm \frac{1}{2k_1}ln\left(\frac{18(5+\sqrt{5})k_1^6{t}^2}{5}\right)+\frac{5ln(720-288\sqrt{5})}{6},t\to +\infty ,\hfill \\ \hfill & x=\frac{(3\sqrt{5}+5)}{10}{k}_1^{2}t\pm \frac{1}{2k_1}ln\left(\frac{18(5+\sqrt{5})k_1^6{t}^2}{5}\right)+\frac{5}{3}ln\frac{390963\sqrt{5-2\sqrt{5}}}{250000},t\to -\infty .\hfill \end{array}$$

(20)

The trajectory corresponding to $k_3$:

$$\begin{array}{cc}\hfill & x=\frac{(3\sqrt{5}+5)}{10}{k}_3^{2}t\pm \frac{1}{2k_3}ln\left(\frac{18(5+\sqrt{5})k_3^6{t}^2}{5}\right)+\frac{5ln(3380-1352\sqrt{5})}{13},t\to +\infty ,\hfill \\ \hfill & x=\frac{(3\sqrt{5}+5)}{10}{k}_3^{2}t\pm \frac{1}{2k_3}ln\left(\frac{18(5+\sqrt{5})k_3^6{t}^2}{5}\right)+\frac{10}{13}ln\frac{1694173\sqrt{5-2\sqrt{5}}}{500000},t\to -\infty .\hfill \end{array}$$

(21)

Two-soliton solutions can be reduced to a breather wave with a special property as long as we add to the module resonance conditions

$$k_1=k_3^{*},{\chi }_1^{\left(0\right)}={\chi }_3^{\left(0\right)*},$$

(22)

where the symbol * stands for conjugate. Figure 6 vividly depicts the dynamic property of the degenerate of the second-order breather solution.

However, the above limit substitution method in Equation (18) does not derive the interaction between triple-pole solutions, so we can promote it further.

Let

$$\begin{array}{cc}\hfill & N=2n,k_2=k_1+ϵ,k_3=k_1+2ϵ,k_4=k_1+3ϵ,\cdots ,k_n=k_1+(n-1)ϵ,\hfill \\ \hfill & k_{n+2}=k_{n+1}+ϵ,k_{n+3}=k_{n+1}+2ϵ,\cdots ,k_{2n}=k_{n+1}+(n-1)ϵ,\hfill \\ \hfill & {\eta }_1^{\left(0\right)}={\chi }_1^{\left(0\right)}+ln\frac{{(-1)}^{n+1}{C}_{n-1}^0}{{ϵ}^{n-1}},{\eta }_2^{\left(0\right)}={\chi }_1^{\left(0\right)}+ln\frac{{(-1)}^{n+2}{C}_{n-1}^1}{{ϵ}^{n-1}},\cdots ,{\eta }_n^{\left(0\right)}={\chi }_1^{\left(0\right)}+ln\frac{{(-1)}^{2n}{C}_{n-1}^{n-1}}{{ϵ}^{n-1}},\hfill \\ \hfill & {\eta }_{n+1}^{\left(0\right)}={\chi }_{n+1}^{\left(0\right)}+ln\frac{{(-1)}^{n+1}{C}_{n-1}^0}{{ϵ}^{n-1}},{\eta }_{n+2}^{\left(0\right)}={\chi }_{n+1}^{\left(0\right)}+ln\frac{{(-1)}^{n+2}{C}_{n-1}^1}{{ϵ}^{n-1}},\cdots ,{\eta }_{2n}^{\left(0\right)}={\chi }_{n+1}^{\left(0\right)}+ln\frac{{(-1)}^{2n}{C}_{n-1}^{n-1}}{{ϵ}^{n-1}},\hfill \\ \hfill & k_1=k_{n+1}^{*},{\xi }_1^{\left(0\right)}={\xi }_{n+1}^{\left(0\right)*},\hfill \end{array}$$

(23)

then the degenerate solution of n-order breather solution will be generated when $ϵ\to 0$. The last row of conditions in Equation (23) are the module resonance constraints. Remove this requirement, and we can acquire the interaction between two triple-pole solutions and two quadruple-pole solutions, and so on. Together with the above resonance conditions, also we can obtain the degenerate solution of the n-order breather solution.

The nonlinear superposition of multiple-pole solutions and single solitons is studied subsequently. Subject to the three-soliton solution, we simply do the transformation (7) and then similarly make $ϵ$ converge to zero. Figure 7 demonstrates the various cases of nonlinear superposition of the double-pole solution and single soliton for different $k_3$. Taking $k_1=2$, when $0<k_3<k_1$, the density plots of the solution after superposition is similar to the shape of double-pole solution (in Figure 2b). And the superposition solution also can be seen as four solutions at t infinity. When $k_3=k_1$, the original form of the multipole solution disappears, forming a special Y-shaped solution. The method used to derive this solution is quite different from the method we commonly use to derive a resonance Y-type solution by making $\exp \left(A_{js}\right)=0$. It is worth investigating further whether this excitation pattern constant. For $k_3>k_1$, the density plots of the superposition solution has five ($k_3=3$) and six ($k_3=5$) tracks at t infinity, respectively.

5. Conclusions

We use the new limit method to generate different degenerate solutions directly from an N-soliton solution by means of the Hirota bilinear method for the bidirectional sixth-order Sawada–Kotera equation. The degenerate solutions include both multiple-pole solutions as shown in Figure 2, Figure 3 and Figure 4. With module resonance conditions, the degenerate solution of a second-order breather solution is as shown in Figure 6. The dynamic properties of these multiple-pole solutions are accurately expressed by Equations (9), (13) and (16). Equations (20), (21) and Figure 5 perfectly prove that the collision between two double-pole solutions is elastic. Compared with the results in the literature [23,24], the findings have similarities with the results we obtained. In the end, we study the superposition solutions consisting of a double-pole solution and different single-soliton solutions. In this context, the mechanism by which the Y-type solution is formed deserves further investigation. With Equation (23), we can obtain the interaction between two n-pole solutions.

We hope that all exact solutions obtained in this paper will be fully used in physics, specifically in plasmas, optics and quantum mechanics. This method still operates for the larger N case. It is simpler to calculate than the inverse scattering method. The methods mentioned in this paper can be used with other integrable systems. A wider range of substituting forms will be studied in our future research.