Quantum Hairy Black Hole Formation and Horizon Quantum Mechanics
Abstract
1. Introduction
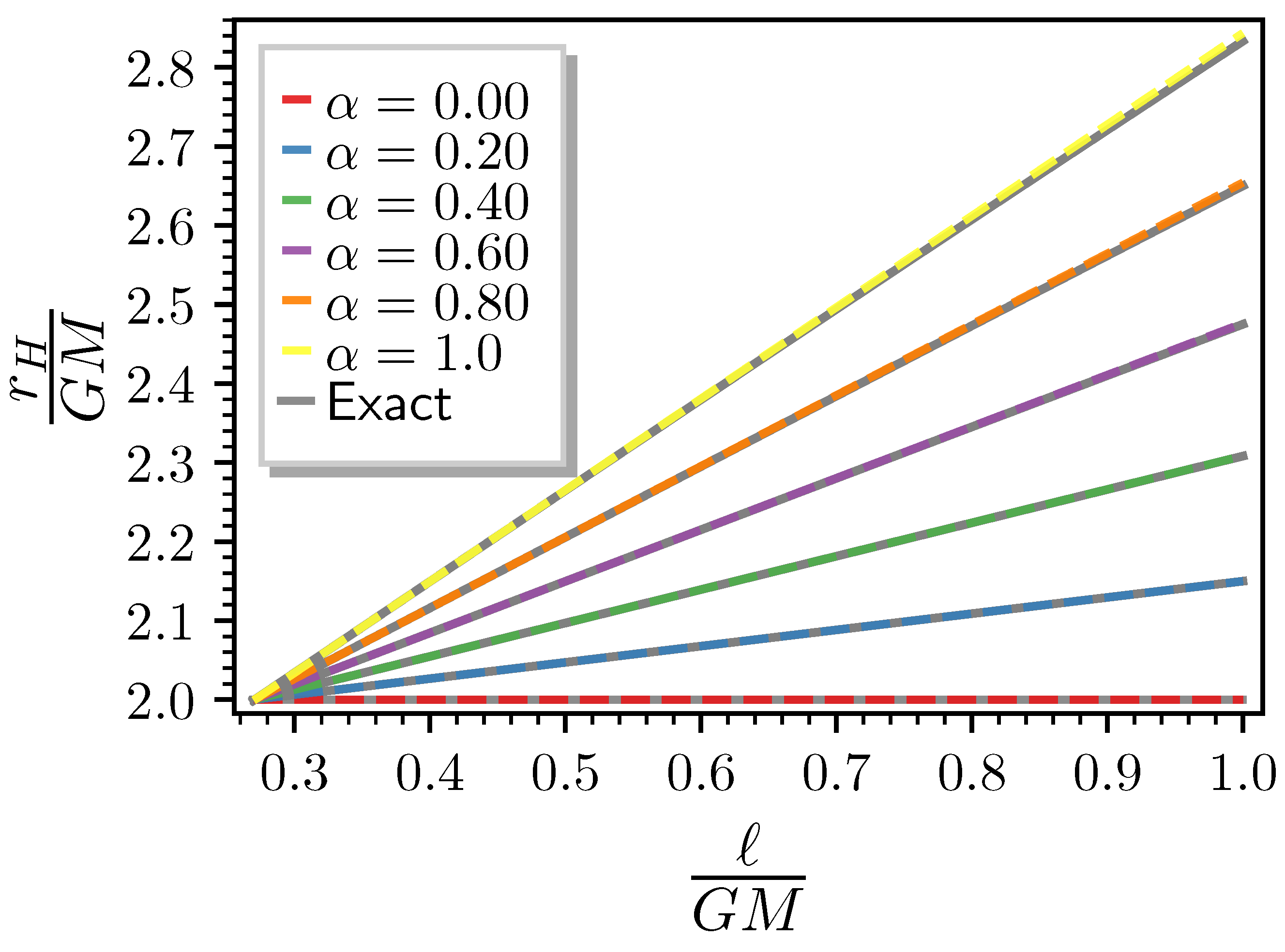
2. Hairy Black Holes and Horizon Radius
3. The Horizon Quantum Mechanics Formalism
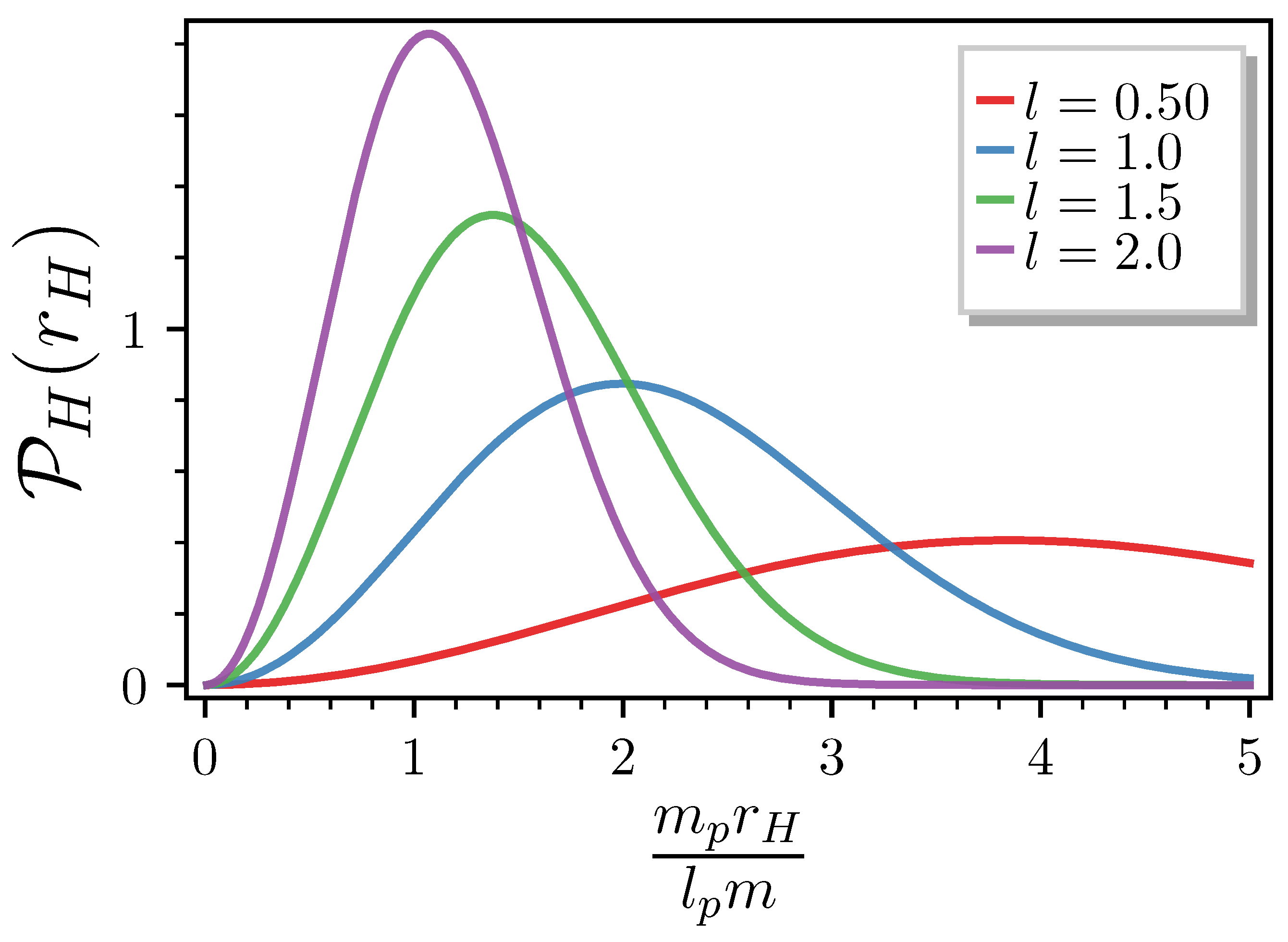
3.1. Gaussian Sources
3.2. HQM and GUP
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | The analytical expression of is huge and little enlightening. |
References
- Hawking, S.W.; Ellis, G.F.R. The Large Scale Structure of Space-Time; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The Mathematical Theory of Black Holes. Fundam. Theor. Phys. 1984, 9, 5–26. [Google Scholar] [CrossRef]
- Frolov, V.P.; Novikov, I.D. (Eds.) Black Hole Physics: Basic Concepts and New Developments; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Cavalieri, R. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Cardoso, V.; Pani, P. Testing the nature of dark compact objects: A status report. Living Rev. Rel. 2019, 22, 4. [Google Scholar] [CrossRef]
- Barack, L.; Cardoso, V.; Nissanke, S.; Sotiriou, T.P.; Askar, A.; Belczynski, C.; Moore, C.J. Black holes, gravitational waves and fundamental physics: A roadmap. Class. Quant. Grav. 2019, 36, 143001. [Google Scholar] [CrossRef]
- Calmet, X. (Ed.) Quantum Aspects of Black Holes; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Wald, R.M. General Relativity; Chicago University Press: Chicago, IL, USA, 1984. [Google Scholar] [CrossRef]
- Faraoni, V. Cosmological and Black Hole Apparent Horizons; Springer: Berlin/Heidelberg, Germany, 2015; Volume 907. [Google Scholar] [CrossRef]
- Ashtekar, A.; Krishnan, B. Dynamical horizons and their properties. Phys. Rev. D 2003, 68, 104030. [Google Scholar] [CrossRef]
- Ashtekar, A.; Galloway, G.J. Some uniqueness results for dynamical horizons. Adv. Theor. Math. Phys. 2005, 9, 1–30. [Google Scholar] [CrossRef]
- Gourgoulhon, E.; Jaramillo, J.L. New theoretical approaches to black holes. New Astron. Rev. 2008, 51, 791–798. [Google Scholar] [CrossRef]
- Calmet, X.; Casadio, R. What is the final state of a black hole merger? Mod. Phys. Lett. A 2018, 33, 1850124. [Google Scholar] [CrossRef]
- Calmet, X.; Kuipers, F. Black holes in quantum gravity. Nuovo Cim. C 2022, 45, 37. [Google Scholar] [CrossRef]
- Casadio, R.; Orlandi, A. Quantum Harmonic Black Holes. J. High Energy Phys. 2013, 08, 025. [Google Scholar] [CrossRef]
- Casadio, R.; Giugno, A.; Micu, O.; Orlandi, A. Black holes as self-sustained quantum states, and Hawking radiation. Phys. Rev. D 2014, 90, 084040. [Google Scholar] [CrossRef]
- Calmet, X.; Casadio, R.; Hsu, S.D.H.; Kuipers, F. Quantum Hair from Gravity. Phys. Rev. Lett. 2022, 128, 111301. [Google Scholar] [CrossRef]
- Will, C.M. The Confrontation between General Relativity and Experiment. Living Rev. Rel. 2014, 17, 4. [Google Scholar] [CrossRef]
- Berti, E.; Barausse, E.; Cardoso, V.; Gualtieri, L.; Pani, P.; Sperhake, U.; Zilhao, M. Testing General Relativity with Present and Future Astrophysical Observations. Class. Quant. Grav. 2015, 32, 243001. [Google Scholar] [CrossRef]
- Kanti, P.; Bakopoulos, A.; Pappas, N. Scalar-Gauss-Bonnet Theories: Evasion of No-Hair Theorems and novel black-hole solutions. PoS 2019, CORFU2018, 091. [Google Scholar] [CrossRef][Green Version]
- Sotiriou, T.P.; Zhou, S.Y. Black hole hair in generalized scalar-tensor gravity: An explicit example. Phys. Rev. D 2014, 90, 124063. [Google Scholar] [CrossRef]
- Cavalcanti, R.T.; Alves, K.d.S.; Hoff da Silva, J.M. Near-Horizon Thermodynamics of Hairy Black Holes from Gravitational Decoupling. Universe 2022, 8, 363. [Google Scholar] [CrossRef]
- Casadio, R.; Cavalcanti, R.T.; Giugno, A.; Mureika, J. Horizon of quantum black holes in various dimensions. Phys. Lett. B 2016, 760, 36–44. [Google Scholar] [CrossRef]
- Arsene, N.; Casadio, R.; Micu, O. Quantum production of black holes at colliders. Eur. Phys. J. C 2016, 76, 384. [Google Scholar] [CrossRef]
- Ovalle, J. Decoupling gravitational sources in general relativity: From perfect to anisotropic fluids. Phys. Rev. D 2017, 95, 104019. [Google Scholar] [CrossRef]
- Ovalle, J. Decoupling gravitational sources in general relativity: The extended case. Phys. Lett. B 2019, 788, 213–218. [Google Scholar] [CrossRef]
- Ovalle, J.; Casadio, R.; Contreras, E.; Sotomayor, A. Hairy black holes by gravitational decoupling. Phys. Dark Univ. 2021, 31, 100744. [Google Scholar] [CrossRef]
- da Rocha, R. MGD Dirac stars. Symmetry 2020, 12, 508. [Google Scholar] [CrossRef]
- Tello-Ortiz, F.; Malaver, M.; Rincón, A.; Gomez-Leyton, Y. Relativistic anisotropic fluid spheres satisfying a non-linear equation of state. Eur. Phys. J. C 2020, 80, 371. [Google Scholar] [CrossRef]
- da Rocha, R. Minimal geometric deformation of Yang-Mills-Dirac stellar configurations. Phys. Rev. D 2020, 102, 024011. [Google Scholar] [CrossRef]
- Fernandes-Silva, A.; Ferreira-Martins, A.J.; da Rocha, R. Extended quantum portrait of MGD black holes and information entropy. Phys. Lett. B 2019, 791, 323–330. [Google Scholar] [CrossRef]
- da Rocha, R. Dark SU(N) glueball stars on fluid branes. Phys. Rev. D 2017, 95, 124017. [Google Scholar] [CrossRef]
- Da Rocha, R.; Tomaz, A.A. Holographic entanglement entropy under the minimal geometric deformation and extensions. Eur. Phys. J. C 2019, 79, 1035. [Google Scholar] [CrossRef]
- Ovalle, J.; Contreras, E.; Stuchlik, Z. Kerr–de Sitter black hole revisited. Phys. Rev. D 2021, 103, 084016. [Google Scholar] [CrossRef]
- Meert, P.; da Rocha, R. Gravitational decoupling, hairy black holes and conformal anomalies. Eur. Phys. J. C 2022, 82, 175. [Google Scholar] [CrossRef]
- Cavalcanti, R.T.; de Paiva, R.C.; da Rocha, R. Echoes of the gravitational decoupling: Scalar perturbations and quasinormal modes of hairy black holes. Eur. Phys. J. Plus 2022, 137, 1185. [Google Scholar] [CrossRef]
- Gross, D.J.; Mende, P.F. String Theory Beyond the Planck Scale. Nucl. Phys. B 1988, 303, 407–454. [Google Scholar] [CrossRef]
- Konishi, K.; Paffuti, G.; Provero, P. Minimum Physical Length and the Generalized Uncertainty Principle in String Theory. Phys. Lett. B 1990, 234, 276–284. [Google Scholar] [CrossRef]
- Amati, D.; Ciafaloni, M.; Veneziano, G. Can Space-Time Be Probed Below the String Size? Phys. Lett. B 1989, 216, 41–47. [Google Scholar] [CrossRef]
- Rovelli, C.; Smolin, L. Discreteness of area and volume in quantum gravity. Nucl. Phys. B 1995, 442, 593–622, Erratum in Nucl. Phys. B 1995, 456, 753–754. [Google Scholar] [CrossRef]
- Scardigli, F. Generalized uncertainty principle in quantum gravity from micro - black hole Gedanken experiment. Phys. Lett. B 1999, 452, 39–44. [Google Scholar] [CrossRef]
- Maggiore, M. A Generalized uncertainty principle in quantum gravity. Phys. Lett. B 1993, 304, 65–69. [Google Scholar] [CrossRef]
- Hossenfelder, S. Minimal Length Scale Scenarios for Quantum Gravity. Living Rev. Rel. 2013, 16, 2. [Google Scholar] [CrossRef]
- Casadio, R.; Micu, O.; Nicolini, P. Minimum length effects in black hole physics. Fundam. Theor. Phys. 2015, 178, 293–322. [Google Scholar] [CrossRef]
- Sprenger, M.; Nicolini, P.; Bleicher, M. Physics on Smallest Scales—An Introduction to Minimal Length Phenomenology. Eur. J. Phys. 2012, 33, 853–862. [Google Scholar] [CrossRef]
- Tawfik, A.N.; Diab, A.M. Review on Generalized Uncertainty Principle. Rept. Prog. Phys. 2015, 78, 126001. [Google Scholar] [CrossRef]
- Casadio, R.; Giugno, A.; Micu, O. Horizon quantum mechanics: A hitchhiker’s guide to quantum black holes. Int. J. Mod. Phys. D 2016, 25, 1630006. [Google Scholar] [CrossRef]
- Casadio, R. Localised particles and fuzzy horizons: A tool for probing Quantum Black Holes. arXiv 2013, arXiv:1305.3195. [Google Scholar]
- Casadio, R.; Giugno, A.; Giusti, A.; Lenzi, M. Quantum Formation of Primordial Black holes. Gen. Rel. Grav. 2019, 51, 103. [Google Scholar] [CrossRef]
- Casadio, R.; Micu, O. Horizon Quantum Mechanics of collapsing shells. Eur. Phys. J. C 2018, 78, 852. [Google Scholar] [CrossRef]
- Casadio, R.; Giugno, A.; Giusti, A. Global and Local Horizon Quantum Mechanics. Gen. Rel. Grav. 2017, 49, 32. [Google Scholar] [CrossRef]
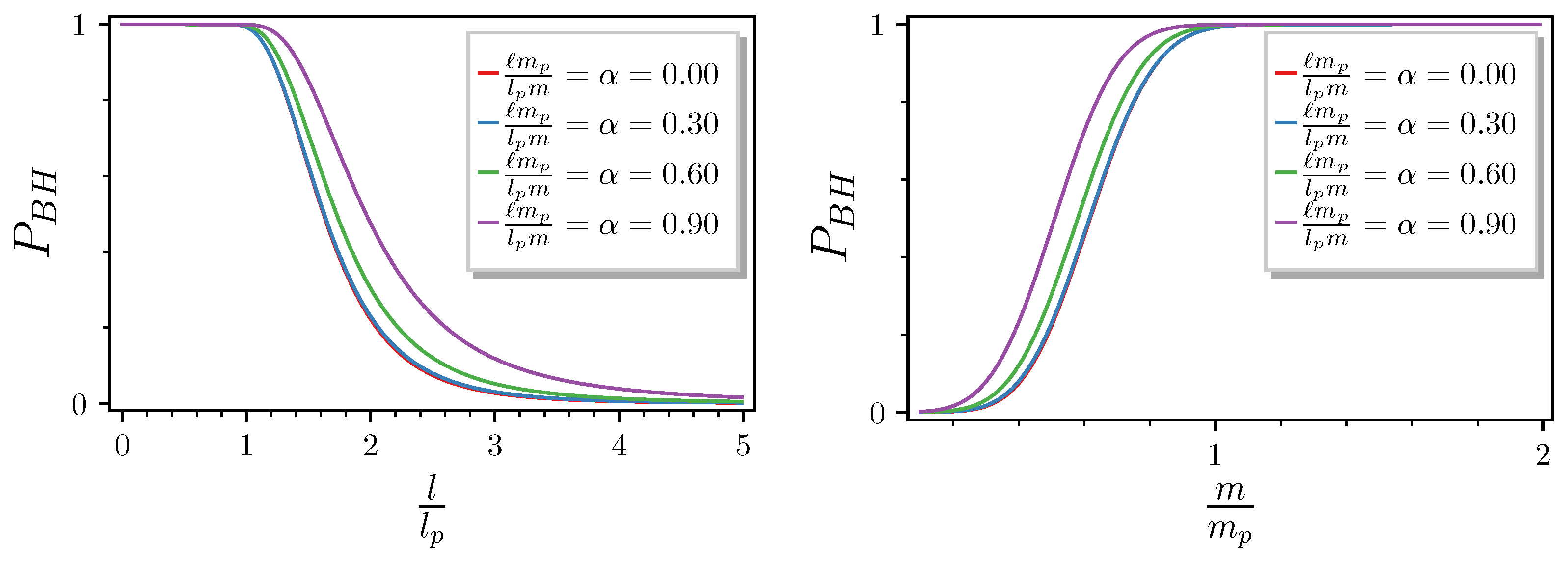


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cavalcanti, R.T.; da Silva, J.M.H. Quantum Hairy Black Hole Formation and Horizon Quantum Mechanics. Universe 2023, 9, 23. https://doi.org/10.3390/universe9010023
Cavalcanti RT, da Silva JMH. Quantum Hairy Black Hole Formation and Horizon Quantum Mechanics. Universe. 2023; 9(1):23. https://doi.org/10.3390/universe9010023
Chicago/Turabian StyleCavalcanti, Rogerio Teixeira, and Julio Marny Hoff da Silva. 2023. "Quantum Hairy Black Hole Formation and Horizon Quantum Mechanics" Universe 9, no. 1: 23. https://doi.org/10.3390/universe9010023
APA StyleCavalcanti, R. T., & da Silva, J. M. H. (2023). Quantum Hairy Black Hole Formation and Horizon Quantum Mechanics. Universe, 9(1), 23. https://doi.org/10.3390/universe9010023







