Abstract
The Hermean average perihelion rate , calculated to the second post-Newtonian (2PN) order with the Gauss perturbing equations and the osculating Keplerian orbital elements, ranges from to microarcseconds per century , depending on the true anomaly at epoch . It is the sum of four contributions: one of them is the direct consequence of the 2PN acceleration entering the equations of motion, while the other three are indirect effects of the 1PN component of the Sun’s gravitational field. An evaluation of the merely formal uncertainty of the experimental Mercury’s perihelion rate recently published by the present author, based on 51 years of radiotechnical data processed with the EPM2017 planetary ephemerides by the astronomers E.V. Pitjeva and N.P. Pitjev, is , corresponding to a relative accuracy of for the combination of the PPN parameters and scaling the well known 1PN perihelion precession. In fact, the realistic uncertainty may be up to ≃10–50 times larger, despite reprocessing the now available raw data of the former MESSENGER mission with a recently improved solar corona model should ameliorate our knowledge of the Hermean orbit. The BepiColombo spacecraft, currently en route to Mercury, might reach a accuracy level in constraining and in an extended mission, despite seems more likely according to most of the simulations currently available in the literature. Thus, it might be that in the not-too-distant future, it will be necessary to include the 2PN acceleration in the Solar System’s dynamics as well.
1. Introduction
The post-Newtonian (PN) approximation (see, e.g., [1,2,3,4,5,6] and references therein) is a computational scheme for solving Einstein’s field equations of their General Theory of Relativity (GTR) relying upon the assumptions that the characteristic speeds of the bodies under consideration are smaller than the speed of light c and that the gravitational fields inside and around them are weak. Nonetheless, as pointed out in [7], such a scheme turned out to be remarkably effective in describing also certain strong-field and fast motion systems such as compact binaries made of at least one dense neutron star and inspiralling pairs of black holes emitting gravitational waves; the reasons for that are largely unknown [7]. Thus, putting the PN approximation to the test in as many different scenarios and at the highest order of approximation as possible is of paramount importance to gain ever-increasing confidence in it.
In its technical realm of validity, the PN approximation has been successfully tested so far only to the first post-Newtonian (1PN) order with, e.g., the orbital motions of planets, asteroids and spacecraft in the Solar System [8,9,10,11,12,13], being its 2PN effects deemed too small to be currently measurable. The 1PN precession of the pericentre was measured also with binary pulsars [14,15] and stars orbiting the supermassive black hole at the center of the Galaxy in Sgr A [16].
The 2PN precession of the pericentre of a two-body system, recently worked out1 [22] in a perturbative way with the Gauss Equations [23] and the standard osculating Keplerian orbital elements [24], was investigated in [25] for the double pulsar PSR J0737-3039A/B [26,27] since it is viewed as a major source of systematic error in the expected future determination of the spin–orbit Lense–Thirring periastron precession [20] since it should fall within the envisaged sensitivity level.
Here, we explore the perspectives of including, a day, the 2PN effects in the dynamics of the Solar System by looking at the perihelion of Mercury and the present and future level of accuracy in knowing its orbit. For the light propagation to the order and its possible astrometric measurements in the Solar System, see, e.g., [28] and references therein. Furthermore, various consequences of modified models of gravity were investigated to the 2PN order; see, e.g., [29,30,31,32,33].
The paper is organized as follows. In Section 2, we review the calculational strategy put forth in [22] to obtain the total 2PN precession of the pericenter of a two-body system. The results are applied in Section 3 to Mercury and compared to the latest figures for the uncertainty in determining its perihelion rate. The role of the ongoing BepiColombo mission in improving the Hermean orbit determination is discussed as well. Section 4 summarizes our findings and offers our conclusions.
2. The 2PN Precession of the Pericenter
The total 2PN net2 precession of the argument of pericenter of a binary system made of two static, spherically symmetric bodies A and B, written in terms of the usual osculating Keplerian orbital elements, is [22] eq. (18), p. 4
where is the gravitational parameter of the two-body system given by the product of the sum of its masses by the Newtonian constant of gravitation G, the dimensionless parameter is given by , , and are the osculating values of the semimajor axis, eccentricity and true anomaly, respectively, at the same arbitrary moment of time [24].
From Equation (2) it can be noted that, to the order of zero in e, the 2PN pericentre precession is independent of .
It should be recalled that Equation (1) does not come only from the direct3 effect of the 2PN acceleration entering the equation of motion (see, e.g., [22] eq. (38), p. 8). Indeed, also two indirect, or mixed, effects related to the 1PN acceleration (see, e.g., [22] eq. (37), p. 7) subtly concur to yield the net shift per orbit to the 2PN level from which (a part of) the precession follows by dividing it by the (Keplerian) orbital period ; see [34] for how to calculate such indirect effects in a different scenario. They are due to the following facts. On the one hand, during an orbital revolution, all the orbital elements entering the right hand side of the Gauss equation for [35], calculated with , in principle, undergo instantaneous variations due to itself changing their values with respect to their fixed Keplerian ones referred to some reference epoch . On the other hand, when the integration over f is performed calculating , the fact that the true anomaly is reckoned from a generally varying line of apsides because of should be taken into account as well. Such features yield two additional corrections to with respect to the usual 1PN one4
which, in the case of , are just of the order of . Finally, as shown in [22], when the total 2PN net precession has to be calculated, the 1PN fractional shift per orbit must be multiplied by the 1PN mean motion , and an expansion in powers of to the order of must be taken. Thus, the precession of Equation (1) comes from the sum of the latter contribution plus the direct rate induced by and the two indirect terms due to .
In [22], it is shown that Equation (1) agrees with other calculations existing in the literature performed with different computational strategies [20,36]. In particular, Equation (1) is in agreement with the expression for the total 2PN pericentre precession, written in terms of the osculating Keplerian orbital elements, which can be inferred from [20] eq. (5.18), p. 158 based on the Damour-Deruelle parameterization [21].
3. The 2PN Perihelion Precession of Mercury
In the case of Sun and Mercury5, Figure 1, displaying the plot of Equation (1) as a function of , shows that the Hermean 2PN precession ranges from to microarcseconds per century .
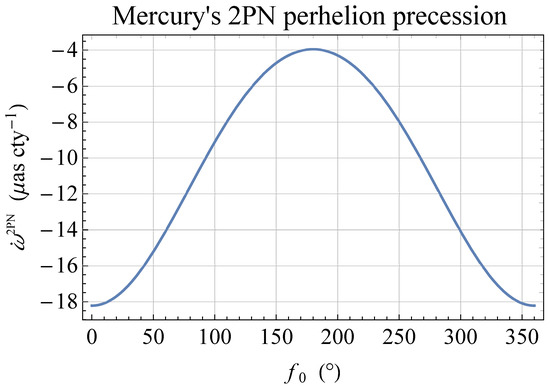
Figure 1.
Total 2PN perihelion precession of Mercury, in , as a function of the true anomaly at epoch according to Equation (1). It turns out that .
About the current accuracy in determining observationally the perihelion precession of Mercury, the present author in [38] tentatively inferred a formal uncertainty as little as
from the planetary ephemerides6 EPM2017 [39]. At first glance, Equation (4) might seem interesting since it is of the same order of magnitude as the 2PN contribution to the Hermean perihelion precession. The dynamical models of7 EPM2017 is accurate to the 1PN level, including, among other things, also the Lense–Thirring effect induced by the Sun’s angular momentum . As far as Mercury is concerned, they are based only on radio tracking data resulting in 1556 normal points over a temporal interval 51 years long (1964–2015); in particular, data collected by the MESSENGER (Mercury Surface, Space Environment, Geochemistry and Ranging) spacecraft from 2011 to 2015 were analyzed. As pointed out in [38,39], realistic accuracies at the time of writing such papers may be ≃10–50 times larger than Equation (4). On the other hand, a new model of solar plasma affecting the spacecraft ranging observations was recently published [40]; it can now be used to reprocess the raw MESSENGER data8 which were recently released9. This should improve the accuracy of our knowledge of Mercury’s orbit. As noted in [38], Equation (4) corresponds to an uncertainty as little as in the combination of the PPN parameters and in front of Equation (3). The ongoing mission to Mercury BepiColombo [41] aims, among other things, to accurately determine and ; according to [42] Table 5, p. 21, an extended mission may reach just the accuracy level in constraining such PPN parameters. The same conclusion is shown also in [43] Table 2, p. 12; see also references therein. However, it should be remarked that most of the scenarios examined in [41,43] envisage an accuracy in constraining and of the order of . Be that as it may, perhaps, we may not be so far away from having to include, one day, also the 2PN terms in Solar System’s dynamics.
In principle, a source of major systematic error which may overwhelm the 2PN perihelion precession is represented by the competing classical effect due to tidal distortion involving the Hermean Love number [44,45]. Such a parameter measures the mass concentration toward the center of a fluid body assumed in hydrostatic equilibrium such as, e.g., a main sequence star. Its possible values range from 0 for the mass point approximation to for a fully homogeneous fluid body [46]. For a binary system, the periastron precession of tidal origin is [46] eq. (3.100), p. 170
where is the semilatus rectum of the two-body relative orbit, and is the equatorial radius of the body A or B. A recent determination of the Love number of Mercury relying upon the analysis of the complete four years of MESSENGER tracking data from March 2011 to April 2015 yields10 [47]
The nominal value of the Hermean contribution11 to Equation (5), calculated with Equation (6), is of the order of a few . Nonetheless, by assuming to model the tidal effects to the level of accuracy of Equation (6), the resultant mismodeled perihelion precession would be well below the 2PN one.
From a practical point of view, experts in planetary data reductions should clarify which part of Equation (1) could be, actually, measured and how. Indeed, given that the 1PN equations of motion are currently included in the dynamical force models of the software routinely adopted to process the data, it may be argued that the indirect components of Equation (1) should have already been measured along with the 1PN precession; if so, only the direct part due to could be detected by explicitly modeling it and estimating, say, a dedicated scaling solve-for parameter. Otherwise, should be modeled in terms of and whose newly estimated values, if known at the level, would account for the 2PN component of the equations of motion as well.
4. Summary and Conclusions
The 2PN pericentre precession of a two-body system made of two static, spherically symmetric masses, obtained with the standard Gauss perturbative equation in terms of the usual osculating Keplerian orbital elements, is reviewed. Both the exact expression (Equation (1)) and an approximated expansion in powers of the eccentricity e up to the order of (Equation (2)) are given. It is recalled that consists of four contributions: a direct term straightforwardly arising from the 2PN acceleration in the equations of motion, and three indirect parts due to the 1PN acceleration itself. In particular, one of the latter ones arises from the expansion to the order of of the product of the well-known fractional 1PN shift per orbit (the ratio of Equation (3) to ) by the 1PN mean motion. The other two indirect contributions come from taking into account also the instantaneous variations of the order of of the orbital elements and the fact that the anomalistic period over which the 1PN shift is integrated is the time interval between two successive crossings of an actually moving pericenter due to itself. The resulting total 2PN precession of Equation (1) depends on the true anomaly at epoch . It is remarked that Equation (1) agrees with other expressions for in the literature obtained with different parameterizations and calculational schemes.
In the case of the Sun and Mercury, the Hermean 2PN perihelion precession, calculated with Equation (1), ranges from to depending on . A recent guess for the formal experimental uncertainty in determining Mercury’s perihelion precession with the EPM2017 planetary ephemerides is , although the realistic uncertainty may be up to ≃10–50 times larger. Nonetheless, the raw data collected during the past MESSENGER mission are now available, and a new, accurate model of the solar corona, usually a major bias impacting the accuracy of ranging measurements, was recently published. Thus, reprocessing the MESSENGER observations with such a new model should improve our knowledge of Mercury in the near future. A level corresponds to an uncertainty of the order of in the PPN combination scaling the 1PN precession. In a few scenarios encompassing an extended mission profile of the BepiColombo spacecraft, currently en route to Mercury, such a level of accuracy in constraining the PPN parameters and may be reached, although seems more plausible according to the majority of the simulations performed so far in the literature. Anyway, perhaps, the time when it will be necessary to model the dynamics of the Solar System at the 2PN order might not be that far away, after all.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
I am indebted to M. Efroimsky for their careful and attentive comments and remarks, and to R.S. Park for clarifications about the Love number of Mercury. I gratefully thanks also G. Tommei and D. Pavlov for useful information.
Conflicts of Interest
The authors declare no conflict of interest.
Notes
| 1 | Among the several calculations existing in the literature with different computational schemes and parameterizations such as, e.g., [17,18,19], see [20] for a derivation based on the Hamilton–Jacobi method and the Damour-Deruelle parameterization [21]. |
| 2 | Here and in the following, the angular brackets denoting the orbital average are omitted. |
| 3 | It is calculated perturbatively in the usual way by evaluating the right hand side of the Gauss equation for [23], calculated with , onto a fixed Keplerian ellipse, and integrating it over a Keplerian orbital period. |
| 4 | It is obtained by keeping a and e fixed during the integration of the right hand side of the Gauss equation for , calculated with , over a Keplerian orbital period. |
| 5 | For a recent comparative study of Mercury’s perihelion advance induced by some classical dynamical effects, see [37]. |
| 6 | EPM stands for Ephemeris of Planets and the Moon. |
| 7 | See https://iaaras.ru/en/dept/ephemeris/epm/2017/ (accessed on 30 December 2022) for details. |
| 8 | Until now, the simpler model of the NASA Jet Propulsion Laboratory (JPL) was pre-applied to the normal points published by it; see https://ssd.jpl.nasa.gov/dat/planets/messenger.txt (accessed on 30 December 2022). |
| 9 | D. Pavlov, private communication to the present author, November 2022. |
| 10 | It has to be meant as the geophysicists’ Love number, which is twice the astronomers’ one, known also as apsidal constant, entering Equation (5) [46] p. 115. |
| 11 | The one due to the Sun’s Love number is much smaller, being, thus, of no concern. |
References
- Damour, T. The problem of motion in Newtonian and Einsteinian gravity. In Three Hundred Years of Gravitation; Hawking, S., Israel, W., Eds.; Cambridge University Press: Cambridge, UK, 1987; pp. 128–198. [Google Scholar]
- Asada, H.; Futamase, T. Chapter 2. Post–Newtonian Approximation: Its Foundation and Applications. Prog. Theor. Phys. Suppl. 1997, 128, 123–181. [Google Scholar] [CrossRef][Green Version]
- Blanchet, L. On the Accuracy of the Post–Newtonian Approximation. In Proceedings of the 2001: A Relativistic Spacetime Odyssey; Ciufolini, I., Dominici, D., Lusanna, L., Eds.; World Scientific: Singapore, 2003; pp. 411–430. [Google Scholar] [CrossRef]
- Blanchet, L. Gravitational Radiation from Post–Newtonian Sources and Inspiralling Compact Binaries. Living Rev. Relativ. 2006, 9, 4. [Google Scholar] [CrossRef] [PubMed]
- Futamase, T.; Itoh, Y. The Post–Newtonian Approximation for Relativistic Compact Binaries. Living Rev. Relativ. 2007, 10, 2. [Google Scholar] [CrossRef] [PubMed]
- Will, C.M. Theory and Experiment in Gravitational Physics, 2nd ed.; Cabridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Will, C.M. On the unreasonable effectiveness of the post-Newtonian approximation in gravitational physics. Proc. Natl. Acad. Sci. USA 2011, 108, 5938–5945. [Google Scholar] [CrossRef] [PubMed]
- Shapiro, I.I.; Ash, M.E.; Smith, W.B. Icarus: Further Confirmation of the Relativistic Perihelion Precession. Phys. Rev. Lett. 1968, 20, 1517–1518. [Google Scholar] [CrossRef]
- Shapiro, I.I.; Pettengill, G.H.; Ash, M.E.; Ingalls, R.P.; Campbell, D.B.; Dyce, R.B. Mercury’s Perihelion Advance: Determination by Radar. Phys. Rev. Lett. 1972, 28, 1594–1597. [Google Scholar] [CrossRef]
- Shapiro, I.I.; Smith, W.B.; Ash, M.E.; Herrick, S. General Relativity and the Orbit of Icarus. Astron. J. 1971, 76, 588. [Google Scholar] [CrossRef]
- Shapiro, I.I. Solar system tests of general relativity: Recent results and present plans. In Proceedings of the General Relativity and Gravitation, 1989; Ashby, N., Bartlett, D.F., Wyss, W., Eds.; Cambridge University Press: Cambridge, UK, 1990; pp. 313–330. [Google Scholar]
- Lucchesi, D.M.; Peron, R. Accurate Measurement in the Field of the Earth of the General-Relativistic Precession of the LAGEOS II Pericenter and New Constraints on Non–Newtonian Gravity. Phys. Rev. Lett. 2010, 105, 231103. [Google Scholar] [CrossRef]
- Lucchesi, D.M.; Peron, R. LAGEOS II pericenter general relativistic precession (1993-2005): Error budget and constraints in gravitational physics. Phys. Rev. D 2014, 89, 082002. [Google Scholar] [CrossRef]
- Kramer, M.; Stairs, I.H.; Manchester, R.N.; McLaughlin, M.A.; Lyne, A.G.; Ferdman, R.D.; Burgay, M.; Lorimer, D.R.; Possenti, A.; D’Amico, N.; et al. Tests of General Relativity from Timing the Double Pulsar. Science 2006, 314, 97–102. [Google Scholar] [CrossRef]
- Kramer, M.; Stairs, I.H.; Manchester, R.N.; Wex, N.; Deller, A.T.; Coles, W.A.; Ali, M.; Burgay, M.; Camilo, F.; Cognard, I.; et al. Strong-Field Gravity Tests with the Double Pulsar. Phys. Rev. X 2021, 11, 041050. [Google Scholar] [CrossRef]
- Gravity Collaboration; Abuter, R.; Amorim, A.; Bauböck, M.; Berger, J.P.; Bonnet, H.; Brandner, W.; Cardoso, V.; Clénet, Y.; de Zeeuw, P.T.; et al. Detection of the Schwarzschild precession in the orbit of the star S2 near the Galactic centre massive black hole. Astron. Astrophys. 2020, 636, L5. [Google Scholar] [CrossRef]
- Schäfer, G.; Wex, N. Second post-Newtonian motion of compact binaries. Phys. Lett. A 1993, 174, 196–205. [Google Scholar] [CrossRef]
- Wex, N. The second post-Newtonian motion of compact binary-star systems with spin. Class. Quantum Gravity 1995, 12, 983–1005. [Google Scholar] [CrossRef]
- Tucker, A.; Will, C.M. Pericenter advance in general relativity: Comparison of approaches at high post-Newtonian orders. Class. Quantum Gravity 2019, 36, 115001. [Google Scholar] [CrossRef]
- Damour, T.; Schäfer, G. Higher-order relativistic periastron advances and binary pulsars. Nuovo Cimento B 1988, 101, 127–176. [Google Scholar] [CrossRef]
- Damour, T.; Deruelle, N. General relativistic celestial mechanics of binary systems. I. The post-Newtonian motion. Ann. De L’Institut Henri Poincaré Sect. A 1985, 43, 107–132. [Google Scholar]
- Iorio, L. On the 2PN Periastron Precession of the Double Pulsar PSR J0737-3039A/B. Universe 2021, 7, 443. [Google Scholar] [CrossRef]
- Kopeikin, S.M.; Efroimsky, M.; Kaplan, G. Relativistic Celestial Mechanics of the Solar System; Wiley-VCH: Weinheim, Germany, 2011. [Google Scholar] [CrossRef]
- Klioner, S.A.; Kopeikin, S.M. The Post-Keplerian Orbital Representations of the Relativistic Two-Body Problem. Astrophys. J. 1994, 427, 951. [Google Scholar] [CrossRef]
- Hu, H.; Kramer, M.; Wex, N.; Champion, D.J.; Kehl, M.S. Constraining the dense matter equation-of-state with radio pulsars. Mon. Not. R. Astron. Soc. 2020, 497, 3118–3130. [Google Scholar] [CrossRef]
- Burgay, M.; D’Amico, N.; Possenti, A.; Manchester, R.N.; Lyne, A.G.; Joshi, B.C.; McLaughlin, M.A.; Kramer, M.; Sarkissian, J.M.; Camilo, F.; et al. An increased estimate of the merger rate of double neutron stars from observations of a highly relativistic system. Nature 2003, 426, 531–533. [Google Scholar] [CrossRef] [PubMed]
- Lyne, A.G.; Burgay, M.; Kramer, M.; Possenti, A.; Manchester, R.N.; Camilo, F.; McLaughlin, M.A.; Lorimer, D.R.; D’Amico, N.; Joshi, B.C.; et al. A Double-Pulsar System: A Rare Laboratory for Relativistic Gravity and Plasma Physics. Science 2004, 303, 1153–1157. [Google Scholar] [CrossRef]
- Deng, X.M. The second post-Newtonian light propagation and its astrometric measurement in the solar system. Int. J. Mod. Phys. D 2015, 24, 1550056. [Google Scholar] [CrossRef]
- Xie, Y.; Huang, T.Y. Second post-Newtonian approximation of Einstein-aether theory. Phys. Rev. D 2008, 77, 124049. [Google Scholar] [CrossRef]
- Xie, Y.; Ni, W.T.; Dong, P.; Huang, T.Y. Second post-Newtonian approximation of scalar-tensor theory of gravity. Adv. Space Res. 2009, 43, 171–180. [Google Scholar] [CrossRef]
- Deng, X.M.; Xie, Y. Two-post-Newtonian light propagation in the scalar-tensor theory: An N-point mass case. Phys. Rev. D 2012, 86, 044007. [Google Scholar] [CrossRef]
- Deng, X.M. Two-post-Newtonian approximation of the scalar-tensor theory with an intermediate-range force for general matter. Sci. China Phys. Mech. Astron. 2015, 58, 1–8. [Google Scholar] [CrossRef]
- Deng, X.M. The second post-Newtonian light propagation and its astrometric measurement in the Solar System: Light time and frequency shift. Int. J. Mod. Phys. D 2016, 25, 1650082. [Google Scholar] [CrossRef]
- Iorio, L. Post–Newtonian direct and mixed orbital effects due to the oblateness of the central body. Int. J. Mod. Phys. D 2015, 24, 1550067. [Google Scholar] [CrossRef]
- Mioc, V.; Radu, E. Perturbations in the anomalistic period of artificial satellites caused by the direct solar radiation pressure. Astron. Nachrichten 1979, 300, 313–315. [Google Scholar] [CrossRef]
- Kopeikin, S.M.; Potapov, V.A. Relativistic shift of the periastron of a double pulsar in the post-post-Newtonian approximation of General Relativity. Astron. Rep. 1994, 38, 104–114. [Google Scholar]
- Pogossian, S.P. Comparative study of Mercury’s perihelion advance. Celest. Mech. Dyn. Astron. 2022, 134, 33. [Google Scholar] [CrossRef]
- Iorio, L. Calculation of the Uncertainties in the Planetary Precessions with the Recent EPM2017 Ephemerides and their Use in Fundamental Physics and Beyond. Astron. J. 2019, 157, 220. [Google Scholar] [CrossRef]
- Pitjeva, E.V.; Pitjev, N.P. Masses of the Main Asteroid Belt and the Kuiper Belt from the Motions of Planets and Spacecraft. Astron. Lett. 2018, 44, 554–566. [Google Scholar] [CrossRef]
- Aksim, D.; Pavlov, D. Improving the solar wind density model used in processing of spacecraft ranging observations. Mon. Not. R. Astron. Soc. 2022, 514, 3191–3201. [Google Scholar] [CrossRef]
- Benkhoff, J.; Murakami, G.; Baumjohann, W.; Besse, S.; Bunce, E.; Casale, M.; Cremosese, G.; Glassmeier, K.H.; Hayakawa, H.; Heyner, D.; et al. BepiColombo - Mission Overview and Science Goals. Space Sci. Rev. 2021, 217, 90. [Google Scholar] [CrossRef]
- Iess, L.; Asmar, S.W.; Cappuccio, P.; Cascioli, G.; De Marchi, F.; di Stefano, I.; Genova, A.; Ashby, N.; Barriot, J.P.; Bender, P.; et al. Gravity, Geodesy and Fundamental Physics with BepiColombo’s MORE Investigation. Space Sci. Rev. 2021, 217, 21. [Google Scholar] [CrossRef]
- van der Zwaard, R.; Dirkx, D. The Influence of Dynamic Solar Oblateness on Tracking Data Analysis from Past and Future Mercury Missions. Remote Sens. 2022, 14, 4139. [Google Scholar] [CrossRef]
- Love, A.E.H. Some Problems of Geodynamics; Cambridge University Press: Cambridge, UK, 1911. [Google Scholar]
- Kopal, Z. Close Binary Systems; Chapman & Hall: London, UK, 1959. [Google Scholar]
- Poisson, E.; Will, C.M. Gravity; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Konopliv, A.S.; Park, R.S.; Ermakov, A.I. The Mercury gravity field, orientation, love number, and ephemeris from the MESSENGER radiometric tracking data. Icarus 2020, 335, 113386. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).