Chaos in a Magnetized Brane-World Spacetime Using Explicit Symplectic Integrators
Abstract
1. Introduction
2. Construction of Explicit Sympletic Intergrators in a Magnetized Brane-World Spacetime
2.1. Magnetized Brane-World Spacetime
2.2. Construction of Explicit Sympletic Intergrators
3. Numerical Simulations
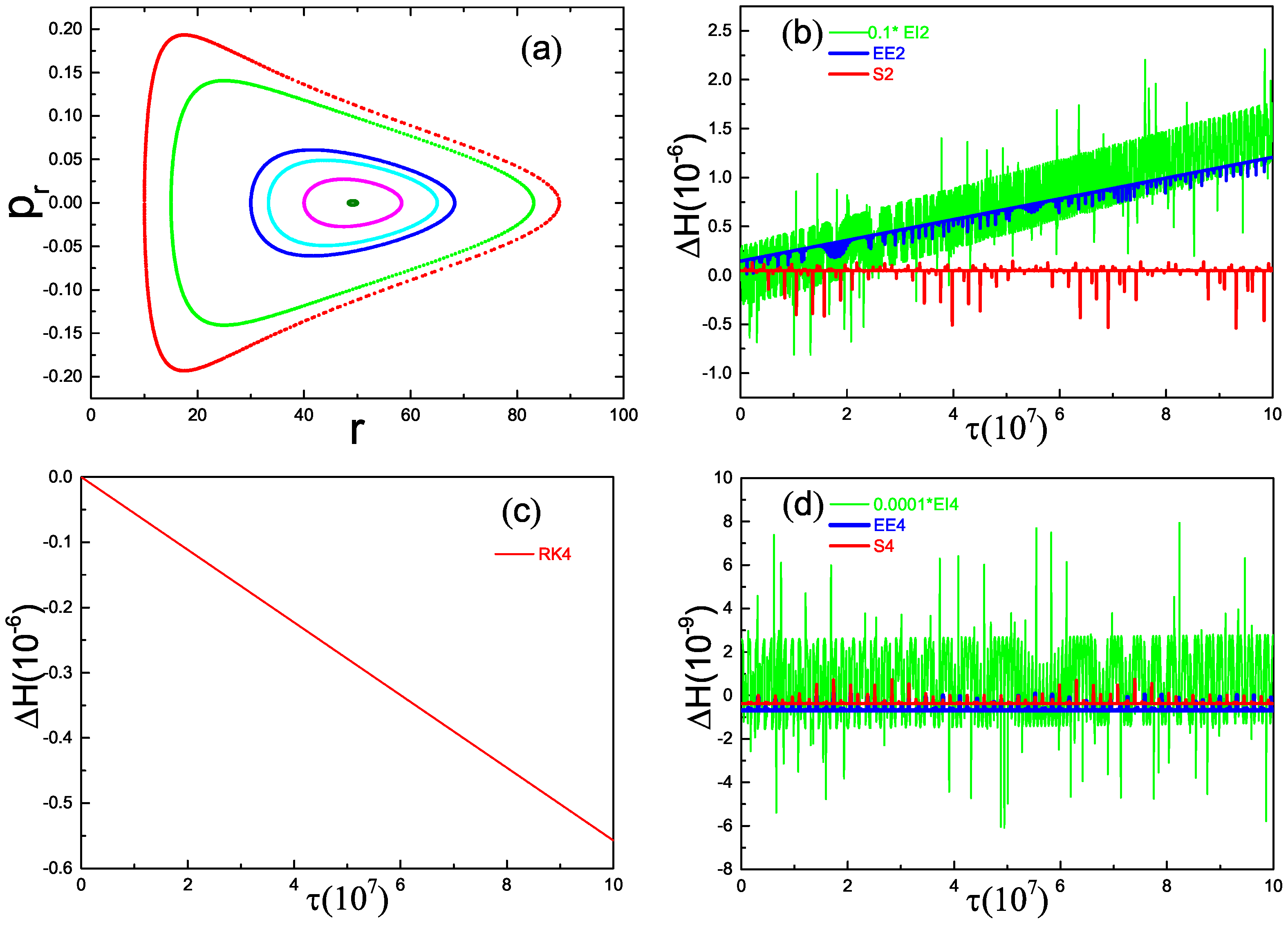
3.1. Performance Evaluation of the Explicit Sympletic Intergrators
3.2. Dependence of the Orbital Dynamics on the Parameters
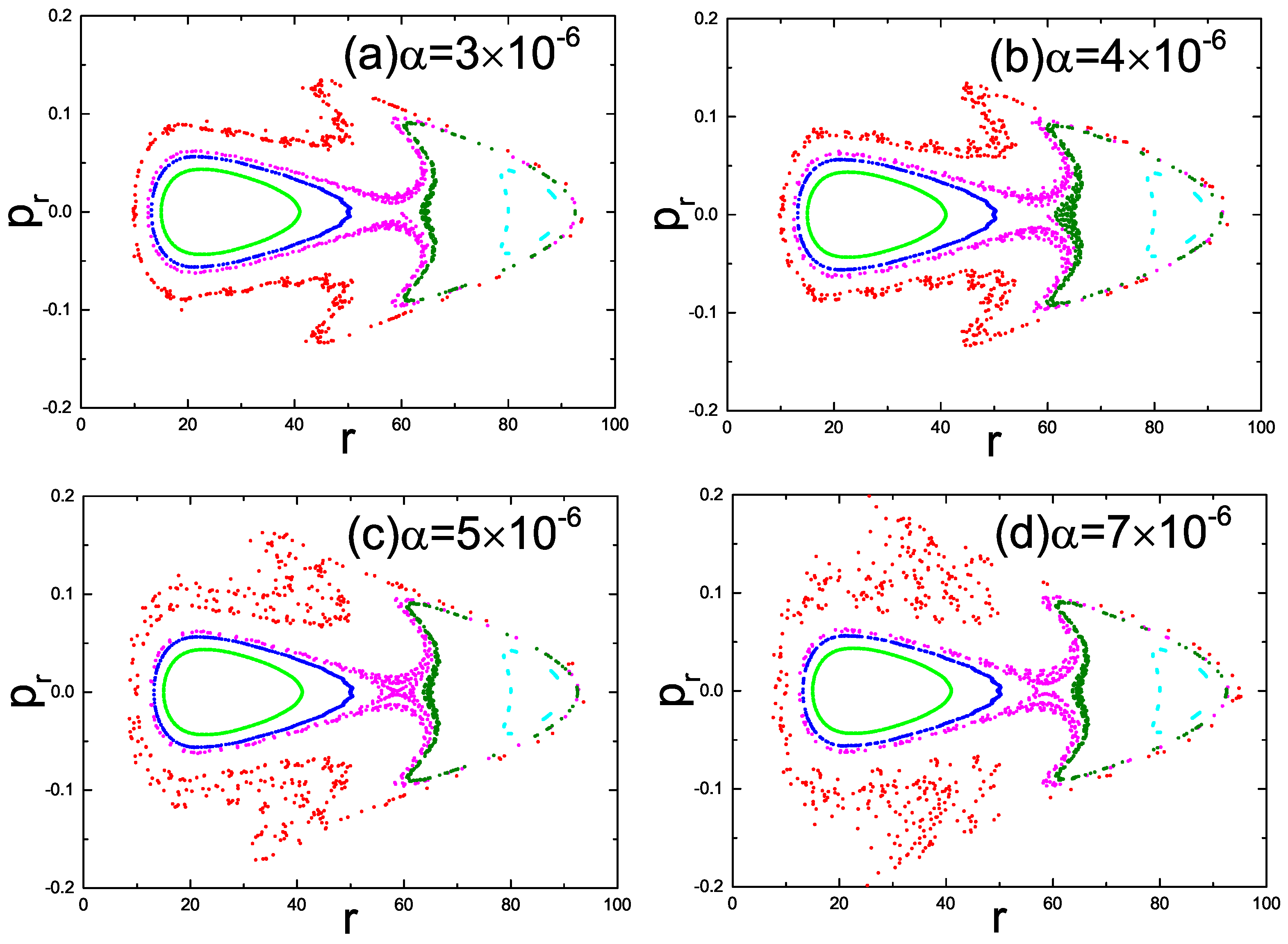
3.2.1. Orbital Dynamics Influenced by the Electromagnetic Parameter
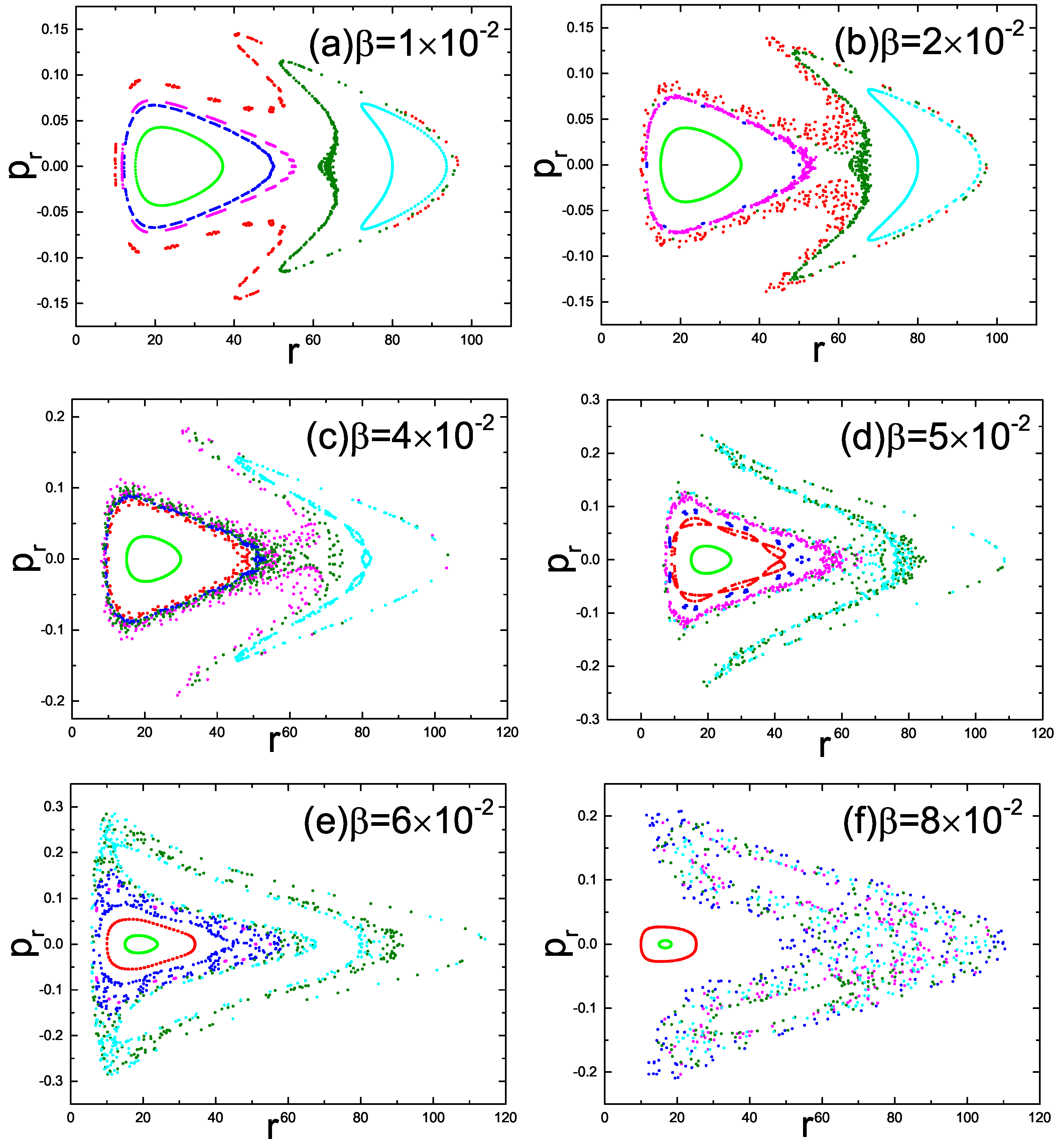
3.2.2. Orbital Dynamics Influenced by the Cosmological Parameter
3.2.3. Orbital Dynamics Influenced by the Dark Matter Parameter
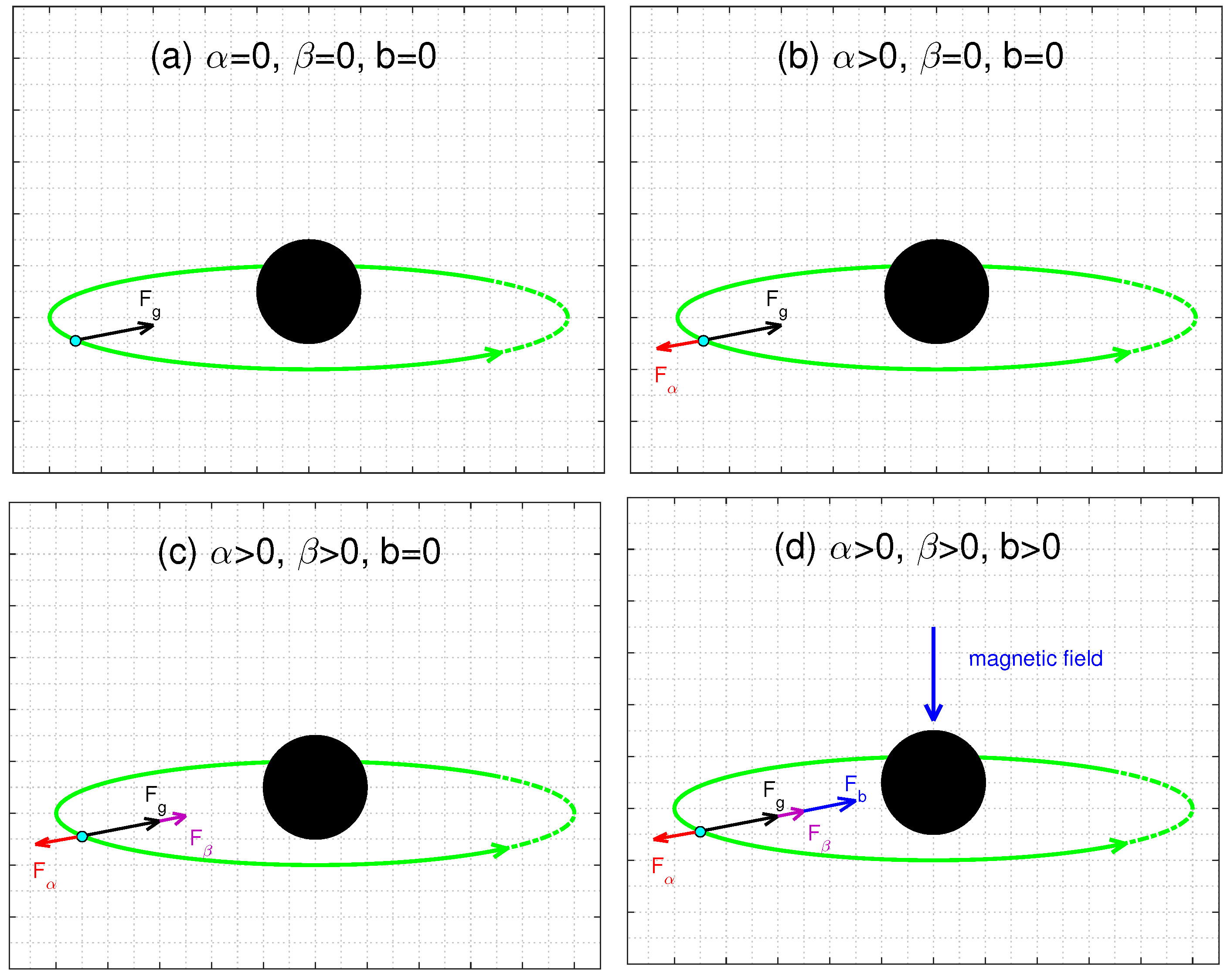
3.3. Explanation to the Influences of the Parameters on Chaotic Behavior
4. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- The Event Horizon Telescope Collaboration. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. Lett. 2019, 875, L1. [Google Scholar] [CrossRef]
- The Event Horizon Telescope Collaboration. First M87 Event Horizon Telescope Results. VII. Polarization of the Ring. Astrophys. J. Lett. 2021, 910, 12. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Dimopoulos, S.; Dvali, G. The Hierarchy Problem and New Dimensions at a Millimeter. Phys. Lett. B 1998, 429, 263–272. [Google Scholar] [CrossRef]
- Randall, L.; Sundrum, R. An Alternative to Compactification. Phys. Rev. Lett. 1999, 83, 4690–4693. [Google Scholar] [CrossRef]
- Deng, X.M. Periodic orbits around brane-world black holes. Eur. Phys. J. C 2020, 80, 489. [Google Scholar] [CrossRef]
- Brans, C.; Dicke, R.H. Mach’s Principle and a Relativistic Theory of Gravitation. Phys. Rev. 1961, 124, 925. [Google Scholar] [CrossRef]
- Brans, C. Mach’s Principle and a Relativistic Theory of Gravitation. II. Phys. Rev. 1961, 125, 2194. [Google Scholar] [CrossRef]
- Chen, X.; Kamionkowski, M. Cosmic microwave background temperature and polarization anisotropy in Brans-Dicke cosmology. Phys. Rev. D 1999, 60, 104036. [Google Scholar] [CrossRef]
- Damour, T.; Nordtvedt, K. General relativity as a cosmological attractor of tensor-scalar theories. Phys. Rev. Lett. 1993, 70, 2217–2219. [Google Scholar] [CrossRef]
- Minas, G.; Saridakis, E.N.; Stavrinos, P.C.; Triantafyllopoulos, A. Bounce Cosmology in Generalized Modified Gravities. Universe 2019, 5, 74. [Google Scholar] [CrossRef]
- Deng, X.; Xie, Y. Solar System tests of a scalar-tensor gravity with a general potential: Insensitivity of light deflection and Cassini tracking. Phys. Rev. D 2016, 93, 044013. [Google Scholar] [CrossRef]
- Deng, X. Two-post-Newtonian approximation of the scalar-tensor theory with an intermediate-range force for general matter. Sci. China Phys. Mech. Astron. 2015, 58, 1–8. [Google Scholar] [CrossRef]
- Deng, X.M.; Xie, Y. Two-post-Newtonian light propagation in the scalar-tensor theory: An N-point mass case. Phys. Rev. D 2012, 86, 044007. [Google Scholar] [CrossRef]
- Deng, X.M. Constraints on a scalar-tensor theory with an intermediate-range force by binary pulsars. Sci. China G: Phys. Astron. 2011, 54, 2071. [Google Scholar] [CrossRef]
- Gong, Y.; Papantonopoulos, E.; Yi, Z. Constraints on scalar-tensor theory of gravity by the recent observational results on gravitational waves. Eur. Phys. J. C 2018, 78, 738. [Google Scholar] [CrossRef]
- Jacobson, T. Einstein-æther gravity: A status report. Proc. Sci. (Quantum Emergent Gravity Theory Phenomenol.) 2007, 43, 020. [Google Scholar]
- Rosen, N. General relativity and flat space. II. Phys. Rev. 1940, 57, 150–153. [Google Scholar] [CrossRef]
- Rosen, N. A bi-metric theory of gravitation. Gen. Relativ. Gravit. 1973, 4, 435–447. [Google Scholar] [CrossRef]
- Drummond, I.T. Bimetric gravity and “dark matter”. Phys. Rev. D 2001, 63, 043503. [Google Scholar] [CrossRef]
- Tamaki, T. Post-Newtonian parameters in the tensor-vector-scalar theory. Phys. Rev. D 2008, 77, 124020. [Google Scholar] [CrossRef]
- Lasky, P.D.; Sotani, H.; Giannios, D. Structure of neutron stars in tensor-vector-scalar theory. Phys. Rev. D 2008, 78, 104019. [Google Scholar] [CrossRef]
- Skordis, C. The tensor-vector-scalar theory and its cosmology. Class. Quantum Grav. 2009, 26, 143001. [Google Scholar] [CrossRef]
- Freire, P.C.C.; Wex, N.; Esposito-Farèse, G.; Verbiest, J.P.W.; Bailes, M.; Jacoby, B.A.; Kramer, M.; Stairs, I.H.; Antoniadis, J.; Janssen, G.H. The relativistic pulsar-white dwarf binary PSR J1738+0333—II. The most stringent test of scalar-tensor gravity. Mon. Not. R. Astron. Soc. 2012, 423, 3328–3343. [Google Scholar] [CrossRef]
- Moffat, J.W. Scalar-tensor-vector gravity theory. J. Cosmol. Astropart. Phys. 2006, 3, 4. [Google Scholar] [CrossRef]
- Deng, X.M.; Xie, Y.; Huang, T.Y. Modified scalar-tensor-vector gravity theory and the constraint on its parameters. Phys. Rev. D 2009, 79, 044014. [Google Scholar] [CrossRef]
- Hehl, F.W.; Von der Heyde, P.; Kerlick, G.D.; Nester, J.M. General relativity with spin and torsion: Foundations and prospects. Rev. Mod. Phys. 1976, 48, 393. [Google Scholar] [CrossRef]
- Trautman, A. Einstein-Cartan theory. Encycl. Math. Phys. 2006, 2, 189–195. [Google Scholar]
- Capozziello, S.; Nojiri, S.; Odintsov, S.D.; Troisi, A. Cosmological viability of f(R)-gravity as an ideal fluid and its compatibility with a matter dominated phase. Phys. Lett. B 2006, 639, 135. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Faraoni, V. f(R) theories of gravity. Rev. Mod. Phys. 2010, 82, 451–497. [Google Scholar] [CrossRef]
- Nojiri, S.I.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rep. 2011, 505, 59–144. [Google Scholar] [CrossRef]
- De Felice, A.; Gérard, J.M.; Suyama, T. Cosmological perturbation in f(R,G) theories with a perfect fluid. Phys. Rev. D 2010, 82, 063526. [Google Scholar]
- Deng, X.M.; Xie, Y. Solar System’s Bounds on the Extra Acceleration of f(R, T) Gravity Revisited. Int. J. Theor. Phys. 2015, 54, 1739–1749. [Google Scholar] [CrossRef]
- Felice, A.D.; Tsujikawa, S. Construction of cosmologically viable f(G) gravity models. Phys. Lett. B 2009, 675, 1–8. [Google Scholar] [CrossRef]
- Deng, X.M.; Xie, Y. Improved Solar System bounds on the cosmologically viable f(G) gravity. Astrophys. Space Sci. 2017, 362, 59. [Google Scholar] [CrossRef]
- Silva, M.V.d.S.; Rodrigues, M.E. Regular black holes in f(G) gravity. Eur. Phys. J. C 2018, 78, 638. [Google Scholar] [CrossRef]
- Ho<i>r</i>ˇava, P. Quantum gravity at a Lifshitz point. Phys. Rev. D 2009, 79, 084008. [Google Scholar]
- Hořava, P. Spectral dimension of the universe in quantum gravity at a Lifshitz point. Phys. Rev. Lett. 2009, 102, 161301. [Google Scholar] [CrossRef]
- Wang, A. Vector and tensor perturbations in Horava-Lifshitz cosmology. Phys. Rev. D 2010, 82, 124063. [Google Scholar] [CrossRef]
- Chow, N.; Khoury, J. Galileon Cosmology. Phys. Rev. D 2009, 80, 024037. [Google Scholar] [CrossRef]
- Ali, A.; Gannouji, R.; Sami, M. Modified gravity à la Galileon: Late time cosmic acceleration and observational constraints. Phys. Rev. D 2010, 82, 103015. [Google Scholar] [CrossRef]
- Appelquist, T.; Chodos, A. Quantum Effects in Kaluza-Klein Theories. Phys. Rev. Lett. 1983, 50, 141. [Google Scholar] [CrossRef]
- Overduin, J.M.; Wesson, P.S. Kaluza-Klein gravity. Phys. Rep. 1997, 283, 303–380. [Google Scholar] [CrossRef]
- Deng, X.M.; Xie, Y. Improved upper bounds on Kaluza-Klein gravity with current Solar System experiments and observations. Eur. Phys. J. C 2015, 75, 539. [Google Scholar] [CrossRef]
- Langlois, D.; Maartens, R.; Wands, D. Gravitational waves from inflation on the brane. Phys. Lett. B 2000, 489, 259–267. [Google Scholar] [CrossRef]
- Neronov, A.; Sachs, I. On metric perturbations in brane-world scenarios. Phys. Lett. B 2001, 513, 173–178. [Google Scholar] [CrossRef]
- Bostock, P.; Gregory, R.; Navarro, I.; Santiago, J. Einstein gravity on the codimension 2-brane? Phys. Rev. Lett. 2004, 92, 221601. [Google Scholar] [CrossRef]
- Charmousis, C.; Zegers, R. Einstein gravity on an even codimension brane. Phys. Rev. D 2005, 72, 064005. [Google Scholar] [CrossRef]
- Kobayashi, T.; Shiromizu, T.; Deruelle, N. Low energy effective gravitational equations on a Gauss-Bonnet brane. Phys. Rev. D 2006, 74, 104031. [Google Scholar] [CrossRef]
- Zipoy, D.M. Topology of Some Spheroidal Metrics. J. Math. Phys. 1966, 7, 1137. [Google Scholar] [CrossRef]
- Voorhees, B.H. Static Axially Symmetric Gravitational Fields. Phys. Rev. D 1970, 2, 2119. [Google Scholar] [CrossRef]
- Psaltis, D.; Perrodin, D.; Dienes, K.R.; Mocioiu, I. Kerr Black Holes Are Not Unique to General Relativity. Phys. Rev. Lett. 2008, 100, 091101. [Google Scholar] [CrossRef] [PubMed]
- Schwarzschild, K. On the Gravitational Field of a Mass Point according to Einstein’s Theory. Stizber. Deut. Akad. Wiss. Math. Phys. 1916, 189–196. [Google Scholar]
- Reissner, H. On the Eigengravitation of the electric Fields according to the Einstein Theory. Annalen der Physik 1916, 50, 106. [Google Scholar] [CrossRef]
- Nordström, G. On the energy of the gravitation field in Einstein’s theory. Proc. Kon. Ned. Akad. Wet. 1918, 20, 1238. [Google Scholar]
- Kerr, R.P. Gravitational field of a spinning mass as an example of algebraically special metrics. Phys. Rev. Lett. 1963, 11, 237–238. [Google Scholar] [CrossRef]
- Sun, W.; Wang, Y.; Liu, Y.F.; Wu, X. Applying explicit symplectic integrator to study chaos of charged particles around magnetized Kerr black hole. Eur. Phys. J. C 2021, 81, 785. [Google Scholar] [CrossRef]
- Sun, X.; Wu, X.; Wang, Y.; Deng, C.; Liu, B.R.; Liang, E.W. Dynamics of Charged Particles Moving around Kerr Black Hole with Inductive Charge and External Magnetic Field. Universe 2021, 7, 410. [Google Scholar] [CrossRef]
- Hu, A.R.; Huang, G.Q. Dynamics of charged particles in the magnetized γ spacetime. Eur. Phys. J. Plus. 2021, 136, 1210. [Google Scholar] [CrossRef]
- Yang, D.; Cao, W.; Zhou, N.; Zhang, H.; Liu, W.; Wu, X. Chaos in a Magnetized Modified Gravity Schwarzschild Spacetime. Universe 2022, 8, 320. [Google Scholar] [CrossRef]
- Polcar, L.; Semerák, O. Free motion around black holes with discs or rings: Between integrability and chaos. VI. The Melnikov method. Phys. Rev. D 2019, 100, 103013. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, H. Chaotic dynamics in a superposed Weyl spacetime. Astrophys. J. 2006, 652, 1466. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Kološ, M. Acceleration of the charged particles due to chaotic scattering in the combined black hole gravitational field and asymptotically uniform magnetic field. Eur. Phys. J. C 2016, 76, 32. [Google Scholar] [CrossRef]
- Cunha, P.V.P.; Herdeiro, C.A.R.; Radu, E.; Rúnarsson, H.F. Shadows of Kerr Black Holes with Scalar Hair. Phys. Rev. Lett. 2015, 115, 211102. [Google Scholar] [CrossRef]
- Cunha, P.V.P.; Grover, J.; Herdeiro, C.; Radu, E.; Rúnarsson, H.; Wittig, A. Chaotic lensing around boson stars and Kerr black holes with scalar hair. Phys. Rev. D 2016, 94, 104023. [Google Scholar] [CrossRef]
- Takahashi, M.; Koyama, H. Chaotic motion of charged particles in an electromagnetic field surrounding a rotating black hole. Astrophys. J. 2009, 693, 472–485. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, W.; Liu, F.Y.; Wu, X. Construction of Explicit Symplectic Integrators in General Relativity. I. Schwarzschild Black Holes. Astrophys. J. 2021, 907, 66. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, W.; Liu, F.Y.; Wu, X. Construction of Explicit Symplectic Integrators in General Relativity. II. Reissner-Nordstrom Black Holes. Astrophys. J. 2021, 909, 22. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, W.; Liu, F.Y.; Wu, X. Construction of Explicit Symplectic Integrators in General Relativity. III. Reissner-Nordstrom-(anti)-de Sitter Black Holes. Astrophys. J. Suppl. Ser. 2021, 254, 8. [Google Scholar] [CrossRef]
- Karas, V.; Vokrouhlický, D. Chaotic motion of test particles in the Ernst space-time. Gen. Relativ. Gravit. 1992, 24, 729–743. [Google Scholar] [CrossRef]
- Li, D.; Wu, X. Chaotic motion of neutral and charged particles in a magnetized Ernst-Schwarzschild spacetime. Eur. Phys. J. Plus. 2019, 134, 96. [Google Scholar] [CrossRef]
- Lukes-Gerakopoulos, G. The non-integrability of the Zipoy-Voorhees metric. Phys. Rev. D 2012, 86, 044013. [Google Scholar] [CrossRef]
- Yi, M.; Wu, X. Dynamics of charged particles around a magnetically deformed Schwarzschild black hole. Phys. Scr. 2020, 95, 085008. [Google Scholar] [CrossRef]
- Zhang, H.X.; Zhou, N.Y.; Liu, W.F.; Wu, X. Charged Particle Motions near Non-Schwarzschild Black Holes with External Magnetic Fields in Modified Theories of Gravity. Universe 2021, 7, 488. [Google Scholar] [CrossRef]
- Nacozy, P.E. The use of integrals in numerical integrations of the N-body problem. In International Astronomical Union Colloquium; Cambridge University Press: Cambridge, UK, 1971; Volume 10, p. 40. [Google Scholar]
- Fukushima, T. Efficient orbit integration by dual scaling for consistency of Kepler energy and Laplace integral. Astron. J. 2003, 126, 2567. [Google Scholar] [CrossRef]
- Ma, D.Z.; Wu, X.; Zhu, J.F. Velocity scaling method to correct individual Kepler energies. New Astron. 2008, 13, 216–223. [Google Scholar] [CrossRef]
- Wang, S.C.; Wu, X.; Liu, F.Y. Implementation of the velocity scaling method for elliptic restricted three-body problems. Mon. Not. R. Astron. Soc. 2016, 463, 1352. [Google Scholar] [CrossRef]
- Wang, S.C.; Huang, G.Q.; Wu, X. Simulations of dissipative circular restricted three-body problems using the velocity-scaling correction method. Astron. J. 2018, 155, 67. [Google Scholar] [CrossRef]
- Deng, C.; Wu, X.; Liang, E.W. The use of Kepler solver in numerical integrations of quasi-Keplerian orbits. Mon. Not. R. Astron. Soc. 2020, 496, 2946–2961. [Google Scholar] [CrossRef]
- Chorin, A.; Huges, T.J.; McCracken, M.F.; Marsden, J.E. Product formulas and numerical algorithms. Commun. Pure Appl. Math. 1978, 31, 205–256. [Google Scholar] [CrossRef]
- Hu, S.Y.; Wu, X.; Huang, G.Q.; Liang, E.W. A Novel Energy-conserving Scheme for Eight-dimensional Hamiltonian Problems. Astrophys. J. 2019, 887, 191. [Google Scholar] [CrossRef]
- Hu, S.Y.; Wu, X.; Liang, E.W. An Energy-conserving Integrator for Conservative Hamiltonian Systems with Ten-dimensional Phase Space. Astrophys. J. Suppl. Ser. 2021, 235, 55. [Google Scholar] [CrossRef]
- Hu, S.Y.; Wu, X.; Liang, E.W. Construction of second-order six-dimensional Hamiltonian-conserving scheme. Astrophys. J. Suppl. Ser. 2021, 257, 40. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, X.; Liang, E. Adjustment of Force-Gradient Operator in Symplectic Methods. Mathematics 2021, 9, 2718. [Google Scholar] [CrossRef]
- Wisdom, J.; Holman, M. Symplectic maps for the n-body problem. Astron. J. 1991, 102, 1528–1538. [Google Scholar] [CrossRef]
- Forest, E.; Ruth, R.D. Fourth-order symplectic integration. Physica D 1990, 43, 105–117. [Google Scholar] [CrossRef]
- Yoshida, H. Construction of higher order symplectic integrators. Phys. Lett. A 1990, 150, 262–268. [Google Scholar] [CrossRef]
- Feng, K. Symplectic Geometry and Numerical Methods in Fluid Dynamics. In Tenth International Conference on Numerical Methods in Fluid Dynamics. Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 1986; Volume 264, pp. 1–7. [Google Scholar]
- Brown, J.D. Midpoint rule as a variational-symplectic integrator: Hamiltonian systems. Phys. Rev. D 2006, 73, 024001. [Google Scholar] [CrossRef]
- Liao, X.H. Symplectic integrator for general near-integrable Hamiltonian system. Celest. Mech. Dyn. Astron. 1997, 66, 243–253. [Google Scholar] [CrossRef]
- Lubich, C.; Walther, B.; Brügmann, B. Symplectic integration of post-Newtonian equations of motion with spin. Phys. Rev. D 2010, 81, 104025. [Google Scholar] [CrossRef]
- Zhong, S.Y.; Wu, X.; Liu, S.Q.; Deng, X.F. Global symplectic structure-preserving integrators for spinning compact binaries. Phys. Rev. D 2010, 82, 124040. [Google Scholar] [CrossRef]
- Pihajoki, P. Explicit methods in extended phase space for inseparable Hamiltonian problems. Celest. Mech. Dyn. Astron. 2015, 121, 211–231. [Google Scholar] [CrossRef]
- Liu, L.; Wu, X.; Huang, G.Q.; Liu, F.Y. Higher order explicit symmetric integrators for inseparable forms of coordinates and momenta. Mon. Not. R. Astron. Soc. 2016, 459, 1968–1976. [Google Scholar] [CrossRef][Green Version]
- Wu, Y.L.; Wu, X. An optimized Forest-Ruth-like algorithm in extended phase space. Int. J. Mod. Phys. C 2018, 29, 1850006. [Google Scholar] [CrossRef]
- Pan, G.F.; Wu, X.; Liang, E.W. Extended phase-space symplectic-like integrators for coherent post-Newtonian Euler-Lagrange equations. Phys. Rev. D 2021, 104, 044055. [Google Scholar] [CrossRef]
- Luo, J.J.; Wu, X.; Huang, G.Q.; Liu, F.Y. Explicit symplectic-like integrators with midpoint permutations for spinning compact binaries. Astrophys. J. 2017, 834, 64. [Google Scholar] [CrossRef]
- Wu, X.; Wang, Y.; Sun, W.; Liu, F.Y. Construction of Explicit Symplectic Integrators in General Relativity. IV. Kerr Black Holes. Astrophys. J. 2021, 914, 63. [Google Scholar] [CrossRef]
- Zhou, N.; Zhang, H.; Liu, W.; Wu, X. Note on Construction of Explicit Symplectic Integrators for Schwarzschild Spacetimes. Astrophys. J. 2022, 927, 160. [Google Scholar] [CrossRef]
- Mikkola, S. Practical symplectic methods with time transformation for the few-body problem. Celest. Mech. Dyn. Ast. 1997, 67, 145–165. [Google Scholar] [CrossRef]
- Heydari-Fard, M.; Shirazi, M.; Jalalzadeh, S.; Sepangi, H.R. Accelarating universe in brane gravity with confining potential. Phys. Lett. B 2006, 640, 1–6. [Google Scholar] [CrossRef]
- Heydari-Fard, M.; Razmi, H.; Sepangi, H.R. Brane-World Black Hole Solutions via a Confining Potential. Phys. Rev. D 2007, 76, 066002. [Google Scholar] [CrossRef]
- Gurzadyan, V.G. On the common nature of dark matter and dark energy: Galaxy groups. Eur. Phys. J. Plus. 2019, 134, 14. [Google Scholar] [CrossRef]
- Gurzadyan, V.G.; Stepanian, A. The cosmological constant derived via galaxy groups and clusters. Eur. Phys. J. C 2019, 79, 169. [Google Scholar] [CrossRef]
- Zwicky, F. On the large scale distribution of matter in the universe. Phys. Rev. 1942, 61, 489. [Google Scholar] [CrossRef]
- Takamiya, T.; Sofue, Y. Radial distribution of the mass-to-luminosity ratio in spiral galaxies and massive dark cores. Astrophys. J. 2000, 534, 670. [Google Scholar] [CrossRef]
- Honma, M.; Nagayama, T.; Ando, K.; Bushimata, T. Fundamental parameters of the Milky Way galaxy based on VLBI astrometry. Astron. Soc. Japan. 2012, 64, 136. [Google Scholar]
- Sofue, Y. Rotation Curve and Mass Distribution in the Galactic Center—From Black Hole to Entire Galaxy. Astron. Soc. Japan 2013, 65, 118. [Google Scholar] [CrossRef]
- Shaymatova, S.; Malafarinaf, D.; Ahmedov, B. Effect of perfect fluid dark matter on particle motion around a static black hole immersed in an external magnetic field. Phys. Dark Univ. 2021, 34, 100891. [Google Scholar] [CrossRef]
- Wu, P.; Yu, H. Observational constraints on f(T) theory. Phys. Lett. B 2010, 693, 415–420. [Google Scholar] [CrossRef]
- Xie, Y.; Deng, X.M. f(T) gravity: Effects on astronomical observation and Solar system experiments and upper bounds. Mon. Not. R. Astron. Soc. 2013, 433, 3584. [Google Scholar] [CrossRef]
- Deng, X.M. Probing f(T) gravity with gravitational time advancement. Class. Quant. Grav. 2018, 35, 175013. [Google Scholar] [CrossRef]
- Deng, X.M. Geodesics and periodic orbits around quantum-corrected black holes. Phys. Dark. Univ. 2020, 30, 100629. [Google Scholar] [CrossRef]
- Lin, H.Y.; Deng, X.M. Rational orbits around 4D Einstein-Lovelock black holes. Phys. Dark. Univ. 2021, 31, 100745. [Google Scholar] [CrossRef]
- Liu, Y.C.; Feng, J.X.; Shu, F.W.; Wang, A.Z. Extended geometry of Gambini-Olmedo-Pullin polymer black hole and its quasinormal spectrum. Phys. Rev. D 2021, 104, 106001. [Google Scholar] [CrossRef]
- Astier, P.; Pain, R. Observational evidence of the accelerated expansion of the universe. Comptes Rendus Phys. 2012, 13, 521. [Google Scholar] [CrossRef]
- Padmanabhan, T. Accelerated expansion of the universe driven by tachyonic matter. Phys. Rev. D 2002, 66, 021301. [Google Scholar] [CrossRef]
- Schrabback, T.; Hartlap, J.; Joachimi, B.; Kilbinger, M.; Simon, P.; Benabed, K.; Brada, M.; Eifler, T.; Erben, T.; Fassnacht, C.D.; et al. Evidence of the accelerated expansion of the Universe from weak lensing tomography with COSMOS? Astron. Astrophys. 2010, 516, 63. [Google Scholar] [CrossRef]
- Carter, B. Global Structure of the Kerr Family of Gravitational Fields. Phys. Rev. 1968, 174, 1559. [Google Scholar] [CrossRef]
- Cao, W.; Liu, W.; Wu, X. Integrability of Kerr-Newman spacetime with cloud strings, quintessence and electromagnetic field. Phys. Rev. D 2022, 105, 124039. [Google Scholar] [CrossRef]

| Method | EI2 | EE2 | S2 | RK4 | EI4 | EE4 | S4 |
|---|---|---|---|---|---|---|---|
| h = 1 | |||||||
| h = 0.1 |
| Method | EI2 | EE2 | S2 | RK4 | EI4 | EE4 | S4 |
|---|---|---|---|---|---|---|---|
| h = 1 | 64.98 | 17.28 | 25.56 | 20.06 | 362.16 | 49.92 | 75.20 |
| h = 0.1 | 317.56 | 155.53 | 276.98 | 208.11 | 853.83 | 503.08 | 763.02 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, A.; Huang, G. Chaos in a Magnetized Brane-World Spacetime Using Explicit Symplectic Integrators. Universe 2022, 8, 369. https://doi.org/10.3390/universe8070369
Hu A, Huang G. Chaos in a Magnetized Brane-World Spacetime Using Explicit Symplectic Integrators. Universe. 2022; 8(7):369. https://doi.org/10.3390/universe8070369
Chicago/Turabian StyleHu, Airong, and Guoqing Huang. 2022. "Chaos in a Magnetized Brane-World Spacetime Using Explicit Symplectic Integrators" Universe 8, no. 7: 369. https://doi.org/10.3390/universe8070369
APA StyleHu, A., & Huang, G. (2022). Chaos in a Magnetized Brane-World Spacetime Using Explicit Symplectic Integrators. Universe, 8(7), 369. https://doi.org/10.3390/universe8070369





