Abstract
In situ recordings by the solar Wind spacecraft reveal the ubiquitousness of alpha particles, whose drift velocities to the background proton are generally less than or equal to the local Alfvén velocity . The alpha beam instability plays a significant role in the alpha beam deceleration in the solar wind; nonetheless, the detailed mechanism of deceleration remains unclear. By using the linear Vlasov equation of the PDRK/B0 solver, the present work investigates the kinetic instability caused by both the alpha beam and the electron temperature anisotropy in the solar wind and assesses the effects of the electron temperature anisotropy on such instability. The results show that both anisotropic electrons and alpha beams lead to the excitation of several plasma waves, and the wave frequency, growth rate, and polarization properties are sensitive to the electron temperature anisotropy (), the parallel electron beta (), and the alpha beam drift velocity (). With an excess parallel temperature , the parallel magnetosonic/whistler (PM/W), parallel Alfvén wave (PAW), and oblique Alfvén/ion cyclotron (OA/IC) instabilities could be generated, while for an excess perpendicular temperature , the PM/W, OA/IC, parallel whistler (PW), and kinetic Alfvén wave (KAW) instabilities could grow. In the region of , the thresholds of the PM/W, PAW, and OA/IC instabilities extend to lower drift velocity . In the region of , the thresholds of the PM/W and OA/IC instabilities increase, while those of the PW and KAW instabilities are shifted to lower . The current study presents a comprehensive overview for alpha beam instabilities that limit the alpha beam drift velocity in the solar wind.
1. Introduction
In situ observations have shown that the solar wind plasma often comprises protons, electrons, and other ion particles [1,2,3]. Except for protons, alpha particles represent the most common ions with the number density approximately 5% of the total number density in the solar wind [4,5]. Alpha particles generally propagate faster compared with the background protons, with their drift velocity related to the background protons being less than or close to the local Alfvén velocity [6,7,8]. During solar wind propagation from the Sun into the interplanetary medium, the local Alfvén velocity decreases with increasing heliocentric distance because of the expansion of the magnetic field. The limitation of the normalized alpha beam drift velocity indicates that a mechanism governs alpha beam deceleration [9,10,11]. Moreover, the alpha beam is a useful indicator of plasma heating and acceleration in the solar wind.
Both linear Vlasov theory and hybrid simulations demonstrated that the drift velocity between the alpha particle and proton may cause several types of alpha/proton instabilities, including magnetosonic/whistler (M/W) and Alfvén/ion cyclotron (A/IC) instabilities [12,13,14,15,16,17,18,19]. The M/W instability tends to show effective excitation in the high beta region of , where represents the plasma thermal pressure/magnetic pressure ratio, mainly propagating parallel to the background magnetic field (i.e., parallel magnetosonic/whistler (PM/W) instability). The A/IC instability likely grows in the low beta region of and is oblique to the field (i.e., oblique Alfvén/ion cyclotron (A/IC) instability). The kinetic energy of alpha beams can be transformed into the wave energy because of interactions between the wave and the particle, which leads to the growth of plasma waves and the deceleration of alpha beams [20,21].
On the other hand, solar wind electrons deviate significantly from local thermodynamic equilibrium, exhibiting temperature anisotropy (i.e., ) [22,23,24,25,26,27]. Electron temperature anisotropy has a wide range with as the plasma beta [28,29,30,31]. These anisotropic electrons can provide important free energy to affect wave generation. Michno et al. [32] analyzed the effect of anisotropic electrons on the solar wind proton temperature anisotropy threshold. Using hybrid simulations, Ahmadi et al. [33] investigated the impact of the electron temperature anisotropy on the proton mirror instability and found that the electron temperature anisotropy promotes the excitation of the electron whistler instability. Shaaban et al. [34] studied the effect of the electron temperature anisotropy on electromagnetic beam instabilities. Xiang et al. [35] studied the proton beam instability under the electron temperature anisotropy.
Using the Wind spacecraft, Maruca et al. [36] investigated the kinetic instabilities driven by temperature anisotropies of the proton and alpha, and they found that the temperature anisotropies of the proton and alpha can trigger various instabilities and, in turn, are constrained by the instability thresholds. Based on hybrid simulations, Lu et al. [37] investigated the nonlinear evolution of parallel and oblique alpha beam instabilities. Gao et al. [38] further studied the heating of the background protons by these instabilities. Recently, Zhang et al. [39] investigated the effects of the alpha and proton temperature anisotropy on the alpha beam instability in the solar wind, demonstrating that the alpha and proton temperature anisotropy could limit the alpha beam drift velocity to a value close to or below the local Alfvén velocity. However, the role of the electron temperature anisotropy on the alpha beam instability remains unexamined. In the current study, the kinetic instability induced by the alpha beam and electron temperature anisotropy will be evaluated, as well as the impacts of the electron temperature anisotropy on the wave frequency, growth rate, threshold conditions, and polarization properties. The present results could help understand the constraining mechanism of the alpha beams in the solar wind.
2. Plasma Model and Wave Equation
Plasma waves and instabilities in collisionless and nonrelativistic plasmas are governed by the Vlasov equation [40].
where , , and represent the charge, mass, and distribution function of the species s, respectively. , , and e correspond to the ambient proton, the alpha beam, and the ambition electron, respectively. , , and represent the perturbed electric field, perturbed magnetic field, and perturbed velocity, respectively. Here, the background magnetic field is parallel to the z axis, i.e., . In the solar wind, electron/ion velocity distributions frequently exhibit non-thermal features, including particle beam and temperature anisotropy [41,42]. We consider the unperturbed distribution function following a drifting bi-Maxwellian as [43]:
where and denote the density and the drift velocity and and are the perpendicular and parallel thermal velocities regarding the field.
In the above expressions, , , , , , , , , and , , , are the Boltzmann constant, permittivity, charge, mass, number density, and drift velocity, respectively. represents the nth-order modified Bessel function with the argument , and represents the standard plasma dispersion function. Here, the wave vector is .
To solve the wave equation of Equation (3), we adopted the PDRK/B0 solver to numerically calculate the wave frequency, growth rate, and polarization. This method is based on the standard matrix eigenvalue technique for solving an equivalent linear wave equation, which is obtained from Equation (3). Therefore, the PDRK can give the totality of solutions of waves at arbitrary propagation angles.
In the alpha beam model, we assumed both the charge-neutral and current-neutral conditions, i.e., and , which indicate that the alpha beam current can be compensated by the background electron current due to the drift motion of electrons. The plasma parameters m−3, , , T, and are employed in the following calculations.
3. Alpha Beam Instability Induced by Electron Temperature Anisotropy
3.1. Alpha Beam Instability with Excess Parallel Electron Temperature Anisotropy
We assessed the wave dispersion and polarization features of the alpha beam instability for and systematically analyzed the electron temperature anisotropy effects on the wave frequency, growth rate, and polarization.
Figure 1 shows the variations of the real frequency (), maximum growth rate (), and polarization () in the parallel electron beta plane and the alpha beam drift velocity for various electron temperature anisotropies and propagation angles: (a) , (b) , (c) , ; (d) , . The tree curves show the contours at the maximum growth rates , , and , respectively. The curved line with is the instability threshold. As shown in Figure 1a,b, at a PM/W instability, the threshold velocity () decreases with growing without the electron temperature anisotropy (i.e., ). At , the PM/W and parallel Alfvén wave (PAW) instabilities could occur, and the unstable area is overtly enlarged in comparison with the condition of . In particular, PAW instability dominates in the region of and , while the PM/W instability with higher growth becomes very strong in the region of . With oblique propagation (), depicted in Figure 1c,d, only the OA/IC instability occurs. A threshold velocity of firstly increases and then decreases with rising . For , a threshold velocity of the OA/IC instability extends to a reduced value (), and the unstable region widens, in particular with .
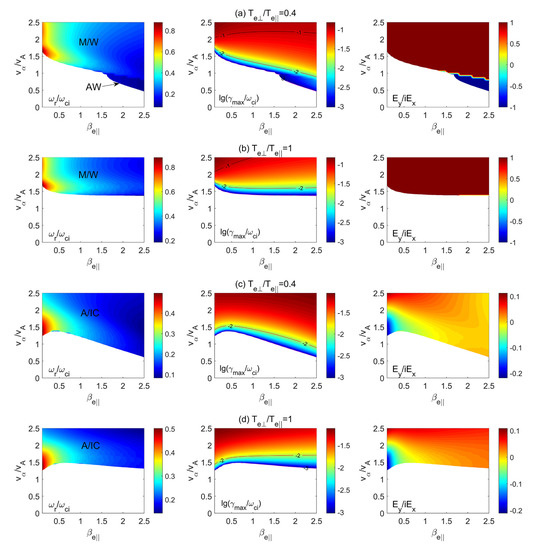
Figure 1.
Color bar distributions of the real frequency (), maximum growth rate (), and polarization () in the plane of the parallel electron beta () and alpha beam drift velocity () for various electron temperature anisotropies and propagation angles: (a) , ; (b) , ; (c) , ; (d) , .
Figure 2 shows the distributions of the real frequency (), maximum growth rate (), and polarization () in the plane of the normalized wave number and propagation angle for various electron temperature anisotropies: (a) , (b) , and (c) 1, with . The alpha beam drift velocity was used. As depicted in Figure 2, the alpha beam efficiently drives the PM/W and OA/IC instabilities in the low-beta region. For the PM/W, the frequency is located in , the propagation angle ranges from to , and the wavenumber is . When the propagation angle , its growth rate is the largest. For the OA/IC wave, the wave frequency is located in , the propagation angle is , and the wavenumber ranges from 0.1 to 2.5. When the propagation angle , its growth rate is the largest. Moreover, as increases from 0.4 to 1, , , and for the PM/W and OA/IC waves mostly remain unchanged.
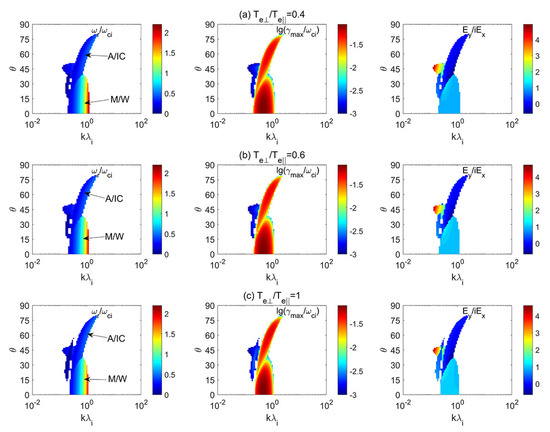
Figure 2.
Color bar distributions of the real frequency (), maximum growth rate (), and polarization () in the plane of the normalized wavelength () and propagation angle () for various electron temperature anisotropies: (a) , (b) , and (c) 1 in a plasma with low beta . The alpha beam drift velocity was used.
Figure 3 uses the same plasma parameters as those in Figure 2, except . In Figure 3, it can be seen that, in the case of and , the alpha/proton instability induces both the PM/W and OA/IC instabilities, which correspond to diverse propagation angles of ∼ and ∼, respectively. The wavenumber of the PM/W is ∼, while that of the OA/IC wave is ∼. For , both the OA/IC and PM/W have increased propagation angles for ∼ and ∼, respectively, compared to those obtained with . For , the PM/W and OA/IC waves dominate in diverse levels of ∼ and ∼, respectively. As decreases from 1 to 0.4, the ranges of the propagation angle and wavenumber for both the PM/W and OA/IC waves are enlarged. Unlike the case of low beta , the wave features (, , and ) for both the PM/W and OA/IC instabilities are sensitive to .
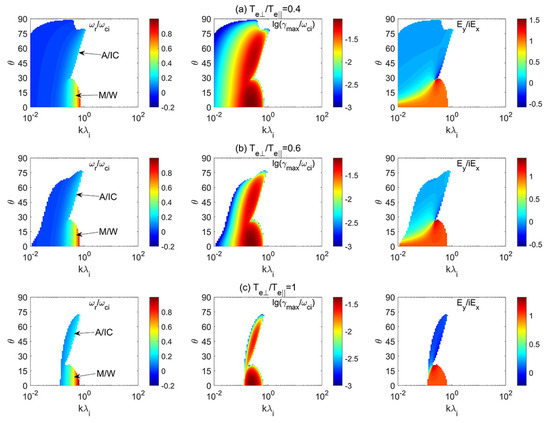
Figure 3.
Color bar distributions of the real frequency (), maximum growth rate (), and polarization () in the plane of the normalized wavelength () and propagation angle () for various electron temperature anisotropies: (a) , (b) , and (c) 1 in a plasma with high beta . The alpha beam drift velocity was used.
In Figure 4, Figure 5 and Figure 6, the propagation angle for the PM/W and PAW instabilities is used and the propagation angle for the OA/IC instability. Figure 4 presents the real frequency () and maximum growth rate () versus the alpha beam drift velocity () for (a) the PM/W instability with , (b) the PM/W instability with , and (c) the PAW instability with . In Figure 4a,b, the black, red, and blue lines represent , , and 1; in Figure 4c, these lines represent , , and . In Figure 4, the maximum growth rates for both the PM/W and PAW instabilities increase with . The maximum growth rate of the PM/W instability is weakly dependent on for the low-beta case of , while a stronger dependence is obtained for the high-beta case of . Moreover, the maximum growth rate of the PAW instability is strongly dependent on for the high-beta case of .
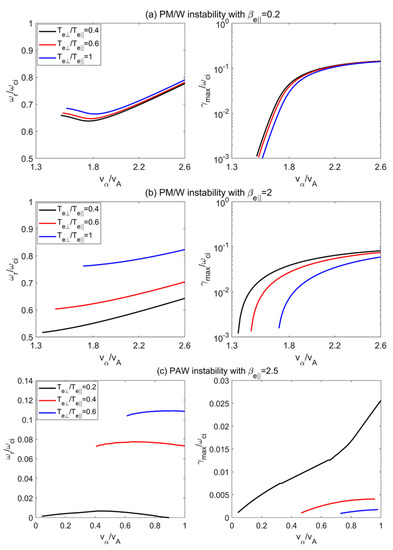
Figure 4.
The real frequency () and maximum growth rate () versus the alpha beam drift velocity () for (a) the PM/W instability with , (b) the PM/W instability with , and (c) the PAW instability with . In (a,b), the black, red, and blue lines represent electron temperature anisotropies at , , and 1, and in (c), these lines represent , , and , respectively.
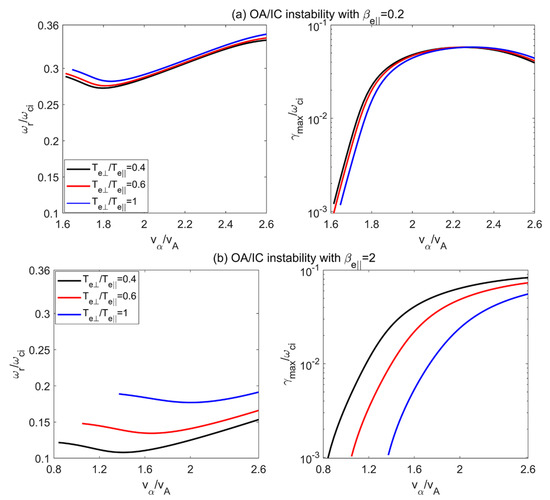
Figure 5.
The real frequency () and maximum growth rate () versus the alpha beam drift velocity () for the OA/IC instability with (a) and (b) 2, where the black, red, and blue lines represent electron temperature anisotropies at , , and 1, respectively.
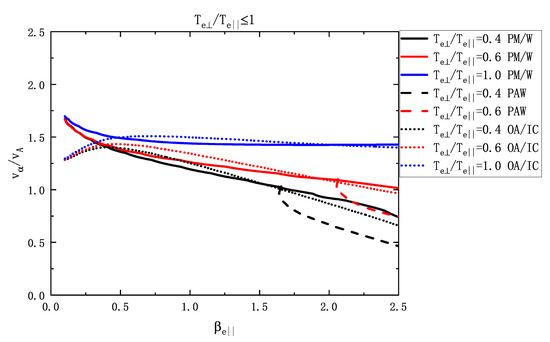
Figure 6.
The instability threshold as a function of and in the region of , where the solid, dashed, and dotted lines represent the PM/W, PAW, and OA/IC instabilities, respectively, and the black, red, and blue lines correspond to , , and 1, respectively.
Figure 5 depicts the real frequency () and maximum growth rate () versus the alpha beam drift velocity () for the OA/IC instability at (a) and (b) 2, where the black, red, and blue lines represent , , and 1, respectively. It can be seen in Figure 5 that, with increasing , the maximum growth rate of the OA/IC instability increases rapidly at , while remaining nearly constant at . The maximum growth rate of the OA/IC instability decreases with increasing . This trend is more obvious in the high-beta case of .
Next, we analyze how the electron temperature anisotropy affects the instability thresholds. Figure 6 displays the instability thresholds as a function of the parallel electron beta () and the alpha beam drift velocity () with , where solid, dotted, and dashed lines represent the PM/W, OA/IC, and PAW instabilities, respectively. As shown in Figure 6, for , the threshold velocity for the PM/W, OA/IC, and PAW instabilities gradually decreases with decreasing , especially in the region of . This indicates that the electron temperature anisotropy with could reduce the threshold velocity (). For , the PAW instability has a threshold velocity lower than both the PM/W and OA/IC instabilities as , implying that the PAW instability becomes important when .
3.2. Alpha Beam Instability with Excess Perpendicular Electron Temperature Anisotropy
We then investigated the alpha beam instability associated with and analyzed the effects of the electron temperature anisotropy on such instability.
Figure 7 shows the color bar distributions of the real frequency (), maximum growth rate (), and polarization () in the plane of the parallel electron beta and the alpha beam drift velocity () for (a) and , (b) and , (c) and , and (d) and . For parallel propagation cases with depicted in Figure 7a,b, besides the PM/W instability, the parallel whistler (PW) instability could be generated when . The PW instability has high-frequency waves with and . The unstable region at is overtly enlarged in comparison with that obtained at . For the oblique propagation cases of depicted in Figure 7c,d, only the OA/IC instability occurs. For , the threshold velocity of the OA/IC instability increases with .
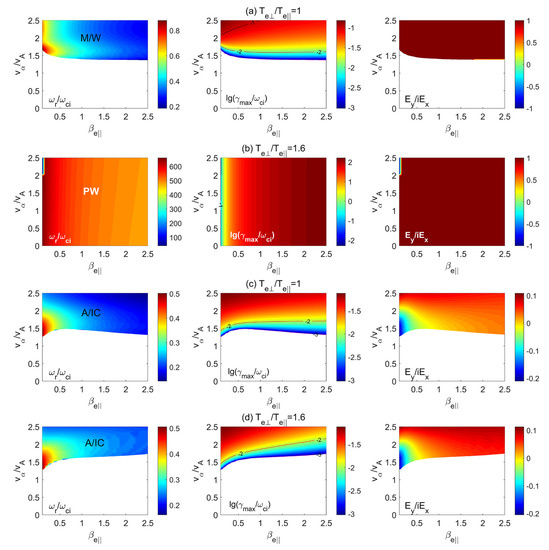
Figure 7.
Color bar distributions of the real frequency (), maximum growth rate (), and polarization () in the plane of the parallel electron beta () and the alpha beam drift velocity () for (a) and , (b) and , (c) and , and (d) and .
Figure 8 shows the color bar distributions of the real frequency (), maximum growth rate (), and polarization () in the plane of the parallel electron beta and the alpha beam drift velocity () at for (a) , (b) , and (c) . As can be seen from Figure 8a, for the OA/IC instability, the threshold velocity () increases with in the case of no electron temperature anisotropy (i.e., ). For (1.6), the KAW instability dominates the unstable region at (1.2), with a threshold velocity independent of . This indicates that the major free energy for exciting the KAW is the electron temperature anisotropy.
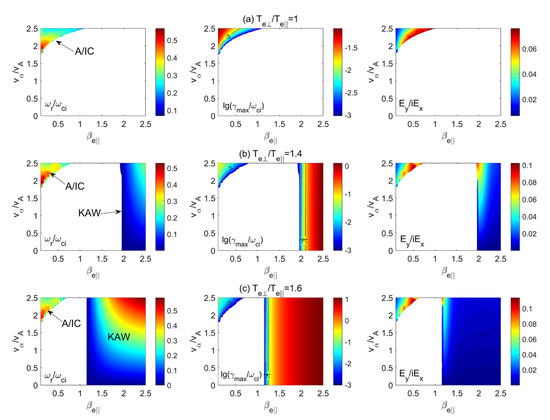
Figure 8.
Color bar distributions of the real frequency (), maximum growth rate (), and polarization () in the plane of the parallel electron beta () and the alpha beam drift velocity () at for (a) , (b) , and (c) .
Figure 9 depicts the color bar distributions of the real frequency (), maximum growth rate (), and polarization () in the plane of and for (a) , (b) , and (c) in a plasma with . The alpha beam drift velocity was adopted. In Figure 9, it can be found that in the case of , alpha beams trigger both the PM/W and OA/IC waves. For , the PW and KAW instabilities exist. For , the PM/W, PW, OA/IC, and KAW instabilities dominate in diverse regimes, including , , , and , respectively. For , the wave frequencies of the PM/W, PW, OA/IC, and KAW are located in ∼, 500∼600, ∼, and 0∼, which correspond to the wavenumber ∼∼, ∼, ∼, and ∼, respectively.
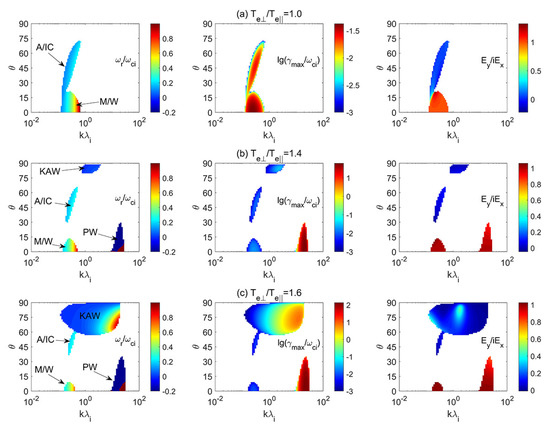
Figure 9.
Color bar distributions of the real frequency (), maximum growth rate (), and polarization () in the plane of and for (a) , (b) , and (c) in a plasma with high beta . The alpha beam drift velocity was used.
In Figure 10, Figure 11 and Figure 12, the propagation angle for the PM/W and PW instabilities is used, for the OA/IC instability, and for the KAW instability. Figure 10 depicts the real frequency () and maximum growth rate () versus the alpha beam drift velocity () for (a) the PM/W instability with , (b) the PM/W instability with , and (c) the PW instability with . In Figure 10a,b, the black, red, and blue lines represent , , and , and in Figure 10c, these lines represent , , and . From Figure 10, with , the maximum growth rate of the PM/W instability increases, whereas that of the PW instability is nearly constant. Moreover, the maximum growth rate of the PM/W instability has a weak dependence on for the low-beta case of , while for the PM/W and PW instabilities, the dependence is stronger for the high-beta case of .
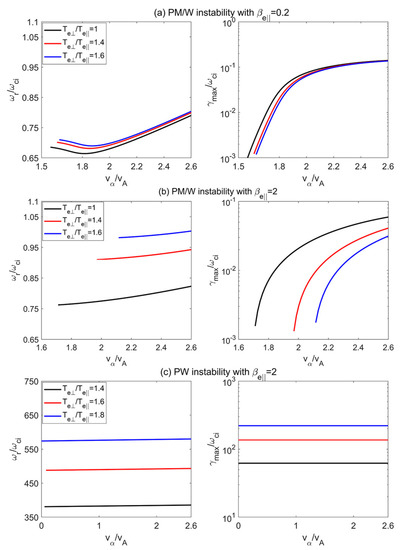
Figure 10.
The real frequency () and maximum growth rate () versus the alpha beam drift velocity () for (a) the PM/W instability with , (b) the PM/W instability with , and (c) the PW instability with . In (a,b), the black, red, and blue lines represent electron temperature anisotropies at , , and , and in (c), these lines represent electron temperature anisotropies at , , and , respectively.
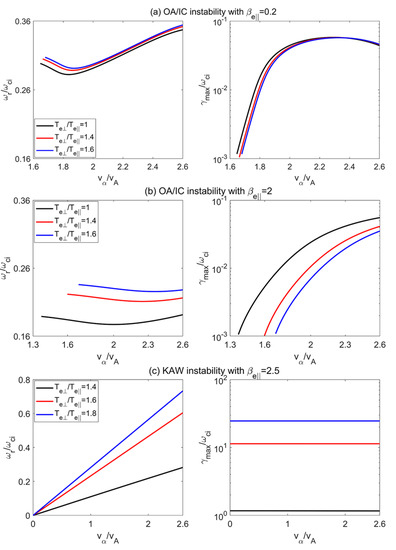
Figure 11.
The real frequency () and maximum growth rate () versus the alpha beam drift velocity () for (a) the OA/IC instability with , (b) the OA/IC instability with , and (c) the KAW instability with . In (a,b), the black, red, and blue lines represent electron temperature anisotropies at , , and , and in (c), these lines correspond to , , and , respectively.
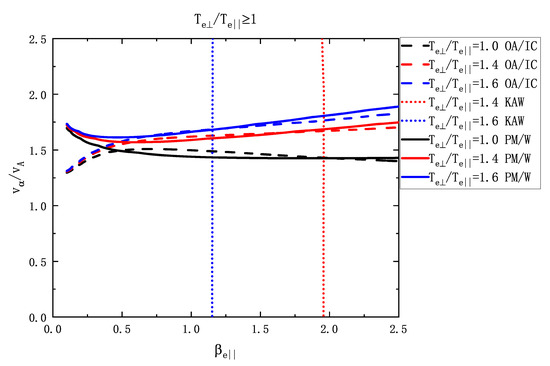
Figure 12.
The same as Figure 6, but for , where the solid, dotted, and dashed lines represent the PM/W, KAW, and OA/IC instabilities, respectively, and the black, red, and blue lines represent , , and , respectively.
Figure 11 is similar to Figure 10, except for (a) the OA/IC instability with , (b) the OA/IC instability with , and (c) the KAW instability with . In Figure 11a,b, the black, red, and blue lines represent , , and , and in Figure 11c, these lines represent , , and . Figure 11 reveals that the maximum growth rate of the OA/IC instability strongly depends on the alpha beam drift velocity (), while that of the KAW instability is independent of . Moreover, as increases, the maximum growth rate of the OA/IC instability varies slightly at and decreases at , while that of the KAW instability increases for the high-beta case of .
In addition, we also considered the effects of the electron temperature anisotropy on the instability thresholds with . Figure 12 displays the instability thresholds as a function of the parallel electron beta () and the alpha beam drift velocity (), where the solid, dotted, and dashed lines represent the PM/W, KAW, and OA/IC instabilities, respectively. As shown in Figure 12, with , the threshold velocities of the PM/W and OA/IC instabilities increase. The KAW instability threshold extends to a wider unstable region of lower and with increasing .
The physical mechanism of the instability is described below. The plasma can be viewed as flowing along the magnetic flux, and when the flux tube is bent slightly, the plasma will create an upward centrifugal force, , where R is the curvature radius of the flux tube. The thermal pressure gradient force, , and magnetic tension, , resist the centrifugal force [43]. In the absence of any free energy, the flux tube satisfies the force balance (i.e., ). However, the presence of electron temperature anisotropy and alpha beam drift velocity will give rise to a larger centrifugal force , and the force balance condition is broken, leading to instability.
4. Discussion and Conclusions
Solar wind measurements often show that the drift velocity () between the alpha beam and the background proton is in the order of the local Alfvén velocity () as the solar wind plasma flows away from the Sun into the interplanetary medium. Alpha beam instability has been proposed to constrain the drift velocity of alpha beams in the solar wind [12,14]. However, how the alpha beams decelerate remains unknown. In this paper, the kinetic instabilities induced by both the alpha beam and the electron temperature anisotropy in the solar wind were assessed, along with the effects of the electron temperature anisotropy on these instabilities.
The results showed that the wave frequency, growth rate, and polarization features are affected by the electron temperature anisotropy (), the parallel electron beta (), and the alpha beam drift velocity (). With an excess parallel temperature , the PM/W, PAW, and OA/IC instabilities could be generated. At , as decreases, the growth rates of the PM/W, PAW, and OA/IC waves increase, and the threshold velocities of the three waves are shifted to lower values of . With an excess perpendicular temperature , the PM/W, OA/IC, PW, and KAW instabilities could be driven. At , as increases, the growth rates for the PM/W and OA/IC instabilities decrease, while those of the PW and KAW instabilities increase. The threshold velocities of the PM/W and OA/IC instabilities are shifted to larger values of with rising .
We note that the growth rate of the PM/W, OA/IC, and PAW is , and that of the KAW is . For a typical magnetic field of 5 nT in the solar wind at 1 AU [45], the relaxation time of the former waves is 2087.7–20.88 s, and that of latter wave is 2.09–0.21 s, which are much smaller than the expanding time of the solar wind. This indicates that the linear wave–particle interaction of these waves can effectively occur in the solar wind.
In the solar wind, the temperature anisotropies of the alpha particles and protons are also important. Based on hybrid simulations, Lu et al. [37] studied the nonlinear evolution of alpha beam instability in the presence of proton and alpha temperature anisotropies, demonstrating that the alpha temperature anisotropy with is inclined to enhance the amplitudes of both the M/W and A/IC waves, while the proton temperature anisotropy with tends to reduce the amplitudes of these waves. Recently, Using the linear Vlasov theory, Zhang et al. [39] investigated the effects of the alpha and proton temperature anisotropies on the alpha beam instability in the solar wind, and they found that the alpha and proton temperature anisotropies can further limit the alpha beam drift velocity from to . Comparing our results with the work of Zhang et al. [39], the presence of the electron temperature anisotropy can result in not only a larger growth rate and a lower threshold velocity of the PM/W and OA/IC instabilities, but also the generation of extra waves, i.e., the PAW and KAW.
Our physical model could provide a reasonable mechanism for alpha beam deceleration in the solar wind. When the solar wind plasma flows away from the Sun into the interplanetary medium, the drift velocity of the alpha beams is nearly constant, while the local Alfvén velocity is reduced by the magnetic field expansion. This indicates that the normalized drift velocity increases with heliocentric distance. When exceeds the instability thresholds of the PM/W and/or OA/IC waves, these waves could be excited. During the process of wave generation, a part of the kinetic energy of the alpha beams is transformed into wave energy, followed by the reduction of the drift velocity of the alpha beams for a lowering threshold velocity (i.e., ). However, the alpha beams can be further slowed down by the electron temperature anisotropy. In the solar wind, is not a fixed value. For , the PM/W, PAW, and OA/IC instabilities can further decelerate the alpha beams, while for , the KAW instability can further constrain the drift velocity of the alpha beams. Anisotropic electrons induce a further deceleration of the alpha beams to below the local Alfvén velocity (i.e., ), corroborating the solar wind measurements. This work can provide important implications for alpha beam deceleration in the solar wind.
We also considered the feasible applications to the magnetosheath. The electron temperature anisotropy accompanied by various plasma instabilities is often observed in the magnetosheath [33], where the plasma beta is larger than or close to 1 (i.e., ). Our results showed that, when , the effect of electron temperature anisotropy on alpha beam instability is more significant, and the excited OA/IC, PM/W, PAW, and KAW play a more important role in the deceleration of alpha particles ().
It is worth noting that the instability thresholds obtained from the linear Vlasov theory can provide an upper boundary imposed on the observed distribution of alpha beam drift velocity, but the specific wave–particle interactions are not fully understood. The solar wind is a turbulent medium. The linear Vlasov theory is usually applicable to the turbulence associated with short-wavelength and small-amplitude microinstabilities [46]. The present results are helpful in understanding the generation of kinetic instabilities and the deceleration of alpha beams in the solar wind, as well as in the magnetosheath.
Author Contributions
Investigation, S.-Y.L. and L.X.; writing—original draft preparation, S.-Y.L. and L.X.; writing—review and editing, S.-Y.L., L.X., Q.-H.L., W.-L.Z. and H.-W.Y. All authors have read and agreed to the published version of the manuscript.
Funding
The present study was funded by the NSFC (Nos. 12103018, 11690034, and 12075084) and the Science and Technology Innovation Program of Hunan Province (2020RC2049).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We are grateful to Guoqing Zhao at Luoyang Normal University for useful discussions and valuable suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bame, S.J.; Asbridge, J.R.; Feldman, W.C.; Gosling, J.T. Evidence for a structure-free state at high solar wind speeds. J. Geophys. Res. 1977, 82, 1487–1492. [Google Scholar] [CrossRef]
- Pierrard, V.; Lazar, M.; Poedts, S.; Štverák, Š.; Maksimovic, M.; Trávníček, P.M. The Electron Temperature and Anisotropy in the Solar Wind. Comparison of the Core and Halo Populations. Sol. Phys. 2016, 291, 2165–2179. [Google Scholar] [CrossRef]
- Verscharen, D.; Bourouaine, S.; Chandran, B.D.G.; Maruca, B.A. A Parallel-propagating Alfvénic Ion-beam Instability in the High-beta Solar Wind. Astrophys. J. 2013, 773, 8. [Google Scholar] [CrossRef]
- Steinberg, J.T.; Lazarus, A.J.; Ogilvie, K.W.; Lepping, R.; Byrnes, J. Differential flow between solar wind protons and alpha particles: First WIND observations. Geophys. Res. Lett. 1996, 23, 1183–1186. [Google Scholar] [CrossRef]
- Neugebauer, M.; Goldstein, B.E.; Smith, E.J.; Feldman, W.C. Ulysses observations of differential alpha-proton streaming in the solar wind. J. Geophys. Res. 1996, 101, 17047–17055. [Google Scholar] [CrossRef]
- Borovsky, J.E. The plasma structure of coronal hole solar wind: Origins and evolution. J. Geophys. Res. Space Phys. 2016, 121, 5055–5087. [Google Scholar] [CrossRef]
- Ďurovcová, T.; Němeček, Z.; Šafránková, J. Evolution of the α-proton Differential Motion across Stream Interaction Regions. Astrophys. J. 2019, 873, 24. [Google Scholar] [CrossRef]
- Ebert, R.W.; McComas, D.J.; Elliott, H.A.; Forsyth, R.J.; Gosling, J.T. Bulk properties of the slow and fast solar wind and interplanetary coronal mass ejections measured by Ulysses: Three polar orbits of observations. J. Geophys. Res. Space Phys. 2009, 114. [Google Scholar] [CrossRef]
- Goldstein, B.E.; Neugebauer, M.; Zhang, L.D.; Gary, S.P. Observed constraint on proton-proton relative velocities in the solar wind. Geophys. Res. Lett. 2000, 27, 53–56. [Google Scholar] [CrossRef]
- Gomberoff, L.; Gnavi, G.; Gratton, F.T. Minor heavy ion electromagnetic beam-plasma interactions in the solar wind. J. Geophys. Res. 1996, 101, 13517–13522. [Google Scholar] [CrossRef]
- Marsch, E.; Livi, S. Observational evidence for marginal stability of solar wind ion beams. J. Geophys. Res. 1987, 92, 7263–7268. [Google Scholar] [CrossRef]
- Gary, S.P.; Yin, L.; Winske, D.; Reisenfeld, D.B. Electromagnetic alpha/proton instabilities in the solar wind. Geophys. Res. Lett. 2000, 27, 1355–1358. [Google Scholar] [CrossRef]
- Gary, S.P.; Jian, L.K.; Broiles, T.W.; Stevens, M.L.; Podesta, J.J.; Kasper, J.C. Ion-driven instabilities in the solar wind: Wind observations of 19 March 2005. J. Geophys. Res. 2016, 121, 30–41. [Google Scholar] [CrossRef]
- Gary, S.P.; Yin, L.; Winske, D.; Reisenfeld, D.B. Alpha/proton magnetosonic instability in the solar wind. J. Geophys. Res. 2000, 105, 20989–20996. [Google Scholar] [CrossRef]
- Revathy, P. Magnetosonic instability driven by an alpha particle beam in the solar wind. J. Geophys. Res. 1978, 83, 5750–5752. [Google Scholar] [CrossRef]
- Verscharen, D.; Chandran, B.D.G.; Bourouaine, S.; Hollweg, J.V. Deceleration of Alpha Particles in the Solar Wind by Instabilities and the Rotational Force: Implications for Heating, Azimuthal Flow, and the Parker Spiral Magnetic Field. Astrophys. J. 2015, 806, 157. [Google Scholar] [CrossRef]
- Verscharen, D.; Bourouaine, S.; Chandran, B.D.G. Instabilities Driven by the Drift and Temperature Anisotropy of Alpha Particles in the Solar Wind. Astrophys. J. 2013, 773, 163. [Google Scholar] [CrossRef]
- Li, X.; Habbal, S.R. Proton/alpha magnetosonic instability in the fast solar wind. J. Geophys. Res. 2000, 105, 7483–7489. [Google Scholar] [CrossRef]
- Xiang, L.; Wu, D.J.; Chen, L. Effect of alpha beams on low-frequency electromagnetic waves driven by proton beams. Astrophys. J. 2018, 869, 64. [Google Scholar] [CrossRef]
- Bourouaine, S.; Verscharen, D.; Chandran, B.D.G.; Maruca, B.A.; Kasper, J.C. Limits on Alpha Particle Temperature Anisotropy and Differential Flow from Kinetic Instabilities: Solar Wind Observations. Astrophys. J. 2013, 777, L3. [Google Scholar] [CrossRef] [Green Version]
- Sun, H.; Zhao, J.; Xie, H.; Wu, D. On Kinetic Instabilities Driven By Ion Temperature Anisotropy and Differential Flow in the Solar Wind. Astrophys. J. 2019, 884, 44. [Google Scholar] [CrossRef]
- Klein, K.G.; Howes, G.G. Predicted impacts of proton temperature anisotropy on solar wind turbulence. Phys. Plasmas 2015, 22, 032903. [Google Scholar] [CrossRef]
- Masood, W.; Schwartz, S.J. Observations of the development of electron temperature anisotropies in Earth’s magnetosheath. J. Geophys. Res. Space Phys. 2008, 113. [Google Scholar] [CrossRef]
- Feldman, W.C.; Asbridge, J.R.; Bame, S.J.; Montgomery, M.D.; Gary, S.P. Solar wind electrons. J. Geophys. Res. 1975, 80, 4181–4196. [Google Scholar] [CrossRef]
- Pilipp, W.G.; Miggenrieder, H.; Montgomery, M.D.; Mühlhäuser, K.-H.; Rosenbauer, H.; Schwenn, R. Characteristics of electron velocity distribution functions in the solar wind derived from the helios plasma experiment. J. Geophys. Res. 1987, 92, 1075–1092. [Google Scholar] [CrossRef]
- ŠtveráK, Š.; Trávníček, P.; Maksimovic, M.; Marsch, E.; Fazakerley, A.N.; Scime, E.E. Electron temperature anisotropy constraints in the solar wind. J. Geophys. Res. Space Phys. 2008, 113, A03103. [Google Scholar] [CrossRef]
- Sun, H.; Zhao, J.; Liu, W.; Xie, H.; Wu, D. Electron Temperature Anisotropy and Electron Beam Constraints from Electron Kinetic Instabilities in the Solar Wind. Astrophys. J. 2020, 902, 59. [Google Scholar] [CrossRef]
- Bale, S.D.; Kasper, J.C.; Howes, G.G.; Quataert, E.; Salem, C.; Sundkvist, D. Magnetic Fluctuation Power Near Proton Temperature Anisotropy Instability Thresholds in the Solar Wind. Phys. Rev. Lett. 2009, 103, 211101. [Google Scholar] [CrossRef]
- Vafin, S.; Lazar, M.; Fichtner, H.; Schlickeiser, R.; Drillisch, M. Solar wind temperature anisotropy constraints from streaming instabilities. Astron. Astrophys. 2018, 613, A23. [Google Scholar] [CrossRef]
- Hellinger, P.; Trávníček, P.; Kasper, J.C.; Lazarus, A.J. Solar wind proton temperature anisotropy: Linear theory and WIND/SWE observations. Geophys. Res. Lett. 2006, 33, L09101. [Google Scholar] [CrossRef] [Green Version]
- Maruca, B.A.; Kasper, J.C.; Bale, S.D. What Are the Relative Roles of Heating and Cooling in Generating Solar Wind Temperature Anisotropies? Phys. Rev. Lett. 2011, 107, 201101. [Google Scholar] [CrossRef] [PubMed]
- Michno, M.J.; Lazar, M.; Yoon, P.H.; Schlickeiser, R. Effects of Electrons on the Solar Wind Proton Temperature Anisotropy. Astrophys. J. 2014, 781, 49. [Google Scholar] [CrossRef]
- Ahmadi, N.; Germaschewski, K.; Raeder, J. Effects of electron temperature anisotropy on proton mirror instability evolution. J. Geophys. Res. Space Phys. 2016, 6, 5350–5365. [Google Scholar] [CrossRef]
- Shaaban, S.M.; Lazar, M.; Yoon, P.H.; Poedts, S. Beaming electromagnetic (or heat-flux) instabilities from the interplay with the electron temperature anisotropies. Phys. Plasmas 2018, 25, 082105. [Google Scholar] [CrossRef]
- Xiang, L.; Lee, K.H.; Wu, D.J.; Lee, L.C. Effects of Electron Temperature Anisotropy on Proton-beam Instability in the Solar Wind. Astrophys. J. 2020, 899, 61. [Google Scholar] [CrossRef]
- Maruca, B.A.; Kasper, J.C.; Gary, S.P. Instability-driven Limits on Helium Temperature Anisotropy in the Solar Wind: Observations and Linear Vlasov Analysis. Astrophys. J. 2012, 748, 137. [Google Scholar] [CrossRef]
- Lu, Q.M.; Xia, L.D.; Wang, S. Hybrid simulations of parallel and oblique electromagnetic alpha/proton instabilities in the solar wind. J. Geophys. Res. 2006, 111, A09101. [Google Scholar] [CrossRef]
- Gao, X.; Lu, Q.; Li, X.; Huang, C.; Wang, S. Heating of the background plasma by obliquely propagating Alfven waves excited in the electromagnetic alpha/proton instability. Phys. Plasmas 2012, 19, 032901. [Google Scholar] [CrossRef]
- Zhang, W.-L.; Xiang, L.; Li, Q.-H.; Lang, S.-Y.; Yu, H.-W. Alpha/proton Instability in the Presence of Proton and Alpha Temperature Anisotropy and its Application to the Deceleration of Alpha Particles in the Solar Wind. Res. Astron. Astrophys. 2022, 22, 015018. [Google Scholar] [CrossRef]
- Wu, D.J. Kinetic Alfvén Waves: Theory, Experience, and Application; Science Press: Beijing, China, 2012. [Google Scholar]
- Marsch, E.; Schwenn, R.; Rosenbauer, H.; Muehlhaeuser, K.-H.; Pilipp, W.; Neubauer, F.M. Solar wind protons: Three-dimensional velocity distributions and derived plasma parameters measured between 0.3 and 1 AU. J. Geophys. Res. 1982, 87, 52–72. [Google Scholar] [CrossRef]
- Marsch, E.; Rosenbauer, H.; Schwenn, R.; Muehlhaeuser, K.-H.; Neubauer, F.M. Solar wind helium ions: Obsevations of the Helios solar probes between 0.3 and 1 AU. J. Abbr. 1982, 1, 35–51. [Google Scholar] [CrossRef]
- Xiang, L.; Lee, K.H.; Wu, D.J.; Yu, H.W.; Lee, L.C. Linear and nonlinear effects of proton temperature anisotropy on proton-beam instability in the solar wind. Astrophys. J. 2021, 916, 30. [Google Scholar] [CrossRef]
- Stix, T.H. Waves in Plasmas; American Institute of Physics: New York, NY, USA, 1992. [Google Scholar]
- Li, Q.H.; Yang, L.; Xiang, L.; Wu, D.J. Spatial Distribution of Electromagnetic Waves near the Proton Cyclotron Frequency in ICME Sheath Regions Associated with Quasi-perpendicular Shocks: Wind Observations. Astrophys. J. 2020, 892, 98. [Google Scholar] [CrossRef]
- Gary, S.P.; Bandyopadhyay, R.; Qudsi, R.A.; Matthaeus, W.H.; Maruca, B.A.; Parashar, T.N.; Roytershteyn, V. Particle-in-cell Simulations of Decaying Plasma Turbulence: Linear Instabilities versus Nonlinear Processes in 3D and 2.5D Approximations. Astrophys. J. 2020, 901, 160. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).