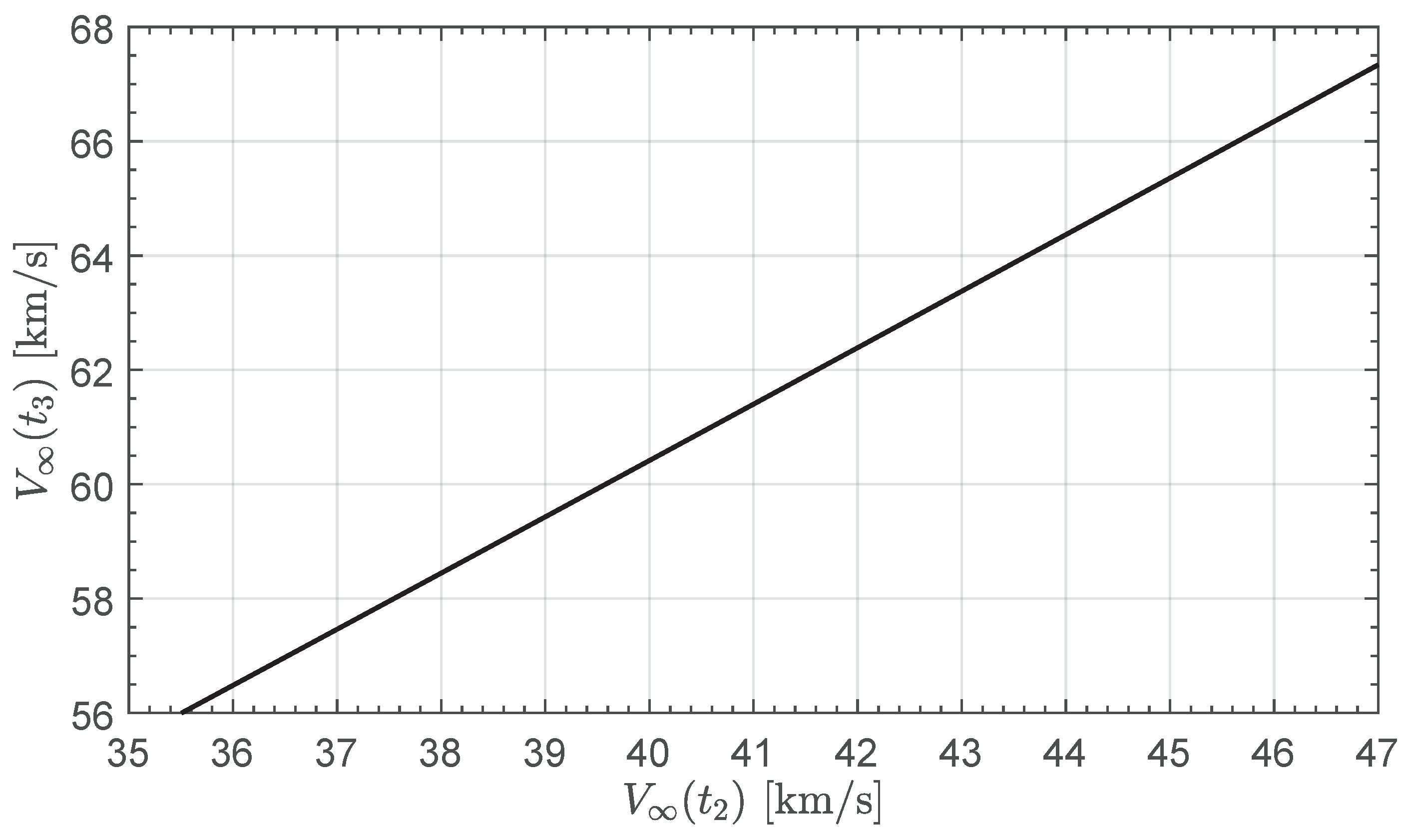1. Introduction
Reaching the boundaries and escaping from the solar system within a time interval on the order of the human working lifetime is currently one of the most complex space mission scenarios from a trajectory analysis viewpoint [
1]. Such a fascinating and advanced mission would be of great scientific interest to obtain information and solve fundamental physical questions about the formation mechanism of the heliospheric boundary, the nature of the nearby interstellar medium [
2], the structure and dynamics of the heliosphere, and the distribution of matter in this part of interplanetary space [
3]. Many, if not all, of these issues can only be solved through in situ measurements such as plasma density, ionization state, dust composition and magnetic field strength [
4]. However, missions towards (and even beyond) the heliopause region represent a technological challenge [
5], as they require the use of advanced propulsion systems [
6] to guarantee a cruise velocity of at least 10 au/year if the spacecraft has to be able to reach the desired (very long) distance, greater than 100 au, in a reasonable time interval.
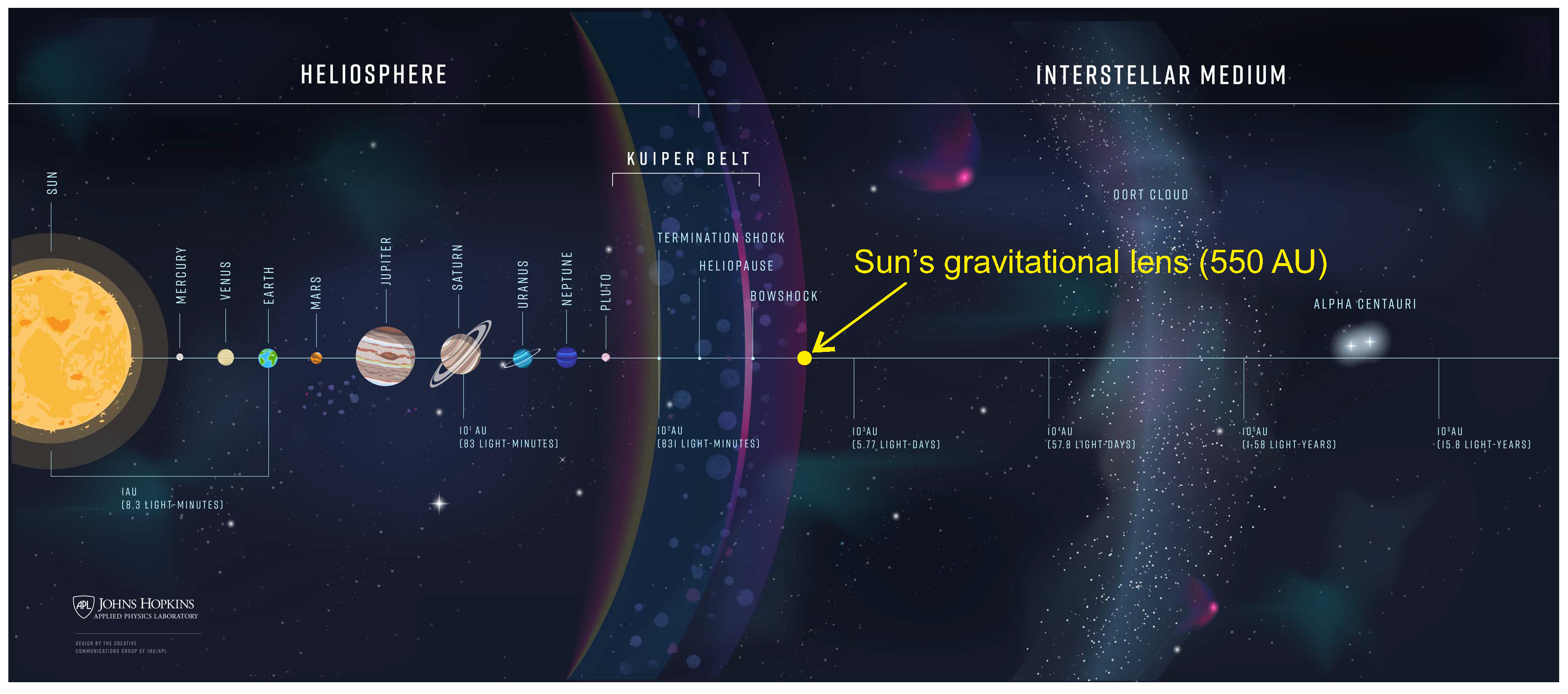
An even more futuristic and hard to manage project from a technological side is the dream to arrive at the Sun’s gravitational focus (SGF). According to general relativity theory, a massive object such as the Sun is able to deflect the light beams passing around it and to converge them at a focus. This effect implies that the Sun might be used as a sort of gravitational lens. However, differently from what happens in classical optics where the lens focus coincides with a single point, the gravitational effect causes the light beams passing at different distances from the Sun’s surface to converge at different points aligned along a straight line, which theoretically extends from about 550 au to the interstellar space (infinity), see
Figure 1.
A light sensor placed at the focal region could therefore obtain images of exoplanets, some tens of light years far away, with a surface resolution of about 10 km for an Earth-like planet [
7]. Note, however, that such a scenario requires staring almost at the Sun, with evident limitations for practical astronomy. This concept, first proposed by Eshleman [
8] in 1979, has much attracted the attention of the scientific community, with many proposals for possible (and exotic) future missions [
9,
10,
11]. A number of advances that could be obtained from a robotic mission to the SGF are in depth discussed by Maccone [
12]. Such a fascinating mission concept may also be thought of as a necessary first step toward a future interstellar mission [
13,
14]. Even though a number of technical difficulties exist in translating the original idea into feasible achievements, including severe problems related to the telescope pointing requirements, the signal to noise ratio due to the solar corona and the focal blur [
15], new studies on advanced missions to SGF continue to appear [
16,
17].
A possible way to address these complex problems is to decrease the mass of the scientific probe to be launched by distributing the whole payload among a fleet of smaller spacecraft, which could be deployed along an Einstein ring as illustrated in
Figure 2. Among other advantages, a vehicle mass reduction implies higher spacecraft accelerations (assuming the thrust magnitude is unchanged) as well as increased escape velocities.
The enormous distances to reach during a (very long) space journey to the SGF make the transfer trajectory a very challenging task to plan, and so is the selection of a suitable propulsion system, capable of providing the required demanding
and, more in general, the design of a space vehicle that must effectively operate along flight times of some tens of years [
17]. An effective outline of the above ideas is offered by the Hesperides mission proposal [
18], originally suggested by Matloff in 2014 as an evolution of a previous Helios and Prometheus concept, which dates back to 2007 [
19]. The main aim of Hesperides mission is to reach a distance of about 600 au from the Sun, comparable with that of the SGF, within approximately five decades. An interesting aspect of the Hesperides mission is the combination of a nuclear electric propulsion system and a solar sail that are jointly exploited to reach the required solar system escape velocity. However the trajectory analysis reported in [
18] is very simplified and is essentially concentrated on obtaining a rough estimate of the main design parameters necessary to meet the mission requirements, that is, mission times and final distances.
The aim of this paper is to revisit the Hesperides mission concept and to analyze it in an optimal and parametric way, by obtaining a more accurate estimate of both the (optimal) transfer trajectory and the flight times. It will be shown that a substantial performance improvement with respect to the original study [
18] is a feasible result.
2. Spacecraft Characteristics and Baseline Mission Description
For illustrative purposes, the spacecraft arrangement and the baseline mission concept are taken from the original Hesperides proposal [
18]. In particular, the solar sail is approximated as a thin disc with a radius of 146 m and a mass-to-area ratio equal to 0.003 kg/m
2. The electric propulsion system uses xenon propellant exhausted at a constant mass flow rate and its specific impulse is
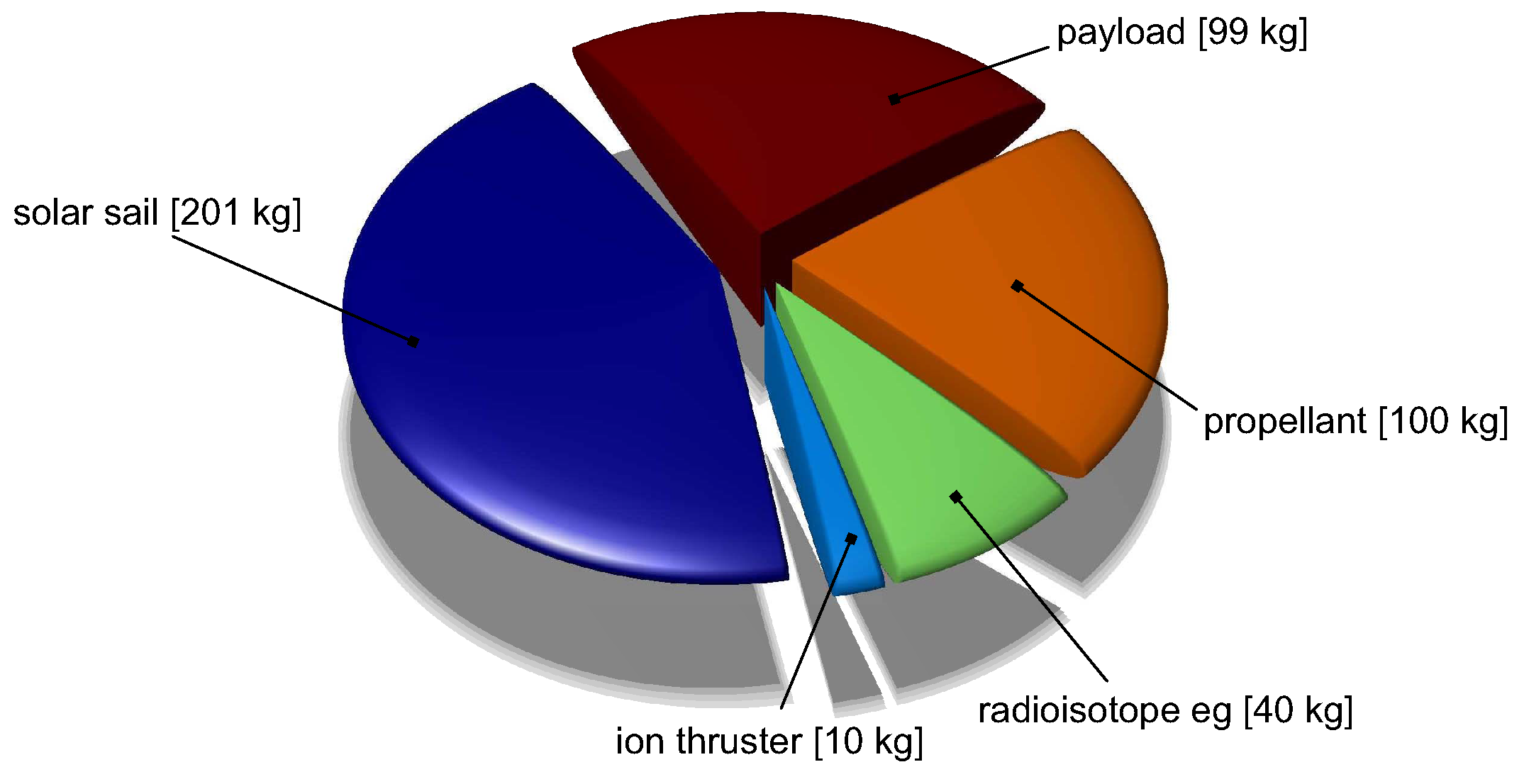
. An estimate of the masses of the main spacecraft subsystems is reported in
Table 1 and is illustrated in the pie chart of
Figure 3.
The baseline mission [
18] may be divided into the following four main phases:
Pre-perihelion phase. The spacecraft is launched from Earth toward an heliocentric orbit with perihelion distance and aphelion distance . The required initial hyperbolic excess velocity is provided by an upper stage of the launcher, and the spacecraft reaches the target orbit with a flight time of about 2 years without using the solar sail or the electric thruster. In particular, the spacecraft mass in this phase is constant and equal to 450 kg.
Solar sail acceleration. When the spacecraft is at the perihelion of the heliocentric orbit (end of phase 1) the solar sail is unfurled with a Sun-facing attitude [
20,
21,
22,
23], that is, its nominal plane is oriented normal to the Sun. In this phase, the spacecraft is continuously accelerated by the solar sail induced thrust until it reaches a solar distance of 5 au, when the sail propulsive acceleration becomes ineffective and is therefore jettisoned. During this whole phase, the spacecraft mass remains equal to 450 kg. The flight time of this phase is about 1 year.
Radioisotope-electric propulsion. This phase starts when the solar sail is discarded, so that the spacecraft mass suddenly reduces to 249 kg. The radioisotope-electric thruster is switched on and is continuously operated until the whole available xenon propellant is exhausted at a constant mass flow rate . Since the total propellant mass is 100 kg, the phase (time) length is 10 years. During this phase the induced thrust is nearly along the radial direction, so that the spacecraft (heliocentric) hyperbolic excess velocity increases from about 35.5 km/s to 56 km/s, at a distance of about 100 au away from the Sun. At the end of this phase, the spacecraft mass is reduced to 149 kg.
Cruise to 600 au. The last (baseline) trajectory part is a coasting phase with a constant velocity (with respect the Sun), equal to that reached at the end of phase 3. The spacecraft continues its (Keplerian) flight for about 42.5 years until it reaches a target distance of 600 au from the Sun. The spacecraft mass in this phase is constant and equal to 149 kg.
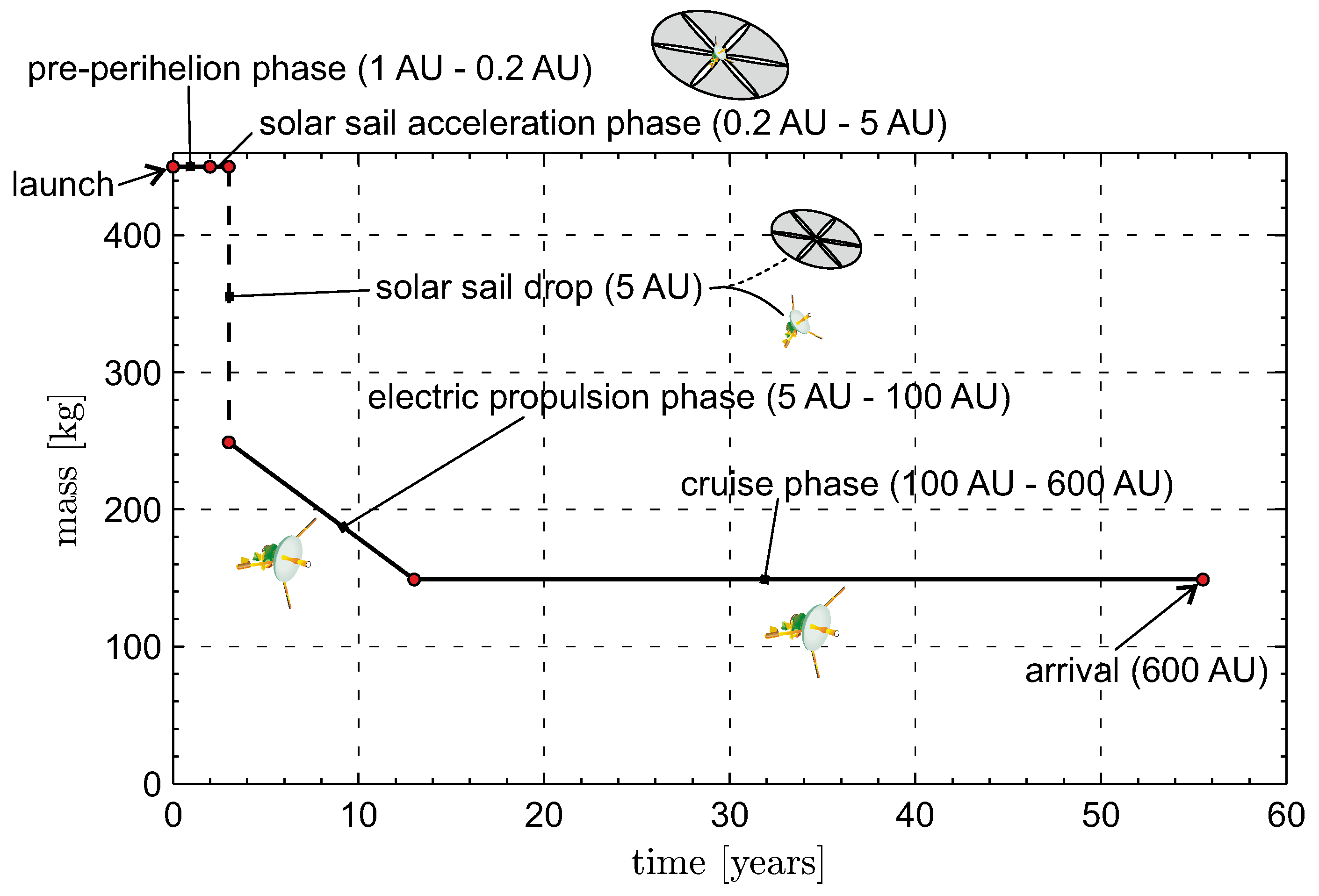
Accordingly, the total mission length is the sum of the flight times required to complete the previous four phases, that is,
.
Figure 4 summarizes the spacecraft mass variation during the four phases and the mission flight times.
3. Mission Optimization
The baseline mission is now reassessed within an optimal framework with the aim of investigating to what extent it may be improved. To that end, according to [
18], a simplified two-dimensional model is used to describe the heliocentric spacecraft dynamics. More precisely, introduce a (heliocentric) polar reference frame
, where
O is the Sun’s center of mass, with orthogonal radial and transverse unit vectors
and
, respectively; see
Figure 5. In this reference frame, the polar angle
is measured counterclockwise from the Sun-spacecraft line at time
.
The spacecraft equations of motion in
may be written as
where
r is the distance from the Sun,
is the Sun’s gravitational parameter,
u and
v are the radial and transverse component of the spacecraft velocity, while
and
are the radial and transverse component of the spacecraft propulsive acceleration vector
.
When the spacecraft is propelled by the solar sail, the propulsive acceleration components are
where
is the spacecraft characteristic acceleration, that is, the acceleration magnitude induced by the solar sail when its nominal plane is perpendicular to the Sun-spacecraft line at a distance
, and
is the sail pitch angle measured counterclockwise from the Sun-spacecraft line; see
Figure 5. The solar sail is here described through an augmented ideal force model [
24,
25] without degradation [
26,
27,
28] or wrinkles [
29]. In this context, the sail is assumed to maintain a flat surface, and the direction of the propulsive acceleration vector is normal to the sail nominal plane in the direction opposite to the Sun. The non-complete reflectivity of the sail film [
30] is modeled by introducing a sort of sail efficiency factor
, which quantifies the amount of reflected rays when compared to an ideal (specular) reflection case. Accordingly, the spacecraft characteristic acceleration may be written as
where
is the solar radiation pressure at
,
66,966
is the sail area and
m is the spacecraft mass. In the simulations it has been assumed [
18] that
. With the aid of Equation (
7) and using the data of
Table 1, the spacecraft characteristic acceleration is therefore
.
When the spacecraft is propelled by the electric thruster, the propulsive acceleration vector components are instead written as
where
is the standard gravitational acceleration, and
is the classical thrust angle measured counterclockwise from the radial direction. The spacecraft mass variation with time is therefore
For comparative purposes, the mission has been divided into the same phases as the baseline proposal, and each phase has been individually optimized using an indirect approach. Details about the optimization method may be found in previous works by the authors [
31,
32,
33]. In particular, the spacecraft equations of motion have been numerically integrated using a variable order Adams–Bashforth–Moulton solver scheme, with absolute and relative errors of
, while the associated two-point boundary value problem has been solved (with an absolute error less than
) through gradient-based methods.
The main difference with respect to [
18] is that the spacecraft is now assumed to leave the Earth’s sphere of influence with zero hyperbolic excess velocity relative to the planet and the required thrust in the pre-perihelion phase is provided by the solar sail, which is therefore unfurled at the beginning of phase 1.
3.1. Phase 1
This phase has been analyzed under the assumption that the spacecraft is propelled by the solar sail only. Three possible cases have been considered, which vary according to the different strategy used to reach a desired perihelion distance .
3.1.1. Case a
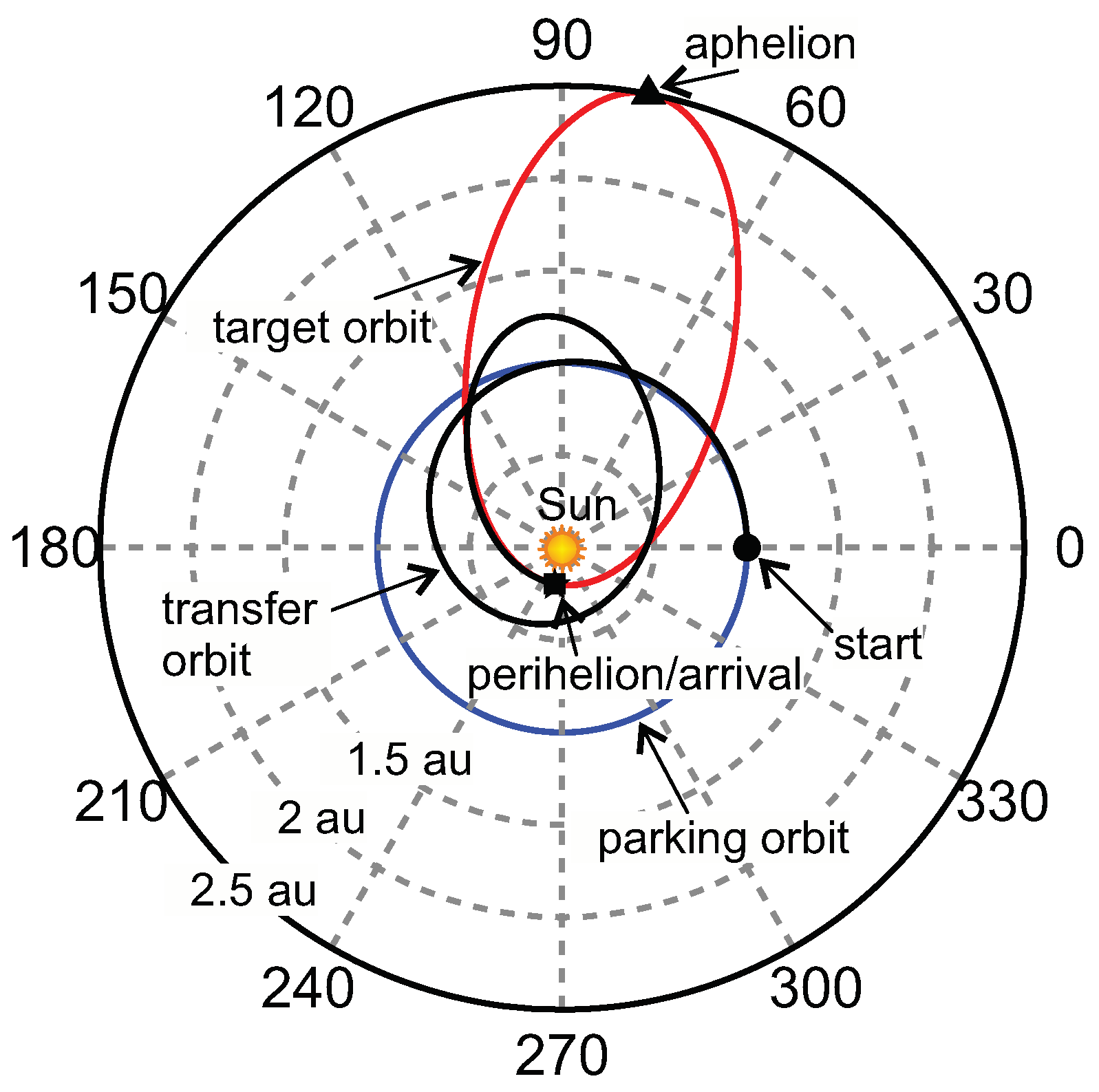
The first strategy is to minimize the transfer time necessary for the spacecraft to reach the heliocentric desired orbit (that is, the elliptic orbit with and ). In this case, the arrival point along the desired orbit is left free and is an output of the optimization process. The time required to complete this phase is , where is the time interval to coast from the insertion point, where the spacecraft enters into the desired orbit, to the orbit perihelion.
Figure 6 shows the transfer trajectory, where the black square coincides with the arrival, that is, the insertion point along the desired heliocentric orbit. The spacecraft true anomaly at insertion point is roughly
. The minimum time to reach the desired orbit is about
and the characteristics of the spacecraft osculating orbit during the transfer trajectory are illustrated in
Figure 7 along with the optimal sail steering law
.
Since the insertion point along the desired orbit is placed forward the perihelion, the spacecraft needs a long time, that is, about , to reach the perihelion with a coasting flight. The total time necessary to complete this phase is roughly .
3.1.2. Case b
The second strategy is to look for the transfer trajectory to the desired orbit with the constraint that the arrival point coincides just with the (desired) orbit perihelion. In this case, the minimum time to reach the perihelion is
, which is, of course, greater than
of the previous case. Note, however, that
because the final point coincides by assumption with the perihelion and no additional coasting phase is required.
Figure 8 shows the transfer trajectory, while the characteristics of the spacecraft osculating orbit along the transfer trajectory and the optimal sail steering law are illustrated in
Figure 9.
3.1.3. Case c
The third strategy is to minimize the flight time to reach a minimum distance from the Sun of
with zero radial velocity, while the transverse velocity is left free. In this case, the minimum transfer time is
, with a remarkable time saving (about
) with respect to
. However, the final osculating orbit (in red color in
Figure 10) has an eccentricity equal to
only. Therefore, the transverse velocity at the arrival point, equal to
, is substantially smaller than that of cases a and b, where the perihelion velocity is about
. Since a high transversal velocity is a fundamental requirement for minimizing the flight time in the succeeding phases, this case actually does not offer an useful option for the whole mission viewpoint. For the sake of completeness
Figure 11 shows the characteristics of the spacecraft osculating orbit along the transfer trajectory, the radial and circumferential velocity components and the optimal sail steering law. Note, in particular, that the velocity at the end of the phase is purely circumferential, since the radial component is zero.
3.2. Phase 2
This phase starts when the spacecraft is at a distance equal to
from the Sun and, according to the previous analysis, we consider the case 1b, with a starting velocity equal to
(fully along the transverse direction). For comparative purposes with the baseline mission, this phase has been studied by minimizing the time required to reach a distance of
with the same hyperbolic excess velocity as that reported in [
18], that is,
. The osculating parameters and the spacecraft velocity components are shown in
Figure 12 along with the sail optimal steering law. The flight time in this phase is
. Note that the final absolute velocity is nearly radial, that is, the transverse component is
, while the radial component is about
. The total flight time to reach a distance of
from the Sun is therefore
.
3.3. Single Optimization of Phases 1 and 2
The previous two phases may be also analyzed within a single optimization problem, by looking for the minimum time trajectory that transfers the spacecraft from the Earth’s (circular) orbit to a heliocentric distance of
, where the vehicle arrives with a hyperbolic excess velocity
. In this case, the spacecraft initially tends to approach the Sun to exploit a solar photonic assist maneuver that dramatically increases its available thrust [
34,
35,
36,
37]. It is therefore necessary to add a constraint on the minimum distance at which the spacecraft pass by the Sun. Details about the practical implementation of such constraint within an optimization problem may be found in [
38]. For compatibility purposes with the previous analysis, such a minimum distance is set to
, which is equal to the perigee distance of the heliocentric target orbit described in phase 1.
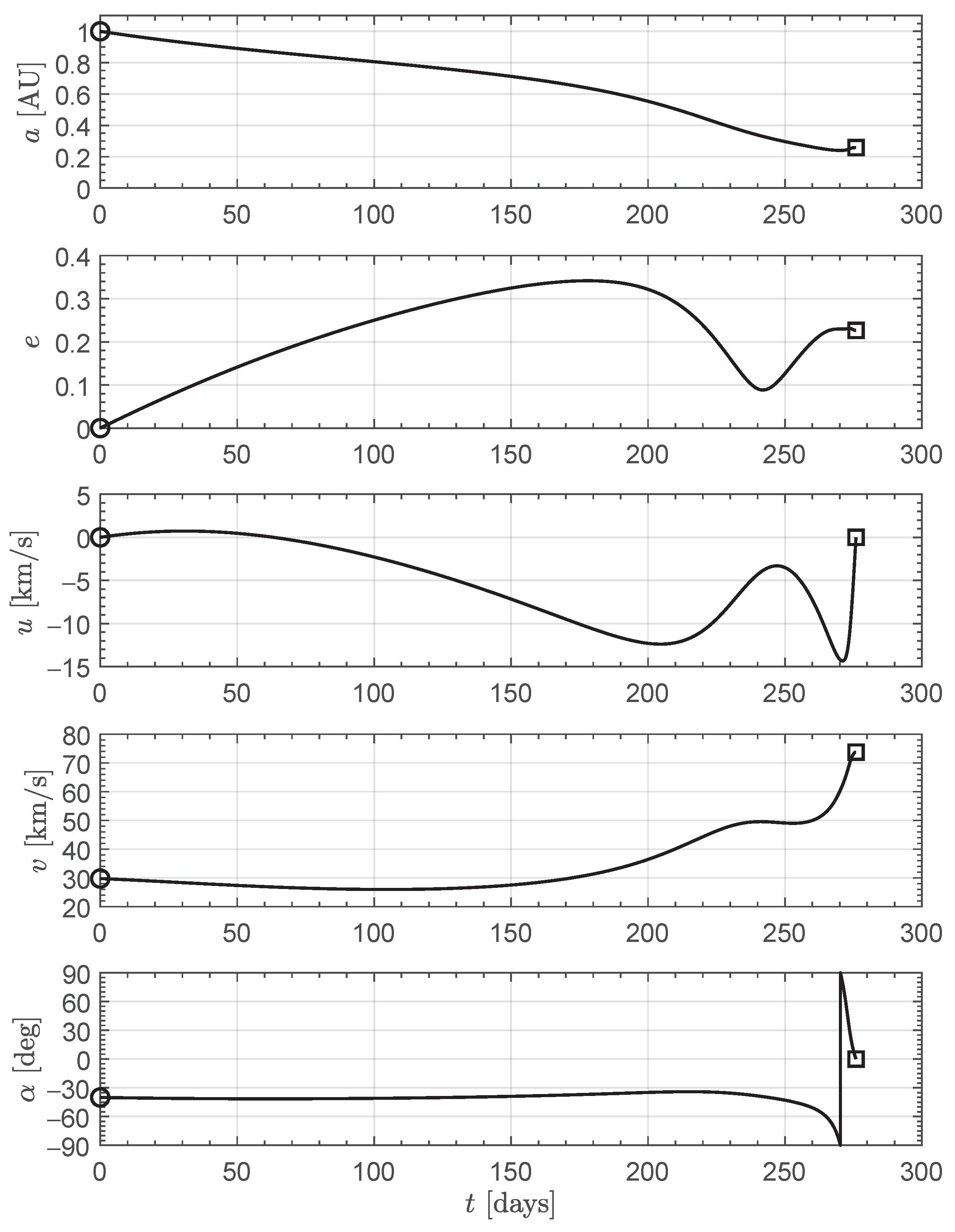
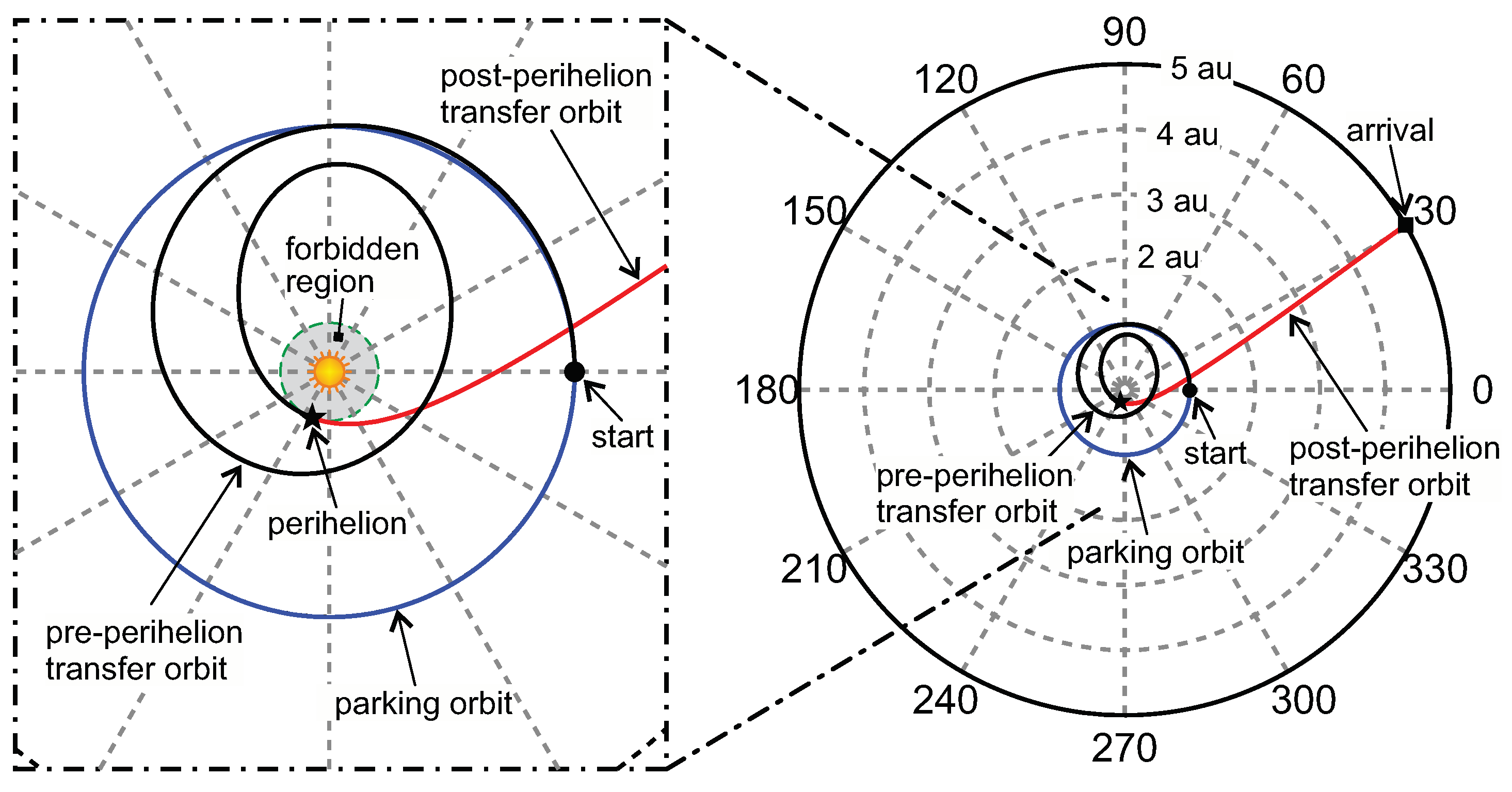
Figure 13 shows that the resulting trajectory is actually tangent to a circle with radius equal to
(the forbidden region). The spacecraft reaches the minimum distance from the Sun after about
when the transverse velocity takes its maximum value and then quickly decreases, as is shown in
Figure 14. Note that in the post-perihelion trajectory the sail is nearly normal to the Sun-spacecraft direction (that is,
) and the spacecraft velocity is almost radial. The total flight time to complete the whole phase is
, which is smaller than the sum of the times necessary to complete phases 1 and 2 alone (the time saving is about
). Note that such time saving may be used to increase the hyperbolic excess velocity when the spacecraft reaches the distance of
. For example, by solving an optimization problem that maximizes
for a fixed flight time, it is possible to look for solutions that provide important improvements over the whole mission time. This parametric analysis will be discussed later on.
3.4. Phase 3
At the end of phase 2 the solar sail becomes ineffective and is therefore jettisoned. The spacecraft is accelerated by the radioisotope-electric thruster that continuously operates for a time length of
until the whole xenon propellant is exhausted at a constant mass flow rate. In this part of the mission, the optimization consists in maximizing the hyperbolic excess speed at the phase end.
Figure 15 shows the main characteristics of the spacecraft trajectory along with the optimal steering law. The spacecraft eventually reaches a solar distance of
with a final hyperbolic excess velocity
, equal to that of the baseline mission [
18].
3.5. Phase 4
The last trajectory part is a coasting phase with constant velocity in which the spacecraft continues its flight until it reaches a distance of from the Sun. The spacecraft mass in this phase remains constant and equal to . Since the initial hyperbolic excess velocity is the same as that reported in the baseline mission, the time interval necessary to complete this phase is also the same.
The total mission time, that is, the sum of the times necessary to complete the four phases, is equal to . This time interval should be compared with that estimated in the baseline mission, that is . Note that the difference between the optimal time and the flight time in the baseline mission is only due to the time saving obtained in phases 1 and 2. This is a consequence of the assumption according to which the hyperbolic excess velocity at the end of phase 2 is the same as that of the baseline mission. However, the total mission time may be substantially reduced by increasing the value of the hyperbolic excess velocity, as will be shown in the parametric analysis of the next section.
4. Parametric Analysis
Since the longer part of the travel involves the electric-based propulsion phase and the final coasting phase, it is reasonable to look for a different strategy aimed at reducing the flight times in these two mission stages. This is possible by maximizing
, that is, the hyperbolic excess velocity at the end of phase 2. The results are shown in
Figure 16, where each point in the graph is the solution of an optimal problem in which the final time
is fixed.
Note that the results start from
(when
), which corresponds to the optimization point of phases 1 and 2. It is clear from the figure that the hyperbolic excess speed may be substantially increased by extending the time interval that exploits the solar photonic assist maneuver.
Figure 17 shows how the hyperbolic excess velocity at the end of phase 3 linearly increases with
. The effect of a change in the hyperbolic speed is better appreciated in
Figure 18, which reports the total mission time as a function of
.
The minimum value of the hyperbolic excess velocity in the figure coincides with the one chosen in the baseline mission. When is increased up to the total mission time is , that is, about smaller than that estimated with the baseline mission. Further performance improvements (that is, additional decrease of total mission times) are of course possible by additionally increasing with a prolonged action of the solar sail within phase two. The corresponding trajectories are characterized by multiple revolutions around the Sun to gain as much energy as possible before reaching the required distance of .
5. Conclusions
In this paper, we have analyzed the times necessary to reach the Sun’s gravitational focus with a baseline reference mission taken from Hesperides proposal. To that end, the problem has been studied in an optimal framework, by dividing the mission into a phase in which the spacecraft is propelled by a solar sail, one in which the spacecraft is propelled by an electric thruster, and a final Keplerian arc. The optimal use of a high-performance solar sail in the first phase of the trajectory allows the spacecraft to obtain a hyperbolic excess velocity of in about . The spacecraft is then further accelerated by means of a radioisotope-electric thruster that continuously operates for a time length of and the required distance of is reached in about .
Further performance improvements (in terms of total flight time) are of course possible by additionally increasing the hyperbolic excess velocity using a prolonged phase of solar photonic assist maneuver. The flight times estimated in this study suggest that the Sun’s gravitational focus may be reached in a time interval well below with a near future technology. The natural extension of this paper is to analyze the performance of such a hybrid propulsion system in a more classical (robotic) mission scenario, in which a deep space probe reaches the outer region of the Solar System and the heliopause.