Dynamics of a Cosmological Model in f(R,T) Gravity: I. On Invariant Planes
Abstract
:1. Introduction
2. Cosmological Equation in Gravity
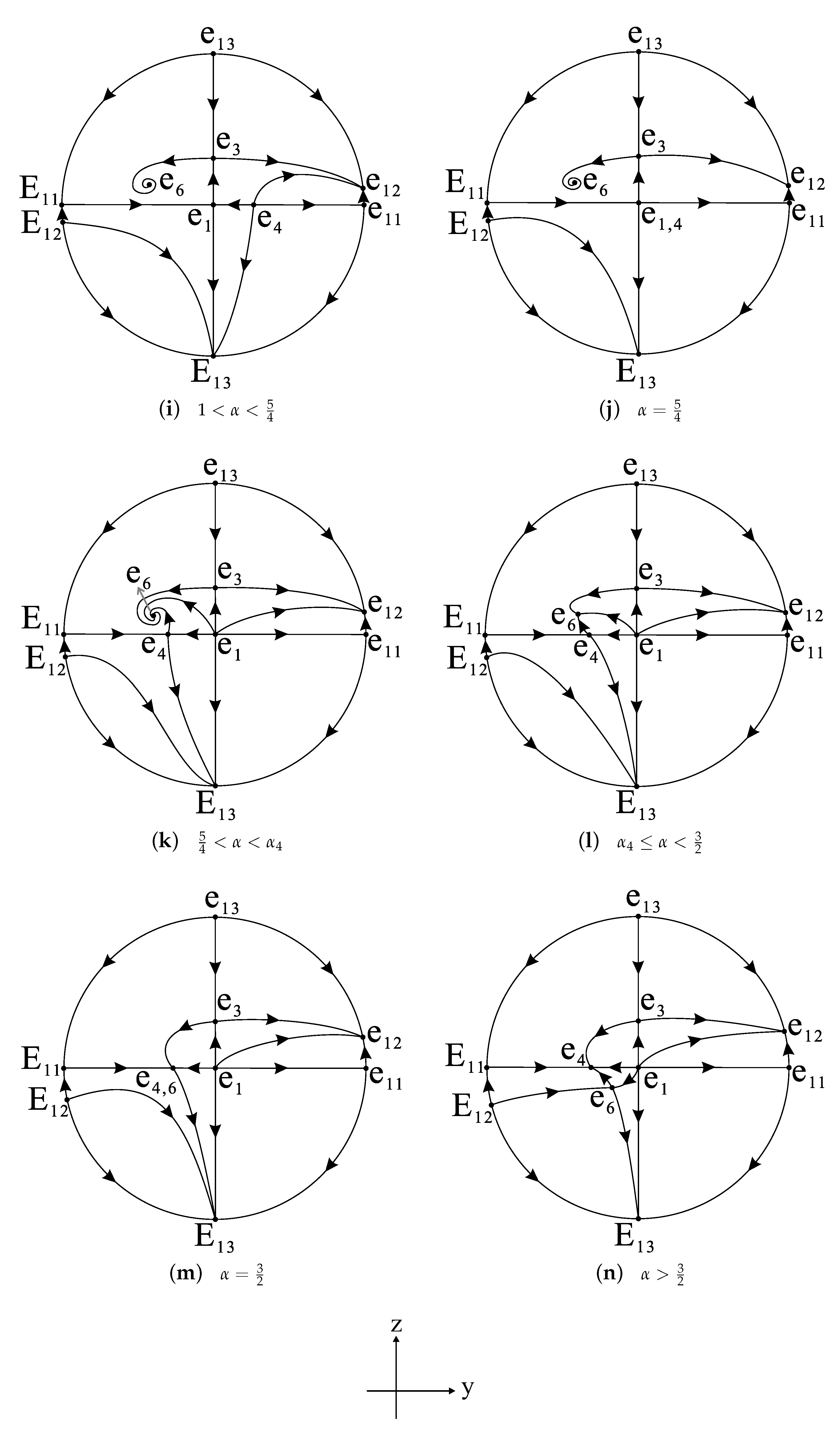
3. Phase Portraits on Invariant Planes and Cosmological Solutions
3.1. Phase Portraits on the Invariant Plane and Cosmological Solutions
3.2. Phase Portraits on the Invariant Plane and Cosmological Solutions
3.3. Phase Portraits on the Invariant Plane and Cosmological Solutions
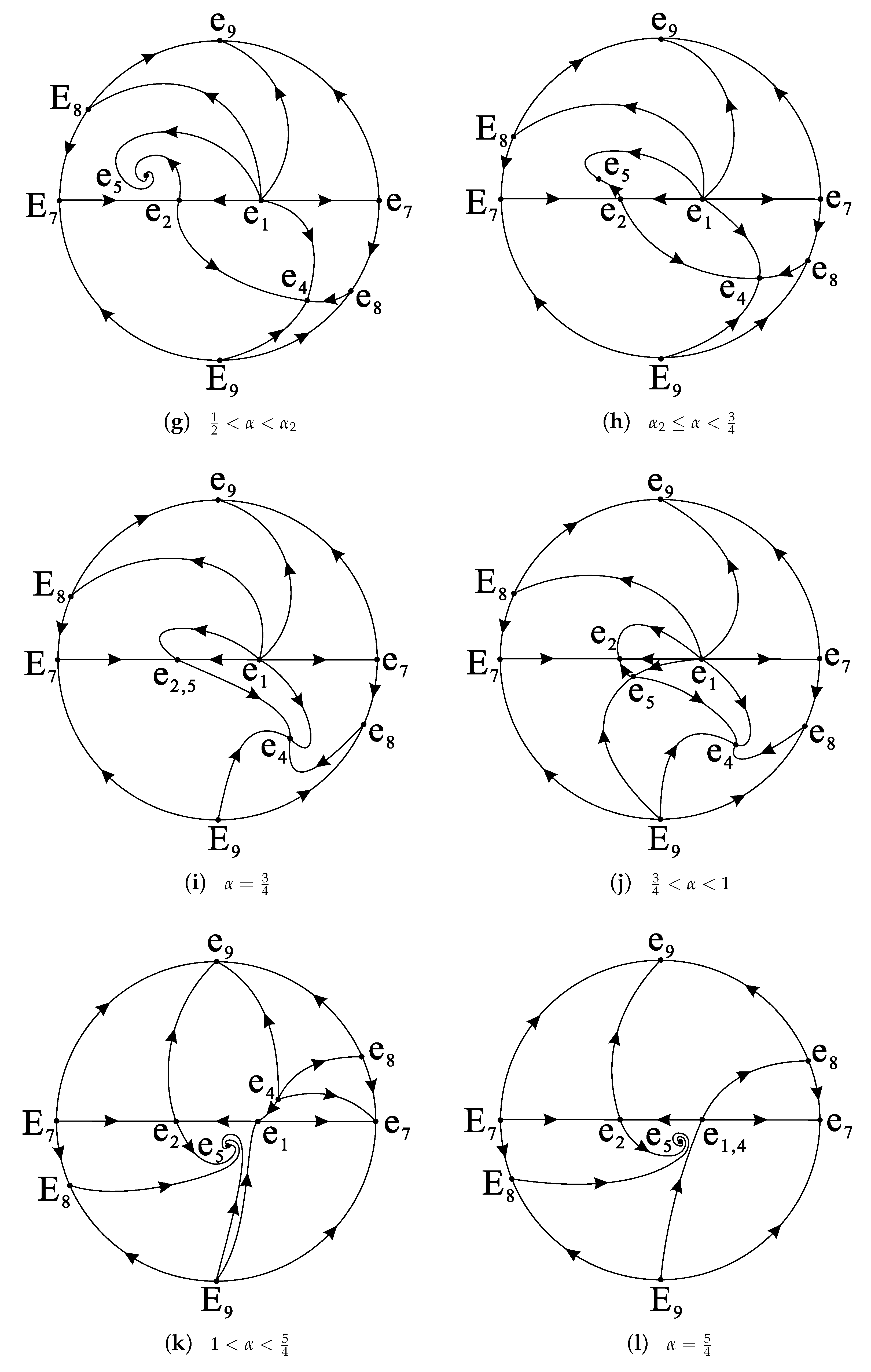
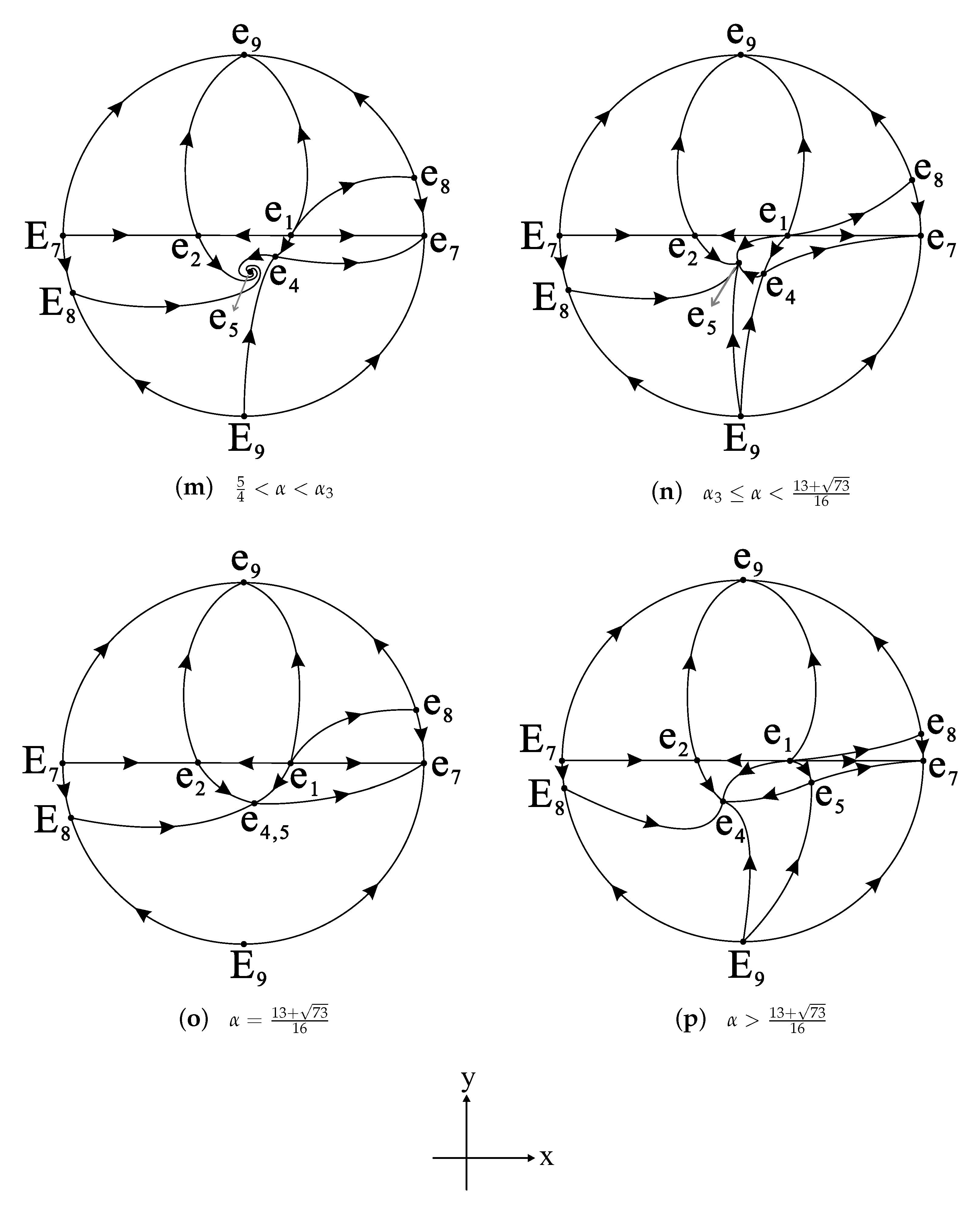
3.4. Equilibrium Points on the Poincaré Sphere at Infinity
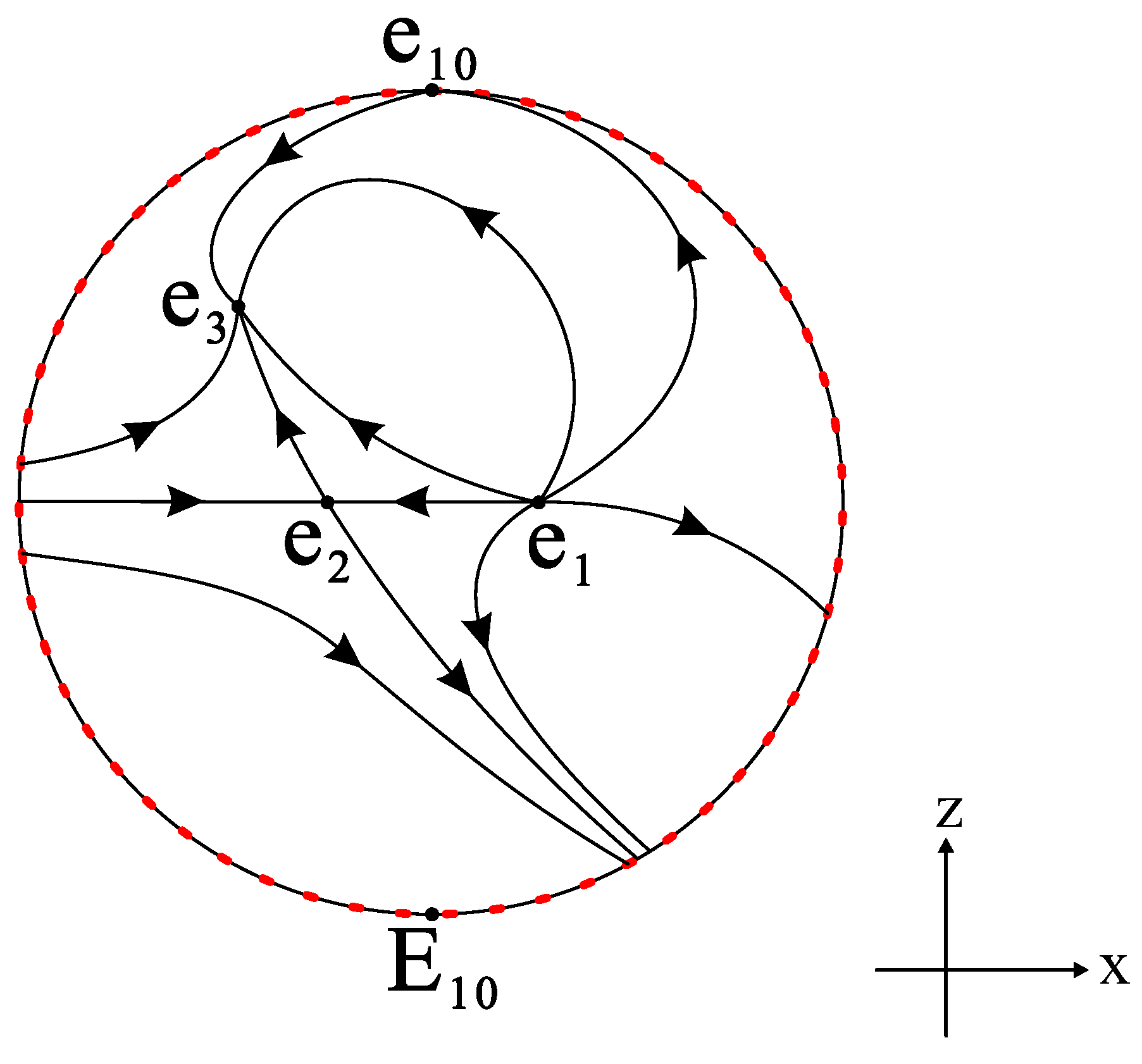
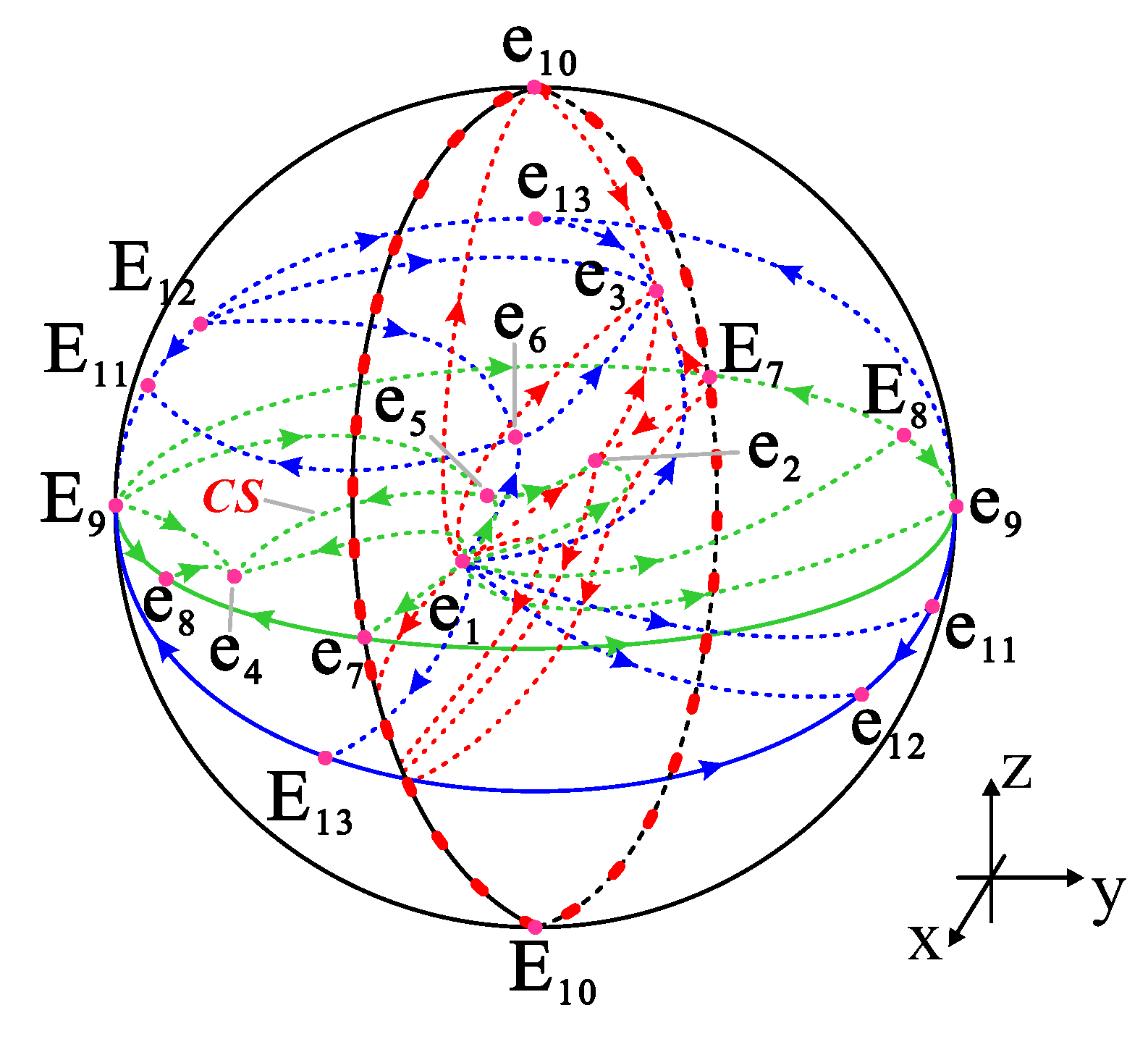
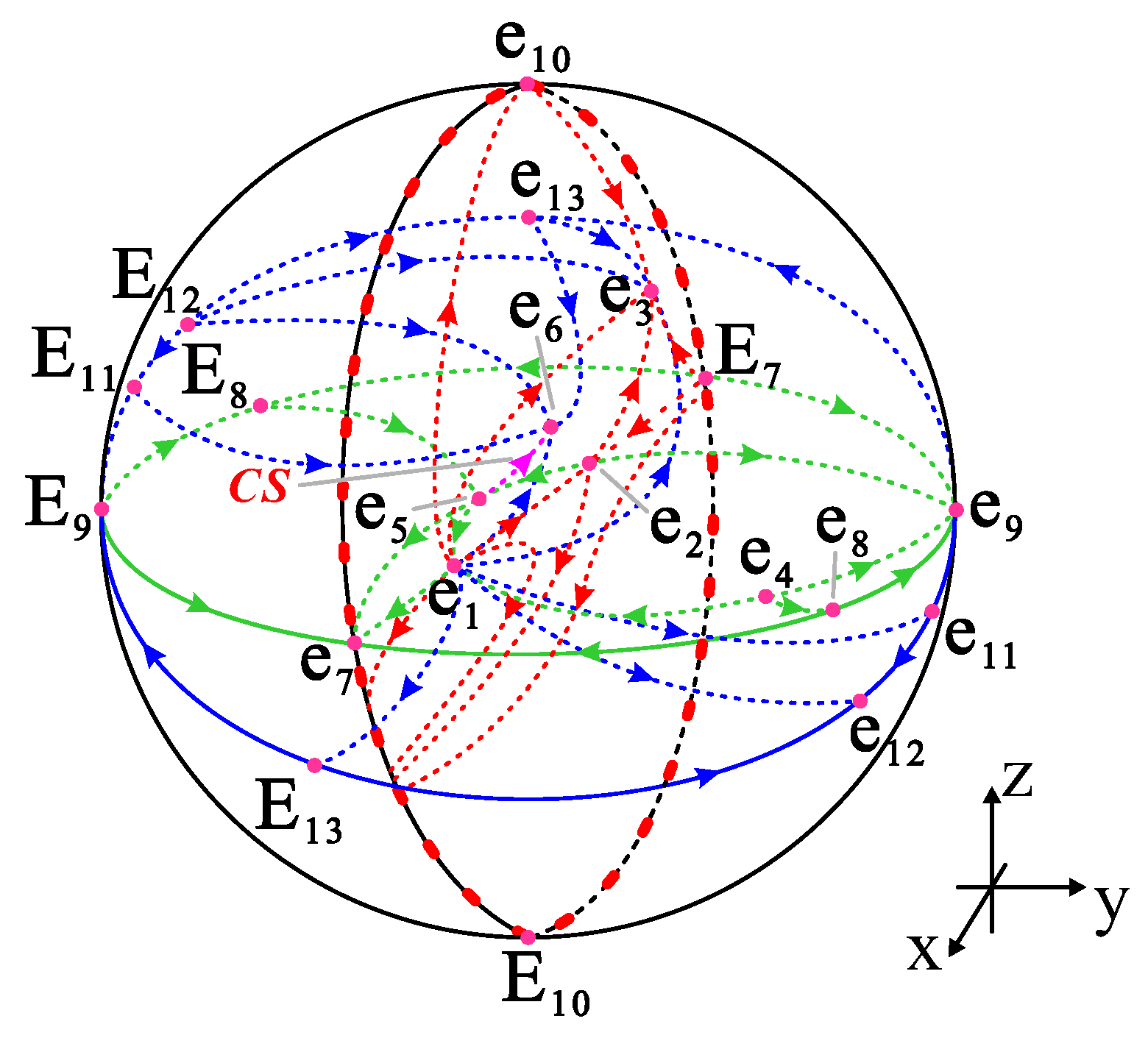
4. The Case in 3D
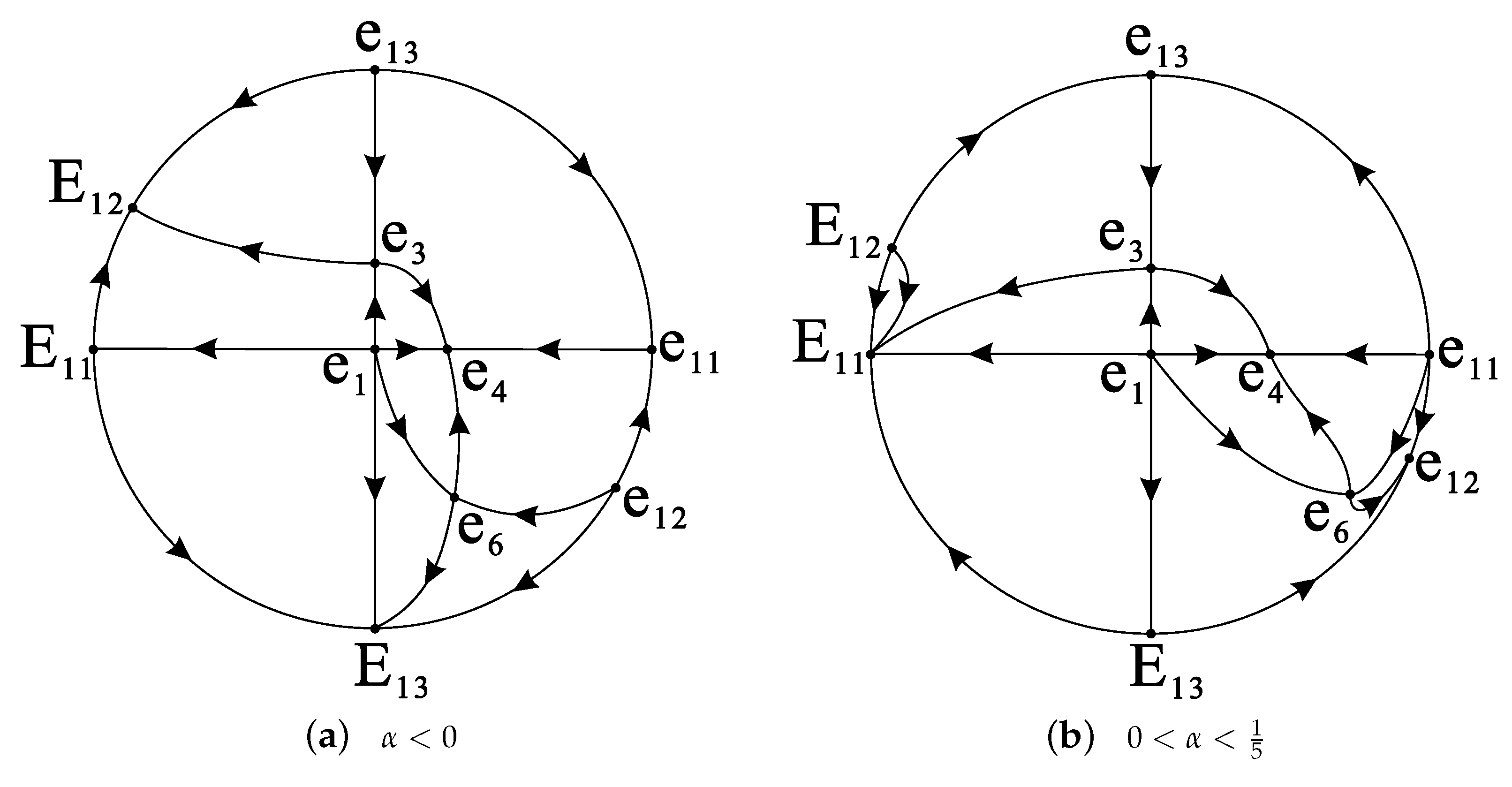
5. The Form
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Will, C.M.; Anderson, J.L. Theory and experiment in gravitational physics. Am. J. Phys. 1994, 62, 1153. [Google Scholar] [CrossRef]
- Turyshev, S.G. Experimental tests of general relativity: Recent progress and future directions. Physics-Uspekhi 2009, 52, 1. [Google Scholar] [CrossRef] [Green Version]
- Iorio, L.; Lichteneggrr, H.I.M.; Ruggiero, M.L.; Corda, C. Phenomenology of the Lense-Thirring effect in the solar system. Astrophys. Space. Sci. 2011, 331, 351–395. [Google Scholar] [CrossRef] [Green Version]
- Peeebles, P.J.E. Testing general relativity on the scales of cosmology. arXiv 2004, arXiv:astro-ph/0410284. [Google Scholar]
- Bennett, C.L.; Bay, M.; Halpern, M.; Hinshaw, G.; Jackson, C.; Jarosik, N.; Kogut, A.; Limon, M.; Meyer, S.S.; Page, L.; et al. The microwave anisotropy probe* mission. Astrophys. J. 2003, 583, 1. [Google Scholar] [CrossRef] [Green Version]
- Farajollahi, H.; Farhoudi, M.; Shojaie, H. On dynamics of Brans–Dicke theory of gravitation. Int. J. Theor. Phys. 2010, 49, 2558–2568. [Google Scholar] [CrossRef] [Green Version]
- Bahrehbakhsh, A.F.; Farhoudi, M.; Shojaie, H. FRW cosmology from five dimensional vacuum Brans–Dicke theory. Gen. Relativ. Gravit. 2011, 43, 847–869. [Google Scholar] [CrossRef] [Green Version]
- De Felice, A.; Tsujikawa, S. f(R) Theories. Living. Rev. Relativ. 2010, 13, 3. [Google Scholar] [CrossRef] [Green Version]
- Capozziello, S.; De Laurentis, M. Extended theories of gravity. Phys. Rep. 2011, 509, 167–321. [Google Scholar] [CrossRef] [Green Version]
- Nojiri, S.; Odintsov, S.D.; Mittal, A. Unified cosmic history in modified gravity: From f(R) theory to Lorentz non-invariant models. Phys. Rep. 2011, 505, 59–144. [Google Scholar] [CrossRef] [Green Version]
- Starobinsky, A.A. Disappearing cosmological constant in f(R) gravity. JETP. Lett. 2007, 86, 157–163. [Google Scholar] [CrossRef] [Green Version]
- Tsujikawa, S. Observational signatures of f(R) dark energy models that satisfy cosmological and local gravity constraints. Phys. Rev. D Part. Fields. 2007, 77, 315–317. [Google Scholar] [CrossRef] [Green Version]
- Nojiri, S.; Odintsov, S.D.; Sáez-Gómez, D. Cosmological reconstruction of realistic modified f(R) gravities. Phys. Lett. B 2009, 681, 74–80. [Google Scholar] [CrossRef] [Green Version]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Unifying inflation with early and late-time dark energy in f(R) gravity. Phys. Dark Universe 2020, 29, 100602. [Google Scholar] [CrossRef]
- Hu, W.; Sawicki, I. Models of f(R) cosmic acceleration that evade solar-system tests. Astrophys. Space Sci. 2007, 76, 064004. [Google Scholar] [CrossRef] [Green Version]
- Bergliaffa, S.E.P. Constraining f(R) theories with the energy conditions. New Astron. 2006, 642, 311–314. [Google Scholar]
- Santos, J.; Alcaniz, J.S.; Reboucas, M.J.; Carvalho, F.C. Energy conditions in f(R) gravity. Phys. Rev. D 2007, 76, 083513. [Google Scholar] [CrossRef] [Green Version]
- Amendola, L.; Tsujikawa, S. Phantom crossing, equation-of-state singularities, and local gravity constraints in f(R) models. Phys. Lett. B 2008, 660, 125–132. [Google Scholar] [CrossRef] [Green Version]
- Pan, Y.; He, Y.; Qi, J.Z.; Li, J.; Cao, S.; Liu, T.H.; Wang, J. Testing f(R) gravity with the simulated data of gravitational waves from the Einstein Telescope. Astrophys. J. 2021, 911, 135. [Google Scholar] [CrossRef]
- Bertolami, O.; Boehmer, C.G.; Harko, T.; Lobo, F.S.N. Extra force in f(R) modified theories of gravity. Phys. Rev. D 2007, 75, 104016. [Google Scholar] [CrossRef] [Green Version]
- Harko, T. Modified gravity with arbitrary coupling between matter and geometry. Phys. Lett. B 2008, 669, 376–379. [Google Scholar] [CrossRef] [Green Version]
- Harko, T.; Lobo, F.S.N. f(R,Lm) gravity. Eur. Phys. J. C 2010, 70, 373–379. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.N.; Nojiri, S.; Odintsov, S.D. f(R,T) gravity. Appl. Math. Nonlinear Sci. 2011, 84, 024020. [Google Scholar] [CrossRef] [Green Version]
- Sun, G.; Huang, Y.C. The cosmology in f(R,τ) gravity without dark energy. Int. J. Mod. Phys. D 2016, 25, 1650038. [Google Scholar] [CrossRef] [Green Version]
- Zaregonbadi, R.; Farhoudi, M.; Riazi, N. Dark matter from f(R,T) gravity. Phys. Rev. D 2016, 94, 084052. [Google Scholar] [CrossRef] [Green Version]
- Bhattacharjee, S.; Sahoo, P.K. Redshift drift in f(R,T) gravity. New Astron. 2020, 81, 101425. [Google Scholar] [CrossRef]
- Moraes, P.H.R.S.; Sahoo, P.K. Nonexotic matter wormholes in a trace of the energy-momentum tensor squared gravity. Phys. Rev. D 2018, 57, 024007. [Google Scholar] [CrossRef] [Green Version]
- Bhatti, M.Z.; Yousaf, Z.; Ilyas, M. Existence of wormhole solutions and energy conditions in f(R,T) gravity. J. Astrophys. 2018, 39, 1–11. [Google Scholar] [CrossRef]
- Sharif, M.; Zubair, M. Thermodynamics in f(R,T) theory of gravity. J. Cosmol. Astropart. Phys. 2012, 2012, 028. [Google Scholar] [CrossRef] [Green Version]
- Houndjo, M.J.S.; Alvarenga, F.G.; Rodrigues, M.E.; Jardim, D.F.; Myrzakulov, R. Thermodynamics in Little Rip cosmology in the framework of a type of f(R,T) gravity. Eur. Phys. J. Plus 2014, 129, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Bhattacharjee, S.; Sahoo, P.K. Comprehensive analysis of a non-singular bounce in f(R,T) gravitation. Phys. Dark Universe 2020, 28, 100537. [Google Scholar] [CrossRef] [Green Version]
- Sahoo, P.; Bhattacharjee, S.; Tripathy, S.K.; Sahoo, P.K. Bouncing scenario in f(R,T) gravity. Mod. Phys. Lett. A 2020, 35, 2050095. [Google Scholar] [CrossRef]
- Sahoo, P.K.; Bhattacharjee, S. Gravitational baryogenesis in non-minimal coupled f(R,T) gravity. Int. J. Theor. Phys. 2020, 59, 1451–1459. [Google Scholar] [CrossRef] [Green Version]
- Alvarenga, F.G.; De La Cruz-Dombriz, A.; Houndjo, M.J.S.; Rodrigues, M.E.; Sáez-Gómez, D. Dynamics of scalar perturbations in f(R,T) gravity. Phys. Rev. D 2013, 87, 103526. [Google Scholar] [CrossRef] [Green Version]
- Alves, M.E.S.; Moraes, P.H.R.S.; De Araujo, J.C.N.; Malheiro, M. Gravitational waves in f(R,T) and f(R,Tϕ) theories of gravity. Phys. Rev. D 2016, 94, 024032. [Google Scholar] [CrossRef] [Green Version]
- Sharif, M.; Siddiqa, A. Propagation of polar gravitational waves in f(R,T) scenario. Gen. Relativ. Gravit. 2019, 51, 74. [Google Scholar] [CrossRef] [Green Version]
- Houndjo, M.J.S. Reconstruction of f(R,T) gravity describing matter dominated and accelerated phases. Int. J. Mod. Phys. D 2012, 21, 1250003. [Google Scholar] [CrossRef] [Green Version]
- Sharif, M.; Zubair, M. Cosmological reconstruction and stability in f(R,T) gravity. Gen. Relativ. Gravit. 2014, 46, 1723. [Google Scholar] [CrossRef]
- Singh, C.P.; Singh, V. Reconstruction of modified f(R,T) gravity with perfect fluid cosmological models. Gen. Relativ. Gravit. 2014, 46, 1696. [Google Scholar] [CrossRef]
- Shabani, H.; Farhoudi, M. Cosmological and solar system consequences of f(R,T) gravity models. Phys. Rev. D 2014, 90, 044031. [Google Scholar] [CrossRef] [Green Version]
- Shabani, H.; Farhoudi, M. f(R,T) cosmological models in phase space. Phys. Rev. D 2013, 88, 044048. [Google Scholar] [CrossRef] [Green Version]
- Baffou, E.H.; Kpadonou, A.V.; Rodrigues, M.E.; Houndjo, M.J.S.; Tossa, J. Cosmological viable f(R,T) dark energy model: Dynamics and stability. Astrophys. Space. Sci. 2015, 356, 173–180. [Google Scholar] [CrossRef] [Green Version]
- Sharma, U.K.; Pradhan, A. Propagation of polar gravitational waves in f(R,T) scenario. Int. J. Geom. Methods Mod. Phys. 2018, 15, 1850014. [Google Scholar] [CrossRef]
- Abchouyeh, M.A.; Mirza, B.; Shahidi, P.; Oboudiat, F. Late time dynamics of f(R,T,RμνTμν) gravity. Int. J. Geom. Methods Mod. Phys. 2020, 17, 2050008. [Google Scholar] [CrossRef] [Green Version]
- Gonçalves, T.B.; Rosa, J.L.; Lobo, F.S.N. Cosmology in the novel scalar-tensor representation of f(R,T) gravity. arXiv 2021, arXiv:2112.03652. [Google Scholar]
- Santos, A.F. Gödel solution in f(R,T) gravity. Mod. Phys. Lett. A 2013, 28, 1350141. [Google Scholar] [CrossRef] [Green Version]
- Guo, J.Q.; Frolov, A.V. Cosmological dynamics in f(R) dravity. Phys. Rev. D 2013, 88, 124036. [Google Scholar] [CrossRef] [Green Version]
- Zonunmawia, H.; Khyllep, W.; Dutta, J.; Järv, L. Cosmological dynamics of brane gravity: A grobal dynamical system perspective. Phys. Rev. D 2018, 98, 083532. [Google Scholar] [CrossRef] [Green Version]
- Gao, F.B.; Llibre, J. Global dynamics of the Hořava-Lifshitz cosmological model in a non-flat universe with non-zero cosmological constant. Universe 2021, 7, 445. [Google Scholar] [CrossRef]
- Singh, A.; Singh, G.P.; Pradhan, A. Cosmic dynamics and qualitative study of Rastall model with spatial curvature. arXiv 2022, arXiv:2205.13934. [Google Scholar] [CrossRef]
- Amendola, L. Coupled quintessence. Phys. Rev. D 2000, 62, 043511. [Google Scholar] [CrossRef] [Green Version]
- Dumortier, F.; Llibre, J.; Ateés, J.C. Qualitative Theory of Planar Differential Syetems; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Cima, A.; Llibre, J. Bounded polynomial vector fields. Trans. Am. Math. Soc. 1990, 318, 557–579. [Google Scholar] [CrossRef]
- Álvarez, M.J.; Pugh, C.C.; Shub, M. Invariant Manifolds; Springer: Berlin/Heidelberg, Germany, 1977. [Google Scholar]



| Equilibrium Points | Coordinates | Scale Factor | ||
|---|---|---|---|---|
| () | 0 | |||
| () | 2 | |||
| () | 0 | |||
| () | 0 | |||
| () | ||||
| () | 0 |
| Values of | Finite Equilibrium Points |
|---|---|
| or or | is an unstable node, , , and are saddles, is a stable node |
| or | is an unstable node, , , and are saddles, and have a 2DSM |
or or | is an unstable node, , , and are saddles, is a stable node |
| is an unstable node, and are saddles, and have a 1DUM and a 1DSM, is a stable node | |
| is an unstable node, , and are saddles, is a NHEP, is a stable node | |
| is an unstable node, and are saddles, and have a 2DSM, is a NHEP | |
| is an unstable node, , and are saddles, is a stable node, is a NHEP | |
| is an unstable node, and are saddles, and are stable nodes, is a NHEP | |
| or | is an unstable node, , , and are saddles, and are stable nodes |
| is an unstable node, and have a 1DUM and a 1DSM, and are stable nodes, is a saddle | |
| , , and is a saddle, is an unstable node, and are NHEPs | |
| and have a 2DUM, and are saddles, and are NHEPs | |
| is an unstable node, , , and are saddles, and are NHEPs | |
or | is an unstable node, , , , and are saddles, is a NHEP |
| is an unstable node, and are saddles, and have a 1DUM and a 1DSM, is a NHEP |
| Values of | Finite Equilibrium Points | Infinite Equilibrium Points |
|---|---|---|
| is an unstable node, and are saddles, is a stable node | is a stable node, is a saddle, is an unstable node | |
| is an unstable node, and are saddles, is a stable node | is a saddle, and are stable nodes | |
| is an unstable node, is a saddle, and are saddle-nodes | is a saddle, and are stable nodes | |
| is an unstable node, and are saddles, is a stable node | is a saddle, and are stable nodes | |
| is an unstable node, and are saddles, is a stable focus | is a saddle, and are stable nodes | |
| is an unstable node, is a saddle, is a stable focus | is a saddle, is a saddle-node, is a stable node | |
| is an unstable node, is a saddle, is a stable node, is a stable focus | and are saddles, is a stable node | |
| is an unstable node, is a saddle, and are stable nodes | and are saddles, is a stable node | |
| is an unstable node, and are saddle-nodes, is a stable node | and are saddles, is a stable node | |
| is an unstable node, and are stable nodes, is a saddle | and are saddles, is a stable node | |
| and are saddles, is an unstable node, is a stable focus | and are stable nodes, is a saddle | |
| and are saddle-nodes, is a saddle, is a stable focus | and are stable nodes, is a saddle | |
| is an unstable node, and are saddles, is a stable focus | and are stable nodes, is a saddle | |
| is an unstable node, and are saddles, is a stable node | and are stable nodes, is a saddle | |
| is an unstable node, is a saddle, and are saddle-nodes | and are stable nodes, is a saddle | |
| is an unstable node, and are saddles, is a stable node | and are stable nodes, is a saddle |
| Values of | Finite Equilibrium Points | Infinite Equilibrium Points |
|---|---|---|
| is an unstable node, and are saddles, is a stable node | is a saddle, and are unstable nodes | |
| is an unstable node, and are saddles, is a stable node | is an unstable node, is a stable node, is a saddle | |
| is an unstable node, is a saddle, and are saddle-nodes | is an unstable node, is a stable node, is a saddle | |
| is an unstable node, and are saddles, is a stable node | is an unstable node, is a stable node, is a saddle | |
| is an unstable node, and are saddle-nodes, is a saddle | is an unstable node, is a stable node, is a saddle | |
| is an unstable node, is a stable node, and are saddles | is an unstable node, is a stable node, is a saddle | |
| is an unstable node, is a stable node, is a saddle | is a saddle-node, is a stable node, is a saddle | |
| is an unstable node, and are stable nodes, is a saddle | and are saddles, is a stable node | |
| and are saddles, is an unstable node, is a stable focus | is a saddle, is a stable node, is an unstable node | |
| and are saddle-nodes, is a saddle, is a stable focus | is a saddle, is a stable node, is an unstable node | |
| is an unstable node, and are saddles, is a stable focus | is a saddle, is a stable node, is an unstable node | |
| is an unstable node, and are saddles, is a stable node | is a saddle, is a stable node, is an unstable node | |
| is an unstable node, is a saddle, and are saddle-nodes | is a saddle, is a stable node, is an unstable node | |
| is an unstable node, and are saddles, is a stable node | is a saddle, is a stable node, is an unstable node |
| Equilibrium Points | Coordinates | ||
|---|---|---|---|
| () | 0 | ||
| () | 2 | ||
| () | 0 | ||
| () | 0 | ||
| () | 0 | ||
| () | |||
| () | 0 | ||
| () | 0 |
| Equilibrium Points | Eigenvalues |
|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Wang, R.; Gao, F. Dynamics of a Cosmological Model in f(R,T) Gravity: I. On Invariant Planes. Universe 2022, 8, 365. https://doi.org/10.3390/universe8070365
Liu J, Wang R, Gao F. Dynamics of a Cosmological Model in f(R,T) Gravity: I. On Invariant Planes. Universe. 2022; 8(7):365. https://doi.org/10.3390/universe8070365
Chicago/Turabian StyleLiu, Jianwen, Ruifang Wang, and Fabao Gao. 2022. "Dynamics of a Cosmological Model in f(R,T) Gravity: I. On Invariant Planes" Universe 8, no. 7: 365. https://doi.org/10.3390/universe8070365
APA StyleLiu, J., Wang, R., & Gao, F. (2022). Dynamics of a Cosmological Model in f(R,T) Gravity: I. On Invariant Planes. Universe, 8(7), 365. https://doi.org/10.3390/universe8070365






