Near-Horizon Thermodynamics of Hairy Black Holes from Gravitational Decoupling
Abstract
:1. Introduction
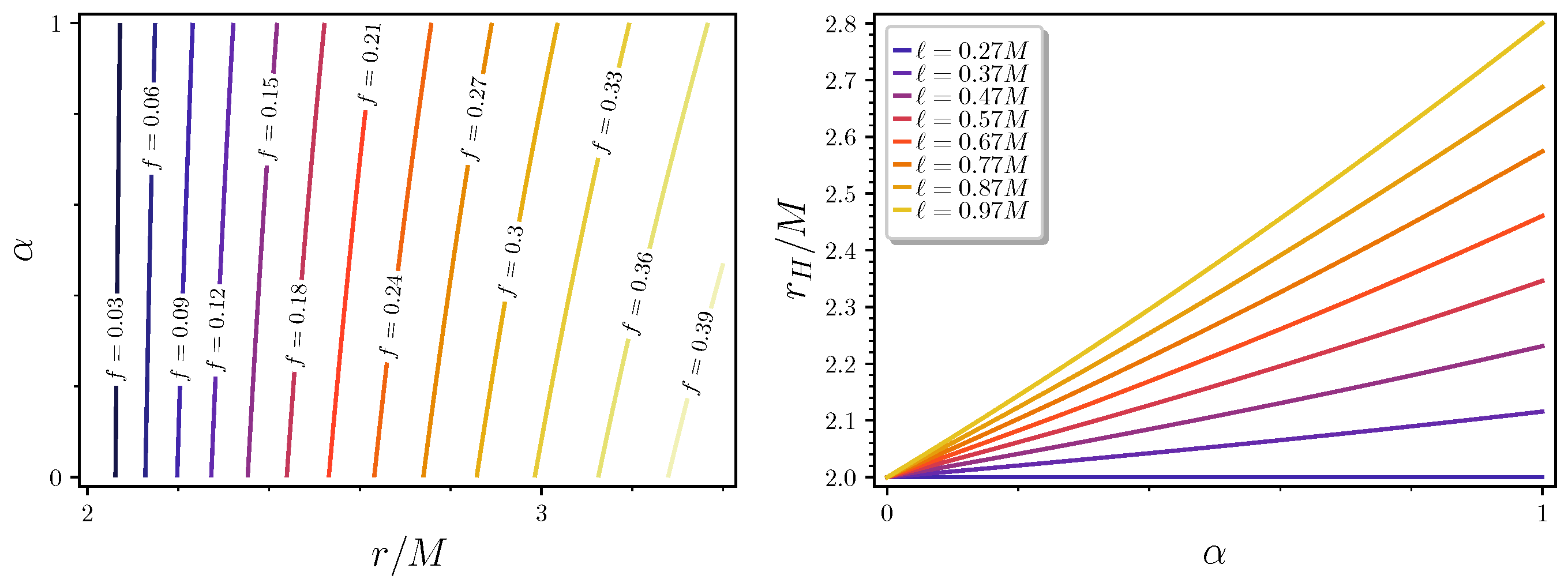
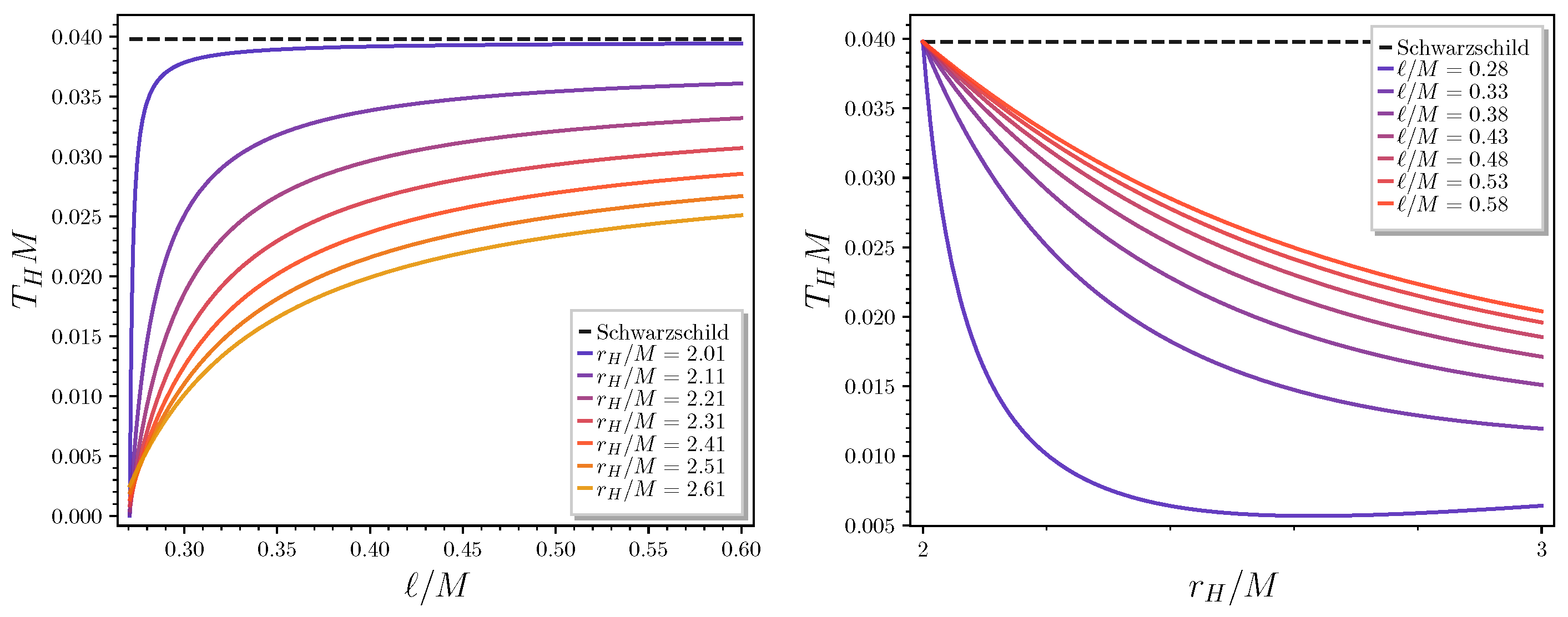
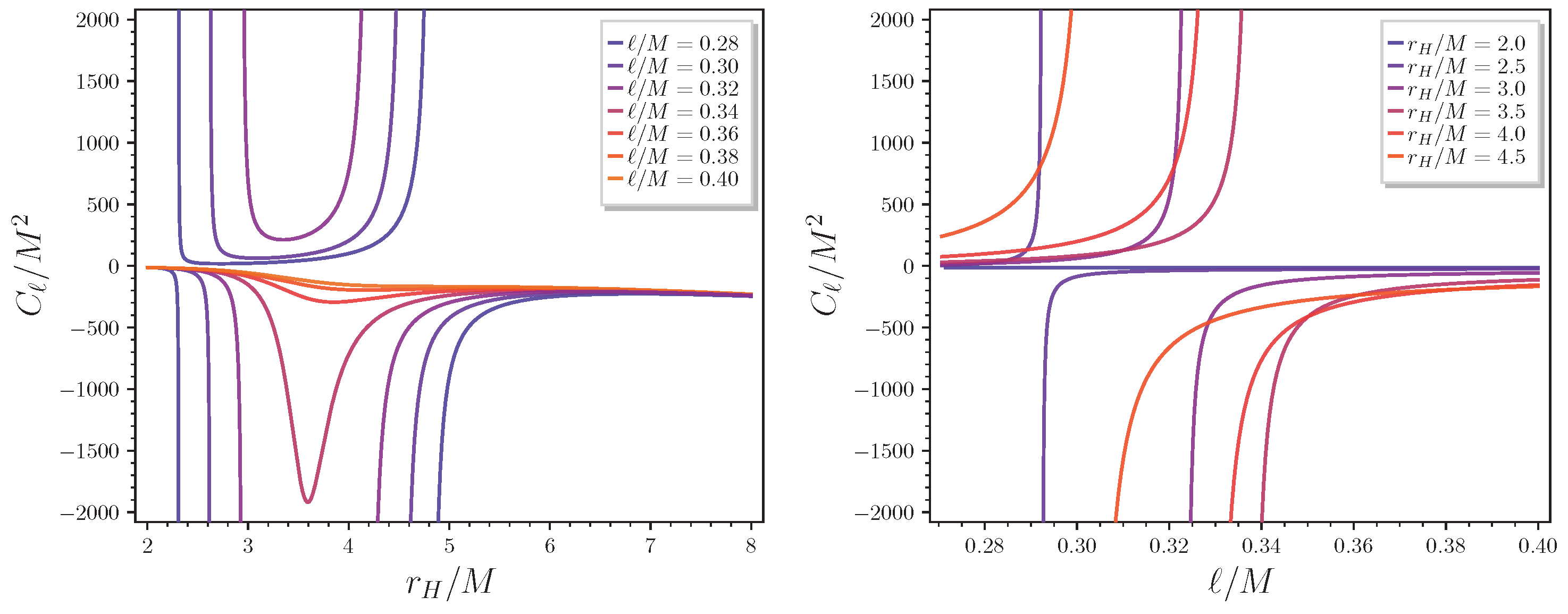
2. Hairy Horizons and Gravitational Decoupling
3. Quantum Effects near the Horizon
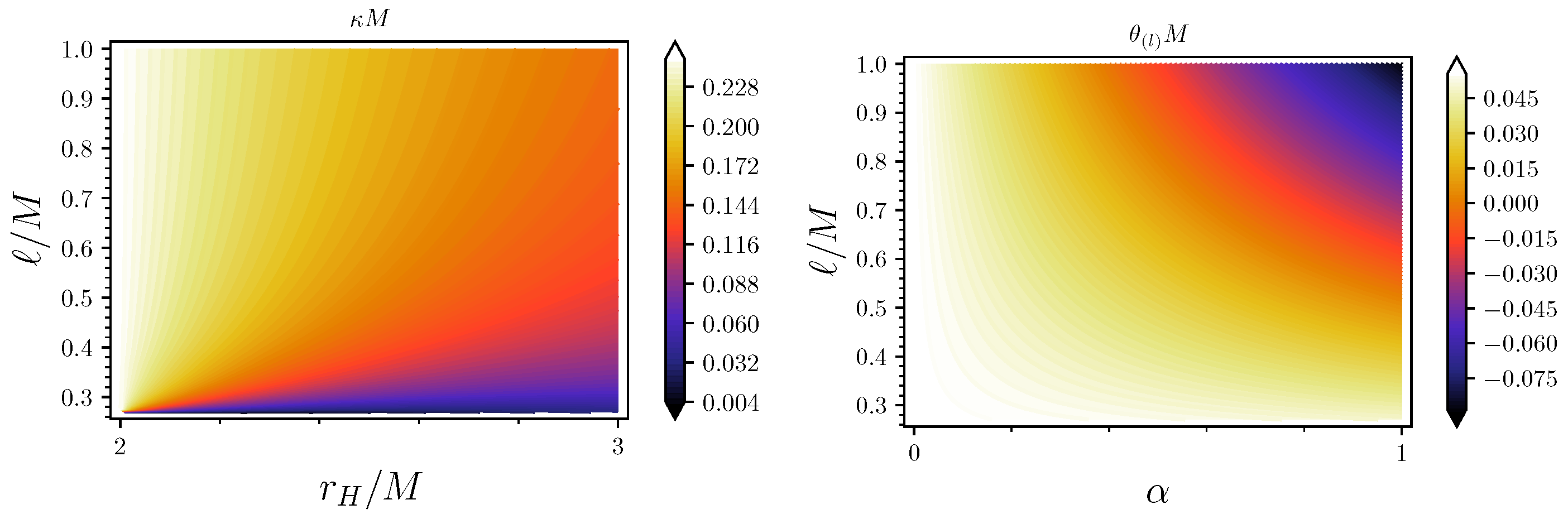
3.1. GUP and Generalized Dirac Equation
3.2. Corrected Fermionic Tunneling through Hairy Horizon
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cardoso, V.; Pani, P. Testing the nature of dark compact objects: A status report. Living Rev. Rel. 2019, 22, 4. [Google Scholar] [CrossRef] [Green Version]
- Romero, G.E.; Vila, G.S. Introduction to Black Hole Astrophysics; Springer: Berlin/Heidelberg, Germany, 2013; Volume 876. [Google Scholar]
- Calmet, X. Quantum Aspects of Black Holes; Springer: Berlin/Heidelberg, Germany, 2015; Volume 178. [Google Scholar]
- Gillessen, S.; Eisenhauer, F.; Trippe, S.; Alexander, T.; Genzel, R.; Martins, F.; Ott, T. Monitoring stellar orbits around the Massive Black Hole in the Galactic Center. Astrophys. J. 2009, 692, 1075–1109. [Google Scholar] [CrossRef] [Green Version]
- Ghez, A.M.; Salim, S.; Weinberg, N.N.; Lu, J.R.; Do, T.; Dunn, J.K.; Matthews, K.; Morris, M.R.; Yelda, S.; Becklin, E.E. Measuring Distance and Properties of the Milky Way’s Central Supermassive Black Hole with Stellar Orbits. Astrophys. J. 2008, 689, 1044–1062. [Google Scholar] [CrossRef] [Green Version]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; Bintley, D.; et al. First M87 Event Horizon Telescope Results. V. Physical Origin of the Asymmetric Ring. Astrophys. J. Lett. 2019, 875, L1. [Google Scholar]
- Frolov, V.P.; Zelnikov, A. Introduction to Black Hole Physics; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Faraoni, V. Cosmological and Black Hole Apparent Horizons; Springer: Berlin/Heidelberg, Germany, 2015; Volume 907, ISBN 978-3-319-19239-0/978-3-319-19240-6. [Google Scholar]
- Wald, R.M. General Relativity; Chicago University Press: Chicago, IL, USA, 1984. [Google Scholar]
- Ashtekar, A.; Galloway, G.J. Some uniqueness results for dynamical horizons. Adv. Theor. Math. Phys. 2005, 9, 1–30. [Google Scholar] [CrossRef] [Green Version]
- Gourgoulhon, E.; Jaramillo, J.L. New theoretical approaches to black holes. New Astron. Rev. 2008, 51, 791–798. [Google Scholar] [CrossRef] [Green Version]
- Chrusciel, P. Geometry of Black Holes; International Series of Monographs on Physics; Oxford University Press: Oxford, UK, 2020; ISBN 978-0-19-885541-5. [Google Scholar]
- Babichev, E.; Charmousis, C. Dressing a black hole with a time-dependent Galileon. JHEP 2014, 8, 106. [Google Scholar] [CrossRef] [Green Version]
- Cavalcanti, R.T.; da Silva, A.G.; da Rocha, R. Strong deflection limit lensing effects in the minimal geometric deformation and Casadio-Fabbri-Mazzacurati solutions. Class. Quant. Grav. 2016, 33, 215007. [Google Scholar] [CrossRef] [Green Version]
- Ovalle, J. Decoupling gravitational sources in general relativity: From perfect to anisotropic fluids. Phys. Rev. D 2017, 95, 104019. [Google Scholar] [CrossRef] [Green Version]
- Ovalle, J. Decoupling gravitational sources in general relativity: The extended case. Phys. Lett. B 2019, 788, 213–218. [Google Scholar] [CrossRef]
- Ovalle, J.; Casadio, R.; Contreras, E.; Sotomayor, A. Hairy black holes by gravitational decoupling. Phys. Dark Univ. 2021, 31, 100744. [Google Scholar] [CrossRef]
- Da Rocha, R. MGD Dirac Stars. Symmetry 2020, 12, 508. [Google Scholar] [CrossRef] [Green Version]
- Tello-Ortiz, F.; Malaver, M.; Rincón, A.; Gomez-Leyton, Y. Relativistic anisotropic fluid spheres satisfying a non-linear equation of state. Eur. Phys. J. C 2020, 80, 371. [Google Scholar] [CrossRef]
- Da Rocha, R. Minimal geometric deformation of Yang-Mills-Dirac stellar configurations. Phys. Rev. D 2020, 102, 024011. [Google Scholar] [CrossRef]
- Fernandes-Silva, A.; Ferreira-Martins, A.J.; da Rocha, R. Extended quantum portrait of MGD black holes and information entropy. Phys. Lett. 2019, B791, 323–330. [Google Scholar] [CrossRef]
- Da Rocha, R. Dark SU(N) glueball stars on fluid branes. Phys. Rev. 2017, D95, 124017. [Google Scholar] [CrossRef] [Green Version]
- Da Rocha, R.; Tomaz, A.A. Holographic entanglement entropy under the minimal geometric deformation and extensions. Eur. Phys. J. C 2019, 79, 1035. [Google Scholar] [CrossRef]
- Ovalle, J.; Contreras, E.; Stuchlik, Z. Kerr-de Sitter black hole revisited. Phys. Rev. D 2021, 103, 084016. [Google Scholar] [CrossRef]
- Meert, P.; da Rocha, R. Gravitational decoupling, hairy black holes and conformal anomalies. Eur. Phys. J. C 2022, 82, 175. [Google Scholar] [CrossRef]
- Cavalcanti, R.T.; de Paiva, R.C.; da Rocha, R. Echoes of the gravitational decoupling: Scalar perturbations and quasinormal modes of hairy black holes. arXiv 2022, arXiv:2203.08740. [Google Scholar]
- Gross, D.J.; Mende, P.F. String theory beyond the Planck scale. Nucl. Phys. B 1988, 303, 407–454. [Google Scholar] [CrossRef]
- Amati, D.; Ciafaloni, M.; Veneziano, G. Can spacetime be probed below the string size? Phys. Lett. B 1989, 216, 41–47. [Google Scholar] [CrossRef] [Green Version]
- Rovelli, C.; Smolin, L. Discreteness of area and volume in quantum gravity. Nucl. Phys. B 1995, 442, 593–622, Erratum in Nucl. Phys. B 1995, 456, 753–754. [Google Scholar] [CrossRef] [Green Version]
- Scardigli, F. Generalized uncertainty principle in quantum gravity from micro-black hole gedanken experiment. Phys. Lett. B 1999, 452, 39–44. [Google Scholar] [CrossRef] [Green Version]
- Hoff da Silva, J.M.; Beghetto, D.; Cavalcanti, R.T.; Da Rocha, R. Exotic fermionic fields and minimal length. Eur. Phys. J. C 2020, 80, 727. [Google Scholar] [CrossRef]
- Hossenfelder, S. Minimal Length Scale Scenarios for Quantum Gravity. Living Rev. Rel. 2013, 16, 2. [Google Scholar] [CrossRef] [Green Version]
- Tawfik, A.N.; Diab, A.M. A review of the generalized uncertainty principle. Rept. Prog. Phys. 2015, 78, 126001. [Google Scholar] [CrossRef] [Green Version]
- Bishop, M.; Contreras, J.; Singleton, D. A Subtle Aspect of Minimal Lengths in the Generalized Uncertainty Principle. Universe 2022, 8, 192. [Google Scholar] [CrossRef]
- Ashtekar, A.; Krishnan, B. Isolated and Dynamical Horizons and Their Applications. Living Rev. Rel. 2004, 7, 10. [Google Scholar] [CrossRef] [Green Version]
- Hawking, S.W.; Page, D.N. Thermodynamics of black holes in anti-de Sitter space. Commun. Math. Phys. 1983, 87, 577. [Google Scholar] [CrossRef]
- Kempf, A.; Mangano, G.; Mann, R.B. Hilbert space representation of the minimal length uncertainty relation. Phys. Rev. D 1995, 52, 1108–1118. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Greiner, W. Relativistic Quantum Mechanics; Springer: Berlin/Heidelberg, Germany, 2000; Volume 2. [Google Scholar]
- Nozari, K.; Saghafi, S. Natural cutoffs and quantum tunneling from black hole horizon. JHEP 2012, 11, 5. [Google Scholar] [CrossRef] [Green Version]
- Nozari, K.; Karami, M. Minimal Length and Generalized Dirac Equation. Mod. Phys. Lett. A 2005, 20, 3095–3104. [Google Scholar] [CrossRef] [Green Version]
- Hossenfelder, S.; Bleicher, M.; Hofmann, S.; Ruppert, J.; Scherer, S.; Stoecker, H. Signatures in the Planck regime. Phys. Lett. B 2003, 575, 85–99. [Google Scholar] [CrossRef]
- Chen, D.; Wu, H.; Yang, H. Observing remnants by fermions’ tunneling. JCAP 2014, 3, 36. [Google Scholar] [CrossRef] [Green Version]
- Page, D.N. Particle emission rates from a black hole: Massless particles from an uncharged, nonrotating hole. Phys. Rev. D 1976, 13, 198–206. [Google Scholar] [CrossRef]
- Kerner, R.; Mann, R.B. Fermions tunnelling from black holes. Class. Quant. Grav. 2008, 25, 095014. [Google Scholar] [CrossRef]
- Barducci, A.; Casalbuoni, R.; Lusanna, L. Supersymmetries and the pseudoclassical relativistic electron. Nuovo Cim. A 1976, 35, 377. [Google Scholar] [CrossRef]
- Vanzo, L.; Acquaviva, G.; Di Criscienzo, R. Tunnelling methods and Hawking’s radiation: Achievements and prospects. Class. Quant. Grav. 2011, 28, 183001. [Google Scholar] [CrossRef]
- Cavalcanti, R.; da Rocha, R. Dark Spinors Hawking Radiation in String Theory Black Holes. Adv. High Energy Phys. 2016, 2016, 4681902. [Google Scholar] [CrossRef] [Green Version]
- Casadio, R.; Nicolini, P.; da Rocha, R. Generalised uncertainty principle Hawking fermions from minimally geometric deformed black holes. Class. Quant. Grav. 2018, 35, 185001. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cavalcanti, R.T.; Alves, K.d.S.; Hoff da Silva, J.M. Near-Horizon Thermodynamics of Hairy Black Holes from Gravitational Decoupling. Universe 2022, 8, 363. https://doi.org/10.3390/universe8070363
Cavalcanti RT, Alves KdS, Hoff da Silva JM. Near-Horizon Thermodynamics of Hairy Black Holes from Gravitational Decoupling. Universe. 2022; 8(7):363. https://doi.org/10.3390/universe8070363
Chicago/Turabian StyleCavalcanti, Rogerio Teixeira, Kelvin dos Santos Alves, and Julio Marny Hoff da Silva. 2022. "Near-Horizon Thermodynamics of Hairy Black Holes from Gravitational Decoupling" Universe 8, no. 7: 363. https://doi.org/10.3390/universe8070363
APA StyleCavalcanti, R. T., Alves, K. d. S., & Hoff da Silva, J. M. (2022). Near-Horizon Thermodynamics of Hairy Black Holes from Gravitational Decoupling. Universe, 8(7), 363. https://doi.org/10.3390/universe8070363






