Shadow and Weak Deflection Angle of a Black Hole in Nonlocal Gravity
Abstract
:1. Introduction
2. A Brief Review of the Nonlocal Gravity
2.1. Model A
2.2. Model B
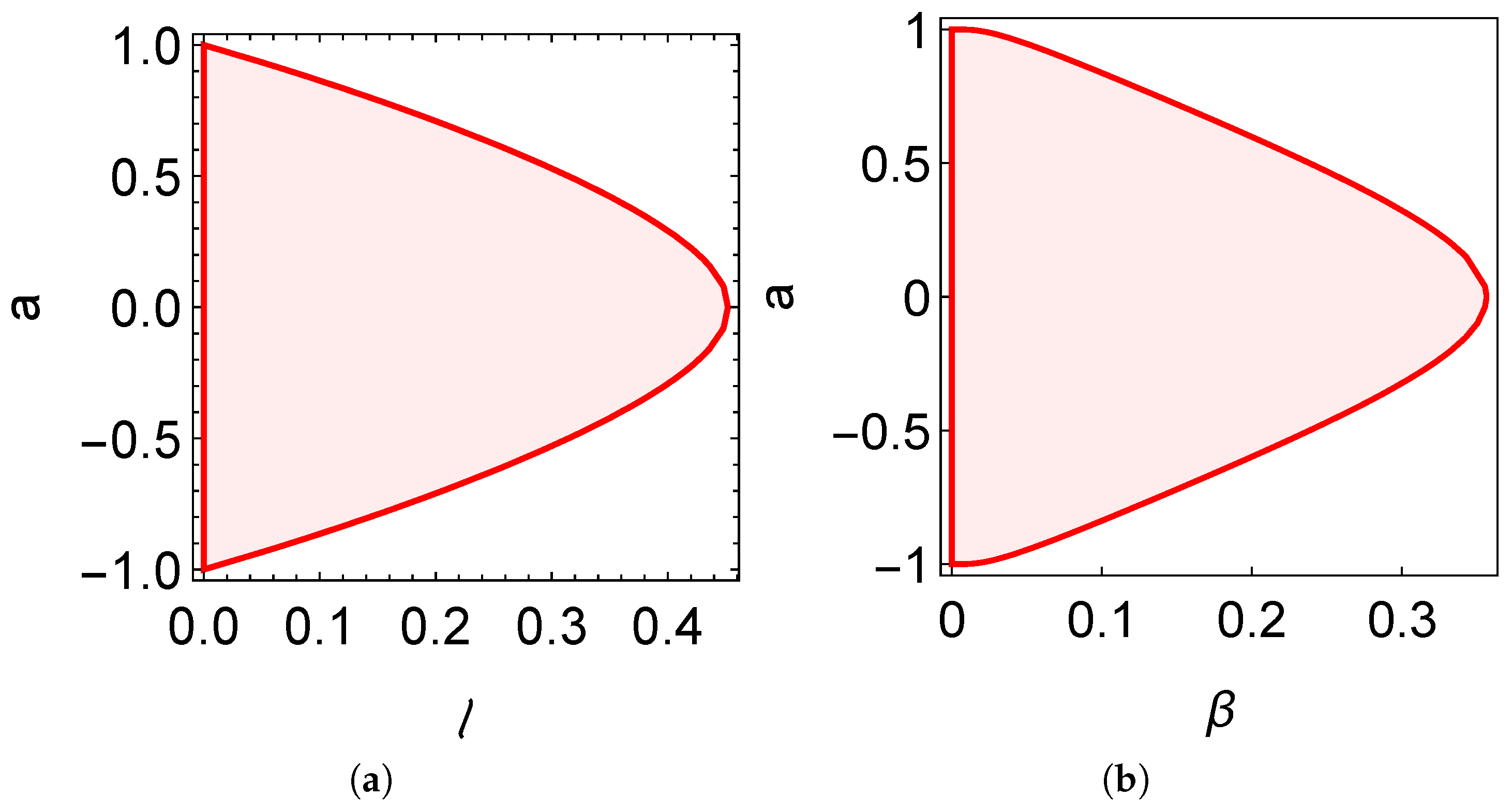
3. Spinning Nonlocal Black Hole and Circular Photon Orbits
3.1. Equations of Null Geodesic Motion
3.2. Unstable Circular Photon Orbits
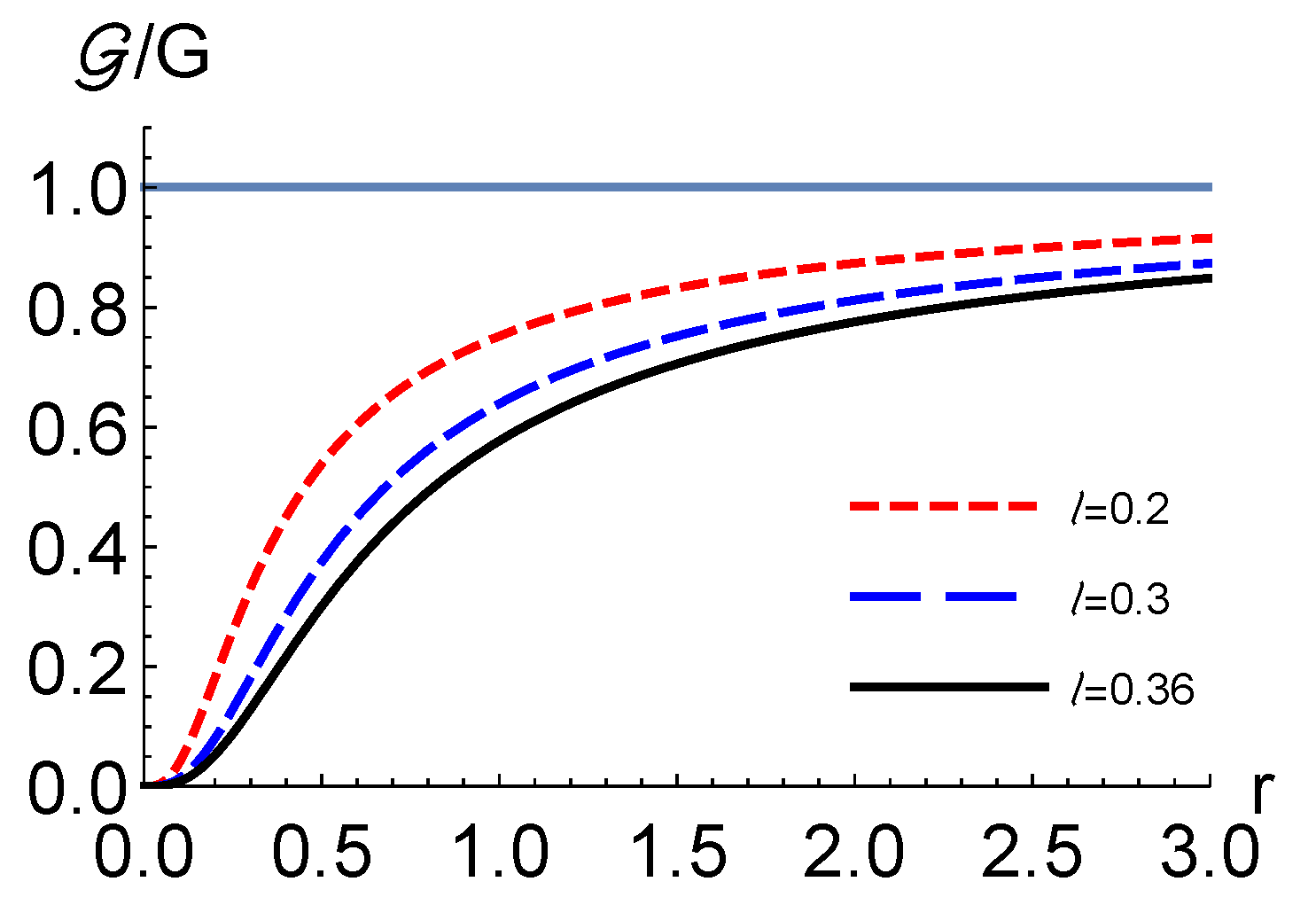
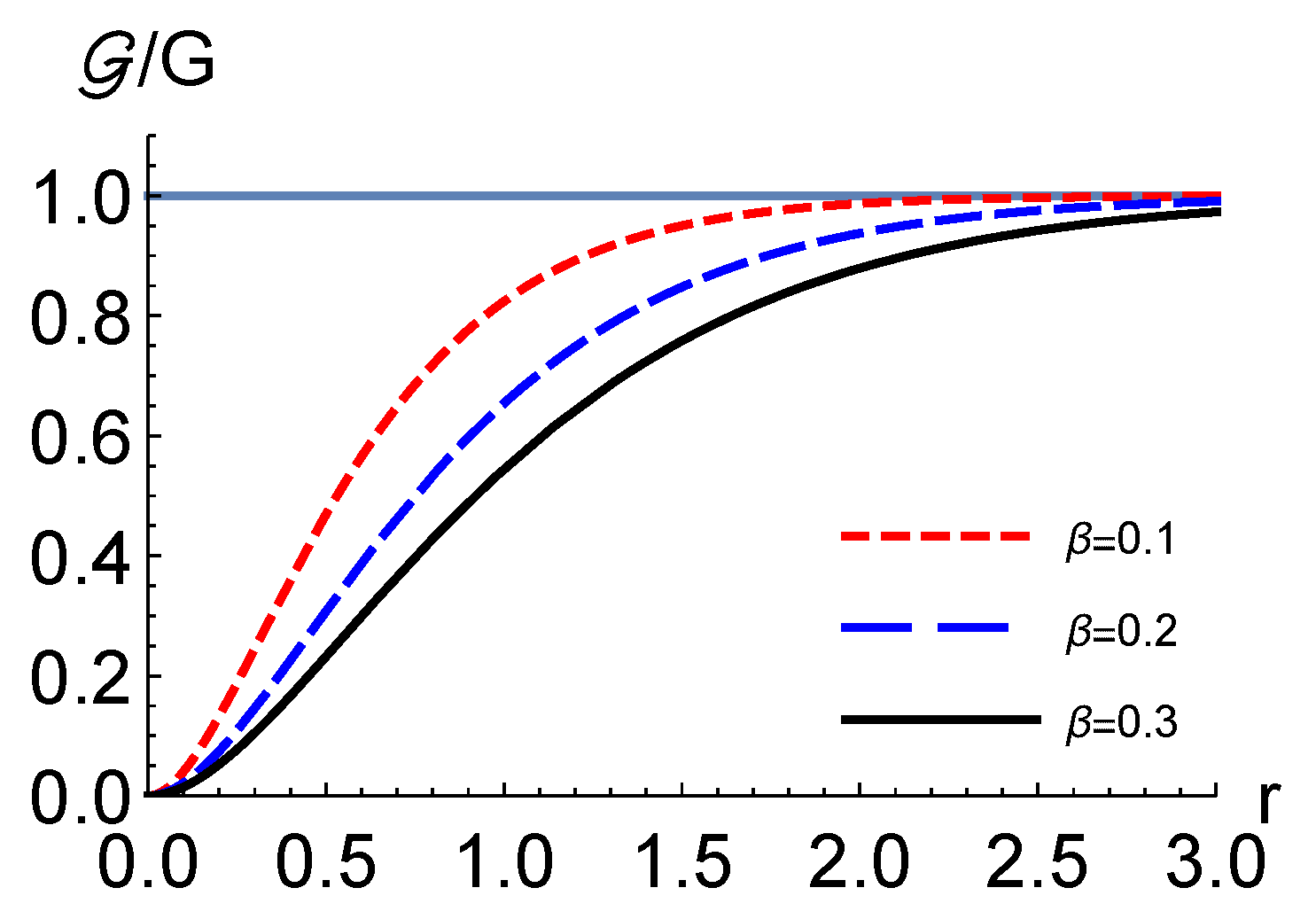
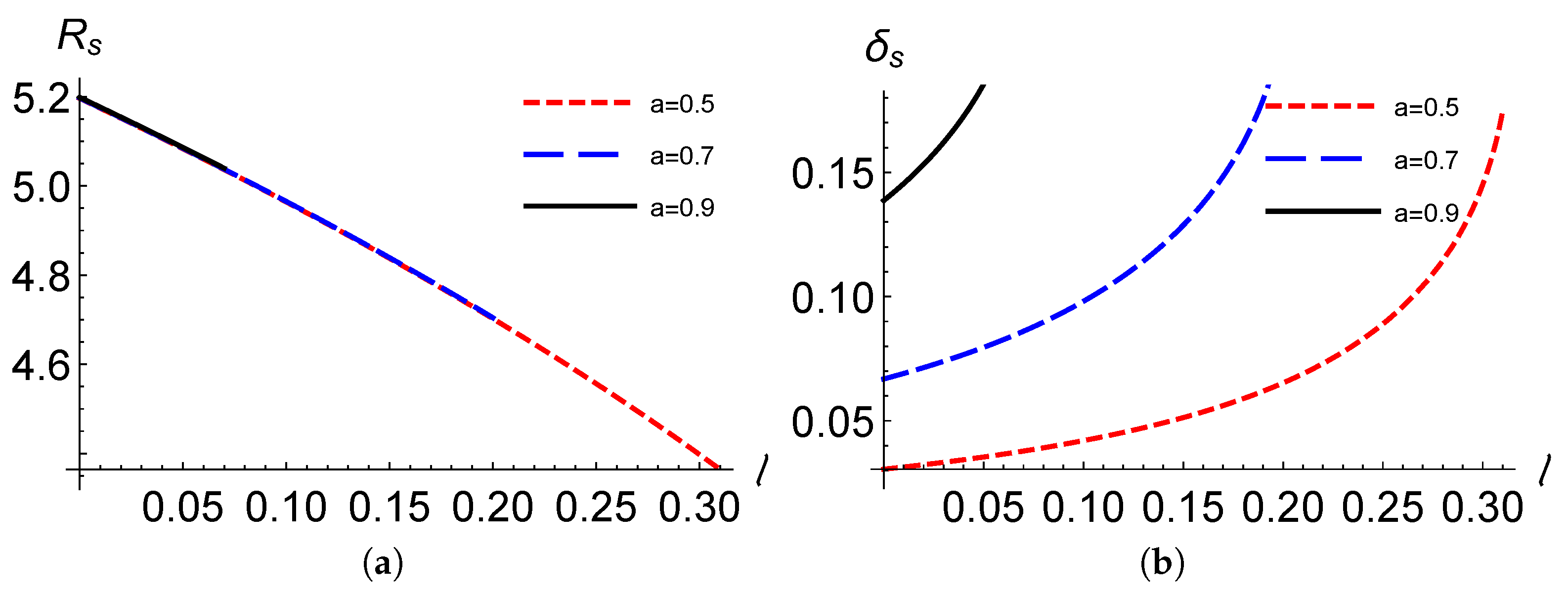
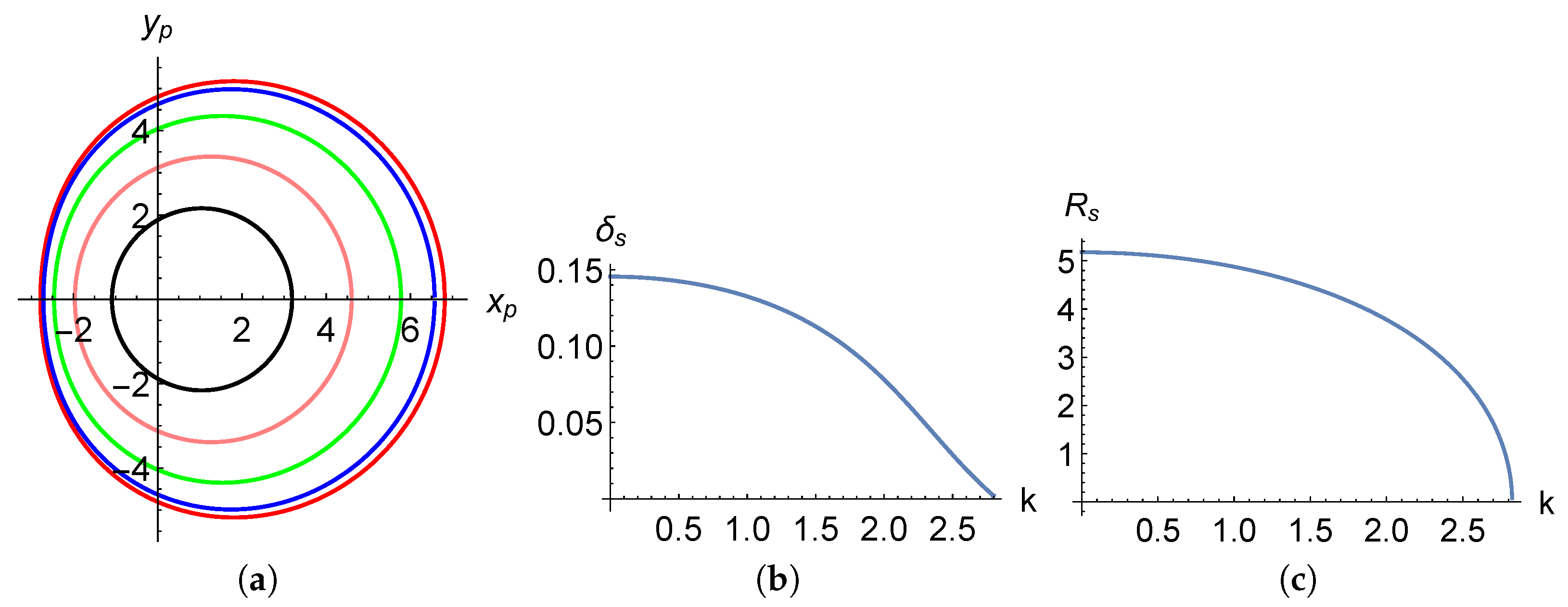
4. Shadow of Black Hole
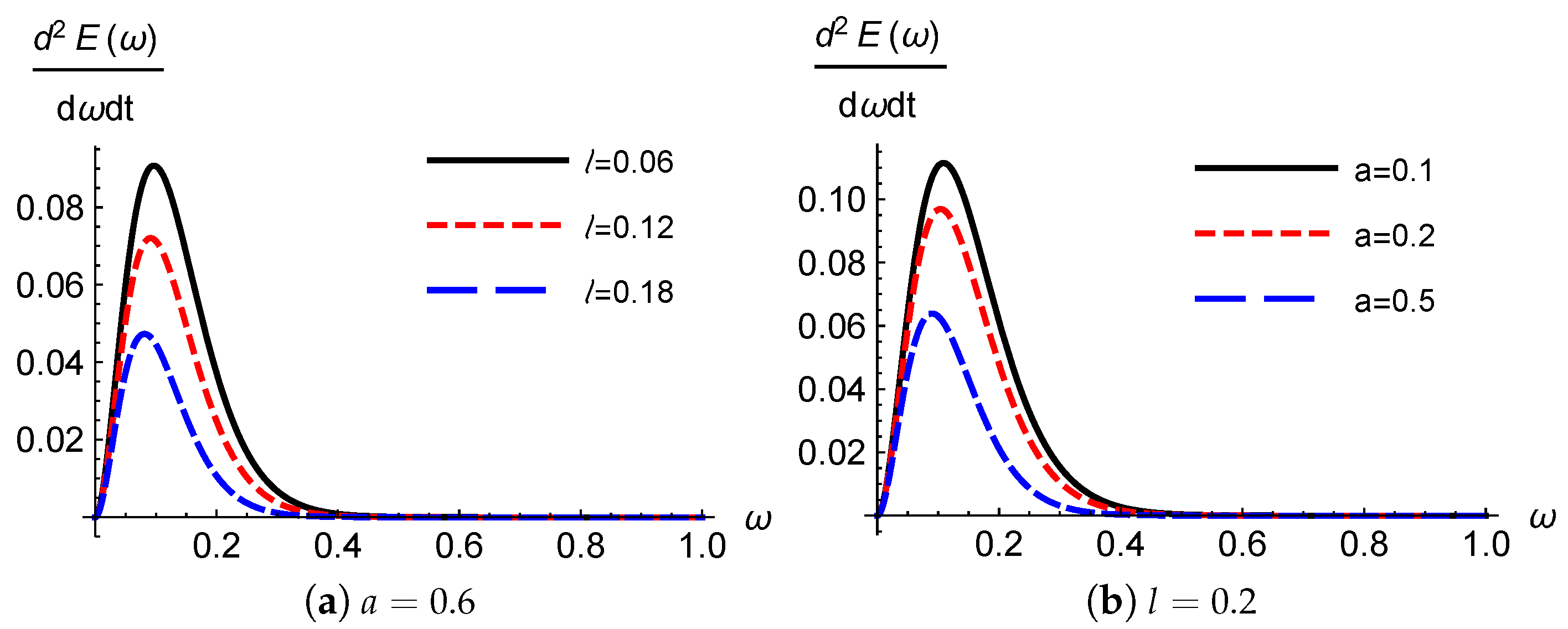
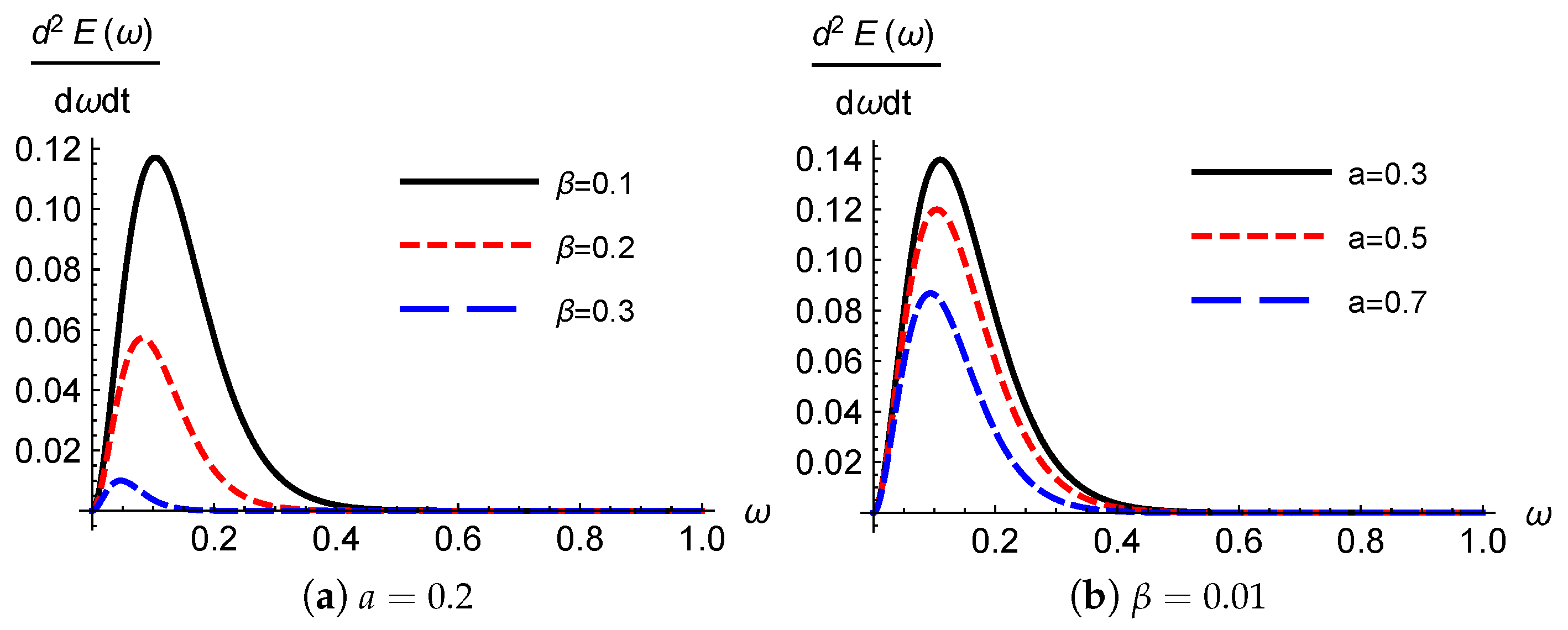
5. Energy Emission Rate
6. The Case with Plasma
7. Gravitational Deflection of Light by Black Hole
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Takahashi, R. It Shapes and positions of black hole shadows in accretion disks and spin parameters of black holes. Astrophys. J. 2004, 611, 996. [Google Scholar] [CrossRef]
- Tsukamoto, N.; Li, Z.L.; Bambi, C. Constraining the spin and the deformation parameters from the black hole shadow. JCAP 2014, 1406, 043. [Google Scholar] [CrossRef] [Green Version]
- Zakharov, A.F.; Paolis, F.D.; Ingrosso, G.; Nucita, A.A. Measuring the black hole parameters in the galactic center with RADIOASTRON. New Astron. 2005, 10, 479. [Google Scholar] [CrossRef]
- Hioki, K.; Maeda, K. Measurement of the Kerr spin parameter by observation of a compact object’s shadow. Phys. Rev. D 2009, 80, 024042. [Google Scholar] [CrossRef] [Green Version]
- Zakharov, A.F. Constraints on a charge in the Reissner-Nordström metric for the black hole at the Galactic Center. Phys. Rev. D 2014, 90, 062007. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.L.; Bambi, C. Measuring the Kerr spin parameter of regular black holes from their shadow. JCAP 2014, 1401, 041. [Google Scholar] [CrossRef] [Green Version]
- Neves, J.C.S. Constraining the tidal charge of brane black holes using their shadows. Eur. Phys. J. C 2020, 80, 717. [Google Scholar] [CrossRef]
- Amarilla, L.; Eiroa, E.F.; Giribet, G. Null geodesics and shadow of a rotating black hole in extended Chern-Simons modified gravity. Phys. Rev. D 2010, 81, 124045. [Google Scholar] [CrossRef] [Green Version]
- Moffat, J.W. Modified Gravity Black Holes and their Observable Shadows. Eur. Phys. J. C 2015, 75, 130. [Google Scholar] [CrossRef]
- Amarilla, L.; Eiroa, E.F. Shadow of a rotating braneworld black hole. Phys. Rev. D 2012, 85, 064019. [Google Scholar] [CrossRef] [Green Version]
- Amarilla, L.; Eiroa, E.F. Shadow of a Kaluza-Klein rotating dilaton black hole. Phys. Rev. D 2013, 87, 044057. [Google Scholar] [CrossRef] [Green Version]
- Synge, J.L. The escape of photons from gravitationally intense stars. Mon. Not. Roy. Astron. Soc. 1966, 131, 463. [Google Scholar] [CrossRef]
- Luminet, J.P. Image of a spherical black hole with thin accretion disk. Astron. Astrophys. 1979, 75, 228. [Google Scholar]
- Bardeen, J.M. Timelike and Null Geodesics of the Kerr Metric; Gordon and Breach: New York, NY, USA, 1973. [Google Scholar]
- Mishra, A.K.; Chakraborty, S.; Sarkar, S. Understanding photon sphere and black hole shadow in dynamically evolving spacetimes. Phys. Rev. D 2019, 99, 104080. [Google Scholar] [CrossRef] [Green Version]
- Perlick, V.; Tsupko, O.Y.; Bisnovatyi-Kogan, G.S. Black hole shadow in an expanding universe with a cosmological constant. Phys. Rev. D 2018, 97, 104062. [Google Scholar] [CrossRef] [Green Version]
- Haroon, S.; Jamil, M.; Jusu, K.; Lin, K.; Mann, R.B. Shadow and Deflection Angle of Rotating Black Holes in Perfect Fluid Dark Matter with a Cosmological Constant. Phys. Rev. D 2019, 99, 044015. [Google Scholar] [CrossRef] [Green Version]
- Grenzebach, A.; Perlick, V.; Lämmerzahl, C. Photon Regions and Shadows of Kerr-Newman-NUT Black Holes with a Cosmological Constant. Phys. Rev. D 2014, 89, 124004. [Google Scholar] [CrossRef] [Green Version]
- Li, P.C.; Guo, M.Y.; Chen, B. Shadow of a Spinning Black Hole in an Expanding Universe. Phys. Rev. D 2020, 101, 084041. [Google Scholar] [CrossRef] [Green Version]
- Amir, M.; Ghosh, S.G. Shapes of rotating nonsingular black hole shadows. Phys. Rev. D 2016, 94, 024054. [Google Scholar] [CrossRef] [Green Version]
- Abdujabbarov, A.; Amir, M.; Ahmedov, B.; Ghosh, S.G. Shadow of rotating regular black holes. Phys. Rev. D 2016, 93, 104004. [Google Scholar] [CrossRef] [Green Version]
- Younsi, Z.; Zhidenko, A.; Rezzolla, L.; Konoplya, R.; Mizuno, Y. New method for shadow calculations: Application to parametrized axisymmetric black holes. Phys. Rev. D 2016, 94, 084025. [Google Scholar] [CrossRef] [Green Version]
- Jusufi, K. Connection Between the Shadow Radius and Quasinormal Modes in Rotating Spacetimes. Phys. Rev. D 2020, 101, 124063. [Google Scholar] [CrossRef]
- Konoplya, R.A. Quantum corrected black holes: Quasinormal modes, scattering, shadows. Phys. Lett. B 2020, 804, 135363. [Google Scholar] [CrossRef]
- Liu, C.; Zhu, T.; Wu, Q.; Jusufi, K.; Jamil, M.; Azreg-Anou, M.; Wang, A.Z. Shadow and Quasinormal Modes of a Rotating Loop Quantum Black Hole. Phys. Rev. D 2020, 101, 084001. [Google Scholar] [CrossRef] [Green Version]
- Atamurotov, F.; Abdujabbarov, A.; Ahmedov, B. Shadow of rotating non-Kerr black hole. Phys. Rev. D 2013, 88, 064004. [Google Scholar] [CrossRef]
- Wei, S.W.; Liu, Y.X. Observing the shadow of Einstein-Maxwell-Dilaton-Axion black hole. JCAP 2013, 1311, 063. [Google Scholar] [CrossRef] [Green Version]
- Lu, R.S.; Broderick, A.E.; Baron, F.; Monnier, J.D.; Fish, V.L.; Doeleman, S.S.; Pankratius, V. Imaging the Supermassive Black Hole Shadow and Jet Base of M87 with the Event Horizon Telescope. Astrophys. J. 2014, 788, 120. [Google Scholar] [CrossRef]
- Papnoi, U.; Atamurotov, F.; Ghosh, S.G.; Ahmedov, B. Shadow of five-dimensional rotating Myers-Perry black hole. Phys. Rev. D 2014, 90, 024073. [Google Scholar] [CrossRef] [Green Version]
- Moffat, J.W. Black Holes in Modified Gravity (MOG). Eur. Phys. J. C 2015, 75, 175. [Google Scholar] [CrossRef]
- Cunha, P.V.P.; Herdeiro, C.A.R.; Radu, E.; Runarsson, H.F. Shadows of Kerr black holes with scalar hair. Phys. Rev. Lett. 2015, 115, 211102. [Google Scholar] [CrossRef] [Green Version]
- Cunha, P.V.P.; Herdeiro, C.A.R.; Kleihaus, B.; Kunz, J.; Radu, E. Shadows of Einstein-dilaton-Gauss-Bonnet black holes. Phys. Lett. B 2017, 768, 373. [Google Scholar] [CrossRef]
- Bisnovatyi-Kogan, G.S.; Tsupko, O.Y. Shadow of a black hole at cosmological distances. Phys. Rev. D 2018, 98, 084020. [Google Scholar] [CrossRef] [Green Version]
- Wei, S.W.; Zou, Y.C.; Liu, Y.X.; Mann, R.B. Curvature radius and Kerr black hole shadow. JCAP 2019, 1908, 030. [Google Scholar] [CrossRef] [Green Version]
- Gralla, S.E.; Holz, D.E.; Wald, R.M. Black Hole Shadows, Photon Rings, and Lensing Rings. Phys. Rev. D 2019, 100, 024018. [Google Scholar] [CrossRef] [Green Version]
- Kumar, R.; Ghosh, S.G.; Wang, A.Z. Gravitational deflection of light and shadow cast by rotating Kalb-Ramond black holes. Phys. Rev. D 2020, 101, 104001. [Google Scholar] [CrossRef]
- Guo, M.Y.; Li, P.C. Innermost stable circular orbit and shadow of the 4D Einstein-Gauss-Bonnet black hole. Eur. Phys. J. C 2020, 80, 588. [Google Scholar] [CrossRef]
- Virbhadra, K.S.; Ellis, G.F.R. Schwarzschild black hole lensing. Phys. Rev. D 2000, 62, 084003. [Google Scholar] [CrossRef] [Green Version]
- Virbhadra, K.S.; Ellis, G.F.R. Gravitational lensing by naked singularities. Phys. Rev. D 2002, 65, 103004. [Google Scholar] [CrossRef]
- Bozza, V. Gravitational lensing in the strong field limit. Phys. Rev. D 2002, 66, 103001. [Google Scholar] [CrossRef] [Green Version]
- Perlick, V. On the Exact gravitational lens equation in spherically symmetric and static space-times. Phys. Rev. D 2004, 69, 064017. [Google Scholar] [CrossRef] [Green Version]
- Hoekstra, H.; Yee, H.K.C.; Gladders, M.D. Properties of galaxy dark matter halos from weak lensing. Astrophys. J. 2004, 606, 67. [Google Scholar] [CrossRef] [Green Version]
- Gallo, E.; Moreschi, O.M. Gravitational lens optical scalars in terms of energy-momentum distributions. Phys. Rev. D 2011, 83, 083007. [Google Scholar] [CrossRef] [Green Version]
- Nam, C.H. Implications for the hierarchy problem, inflation and geodesic motion from fiber fabric of spacetime. Eur. Phys. J. C 2021, 81, 1102. [Google Scholar] [CrossRef]
- Gibbons, G.W.; Werner, M.C. Applications of the Gauss-Bonnet theorem to gravitational lensing. Class. Quant. Grav. 2008, 25, 235009. [Google Scholar] [CrossRef]
- Werner, M.C. Gravitational lensing in the Kerr-Randers optical geometry. Gen. Relativ. Gravit. 2012, 44, 3047. [Google Scholar] [CrossRef] [Green Version]
- Jusufi, K. Gravitational lensing by Reissner-Nordstrom black holes with topological defects. Astrophys. Space Sci. 2016, 361, 24. [Google Scholar] [CrossRef] [Green Version]
- Jusufi, K.; Werner, M.C.; Banerjee, A.; Övgün, A. Light deflection by a rotating global monopole spacetime. Phys. Rev. D 2017, 95, 104012. [Google Scholar] [CrossRef] [Green Version]
- Jusufi, K.; Övgün, A. Gravitational lensing by rotating wormholes. Phys. Rev. D 2018, 97, 024042. [Google Scholar] [CrossRef] [Green Version]
- Jusufi, K.; Övgün, A.; Saavedra, J.; Vasquez, Y.; Gonzalez, P.A. Deflection of light by rotating regular black holes using the Gauss-Bonnet theorem. Phys. Rev. D 2018, 97, 124024. [Google Scholar] [CrossRef] [Green Version]
- Arakida, H. Light deflection and Gauss-Bonnet theorem: Definition of total deflection angle and its applications. Gen. Relativ. Gravit. 2018, 50, 48. [Google Scholar] [CrossRef] [Green Version]
- Övgün, A.; Gyulchev, G.; Jusufi, K. Weak Gravitational lensing by phantom black holes and phantom wormholes using the Gauss-Bonnet theorem. Ann. Phys. 2019, 406, 152. [Google Scholar] [CrossRef] [Green Version]
- Javed, W.; Babar, R.; Övgün, A. The effect of the Brane-Dicke coupling parameter on weak gravitational lensing by wormholes and naked singularities. Phys. Rev. D 2019, 99, 084012. [Google Scholar] [CrossRef] [Green Version]
- Kumar, R.; Ghosh, S.G.; Wang, A.Z. Shadow cast and deflection of light by charged rotating regular black holes. Phys. Rev. D 2019, 100, 124024. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z. Geometrization of light bending and its application to SdS spacetime. Class. Quant. Grav. 2022, 39, 015003. [Google Scholar] [CrossRef]
- Jusufi, K. Gravitational deflection of relativistic massive particles by Kerr black holes and Teo wormholes viewed as a topological effect. Phys. Rev. D 2018, 98, 064017. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.H.; Jia, J.J. The finite-distance gravitational deflection of massive particles in stationary spacetime: A Jacobi metric approach. Eur. Phys. J. C 2020, 80, 157. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.H.; Duan, Y.J.; Jia, J.J. The deflection of charged massive particles by a 4-Dimensional charged Einstein-Gauss-Bonnet black hole. arXiv 2020, arXiv:2012.14226. [Google Scholar]
- Ono, T.; Ishihara, A.; Asada, H. Gravitomagnetic bending angle of light with finite-distance corrections in stationary axisymmetric spacetimes. Phys. Rev. D 2017, 96, 104037. [Google Scholar] [CrossRef] [Green Version]
- Ono, T.; Ishihara, A.; Asada, H. Deflection angle of light for an observer and source at finite distance from a rotating wormhole. Phys. Rev. D 2018, 98, 044047. [Google Scholar] [CrossRef] [Green Version]
- Crisnejo, G.; Gallo, E.; Rogers, A. Finite distance corrections to the light deflection in a gravitational field with a plasma medium. Phys. Rev. D 2019, 99, 124001. [Google Scholar] [CrossRef] [Green Version]
- Muhleman, D.O.; Johnston, I.D. Radio propagation in the solar gravitational field. Phys. Rev. Lett. 1966, 17, 455. [Google Scholar] [CrossRef]
- Muhleman, D.O.; Ekers, R.D.; Fomalont, E.B. Radio interferometric test of the general relativistic light bending near the sun. Phys. Rev. Lett. 1970, 24, 1377. [Google Scholar] [CrossRef]
- Perlick, V. Ray Optics, Fermat’s Principle, and Applications to General Relatively; Springer: Berlin, Germany, 2000. [Google Scholar]
- Bisnovatyi-Kogan, G.S.; Tsupko, O.Y. Gravitational lensing in a non-uniform plasma. Not. Roy. Astron. Soc. 2010, 404, 1790. [Google Scholar] [CrossRef] [Green Version]
- Rogers, A. Frequency-dependent effects of gravitational lensing within plasma. Mon. Not. Roy. Astron. Soc. 2015, 451, 17. [Google Scholar] [CrossRef]
- Morozova, V.; Ahmedov, B.; Tursunov, A. Gravitational lensing by a rotating massive object in a plasma. Astrophys. Space Sci. 2013, 346, 513. [Google Scholar] [CrossRef] [Green Version]
- Benavides-Gallego, C.A.; Abdujabbarov, A.A.; Bambi, C. Gravitational lensing for a boosted Kerr black hole in the presence of plasma. Eur. Phys. J. C 2018, 78, 694. [Google Scholar] [CrossRef]
- Crisnejo, G.; Gallo, E. Weak lensing in a plasma medium and gravitational deflection of massive particles using the Gauss-Bonnet theorem. A unified treatment. Phys. Rev. D 2018, 97, 124016. [Google Scholar] [CrossRef] [Green Version]
- Bisnovatyi-Kogan, G.; Tsupko, O. Gravitational Lensing in Presence of Plasma: Strong Lens Systems, Black Hole Lensing and Shadow. Universe 2017, 3, 57. [Google Scholar] [CrossRef] [Green Version]
- Atamurotov, F.; Ahmedov, B. Optical properties of black hole in the presence of plasma: Shadow. Phys. Rev. D 2015, 92, 084005. [Google Scholar] [CrossRef] [Green Version]
- Perlick, V.; Tsupko, O.Y.; Bisnovatyi-Kogan, G.S. Influence of a plasma on the shadow of a spherically symmetric black hole. Phys. Rev. D 2015, 92, 104031. [Google Scholar] [CrossRef] [Green Version]
- Perlick, V.; Tsupko, O.Y. Light propagation in a plasma on Kerr spacetime: Separation of the Hamilton-Jacobi equation and calculation of the shadow. Phys. Rev. D 2017, 95, 104003. [Google Scholar] [CrossRef] [Green Version]
- Yan, H.P. Influence of a plasma on the observational signature of a high-spin Kerr black hole. Phys. Rev. D 2019, 99, 084050. [Google Scholar] [CrossRef] [Green Version]
- Bisnovatyi-Kogan, G.S.; Tsupko, O.Y. Gravitational Lensing in Plasmic Medium. Plasma Phys. Rep. 2015, 41, 562. [Google Scholar] [CrossRef] [Green Version]
- Das, S.; Vagenas, E.C. Universality of Quantum Gravity Corrections. Phys. Rev. Lett. 2008, 101, 221301. [Google Scholar] [CrossRef] [Green Version]
- Masood, S.; Faizal, M.; Zaz, Z.; Ali, A.F.; Raza, J.; Shah, M.B. The most general form of deformation of the Heisenberg algebra from the generalized uncertainty principle. Phys. Lett. B 2016, 763, 218. [Google Scholar] [CrossRef] [Green Version]
- Modesto, L.; Shapiro, I.L. Superrenormalizable quantum gravity with complex ghosts. Phys. Lett. B 2016, 755, 279. [Google Scholar] [CrossRef]
- Modesto, L. Super-renormalizable or finite Lee-Wick quantum gravity. Nucl. Phys. B 2016, 909, 584. [Google Scholar] [CrossRef] [Green Version]
- Faizal, M.; Ali, A.F.; Nassar, A. Generalized uncertainty principle as a consequence of the effective field theory. Phys. Lett. B 2017, 765, 238. [Google Scholar] [CrossRef]
- Elizalde, E.; Odintsov, S.D. A Renormalization group improved nonlocal gravitational effective Lagrangian. Mod. Phys. Lett. A 1995, 10, 1821. [Google Scholar] [CrossRef]
- Modesto, L.; Moffat, J.W.; Nicolini, P. Black holes in an ultraviolet complete quantum gravity. Phys. Lett. B 2011, 695, 397. [Google Scholar] [CrossRef] [Green Version]
- Chicone, C.; Mashhoon, B. Linearized Gravitational Waves in Nonlocal General Relativity. Phys. Rev. D 2013, 87, 064015. [Google Scholar] [CrossRef] [Green Version]
- Joshi, P.; Kumar, U.; Panda, S. Hamiltonian formalism for nonlocal gravity models. Int. J. Geom. Meth. Mod. Phys. 2022, 19, 2250036. [Google Scholar] [CrossRef]
- Moffat, J.W. Ultraviolet Complete Quantum Gravity. Eur. Phys. J. Plus 2011, 126, 43. [Google Scholar] [CrossRef] [Green Version]
- Biswas, T.; Koivisto, T.; Mazumdar, A. Towards a resolution of the cosmological singularity in non-local higher derivative theories of gravity. JCAP 2010, 1011, 008. [Google Scholar] [CrossRef] [Green Version]
- Modesto, L. Super-renormalizable Quantum Gravity. Phys. Rev. D 2012, 86, 044005. [Google Scholar] [CrossRef] [Green Version]
- Modesto, L.; Rachwal, L. Super-renormalizable and finite gravitational theories. Nucl. Phys. B 2014, 889, 228. [Google Scholar] [CrossRef] [Green Version]
- Maggiore, M. Phantom dark energy from nonlocal infrared modifications of general relativity. Phys. Rev. D 2014, 89, 043008. [Google Scholar] [CrossRef] [Green Version]
- Narain, G.; Li, T.J. Ultraviolet complete dark energy model. Phys. Rev. D 2018, 97, 083523. [Google Scholar] [CrossRef] [Green Version]
- Kumar, U.; Panda, S.; Patel, A. Metric for Rotating object in Infrared Corrected Nonlocal Gravity Model. Phys. Rev. D 2018, 98, 124040. [Google Scholar] [CrossRef] [Green Version]
- Tian, S.X.; Zhu, Z.H. Revisiting scalar and tensor perturbations in a nonlocal gravity. Phys. Rev. D 2019, 100, 124059. [Google Scholar] [CrossRef] [Green Version]
- Dirian, Y.; Foffa, S.; Khosravi, N.; Kunz, M.; Maggiore, M. Cosmological perturbations and structure formation in nonlocal infrared modifications of general relativity. JCAP 2014, 1406, 033. [Google Scholar] [CrossRef] [Green Version]
- Dirian, Y.; Foffa, S.; Kunz, M.; Maggiore, M.; Pettorino, V. Non-local gravity and comparison with observational datasets. JCAP 2015, 1504, 044. [Google Scholar] [CrossRef] [Green Version]
- Dirian, Y.; Foffa, S.; Kunz, M.; Maggiore, M.; Pettorino, V. Non-local gravity and comparison with observational datasets. II. Updated results and Bayesian model comparison with ΛCDM. JCAP 2016, 1605, 068. [Google Scholar] [CrossRef] [Green Version]
- Nicolini, P. Nonlocal and generalized uncertainty principle black holes. arXiv 2012, arXiv:1202.2102. [Google Scholar]
- Isi, M.; Mureika, J.; Nicolini, P. Self-Completeness and the Generalized Uncertainty Principle. JHEP 2013, 1311, 139. [Google Scholar] [CrossRef] [Green Version]
- Frolov, V.P. Mass-gap for black hole formation in higher derivative and ghost free gravity. Phys. Rev. Lett. 2015, 115, 051102. [Google Scholar] [CrossRef] [PubMed]
- Knipfer, M.; Köppel, S.; Mureika, J.; Nicolini, P. Generalized Uncertainty Principle and Black Holes in Higher Dimensional Self-Complete Gravity. JCAP 2019, 1908, 008. [Google Scholar] [CrossRef] [Green Version]
- Platania, A. Dynamical renormalization of black-hole spacetimes. Eur. Phys. J. C 2019, 79, 470. [Google Scholar] [CrossRef]
- Nicolini, P.; Smailagic, A.; Spallucci, E. Noncommutative geometry inspired Schwarzschild black hole. Phys. Lett. B 2006, 632, 547. [Google Scholar] [CrossRef] [Green Version]
- Platania, A. From renormalization group flows to cosmology. Front. Phys. 2020, 8, 188. [Google Scholar] [CrossRef]
- Knorr, B.; Platania, A. Sifting quantum black holes through the principle of least action. arXiv 2022, arXiv:2202.01216. [Google Scholar]
- Newman, E.; Janis, A. Note on the Kerr spinning particle metric. J. Math. Phys. 1965, 6, 915. [Google Scholar] [CrossRef]
- Newman, E.T.; Couch, R.; Chinnapared, K.; Exton, A.; Prakash, A.; Torrence, R. Metric of a Rotating, Charged Mass. J. Math. Phys. 1965, 6, 918. [Google Scholar] [CrossRef]
- Johannsen, T.; Psaltis, D. A Metric for Rapidly Spinning Black Holes Suitable for Strong-Field Tests of the No-Hair Theorem. Phys. Rev. D 2011, 83, 124015. [Google Scholar] [CrossRef] [Green Version]
- Bambi, C.; Modesto, L. Rotating regular black holes. Phys. Lett. B 2013, 721, 329. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, S.G.; Maharaj, S.D. Radiating Kerr-like regular black hole. Eur. Phys. J. C 2015, 75, 7. [Google Scholar] [CrossRef] [Green Version]
- Jusufi, K.; Jamil, M.; Chakrabarty, H.; Wu, Q.; Bambi, C.; Wang, A. Rotating regular black holes in conformal massive gravity. Phys. Rev. D 2020, 101, 044035. [Google Scholar] [CrossRef] [Green Version]
- Azreg-Aïnou, M. Generating rotating regular black hole solutions without complexification. Phys. Rev. D 2014, 90, 064041. [Google Scholar] [CrossRef] [Green Version]
- Chandrasekhar, S. The Mathematical Theory of Black Holes; Oxford University Press: New York, NY, USA, 1983. [Google Scholar]
- Bardeen, J.M.; Press, W.H.; Teukolsky, S.A. Rotating black holes: Locally nonrotating frames, energy extraction, and scalar synchrotron radiation. Astrophys. J. 1972, 178, 347. [Google Scholar] [CrossRef]
- Cunningham, C.T.; Bardeen, J.M. The optical appearance of a star orbiting an extreme Kerr black hole. Astrophys. J. 1973, 183, 237. [Google Scholar] [CrossRef]
- Cunningham, C.T. The effects of redshifts and focusing on the spectrum of an accretion disk around a Kerr black hole. Astrophys. J. 1975, 202, 788. [Google Scholar] [CrossRef]
- Carter, B. Hamilton-Jacobi and Schrodinger separable solutions of Einstein’s equations. Commun. Math. Phys. 1968, 10, 280. [Google Scholar] [CrossRef]
- Event Horizon Telescope Collaboration; Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.; Ball, D.; Baloković, M.; Barrett, J.; et al. First M87 Event Horizon Telescope Results. I. The shadow of the supermassive black hole. Astrophys. J. 2019, 875, L1. [Google Scholar]
- Bambi, C.; Freese, K.; Vagnozzi, S.; Visinelli, L. Testing the rotational nature of the supermassive object M87* from the circularity and size of its first image. Phys. Rev. D 2019, 100, 044057. [Google Scholar] [CrossRef] [Green Version]
- Mashhoon, B. Scattering of Electromagnetic Radiation from a Black Hole. Phys. Rev. D 1973, 7, 2807. [Google Scholar] [CrossRef]
- Parikh, M.K.; Wilczek, F. Hawking radiation as tunneling. Phys. Rev. Lett. 2000, 85, 5042. [Google Scholar] [CrossRef] [Green Version]
- Padmanabhan, T. Gravity and the thermodynamics of horizons. Phys. Rept. 2005, 406, 49. [Google Scholar] [CrossRef] [Green Version]




| 0.00 | 5.196 | 0.030 | 5.197 | 0.066 | 5.198 | 0.138 |
| 0.03 | 5.129 | 0.033 | 5.130 | 0.073 | 5.132 | 0.162 |
| 0.05 | 5.083 | 0.035 | 5.084 | 0.079 | 5.086 | 0.185 |
| 0.13 | 4.889 | 0.047 | 4.890 | 0.114 | — | — |
| 0.15 | 4.837 | 0.051 | 4.839 | 0.128 | — | — |
| 0.18 | 4.757 | 0.058 | 4.759 | 0.161 | — | — |
| 0.23 | 4.616 | 0.077 | — | — | — | — |
| 0.00 | 5.1961 | 0.0045 | 5.1964 | 0.0305 | 5.1979 | 0.0954 |
| 0.05 | 5.1960 | 0.0045 | 5.1963 | 0.0307 | 5.1978 | 0.0988 |
| 0.10 | 5.1919 | 0.0049 | 5.1923 | 0.0347 | 5.1939 | 0.1354 |
| 0.15 | 5.1753 | 0.0060 | 5.1758 | 0.0453 | — | — |
| 0.20 | 5.1408 | 0.0081 | 5.1416 | 0.0682 | — | — |
| 0.25 | 5.0853 | 0.0117 | — | — | — | — |
| 0.30 | 5.0051 | 0.0189 | — | — | — | — |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, Q.-M.; Wei, S.-W.; Zhao, L.; Liu, Y.-X.; Zhang, X. Shadow and Weak Deflection Angle of a Black Hole in Nonlocal Gravity. Universe 2022, 8, 341. https://doi.org/10.3390/universe8070341
Fu Q-M, Wei S-W, Zhao L, Liu Y-X, Zhang X. Shadow and Weak Deflection Angle of a Black Hole in Nonlocal Gravity. Universe. 2022; 8(7):341. https://doi.org/10.3390/universe8070341
Chicago/Turabian StyleFu, Qi-Ming, Shao-Wen Wei, Li Zhao, Yu-Xiao Liu, and Xin Zhang. 2022. "Shadow and Weak Deflection Angle of a Black Hole in Nonlocal Gravity" Universe 8, no. 7: 341. https://doi.org/10.3390/universe8070341
APA StyleFu, Q.-M., Wei, S.-W., Zhao, L., Liu, Y.-X., & Zhang, X. (2022). Shadow and Weak Deflection Angle of a Black Hole in Nonlocal Gravity. Universe, 8(7), 341. https://doi.org/10.3390/universe8070341








