GRMHD Simulations and Modeling for Jet Formation and Acceleration Region in AGNs
Abstract
1. Introduction
2. Jet Formation from Geometrically Thin Accretion Disk
2.1. Jet Formation from Tilted Thin Disks
2.2. Thin Disk Simulations in Non-Ideal GRMHD
3. Jet Formation from Geometrically Thick Magnetized Torii
3.1. GRMHD Simulations in the MAD Regime
3.2. Different Magnetic Field Configurations
3.3. Jet Formation from Tilted Thick Torii
3.4. Geometrically Thick Torus Simulations in Non-Ideal GRMHD
4. Jet Formation in Radiative GRMHD Simulations
5. Jet Formation without Disk
6. Jet Modeling from GRMHD Simulations
7. Discussion and Summary
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ADAF | Advection-Dominated Accretion Flow |
| AGN | Active Galactic Nuclei |
| AMR | Adaptive Mesh Refinement |
| BH | Black Hole |
| EHTC | Event Horizon Telescope Collaboration |
| GR | General Relativity |
| GRMHD | General Relativistic Magnetohydrodynamics |
| GRRT | General Relativistic Radiative Transfer |
| MAD | Magnetically Arrested Disk |
| MHD | Magnetohydrodynamics |
| MRI | Magnetorotational Instability |
| SANE | Standard Accretion and Normal Evolution |
| PFD | Poynting Flux Dominated |
| RIAF | Radiatively Inefficient Accretion Flow |
| WR | Wolf–Rayet |
References
- Begelman, M.C.; Blandford, R.D.; Rees, M.J. Theory of extragalactic radio sources. Rev. Mod. Phys. 1984, 56, 255–351. [Google Scholar] [CrossRef]
- de Gouveia Dal Pino, E.M. Astrophysical jets and outflows. Adv. Space Res. 2005, 35, 908–924. [Google Scholar] [CrossRef]
- Beskin, V.S. Magnetohydrodynamic models of astrophysical jets. Phys. Uspekhi 2010, 53, 1199–1233. [Google Scholar] [CrossRef]
- Blandford, R.D.; Znajek, R.L. Electromagnetic extraction of energy from Kerr black holes. Mon. Not. R. Astron. Soc. 1977, 179, 433–456. [Google Scholar] [CrossRef]
- Blandford, R.D.; Payne, D.G. Hydromagnetic flows from accretion disks and the production of radio jets. Mon. Not. R. Astron. Soc. 1982, 199, 883–903. [Google Scholar] [CrossRef]
- Bisnovatyi-Kogan, G.S.; Lovelace, R.V.E. Advective accretion disks and related problems including magnetic fields. New Astron. Rev. 2001, 45, 663–742. [Google Scholar] [CrossRef]
- Aloy, M.A.; Rezzolla, L. A Powerful Hydrodynamic Booster for Relativistic Jets. Astrophys. J. Lett. 2006, 640, L115–L118. [Google Scholar] [CrossRef]
- Mizuno, Y.; Hardee, P.; Hartmann, D.H.; Nishikawa, K.I.; Zhang, B. A Magnetohydrodynamic Boost for Relativistic Jets. Astrophys. J. 2008, 672, 72–82. [Google Scholar] [CrossRef]
- Hawley, J.F.; Smarr, L.L.; Wilson, J.R. A numerical study of nonspherical black hole accretion. I Equations and test problems. Astrophys. J. 1984, 277, 296–311. [Google Scholar] [CrossRef]
- Koide, S.; Meier, D.L.; Shibata, K.; Kudoh, T. General Relativistic Simulations of Early Jet Formation in a Rapidly Rotating Black Hole Magnetosphere. Astrophys. J. 2000, 536, 668–674. [Google Scholar] [CrossRef]
- De Villiers, J.P.; Hawley, J.F. A Numerical Method for General Relativistic Magnetohydrodynamics. Astrophys. J. 2003, 589, 458–480. [Google Scholar] [CrossRef]
- Gammie, C.F.; McKinney, J.C.; Tóth, G. HARM: A Numerical Scheme for General Relativistic Magnetohydrodynamics. Astrophys. J. 2003, 589, 444–457. [Google Scholar] [CrossRef]
- Baiotti, L.; Hawke, I.; Montero, P.J.; Löffler, F.; Rezzolla, L.; Stergioulas, N.; Font, J.A.; Seidel, E. Three-dimensional relativistic simulations of rotating neutron-star collapse to a Kerr black hole. Phys. Rev. D 2005, 71, 024035. [Google Scholar] [CrossRef]
- Duez, M.D.; Liu, Y.T.; Shapiro, S.L.; Stephens, B.C. Relativistic magnetohydrodynamics in dynamical spacetimes: Numerical methods and tests. Phys. Rev. D 2005, 72, 024028. [Google Scholar] [CrossRef]
- Anninos, P.; Fragile, P.C.; Salmonson, J.D. Cosmos++: Relativistic Magnetohydrodynamics on Unstructured Grids with Local Adaptive Refinement. Astrophys. J. 2005, 635, 723–740. [Google Scholar] [CrossRef]
- Antón, L.; Zanotti, O.; Miralles, J.A.; Martí, J.M.; Ibáñez, J.M.; Font, J.A.; Pons, J.A. Numerical 3+1 General Relativistic Magnetohydrodynamics: A Local Characteristic Approach. Astrophys. J. 2006, 637, 296–312. [Google Scholar] [CrossRef]
- Mizuno, Y.; Nishikawa, K.I.; Koide, S.; Hardee, P.; Fishman, G.J. RAISHIN: A High-Resolution Three-Dimensional General Relativistic Magnetohydrodynamics Code. arXiv 2006, arXiv:astro-ph/0609004. [Google Scholar]
- Del Zanna, L.; Zanotti, O.; Bucciantini, N.; Londrillo, P. ECHO: A Eulerian conservative high-order scheme for general relativistic magnetohydrodynamics and magnetodynamics. Astron. Astrophys. 2007, 473, 11–30. [Google Scholar] [CrossRef]
- Giacomazzo, B.; Rezzolla, L. WhiskyMHD: A new numerical code for general relativistic magnetohydrodynamics. Class. Quantum Gravity 2007, 24, S235–S258. [Google Scholar] [CrossRef]
- Etienne, Z.B.; Paschalidis, V.; Haas, R.; Mösta, P.; Shapiro, S.L. IllinoisGRMHD: An open-source, user-friendly GRMHD code for dynamical spacetimes. Class. Quantum Gravity 2015, 32, 175009. [Google Scholar] [CrossRef]
- White, C.J.; Stone, J.M.; Gammie, C.F. An Extension of the Athena++ Code Framework for GRMHD Based on Advanced Riemann Solvers and Staggered-mesh Constrained Transport. Astrophys. J. Suppl. 2016, 225, 22. [Google Scholar] [CrossRef]
- Zanotti, O.; Dumbser, M. A high order special relativistic hydrodynamic and magnetohydrodynamic code with space-time adaptive mesh refinement. Comput. Phys. Commun. 2015, 188, 110–127. [Google Scholar] [CrossRef]
- Porth, O.; Olivares, H.; Mizuno, Y.; Younsi, Z.; Rezzolla, L.; Moscibrodzka, M.; Falcke, H.; Kramer, M. The black hole accretion code. Comput. Astrophys. Cosmol. 2017, 4, 1. [Google Scholar] [CrossRef]
- Olivares, H.; Porth, O.; Davelaar, J.; Most, E.R.; Fromm, C.M.; Mizuno, Y.; Younsi, Z.; Rezzolla, L. Constrained transport and adaptive mesh refinement in the Black Hole Accretion Code. Astron. Astrophys. 2019, 629, A61. [Google Scholar] [CrossRef]
- Liska, M.; Chatterjee, K.; Tchekhovskoy, A.; Yoon, D.; van Eijnatten, D.; Hesp, C.; Markoff, S.; Ingram, A.; van der Klis, M. H-AMR: A New GPU-accelerated GRMHD Code for Exascale Computing with 3D Adaptive Mesh Refinement and Local Adaptive Time-stepping. arXiv 2019, arXiv:1912.10192. [Google Scholar]
- Chi-Kit Cheong, P.; Tsz-Lok Lam, A.; Ho-Yin Ng, H.; Li, T.G.F. Gmunu: Paralleled, grid-adaptive, general-relativistic magnetohydrodynamics in curvilinear geometries in dynamical spacetimes. arXiv 2020, arXiv:2012.07322. [Google Scholar]
- Rezzolla, L.; Zanotti, O. Relativistic Hydrodynamics; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Font, J.A. Numerical Hydrodynamics in General Relativity. Living Rev. Relativ. 2003, 6, 4. [Google Scholar] [CrossRef]
- Martí, J.M.; Müller, E. Grid-based Methods in Relativistic Hydrodynamics and Magnetohydrodynamics. Living Rev. Comput. Astrophys. 2015, 1, 3. [Google Scholar] [CrossRef]
- Sądowski, A.; Narayan, R.; Tchekhovskoy, A.; Zhu, Y. Semi-implicit scheme for treating radiation under M1 closure in general relativistic conservative fluid dynamics codes. Mon. Not. R. Astron. Soc. 2013, 429, 3533–3550. [Google Scholar] [CrossRef]
- McKinney, J.C.; Tchekhovskoy, A.; Sadowski, A.; Narayan, R. Three-dimensional general relativistic radiation magnetohydrodynamical simulation of super-Eddington accretion, using a new code HARMRAD with M1 closure. Mon. Not. R. Astron. Soc. 2014, 441, 3177–3208. [Google Scholar] [CrossRef]
- Takahashi, H.R.; Ohsuga, K.; Kawashima, T.; Sekiguchi, Y. Formation of Overheated Regions and Truncated Disks around Black Holes: Three-dimensional General Relativistic Radiation-magnetohydrodynamics Simulations. Astrophys. J. 2016, 826, 23. [Google Scholar] [CrossRef]
- Bucciantini, N.; Del Zanna, L. A fully covariant mean-field dynamo closure for numerical 3 + 1 resistive GRMHD. Mon. Not. R. Astron. Soc. 2013, 428, 71–85. [Google Scholar] [CrossRef]
- Dionysopoulou, K.; Alic, D.; Palenzuela, C.; Rezzolla, L.; Giacomazzo, B. General-relativistic resistive magnetohydrodynamics in three dimensions: Formulation and tests. Phys. Rev. D 2013, 88, 044020. [Google Scholar] [CrossRef]
- Chandra, M.; Gammie, C.F.; Foucart, F.; Quataert, E. An Extended Magnetohydrodynamics Model for Relativistic Weakly Collisional Plasmas. Astrophys. J. 2015, 810, 162. [Google Scholar] [CrossRef]
- Chandra, M.; Foucart, F.; Gammie, C.F. grim: A Flexible, Conservative Scheme for Relativistic Fluid Theories. Astrophys. J. 2017, 837, 92. [Google Scholar] [CrossRef]
- Del Zanna, L.; Bucciantini, N. Covariant and 3 + 1 equations for dynamo-chiral general relativistic magnetohydrodynamics. Mon. Not. R. Astron. Soc. 2018, 479, 657–666. [Google Scholar] [CrossRef]
- Ripperda, B.; Bacchini, F.; Porth, O.; Most, E.R.; Olivares, H.; Nathanail, A.; Rezzolla, L.; Teunissen, J.; Keppens, R. General-relativistic Resistive Magnetohydrodynamics with Robust Primitive-variable Recovery for Accretion Disk Simulations. Astrophys. J. Suppl. 2019, 244, 10. [Google Scholar] [CrossRef]
- Fender, R.P.; Belloni, T.M.; Gallo, E. Towards a unified model for black hole X-ray binary jets. Mon. Not. R. Astron. Soc. 2004, 355, 1105–1118. [Google Scholar] [CrossRef]
- Markoff, S. Sagittarius A* in Context: Daily Flares as a Probe of the Fundamental X-Ray Emission Process in Accreting Black Holes. Astrophys. J. Lett. 2005, 618, L103–L106. [Google Scholar] [CrossRef][Green Version]
- Marrone, D.P.; Moran, J.M.; Zhao, J.H.; Rao, R. An Unambiguous Detection of Faraday Rotation in Sagittarius A*. Astrophys. J. Lett. 2007, 654, L57–L60. [Google Scholar] [CrossRef]
- Ho, L.C. Radiatively Inefficient Accretion in Nearby Galaxies. Astrophys. J. 2009, 699, 626–637. [Google Scholar] [CrossRef]
- Narayan, R.; Yi, I. Advection-dominated Accretion: A Self-similar Solution. Astrophys. J. Lett. 1994, 428, L13. [Google Scholar] [CrossRef]
- Narayan, R.; Yi, I. Advection-dominated Accretion: Underfed Black Holes and Neutron Stars. Astrophys. J. 1995, 452, 710. [Google Scholar] [CrossRef]
- Abramowicz, M.A.; Chen, X.; Kato, S.; Lasota, J.P.; Regev, O. Thermal Equilibria of Accretion Disks. Astrophys. J. Lett. 1995, 438, L37. [Google Scholar] [CrossRef]
- Yuan, F.; Narayan, R. Hot Accretion Flows Around Black Holes. Annu. Rev. Astron. Astrophys. 2014, 52, 529–588. [Google Scholar] [CrossRef]
- Yuan, F.; Quataert, E.; Narayan, R. Nonthermal Electrons in Radiatively Inefficient Accretion Flow Models of Sagittarius A*. Astrophys. J. 2003, 598, 301–312. [Google Scholar] [CrossRef]
- Novikov, I.D.; Thorne, K.S. Astrophysics of black holes. In Black Holes (Les Astres Occlus); Dewitt, C., Dewitt, B.S., Eds.; Gordon & Breach: New York, NY, USA, 1973; pp. 343–450. [Google Scholar]
- Shakura, N.I.; Sunyaev, R.A. Reprint of 1973A&A....24..337S. Black holes in binary systems. Observational appearance. Astron. Astrophys. 1973, 500, 33–51. [Google Scholar]
- Abramowicz, M.A.; Czerny, B.; Lasota, J.P.; Szuszkiewicz, E. Slim Accretion Disks. Astrophys. J. 1988, 332, 646. [Google Scholar] [CrossRef]
- Koide, S.; Shibata, K.; Kudoh, T. General Relativistic Magnetohydrodynamic Simulations of Jets from Black Hole Accretions Disks: Two-Component Jets Driven by Nonsteady Accretion of Magnetized Disks. Astrophys. J. Lett. 1998, 495, L63–L66. [Google Scholar] [CrossRef]
- Koide, S.; Shibata, K.; Kudoh, T. Relativistic Jet Formation from Black Hole Magnetized Accretion Disks: Method, Tests, and Applications of a General RelativisticMagnetohydrodynamic Numerical Code. Astrophys. J. 1999, 522, 727–752. [Google Scholar] [CrossRef]
- Nishikawa, K.I.; Richardson, G.; Koide, S.; Shibata, K.; Kudoh, T.; Hardee, P.; Fishman, G.J. A General Relativistic Magnetohydrodynamic Simulation of Jet Formation. Astrophys. J. 2005, 625, 60–71. [Google Scholar] [CrossRef]
- Hardee, P.; Mizuno, Y.; Nishikawa, K.I. GRMHD/RMHD simulations & stability of magnetized spine-sheath relativistic jets. Astrophys. Space Sci. 2007, 311, 281–286. [Google Scholar] [CrossRef]
- Shafee, R.; McKinney, J.C.; Narayan, R.; Tchekhovskoy, A.; Gammie, C.F.; McClintock, J.E. Three-Dimensional Simulations of Magnetized Thin Accretion Disks around Black Holes: Stress in the Plunging Region. Astrophys. J. Lett. 2008, 687, L25. [Google Scholar] [CrossRef]
- Noble, S.C.; Krolik, J.H.; Hawley, J.F. Dependence of Inner Accretion Disk Stress on Parameters: The Schwarzschild Case. Astrophys. J. 2010, 711, 959–973. [Google Scholar] [CrossRef]
- Noble, S.C.; Krolik, J.H.; Schnittman, J.D.; Hawley, J.F. Radiative Efficiency and Thermal Spectrum of Accretion onto Schwarzschild Black Holes. Astrophys. J. 2011, 743, 115. [Google Scholar] [CrossRef]
- Penna, R.F.; McKinney, J.C.; Narayan, R.; Tchekhovskoy, A.; Shafee, R.; McClintock, J.E. Simulations of magnetized discs around black holes: Effects of black hole spin, disc thickness and magnetic field geometry. Mon. Not. R. Astron. Soc. 2010, 408, 752–782. [Google Scholar] [CrossRef]
- Avara, M.J.; McKinney, J.C.; Reynolds, C.S. Efficiency of thin magnetically arrested discs around black holes. Mon. Not. R. Astron. Soc. 2016, 462, 636–648. [Google Scholar] [CrossRef]
- Dihingia, I.K.; Vaidya, B.; Fendt, C. Jets, disc-winds, and oscillations in general relativistic, magnetically driven flows around black hole. Mon. Not. R. Astron. Soc. 2021, 505, 3596–3615. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Petterson, J.A. The Lense-Thirring Effect and Accretion Disks around Kerr Black Holes. Astrophys. J. Lett. 1975, 195, L65. [Google Scholar] [CrossRef]
- Liska, M.; Hesp, C.; Tchekhovskoy, A.; Ingram, A.; van der Klis, M.; Markoff, S. Formation of precessing jets by tilted black hole discs in 3D general relativistic MHD simulations. Mon. Not. R. Astron. Soc. 2018, 474, L81–L85. [Google Scholar] [CrossRef]
- Liska, M.; Hesp, C.; Tchekhovskoy, A.; Ingram, A.; van der Klis, M.; Markoff, S.B.; Van Moer, M. Disc tearing and Bardeen-Petterson alignment in GRMHD simulations of highly tilted thin accretion discs. Mon. Not. R. Astron. Soc. 2021, 507, 983–990. [Google Scholar] [CrossRef]
- Qian, Q.; Fendt, C.; Vourellis, C. Jet Launching in Resistive GR-MHD Black Hole-Accretion Disk Systems. Astrophys. J. 2018, 859, 28. [Google Scholar] [CrossRef]
- Vourellis, C.; Fendt, C.; Qian, Q.; Noble, S.C. GR-MHD Disk Winds and Jets from Black Holes and Resistive Accretion Disks. Astrophys. J. 2019, 882, 2. [Google Scholar] [CrossRef]
- Balbus, S.A.; Hawley, J.F. A Powerful Local Shear Instability in Weakly Magnetized Disks. I. Linear Analysis. Astrophys. J. 1991, 376, 214. [Google Scholar] [CrossRef]
- Balbus, S.A.; Hawley, J.F. Instability, turbulence, and enhanced transport in accretion disks. Rev. Mod. Phys. 1998, 70, 1–53. [Google Scholar] [CrossRef]
- De Villiers, J.P.; Hawley, J.F. Global General Relativistic Magnetohydrodynamic Simulations of Accretion Tori. Astrophys. J. 2003, 592, 1060–1077. [Google Scholar] [CrossRef]
- McKinney, J.C.; Gammie, C.F. A Measurement of the Electromagnetic Luminosity of a Kerr Black Hole. Astrophys. J. 2004, 611, 977–995. [Google Scholar] [CrossRef]
- McKinney, J.C. General relativistic magnetohydrodynamic simulations of the jet formation and large-scale propagation from black hole accretion systems. Mon. Not. R. Astron. Soc. 2006, 368, 1561–1582. [Google Scholar] [CrossRef]
- McKinney, J.C.; Blandford, R.D. Stability of relativistic jets from rotating, accreting black holes via fully three-dimensional magnetohydrodynamic simulations. Mon. Not. R. Astron. Soc. 2009, 394, L126–L130. [Google Scholar] [CrossRef]
- De Villiers, J.P.; Hawley, J.F.; Krolik, J.H. Magnetically Driven Accretion Flows in the Kerr Metric. I. Models and Overall Structure. Astrophys. J. 2003, 599, 1238–1253. [Google Scholar] [CrossRef]
- De Villiers, J.P.; Hawley, J.F.; Krolik, J.H.; Hirose, S. Magnetically Driven Accretion in the Kerr Metric. III. Unbound Outflows. Astrophys. J. 2005, 620, 878–888. [Google Scholar] [CrossRef]
- Hirose, S.; Krolik, J.H.; De Villiers, J.P.; Hawley, J.F. Magnetically Driven Accretion Flows in the Kerr Metric. II. Structure of the Magnetic Field. Astrophys. J. 2004, 606, 1083–1097. [Google Scholar] [CrossRef]
- Hawley, J.F.; Krolik, J.H. Magnetically Driven Jets in the Kerr Metric. Astrophys. J. 2006, 641, 103–116. [Google Scholar] [CrossRef]
- Beckwith, K.; Hawley, J.F.; Krolik, J.H. The Influence of Magnetic Field Geometry on the Evolution of Black Hole Accretion Flows: Similar Disks, Drastically Different Jets. Astrophys. J. 2008, 678, 1180–1199. [Google Scholar] [CrossRef]
- Narayan, R.; SÄ dowski, A.; Penna, R.F.; Kulkarni, A.K. GRMHD simulations of magnetized advection-dominated accretion on a non-spinning black hole: Role of outflows. Mon. Not. R. Astron. Soc. 2012, 426, 3241–3259. [Google Scholar] [CrossRef]
- Sądowski, A.; Narayan, R.; Penna, R.; Zhu, Y. Energy, momentum and mass outflows and feedback from thick accretion discs around rotating black holes. Mon. Not. R. Astron. Soc. 2013, 436, 3856–3874. [Google Scholar] [CrossRef]
- Porth, O.; Chatterjee, K.; Narayan, R.; Gammie, C.F.; Mizuno, Y.; Anninos, P.; Baker, J.G.; Bugli, M.; Chan, C.k.; Davelaar, J.; et al. The Event Horizon General Relativistic Magnetohydrodynamic Code Comparison Project. Astrophys. J. Suppl. 2019, 243, 26. [Google Scholar] [CrossRef]
- Vlahakis, N.; Königl, A. Relativistic Magnetohydrodynamics with Application to Gamma-Ray Burst Outflows. I. Theory and Semianalytic Trans-Alfvénic Solutions. Astrophys. J. 2003, 596, 1080–1103. [Google Scholar] [CrossRef]
- Beskin, V.S.; Nokhrina, E.E. The effective acceleration of plasma outflow in the paraboloidal magnetic field. Mon. Not. R. Astron. Soc. 2006, 367, 375–386. [Google Scholar] [CrossRef]
- Lyubarsky, Y. Asymptotic Structure of Poynting-Dominated Jets. Astrophys. J. 2009, 698, 1570–1589. [Google Scholar] [CrossRef]
- Pu, H.Y.; Nakamura, M.; Hirotani, K.; Mizuno, Y.; Wu, K.; Asada, K. Steady General Relativistic Magnetohydrodynamic Inflow/Outflow Solution Along Large-Scale Magnetic Fields that Thread a Rotating Black Hole. Astrophys. J. 2015, 801, 56. [Google Scholar] [CrossRef]
- McKinney, J.C.; Narayan, R. Disc-jet coupling in black hole accretion systems—I. General relativistic magnetohydrodynamical models. Mon. Not. R. Astron. Soc. 2007, 375, 513–530. [Google Scholar] [CrossRef]
- Nakamura, M.; Asada, K.; Hada, K.; Pu, H.Y.; Noble, S.; Tseng, C.; Toma, K.; Kino, M.; Nagai, H.; Takahashi, K.; et al. Parabolic Jets from the Spinning Black Hole in M87. Astrophys. J. 2018, 868, 146. [Google Scholar] [CrossRef]
- McKinney, J.C.; Narayan, R. Disc-jet coupling in black hole accretion systems—II. Force-free electrodynamical models. Mon. Not. R. Astron. Soc. 2007, 375, 531–547. [Google Scholar] [CrossRef]
- Komissarov, S.S.; Barkov, M.V.; Vlahakis, N.; Königl, A. Magnetic acceleration of relativistic active galactic nucleus jets. Mon. Not. R. Astron. Soc. 2007, 380, 51–70. [Google Scholar] [CrossRef]
- Komissarov, S.S.; Vlahakis, N.; Königl, A.; Barkov, M.V. Magnetic acceleration of ultrarelativistic jets in gamma-ray burst sources. Mon. Not. R. Astron. Soc. 2009, 394, 1182–1212. [Google Scholar] [CrossRef]
- Tchekhovskoy, A.; McKinney, J.C.; Narayan, R. Simulations of ultrarelativistic magnetodynamic jets from gamma-ray burst engines. Mon. Not. R. Astron. Soc. 2008, 388, 551–572. [Google Scholar] [CrossRef]
- Tchekhovskoy, A.; Narayan, R.; McKinney, J.C. Black Hole Spin and The Radio Loud/Quiet Dichotomy of Active Galactic Nuclei. Astrophys. J. 2010, 711, 50–63. [Google Scholar] [CrossRef]
- Chatterjee, K.; Liska, M.; Tchekhovskoy, A.; Markoff, S.B. Accelerating AGN jets to parsec scales using general relativistic MHD simulations. Mon. Not. R. Astron. Soc. 2019, 490, 2200–2218. [Google Scholar] [CrossRef]
- Begelman, M.C. Instability of Toroidal Magnetic Field in Jets and Plerions. Astrophys. J. 1998, 493, 291–300. [Google Scholar] [CrossRef]
- Giannios, D.; Spruit, H.C. The role of kink instability in Poynting-flux dominated jets. Astron. Astrophys. 2006, 450, 887–898. [Google Scholar] [CrossRef]
- Mizuno, Y.; Lyubarsky, Y.; Nishikawa, K.I.; Hardee, P.E. Three-Dimensional Relativistic Magnetohydrodynamic Simulations of Current-Driven Instability. I. Instability of a Static Column. Astrophys. J. 2009, 700, 684–693. [Google Scholar] [CrossRef]
- Mizuno, Y.; Hardee, P.E.; Nishikawa, K.I. Three-dimensional Relativistic Magnetohydrodynamic Simulations of Current-driven Instability with a Sub-Alfvénic Jet: Temporal Properties. Astrophys. J. 2011, 734, 19. [Google Scholar] [CrossRef]
- Mizuno, Y.; Lyubarsky, Y.; Nishikawa, K.I.; Hardee, P.E. Three-dimensional Relativistic Magnetohydrodynamic Simulations of Current-driven Instability. III. Rotating Relativistic Jets. Astrophys. J. 2012, 757, 16. [Google Scholar] [CrossRef]
- Mizuno, Y.; Hardee, P.E.; Nishikawa, K.I. Spatial Growth of the Current-driven Instability in Relativistic Jets. Astrophys. J. 2014, 784, 167. [Google Scholar] [CrossRef]
- Singh, C.B.; Mizuno, Y.; de Gouveia Dal Pino, E.M. Spatial Growth of Current-driven Instability in Relativistic Rotating Jets and the Search for Magnetic Reconnection. Astrophys. J. 2016, 824, 48. [Google Scholar] [CrossRef]
- Kadowaki, L.H.S.; de Gouveia Dal Pino, E.M.; Medina-Torrejón, T.E.; Mizuno, Y.; Kushwaha, P. Fast Magnetic Reconnection Structures in Poynting Flux-dominated Jets. Astrophys. J. 2021, 912, 109. [Google Scholar] [CrossRef]
- Medina-Torrejón, T.E.; de Gouveia Dal Pino, E.M.; Kadowaki, L.H.S.; Kowal, G.; Singh, C.B.; Mizuno, Y. Particle Acceleration by Relativistic Magnetic Reconnection Driven by Kink Instability Turbulence in Poynting Flux-Dominated Jets. Astrophys. J. 2021, 908, 193. [Google Scholar] [CrossRef]
- Tchekhovskoy, A.; McKinney, J.C.; Narayan, R. Efficiency of Magnetic to Kinetic Energy Conversion in a Monopole Magnetosphere. Astrophys. J. 2009, 699, 1789–1808. [Google Scholar] [CrossRef]
- Komissarov, S.S.; Vlahakis, N.; Königl, A. Rarefaction acceleration of ultrarelativistic magnetized jets in gamma-ray burst sources. Mon. Not. R. Astron. Soc. 2010, 407, 17–28. [Google Scholar] [CrossRef]
- Mizuno, Y.; Gómez, J.L.; Nishikawa, K.I.; Meli, A.; Hardee, P.E.; Rezzolla, L. Recollimation Shocks in Magnetized Relativistic Jets. Astrophys. J. 2015, 809, 38. [Google Scholar] [CrossRef]
- Gómez, J.L.; Lobanov, A.P.; Bruni, G.; Kovalev, Y.Y.; Marscher, A.P.; Jorstad, S.G.; Mizuno, Y.; Bach, U.; Sokolovsky, K.V.; Anderson, J.M.; et al. Probing the Innermost Regions of AGN Jets and Their Magnetic Fields with RadioAstron. I. Imaging BL Lacertae at 21 Microarcsecond Resolution. Astrophys. J. 2016, 817, 96. [Google Scholar] [CrossRef]
- Mizuno, Y.; Younsi, Z.; Fromm, C.M.; Porth, O.; De Laurentis, M.; Olivares, H.; Falcke, H.; Kramer, M.; Rezzolla, L. The current ability to test theories of gravity with black hole shadows. Nat. Astron. 2018, 2, 585–590. [Google Scholar] [CrossRef]
- Olivares, H.; Younsi, Z.; Fromm, C.M.; De Laurentis, M.; Porth, O.; Mizuno, Y.; Falcke, H.; Kramer, M.; Rezzolla, L. How to tell an accreting boson star from a black hole. Mon. Not. R. Astron. Soc. 2020, 497, 521–535. [Google Scholar] [CrossRef]
- Igumenshchev, I.V.; Narayan, R.; Abramowicz, M.A. Three-dimensional Magnetohydrodynamic Simulations of Radiatively Inefficient Accretion Flows. Astrophys. J. 2003, 592, 1042–1059. [Google Scholar] [CrossRef]
- Igumenshchev, I.V. Magnetically Arrested Disks and the Origin of Poynting Jets: A Numerical Study. Astrophys. J. 2008, 677, 317–326. [Google Scholar] [CrossRef]
- Narayan, R.; Igumenshchev, I.V.; Abramowicz, M.A. Magnetically Arrested Disk: An Energetically Efficient Accretion Flow. Publ. Astron. Soc. Jpn. 2003, 55, L69–L72. [Google Scholar] [CrossRef]
- Tchekhovskoy, A.; McKinney, J.C. Prograde and retrograde black holes: Whose jet is more powerful? Mon. Not. R. Astron. Soc. 2012, 423, L55–L59. [Google Scholar] [CrossRef]
- McKinney, J.C.; Tchekhovskoy, A.; Blandford, R.D. General relativistic magnetohydrodynamic simulations of magnetically choked accretion flows around black holes. Mon. Not. R. Astron. Soc. 2012, 423, 3083–3117. [Google Scholar] [CrossRef]
- Tchekhovskoy, A.; Narayan, R.; McKinney, J.C. Efficient generation of jets from magnetically arrested accretion on a rapidly spinning black hole. Mon. Not. R. Astron. Soc. 2011, 418, L79–L83. [Google Scholar] [CrossRef]
- White, C.J.; Stone, J.M.; Quataert, E. A Resolution Study of Magnetically Arrested Disks. Astrophys. J. 2019, 874, 168. [Google Scholar] [CrossRef]
- Narayan, R.; Chael, A.; Chatterjee, K.; Ricarte, A.; Curd, B. Jets in Magnetically Arrested Hot Accretion Flows: Geometry, Power and Black Hole Spindown. arXiv 2021, arXiv:2108.12380. [Google Scholar]
- Fromm, C.M.; Cruz-Osorio, A.; Mizuno, Y.; Nathanail, A.; Younsi, Z.; Porth, O.; Davelaar, J.; Falke, H.; Kramer, M.; Rezzolla, L. Impact of non-thermal particles on the spectral and structural properties of M87. Astron. Astrophys. 2021, submitted.
- Dexter, J.; Jiménez-Rosales, A.; Ressler, S.M.; Tchekhovskoy, A.; Bauböck, M.; de Zeeuw, P.T.; Eisenhauer, F.; von Fellenberg, S.; Gao, F.; Genzel, R.; et al. A parameter survey of Sgr A* radiative models from GRMHD simulations with self-consistent electron heating. Mon. Not. R. Astron. Soc. 2020, 494, 4168–4186. [Google Scholar] [CrossRef]
- Porth, O.; Mizuno, Y.; Younsi, Z.; Fromm, C.M. Flares in the Galactic Centre—I. Orbiting flux tubes in magnetically arrested black hole accretion discs. Mon. Not. R. Astron. Soc. 2021, 502, 2023–2032. [Google Scholar] [CrossRef]
- Wong, G.N.; Du, Y.; Prather, B.S.; Gammie, C.F. The Jet-disk Boundary Layer in Black Hole Accretion. Astrophys. J. 2021, 914, 55. [Google Scholar] [CrossRef]
- Event Horizon Telescope Collaboration; Akiyama, K.; Algaba, J.C.; Alberdi, A.; Alef, W.; Anantua, R.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; et al. First M87 Event Horizon Telescope Results. VIII. Magnetic Field Structure near The Event Horizon. Astrophys. J. Lett. 2021, 910, L13. [Google Scholar] [CrossRef]
- Zamaninasab, M.; Clausen-Brown, E.; Savolainen, T.; Tchekhovskoy, A. Dynamically important magnetic fields near accreting supermassive black holes. Nature 2014, 510, 126–128. [Google Scholar] [CrossRef] [PubMed]
- Nemmen, R.S.; Tchekhovskoy, A. On the efficiency of jet production in radio galaxies. Mon. Not. R. Astron. Soc. 2015, 449, 316–327. [Google Scholar] [CrossRef]
- Beckwith, K.; Hawley, J.F.; Krolik, J.H. Transport of Large-Scale Poloidal Flux in Black Hole Accretion. Astrophys. J. 2009, 707, 428–445. [Google Scholar] [CrossRef]
- Barkov, M.V.; Baushev, A.N. Accretion of a massive magnetized torus on a rotating black hole. New Astron. 2011, 16, 46–56. [Google Scholar] [CrossRef]
- White, C.J.; Quataert, E.; Gammie, C.F. The Structure of Radiatively Inefficient Black Hole Accretion Flows. Astrophys. J. 2020, 891, 63. [Google Scholar] [CrossRef]
- Nathanail, A.; Fromm, C.M.; Porth, O.; Olivares, H.; Younsi, Z.; Mizuno, Y.; Rezzolla, L. Plasmoid formation in global GRMHD simulations and AGN flares. Mon. Not. R. Astron. Soc. 2020, 495, 1549–1565. [Google Scholar] [CrossRef]
- Nathanail, A.; Mpisketzis, V.; Porth, O.; Fromm, C.M.; Rezzolla, L. Magnetic reconnection and plasmoid formation in three-dimensional accretion flows around black holes. arXiv 2021, arXiv:2111.03689. [Google Scholar]
- Ripperda, B.; Bacchini, F.; Philippov, A.A. Magnetic Reconnection and Hot Spot Formation in Black Hole Accretion Disks. Astrophys. J. 2020, 900, 100. [Google Scholar] [CrossRef]
- Chashkina, A.; Bromberg, O.; Levinson, A. GRMHD simulations of BH activation by small scale magnetic loops: Formation of striped jets and active coronae. Mon. Not. R. Astron. Soc. 2021, 508, 1241–1252. [Google Scholar] [CrossRef]
- Brandenburg, A.; Nordlund, A.; Stein, R.F.; Torkelsson, U. Dynamo-generated Turbulence and Large-Scale Magnetic Fields in a Keplerian Shear Flow. Astrophys. J. 1995, 446, 741. [Google Scholar] [CrossRef]
- Liska, M.; Tchekhovskoy, A.; Quataert, E. Large-scale poloidal magnetic field dynamo leads to powerful jets in GRMHD simulations of black hole accretion with toroidal field. Mon. Not. R. Astron. Soc. 2020, 494, 3656–3662. [Google Scholar] [CrossRef]
- Komissarov, S.S. Magnetized tori around Kerr black holes: Analytic solutions with a toroidal magnetic field. Mon. Not. R. Astron. Soc. 2006, 368, 993–1000. [Google Scholar] [CrossRef]
- Wielgus, M.; Fragile, P.C.; Wang, Z.; Wilson, J. Local stability of strongly magnetized black hole tori. Mon. Not. R. Astron. Soc. 2015, 447, 3593–3601. [Google Scholar] [CrossRef]
- Fragile, P.C.; Sądowski, A. On the decay of strong magnetization in global disc simulations with toroidal fields. Mon. Not. R. Astron. Soc. 2017, 467, 1838–1843. [Google Scholar] [CrossRef]
- Bugli, M.; Guilet, J.; Müller, E.; Del Zanna, L.; Bucciantini, N.; Montero, P.J. Papaloizou-Pringle instability suppression by the magnetorotational instability in relativistic accretion discs. Mon. Not. R. Astron. Soc. 2018, 475, 108–120. [Google Scholar] [CrossRef]
- Fragile, P.C.; Blaes, O.M.; Anninos, P.; Salmonson, J.D. Global General Relativistic Magnetohydrodynamic Simulation of a Tilted Black Hole Accretion Disk. Astrophys. J. 2007, 668, 417–429. [Google Scholar] [CrossRef]
- Fragile, P.C.; Blaes, O.M. Epicyclic Motions and Standing Shocks in Numerically Simulated Tilted Black Hole Accretion Disks. Astrophys. J. 2008, 687, 757–766. [Google Scholar] [CrossRef]
- White, C.J.; Quataert, E.; Blaes, O. Tilted Disks around Black Holes: A Numerical Parameter Survey for Spin and Inclination Angle. Astrophys. J. 2019, 878, 51. [Google Scholar] [CrossRef]
- Chatterjee, K.; Younsi, Z.; Liska, M.; Tchekhovskoy, A.; Markoff, S.B.; Yoon, D.; van Eijnatten, D.; Hesp, C.; Ingram, A.; van der Klis, M.B.M. Observational signatures of disc and jet misalignment in images of accreting black holes. Mon. Not. R. Astron. Soc. 2020, 499, 362–378. [Google Scholar] [CrossRef]
- Mahadevan, R.; Quataert, E. Are Particles in Advection-dominated Accretion Flows Thermal? Astrophys. J. 1997, 490, 605–618. [Google Scholar] [CrossRef]
- Foucart, F.; Chandra, M.; Gammie, C.F.; Quataert, E. Evolution of accretion discs around a kerr black hole using extended magnetohydrodynamics. Mon. Not. R. Astron. Soc. 2016, 456, 1332–1345. [Google Scholar] [CrossRef]
- Foucart, F.; Chandra, M.; Gammie, C.F.; Quataert, E.; Tchekhovskoy, A. How important is non-ideal physics in simulations of sub-Eddington accretion on to spinning black holes? Mon. Not. R. Astron. Soc. 2017, 470, 2240–2252. [Google Scholar] [CrossRef]
- Tomei, N.; Del Zanna, L.; Bugli, M.; Bucciantini, N. General relativistic magnetohydrodynamic dynamo in thick accretion discs: Fully non-linear simulations. Mon. Not. R. Astron. Soc. 2020, 491, 2346–2359. [Google Scholar] [CrossRef]
- Bugli, M.; Del Zanna, L.; Bucciantini, N. Dynamo action in thick discs around Kerr black holes: High-order resistive GRMHD simulations. Mon. Not. R. Astron. Soc. 2014, 440, L41–L45. [Google Scholar] [CrossRef]
- Fragile, P.C.; Meier, D.L. General Relativistic Magnetohydrodynamic Simulations of the Hard State as a Magnetically Dominated Accretion Flow. Astrophys. J. 2009, 693, 771–783. [Google Scholar] [CrossRef]
- Dibi, S.; Drappeau, S.; Fragile, P.C.; Markoff, S.; Dexter, J. General relativistic magnetohydrodynamic simulations of accretion on to Sgr A*: How important are radiative losses? Mon. Not. R. Astron. Soc. 2012, 426, 1928–1939. [Google Scholar] [CrossRef]
- Yoon, D.; Chatterjee, K.; Markoff, S.B.; van Eijnatten, D.; Younsi, Z.; Liska, M.; Tchekhovskoy, A. Spectral and imaging properties of Sgr A* from high-resolution 3D GRMHD simulations with radiative cooling. Mon. Not. R. Astron. Soc. 2020, 499, 3178–3192. [Google Scholar] [CrossRef]
- Ryan, B.R.; Dolence, J.C.; Gammie, C.F. bhlight: General Relativistic Radiation Magnetohydrodynamics with Monte Carlo Transport. Astrophys. J. 2015, 807, 31. [Google Scholar] [CrossRef]
- Ryan, B.R.; Ressler, S.M.; Dolence, J.C.; Tchekhovskoy, A.; Gammie, C.; Quataert, E. The Radiative Efficiency and Spectra of Slowly Accreting Black Holes from Two-temperature GRRMHD Simulations. Astrophys. J. Lett. 2017, 844, L24. [Google Scholar] [CrossRef]
- Ryan, B.R.; Ressler, S.M.; Dolence, J.C.; Gammie, C.; Quataert, E. Two-temperature GRRMHD Simulations of M87. Astrophys. J. 2018, 864, 126. [Google Scholar] [CrossRef]
- Yao, P.Z.; Dexter, J.; Chen, A.Y.; Ryan, B.R.; Wong, G.N. Radiation GRMHD simulations of M87: Funnel properties and prospects for gap acceleration. Mon. Not. R. Astron. Soc. 2021, 507, 4864–4878. [Google Scholar] [CrossRef]
- Farris, B.D.; Li, T.K.; Liu, Y.T.; Shapiro, S.L. Relativistic radiation magnetohydrodynamics in dynamical spacetimes: Numerical methods and tests. Phys. Rev. D 2008, 78, 024023. [Google Scholar] [CrossRef]
- Fragile, P.C.; Gillespie, A.; Monahan, T.; Rodriguez, M.; Anninos, P. Numerical Simulations of Optically Thick Accretion onto a Black Hole. I. Spherical Case. Astrophys. J. Suppl. 2012, 201, 9. [Google Scholar] [CrossRef]
- Sądowski, A.; Narayan, R.; McKinney, J.C.; Tchekhovskoy, A. Numerical simulations of super-critical black hole accretion flows in general relativity. Mon. Not. R. Astron. Soc. 2014, 439, 503–520. [Google Scholar] [CrossRef]
- Sądowski, A.; Narayan, R.; Tchekhovskoy, A.; Abarca, D.; Zhu, Y.; McKinney, J.C. Global simulations of axisymmetric radiative black hole accretion discs in general relativity with a mean-field magnetic dynamo. Mon. Not. R. Astron. Soc. 2015, 447, 49–71. [Google Scholar] [CrossRef]
- McKinney, J.C.; Dai, L.; Avara, M.J. Efficiency of super-Eddington magnetically-arrested accretion. Mon. Not. R. Astron. Soc. 2015, 454, L6–L10. [Google Scholar] [CrossRef]
- Sądowski, A.; Narayan, R. Three-dimensional simulations of supercritical black hole accretion discs—Luminosities, photon trapping and variability. Mon. Not. R. Astron. Soc. 2016, 456, 3929–3947. [Google Scholar] [CrossRef]
- Mizuno, Y.; Yamada, S.; Koide, S.; Shibata, K. General Relativistic Magnetohydrodynamic Simulations of Collapsars. Astrophys. J. 2004, 606, 395–412. [Google Scholar] [CrossRef]
- Mizuno, Y.; Yamada, S.; Koide, S.; Shibata, K. General Relativistic Magnetohydrodynamic Simulations of Collapsars: Rotating Black Hole Cases. Astrophys. J. 2004, 615, 389–401. [Google Scholar] [CrossRef]
- Garain, S.K.; Balsara, D.S.; Chakrabarti, S.K.; Kim, J. Effects of Magnetic Field Loops on the Dynamics of Advective Accretion Flows and Jets around a Schwarzschild Black Hole. Astrophys. J. 2020, 888, 59. [Google Scholar] [CrossRef]
- Ressler, S.M.; Quataert, E.; White, C.J.; Blaes, O. Magnetically modified spherical accretion in GRMHD: Reconnection-driven convection and jet propagation. Mon. Not. R. Astron. Soc. 2021, 504, 6076–6095. [Google Scholar] [CrossRef]
- Ressler, S.M.; White, C.J.; Quataert, E.; Stone, J.M. Ab Initio Horizon-scale Simulations of Magnetically Arrested Accretion in Sagittarius A* Fed by Stellar Winds. Astrophys. J. Lett. 2020, 896, L6. [Google Scholar] [CrossRef]
- Ressler, S.M.; Quataert, E.; Stone, J.M. The surprisingly small impact of magnetic fields on the inner accretion flow of Sagittarius A* fueled by stellar winds. Mon. Not. R. Astron. Soc. 2020, 492, 3272–3293. [Google Scholar] [CrossRef]
- Goddi, C.; Falcke, H.; Kramer, M.; Rezzolla, L.; Brinkerink, C.; Bronzwaer, T.; Davelaar, J.R.J.; Deane, R.; de Laurentis, M.; Desvignes, G.; et al. BlackHoleCam: Fundamental physics of the galactic center. Int. J. Mod. Phys. D 2017, 26, 1730001-239. [Google Scholar] [CrossRef]
- Younsi, Z.; Zhidenko, A.; Rezzolla, L.; Konoplya, R.; Mizuno, Y. New method for shadow calculations: Application to parametrized axisymmetric black holes. Phys. Rev. D 2016, 94, 084025. [Google Scholar] [CrossRef]
- Bronzwaer, T.; Davelaar, J.; Younsi, Z.; Mościbrodzka, M.; Olivares, H.; Mizuno, Y.; Vos, J.; Falcke, H. Visibility of black hole shadows in low-luminosity AGN. Mon. Not. R. Astron. Soc. 2021, 501, 4722–4747. [Google Scholar] [CrossRef]
- Fuerst, S.V.; Wu, K. Radiation transfer of emission lines in curved space-time. Astron. Astrophys. 2004, 424, 733–746. [Google Scholar] [CrossRef]
- Noble, S.C.; Leung, P.K.; Gammie, C.F.; Book, L.G. Simulating the emission and outflows from accretion discs. Class. Quantum Gravity 2007, 24, S259–S274. [Google Scholar] [CrossRef]
- Dexter, J.; Agol, E. A Fast New Public Code for Computing Photon Orbits in a Kerr Spacetime. Astrophys. J. 2009, 696, 1616–1629. [Google Scholar] [CrossRef]
- Younsi, Z.; Wu, K.; Fuerst, S.V. General relativistic radiative transfer: Formulation and emission from structured tori around black holes. Astron. Astrophys. 2012, 545, A13. [Google Scholar] [CrossRef]
- Chan, C.k.; Psaltis, D.; Özel, F. GRay: A Massively Parallel GPU-based Code for Ray Tracing in Relativistic Spacetimes. Astrophys. J. 2013, 777, 13. [Google Scholar] [CrossRef]
- Dexter, J. A public code for general relativistic, polarised radiative transfer around spinning black holes. Mon. Not. R. Astron. Soc. 2016, 462, 115–136. [Google Scholar] [CrossRef]
- Chan, C.k.; Medeiros, L.; Özel, F.; Psaltis, D. GRay2: A General Purpose Geodesic Integrator for Kerr Spacetimes. Astrophys. J. 2018, 867, 59. [Google Scholar] [CrossRef]
- Pu, H.Y.; Yun, K.; Younsi, Z.; Yoon, S.J. Odyssey: A Public GPU-based Code for General Relativistic Radiative Transfer in Kerr Spacetime. Astrophys. J. 2016, 820, 105. [Google Scholar] [CrossRef]
- Bronzwaer, T.; Davelaar, J.; Younsi, Z.; Mościbrodzka, M.; Falcke, H.; Kramer, M.; Rezzolla, L. RAPTOR. I. Time-dependent radiative transfer in arbitrary spacetimes. Astron. Astrophys. 2018, 613, A2. [Google Scholar] [CrossRef]
- Mościbrodzka, M.; Gammie, C.F. IPOLE—Semi-analytic scheme for relativistic polarized radiative transport. Mon. Not. R. Astron. Soc. 2018, 475, 43–54. [Google Scholar] [CrossRef]
- Bronzwaer, T.; Younsi, Z.; Davelaar, J.; Falcke, H. RAPTOR. II. Polarized radiative transfer in curved spacetime. Astron. Astrophys. 2020, 641, A126. [Google Scholar] [CrossRef]
- Kawashima, T.; Ohsuga, K.; Takahashi, H.R. RAIKOU: A General Relativistic, Multi-wavelength Radiative Transfer Code. arXiv 2021, arXiv:2108.05131. [Google Scholar]
- Broderick, A.E.; Loeb, A. Imaging the Black Hole Silhouette of M87: Implications for Jet Formation and Black Hole Spin. Astrophys. J. 2009, 697, 1164–1179. [Google Scholar] [CrossRef]
- Lu, R.S.; Broderick, A.E.; Baron, F.; Monnier, J.D.; Fish, V.L.; Doeleman, S.S.; Pankratius, V. Imaging the Supermassive Black Hole Shadow and Jet Base of M87 with the Event Horizon Telescope. Astrophys. J. 2014, 788, 120. [Google Scholar] [CrossRef]
- Jeter, B.; Broderick, A.E.; Gold, R. Differentiating disc and black hole-driven jets with EHT images of variability in M87. Mon. Not. R. Astron. Soc. 2020, 493, 5606–5616. [Google Scholar] [CrossRef]
- Takahashi, K.; Toma, K.; Kino, M.; Nakamura, M.; Hada, K. Fast-spinning Black Holes Inferred from Symmetrically Limb-brightened Radio Jets. Astrophys. J. 2018, 868, 82. [Google Scholar] [CrossRef]
- Pu, H.Y.; Wu, K.; Younsi, Z.; Asada, K.; Mizuno, Y.; Nakamura, M. Observable Emission Features of Black Hole GRMHD Jets on Event Horizon Scales. Astrophys. J. 2017, 845, 160. [Google Scholar] [CrossRef]
- Shcherbakov, R.V.; Penna, R.F.; McKinney, J.C. Sagittarius A* Accretion Flow and Black Hole Parameters from General Relativistic Dynamical and Polarized Radiative Modeling. Astrophys. J. 2012, 755, 133. [Google Scholar] [CrossRef]
- Dexter, J.; McKinney, J.C.; Agol, E. The size of the jet launching region in M87. Mon. Not. R. Astron. Soc. 2012, 421, 1517–1528. [Google Scholar] [CrossRef]
- Mościbrodzka, M.; Falcke, H.; Shiokawa, H.; Gammie, C.F. Observational appearance of inefficient accretion flows and jets in 3D GRMHD simulations: Application to Sagittarius A*. Astron. Astrophys. 2014, 570, A7. [Google Scholar] [CrossRef]
- Mościbrodzka, M.; Falcke, H.; Shiokawa, H. General relativistic magnetohydrodynamical simulations of the jet in M 87. Astron. Astrophys. 2016, 586, A38. [Google Scholar] [CrossRef]
- Chan, C.K.; Psaltis, D.; Özel, F.; Narayan, R.; Sadowski, A. The Power of Imaging: Constraining the Plasma Properties of GRMHD Simulations using EHT Observations of Sgr A*. Astrophys. J. 2015, 799, 1. [Google Scholar] [CrossRef]
- Gold, R.; McKinney, J.C.; Johnson, M.D.; Doeleman, S.S. Probing the Magnetic Field Structure in Sgr A* on Black Hole Horizon Scales with Polarized Radiative Transfer Simulations. Astrophys. J. 2017, 837, 18. [Google Scholar] [CrossRef]
- Mościbrodzka, M.; Falcke, H. Coupled jet-disk model for Sagittarius A*: Explaining the flat-spectrum radio core with GRMHD simulations of jets. Astron. Astrophys. 2013, 559, L3. [Google Scholar] [CrossRef]
- Sharma, P.; Quataert, E.; Hammett, G.W.; Stone, J.M. Electron Heating in Hot Accretion Flows. Astrophys. J. 2007, 667, 714–723. [Google Scholar] [CrossRef]
- Anantua, R.; Ressler, S.; Quataert, E. On the comparison of AGN with GRMHD simulations: I. Sgr A*. Mon. Not. R. Astron. Soc. 2020, 493, 1404–1418. [Google Scholar] [CrossRef]
- Ressler, S.M.; Tchekhovskoy, A.; Quataert, E.; Chandra, M.; Gammie, C.F. Electron thermodynamics in GRMHD simulations of low-luminosity black hole accretion. Mon. Not. R. Astron. Soc. 2015, 454, 1848–1870. [Google Scholar] [CrossRef]
- Mizuno, Y.; Fromm, C.M.; Younsi, Z.; Porth, O.; Olivares, H.; Rezzolla, L. Comparison of the ion-to-electron temperature ratio prescription: GRMHD simulations with electron thermodynamics. Mon. Not. R. Astron. Soc. 2021, 506, 741–758. [Google Scholar] [CrossRef]
- Chael, A.; Narayan, R.; Johnson, M.D. Two-temperature, Magnetically Arrested Disc simulations of the jet from the supermassive black hole in M87. Mon. Not. R. Astron. Soc. 2019, 486, 2873–2895. [Google Scholar] [CrossRef]
- Chael, A.; Rowan, M.; Narayan, R.; Johnson, M.; Sironi, L. The role of electron heating physics in images and variability of the Galactic Centre black hole Sagittarius A*. Mon. Not. R. Astron. Soc. 2018, 478, 5209–5229. [Google Scholar] [CrossRef]
- Howes, G.G. A prescription for the turbulent heating of astrophysical plasmas. Mon. Not. R. Astron. Soc. 2010, 409, L104–L108. [Google Scholar] [CrossRef]
- Kawazura, Y.; Barnes, M.; Schekochihin, A.A. Thermal disequilibration of ions and electrons by collisionless plasma turbulence. Proc. Natl. Acad. Sci. USA 2019, 116, 771–776. [Google Scholar] [CrossRef]
- Rowan, M.E.; Sironi, L.; Narayan, R. Electron and Proton Heating in Transrelativistic Magnetic Reconnection. Astrophys. J. 2017, 850, 29. [Google Scholar] [CrossRef]
- Rowan, M.E.; Sironi, L.; Narayan, R. Electron and Proton Heating in Transrelativistic Guide Field Reconnection. Astrophys. J. 2019, 873, 2. [Google Scholar] [CrossRef]
- Cruz-Osorio, A.; Fromm, C.M.; Mizuno, Y.; Nathanail, A.; Younsi, Z.; Porth, O.; Davelaar, J.; Falke, H.; Kramer, M.; Rezzolla, L. Accurate energetic and morphological modelling of the launching site of the M87 jet. Nat. Astron. 2021; accepted. [Google Scholar]
- Davelaar, J.; Mościbrodzka, M.; Bronzwaer, T.; Falcke, H. General relativistic magnetohydrodynamical κ-jet models for Sagittarius A*. Astron. Astrophys. 2018, 612, A34. [Google Scholar] [CrossRef]
- Vasyliunas, V.M. A survey of low-energy electrons in the evening sector of the magnetosphere with OGO 1 and OGO 3. J. Geophys. Res. 1968, 73, 2839–2884. [Google Scholar] [CrossRef]
- Xiao, F. Modelling energetic particles by a relativistic kappa-loss-cone distribution function in plasmas. Plasma Phys. Control. Fusion 2006, 48, 203–213. [Google Scholar] [CrossRef]
- Pandya, A.; Zhang, Z.; Chandra, M.; Gammie, C.F. Polarized Synchrotron Emissivities and Absorptivities for Relativistic Thermal, Power-law, and Kappa Distribution Functions. Astrophys. J. 2016, 822, 34. [Google Scholar] [CrossRef]
- Marszewski, A.; Prather, B.S.; Joshi, A.V.; Pandya, A.; Gammie, C.F. Updated Transfer Coefficients for Magnetized Plasmas. arXiv 2021, arXiv:2108.10359. [Google Scholar] [CrossRef]
- Davelaar, J.; Olivares, H.; Porth, O.; Bronzwaer, T.; Janssen, M.; Roelofs, F.; Mizuno, Y.; Fromm, C.M.; Falcke, H.; Rezzolla, L. Modeling non-thermal emission from the jet-launching region of M 87 with adaptive mesh refinement. Astron. Astrophys. 2019, 632, A2. [Google Scholar] [CrossRef]
- Ball, D.; Sironi, L.; Özel, F. Electron and Proton Acceleration in Trans-relativistic Magnetic Reconnection: Dependence on Plasma Beta and Magnetization. Astrophys. J. 2018, 862, 80. [Google Scholar] [CrossRef]
- Kim, J.Y.; Krichbaum, T.P.; Lu, R.S.; Ros, E.; Bach, U.; Bremer, M.; de Vicente, P.; Lindqvist, M.; Zensus, J.A. The limb-brightened jet of M87 down to the 7 Schwarzschild radii scale. Astron. Astrophys. 2018, 616, A188. [Google Scholar] [CrossRef]

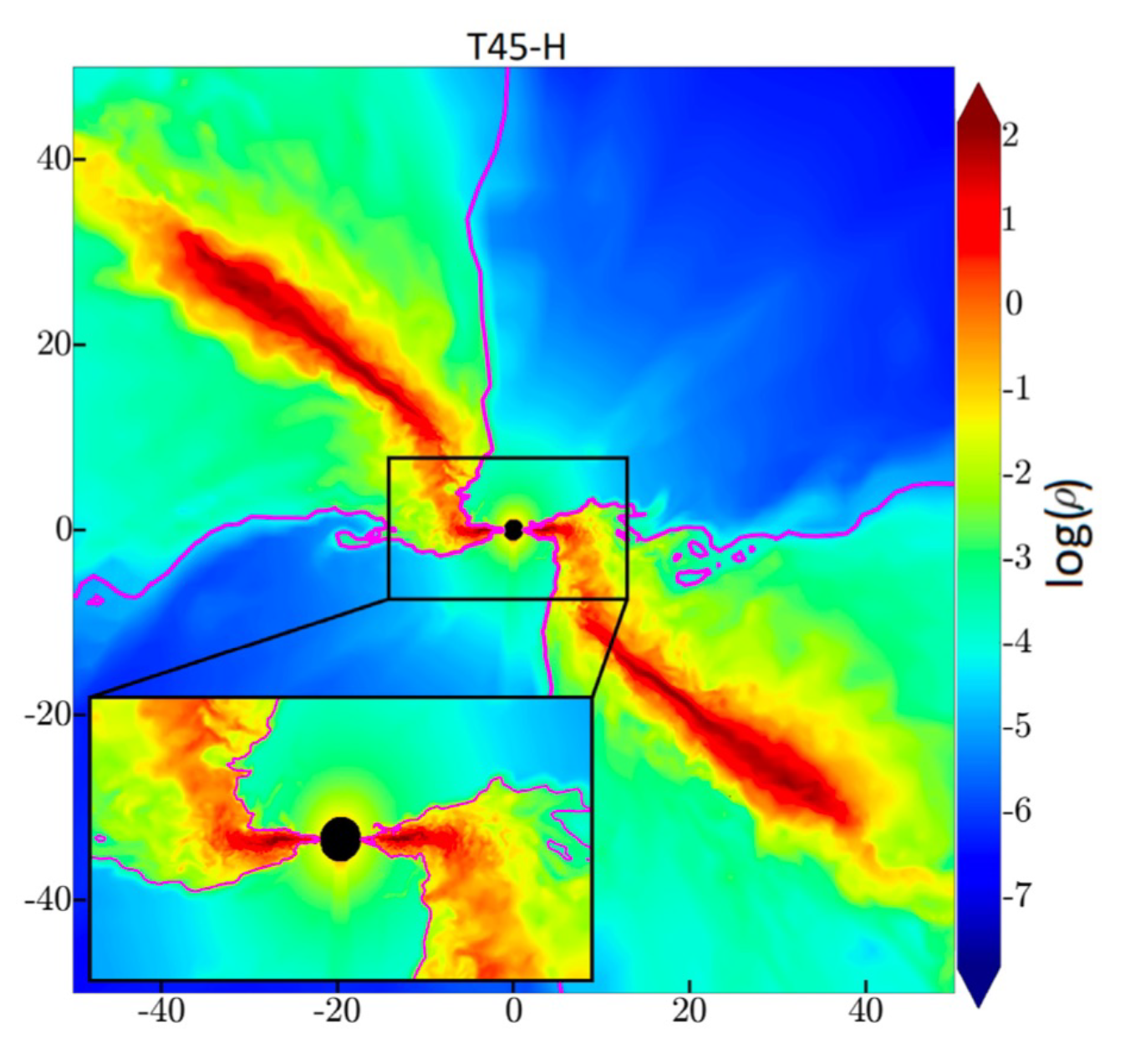


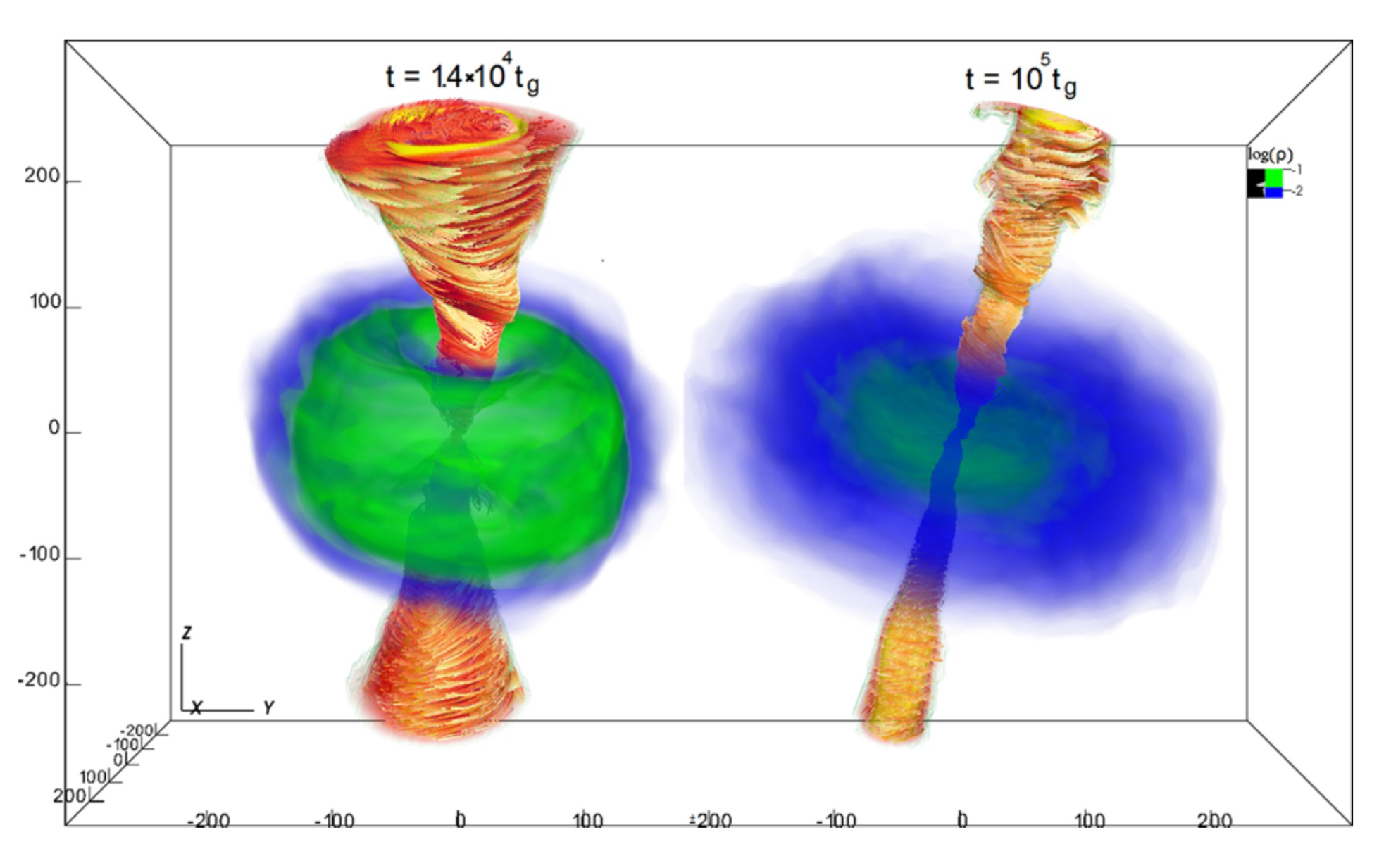


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mizuno, Y. GRMHD Simulations and Modeling for Jet Formation and Acceleration Region in AGNs. Universe 2022, 8, 85. https://doi.org/10.3390/universe8020085
Mizuno Y. GRMHD Simulations and Modeling for Jet Formation and Acceleration Region in AGNs. Universe. 2022; 8(2):85. https://doi.org/10.3390/universe8020085
Chicago/Turabian StyleMizuno, Yosuke. 2022. "GRMHD Simulations and Modeling for Jet Formation and Acceleration Region in AGNs" Universe 8, no. 2: 85. https://doi.org/10.3390/universe8020085
APA StyleMizuno, Y. (2022). GRMHD Simulations and Modeling for Jet Formation and Acceleration Region in AGNs. Universe, 8(2), 85. https://doi.org/10.3390/universe8020085





