Progress in the Simulation and Modelling of Coherent Radio Pulses from Ultra High-Energy Cosmic Particles

Abstract

In the last decade, many experiments have been planned, designed or constructed to detect Ultra High Energy showers produced by cosmic rays or neutrinos using the radio technique. This technique consists in detecting short radio pulses emitted by the showers. When the detected wavelengths are longer than typical shower length scales, the pulses are coherent. Radio emission can be simulated by adding up the contributions of all the particle showers in a coherent way. The first program to use this approach was based on an algorithm developed more than thirty years ago and referred to as “ZHS”. Since then, much progress has been obtained using the ZHS algorithm with different simulation programs to investigate pulses from showers in dense homogeneous media and the atmosphere, applying it to different experimental initiatives, and developing extensions to address different emission mechanisms or special circumstances. We here review this work, primarily led by the authors in collaboration with other scientists, illustrating the connections between different articles, and giving a pedagogical approach to most of the work.

1. Introduction

The study of High Energy particles of astrophysical origin has experienced much development in the past decades. The energy spectrum of cosmic rays is known since the 1960s to extend all the way to energies exceeding 100 EeV (1 EeV $={10}^{18}$eV) [1,2,3,4,5,6]. Cosmic rays are ionized nuclei; in their interactions with matter or radiation in space, they produce secondary neutral and charged pions that, when decaying, produce photons and neutrinos of average energies extending up to roughly $5\%$ of the energy of the constituent nucleons. Photons and neutrinos must reach Ultra High Energies (UHE), above the EeV scale, depending on the yet-unknown mass of the accelerated cosmic-ray nuclei at the highest detected energies. Neutrinos of ${10}^{15}$ eV and above, in contrast to photons, hardly have further interactions even if they are of extragalactic origin, pointing to UHE sources and tracing their production processes. For this reason, the search for neutrinos is one of the highest priorities in multi-messenger astronomy, a reality since 2017 when the coalescence of two neutron stars was spectacularly discovered with combined gravitational waves and gamma-ray detectors, and later followed up in practically all wavelengths [7].

Recent progress in UHE Cosmic-Rays (UHECR) concerning their spectrum, anisotropy of arrival directions and composition measurements [6,8,9,10] have stimulated much experimental, as well as theoretical, activity in the UHE field. Moreover, neutrinos of astrophysical origin have been detected with the IceCube neutrino observatory up to energies of order ${10}^{16}$ eV without an apparent break in the energy spectrum [11,12], which constitutes on its own a clear invitation to extend the energy range into the UHE regime. The detection of UHE neutrinos adds valuable information about the extreme processes taking place in the sources where they are produced, shedding light on the still-unknown nature and origin of UHECR.

The measured fluxes of UHECR have a very low intensity which makes detection challenging, particularly above 100 EeV. Similarly, the measured neutrino spectrum is limited at high energies by the size of the observatories. The predictions of UHE neutrino fluxes in many models make their detection a challenge because of the large target masses that are required, at least tens of Gigatons (close to a mountain 2 km high). A boost in sensitivity is intended to be achieved with the next-generation detectors for both UHE cosmic rays and neutrinos, in particular, those exploiting the so-called radio technique in dielectric media. The idea is to search for coherent, broadband and impulsive radio signals in the MHz to GHz frequency range that are emitted by electromagnetic particle cascades induced by neutrinos interacting both in a dense, dielectric and transparent medium such as ice or the lunar regolith, and in a thinner one, the atmosphere. There are ideas to search for UHE CR and neutrinos using both types of targets, with each type of target requiring very specific and different methods.

During the last two decades, there have been tremendous advances in the radio technique as a means to detect high-energy showers induced by UHECR and UHE neutrinos. These advances are rooted in a very long-term effort that started in the 1950s. As the showers develop, short electromagnetic pulses are emitted with very particular characteristics that derive from the coherent character of the emission induced by the differently charged particles in the shower. The patterns of the emission reflect the space-time distribution of the shower particles and can be used to deduce the shower properties. The potential of the technique is enormous, and as a result, many experiments are now operating, and others are being planned, designed or proposed to measure UHECR or to search for the elusive UHE neutrinos. These experiments are very diverse, ranging from antennas buried in the ice of Antarctica to satellites with antennas orbiting the Moon. This diversity of approach has been possible in part because efforts made to perform realistic calculations of these pulses have been successful, particularly those using detailed simulation programs, increasing our understanding of the emission patterns and allowing conceptual designs that exploit the potential of the technique. In Section 2, we give a non-comprehensive overview of the radio technique and its experimental and theoretical developments.

This article is not intended as a review of the radio technique and the diversity of experiments that are exploiting it. Several reviews with different emphases and dealing with different periods can be found in the literature [13,14,15,16,17,18]. Instead, this paper and in particular Section 2 will be centred on calculations of radio pulses in particle showers both in dense media and in the atmosphere. Different approaches have been followed for this purpose. Some (the so-called macroscopic models) [19,20,21,22,23] are based on analytical or numerical approximations of the currents generated by the charged particles in the shower, solving Maxwell’s equations analytically or numerically. On the other hand, there are several microscopic approaches that simulate the showers themselves [24,25,26,27,28] or sample the particle trajectories from distributions [29], and calculate the pulses as a superposition of the individual contributions to the electric field by each charged particle. Here we mainly deal with the latter, and in particular with the approach of dividing the contribution of each particle track into small steps or sub-tracks. We give a non-exhaustive description of developments of the simulation programs for coherent radio pulses from showers using an algorithm that was introduced in shower simulation programs in 1990 by one of the authors together with F. Halzen and T. Stanev [30]. This approach has been extended and continued up to date. The original program has been remarkably stable and subsequent developments were made by the authors in collaboration with many other scientists1.

This article is structured as follows. We firstly give an overview of radio developments, emphasising calculations based on simulation programs, which is followed by a section that deals with the so-called ZHS algorithm to calculate the electric field from a charged particle track both in the time and frequency domains. Section 4 is dedicated to describing the simulation codes that have used this algorithm to obtain radio pulses from cosmic-ray and neutrino-induced showers in dense media and the atmosphere, mostly ZHS and ZHAireS. In Section 5, we discuss models and parameterizations that help understand the complex radiation patterns obtained and relate them to the physical dimensions and structure of the showers as well as the position of the observer. In Section 6, we address further developments made to the simulation programs to calculate pulses in special situations such as after reflection on the ice cap of Antarctica or the calculation of transition radiation. The last section is dedicated to future prospects.

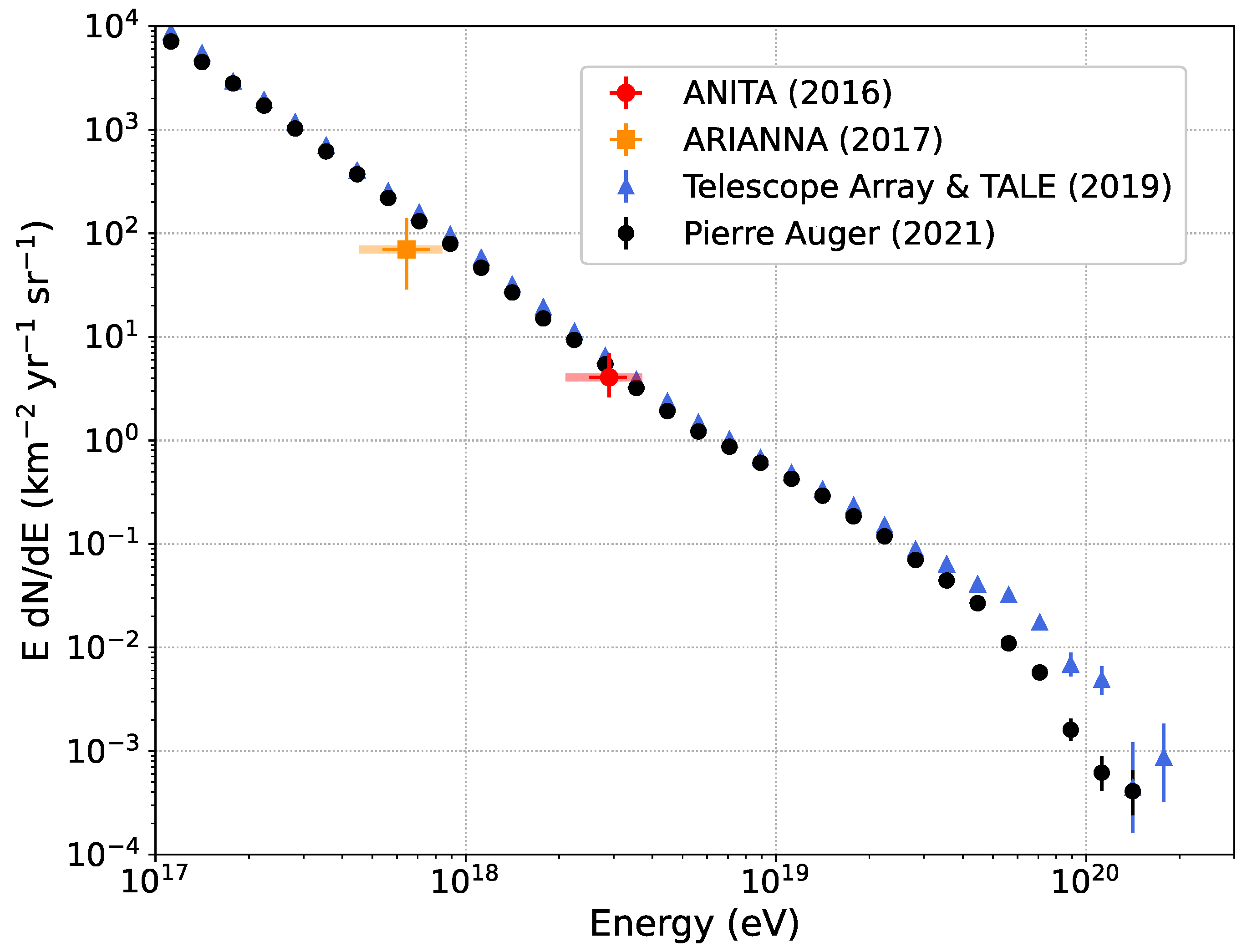
2. Progress in the Radio Technique and (the Role of) Simulation Programs

During the 1950s many efforts were made to find new techniques to detect extensive air showers produced by cosmic rays. The possibility of using the radio technique was already considered by J. Jelley in 1956 [31,32,33], relatively soon after the discovery of light pulses produced by Cherenkov radiation as the shower particles traverse the atmosphere [34]. A first but unsuccessful attempt to detect radio pulses was made by F. Graham-Smith and J. Jelley in Cambridge [35]. The possibility to search for pulses from showers that develop in dense media was suggested in parallel with a different motivation. In the early 1960s, G. Askaryan predicted a mechanism by which showers generate pulses due to a net negative charge that builds up as matter electrons are drawn into the shower and shower positrons are annihilated [36,37]. He also anticipated that coherence effects for wavelengths longer than the shower dimensions would lead to enhanced emission. In the same article, Askaryan proposed, in a visionary exercise, the possibility to use this mechanism to detect neutrino interactions both under the Earth and the Moon’s surface. Motivated by this work, in 1965, J. Jelley, N.A. Porter, T.C. Weekes, F. Graham-Smith, and R.A. Porter discovered radio pulses at 44 MHz in coincidence with an array of Geiger counters that registered air showers [38]. Multiple successful efforts followed, particularly in the UK (see [13] for a review and refs. therein), and during this early period, many of the properties of the radio pulses became understood and related to shower properties [39,40]. Besides the excess charge, several mechanisms were also suggested. Transverse currents that develop in the shower because of the geomagnetic field [41,42], often referred to as the geomagnetic effect, was shown to be the dominant mechanism in some early experiments [43,44]. Despite the successful detection of cosmic-ray showers, the community began to lose interest in the technique around 1975. This was possibly due to a combination of circumstances such as the lack of precise knowledge about the details of the emission, difficulties in obtaining systematic results between experiments, technical problems to make triggering systems with radio detectors alone, and disturbance by atmospheric effects such as the atmospheric electric fields created by distant thunderstorms [45].

While the research to improve the detection of air showers has focused on the fluorescence and Cherenkov techniques, the attractive challenge of detecting astrophysical neutrinos also using Cherenkov light in the ocean, as proposed in 1975 [46], revived the idea of Askaryan in the 1980s as an alternative [47,48]. In the early 1990s, Antarctic ice was considered a target medium to detect Cherenkov light from neutrino interactions in the AMANDA proposal [49]. Since radio waves can travel distances on the kilometre scale in cold ice, the radio technique in ice was also considered [50].

To calculate pulses in detail, a numerical algorithm was developed in 1990 by F. Halzen, T. Stanev and E. Zas [30] from first principles (Maxwell’s equations) to calculate the contributions of small particle tracks in a shower to the generation of the radio pulses. In addition, a program was also prepared to simulate electromagnetic showers in dense media [24,30], particularly in ice, capable of adding coherently the electric field contributions from all the particle tracks of the shower and thus obtaining the details of the emitted pulses2. The program was developed with special care to account accurately for the lateral deviation of the particles and their time delays since these play a crucial role in the interference effects of the radio emission from different tracks [24]. The results obtained were revealing since they quantified the excess charge in the shower to be of order 20–30%, mainly produced by Compton and Bhabha scattering with a smaller contribution from positron annihilation. The calculations reinforced the potential of the technique for the detection of high-energy showers due to the coherent properties of the emission for wavelengths comparable to the shower dimensions.

New projects to search for astrophysical neutrinos and the ZHS calculations stimulated proposals using the radio technique nearly 40 years after Askaryan’s original proposal. The first initiatives using the radio technique came to light by searching for coherent pulses on the Moon with radio telescopes [51,52] and in ice with a prototype of an antenna array, RICE [53], in synergy with the AMANDA project at the South Pole [49]. At the turn of the century, the proposed mechanism was confirmed at an accelerator experiment [54], and ZHS simulations were shown to be in agreement with uncertainties. This milestone was followed by the ANtartic Impulsive Transient Antenna (ANITA) project [55], a multiple antenna system flown in a super-pressure balloon to the stratosphere and designed to detect pulses produced by neutrinos interacting under the ice cap. The prototype flight, ANITA-lite, provided the first competitive flux bounds with the radio technique [56] in 2004. More importantly, the first ANITA flight led to the serendipitous measurement of radio pulses induced by cosmic-ray showers, most of them from downward-going showers after reflection on the surface of the ice cap [57]. Even though shower pulses had been detected in the atmosphere above 500 MHz in the 1960s [58,59], the detection of cosmic rays came as a surprise because the ANITA system was pointing down to the ice, and moreover, it was designed to work in a radio band from 200 MHz to 1.2 GHz, corresponding to wavelengths much smaller than the shower dimensions, so that the coherence from different shower regions was expected to be washed out [60]. ANITA pulses were later shown to be consistent with the geomagnetic and excess charge emission mechanisms of the air showers [61].

Other initiatives to measure radio pulses in the atmosphere were also developed at the turn of the century. The LOPES antenna array [62] located in Karlsruhe, Germany, in coincidence with KASCADE, a reference air shower particle array, was a successful prototype setup [63] constructed to study the viability as a shower detector of the existing low-frequency radio astronomical array LOFAR [64,65]. The CODALEMA [66] radio array was a dedicated installation of antennas with a small scintillator surface array in Nançay, France.

In parallel, attempts were made to calculate the radio pulses in the atmosphere using both Monte Carlo simulations [67,68], based on coherent geo-synchrotron radiation of shower particles [69], and analytic approximations of the transverse currents generated in the magnetic field of the Earth [20,21]. The two approaches gave qualitatively different pulses, and the theoretical situation remained unresolved for a while, with the latter providing a better description of the pulses. On the experimental side, more initiatives were undertaken, such as the search for cosmic-ray showers with LOFAR [65], Tunka-Rex [70,71], and the construction of new R&D radio installations within the Pierre Auger Observatory, namely RAuger [72] and, most importantly, AERA [73].

While pulses in different media had been studied in detail using ZHS, the simulation setup was limited to electromagnetic showers, it did not account for the magnetic field and was only valid for homogeneous media. These limitations were bypassed through the exportation of the algorithm (ZHS) to calculate the electric field from sub-track contributions to a standard shower simulation program, AIRES [74], to give ZHAireS [25]. These simulations rapidly confirmed the bipolar structure of the pulse obtained in analytical approaches. In parallel, a similar approach was undertaken based on the CORSIKA code [75], another state-of-the-art simulation program for air showers, implementing a very similar approach for radio pulses, the “end-point” algorithm [76]. This was used to produce first REAS3 [26] and, later on, CoREAS [28] which accounts for the variable refractive index of the atmosphere. Simulations made with ZHAireS and CoREAS give consistent results between themselves [77] and when compared to data [78,79]. Both are at present the two reference simulation codes for radio pulses from air showers.

After these simulation tools were developed, the fidelity of the pulse simulation could be soon confirmed indirectly because it allowed detailed shower simulation and reconstruction of data from three (among other) experiments that led to outstanding results. An independent measurement of the EeV cosmic-ray spectrum was obtained by reconstructing the ANITA cosmic-ray events [61] (see Figure 9 in Section 6.1), showing that shower reconstruction was possible using antennas in a single location. The potential of radio measurements to measure the position of the shower maximum was shown using LOFAR data [80], and recently with AERA [81], demonstrating that the technique had potential for composition measurements. A strong correlation was found between the emitted energy in the 30-80 MHz frequency band measured with AERA and the shower energy measured with the Pierre Auger Observatory data [79]. This gave prospects that the radio technique would provide an independent and reliable energy calibration method for air showers, which is likely to be one of the next big advances to follow.

The radio technique has received a lot of attention lately because subsequent studies of ANITA data (flights I [82], III [83] and IV [84]) revealed a few “anomalous” events coming from the surface of the ice with dominantly horizontal polarization, that is consistent with showers that develop in the air with the emission dominated by the geomagnetic mechanism. These events do not have the polarity inversion that is expected as the pulses are reflected on the ice cap, and for this reason, they are, in principle, consistent with showers developing upwards, such as those that could be expected from the decay of exiting tau leptons produced by charged current neutrino interactions within the ice cap. However, in this hypothesis, the deduced neutrino fluxes under Standard Model assumptions are comfortably ruled out by flux limits obtained both with the Pierre Auger cosmic-ray Observatory in Argentina [85], with the IceCube neutrino detector at the South Pole [86], and with the search for pulses from neutrino-induced showers inside the ice cap with ANITA itself [87]. Many theoretical interpretations of the origin of these pulses have been put forward, often invoking physics beyond the Standard Model (see [88] for a review), and the explanation still remains a mystery.

In the last years, an explosion of initiatives has followed to search for high-energy showers both in dense media, such as ice [15] or the lunar regolith [89], and in the atmosphere, driven by UHECR studies and by UHE neutrino searches (see [15,16,17,18] for recent reviews). While dense media are attractive for neutrino searches, they can be also used to detect cosmic rays, for instance, by searching for radio pulses produced just under the Moon’s surface [89]. Similarly, while air showers are natural to study cosmic rays, they can also be used to search for neutrino interactions, particularly for tau leptons that exit the Earth after a charged current interaction turns a tau neutrino into a tau lepton just below the surface [90,91].

This field is mature enough to be rapidly growing with new planned experimental setups [92,93,94,95,96,97,98], but at the same time, there are still aspects that require further development, such as exploring other mechanisms leading to coherent pulses like transition radiation [99,100], or the full development of dedicated interferometric approaches [101] that are likely to provide new opportunities for the future.

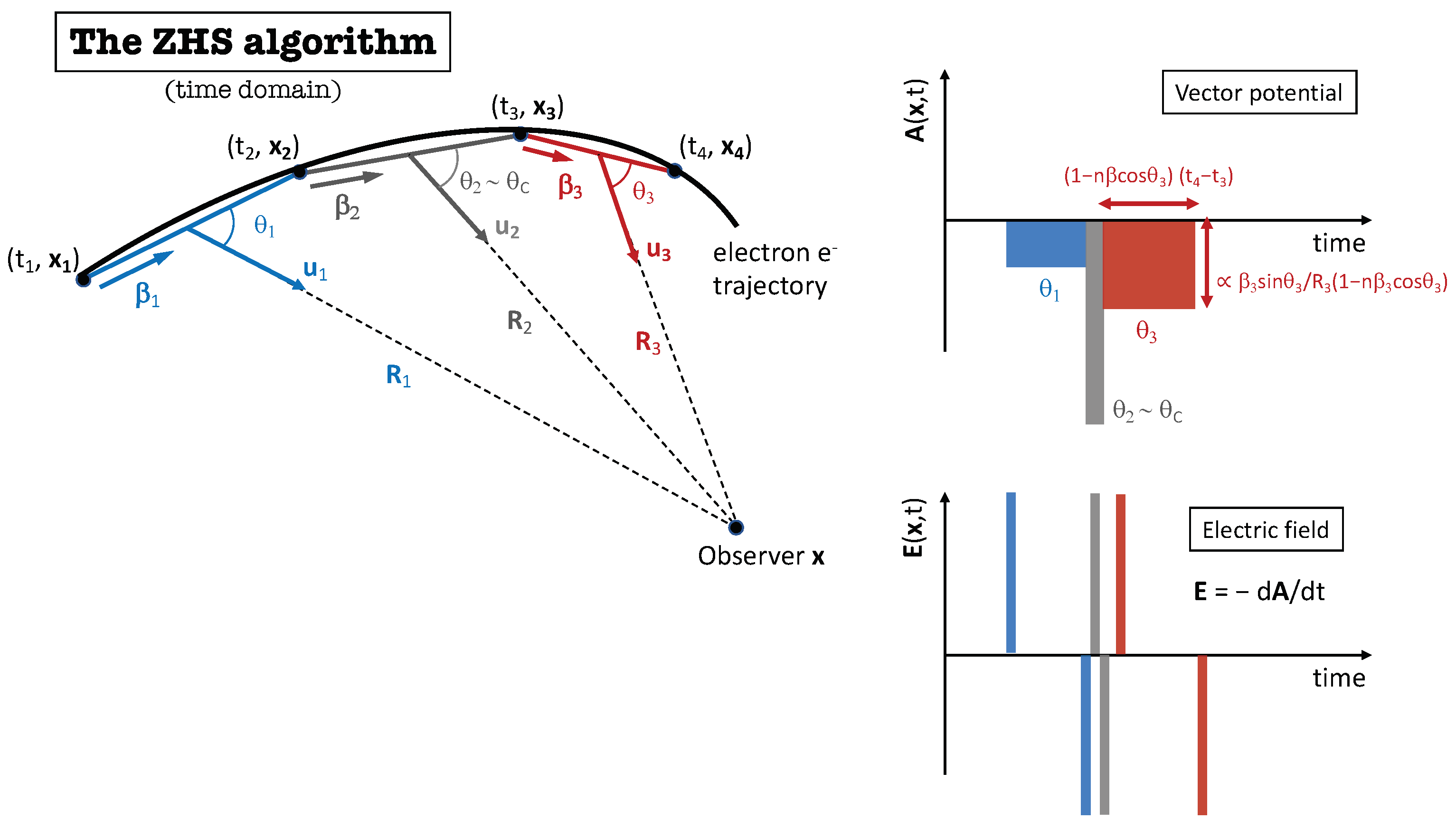
3. Radiation from Particle Tracks in a Medium: The ZHS Algorithm

When shower particles go through a medium, they induce radiation due to interactions with the particles in the medium. Since shower particles are typically travelling at speeds higher than that of light in the medium, Cherenkov radiation is expected. This radiation extends beyond the optical band, into radio frequencies in transparent media such as ice, air, sand, salt, and the lunar regolith. Attenuation lengths of radio waves in these materials are also long enough to make them attractive for particle detection. For sufficiently long wavelengths, the induced emission becomes coherent and shock pulses are generated in the Cherenkov direction. This applies not only to Cherenkov radiation but to any sort of radiation. Since the early days, several other mechanisms have also been invoked such as Coulomb-field bremsstrahlung, transition radiation, synchrotron radiation, and transverse currents induced by the geomagnetic field (also referred to as dipole Cherenkov radiation) [102]. The fact is that all these mechanisms stem from Maxwell’s equations, and their separation is sometimes artificial. In all these cases, at low frequencies the emission is coherent, and the electric field intensity of these pulses increases linearly with the number of shower particles, scaling with the shower energy so that it becomes favourable to detect high-energy showers.

To calculate the radiation from a charged particle trajectory (belonging for instance to a particle shower), the problem is split using the superposition principle of electromagnetism into the contributions of a number of arbitrarily small sub-tracks, in which individual particles are assumed to be travelling at a constant speed. It is assumed that, provided the track is sufficiently small, several approximations can be made to calculate the emission (see below). In this approach, the electric field is simply obtained by summing the contributions from all the sub-tracks of the shower taking into account their relative phases (times) when working in the frequency (time) domain.

The formula to obtain the contribution of the electric field to the total radiated pulse of a small sub-track was originally obtained in the frequency domain [24]. Working in the frequency domain turned out to be more adequate to relate the apparent diffractive properties of the pulse as a function of frequency to the physical dimensions of the shower. It was only much later that the algorithm was addressed in the time domain [25], which has other advantages and is easier to implement numerically. The two approaches have been shown to be completely equivalent in [25].

3.1. Time Domain

Radiation produced within a linear, homogeneous and isotropic medium can be calculated with Maxwell’s equations in matter, in which the induced current and polarization effects are automatically considered by the displacement field, $\mathbf{D}={ϵ}_r{ϵ}_0\mathbf{E}$, and by the magnetizing field, $\mathbf{H}={\left({\mu }_r{\mu }_0\right)}^{-1}\mathbf{B}$, where $\mathbf{E}$ and $\mathbf{B}$ are respectively the electric and magnetic fields, and ${\mu }_r$$\left({\mu }_0\right)$ and ${ϵ}_r$$\left({ϵ}_0\right)$ are respectively the relative (free space) permeability and permittivity. The corresponding speed of light in the medium is that of vacuum c divided by the refractive index $n=\sqrt{{ϵ}_r{\mu }_r}$.

The electric and magnetic fields can be formally obtained by introducing the vector ($\mathbf{A}$) and scalar potentials ($\varphi$):

$$\begin{array}{cc}\hfill \mathbf{B}& =\nabla \times \mathbf{A}\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill \mathbf{E}& =-\frac{\partial \mathbf{A}}{\partial t}-\nabla \varphi ,\hfill \end{array}$$

(2)

that, by construction, satisfy $\nabla ·\mathbf{B}=0$ and $\nabla \times \mathbf{E}=-\frac{\partial \mathbf{B}}{\partial t}$. In the transverse gauge ($\nabla ·\mathbf{A}=0$), the two remaining Maxwell’s equations become:

$$\begin{array}{cc}\hfill {\nabla }^2\varphi & =-\frac{\rho }{ϵ}\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill {\nabla }^2\mathbf{A}-\mu ϵ\frac{{\partial }^2\mathbf{A}}{{\partial }^{2}t}& =-\mu {\mathbf{J}}_{\perp },\hfill \end{array}$$

(4)

where ${\mathbf{J}}_{\perp }$ is the divergenceless component of the current, also referred to as the transverse current because, in the limit of observation at large distances from the source, it can be shown to correspond to the component of the current density perpendicular to the direction of observation (specified by a unit vector $\widehat{\mathbf{u}}$), i.e., ${\mathbf{J}}_{\perp }=-\widehat{\mathbf{u}}\times (\widehat{\mathbf{u}}\times \mathbf{J})$.

Maxwell’s equations for $\varphi$ and $\mathbf{A}$ can be solved using Green’s functions. For the electrostatic potential, this gives the familiar solution of Poisson’s equation, as a space integral of the instantaneous charge distribution $\rho ({\mathbf{x}}^{\prime },t)$ at a space-time position $({\mathbf{x}}^{\prime },t)$:

$$\begin{array}{cc}\hfill \varphi (\mathbf{x},t)& =\frac{1}{4\pi ϵ}\int \frac{\rho ({\mathbf{x}}^{\prime },t)}{|\mathbf{x}-{\mathbf{x}}^{\prime }|}{d}^3{\mathbf{x}}^{\prime },\hfill \end{array}$$

with $(\mathbf{x},t)$ the observer’s position and time.

For the vector potential, the solution of the wave equation gives:

$$\begin{array}{cc}\hfill \mathbf{A}(\mathbf{x},t)& =\frac{\mu }{4\pi }\int \frac{{\mathbf{J}}_{\perp }({\mathbf{x}}^{\prime },t^{\prime })}{|\mathbf{x}-{\mathbf{x}}^{\prime }|}\delta \left(\sqrt{\mu ϵ}|\mathbf{x}-{\mathbf{x}}^{\prime }|-(t-t^{\prime })\right)d^3{\mathbf{x}}^{\prime }d{t}^{\prime }.\hfill \end{array}$$

(5)

The $\delta$-function in Equation (5) gives the familiar retarded condition for the space integral. To calculate the vector potential at a given time t in the observing position $\mathbf{x}$, the current at the position ${\mathbf{x}}^{\prime }$ needs to be evaluated at time $t^{\prime }$ so that the time interval $(t-t^{\prime })$ equals the travel time from ${\mathbf{x}}^{\prime }$ to $\mathbf{x}$ at the speed of light $c/n$ in the medium.

We consider a track corresponding to a particle moving at constant velocity $\mathbf{v}$ between two points at times $t_1$ and $t_2$, and, without loss of generality, take the equation of motion so that a point ${\mathbf{x}}_{\mathbf{0}}^{\prime }$ of the track corresponds to $t=0$. At large distances, the resulting transverse current density entering in Equation (5) reads:

$${\mathbf{J}}_{\perp }({\mathbf{x}}^{\prime },t^{\prime })=e{\mathbf{v}}_{\perp }{\delta }^3\left({\mathbf{x}}^{\prime }-{\mathbf{x}}_{\mathbf{0}}^{\prime }-\mathbf{v}{t}^{\prime }\right)\left[\Theta (t^{\prime }-t_1)-\Theta (t^{\prime }-t_2)\right],$$

(6)

where $-e$ is the charge of an electron, ${\mathbf{v}}_{\perp }=-\widehat{\mathbf{u}}\times (\widehat{\mathbf{u}}\times \mathbf{v})$ is the projection of the velocity onto a plane perpendicular to $\widehat{\mathbf{u}}$ and $\Theta \left(x\right)$ is the Heaviside step function. We note that $|{\mathbf{v}}_{\perp }|=vsin\theta$, with $\theta$ the observation angle relative to the particle track (between $\mathbf{v}$ and $\widehat{\mathbf{u}}$) given by $cos\theta =\widehat{\mathbf{u}}·\widehat{\mathbf{v}}$.

Substituting ${\mathbf{J}}_{\perp }$ into Equation (5), we can obtain a simple expression in the Fraunhofer limit. In this limit, the distance $|\mathbf{x}-{\mathbf{x}}^{\prime }| = |\mathbf{x}-{\mathbf{x}}_{\mathbf{0}}^{\prime }-\mathbf{v}{t}^{\prime }|$ is simply approximated by $R-\mathbf{v}·\widehat{\mathbf{u}}{t}^{\prime }$ with $R=|\mathbf{x}-{\mathbf{x}}_{\mathbf{0}}^{\prime }|$, and taking the observation distance $|\mathbf{x}-{\mathbf{x}}^{\prime }| \simeq R$ in the denominator as a constant but accounting for the time delays between contributions from different points of the sub-track. It is easy to show [25] that the resulting $\delta$-function in Equation (5) can be written as:

$$\delta \left(t^{\prime }(1-n\beta cos\theta )-(t-\frac{nR}{c})\right)=\frac{1}{|1-n\beta cos\theta |}\delta \left(t^{\prime }-\frac{t-\frac{nR}{c}}{1-n\beta cos\theta }\right).$$

(7)

The factor $(1-n\beta cos\theta )$ becomes zero for observation at the Cherenkov angle ${\theta }_C$ defined as $cos{\theta }_C=1/n\beta$. With the $\delta$-function expressed in this form, integration implies replacing $t^{\prime }$ in the two-step functions of ${\mathbf{J}}_{\perp }({\mathbf{x}}^{\prime },t^{\prime })$ in Equation (6) by $\frac{t-nR/c}{1-n\beta cos\theta }$. There is a subtlety with the sign. As the observation angle changes from being larger to smaller than the Cherenkov angle, the $(1-n\beta cos\theta )$-factor changes sign from positive to negative. The standard property of the $\Theta$-function:

$$\Theta \left(ax\right)=\left\{\begin{array}{c}\Theta \left(x\right)\mathrm{if}a>0,\hfill \\ 1-\Theta \left(x\right)\mathrm{if}a<0\hfill \end{array}\right.$$

applies because here $a={(1-n\beta cos\theta )}^{-1}$ changes sign. This implies a change of sign in the numerator involving the difference of the two-step functions of Equation (6) that compensates for the implicit change of sign of the modulus operation that appears in the denominator of Equation (7), so that Equation (5) becomes:

$$\mathbf{A}=\frac{\mu e}{4\pi R}{\mathbf{v}}_{\perp }\frac{\Theta (t-\frac{nR}{c}-(1-n\beta cos\theta )t_1)-\Theta (t-\frac{nR}{c}-(1-n\beta cos\theta )t_2)}{(1-n\beta cos\theta )}.$$

(8)

Equation (8) states that the contribution of a single straight charged-particle track is simply a top-hat function with a time interval between the two edges given by $(1-n\beta cos\theta )\delta t$, which is proportional to the time interval between the endpoints of the track $\delta t=t_2-t_1$. The normalization factor, $(1-n\beta cos\theta )$, reduces the time interval as the observation angle approaches the Cherenkov direction so that it becomes zero at ${\theta }_C$. This is illustrated in Figure 1, where three sub-tracks give different contributions to the vector potential at the observer’s position depending on the viewing angle of the sub-track as seen by the observer.

The electric field is given by minus the time derivative of the vector potential, see Equation (2). Differentiating the top-hat function in Equation (8) gives two $\delta$-functions of opposite sign at each end of the particle track, as illustrated in Figure 1. Because of the negative sign of the time derivative of $\mathbf{A}$, the first pulse is negative while the second is positive. This, in turn, defines the polarity of the bipolar pulse obtained.

Equation (8) has a well-defined limit as $\theta$ approaches the Cherenkov angle. Multiplying and dividing by $\delta t=t_2-t_1$, the formal definition of the $\delta$-function is obtained3:

$$R\mathbf{A}(t,{\theta }_C)=\left[\frac{e{\mu }_r}{4\pi {ϵ}_0{c}^2}\right]\delta \left(t-\frac{nR}{c}\right){\mathbf{v}}_{\perp }\delta t.$$

(9)

Differentiation of the $\delta$-function in Equation (9) must be interpreted as the limiting case of the derivative of a top-hat function when the time interval between the two $\Theta$-functions goes to zero. In the limit, two opposite $\delta$-functions are obtained, separated now by an infinitesimal time interval as $(1-n\beta cos\theta )\delta t$ tends to zero. There is continuity; as $\theta$ approaches ${\theta }_C$, the time difference between the two opposite pulses associated to the end points of the track shrinks and becomes zero in the limit.

A technical problem arises in the numerical evaluation of the $\delta$-function that is ill-defined. The solution is to replace it with top-hat functions of small but finite time width. The receiving system always has a limited bandwidth, and time variations cannot be much smaller than the inverse of the highest frequency. By choosing a sufficiently small time width for the approximation, which is well below the inverse high-frequency limit of the system, the results are guaranteed to give reliable electric field amplitudes [25]. If one is interested in the actual pulse, there are other limiting factors for the large frequency components, due to the linear response of the medium breaking down, a limited acceleration of the charges or quantum mechanical effects.

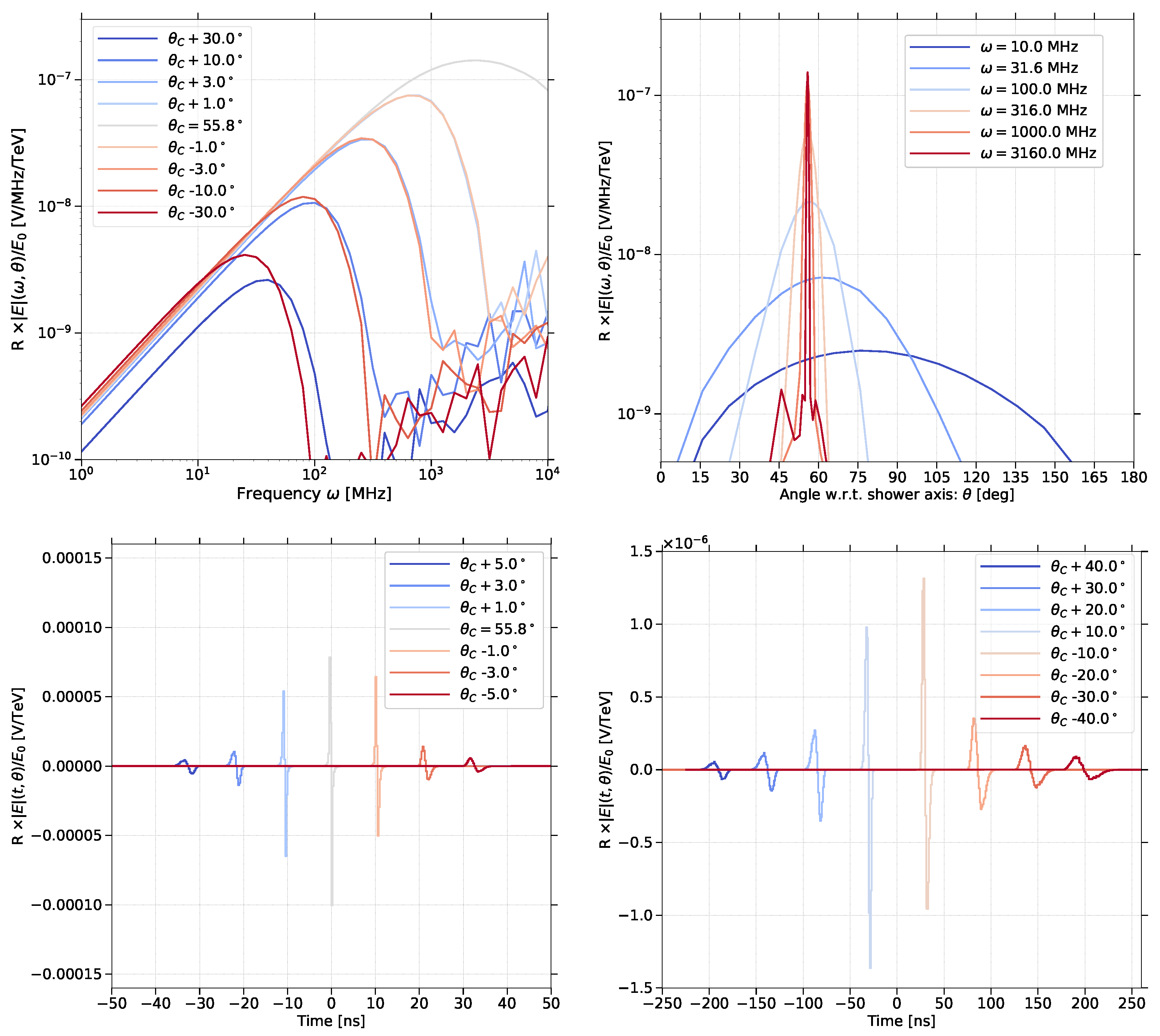
3.2. Frequency Domain

The expression for the electric field of a straight and finite charged-particle track can be also obtained directly in the frequency domain [24]. Here it is easier to take the time derivative of Equation (8) first and then Fourier-transform it. Following the (unusual) convention in ref. [24]4

$$\tilde{f}\left(\omega \right)=2{\int }_{-\infty }^{\infty }f\left(t\right)e^{i\omega t}dt,$$

it is straightforward to get:

$$\mathbf{E}(\omega ,\mathbf{x})=-\frac{e\mu }{2\pi }\frac{1}{R}{\mathbf{v}}_{\perp }\frac{{\mathrm{e}}^{i\omega \left[\frac{nR}{c}+(1-n\beta cos\theta )\right]{\mathrm{t}}_1}-{\mathrm{e}}^{i\omega \left[\frac{nR}{c}+(1-n\beta cos\theta )\right]{\mathrm{t}}_2}}{(1-n\beta cos\theta )}.$$

(10)

Using $k=\frac{n\omega }{c}$, Equation (10) is equivalent to the original expression, Equation (12) in Ref. [24]:

$$\mathbf{E}(\omega ,\mathbf{x})=\frac{e{\mu }_r}{2\pi {ϵ}_0{\mathrm{c}}^2}i\omega \frac{{\mathrm{e}}^{ikR}}{R}{\mathrm{e}}^{i(\omega -\mathbf{k}·\mathbf{v}){\mathrm{t}}_1}{\mathbf{v}}_{\perp }\left[\frac{{\mathrm{e}}^{i(\omega -\mathbf{k}·\mathbf{v})\delta \mathrm{t}}-1}{i(\omega -\mathbf{k}·\mathbf{v})}\right].$$

(11)

As can be seen in Equation (10), there are two terms for each sub-track corresponding to the start and the endpoints. It is straightforward to see that if a long straight track of uniform velocity is separated into several sub-tracks, the contribution from the ending point of one sub-track and the starting point of the next sub-track cancel out completely in the Fraunhofer approximation. As a result, we end up with only two terms contributing to the electric field, corresponding to the starting and ending points of the original long track. It also follows that when the particle velocity changes from one sub-track to the next, the cancellation will not be complete, leading to radiated power. If the particle changes its direction interacting with an external magnetic field, it would lead to synchrotron emission, and to bremsstrahlung if it reduces speed. Similarly, if the particle crosses an interface between two media, the boundary conditions can be satisfied with reflected and refracted rays giving rise to transition radiation [99].

The limiting case of Equation (11) in the Cherenkov direction can be obtained by taking the transform of Equation (9) and then multiplying it by $i\omega$ (corresponding to minus the time derivative of the vector potential in the time domain) to give Equation (13) in Ref. [24]:

$$\mathbf{E}(\omega ,\mathbf{x})=\frac{e{\mu }_r}{2\pi {ϵ}_0{\mathrm{c}}^2}\frac{{\mathrm{e}}^{ikR}}{R}{\mathrm{e}}^{i(\omega {\mathrm{t}}_1-\mathbf{k}{\mathbf{x}}_1)}{\mathbf{v}}_{\perp }\delta t.$$

(12)

The electric field amplitude in this limit is proportional (and parallel) to ${\mathbf{v}}_{\perp }\delta t$, i.e., to the projection of the displacement vector onto a plane perpendicular to the observation direction. The contribution to the electric field for an observer in the Cherenkov angle becomes proportional to the total projected track corresponding to the sum of the contributions from all the sub-tracks, as could be expected. Proportionality with the tracklength is characteristic of Cherenkov radiation. It can be shown that the expression for the emission, when converted to radiated power and integrated in a solid angle, leads precisely to the well-known Frank-Tamm’s result [24,103] in the limit of a very large track with uniform velocity. This radiation cannot be separated from Cherenkov radiation.

Expressions (11) and (12) can be directly used to calculate the radio pulse in a shower simulation in the frequency domain. Early work between 1990 and 2010 was exclusively done in the frequency domain, and no further numerical approximations were needed in contrast with the delta function in the time-domain expressions.

3.3. Comparison with the “Endpoints Formulation”

Soon after the calculation of ZHS in the time domain, a similar methodology was presented under the name of “endpoint formulation” [76], emphasizing its potential to calculate the radiation arising from different mechanisms, such as synchrotron, bremsstrahlung and transition radiation. This approach singles out each “acceleration” event at the two endpoints of a sub-track that are treated independently. Particle motion is described by a series of discrete instantaneous acceleration events. In this respect, the methodology is in essence similar to the ZHS one, only that the two terms that appear in the ZHS expression are interpreted as acceleration and deceleration terms in this approach. A practical difference, when used in a shower simulation, is that in the ZHS algorithm the $R^{-1}$ attenuation that is applied to the two terms in the expression for a sub-track is the same (usually taken for the midpoint of the track), while in the endpoints formulation a different value of $R_i$ is independently calculated for each endpoint. In the limit of large R, the difference between the two approaches vanishes, but for sub-tracks that are not short compared to R, there can be numerical differences. In the time-domain implementation of the ZHS algorithm, first, the vector potentials are calculated and summed, and then the time-derivative is taken to calculate the fields (as illustrated in Figure 1) while, equivalently, in the endpoints methodology, the electric fields are calculated and summed directly without obtaining first the vector potentials.

More importantly, when the Cherenkov factor $(1-n\beta \mathrm{c}\mathrm{o}\mathrm{s} \theta )$ becomes zero in the limit $\theta \to {\theta }_C$, only in the ZHS approach the correct and finite limit can be taken [104]. As a result, the shower simulation programs that implement the endpoints algorithm require the use of the ZHS expressions for sub-tracks in which the Cherenkov factor is close to zero, given by Equation (12) in the frequency domain and by minus the time derivative of Equation (9) in the time domain. It is thus not surprising that both formulations, having the same limit as the sub-tracks tend to zero, are able to equivalently describe different radiation mechanisms.

3.4. Comparison with Exact Calculations

The ZHS expressions in Section 3 can also be obtained directly from the exact results for the electromagnetic fields of a finite rectilinear track of a uniformly moving charged particle as obtained in [104]. This tour de force exercise confirmed that the ZHS algorithm does also take into account Cherenkov radiation in contrast to [76] (see also [105]).

Moreover, the exact results for the electromagnetic fields also served to explore the limitations and range of applicability and validity of the ZHS formalism [104], clearly establishing the approximations required to convert the exact calculation into the ZHS expressions. These approximations are:

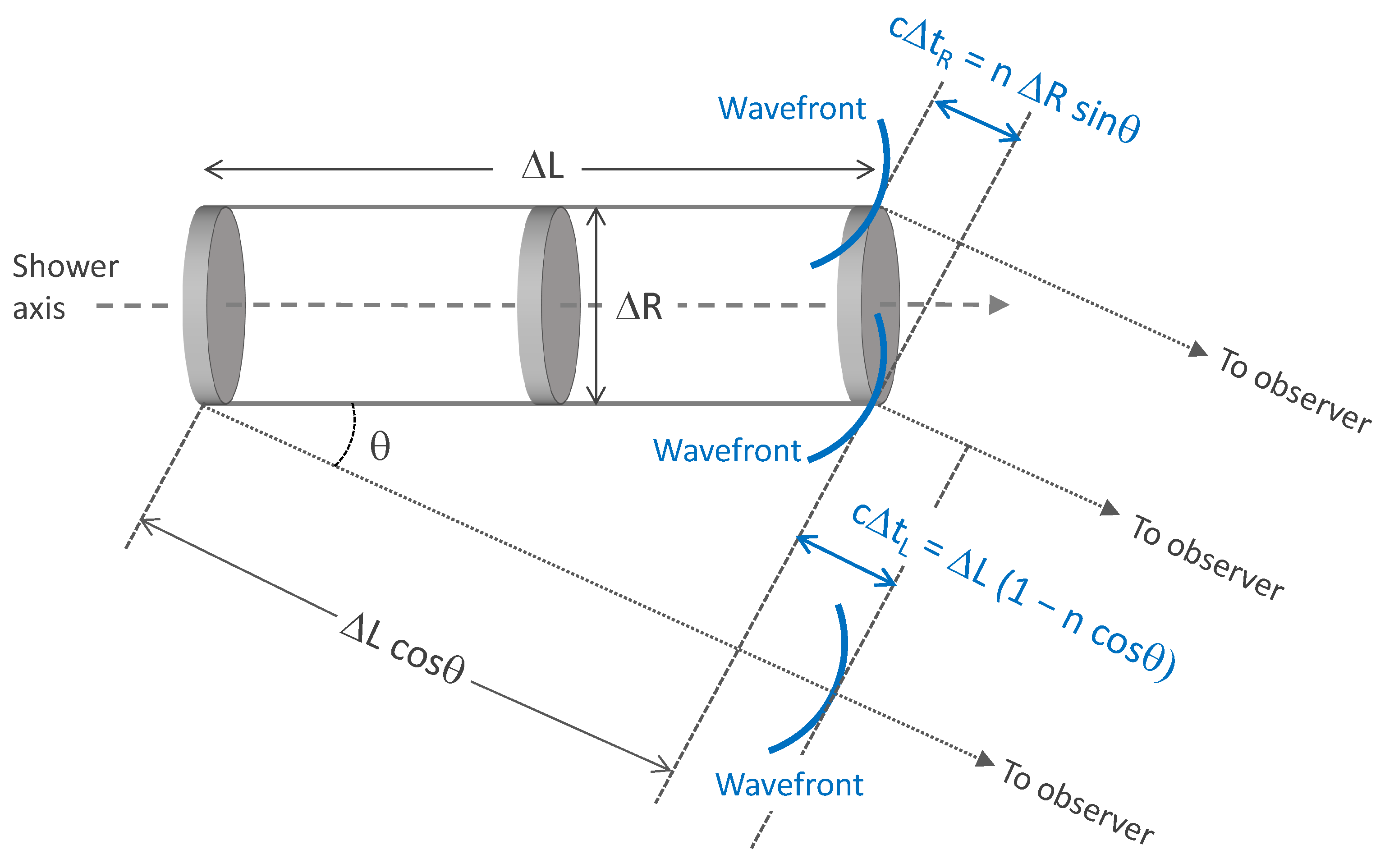
• The observer must be in the "far field" zone, what implies that $kr\simeq kR\gg 1$ where $r=|\mathbf{x}-{\mathbf{x}}^{\prime }|$ is the distance between an arbitrary point of the sub-track ${\mathbf{x}}^{\prime }$ and the observation point at $\mathbf{x}$.
• The distance between points of the sub-track and the observation point must be well approximated by a constant R. The normalization of the electric field is given by $1/r$, so clearly the error is below $L\mathrm{c}\mathrm{o}\mathrm{s} \theta /R$, where $\mathbf{L}$ is the vector that defines the length and direction of the sub-track, and $\theta$ the observation angle relative to the track direction.
• The Fraunhofer condition must hold within the sub-track, that is $kr=k|\mathbf{x}-{\mathbf{x}}^{\prime }|$ with $k=\omega n/c$ should be well approximated by $k(R-\mathbf{L}·\widehat{\mathbf{u}})$ in the calculation of time delays (or phases). This implies that $k{L}^2\mathrm{s}\mathrm{i}{\mathrm{n}}^2 \theta <<R$.

Exact results can be evaluated numerically and have been compared to those obtained using the ZHS calculation to check the range of validity and the accuracy of the approximations.

The first condition is an intrinsic limitation of the ZHS algorithm. For low frequencies and/or small distances that do not satisfy this criterion, a different approximation or the exact expression must be used to include Coulomb terms. For instance, for a frequency $\nu =10$ MHz, the error is of order $10\%$ for an observer at a distance 5 m. The distance limit for a $10\%$ uncertainty scales with the inverse of the frequency, while for a fixed frequency, the fractional error decreases quadratically with distance [104]. The accuracy of the ZHS algorithm is shown to be below the $2\%$ level provided $R>10$ m and $\omega >10$ MHz [104]. Fortunately, these conditions are typically satisfied in the standard frequency bands used both in air-shower and dense-media experiments. Codes have also been developed that use the exact expression [104], which could be particularly important in very low-frequency experiments [106].

Conditions 2 and 3 are less restrictive because the sub-tracks can be made arbitrarily small to improve the accuracy of the calculation. In the first calculation of radio pulses in ice using [30], each electron in the shower was considered as a unique track, ignoring changes in velocity in different interactions. The main improvement to the code was to calculate the contributions to the pulse from the sub-tracks that are naturally used for Monte Carlo particle propagation. These steps were taken at each interaction point, but for low-energy electrons, smaller sub-steps were chosen for more accurate implementation of velocity and direction changes due to ionization and multiple elastic scattering [24]. This resulted in a significant improvement, especially around 1 GHz, although the original calculation already gave quite accurate results. The effect of changing the size of the sub-tracks to further smaller values were also explored for optimization, to estimate the uncertainty of the calculation and to calculate radio pulses in positions where the whole shower could not be treated as being in the Fraunhofer regime [107].

4. Monte Carlo Simulation Codes

Once the method for calculating the contribution to the electric field of sub-tracks is established, the coherent emission from a shower is a matter of careful book-keeping of the relative phases or time delays from all the charged particles of a shower. In principle, the ZHS algorithm can be applied to any shower simulation program. The first code to do this comprehensively was the ZHS code [24]. This was a specifically devised code to evaluate radio pulses from electromagnetic showers in homogeneous ice.

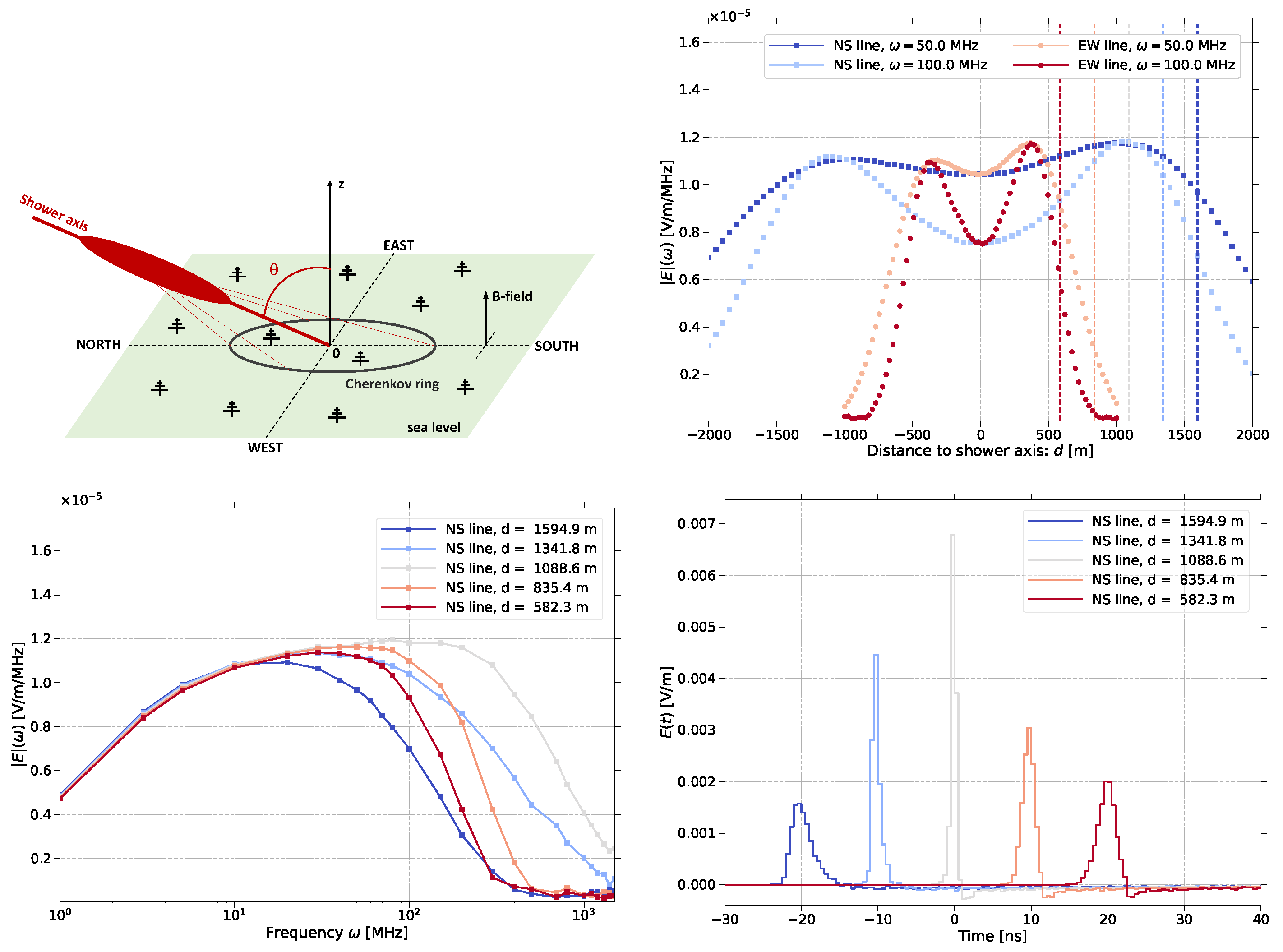
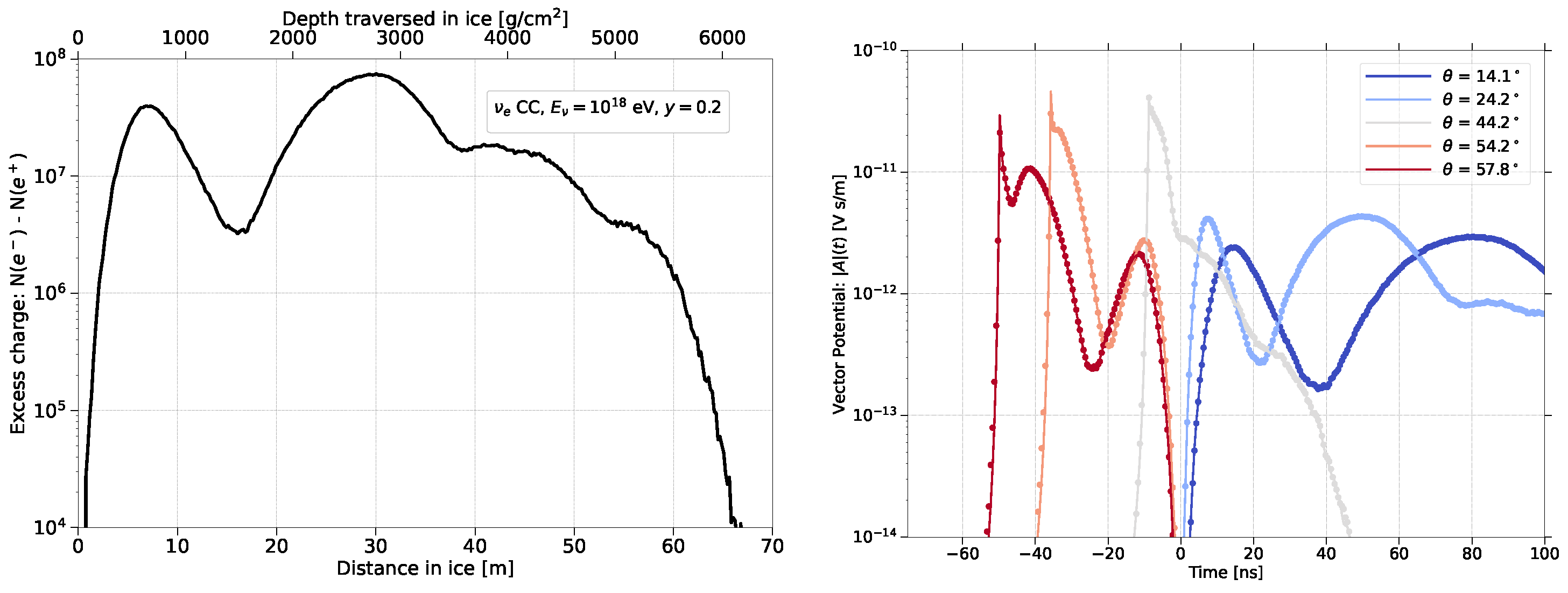
4.1. Electromagnetic Showers in Homogeneous Media: ZHS Code

The ZHS simulation program is based on efficient routines for the simulation of electron-photon cascades developed by T. Stanev and Ch. Vankov [108] that have been improved using the EGS4 package [109] for the simulations of coupled electron-photon transport. The ZHS code was initially developed for homogeneous ice with a radiation length of $X_0=36.08\mathrm{g}{\mathrm{cm}}^{-2}$ and a density of 0.924 g cm${}^{-2}$ and a refractive index of $n=1.78$. Later it was extended to deal with arbitrary homogeneous media [110]. The program takes into account the main interactions of electrons and photons with matter at high energies, bremsstrahlung and pair production in the atomic fields as well as the interactions with atomic electrons, Møller scattering for shower electrons, Bhabha scattering and annihilation for positrons and Compton for photons. These latter interactions are those responsible for the excess charge predicted by Askaryan. The photoelectric effect, which is responsible for the final absorption of the energy, is not accounted for because it is irrelevant for the kinetic energies considered, always above 100 keV. The program also accounts for continuous energy loss and multiple elastic scattering, the latter using Molière’s theory and retaining the first two terms in the Bessel function expansion [111].

For low particle energies, the interaction distance for bremsstrahlung and pair production is much less than the atomic radius, and the required Coulomb field is a point charge of charge Z with corrections according to Koch and Motz [112]. For higher energies, the interaction distance increases, and corrections due to electron screening are considered. At even higher energies, the interaction distance becomes comparable to the typical separation of the atoms and the collective field of multiple atoms results in the Landau-Pomeranchuk-Migdal [113,114,115] (LPM) effect. This occurs at characteristic energy in ice of $61.5\times X_0\left(cm\right)=2200$ TeV [116], above which there is a dramatic reduction of both cross-sections, as well as a suppression of soft bremsstrahlung with important consequences for shower development [117].

Time delays of particles are considered in detail in the phases of the frequency components of the field and are measured relative to a perpendicular plane front moving along the shower axis at the speed of light. Some delays are due to particle velocities smaller than c, and others are purely geometrical because the particles deviate from the shower axis. Account is taken of the time delays associated with multiple scattering and ionization losses as the particles are propagated in the simulation from one interaction to the next. This careful treatment of delays may well be the most important difference relative to other programs for shower simulation.

The ZHS program worked originally in the frequency domain and in the Fraunhofer regime of the shower [24]. It was later extended to work in the Fresnel regime in both the time and frequency domains [25] simply reducing the maximum length of particle sub-tracks. Although originally only showers of energy below $\sim {10}^{15}$ eV could be simulated in a practical amount of time, the implementation of statistical thinning techniques [118,119] allowed the simulation of showers at UHE up to ${10}^{20}$ eV [120].

Results

The first results obtained in ice revealed the power that lies behind the radio technique. The electric field was shown to scale with shower energy as expected for full coherence. The low-frequency part of the spectrum was shown to be directly proportional to the tracklength of electrons minus the tracklength of positrons projected onto the shower axis, the “excess projected tracklength” [24], as can be expected from Equation (12). Moreover, it was apparent that the fluctuations in the amplitude for fixed energy were very small, providing an excellent measurement of the shower energy. This is because the pulse amplitude gets contributions from the whole shower development, and this fact is behind the common statement describing the radio technique as a “calorimetric” measurement.

Because of coherence, the angular pattern and the frequency spectrum both reflect the space-time distribution of the particles in the shower. This fact adds potential to the technique for reconstructing shower properties that can be, for instance, related to the type of primary particle and type of interaction initiating the shower [121]. Pulses in the frequency domain display characteristic diffraction patterns that allowed the identification of the relevant shower scales. The frequency spectrum was shown to rise linearly with frequency (as expected from Cherenkov emission) up to a limiting frequency beyond which the spectral slope gradually changes from positive to negative as the amplitude goes through its maximum value at a turnover frequency, indicating that the emission from all particles ceases to be fully coherent. An example can be seen in the top left panel of Figure 1. The turnover frequency is related to the observation direction, being largest for the Cherenkov angle (${\theta }_C$) and gets progressively smaller as the observation angle departs from ${\theta }_C$ as shown in Figure 1. In ice, the largest turnover frequency (for ${\theta }_c$) is at about 3 GHz which, not surprisingly, has a wavelength of 6 cm comparable to the Molière radius (11 cm) that characterizes the radial scale of the shower. Consequently, the angular distribution of the emission at a given frequency displays a main diffraction peak in the ${\theta }_C$ direction. Its width is inversely related to the frequency, as illustrated in the top right panel of Figure 2. The emission from different points along the shower axis loses coherence as the observation angle departs from ${\theta }_C$, and the turnover frequency becomes smaller as the deviation from the Cherenkov angle increases in either direction.

In the time domain, the pulses are bipolar as can be seen in the bottom panels of Figure 2. There is no change in the polarity of the pulse when observing inside ($\theta <{\theta }_C$) or outside ($\theta >{\theta }_C$) the Cherenkov cone, the pulse always starts being positive and ends being negative regardless of the observation angle. The pulse is the largest and narrowest in time ($\sim 1$ ns) at the Cherenkov angle as the observer receives the radiation from different stages in the longitudinal development of the shower almost at once. Away from ${\theta }_C$, the pulses broaden in time. An apparent violation of causality, a purely relativistic effect, reflects itself in the shape of the pulses inside and outside the Cherenkov cone, where the observer sees respectively first the beginning of the shower and then the end of it and vice-versa. As a result, the pulses look like antisymmetric copies of each other at angles ${\theta }_C\pm \Delta \theta$ for the same value of $\Delta \theta$, an effect that is clearly visible in Figure 2 and can be tracked down to the change of sign of the factor $(1-n\beta cos\theta )$ when crossing the Cherenkov angle.

The ZHS algorithm and simulation program were compared with data (see Section 6 for more details) as well as with other codes. The ZHS algorithm was implemented in the GEANT program for the simulation of particle tracking, to provide a test of the calculation. The two results were in very good qualitative agreement concerning the diffraction patterns of the emission, but the normalization of the electric field amplitude obtained with GEANT was smaller by about $40\%$ [122]. After quite some time, the controversy finally settled, and it turned out that the particle thresholds in GEANT had not been consistently set so that in practice they were larger than those used in ZHS [123]. As a result, the simulated tracklength of the charged particles was reduced, directly implying a reduction of the obtained radio pulse amplitudes as expected.

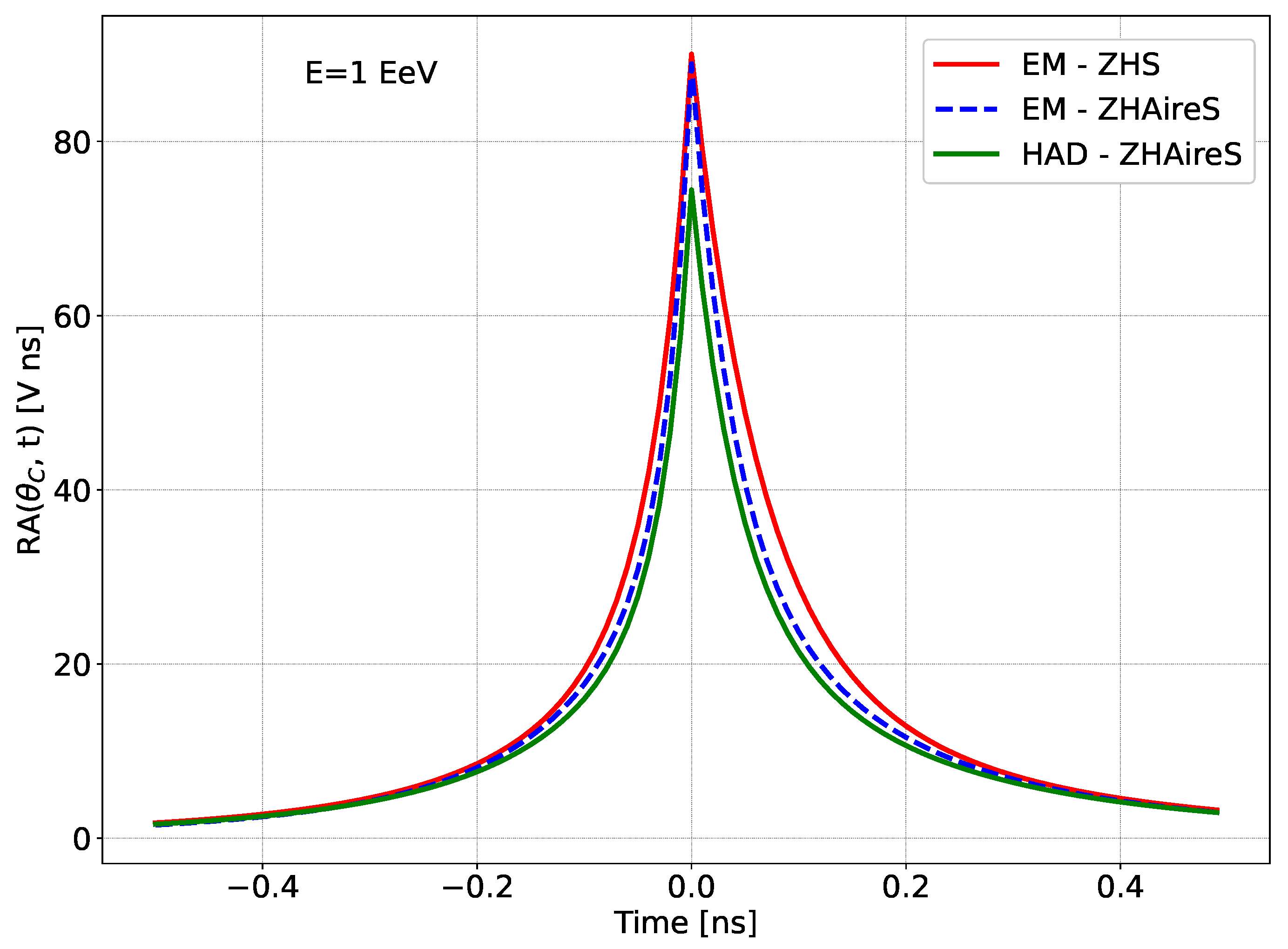
4.2. Air Showers with Hadronic Component: ZHAireS

As stated above, the ZHS algorithm is completely general and can be applied to the calculation of the electric field in a variety of situations as long as a good account of the charged-particle trajectories involved can be performed reliably. In particular, the calculation of the electric field radiated by cosmic-ray and neutrino showers in the air required a simulation program that treats both hadronic and electromagnetic showers in a non-homogeneous medium such as the atmosphere, capabilities that the current version of the ZHS shower simulator does not have. An alternative shower simulation code AIRES [74] was used to calculate radio pulses with the ZHS algorithm. AIRES is a standard and versatile code originally developed to study UHE showers in the atmosphere that includes the relevant interaction cross-sections and decay processes of the main baryons, mesons and leptons involved in shower development. AIRES was first combined with the TIERRAS package [124]5 to allow also the simulation of hadronic showers in homogeneous ice. The resulting code, named ZHAireS [27], was first validated by comparing the results of photon showers in ice with those of both GEANT4 and ZHS. All programs gave consistent results up to energies of ${10}^{19}$ eV. Beyond this energy, the ZHS code ceases to be reliable because it does not treat photoproduction (hadronic) interactions. Almost at the same time, the first calculations of the electric field in cosmic-ray induced showers were performed with ZHAireS, accounting for the varying index of refraction of the atmosphere [27].

Results

ZHAireS simulations of cosmic-ray induced air showers [27] showed that the pulses were bipolar, as can be seen in Figure 3, and dominated by the geomagnetic mechanism (see Section 2), supporting earlier results based on modelling macroscopic currents [20]. Similar results were obtained with CoREAS [28]. The results also clarified the relevance of the refractive index producing a Cherenkov-like ring clearly visible in the pattern of the signal, especially for inclined showers [125]. An example can be seen in Figure 3. Also, these simulations showed that, as expected, the atmospheric refractive index leads to strengthened coherence in directions close to the Cherenkov angle, predicting that coherence could reach up to GHz frequencies [125] (see Figure 3) in spite of the shower dimensions being extremely larger than in ice. There are several reasons for this that can be best understood in terms of time delays. Firstly, the Cherenkov angle ${\theta }_C$ in the air is very small and the time delay due to the lateral spread of the shower is reduced because it depends on $sin{\theta }_C\sim 0.02$ (as shown in Section 5.1) [37]. It can also be shown that for given geometries, the time delays between different regions of the shower increase as the distance to the shower axis rises [125]. At a given frequency, there is, however, a reduced but significant region surrounding the shower axis within which the emission is coherent. As the particle density is peaked around the shower axis, the emission from this reduced region is sufficient to contribute a coherent signal even at GHz. The Cherenkov angle is, however, difficult to define. In the atmosphere, the refractivity $n-1$ can be assumed proportional to air density, and ${\theta }_C$ depends on the altitude ranging between $0.3^{\circ }$ at high altitudes to $1.4^{\circ }$ at ground level. Very inclined showers develop high in the atmosphere, changes in the refractive are less important during shower development when compared to more vertical showers, and the Cherenkov ring at the ground can be estimated by assuming the dominant contribution originates at shower maximum with ${\theta }_C$ calculated at the corresponding altitude. In contrast, for vertical showers, the observer is not within the far distance limit so both the observing direction and the Cherenkov direction change more rapidly as the shower front advances.

5. Simplifying and Understanding Radio Emission through Models

The rich angular and frequency patterns of the simulated pulses obtained in dense media immediately suggested diffraction effects that were clearly related to the space-time distribution of the excess charge, the wavelength of observation and the position of the observer w.r.t. the Cherenkov angle [30]. Electrons and positrons with kinetic energies above hundreds of keV in a dense medium such as clear ice, or above tens of MeV in air, travel at speeds $v\sim c>c/n$ with $n>1$ the refractive index of the medium. This induces purely relativistic “Cherenkov-like” effects that play a crucial role in radio emission. These ideas led to several models and parameterizations that are able to reproduce and extrapolate the results without the need for lengthy calculations. This is particularly important when large amounts of simulations are needed to be combined with detector models both for the design and optimization of detectors and for data analysis. These models in addition give further insight into the radiation patterns.

5.1. The Simplest Model: A Basis for Parameterizations

The simplest model of shower development assumes that the shower is a one-dimensional line of current with constant net negative charge travelling with a speed $v>c/n$ along an effective length $\Delta L$. For the moment, the lateral spread of the shower in the directions perpendicular to the dimension L and the width of the shower front are neglected in the model. When the observation angle, $\theta$, is the Cherenkov angle ${\theta }_C$ ($cos{\theta }_C={\left(n\beta \right)}^{-1}$ if $\beta =v/c$), the travel time of the charge along $\Delta L$ (given by $\Delta L/v$) is equal to the travel time of the radiation emitted (given by $n\Delta Lcos\theta /c$)—see Figure 4. As a consequence, an observer at $\theta ={\theta }_C$ and in the Fraunhofer regime, sees all the wavefronts emitted at different stages along $\Delta L$ at the same time. In the frequency domain, there is constructive interference between the wavefronts at all wavelengths, and the frequency spectrum increases indefinitely. However, if the observer is placed at $\theta \ne {\theta }_C$, the radiation is seen to arrive in a finite interval of time $\Delta t_L(\Delta L,\theta )=\Delta L|1-ncos\theta |/c$ (Figure 4). In this case, the wavefronts from different points along the length L are no longer in phase because the Cherenkov condition is not fulfilled. The angular pattern obtained in simulations resembles that of a single slit with the central peak shifted to the Cherenkov direction and secondary peaks at both sides (see Figure 1). One can relate the width of the slit to the “compressed” length of the shower, due to the factor $(1-n\beta cos\theta )$, as long as it dominates over the lateral distribution. The direct analogy to the slit model is formalized in the following Section 5.2. In the frequency domain, the Fourier amplitude ceases to grow linearly with frequency as destructive interference sets in, reaching a maximum or turnover point at ${\omega }_{\mathrm{cut}}(\Delta L,\theta )\propto \Delta t_L^{-1}$. A purely relativistic effect also occurs: if $\theta <{\theta }_C$, then the observer sees first the end of the shower and then its beginning ($\Delta t_L<0$ in an apparent violation of causality), while the opposite occurs if $\theta >{\theta }_C$ ($\Delta t_L>0$, apparent causality).

We can refine the model above and introduce a transverse scale of the shower, modelling it as a disk of uniform charge and effective radius $\Delta R$ moving along $\Delta L$ at speed $v>c/n$. In this case, even for an observer at ${\theta }_C$, the wavefronts are no longer in phase due to the lateral spread of the shower, and in fact, it is easy to show [24,110,120] that the radiation lasts a time interval $\Delta t_R\simeq n\Delta Rsin{\theta }_C/c$ (see Figure 4). This induces another turnover in the frequency spectrum at ${\omega }_{\mathrm{cut}}\left(R\right)\propto {\Delta t_R}^{-1}$ even at the Cherenkov angle, cutting off the linear behaviour of the electric field with frequency. If the observer is placed at $\theta \ne {\theta }_C$, the wavefronts are not in phase both due to the longitudinal and lateral shower development, and the radiation lasts a finite time interval given by the maximum of time intervals $\Delta t\simeq \max [\Delta t_R(\Delta R,\theta ),\Delta t_L(\Delta L,\theta )]$ inducing a turnover frequency ${\omega }_{\mathrm{cut}}\propto {\Delta t}^{-1}$.

This simple approach links the turnover point in the frequency spectrum for observers in the Cherenkov direction to the lateral shower development, and the turnover at angles away from the Cherenkov direction to the longitudinal shower development. Although this is rather crude, the parameters $\Delta L$ and $\Delta R$ can be adjusted to fit the simulation results and give a fairly accurate description of the spectrum and angular distributions. This model reproduces the frequency at which the interference starts to take place, as well as the angular distribution of the Cherenkov beam, decreasing from its maximum value as the observation direction departs from the Cherenkov angle. It has been exploited to produce educated parameterizations of the features of the radio emission in different dense dielectric media (ice, salt, lunar regolith) [110,120], that match quite accurately the results obtained in Monte Carlo simulations performed with the ZHS and ZHAireS codes. However, they are limited to showers that match the longitudinal distribution assumed. At sufficiently high energies, dramatic changes in the longitudinal distribution can be expected because the LPM effect (see Section 4) increases the length of the shower. This translates into a proportional reduction of the angular width of the pulse as could be expected for a diffraction slit.

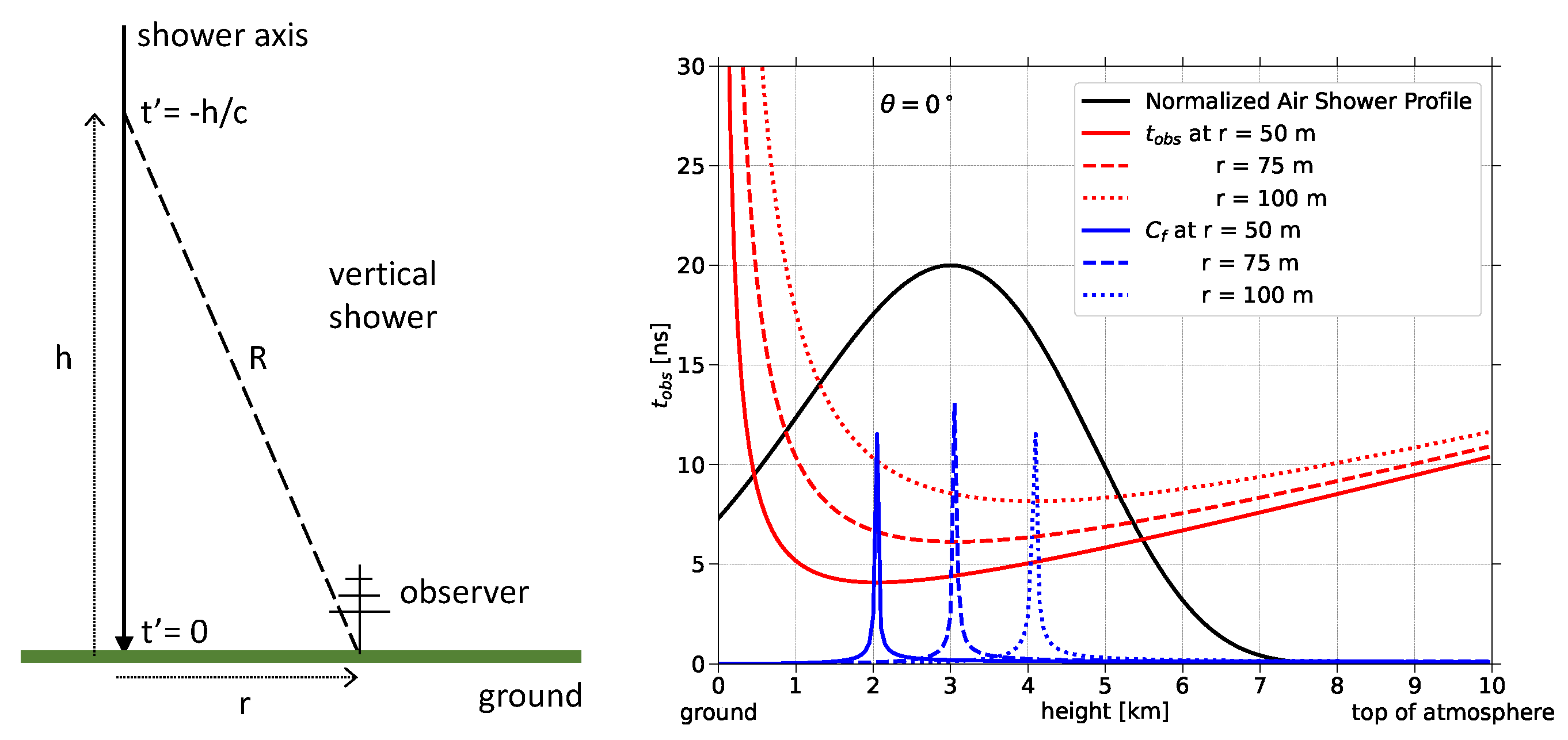
5.2. The 1-Dimensional (1D) Approximation

A quick approach to the problem is obtained in the frequency domain, assuming all particles move at the speed of light along the z-axis, or equivalently neglecting the transverse size of the shower. Clearly, it will be extremely accurate in the far-field limit when the wavelength comfortably exceeds the transverse size as all emissions coming from within the transverse size will be in phase. This corresponds to frequencies below ∼100 MHz in ice from the discussion above.

Taking the Fourier transform of the vector potential in Equation (5) is trivial, and the electric field is just obtained by multiplying by $i\omega$:

$$\begin{array}{cc}\hfill \mathbf{E}(\omega ,\mathbf{x})& =i\omega \frac{\mathrm{e}\mu }{2\pi }\int \frac{{\mathbf{J}}_{\perp }({\mathbf{x}}^{\prime },t^{\prime })}{|\mathbf{x}-{\mathbf{x}}^{\prime }|}{e}^{i\omega t^{\prime }+ik|\mathbf{x}-{\mathbf{x}}^{\prime }|}{d}^3{\mathbf{x}}^{\prime }d{t}^{\prime },\hfill \end{array}$$

(13)

where the retarded condition of the delta function in Equation (5) is responsible for replacing t with $|\mathbf{x}-{\mathbf{x}}^{\prime }|n/c$ in the phase factor $e^{i\omega t}$.

Assuming the particles move at the speed of light in a vacuum on the $z^{\prime }$-axis, the 1-dimensional approximation for the macroscopic current ${\mathbf{J}}_{\perp }$ is a “point-like” current given by

$${\mathbf{J}}_{\perp }({\mathbf{x}}^{\prime },t^{\prime })=eQ\left(z^{\prime }\right)csin\theta {\widehat{\mathbf{v}}}_{\perp }\delta \left(x^{\prime }\right)\delta \left(y^{\prime }\right)\delta \left(z^{\prime }-c{t}^{\prime }\right),$$

where $eQ\left(z^{\prime }\right)c$ is the magnitude of the current6 that rises and falls along the shower direction $z^{\prime }$, and we re-encounter ${\widehat{\mathbf{v}}}_{\perp }$, the unit vector in the direction of the transverse current. The 1D approximation is obtained by substituting this current into Equation (13). The result is proportional to a “modified” Fourier transform of the longitudinal shower development, $Q\left(z^{\prime }\right)$ [107]:

$$\mathbf{E}(\omega ,\mathbf{x})=i\omega \frac{e\mu }{2\pi }\frac{e^{ikR}}{R}csin\theta {\widehat{\mathbf{v}}}_{\perp }\int d{z}^{\prime }Q\left(z^{\prime }\right){\mathrm{e}}^{i\tilde{\omega }{z}^{\prime }/c},$$

where the time integral is replaced by a $z^{\prime }$ integral using $d{z}^{\prime }=cd{t}^{\prime }$, and the frequency $\omega$ has been re-scaled into $\tilde{\omega }=(1-ncos\theta )\omega$, with a time “compression” factor due to retardation. The phase factor $\tilde{\omega }{z}^{\prime }/c$ regulates interference between different shower stages in the longitudinal development. This expression has similarities to one for the diffraction by a slit. As expected, the electric field amplitude scales with $R^{-1}$ and has a $sin\theta$ projection factor due to the transverse current. It also has an overall phase $e^{ikR}$ and a time-derivative factor $i\omega$.

Replacing $Q\left(z\right)$ with a Gaussian approximation for shower maximum gives a good description of the angular diffraction patterns of the Fourier amplitudes obtained at low frequencies and of the change of slope of the frequency spectrum for observation angles that differ from ${\theta }_C$. For $\tilde{\omega }\Delta L/c\sim 1$, $\Delta L$ being an effective shower length, the emission is still partially coherent, and interference effects are relevant. Using $Q\left(z\right)$ as obtained in full simulations and comparing the approximation with the ZHS Monte Carlo results for the amplitudes, they were shown to agree except for the normalization that is increasingly overestimated as the frequency increases and the observer gets closer to the Cherenkov direction, by about $5\%$ ($20\%$) at 100 (300) MHz. This is due to interference between different zones of the lateral spread of the shower front that are unaccounted for in the 1D approximation. This can be corrected with an ad-hoc factor as was independently shown with a fully analytical model [19]. Armed with such a correction, it was possible to obtain reliable results using 1D simulations for very large energies, exploring LPM effects for hadronic and electromagnetic showers and the characteristics of pulses produced by showers induced by neutrinos of different flavours [107,121]. Incidentally, it was also shown that very similar results are obtained if an effective excess number of electrons was considered as $\sim 25\%$ so that $Q\left(z\right)\sim 0.25N\left(z\right)$, $N\left(z\right)$ being the shower size (the number of electrons and positrons).

5.3. The Semi-Analytical Approach

The next natural step is to include the lateral distribution, treating the current density $\mathbf{J}$ as a flat pancake $\delta (z^{\prime }-v{t}^{\prime })$ travelling with velocity $\mathbf{v}$ along the $z^{\prime }$-axis. The net charge profile $Q\left(z^{\prime }\right)$ also spreads laterally in $x^{\prime }$ and $y^{\prime }$ and the transverse current is approximated as:

$$\mathbf{J}({\mathbf{x}}^{\prime },t^{\prime })=\mathbf{v}(r^{\prime },{\varphi }^{\prime },z^{\prime })f(r^{\prime },z^{\prime })Q\left(z^{\prime }\right)\delta (z^{\prime }-v{t}^{\prime }).$$

(14)

Here the function $f(r^{\prime },z^{\prime })$ represents the lateral charge distribution in a plane transverse to $z^{\prime }$, with cylindrical symmetry, $r^{\prime }=\sqrt{{x^{\prime }}^2+{y^{\prime }}^2}$ being the cylindrical radius. The velocity $\mathbf{v}$, close to that of light in a vacuum, is primarily directed in the ${\mathbf{z}}^{\prime }$ direction, allowing for a small transverse component due to the scattering of shower particles. This is a flat disk approximation that ignores the curvature of the shower front that delays the particles relative to those along the $z^{\prime }$-axis. This approximation is expected to be valid provided that these time delays can be ignored, which is correct for frequencies below ∼3 GHz in ice.

With this approximation for the transverse current, the vector potential in Equation (5) is then given by:

$$\begin{array}{cc}\hfill \mathbf{A}(\mathbf{x},t)=& \frac{\mu }{4\pi }{\int }_{-\infty }^{\infty }d{t}^{\prime }{\int }_{-\infty }^{\infty }d{z}^{\prime }Q\left(z^{\prime }\right)\delta (z^{\prime }-v{t}^{\prime })\hfill \\ \hfill & {\int }_0^{\infty }d{r}^{\prime }{r}^{\prime }{\int }_0^{2\pi }d{\varphi }^{\prime }f(r^{\prime },z^{\prime }){\mathbf{v}}_{\perp }(r^{\prime },{\varphi }^{\prime },z^{\prime })\frac{\delta \left(n|\mathbf{x}-{\mathbf{x}}^{\prime }|/c-(t-t^{\prime })\right)}{|\mathbf{x}-{\mathbf{x}}^{\prime }|},\hfill \end{array}$$

(15)

where ${\varphi }^{\prime }$ is the azimuthal angle in cylindrical coordinates, and ${\mathbf{v}}_{\perp }(r^{\prime },{\varphi }^{\prime },z^{\prime })$ generally depends on $r^{\prime }$ and $z^{\prime }$.

Instead of using a standard parameterization of the lateral distribution, as later done in [126], the integral over the lateral distribution in the second line of Equation (15) was directly calculated in the Fraunhofer limit, for observers in the Cherenkov direction, using full simulations of the radio pulse [22] applying the procedure detailed in the following.

For an observer in the direction $\widehat{\mathbf{u}}=\mathbf{x}/\left|\mathbf{x}\right|=(sin\theta cos\varphi ,sin\theta sin\varphi ,cos\theta )$ in spherical coordinates, and assuming $\varphi =0$ without loss of generality, the Fraunhofer approximation implies:

$$|\mathbf{x}-{\mathbf{x}}^{\prime }| \approx R-\widehat{\mathbf{u}}·{\mathbf{x}}^{\prime }=R-z^{\prime }cos\theta -r^{\prime }sin\theta cos{\varphi }^{\prime }.$$

(16)

Again, the denominator $|\mathbf{x}-{\mathbf{x}}^{\prime }|$ in Equation (15) is replaced by a constant R, but for the $\delta$-function we keep the expansion given in Equation (16) and integrate in $t^{\prime }$ to get:

$$\begin{array}{cc}\hfill & \mathbf{A}(\theta ,t)=\frac{\mu }{4\pi R}{\int }_{-\infty }^{\infty }d{z}^{\prime }Q\left(z^{\prime }\right)\hfill \\ \hfill & {\int }_0^{\infty }d{r}^{\prime }{r}^{\prime }{\int }_0^{2\pi }d{\varphi }^{\prime }f(r^{\prime },z^{\prime })\frac{{\mathbf{v}}_{\perp }(r^{\prime },{\varphi }^{\prime },z^{\prime })}{v}\delta \left(z^{\prime }\left[\frac{1}{v}-\frac{ncos\theta }{c}\right]-\frac{n{r}^{\prime }sin\theta cos{\varphi }^{\prime }}{c}+\frac{nR}{c}-t\right).\hfill \end{array}$$

(17)

Evaluating this expression at the Cherenkov angle, as $1/v-ncos{\theta }_C/c=0$, one effectively removes the $z^{\prime }$ dependence in the $\delta$-function7. If we then further assume that the lateral density and the particle velocity depends only very weakly on $z^{\prime }$, i.e., $f(r^{\prime },z^{\prime })\simeq f\left(r^{\prime }\right)$ and $\mathbf{v}(r^{\prime },{\varphi }^{\prime },z^{\prime })\simeq \mathbf{v}(r^{\prime },{\varphi }^{\prime })$, we can factorize Equation (17) into the integral over the longitudinal dimension $z^{\prime }$ in the first line and a form factor $\mathbf{F}$ containing the lateral ($r^{\prime },{\varphi }^{\prime }$) integration8:

$$\mathbf{F}\left(t-\frac{nR}{c}\right)=\frac{1}{sin{\theta }_C}{\int }_0^{\infty }d{r}^{\prime }{r}^{\prime }{\int }_0^{2\pi }d{\varphi }^{\prime }f\left(r^{\prime }\right)\frac{{\mathbf{v}}_{\perp }(r^{\prime },{\varphi }^{\prime })}{v}\delta \left(\frac{nR}{c}-t-\frac{n{r}^{\prime }sin{\theta }_{C}cos{\varphi }^{\prime }}{c}\right).$$

(18)

The vector potential in the Cherenkov direction is then simply expressed as:

$$\mathbf{A}({\theta }_C,t)=\frac{\mu }{4\pi R}\mathbf{F}\left(t-\frac{nR}{c}\right)sin{\theta }_C{\int }_{-\infty }^{\infty }d{z}^{\prime }Q\left(z^{\prime }\right).$$

(19)

The functional shape of the form factor can be numerically evaluated by equating the vector potential in the Cherenkov direction obtained with simulations to Equation (19), taking for $\int d{z}^{\prime }Q\left(z^{\prime }\right)$ the excess projected tracklength obtained in the same simulation, $L{Q}_{\mathrm{tot}}$:

$$F\left(t-\frac{nR}{c}\right)=\frac{4\pi }{\mu }\frac{RA({\theta }_C,t)}{L{Q}_{\mathrm{tot}}}.$$

(20)

This is the modulus of the vector $\mathbf{F}=F\widehat{\mathbf{p}}$. It is easy to show that, because of symmetry, it must be aligned with $\mathbf{p}=\widehat{\mathbf{p}}sin\theta =-\widehat{\mathbf{u}}\times \left[\widehat{\mathbf{u}}\times {\widehat{\mathbf{z}}}^{\prime }\right]$, i.e., in the ${\mathbf{z}}^{\prime }$-$\widehat{\mathbf{u}}$ plane and perpendicular to $\widehat{\mathbf{u}}$.

The final expression for Equation (17) is given as a simple one-dimensional integral involving the longitudinal development of the excess charge $Q\left(z^{\prime }\right)$ that can be obtained from a simulation, model or parameterization:

$$\mathbf{A}(\theta ,t)=\frac{\mu }{4\pi R}\widehat{\mathbf{p}}sin\theta {\int }_{-\infty }^{\infty }d{z}^{\prime }Q\left(z^{\prime }\right)F\left(t-\frac{nR}{c}-z^{\prime }\left[\frac{1}{v}-\frac{ncos\theta }{c}\right]\right).$$

(21)

The argument of the form factor F Equation (20) must now include an extra term, $z^{\prime }(1/v-ncos\theta /c)$, which tends to zero as we approach the Cherenkov angle. The result obtained is valid for all observation angles, a very significant improvement over the 1D model, and gives excellent agreement when compared to simulations up to 3 GHz.

The main assumption in this approach is in the factorization of the current given by Equation (14). The $\delta$-function of $(z^{\prime }-v{t}^{\prime })$ implies a current density established by a shower front that lies in a plane perpendicular to the shower axis which is a point like in the $z^{\prime }$-direction, i.e., has no time width. Clearly, this is a limitation since the shower front has curvature and a finite width, both of which are due to time delays that increase in mean and spread as r rises. Time delays for a shower in a dense medium are typically well below the nanosecond scale. This explains why this approach is so successful in describing the emission up to 3 GHz. In the case of showers in the atmosphere, these delays are typically larger by a factor of order 1000, and so this approach is not expected to perform as precisely.

5.3.1. Results in the Near Field

As with the 1D approximation, the approach can be extended to deal with situations in which the observer is no longer in the far-field region with respect to the longitudinal development of the shower. For an observer located at $(r,\varphi =0,z)$ where the polar angle can be assumed to be zero because of cylindrical symmetry, the distance between the source at $(r^{\prime },{\varphi }^{\prime },z^{\prime })$ and the observation point can be expanded in the Fraunhofer approximation:

$$|\mathbf{x}-{\mathbf{x}}^{\prime }|=\sqrt{r^2+{r^{\prime }}^2-2r{r}^{\prime }cos{\varphi }^{\prime }+{(z-z^{\prime })}^2}\simeq \sqrt{r^2+{(z-z^{\prime })}^2}-r^{\prime }sin\theta cos{\varphi }^{\prime },$$

(22)

where now $sin\theta =r/\sqrt{r^2+{(z-z^{\prime })}^2}$, i.e., the observer direction, $\widehat{\mathbf{u}}\left(z^{\prime }\right)$, is $z^{\prime }$ dependent, unlike in the far-field case. The factor $|\mathbf{x}-{\mathbf{x}}^{\prime }|$ in the denominator of the vector potential in Equation (15) is now only allowed to depend on $z^{\prime }$ (or $t^{\prime }$) approximating it as $\sqrt{r^2+{(z-z^{\prime })}^2}$, so that it remains constant in the form factor integral Equation (18). The Fraunhofer approximation still applies in relation to the lateral distribution, typically of order 10 cm in ice. Substituting into the expression for the vector potential in Equation (15) and following the same steps for the $t^{\prime }$ integral, it becomes:

$$\begin{array}{cc}\hfill \mathbf{A}(r,z,t)=& \frac{\mu }{4\pi }{\int }_{-\infty }^{\infty }d{z}^{\prime }\frac{Q\left(z^{\prime }\right)}{\sqrt{r^2+{(z-z^{\prime })}^2}}{\int }_{-\infty }^{\infty }d{r}^{\prime }{r}^{\prime }f\left(r^{\prime }\right){\int }_0^{2\pi }d{\varphi }^{\prime }\frac{{\mathbf{v}}_{\perp }(r^{\prime },{\varphi }^{\prime },z^{\prime })}{v}\hfill \\ \hfill & \delta \left(\frac{z^{\prime }}{v}+\frac{n\sqrt{r^2+{(z-z^{\prime })}^2}-n{r}^{\prime }sin\theta cos{\varphi }^{\prime }}{c}-t\right),\hfill \end{array}$$

(23)

and the corresponding expression for the form factor becomes remarkably similar to Equation (18) for the far-field case:

$$\begin{array}{cc}\hfill \mathbf{F}\left(t-\frac{z^{\prime }}{v}-\frac{n\sqrt{r^2+{(z-z^{\prime })}^2}}{c}\right)=& {\int }_{-\infty }^{\infty }d{r}^{\prime }{r}^{\prime }{\int }_0^{2\pi }d{\varphi }^{\prime }f\left(r^{\prime }\right)\frac{{\mathbf{v}}_{\perp }(r^{\prime },{\varphi }^{\prime },z^{\prime })}{v}\hfill \\ \hfill & \delta \left(\frac{z^{\prime }}{v}+\frac{n\sqrt{r^2+{(z-z^{\prime })}^2}}{c}-t-\frac{n{r}^{\prime }sin\theta cos{\varphi }^{\prime }}{c}\right).\hfill \end{array}$$

(24)

Only the argument of the $\delta$-function is modified relative to Equation (18). We note however that there is a subtlety because the direction of $\mathbf{F}$, given by ${\mathbf{v}}_{\perp }(r^{\prime },{\varphi }^{\prime },z^{\prime })$, now also depends on $z^{\prime }$ since $\widehat{\mathbf{u}}\left(z^{\prime }\right)$ changes with $z^{\prime }$ as the shower develops. This is conveniently taken into account substituting $(\widehat{\mathbf{p}}sin\theta )$ for $\mathbf{p}\left(z^{\prime }\right)=-\widehat{\mathbf{u}}\left(z^{\prime }\right)\times [\widehat{\mathbf{u}}\left(z^{\prime }\right)\times {\widehat{\mathbf{z}}}^{\prime }]$ into Equation (21).9 This approximation has been shown to give excellent results for instance for showers extending 40 m in length and observers being only 10 m away from the shower axis [22].

5.3.2. Parameterizations of the Form Factor

A parameterization of the form factor was first obtained using Monte Carlo simulations performed with ZHS for electromagnetic showers in ice [22]. The parameterization is asymmetric in time and is given by the following function:

$$RA({\theta }_C,t)=-A_P{E}_{\mathrm{em}}\left\{\begin{array}{cc}exp\left(-\frac{t}{t_{1a}}\right)+{\left(1+\frac{t}{t_{1b}}\right)}^{-{\beta }_1}\hfill & \mathrm{i}\mathrm{f} t > 0\hfill \\ \\ exp\left(-\frac{\left|t\right|}{t_{2a}}\right)+{\left(1+\frac{\left|t\right|}{t_{2b}}\right)}^{-{\beta }_2}\hfill & \mathrm{i}\mathrm{f} t < 0,\hfill \end{array}\right.$$

(25)

with R and t the observer distance and time, and $E_{\mathrm{em}}$ represents the energy transferred to the electromagnetic component of the shower, responsible for the bulk of the radio emission due to the excess negative charge, and which depends on the energy of the primary particle E. The parameters for this calculation can be read in

Table 1. Best fit parameters for the vector potential parameterization of Equation (25) as obtained from fits to electromagnetic (EM) simulations made in ice both with ZHS and ZHAireS as well as for hadronic (HAD) showers with ZHAireS.

Type	Code	${\mathit{A}}_{\mathit{P}}\left[\frac{\mathit{V}\mathbf{ns}}{\mathbf{EeV}}\right]$	${\mathit{t}}_{1\mathit{a}}\left[\mathbf{ns}\right]$	${\mathit{t}}_{1\mathit{b}}\left[\mathbf{ns}\right]$	${\mathit{t}}_{2\mathit{a}}\left[\mathbf{ns}\right]$	${\mathit{t}}_{2\mathit{b}}\left[\mathbf{ns}\right]$	${\mathit{\beta }}_1$	${\mathit{\beta }}_2$
EM	ZHS	45.00	0.0570	0.3484	0.03	0.3279	3.0	3.5
EM	ZHAireS	44.45	0.0348	0.4352	0.0203	0.3823	3.588	4.043
HAD	ZHAireS	40.71	0.0391	0.4277	0.0234	0.3723	3.320	3.687

. The accuracy of this approach is better than 5% when compared to the full simulation. As expected, the normalization scales with $E_{\mathrm{em}}$ and is fairly universal. Fluctuations become less relevant as the energy increases because of statistics. Later, the form factor was recalculated using ZHAireS together with TIERRAS to simulate both electromagnetic (EM) and hadronic (HAD) showers in ice [127]. The same functional form was fitted for both cases, and the best-fit parameters are also indicated in Table 1. The results using ZHS and ZHAireS for electromagnetic showers shown in Figure 5 have slightly different parameters that are possibly due to differences in the space-time distribution of the particles in the shower simulation process. The two parameterizations can be used to roughly estimate the uncertainty of the radio pulse associated with the simulations. For the case of electromagnetic showers, $E=E_{\mathrm{em}}$, while in the case of hadronic showers, typically $E_{\mathrm{em}}<E$ due to the missing energy (energy transferred to the muons and neutrinos in the shower). This explains the lower normalization of the peak of the vector potential for hadronic showers in Figure 5. In this case, a phenomenological relation between E and $E_{\mathrm{em}}$ obtained with Monte Carlo simulations using ZHAireS is [127]:

$$E_{\mathrm{em}}=(a+bϵ+c{ϵ}^2+d\sqrt{ϵ})E,$$

(26)

where $ϵ={log}_{10}\left(\frac{E}{\mathrm{eV}}\right)$ and $a=-21.98905$, $b=-2.32492$, $c=0.019650$ and $d=13.76512$. For instance, for $E={10}^{18}$ eV, $E_{\mathrm{em}}\simeq 0.914\times {10}^{18}$ eV.

These parameterizations, along with the formalism described above, allow simple modelling of more complex showers as produced by neutrino interactions that can have a mixture of electromagnetic and hadronic showers, for instance, in a charged-current electron neutrino interaction, where particularly elongated showers due to the LPM effect can be created. An example of this is shown in Figure 6, where the agreement between full ZHAireS simulations and the model described above is remarkable. A weighted average of the form factors is used in this case. Another important example where this formalism can be very useful is that of a charged-current, tau-neutrino interaction in which two showers are generated separated by the distance the tau lepton takes to decay. All these types of showers have distinctive diffraction patterns that can help to differentiate between them using the radio technique, representing a potential advantage in the determination of the flavour content of the cosmic neutrino beam at UHE [121,127].

We end this part by noting that the model described here can be applied in any dense homogeneous medium in which radio emission is dominated by the Askaryan effect. The only ingredients needed are the longitudinal profile of the excess charge in the shower $Q\left(z^{\prime }\right)$, as can be obtained with a suitable simulation or model, and the values of the parameters of the fit to the form factor in Equation (25) for the medium in consideration. Alternatively, the latter can also be obtained with radio simulations giving the vector potential, such as ZHAireS.

5.4. Modeling Radiation in Air Shower: Near Effects

The radio pulses emitted from air showers were early recognized as being much more complicated than those in dense homogeneous media such as ice. There are several reasons for this. Most importantly, the physical shower dimensions are ∼1000 times larger in air due to the reduced density. The lateral spread of the shower is of order 100 m, exceeding the wavelength of frequency components greater than 3 MHz. In addition, the emission is not necessarily in the far-field region, the relation between observation distance and the shower dimensions being typically less than 1 except for inclined showers, so the Fraunhofer approximation is not appropriate for a macroscopic treatment of the emission in many cases. As a result, interference effects play a more important role in general. Moreover, the density of the atmosphere decreases exponentially with altitude, making these scales different for cosmic-ray showers of different zenith angles and for neutrino-induced showers that are likely to develop at lower altitudes. Another big difference stems from the refractive index of the atmosphere, which is also dependent on altitude. This can bend the trajectory of the radiation from the source to the observer and complicates the calculation of the light travelling time. Furthermore, deviations in the magnetic field of the Earth that break the symmetry of the shower, are known to play a dominant role in the emission (see Section 2), and this depends on the relative orientation of the shower and the magnetic field. Not surprisingly, progress in the simulations and interpretations is more recent than in the case of showers in, for instance, ice.

Still, models are useful both to obtain reliable results rapidly and as a framework to give intuition to the more complex behaviour of the diffraction patterns obtained and their relation to the shower development, the orientation of these showers relative to the observer, the atmosphere and the magnetic field direction, and to the magnetic field intensity.

5.4.1. The One-Dimensional Toy Model

Some insight into the complexity of the problem is gained by considering a vertical shower in which particles propagate at the speed of light c along the axis, ignoring the lateral spread, and an observer located at ground altitude $h=0$ at a distance r, shown in Figure 7. The model assumes a signal proportional to the number of particles at a given altitude h which is attenuated with the distance R to the observer, $R=\sqrt{h^2+r^2}$, and which takes a time $nR/c$ to arrive, assuming a constant refractive index n [25]. The signal is obtained summing the contributions (i.e., integrating) in h. Fixing $t^{\prime }=0$ when the shower reaches $h=0$, the emission at height h happens at a “source-time” $t^{\prime }=-h/c$, and from geometrical considerations the arrival time is simply $t=(n\sqrt{h^2+r^2}-h)/c$. This relation between t and h for a constant refractive index $n=1.0003$ is shown in Figure 7.

The start-time of the electric field pulse is given by the minimum value of t, $t_{\mathrm{start}}=r\sqrt{n^2-1}/c$ that corresponds to $h_{\mathrm{start}}=r/\sqrt{n^2-1}$ at an observation angle equal to the Cherenkov angle, $tan{\theta }_C=\sqrt{n^2-1}$. Emission arriving later can come from two different altitudes, one above and one below $h_{\mathrm{start}}$. This is the well-known apparent violation of causality for emission within the Cherenkov cone, i.e., that above $h_{\mathrm{start}}$.

The amplitude of the electric field depends on the number of particles at altitude h in an interval $\Delta h$ and on $C_f$, the variation of h with observation time t.

$$C_f=\left|\frac{\partial h}{\partial t}\right|=c\left|\frac{\sqrt{r^2+h^2}}{\sqrt{r^2+h^2}-nh}\right|,$$

(27)

which has a singularity in the Cherenkov direction, when $tan{\theta }_C=r/h$. A large value of $C_f$ implies that the emission from a relatively large longitudinal portion of the shower $\Delta h$ contributes to the pulse in a relatively small interval of observer’s time $\Delta t$. The factor $C_f$ is plotted in Figure 7. It is the inverse of the compression factor already discussed in Section 5.4.1. An observer located at a position $r_C$ on the ground such that $h_{\mathrm{start}}$ corresponds to shower maximum, will receive the pulse with the largest amplitude. This corresponds to a Cherenkov-like ring at $r_C\simeq 75$ m in the particular case shown in Figure 7.

We note, however, that the Cherenkov angle in the air is very small, typically ${\theta }_C\sim 1^{\circ }$, and a distance $r=100$ m at ground level corresponds to $h_{\mathrm{s}tart}\sim 6$ km, well above shower maximum which is at an altitude of about 3 km for a vertical shower of ∼${10}^{18}$ eV. Clearly, for this geometry, the model cannot be expected to give good results because the transverse size of the shower cannot be ignored, and it is bound to change the picture. The Cherenkov ring is not always apparent. The model can be extended to an inclined shower simply considering h to be the distance along the shower axis to the ground and r the distance from the observer to the shower axis. The radiation pattern from inclined showers displays a distinct and characteristic Cherenkov ring, which can be interpreted with these simple ideas.

Finally, an estimate of the duration of the pulse can be obtained by calculating the arrival time of the signal $t_{\mathrm{g}}$ when the shower reaches the ground:

$$\Delta t=t_{\mathrm{g}}-t_{\mathrm{start}}=\frac{r}{c}\left(n-\sqrt{n^2-1}\right).$$

In the case of inclined showers that do not reach ground level, $t_{\mathrm{g}}$ should be replaced by the observer time corresponding to the “end” of the shower.

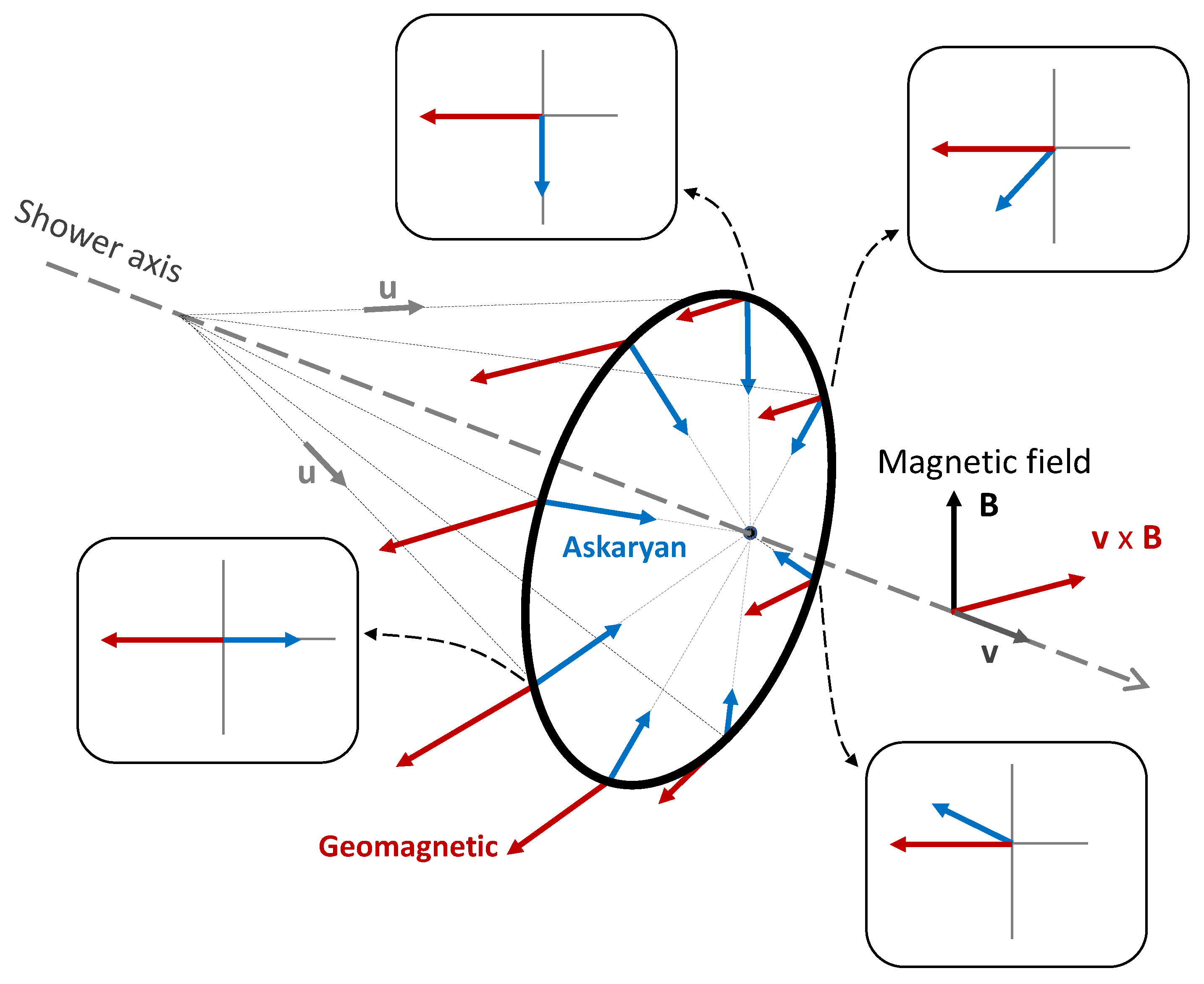
5.4.2. A Superposition Model

Despite being useful to understand the complex relation between observer and source times, shower size and geometry and how the radiation received changes with observer position, the toy model above cannot be used for a reliable calculation of radio emission in air showers. For this purpose, one has to rely on detailed and time-consuming Monte Carlo simulations such as those performed with ZHAireS and CoREAS (see Section 4).

An approach was developed to reduce the computing time that is required to fully describe the pulse at all possible positions at ground level, which would otherwise require intensive computing. It is based on the superposition of two different radiation patterns, one due to the development of the excess charge and the other due to the geomagnetic effect. These two mechanisms have very distinct polarization patterns as sketched in Figure 8.

In the absence of a magnetic field, the polarization that an observer sees, due to the excess charge, is determined by ${\mathbf{J}}_{\perp }$, in the Fraunhofer approximation equal to the component of the current perpendicular to the observing direction $\widehat{\mathbf{u}}$. The polarization plane is thus defined by $\widehat{\mathbf{u}}$ and the shower direction $\widehat{\mathbf{v}}=\widehat{\mathbf{z}}$, and is given by $-\widehat{\mathbf{u}}\times (\widehat{\mathbf{u}}\times \mathbf{v})$. As an observer at a radial distance r rotates about the shower axis, the polarization vector will also rotate to always point to the shower axis for a positive current10.

The current that develops because of the geomagnetic effect is established by the Lorentz force in the direction $(\mathbf{v}\times \mathbf{B})$, that is perpendicular to the shower direction and to the magnetic field. This component of the current must be projected onto a plane perpendicular to the observing direction (parallel to the vector potential). This is achieved, as in the Askaryan case, with a double cross product of the unit direction vector $\widehat{\mathbf{u}}$, i.e., $-\widehat{\mathbf{u}}\times [\widehat{\mathbf{u}}\times (\mathbf{v}\times \mathbf{B})]=(\mathbf{v}\times \mathbf{B})-[\widehat{\mathbf{u}}·(\mathbf{v}\times \mathbf{B})]\widehat{\mathbf{u}}$. This fixes the polarization of the electric field for the geomagnetic mechanism, which is in the opposite direction to the transverse current, as indicated in Figure 8. This vector does not rotate as the observer makes a full rotation about the axis at a distance r. Note that when $\widehat{\mathbf{u}}$ is nearly perpendicular to $(\mathbf{v}\times \mathbf{B})$, the electric field polarization is nearly $-(\mathbf{v}\times \mathbf{B})$. This situation is relatively frequent in practice, and it is quite common to find in the literature $-(\mathbf{v}\times \mathbf{B})$ instead of the complete expression.

A number of assumptions are necessary for the superposition approach:

• The polarization of the electric field due to the excess charge is assumed to be $-\widehat{\mathbf{u}}\times (\widehat{\mathbf{u}}\times \mathbf{v})$, while that of the geomagnetic effect is assumed to approximately be parallel to $-(\mathbf{v}\times \mathbf{B})$.
• The amplitude of the electric field since each mechanism is supposed to have circular symmetry. At a given distance r (perpendicular to the shower axis), the magnitude of each component is constant, i.e., independent of the polar angle.
• Both components can be identified and separated using simulations. The ansatz is that the component of the field due to the excess charge, ${\mathbf{E}}_{\mathrm{Ask}}$, can be directly obtained simulating a shower with the magnetic field “switched” off, while the component due to the geomagnetic effect, ${\mathbf{E}}_{\mathrm{geo}}$, is obtained using a simulation with the magnetic field switched on, $\mathbf{E}$, and subtracting the excess charge from it to obtain ${\mathbf{E}}_{\mathrm{geo}}=\mathbf{E}-{\mathbf{E}}_{\mathrm{Ask}}$.

The implementation of this approach requires the simulation of the electric field vector along a line of observers, the “sampling line” at the ground level which becomes the basic input to deduce the electric field at any other position. The sampling line starts at the core of the shower on the ground and is directed radially outwards in an arbitrary direction. Once the fields are obtained, they give a functional dependence in terms of distance to the shower axis. If this is done at ground level for an inclined shower there are projection effects that are easily accounted for; basically, the distance on the ground must be converted to distance to the shower axis. The asymmetry of the distribution of the pulse amplitudes at the ground is obtained because of the different polarizations of the two components. As an observer rotates about the shower axis at a fixed r, the two components do not change their corresponding absolute value. However, the excess charge component makes a full rotation in the transverse plane while the geomagnetic component approximately points in the same direction. As a result, the two components can be aligned (or antialigned) for observer directions lying in the plane defined by $\mathbf{v}$ and $\mathbf{v}\times \mathbf{B}$, or at right angles when the observing direction is parallel to the plane defined by $\mathbf{v}$ and $\mathbf{B}$ (see Figure 8) [128].

This model reduces the calculation time for a given shower as observed from multiple positions at ground level. The approach has been recently improved and extended to account for observers at different observation planes and allow the calculation of the electric field time traces, an approach named radio-morphing [129].

6. Applications

Throughout the years, very few changes have been made to the actual calculation method and, in particular, to the ZHS algorithm, but the variety of situations in which it could be applied has been enhanced by combining it with other simulation programs, as described before, and also by the introduction of a number of extensions that improved its performance in several ways.

The ZHS code for electromagnetic showers were first combined with one-dimensional shower generators to simulate hadronic showers in ice [130], which allowed the first simulations of neutrino-induced showers [121]. The ZHS code was also extended to be usable in other dense homogeneous media besides ice [110], such as salt, or more importantly, the regolith of the Moon, allowing the sensitivity and potential of experiments using the Moon as a target for UHECR and neutrino interactions to be estimated [89,131]. Later on, specific thinning algorithms for radio calculations were developed and tested [120], allowing the simulation of pulses from showers of energies up to ${10}^{20}$ eV. Another extension of the ZHS code has been the possibility of using the endpoints methodology simultaneously with the ZHS algorithm for the calculation of pulses from the same shower, and the implementation of an exact calculation of the electric field free of all the approximations needed for the ZHS algorithm to work [104]. As stated before, the ZHS algorithm was implemented in AIRES, to benefit from its many capabilities as a shower simulator, to produce ZHAireS that can be used to calculate radio pulses in full 3-dimensional simulations of cosmic-ray and neutrino-induced showers both in dense homogeneous media [25] and in the atmosphere [27]. The extension of the ZHS algorithm to the time-domain [132] made it possible to calculate radio pulses of the same shower in both the Fourier and time domains with both ZHS and ZHAireS.

The most recent extensions made to the calculation of radio pulses with ZHS and ZHAireS deserve explicit and longer mention because they were developed with the intention of explaining measurements made with the ANITA detector system. An important development followed the data analysis of the first ANITA flight that revealed pulses that were compatible with coherent pulses from air showers because they displayed a strong polarization in a horizontal plane, parallel to the ground, as would be expected from the geomagnetic effect [57]. Most of these events were coming from directions below the Earth’s horizon, as seen from the ANITA position, while a few came from directions just above the horizon. The two classes of events display opposite polarity. Those events arriving from below the horizon were interpreted as downward-going cosmic-ray showers whose radio emission is reflected on the ice surface and travels in the upward direction, with the reflection inducing a flip in the polarity.

6.1. Reflected Pulses from Air Showers

The calculation of the reflected pulses had not been previously addressed and was made using ZHAireS as a base simulation, assuming rectilinear propagation of the “light rays” from the shower to the ice cap and after reflection on it [133]. This assumption is adequate as long as the zenith angle of the incoming showers does not exceed $\theta \sim {85}^{\circ }$ [133]. For each particle track in the shower simulation, there is a single point on the ice cap where the ray is reflected to reach the ANITA detector system. If the surface of the ice is assumed to be a horizontal plane, it is trivial to obtain the reflection point and then the direction of the emitted light ray relative to the track. Once the geometry is established, the contribution to the electric field of any track at the ANITA location is calculated, taking into account the Fresnel coefficients at the interface and the total distance of the reflected light ray from the track to the ice cap and then to the ANITA detector at an altitude of ∼36 km.

The developed extension of ZHAireS was used extensively to simulate pulses from air showers incident at high zenith angles. The pulses display a Cherenkov cone which is of order one degree, and the pulse intensity drops as the observation angle departs from the Cherenkov angle as expected. One can, in principle, only obtain a lower bound to the shower energy assuming observation is precisely at the Cherenkov cone. A measurement of the energy implies knowledge about the actual geometry of the emission relative to the shower direction. The simulations performed with ZHAireS revealed that the slope of the frequency spectrum in the ANITA frequency range (200–1200 MHz) is very sensitive to the deviation from the Cherenkov direction. By measuring the spectrum, it is possible to infer the observation angle with respect to the Cherenkov direction, and once this is known, the pulse amplitude at the Cherenkov angle can be inferred, showing that it scales linearly with the shower energy [61]. This is an important result because it demonstrates that it is possible to use radio pulses with detectors at a single location to reconstruct air showers. This finding was the basis of the analysis of the 14 pulses detected in the first ANITA flight, which led to the first measurement of the UHECR spectrum with the radio technique. Only one point was obtained at a mean energy of $2.9\times {10}^{18}$ eV, as displayed in Figure 9. A second point at a mean energy of $6.5\times {10}^{17}$ eV was obtained later with the 38 radio pulses observed with ARIANNA, a detector system with multiple antennas buried at shallow depths in Antarctica on the Ross ice shelf [134].

6.2. Direct Pulses from Air Showers Pointing Upwards

A second development of ZHAireS was also triggered by further analyses of ANITA data. During the first ANITA flight, four events were consistent with air shower pulses pointed in a direction below the horizon. One of them, with an elevation angle of $27.4^{\circ }$ as seen from the ANITA detector (zenith angle $\theta =117.4^{\circ })$, did not display the inverted polarity expected after reflection [82]. A second event below the horizon, with an elevation angle of $35.0^{\circ }$ ($\theta =125.0^{\circ }$) and non-inverted polarity, was also found in the analysis of the third ANITA flight [83]. These events have attracted a lot of attention because they could be compatible with pulses from air showers that develop in an upward direction. Such showers could be due to charged-current tau neutrino interactions under the Earth that produce a tau lepton which exits into the atmosphere where it decays in flight inducing an air shower developing in the upward direction. The pulse intensities allow an estimate of the neutrino energies to be over ∼$2\times {10}^{17}$ eV. The pulse directions imply that the parent neutrinos must have travelled thousands of kilometres under the Earth, well exceeding their mean free path in the Standard Model. First estimates showed that these neutrinos would be highly suppressed (by a factor of at least ∼${10}^{-5}$) due to attenuation in the Earth [82]. A more careful analysis of the events was made in [87] using another development of the ZHAireS code that allowed the simulation of pulses for showers developing in the upward direction. The simulation of these showers, together with the development of a specific program to model tau neutrino propagation and interactions on Earth, NuTauSim [137], led to detailed studies of the pulses expected from tau decays through this mechanism [87]. These studies revealed that the assumption that these events are due to a tau neutrino flux leading to tau decays requires a diffuse flux of UHE neutrinos at least two orders of magnitude above the upper limits set with the IceCube Neutrino observatory and the Pierre Auger Observatory [87]. More recently, four more such events were found at lower elevation angles, just below the horizon [84]. A similar conclusion has been reached with improved analysis of these events using ZHAireS. The assumption that a tau neutrino flux is the origin of these Earth-skimming events is in strong conflict with the limits obtained with IceCube and the Pierre Auger Observatory in the assumption of both a diffuse flux and a flux due to a few point-like sources [138].

6.3. Transition Radiation

A third significant development was also made by introducing in the ZHS code the capability to calculate coherent transition radiation as a shower intercepts the interface between two dense and homogeneous media. This line of work was also motivated by the ANITA anomalous events just described. The hypothesis that was tested was the possibility that neutrinos produced showers just below the surface of the Earth so that the shower exits into the atmosphere. The transition radiation due to all shower particles intercepting the interface is expected to keep some coherence and have a broad angular distribution and could be responsible for the observed events.

This was by far the most involved development from the point of view of the radio simulation because it required a modified prescription to calculate the pulses and combine two media. In the assumption of a shower coming from a dense medium such as ice into a lighter one such as air, the lateral spread of the shower as it intercepts the interface will be determined by the Moliére radius in the dense medium (∼11 cm in ice), which is relatively small compared to the wavelengths of the measured pulses. The ANITA detector can thus be assumed to be within the far distant limit. In addition, the shower develops first in a homogeneous medium, where the effect of the Earth’s magnetic field is believed not to play a significant role due to the reduced dimensions of the shower, of the order of meters in length. It is adequate to use the ZHS program paying a small price for not being able to simulate hadronic showers. The development of the program, dubbed ZHS-TR, was done assuming a perfect plane for the interface and considering only the radiation that was emitted into the atmosphere11.

Transition radiation is treated with the original ZHS algorithm, but when the tracks intercept the interface between the two media, a special procedure must be made to match the boundary conditions implied by the change of the medium. These tracks are subdivided into two, one in ice and the other in the atmosphere. The modification involves the calculation of the electric field of several contributions: (a) Radiation from the portion of the sub-track inside ice (and all other shower tracks that develop in ice) that is refracted into the atmosphere, (b) two contributions to the radiation from the portion of the sub-track that is in the atmosphere (and all other tracks that develop in the atmosphere), one that travels directly to the detector and another one that is emitted back to the interface where it is reflected towards the detector. All of these contributions must be added with care to correctly match their relative phases. This was achieved in the ZHS-TR code in the frequency domain leading to the first full calculation of coherent transition radiation [99].

Results showed that the emitted pulses are proportional to the number of particles that intercept the interface plane, so the most favourable situation is when the shower is close to shower maximum as it crosses the interface. Two favourable directions were clearly apparent in which the pulses have a larger amplitude. One is that of the Cherenkov cone in ice as it gets refracted into the atmosphere, and the second one corresponds to the Cherenkov cone in air, close to the direction of the shower axis, where the second part of the shower develops after the particles have crossed the interface. We will refer to these as the “Cherenkov directions”. The pulse in the Cherenkov direction as defined by the atmosphere is subject to greater uncertainty because the program treats the atmosphere as a homogeneous gas and, more importantly, it does not include the effects of the magnetic field of the Earth, which is known to be responsible for the dominant mechanism for radio pulses induced by atmospheric showers.

All of these conclusions were not so unexpected; in fact, the enhancement around the two Cherenkov directions is not exclusive to transition radiation but common to many other radiation mechanisms. The most important result, more closely linked with transition radiation, concerns the amplitude of the pulses in directions that are very different from those special ones discussed above. This amplitude is typical of order $10\%$ of the highest amplitudes seen in the Cherenkov directions [99], significantly larger than for equivalent directions when there is no transition radiation. The pulses were also shown to be much less directional as could be expected from the lateral distribution of the shower at the interface, which is typically small compared to the wavelengths of interest.

These results are interesting because they imply that showers can be detected from a wider range of directions, and in particular, they could be produced by Earth-skimming neutrinos, alleviating the problem of attenuation in the Earth. Detection in other than the Cherenkov direction would nevertheless imply larger energy thresholds by close to an order of magnitude. These simulations allowed a detailed study of the anomalous ANITA event detected in the first flight, in the assumption that it was due to transition radiation of showers that develop inside the ice and cross the ice cap. The optimistic calculations performed in [139] concluded that this explanation was possible from the point of view of the polarization of the signals, but it was again in strong conflict with limits from other neutrino experiments [139]. The gain in solid angle provided by the wider angular distribution of transition radiation is not enough to compensate for the increased energy threshold and implied loss of sensitivity.

6.4. Accelerator Tests

The viability of the radio technique was also explored at particle physics laboratories, and this has also served for testing the performance of the simulation programs that calculated coherent radio emissions. In the first experiment, showers were generated using a bunch of electrons incident on a large sand target at the Argonne Wakefield Accelerator [54]. In this experiment, coherent emission was detected, attributed both to transition and possibly Cherenkov radiation at different levels.

By changing the bunch of electrons to a bunch of photons from electron bremsstrahlung, the measured radiation was limited, primarily, to coherent Cherenkov in experiments performed at the Stanford Linear Accelerator [140], presenting the first direct experimental evidence for the charge excess in high-energy particle showers and showing results in good agreement with simulations based on ZHS. These experiments have been repeated in rock salt [141] and ice [142] targets.

More recently, a similar experiment has been performed using high-density polyethene and including a strong magnetic field to test the dominant (geo-)magnetic effect in air showers [143]. The setup of this experiment was simulated with GEANT, and the radio emission was calculated using the ZHS algorithm, comparing it to the endpoints methodology. The comparison between simulations and the experiment has been recently made in much greater detail, indicating differences typically below $10\%$, well within estimated uncertainties [144].

7. Prospects for the Future: Some Open Questions

When the original ZHS program to simulate radio pulses was created in 1990 the idea of using coherent radiation to detect neutrinos or other energetic particles was hardly being considered by the community; the radio technique had fallen out of favour earlier on, and only a few scientists considered the possibility to search for neutrinos in ice. The simulations revealed that the pulses had to be rather close to the antennae for showers below ${10}^{15}$ eV, which implied that this alternative would require large numbers of antennae, in addition to substantial research and development into this new technique to build a detector sensitive to neutrinos in this energy range and above. The results obtained with these early simulations gave a good perspective into the angular distribution and frequency spectra of the showers, as well as the scaling with shower energy and demonstrated the potential of the technique, particularly for higher energy showers, that stimulated much of the research that has followed.

Thirty years have passed since then, and the progress has been huge. Coherent radio emission has been studied in multiple media as a means to search for both neutrinos and cosmic rays. Since then, the number of new experiments being proposed has been steadily growing, and interestingly, there is a large diversity of ideas. Many of them have been converted into real experiments. Some others with larger sensitivities are in the planning: Experiments at high elevations like BEACON [93], or carrying arrays of antennas in balloons like PUEO [94], the successor of ANITA. Arrays of antennas in the ice or on the ground, such as RNO-G in Greenland [96]; the GRAND array [92]; the radio component of the AugerPrime detector in Argentina [95]; the radio component of IceCube-Gen2 at the South Pole [145] and the Square-Kilometer array SKA to search for radio pulses produced in neutrino and cosmic-ray showers inside the regolith of the Moon or the atmosphere [146].

The progression does not seem to have come to a halt. On the contrary, many initiatives have been converging into concrete ideas in the past couple of years. The need to calculate radio pulses in different and new circumstances is likely to continue pushing this simulation effort to reach a higher precision level, needed for future experiments measuring cosmic-ray showers and for neutrino signals that will eventually get measured with this technique. New effects will have to be included in the simulations, and effects that have already been addressed will have to be optimized and refined so that the precision of the calculations improves to the few per cent level, which is likely to put the technique at the forefront of the field.