Methodologies to Measure the $\mathcal{CP}$ Structure of the Higgs Yukawa Coupling to Tau Leptons

Abstract

One of the central goals of the Large Hadron Collider has been the search, and later the study, of the Higgs boson. Its coupling structure under charge conjugation and parity ($\mathcal{CP}$) symmetries has been extensively investigated as a probe for new physics. This paper presents a review of the methods collected in the literature to access the $\mathcal{CP}$ structure of the Yukawa coupling of the Higgs boson to tau leptons at proton colliders. A new notation is introduced to classify already existing methods, highlighting their common features and favoring the investigation of new, more performing alternatives.

1. Introduction

In July 2012 the CMS and ATLAS collaborations announced the discovery of the Higgs boson [1,2], opening the exploration of the Higgs sector of particle physics. According to the Standard Model (SM) of particle physics, the Higgs boson is predicted to have spin-parity $J^P=0^{+}$. Its Yukawa couplings to fermions are supposed to be invariant under the operations of charge conjugation and parity ($\mathcal{CP}$). Any anomalous $\mathcal{CP}$-odd component in the Yukawa couplings would constitute a clear sign of new physics, making the study of the structure under $\mathcal{CP}$ symmetry particularly interesting.

The production mechanisms of the Higgs boson at the LHC have been used throughout the years to probe the Higgs coupling to vector bosons and the Yukawa coupling to top quarks. These measurements targeted the direct coupling present in top-associated production (ttH) [3], and the coupling at loop level in the gluon–gluon–fusion process (ggH) [4]. The coupling to $\tau$ leptons does not contribute to the tree-level diagrams of production mechanisms and can be studied in the $H\to {\tau }^{+}{\tau }^{-}$ decay process. Several methods have been proposed in the literature for measuring the $\mathcal{CP}$ structure of the Yukawa coupling of the Higgs boson to $\tau$ leptons. This paper aims at reviewing such methods while providing a common notation that can be used to separate considerations of a phenomenological nature, from the geometrical and experimental ones.

The next section is used to provide a theoretical overview of the Higgs decay process to a $\tau$ pair final state. The symbols used in the paper are also defined. Section 3 provides a review of methods presented in literature for the measurement of the $\mathcal{CP}$ structure of the Yukawa coupling for different decay channels. The final section discusses the features common among the methods described in Section 3 and introduces a notation that can uniformly describe the aforementioned methods. The notation is also applied to already published experimental measurements, with the goal of favoring the combination of different measurements in the future. Analysis techniques that cannot be included in the presented notation are also acknowledged.

2. $\mathcal{CP}$ Structure of the Yukawa Interaction

The Yukawa Lagrangian can be written accounting for both a $\mathcal{CP}$-even and a $\mathcal{CP}$-odd coupling at leading order:

$${\mathcal{L}}_{Y,f}=-{\overline{\psi }}_f^L(y_f+i{\gamma }^5{\tilde{y}}_f)H{\psi }_f^R+h.c.,$$

(1)

where ${\psi }_f$ is the fermionic field, with the suffix ${}^{L\left(R\right)}$ being used to label its left (right) projection under chiral operators. The H represents the excitation of the Higgs field with respect to its vacuum state, ${\gamma }^5$ is the fifth Dirac matrix, and $y_f$ (${\tilde{y}}_f$) is the $\mathcal{CP}$-even ($\mathcal{CP}$-odd) coupling of the Higgs boson to the fermion of interest. The SM prediction corresponds in this notation to ${\tilde{y}}_f=0$ and $y_f=m_f/v$, with $m_f$ being the fermion mass and v the Higgs vacuum expectation value (vev). The branching fractions for Higgs fermionic decays depend only on the squared sum of the couplings, therefore it is useful to parametrize the couplings using a circular coordinate system:

$$\begin{array}{cc}\hfill y_f=& \frac{m_f}{v}\sqrt{{\mathsf{\mu }}_{ff}^H}cos{\mathsf{\Delta }}_{Hff},\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill {\tilde{y}}_f=& \frac{m_f}{v}\sqrt{{\mathsf{\mu }}_{ff}^H}sin{\mathsf{\Delta }}_{Hff}.\hfill \end{array}$$

(3)

Equation (1) is therefore rewritten as:

$$\begin{array}{cc}{\mathcal{L}}_{Y,f}=& -\frac{m_f}{v}\sqrt{{\mathsf{\mu }}_{ff}^H}{\overline{\psi }}_f[cos{\mathsf{\Delta }}_{Hff}\\ & +i{\gamma }^{5}sin{\mathsf{\Delta }}_{Hff}]H{\psi }_f+h.c,\end{array}$$

(4)

with ${\mathsf{\mu }}_{ff}^H$ quantifying the deviation from the SM prediction for the Higgs fermionic branching fractions, while the deviation from a pure $\mathcal{CP}$-even coupling is encoded in the angle ${\mathsf{\Delta }}_{Hff}$, referred to in this text as “$\mathcal{CP}$ mixing angle”. The SM prediction corresponds to ${\mathsf{\mu }}_{ff}^H=1$ and ${\mathsf{\Delta }}_{Hff}=0°$, while a pure $\mathcal{CP}$-odd coupling would be represented by ${\mathsf{\Delta }}_{Hff}=90°$. The Lagrangian presents a linear dependence on the fermionic mass. The properties under the $\mathcal{CP}$ symmetry of the Yukawa interaction can therefore be studied with processes involving third generation charged fermions, i.e., the top and bottom quarks, and the $\tau$ lepton. In this context, the coupling to $\tau$ leptons is unique as it does not contribute to leading order diagrams for the Higgs production at proton colliders. The $\mathcal{CP}$ structure of the Yukawa coupling to $\tau$ leptons can be studied in $H\to {\tau }^{+}{\tau }^{-}$ decays. As shown in the next section, the spin-correlation between $\tau$ leptons carries over to their decay products allowing for the measurement of ${\mathsf{\Delta }}_{H\tau \tau }$.

2.1. $\mathcal{CP}$ Violation in $H\to \tau \tau$ Decays

Equation (4) describes the Yukawa Lagrangian for a generic fermion including both $\mathcal{CP}$-even and $\mathcal{CP}$-odd couplings. For the decay to $\tau$ leptons it can be written, omitting the Hermitian conjugate, as:

$${\mathcal{L}}_{Y,\tau }=-\frac{m_{\tau }}{v}\overline{\tau }({\mathsf{\kappa }}_{\tau }+i{\gamma }^5{\tilde{\mathsf{\kappa }}}_{\tau })H\tau ,$$

(5)

where

$${\mathsf{\kappa }}_{\tau }=\sqrt{{\mathsf{\mu }}_{\tau \tau }^H}cos{\mathsf{\Delta }}_{H\tau \tau }$$

(6)

and

$${\tilde{\mathsf{\kappa }}}_{\tau }=\sqrt{{\mathsf{\mu }}_{\tau \tau }^H}sin{\mathsf{\Delta }}_{H\tau \tau }$$

(7)

are real parameters representing the reduced $\mathcal{CP}$-even and $\mathcal{CP}$-odd Yukawa couplings of the Higgs boson to $\tau$ leptons. The study of the $\mathcal{CP}$ structure of this Yukawa interaction requires computing the $H\to \tau \tau$ decay width differentially with respect to variables that are sensitive to the $\mathcal{CP}$ properties of the coupling structure. As shown in [5], the $H\to \tau \tau$ decay width can be written for pure $\mathcal{CP}$-even (${\mathsf{\kappa }}_{\tau }=1$ and ${\tilde{\mathsf{\kappa }}}_{\tau }=0$) or $\mathcal{CP}$-odd (${\mathsf{\kappa }}_{\tau }=0$ and ${\tilde{\mathsf{\kappa }}}_{\tau }=1$) couplings as a function of the tau leptons polarization $s^{\pm }$:

$$\mathsf{\Gamma }\left(H\left(\frac{\mathcal{CP}-even}{\mathcal{CP}-odd}\right)\to \right.\left.\phantom{\left(\frac{\mathcal{CP}-even}{\mathcal{CP}-odd}\right)}{\tau }^{+}{\tau }^{-}\right)={\mathsf{\Gamma }}^{unpol}\left(1-s_{//}^{-}·s_{//}^{+}\pm s_{\perp }^{-}·s_{\perp }^{+}\right),$$

(8)

where ${\mathsf{\Gamma }}^{unpol}$ represents the decay width calculated integrating over the polarization of the two tau leptons, and $s_{//}^{\pm }$ ($s_{\perp }^{\pm }$) the projection of the ${\tau }^{\pm }$ polarization in the direction parallel (orthogonal) to the tau direction-of-flight. The term $s_{\perp }^{-}·s_{\perp }^{+}$ appears in the equation with a + sign for a pure $\mathcal{CP}$-even coupling and with a − sign for a pure $\mathcal{CP}$-odd one. Equation (8) can then be generalized as shown in [6] to account for a more general admixture between $\mathcal{CP}$-even and $\mathcal{CP}$-odd couplings:

$$\mathsf{\Gamma }(H_{mix}\to \tau \tau )={\mathsf{\Gamma }}^{unpol}(1-s_{//}^{-}{s}_{//}^{+}+s_{\perp }^{-}R\left(2{\mathsf{\Delta }}_{H\tau \tau }\right)s_{\perp }^{+}).$$

(9)

The dependence of the Higgs decay width on the $\mathcal{CP}$ mixing angle is encoded in the matrix $R\left(2{\mathsf{\Delta }}_{H\tau \tau }\right)$, which alters the spin correlation between the tau transverse polarizations depending on the Higgs $\mathcal{CP}$ nature. The analytical form of this matrix can be found in [6] and is addressed later in the text as it depends on the frame of reference in which the vectors are defined. Equation (9) is used to establish the spin correlation between the Higgs boson and the tau leptons it decays to. The spin correlation depends on the transverse components of the tau polarization, which can be accessed via the tau decay products.

2.2. Tau Decays

There are two conventions generally used for describing tau decays:

• decay into a charged particle and a neutral system: ${\tau }^{-}\to N^0{p}^{-}$;
• decay into a tauonic neutrino and charged system: ${\tau }^{-}\to {\nu }_{\tau }{\chi }^{-}$.

This difference in approaches later evolved in distinct methods used to study the $\mathcal{CP}$ properties of the Higgs Yukawa coupling to $\tau$ leptons. The differential decay width in approach 1 can be written as [7]:

$$\mathrm{d}{\mathsf{\Gamma }}_{{\tau }^{-}\to N^0{p}^{-}}=A\left(x\right)\left[1\pm B\left(x\right)(\overrightarrow{s}·\widehat{q})\right]\mathrm{d}x\frac{\mathrm{d}\Omega }{4\mathsf{\pi }},$$

(10)

where $\widehat{q}$ and x are respectively the direction-of-flight of the charged particle $p^{-}$, usually referred to as prong, and the fraction of the $\tau$ momentum it carries, $\overrightarrow{s}$ is the $\tau$ spin, and d$\Omega$ is the infinitesimal element of solid angle. The functions $A\left(x\right)$ and $B\left(x\right)$ are known in literature as spectral functions and their behavior has been described in several publications [7,8,9,10]. The correlation between the $\tau$ spin and the momentum of one charged prong is encoded in the term $B\left(x\right)(\overrightarrow{s}·\widehat{q})$. Equation (10) can be rewritten according to the approach 2, in a Lorentz invariant frame of reference for decays of the form ${\tau }^{-}\to {\nu }_{\tau }{\chi }^{-}$ as [11,12]:

$$\mathrm{d}{\mathsf{\Gamma }}_{{\tau }^{-}\to {\nu }_{\tau }{\chi }^{-}}=\frac{1}{2m_{\tau }}{\left|\mathcal{M}\right|}^2(1+h_{\mu }{s}^{\mu })\mathrm{d}Lips.$$

(11)

This differential expression of the decay width with respect to a Lorentz invariant phase-space ($Lips$) element contains a term analogous to the scalar product $\overrightarrow{s}·\overrightarrow{q}$ found in Equation (10): $h_{\mu }{s}^{\mu }$. The tau spin s is now written as a four-dimensional vector, while $h^{\mu }$ is used to encode the spin-correlation between the $\tau$ lepton and its decay products, and in this paper is referred to as polarimetric vector (analogous terms found in the literature to describe this quantity are: polarimeter vector and tau polarimeter).

2.3. The Acoplanarity Angle

Using either description of the tau decays it is possible to show [13,14] that the $H\to \tau \tau$ cross-section acquires a sinusoidal dependence with respect to the angle between the tau decay planes, i.e., the acoplanarity angle. In approach 1, the tau decay plane is naturally defined by the $\tau$ direction-of-flight and the charged prong momentum. The latter is replaced by the polarimetric vector in approach 2.

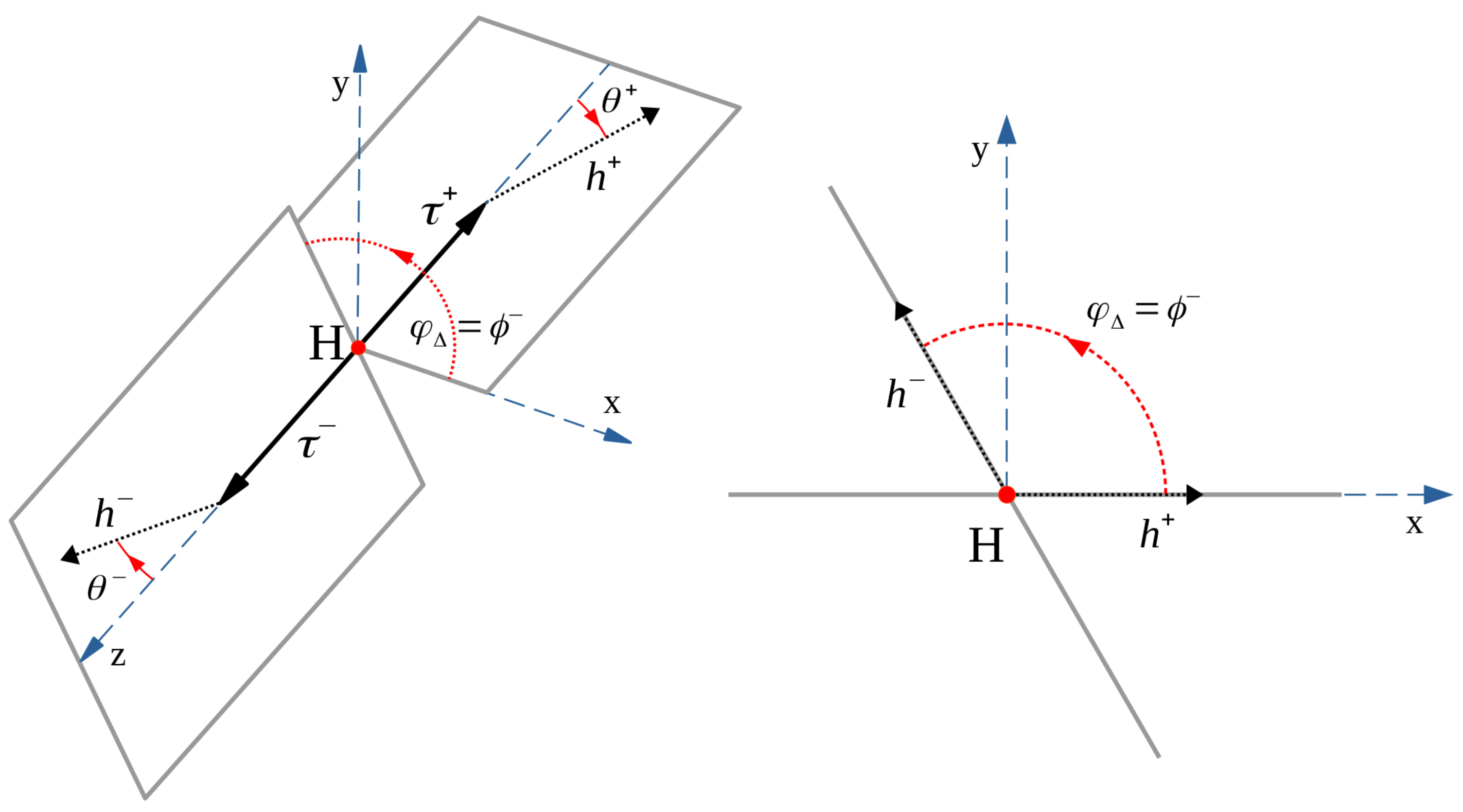
Before discussing the analytical form taken by the $H\to \tau \tau$ cross-section, it is useful to define a specific frame of reference. Figure 1 shows the Higgs rest-frame with the z axis aligned with the ${\tau }^{-}$ direction-of-flight, while the x axis is directed so as to lie on the plane formed by the ${\tau }^{-}$ and its corresponding polarimetric vector ($h^{-}$). The symbols ${\theta }^{\pm }$ and ${\varphi }^{\pm }$ represent the polar and azimuthal angles defining the direction of each polarimetric vector with respect to the corresponding $\tau$ lepton direction-of-flight. In this frame of reference, ${\varphi }^{+}=0°$ and the difference between the two azimuthal angles is

$${\mathsf{\phi }}_{\mathsf{\Delta }}={\varphi }^{-}-{\varphi }^{+}={\varphi }^{-}.$$

(12)

In this frame of reference the R matrix introduced in Equation (9) takes the form [6]:

$$R\left(2{\mathsf{\Delta }}_{H\tau \tau }\right)\simeq \left[\begin{array}{ccc}cos\left(2{\mathsf{\Delta }}_{H\tau \tau }\right)& sin\left(2{\mathsf{\Delta }}_{H\tau \tau }\right)& 0\\ -sin\left(2{\mathsf{\Delta }}_{H\tau \tau }\right)& cos\left(2{\mathsf{\Delta }}_{H\tau \tau }\right)& 0\\ 0& 0& -1\end{array}\right],$$

(13)

and the $H\to \tau \tau$ cross-section can be written, in the limit of ultrarelativistic tau leptons, as [15]:

$$\begin{array}{cc}\hfill \mathrm{d}{\mathsf{\sigma }}_{H\to \tau \tau }& /\mathrm{d}cos{\theta }^{+}\mathrm{d}cos{\theta }^{-}\mathrm{d}{\mathsf{\phi }}_{\Delta }\sim \hfill \\ & \left[1+cos{\theta }^{+}cos{\theta }^{-}-sin{\theta }^{+}sin{\theta }^{-}cos\left({\mathsf{\phi }}_{\mathsf{\Delta }}-2{\mathsf{\Delta }}_{H\tau \tau }\right)\right].\hfill \end{array}$$

(14)

The analogous expression obtained by describing $\tau$ decays with approach 1 is [16]:

$$\mathrm{d}{\mathsf{\sigma }}_{H\to \tau \tau }/\mathrm{d}{x}_{-}\mathrm{d}{x}_{+}\mathrm{d}{\mathsf{\phi }}_{\Delta }\sim 1-B\left(x_{-}\right)B\left(x_{+}\right)\frac{{\mathsf{\pi }}^2}{16}cos\left({\mathsf{\phi }}_{\mathsf{\Delta }}-2{\mathsf{\Delta }}_{H\tau \tau }\right),$$

(15)

with ${\mathsf{\phi }}_{\mathsf{\Delta }}$ representing here the azimuthal difference between the two charged prong momenta.

In both expressions, the term $s_{\perp }^{-}R\left(2{\mathsf{\Delta }}_{H\tau \tau }\right)s_{\perp }^{+}$ of Equation (9) is rewritten as a function of the angle ${\mathsf{\Delta }}_{H\tau \tau }$ and the azimuthal distance between vectors which lie on the tau decay planes. The latter is labeled ${\mathsf{\phi }}_{\mathsf{\Delta }}$ in both equations as the angle between the tau decay planes is a physical observable and therefore cannot depend on the specific approach used to describe the tau lepton decays. Analytically, the acoplanarity angle can be defined based on the vectorial product of the polarimetric vector with its corresponding tau momentum (${\overrightarrow{h}}^{\pm }\times {\overrightarrow{p}}_{\tau }^{\pm }$) [14]:

$${\mathsf{\phi }}_{\mathsf{\Delta }}=\left\{\begin{array}{cc}{\mathsf{\phi }}^{*},\hfill & \mathrm{if}\mathcal{O}\ge 0\hfill \\ 2\mathsf{\pi }-{\mathsf{\phi }}^{*},\hfill & \mathrm{if}\mathcal{O}<0\hfill \end{array}\right.,$$

(16)

where

$${\mathsf{\phi }}^{*}=arccos(\frac{{\overrightarrow{h}}^{-}\times {\overrightarrow{p}}_{\tau }^{-}}{|{\overrightarrow{h}}^{-}\times {\overrightarrow{p}}_{\tau }^{-}|}·\frac{{\overrightarrow{h}}^{+}\times {\overrightarrow{p}}_{\tau }^{+}}{|{\overrightarrow{h}}^{+}\times {\overrightarrow{p}}_{\tau }^{+}|}),$$

(17)

and

$$\mathcal{O}=\frac{({\overrightarrow{h}}^{+}\times {\overrightarrow{h}}^{-})·{\overrightarrow{p}}_{{\tau }^{-}}}{|({\overrightarrow{h}}^{+}\times {\overrightarrow{h}}^{-})·{\overrightarrow{p}}_{{\tau }^{-}}|}.$$

(18)

The variable $\mathcal{O}$ is used in order to define the acoplanarity angle between 0 and 2$\mathsf{\pi }$. One common notation found in literature is to establish a right-hand rule with respect to the $\tau -$ direction-of-flight for the angle definition. This is reflected in the choice of the right-handed coordinate system shown in Figure 1.

The acoplanarity definition in approach 1 is obtained by replacing the ${\overrightarrow{h}}^{\pm }$ vectors with the momentum of the charged decay product of the tau lepton. The difference between the two approaches resides in the factors multiplying the cosine functions: in Equation (15) there is an explicit dependence on the momentum fraction carried by the charged particles, while in Equation (14) the energy dependence is implicit into the polarimetric vector definition. The factor $B\left(x_{-}\right)B\left(x_{+}\right)$ does not have a definite sign, leading to different phase-space regions providing contributions of opposite sign to the $H\to \tau \tau$ cross-section in Equation (15).

2.4. Experimental Challenges at Proton Colliders

The measurement of the acoplanarity angle is affected by several experimental challenges. The average lifetime of tau leptons is $(2.903\pm 0.005)\times {10}^{-13}$ s [17], and therefore mostly decays before its track can be reconstructed by experiments placed at particle colliders. Furthermore, tau leptons decay always via electroweak charged current interaction, producing at least one neutrino. This leads to inefficiencies in the reconstruction of their momentum and, consequently, of the Higgs rest-frame. The next section describes the methods established in literature for the measurement of the acoplanarity angle at particle colliders and how they can overcome these experimental challenges.

3. Experimental Methods

3.1. Impact Parameter Method

The first method was introduced in the literature to measure the acoplanarity angle by describing tau decays according to approach 1. It was also chosen in CMS [18] as the experimental technique to measure the acoplanarity angle when both tau leptons decay to a single charged particle and one or two neutrinos. These decays will be referred to as one prong decays and are used here as the main examples for the application of this method.

For $\tau \to \mathsf{\pi }{\nu }_{\tau }$ decays the polarimetric vector coincides with the 4-momentum of the charged pion and the spectral function $B\left(x\right)$ defined in approach 1 is constant. This means that both approaches would lead to identical experimental definitions of the acoplanarity angle for this decay channel.

For $\tau \to \ell {\nu }_{\tau }{\nu }_{\ell }$, the spectral function is non-constant [7]:

$$B_{\ell }\left(x\right)=\frac{4E-m_{\tau }-\frac{3m_{\ell }^2}{m_{\tau }}}{4E+\frac{m_{\ell }^2}{E}-\frac{3m_{\ell }^2}{m_{\tau }}-3m_{\tau }}x,$$

(19)

where E and $m_{\tau }$ represent the energy and mass of the tau lepton, $m_{\ell }$ the mass of the lepton, and x the fraction of the tau momentum it carries.

The tau momentum instead cannot be reconstructed since the particle decays before interacting with the tracking system of current particle collider experiments. The method proposed in [16] for reconstructing the acoplanarity angle substitutes the tau momentum with the impact parameter of its charged decay product (IP).

In Equation (17) the tau lepton momentum always appears as part of a vectorial product with the charged decay product momentum. The component of the tau momentum parallel to its charged decay product is irrelevant in the acoplanarity angle calculation, allowing the IP to be a good replacement for the tau momentum.

The IP is constructed as shown in Figure 2. The vector connecting the primary interaction vertex (PV) to the point of closest approach (PCA) of the charged particle to the PV is used to approximate the tau lepton direction-of-flight. The IP is then defined as the component of the vector $\overrightarrow{PCA}-\overrightarrow{PV}$ orthogonal to the prong momentum.

Due to its reliance on the IP, this method will be referred to in the text as the “Impact parameter method”. To fully define the method another relevant characteristic is the frame of reference where the IPs and the prong momenta are measured. When both tau leptons decay to a single charged particle of momentum ${\overrightarrow{p}}_p^{\pm }$ and one or two neutrinos, the Higgs rest-frame is replaced by the zero-momentum-frame (ZMF) formed by the two charged particles.

$${\mathsf{\phi }}_{\mathsf{\Delta }}=\left\{\begin{array}{cc}{\mathsf{\phi }}^{*},\hfill & \mathrm{if}\mathcal{O}\ge 0\hfill \\ 2\mathsf{\pi }-{\mathsf{\phi }}^{*},\hfill & \mathrm{if}\mathcal{O}<0\hfill \end{array}\right.,$$

(20)

where

$${\mathsf{\phi }}^{*}=arccos({\overrightarrow{IP}}_{\perp }^{+}·{\overrightarrow{IP}}_{\perp }^{-}),$$

(21)

and

$$\mathcal{O}=({\overrightarrow{IP}}_{\perp }^{+}\times {\overrightarrow{IP}}_{\perp }^{-})·\frac{{\overrightarrow{p}}_p^{-}}{|{\overrightarrow{p}}_p^{-}|}.$$

(22)

This method can also be applied to other decay channels of the tau lepton, provided that the appropriate spectral functions are used and that the ZMF is defined using the momenta of the charged decay products.

3.2. Polarimetric Vector Method

The methods described in this and the following section both rely on the tau lepton decay description of approach 2, with different degrees of approximation.

If the tau lepton momentum and its polarimetric vector can be reconstructed with sufficient precision, the acoplanarity angle can be measured directly using Equation (17). This is experimentally verified for tau lepton decays to three charged pions via the intermediate ${\mathcal{a}}_1$ meson resonance. The presence of three charged particles in the decay allows the identification of the tau lepton decay vertex, providing a more precise reconstruction of its momentum. This in turn allows us to better reconstruct the rest-frame of the tau pair system.

The tau lepton polarimetric vector for the ${\tau }^{\pm }\to {\mathsf{\pi }}^{\pm }{\mathsf{\pi }}^{\pm }{\mathsf{\pi }}^{\mp }{\nu }_{\tau }$ decays can be expressed using the momenta of the three charged pions as described in [12,19]. This decay channel is obtained via a chain of two-body decays using several intermediate mesonic resonances [17], e.g., ${\tau }^{\pm }\to {\mathcal{a}}_1^{\pm }{\nu }_{\tau }\to {\mathsf{\rho }}^0{\mathsf{\pi }}^{\pm }{\nu }_{\tau }\to {\mathsf{\pi }}^{\pm }{\mathsf{\pi }}^{\pm }{\mathsf{\pi }}^{\mp }{\nu }_{\tau }$. The polarimetric vector can be computed numerically using the Monte Carlo (MC) methods described in [8,20,21,22].

3.3. Neutral Pion Method

The last method considered is an approximation of the polarimetric vector method to cases where the rest-frame of the tau pair system is not reconstructed precisely, but some properties of the polarimetric vector are still accessible. In ${\tau }^{\pm }\to {\mathsf{\pi }}^{\pm }{\mathsf{\pi }}^0{\nu }_{\tau }$ decays, for example, the charged and neutral pions are obtained via a $\mathsf{\rho }$ meson decay. The tau lepton polarimetric vector takes the form [21,23]:

$$\overrightarrow{h}=\mathcal{N}(2(q·N)\overrightarrow{q}-q^2\overrightarrow{N})\simeq \mathcal{N}(2m_{\tau }(E_{{\mathsf{\pi }}^{\pm }}-E_{{\mathsf{\pi }}^0})\overrightarrow{q}-q^2\overrightarrow{N}),$$

(23)

with $\mathcal{N}$ normalization factor, $q=(q_0,\overrightarrow{q})$ difference between the charged and neutral pion momenta and $N=(N_0,\overrightarrow{N})$ neutrino momentum, all defined in the tau lepton rest-frame. The second part of the equation is written by neglecting the mass difference between the two pions. This introduces a change of sign in the polarimetric vector definition based on the energy difference between the charged ($E_{{\mathsf{\pi }}^{\pm }}$) and neutral pion ($E_{{\mathsf{\pi }}^0}$). By definition, the polarimetric vector in the $\tau$ rest-frame lays in the same plane as the pions and neutrino. When neglecting the neutrino momentum, in the laboratory frame of reference the tau direction-of-flight also lies in the same plane. Therefore a direction orthogonal to the momenta of the two pions, is approximately also orthogonal to the tau lepton polarimetric vector and momentum:

$$({\overrightarrow{p}}_{{\mathsf{\pi }}^{\pm }}\times {\overrightarrow{p}}_{{\mathsf{\pi }}^0}){\displaystyle //}(\overrightarrow{h}\times {\overrightarrow{p}}_{\tau }).$$

(24)

This observation is at the core of the method introduced in [23] and is here referred to as the “neutral pion method”. The momentum of the charged pion replaces the tau lepton one both in the calculation of the acoplanarity angle and in the definition of the frame of reference where all vectors are defined, namely the ZMF of the charged pion system. The neutral pion momentum replaces instead the polarimetric vector.

To account for the polarimetric vector change of sign with respect to the energy of the two pions, the acoplanarity angle is measured separately in two categories. When both tau leptons decay via intermediate $\mathsf{\rho }$ resonance, such regions are defined based on the sign of the product $y_{+}·y_{-}$, where:

$$y_{\pm }=\frac{E_{{\mathsf{\pi }}^{\pm }}-E_{{\mathsf{\pi }}^0}}{E_{{\mathsf{\pi }}^{\pm }}+E_{{\mathsf{\pi }}^0}}.$$

(25)

As shown in [23], the acoplanarity distribution in the region $y_{+}·y_{-}<0$ assumes a sinusoidal dependence which is affected by a phase shift of $\mathsf{\pi }$ with respect to the distribution for $y_{+}·y_{-}>0$. The two distributions are also generally combined by operating a phase-shift of $\mathsf{\pi }$ to one of them: both in [23] and in [18] the convention used is to apply a phase-shift of $\mathsf{\pi }$ to the acoplanarity angle distribution for events with $y_{+}·y_{-}<0$.

4. Notation for the Acoplanarity Angle Reconstruction

The previous section focused on the methods established in the literature for measuring the acoplanarity angle in order to access the $\mathcal{CP}$ structure of the Yukawa coupling between the Higgs boson and tau leptons. This section is dedicated to underlining the common features observed in the established methods, and proposing a new notation that can be used to unify them.

As previously mentioned, established experimental methods have been developed accounting for the limitation of hadron collider experiments. The impossibility of directly reconstructing neutrinos leads to the following properties not being precisely reconstructed:

• the total tau lepton momentum;
• the tau pair rest-frame;
• the tau lepton polarimetric vector.

The polarimetric vector method estimates the acoplanarity angle using an approximation of the tau lepton polarimetric vectors and their ZMF. This is possible when the decay vertex of the tau lepton is reconstructed with sufficient precision or the neutrinos carry a relatively low fraction of the tau lepton momentum. Events where both tau leptons decay into three charged pions and a neutrino can satisfy this condition. The other methods rely on the ZMF of charged particles as a replacement for the tau lepton pair rest-frame.

The reason behind this substitution can be understood by separating geometrical considerations in the acoplanarity calculation from the physical ones. By definition, the acoplanarity angle is defined as the angle spanned between the two tau decay planes. In order for the angle to be uniquely defined, it must be measured in a reference frame where the two decay planes share one axis in common. If this co-planar axis is defined with a specific direction, it also allows for the angle definition to be extended between 0 and 2$\mathsf{\pi }$.

The ZMF of two particles, each originated by a separate tau lepton decay, naturally satisfies these requirements. The same is verified for the tau pair rest-frame. Furthermore, the ZMF of two prongs provides the following advantages:

• charged particle momenta are generally reconstructed with higher precision compared to neutral particle ones;
• the charge sign can be used to define the axis orientation and, consequently, define the acoplanarity angle between 0 and 2$\mathsf{\pi }$.

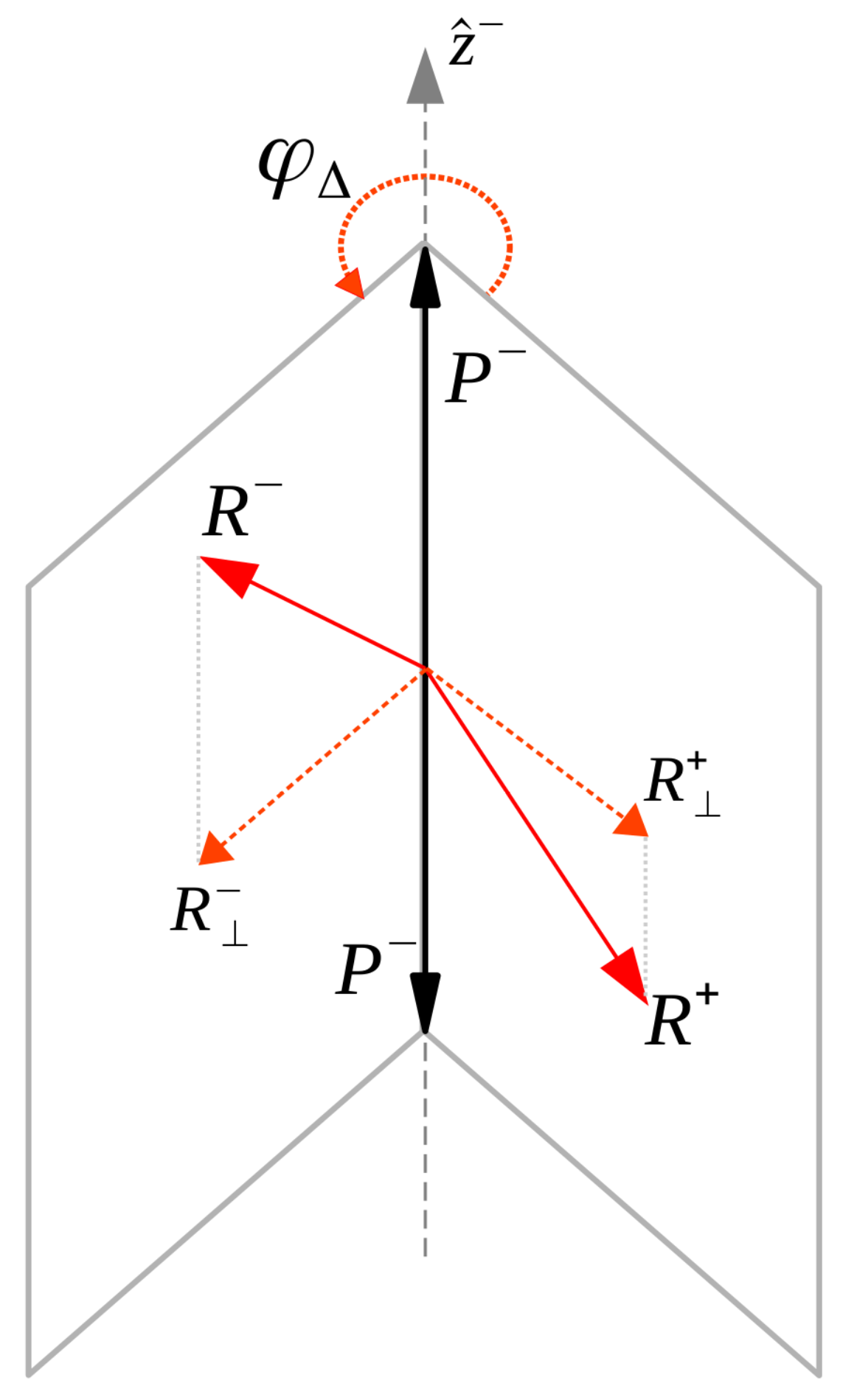
For simplicity let $\widehat{z}$ be an axis, with a defined orientation, which is co-planar to the two tau decay planes in a certain frame of reference. This and other vectors of unitary modules are represented in this section with the symbol $\widehat{}$. If each plane is defined such that its normal (${\widehat{n}}_{1,2}$) has also defined orientation then the acoplanarity angle can be calculated as:

$${\mathsf{\phi }}_{\mathsf{\Delta }}=\left\{\begin{array}{cc}{\mathsf{\phi }}^{*},\hfill & if\mathcal{O}\ge 0\hfill \\ 2\mathsf{\pi }-{\mathsf{\phi }}^{*},\hfill & if\mathcal{O}<0\hfill \end{array}\right.,$$

(26)

where

$${\mathsf{\phi }}^{*}=arccos({\widehat{n}}_1·{\widehat{n}}_2),$$

(27)

and

$$\mathcal{O}=({\widehat{n}}_1\times {\widehat{n}}_2)·\widehat{z}.$$

(28)

The angle ${\mathsf{\phi }}_{\mathsf{\Delta }}$ is uniquely defined once the following conventions are established:

• the direction of $\widehat{z}$;
• which normal is assigned to the ${\tau }^{-}$ decay plane in Equation (28);
• how the orientation of the two normals is determined.

The direction of $\widehat{z}$ was found to be coherently assigned in [6,15,16,23,24,25] to the direction-of-flight of the ${\tau }^{-}$ or of one of its decay products. This convention will be represented in the text by the use of the versor ${\widehat{z}}^{-}$.

Assuming that the azimuthal coordinates of the planes (${\mathsf{\phi }}^{\pm }$) with respect to the ${\widehat{z}}^{-}$ axis are defined following a right-hand rule, choosing the order of the vectors in Equation (28) is equivalent to defining the angle ${\mathsf{\phi }}_{\mathsf{\Delta }}$ either as ${\mathsf{\phi }}^{+}-{\mathsf{\phi }}^{-}$ or ${\mathsf{\phi }}^{-}-{\mathsf{\phi }}^{+}$:

$$\mathcal{O}=\left\{\begin{array}{cc}({\widehat{n}}^{+}\times {\widehat{n}}^{-})·{\widehat{z}}^{-},\hfill & if{\mathsf{\phi }}_{\mathsf{\Delta }}={\mathsf{\phi }}^{-}-{\mathsf{\phi }}^{+}\hfill \\ ({\widehat{n}}^{-}\times {\widehat{n}}^{+})·{\widehat{z}}^{-},\hfill & if{\mathsf{\phi }}_{\mathsf{\Delta }}={\mathsf{\phi }}^{+}-{\mathsf{\phi }}^{-}\hfill \end{array}\right..$$

(29)

The most common convention found in the literature [6,13,24,25] is to define ${\mathsf{\phi }}_{\mathsf{\Delta }}={\mathsf{\phi }}^{-}-{\mathsf{\phi }}^{+}$ and $\mathcal{O}=({\widehat{n}}^{+}\times {\widehat{n}}^{-})·{\widehat{z}}^{-}$, while the opposite choice was found in [15]. In older articles [14,23], the acoplanarity angle was defined between 0 and $\mathsf{\pi }$, making this particular convention irrelevant.

The last convention to establish is the orientation of the normal vectors ${\widehat{n}}^{\pm }$. From the geometrical point of view, a plane can be uniquely defined given two intersecting lines. However, such a definition leaves the orientation of the normal ambiguous. The vectorial product of two non-parallel vectors lying on the same plane can instead be used. In the polarimetric vector method this corresponds to the following definition of the plane normals:

$${\widehat{n}}^{\pm }=\frac{{\overrightarrow{h}}^{\pm }\times {\overrightarrow{p}}_{\tau }^{\pm }}{|{\overrightarrow{h}}^{\pm }\times {\overrightarrow{p}}_{\tau }^{\pm }|}.$$

(30)

The definition of the plane normals in the impact parameter and neutral pion methods is less obvious since the impact parameter and neutral pion momenta are used in the calculation of the acoplanarity angle.

As shown in Section 2.2.3 of [26], Equation (17) can be rewritten in function of the polarimetric vector components orthogonal to the tau lepton momentum defined in the tau pair ZMF (${\overrightarrow{h}}_{\perp }^{\pm }$):

$${\mathsf{\phi }}^{*}=arccos(\frac{{\overrightarrow{h}}^{-}\times {\overrightarrow{p}}_{\tau }^{-}}{|{\overrightarrow{h}}^{-}\times {\overrightarrow{p}}_{\tau }^{-}|}·\frac{{\overrightarrow{h}}^{+}\times {\overrightarrow{p}}_{\tau }^{+}}{|{\overrightarrow{h}}^{+}\times {\overrightarrow{p}}_{\tau }^{+}|})=arccos(-\frac{{\overrightarrow{h}}_{\perp }^{-}}{|{\overrightarrow{h}}_{\perp }^{-}|}·\frac{{\overrightarrow{h}}_{\perp }^{+}}{|{\overrightarrow{h}}_{\perp }^{+}|}).$$

(31)

The negative sign appearing on the right side of the equation is equivalent to a phase-shift of $\mathsf{\pi }$ with respect to the angle computed with the scalar product of the ${\overrightarrow{h}}_{\perp }^{\pm }$ vectors.

Applying the inverse transformation to the acoplanarity angle definition for the impact parameter method results in the following equation:

$${\mathsf{\phi }}^{*}=arccos({\overrightarrow{IP}}_{\perp }^{+}·{\overrightarrow{IP}}_{\perp }^{-})=\mathsf{\pi }-arccos(\frac{{\overrightarrow{IP}}_{\perp }^{-}\times {\overrightarrow{p}}_p^{-}}{|{\overrightarrow{IP}}_{\perp }^{-}\times {\overrightarrow{p}}_p^{-}|}·\frac{{\overrightarrow{IP}}_{\perp }^{+}\times {\overrightarrow{p}}_p^{+}}{|{\overrightarrow{IP}}_{\perp }^{+}\times {\overrightarrow{p}}_p^{+}|}).$$

(32)

The planes are not defined using the same convention in the different methods. However, in each method, the orientation of the decay planes is uniquely defined, allowing the establishment of a common notation for the decay plane definition.

4.1. Common Notation for the Acoplanarity Angle Measurement

All reviewed methods require that the decay plane of a tau lepton is defined by two vectors:

• the momentum of a charged particle: ${\overrightarrow{\mathcal{P}}}^{\pm }$
• a reference vector, non-parallel to the first one: ${\overrightarrow{\mathcal{R}}}^{\pm }$.

The acoplanarity angle is then defined by boosting all vectors in the ZMF of the two charged particle momenta, defined such that:

$${\overrightarrow{P}}^{+}+{\overrightarrow{P}}^{-}=0,$$

(33)

where the vectors ${\overrightarrow{P}}^{\pm }$ are obtained by boosting ${\overrightarrow{\mathcal{P}}}^{\pm }$ in this ZMF.

Let ${\overrightarrow{R}}^{\pm }$ be the vectors corresponding to ${\overrightarrow{\mathcal{R}}}^{\pm }$ in the same frame of reference. As a function of these vectors, the acoplanarity angle can be calculated as:

$${\mathsf{\phi }}_{\mathsf{\Delta }}=\left\{\begin{array}{cc}{\mathsf{\phi }}^{*},\hfill & \mathrm{if}\mathcal{O}\ge 0\hfill \\ 2\mathsf{\pi }-{\mathsf{\phi }}^{*},\hfill & \mathrm{if}\mathcal{O}<0\hfill \end{array}\right.,$$

(34)

where

$${\mathsf{\phi }}^{*}=arccos\left(\frac{{\overrightarrow{R}}_{\perp }^{-}}{|{\overrightarrow{R}}_{\perp }^{-}|}·\frac{{\overrightarrow{R}}_{\perp }^{+}}{|{\overrightarrow{R}}_{\perp }^{+}|}\right),$$

(35)

$$\mathcal{O}=({\overrightarrow{R}}_{\perp }^{+}\times {\overrightarrow{R}}_{\perp }^{-})·{\overrightarrow{P}}^{-},$$

(36)

$${\overrightarrow{R}}_{\perp }^{\pm }={\overrightarrow{R}}^{\pm }-({\overrightarrow{R}}^{\pm }·{\overrightarrow{P}}^{\pm })\frac{{\overrightarrow{P}}^{\pm }}{|{\overrightarrow{P}}^{\pm }|}.$$

(37)

This notation focuses on defining the $\tau$ decay planes before the acoplanarity angle is calculated. A visual representation of the acoplanarity angle defined according to this notation is shown in Figure 3.

Table 1. Summary of the vectors used in the presented notation to reconstruct the acoplanarity angle in order to reproduce the methods described in Section 3. The last column shows the condition for which it is preferable to apply a phase shift of $\mathsf{\pi }$. A-symbol is used to mark methods which do not require such a phase shift, while the $y_{\pm }$ definition can be found in Equation (25).

Method	P1	R1	P2	R2	$\mathsf{\pi }$ Phase-Shift
Impact parameter	${\overrightarrow{p}}_p$	$\overrightarrow{IP}$	${\overrightarrow{p}}_p$	$\overrightarrow{IP}$	-
Neutral pion	${\overrightarrow{p}}_{\mathsf{\pi }}$	${\overrightarrow{p}}_{{\mathsf{\pi }}^0}$	${\overrightarrow{p}}_{\mathsf{\pi }}$	${\overrightarrow{p}}_{{\mathsf{\pi }}^0}$	$y_{+}·y_{-}<0$
Polarimetric vector	${\overrightarrow{p}}_{\tau }$	$\overrightarrow{h}$	${\overrightarrow{p}}_{\tau }$	$\overrightarrow{h}$	-

summarizes how the methods described in Section 3 can be expressed in the proposed notation. Indices 1 and 2 are used instead of the charge for keeping the notation more general. In some circumstances, it is preferable to apply a phase-shift of $\mathsf{\pi }$ to the angle definition, in order to improve the sensitivity to the $\mathcal{CP}$ mixing angle ${\mathsf{\Delta }}_{H\tau \tau }$. This is expressed in the last column of Table 1, as the recommended condition under which to apply a

$${\mathsf{\phi }}_{\mathsf{\Delta }}\to {\mathsf{\phi }}_{\mathsf{\Delta }}+\mathsf{\pi }$$

(38)

transformation to the acoplanarity angle. This notation allows to define the acoplanarity angle uniformly among different decay channels. With respect to some established methods, the only difference in the sinusoidal dependence of the $H\to \tau \tau$ cross-section is a redefinition of the angle ${\mathsf{\phi }}^{*}$ to $\mathsf{\pi }-{\mathsf{\phi }}^{*}$.

Multi-body decays do, in general, offer multiple possibilities for the decay plane reconstruction. For example, in ${\tau }^{-}\to {\nu }_{\tau }{\mathcal{a}}_1^{-}\to {\nu }_{\tau }{\mathsf{\pi }}^{-}{\mathsf{\pi }}^0{\mathsf{\pi }}^0$ decays a total of three particles are reconstructed in the final state, a charged pion and two neutral ones. Depending on the resolution of the specific experiment, the decay plane for this channel could be reconstructed using:

• the total momentum of the three pions ($\overrightarrow{\mathcal{P}}$) and the $\tau$ polarimetric vector ($\overrightarrow{\mathcal{R}}$);
• the total momentum of the three pions ($\overrightarrow{\mathcal{P}}$) and the impact parameter of the ${\mathsf{\pi }}^{-}$ ($\overrightarrow{\mathcal{R}}$);
• the ${\mathsf{\pi }}^{-}$ momentum ($\overrightarrow{\mathcal{P}}$) and the sum of the two ${\mathsf{\pi }}^0$ momenta ($\overrightarrow{\mathcal{R}}$), applying a phase shift of $\mathsf{\pi }$ based on the energy difference between the charged pion and the neutral ones.

In the last case the phase shift could be applied applied when:

$$y_{-}^{{\mathcal{a}}_1}=\frac{E_{{\mathsf{\pi }}^{-}}-E_{{\mathsf{\pi }}^0{\mathsf{\pi }}^0}}{E_{{\mathsf{\pi }}^{-}}+E_{{\mathsf{\pi }}^0{\mathsf{\pi }}^0}}<0,$$

(39)

where the subfix ${\mathsf{\pi }}^0{\mathsf{\pi }}^0$ represents the neutral pion system. This particular option is made assuming that it is not possible to reliably identify the ${\mathsf{\pi }}^0$ coming from the ${\mathsf{\rho }}^{-}$ decay in the decay chain ${\mathcal{a}}_1^{-}\to {\mathsf{\rho }}^{-}(\to {\mathsf{\pi }}^{-}{\mathsf{\pi }}^0){\mathsf{\pi }}^0$. Taking into account the two-body decay chain, the mass of the mesonic resonances, and assuming that the ${\mathsf{\rho }}^{-}$ meson can be precisely reconstructed, the value for which a phase-shift should be applied can be corrected as follows [25]:

$$y_{-}^{{\mathcal{a}}_1}=\frac{E_{{\mathsf{\rho }}^{-}}-E_{{\mathsf{\pi }}^0}}{E_{{\mathsf{\rho }}^{-}}+E_{{\mathsf{\pi }}^0}}-\frac{m_{{\mathcal{a}}_1}^2-m_{{\mathsf{\pi }}^0}^2-m_{{\mathsf{\rho }}^{-}}^2}{m_{{\mathcal{a}}_1}^2},$$

(40)

where $m_X$ represents the mass of the meson X, with $X\in \{{\mathcal{a}}_1,\mathsf{\rho },{\mathsf{\pi }}^0\}$.

Another consideration can be made for $\tau$ decays involving kaons, or other mesons. Given that kaons and pions have the same spin-parity, the only parameters affected in this notation are the $y_{\pm }$ variables which should be corrected to account for the different meson mass.

The choice of the specific method to reconstruct the $\tau$ decay plane falls beyond the scope of this article, as the sensitivity obtained from each pair of vectors is heavily dependent on the energy and momentum resolution of a specific experiment. However, the use of this common notation allows us to naturally combine measurements performed with different methods.

4.2. Measurements Overview

This section is dedicated to addressing measurements performed at hadron colliders for the measurement of the $\mathcal{CP}$ mixing angle and show how the methods they used can be rewritten with the notation proposed in this paper. In 2019, the ATLAS Collaboration released prospects for the measurement of the $\mathcal{CP}$ mixing angle in $H\to \tau \tau$ decays at the HL-LHC [27]. The $\tau$ pair decay channel addressed was ${\tau }^{+}{\tau }^{-}\to {\nu }_{\tau }{\overline{\nu }}_{\tau }{\mathsf{\rho }}^{+}{\mathsf{\rho }}^{-}$, and the acoplanarity angle was reconstructed using the neutral pion method. The equivalent description based on defining the decay planes can be retrieved from Table 1.

The measurement of the $\mathcal{CP}$ structure of the Higgs Yukawa coupling to tau leptons in CMS (2021) [18] and its combination with other Yukawa couplings (2022) [28] treated multiple $\tau$ decay channels and combined them to constrain the $\mathcal{CP}$ mixing angle.

Table 2. Summary of the vectors used to reconstruct the acoplanarity angle in the decay channels analyzed in [18,26,28]. Note that for ${\tau }_{{\mathcal{a}}_1^{3\mathcal{Pr}}}$ decays the sign is written explicitly to identify the pion having the same sign as the decaying $\tau$ lepton, and the one having the opposite sign.

Channel	P1	R1	P2	R2	$\mathsf{\pi }$ Phase-Shift
${\tau }_{\mathsf{\mu },\mathcal{e},\mathsf{\pi }}\times {\tau }_{\mathsf{\mu },\mathcal{e},\mathsf{\pi }}$	${\overrightarrow{p}}_{\mathsf{\mu },\mathcal{e},\mathsf{\pi }}$	${\overrightarrow{IP}}_{\mathsf{\mu },\mathcal{e},\mathsf{\pi }}$	${\overrightarrow{p}}_{\mathsf{\mu },\mathcal{e},\mathsf{\pi }}$	${\overrightarrow{IP}}_{\mathsf{\mu },\mathcal{e},\mathsf{\pi }}$	-
${\tau }_{\mathsf{\mu },\mathcal{e},\mathsf{\pi }}\times {\tau }_{\mathsf{\rho }}$	${\overrightarrow{p}}_{\mathsf{\mu },\mathcal{e},\mathsf{\pi }}$	${\overrightarrow{IP}}_{\mathsf{\mu },\mathcal{e},\mathsf{\pi }}$	${\overrightarrow{p}}_{{\mathsf{\pi }}^{\pm }}$	${\overrightarrow{p}}_{{\mathsf{\pi }}^0}$	$y_{\mathsf{\rho }}<0$
${\tau }_{\mathsf{\mu },\mathcal{e},\mathsf{\pi }}\times {\tau }_{{\mathcal{a}}_1^{1\mathcal{Pr}}}$	${\overrightarrow{p}}_{\mathsf{\mu },\mathcal{e},\mathsf{\pi }}$	${\overrightarrow{IP}}_{\mathsf{\mu },\mathcal{e},\mathsf{\pi }}$	${\overrightarrow{p}}_{{\mathsf{\pi }}^{\pm }}$	${\overrightarrow{p}}_{{\mathsf{\pi }}^0{\mathsf{\pi }}^0}$	$y_{{\mathcal{a}}_1^{1\mathcal{Pr}}}<0$
${\tau }_{\mathsf{\mu },\mathcal{e},\mathsf{\pi }}\times {\tau }_{{\mathcal{a}}_1^{3\mathcal{Pr}}}^{\pm }$	${\overrightarrow{p}}_{\mathsf{\mu },\mathcal{e},\mathsf{\pi }}$	${\overrightarrow{IP}}_{\mathsf{\mu },\mathcal{e},\mathsf{\pi }}$	${\overrightarrow{p}}_{{\mathsf{\pi }}^{\pm }}$	${\overrightarrow{p}}_{{\mathsf{\pi }}^{\mp }}$	$y_{{\mathcal{a}}_1^{3\mathcal{Pr}}}<0$
${\tau }_{\mathsf{\rho }}\times {\tau }_{\mathsf{\rho }}$	${\overrightarrow{p}}_{\mathsf{\pi }}$	${\overrightarrow{p}}_{{\mathsf{\pi }}^0}$	${\overrightarrow{p}}_{\mathsf{\pi }}$	${\overrightarrow{p}}_{{\mathsf{\pi }}^0}$	$y_{\mathsf{\rho }}·y_{\mathsf{\rho }}<0$
${\tau }_{\mathsf{\rho }}\times {\tau }_{{\mathcal{a}}_1^{1\mathcal{Pr}}}$	${\overrightarrow{p}}_{\mathsf{\pi }}$	${\overrightarrow{p}}_{{\mathsf{\pi }}^0}$	${\overrightarrow{p}}_{\mathsf{\pi }}$	${\overrightarrow{p}}_{{\mathsf{\pi }}^0{\mathsf{\pi }}^0}$	$y_{\mathsf{\rho }}·y_{{\mathcal{a}}_1^{1\mathcal{Pr}}}<0$
${\tau }_{\mathsf{\rho }}\times {\tau }_{{\mathcal{a}}_1^{3\mathcal{Pr}}}^{\pm }$	${\overrightarrow{p}}_{\mathsf{\pi }}$	${\overrightarrow{p}}_{{\mathsf{\pi }}^0}$	${\overrightarrow{p}}_{{\mathsf{\pi }}^{\pm }}$	${\overrightarrow{p}}_{{\mathsf{\pi }}^{\mp }}$	$y_{\mathsf{\rho }}·y_{{\mathcal{a}}_1^{3\mathcal{Pr}}}<0$
${\tau }_{{\mathcal{a}}_1^{1\mathcal{Pr}}}\times {\tau }_{{\mathcal{a}}_1^{3\mathcal{Pr}}}^{\pm }$	${\overrightarrow{p}}_{\mathsf{\pi }}$	${\overrightarrow{p}}_{{\mathsf{\pi }}^0{\mathsf{\pi }}^0}$	${\overrightarrow{p}}_{{\mathsf{\pi }}^{\pm }}$	${\overrightarrow{p}}_{{\mathsf{\pi }}^{\mp }}$	$y_{{\mathcal{a}}_1^{1\mathcal{Pr}}}·y_{{\mathcal{a}}_1^{3\mathcal{Pr}}}<0$
${\tau }_{{\mathcal{a}}_1^{3\mathcal{Pr}}}\times {\tau }_{{\mathcal{a}}_1^{3\mathcal{Pr}}}$	${\overrightarrow{p}}_{\tau }$	$\overrightarrow{h}$	${\overrightarrow{p}}_{\tau }$	$\overrightarrow{h}$	-

summarizes the decay planes definitions equivalent to the methods used in [18,28]. The analytical expressions for the $y_X$ values shown in the table are reported here for the convenience of the reader:

$$y_{\mathsf{\rho }}=\frac{E_{\mathsf{\pi }}-E_{{\mathsf{\pi }}^0}}{E_{\mathsf{\pi }}+E_{{\mathsf{\pi }}^0}},y_{{\mathcal{a}}_1^{1\mathcal{Pr}}}=\frac{E_{\mathsf{\pi }}-E_{{\mathsf{\pi }}^0{\mathsf{\pi }}^0}}{E_{\mathsf{\pi }}+E_{{\mathsf{\pi }}^0{\mathsf{\pi }}^0}},y_{{\mathcal{a}}_1^{3\mathcal{Pr}}}=\frac{E_{{\mathsf{\pi }}^{\pm }}-E_{{\mathsf{\pi }}^{\mp }}}{E_{{\mathsf{\pi }}^{\pm }}+E_{{\mathsf{\pi }}^{\mp }}}.$$

(41)

In this measurement, planes associated with one prong $\tau$ lepton decays without neutral pions were defined according to the impact parameter method. The polarimetric vector method was applied for cases where both $\tau$ leptons decayed into three charged pions, and variations of the neutral pion method were used for all other cases where a mesonic resonance was involved. When only one $\tau$ lepton decayed to three charged pions, the decay plane was defined by the two oppositely charged pions having an invariant mass closer to the $\mathsf{\rho }$ meson resonance.

A notable exception from the notation expressed in this article is the direct measurement of the $\mathcal{CP}$ mixing angle using machine learning (ML) techniques [25]. The use of regression ML techniques to access the $\mathcal{CP}$ mixing angle does not require the direct reconstruction of the acoplanarity angle nor of the $\tau$ decay planes and therefore cannot be directly compared with the notation shown in this article.

5. Conclusions

With the increasing amount of proton–proton collisions recorded at LHC experiments, the study of the $\mathcal{CP}$ structure of the Yukawa coupling between the Higgs boson and tau leptons has become more interesting for measurements. As more experiments target the measurement of the $\mathcal{CP}$ mixing angle ${\mathsf{\Delta }}_{H\tau \tau }$, more interest has been placed on techniques to measure the angle between the $\tau$ decay planes. The use of the common notation proposed in this paper would favor the future combination of measurements performed by different experiments and with potentially different techniques. The presented notation offers a clear separation between the geometric calculation of the angle between the $\tau$ decay planes and the experimental considerations related to the vectors used to define the decay planes themselves. For measurements of the $\mathcal{CP}$ mixing angle already available in the literature, the equivalent description using the decay plane definition is also presented.