A Short Overview on Low Mass Scalars at Future Lepton Colliders
Abstract
1. Introduction
2. Models
2.1. Singlet Extensions
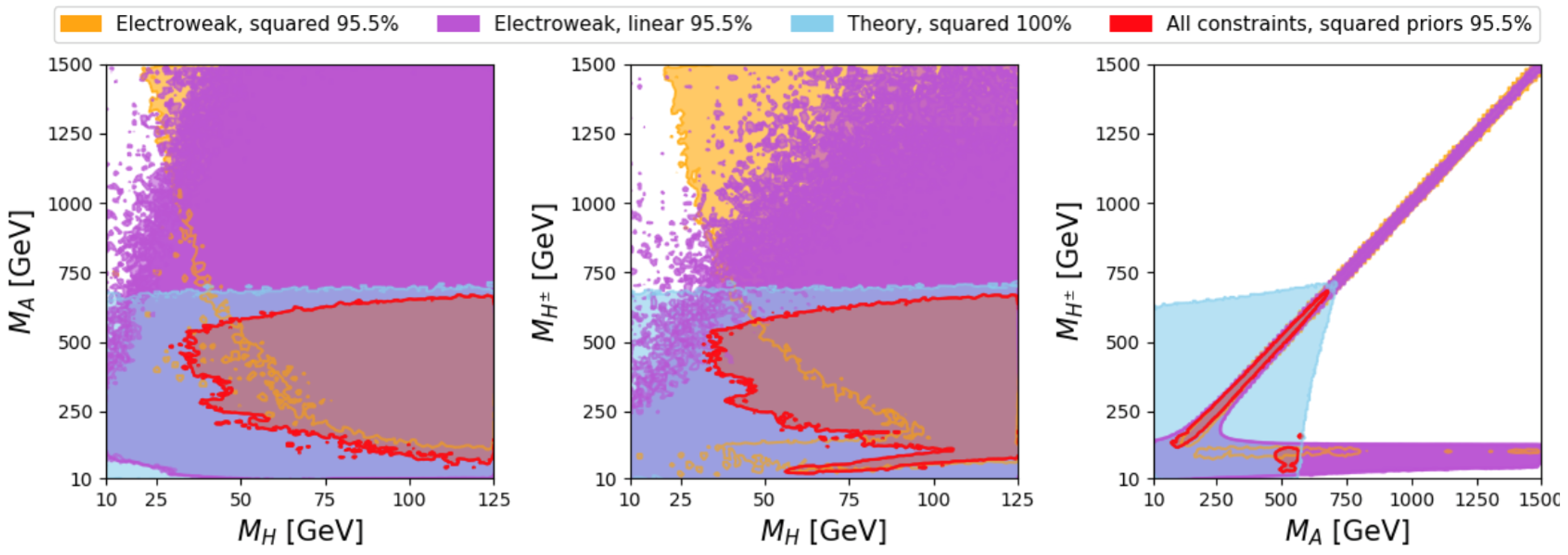
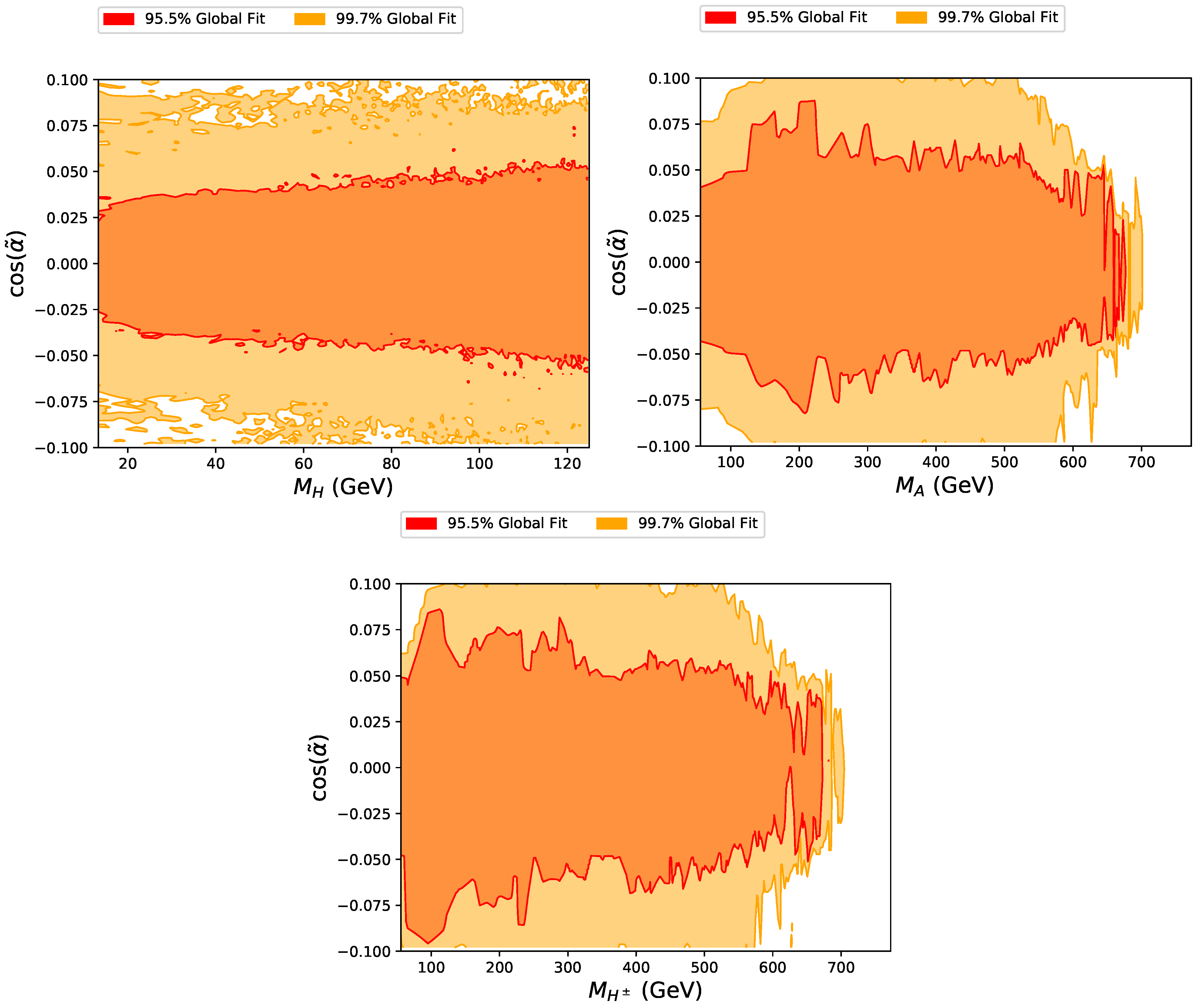
2.2. Two Higgs Doublet Models
2.3. Other Extensions
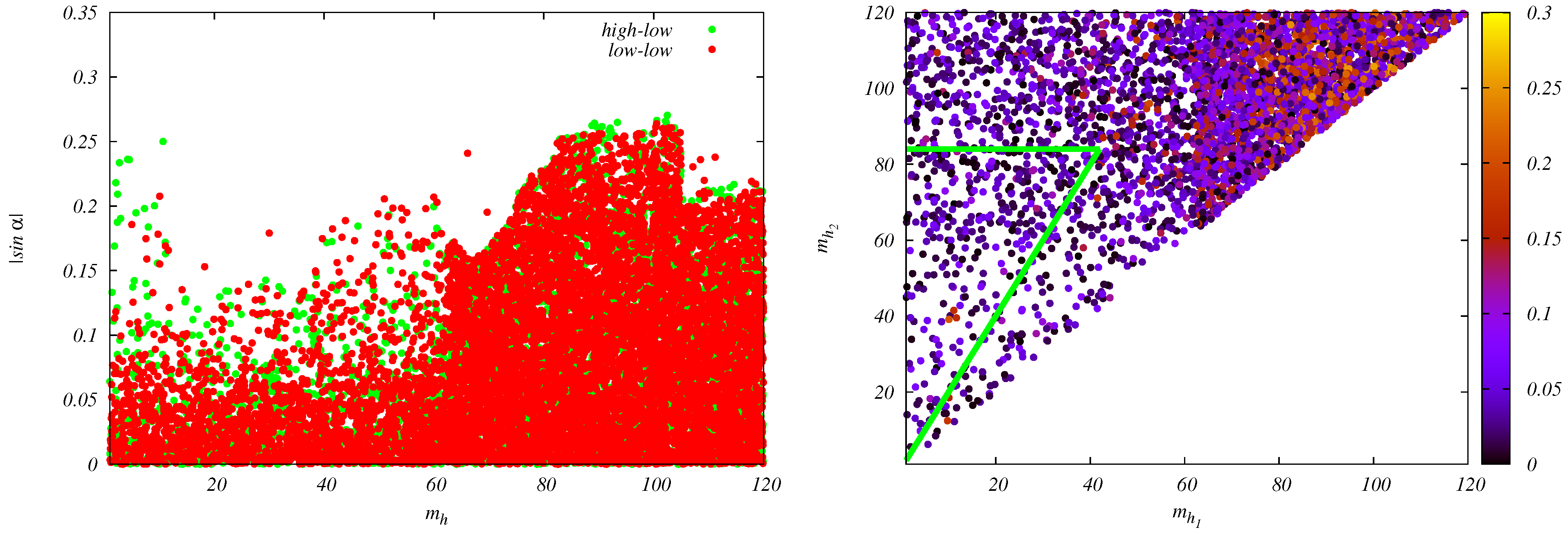
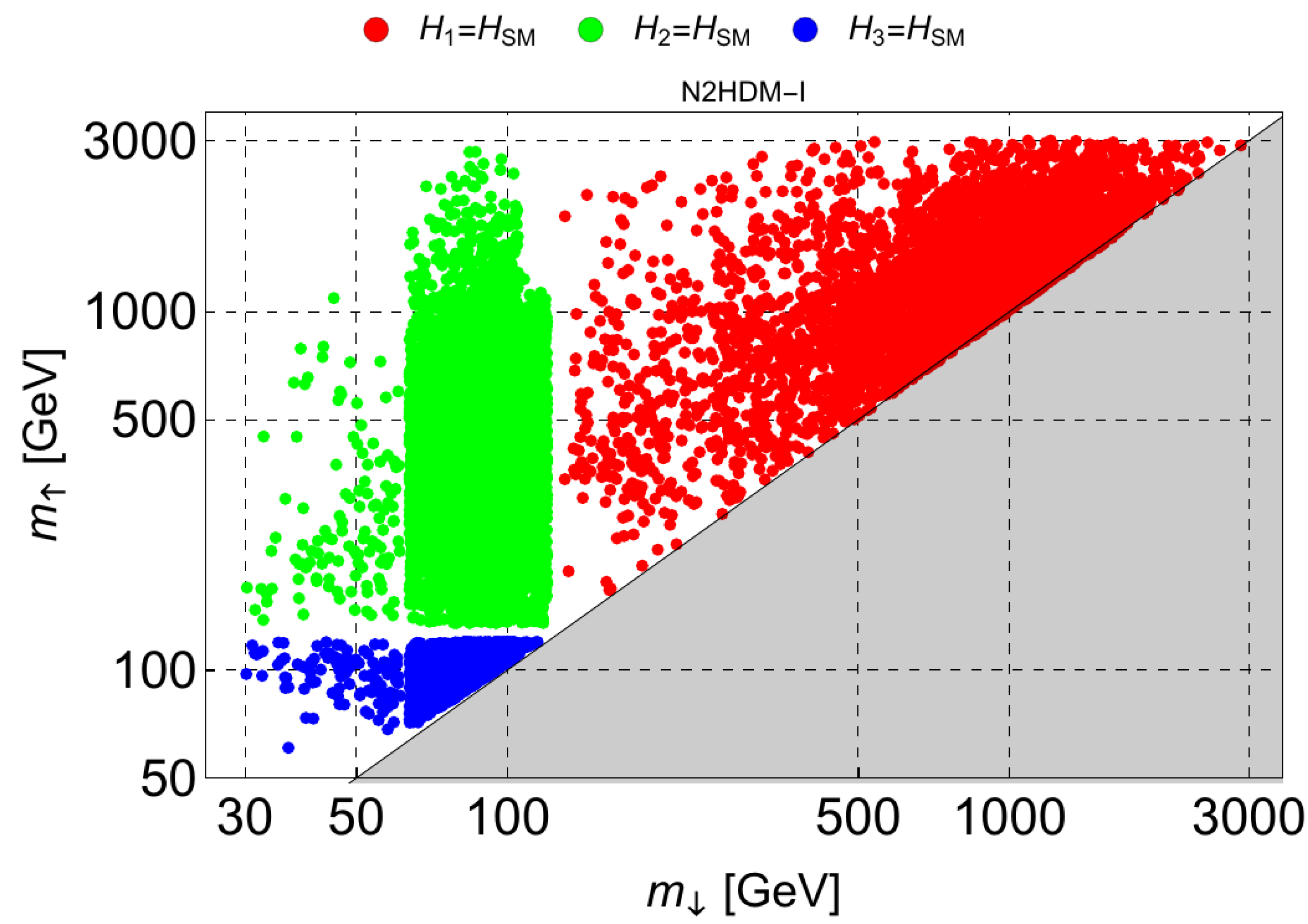
2.3.1. N2HDM
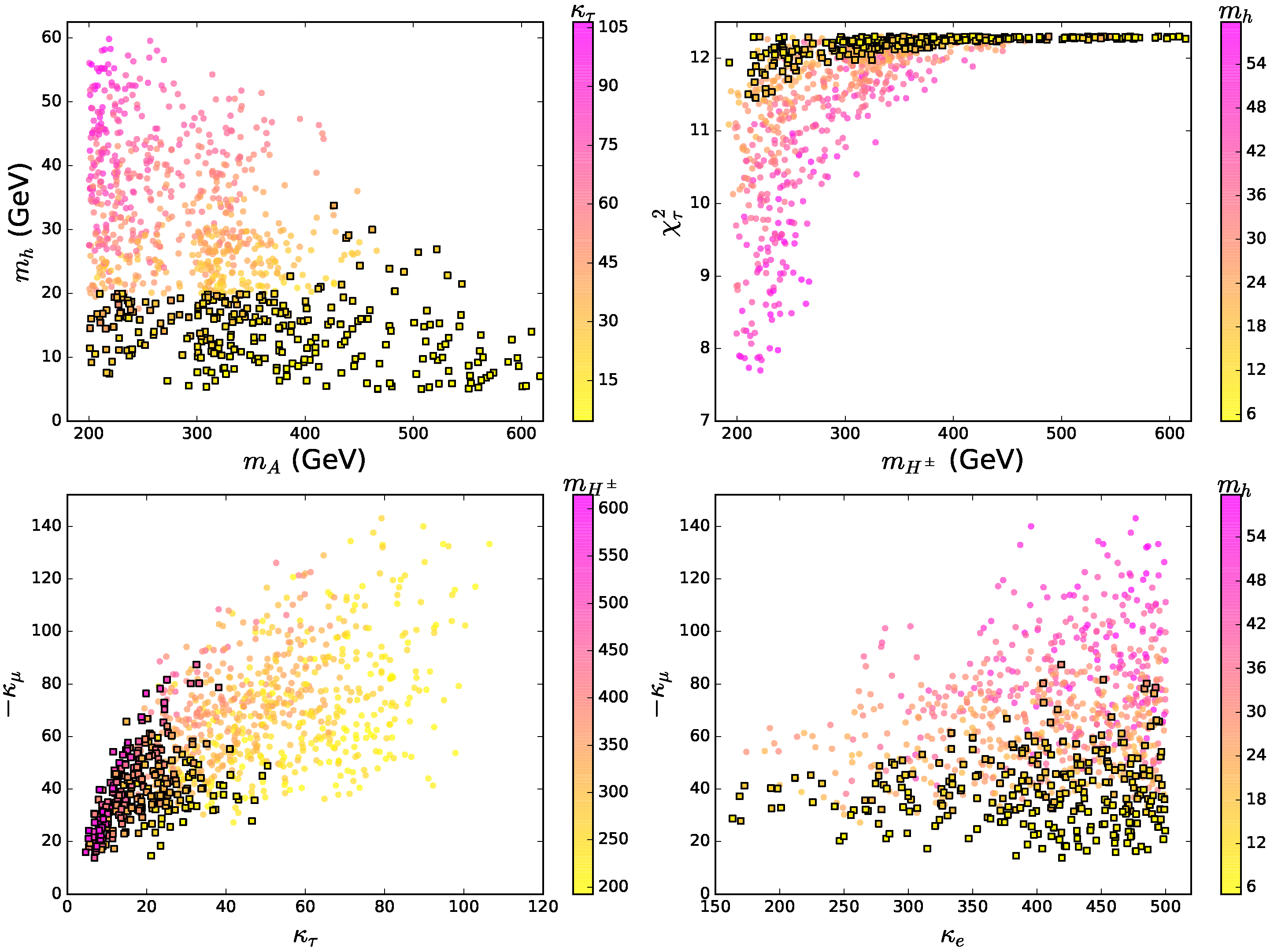
2.3.2. Lepton-Specific Inert Doublet Model
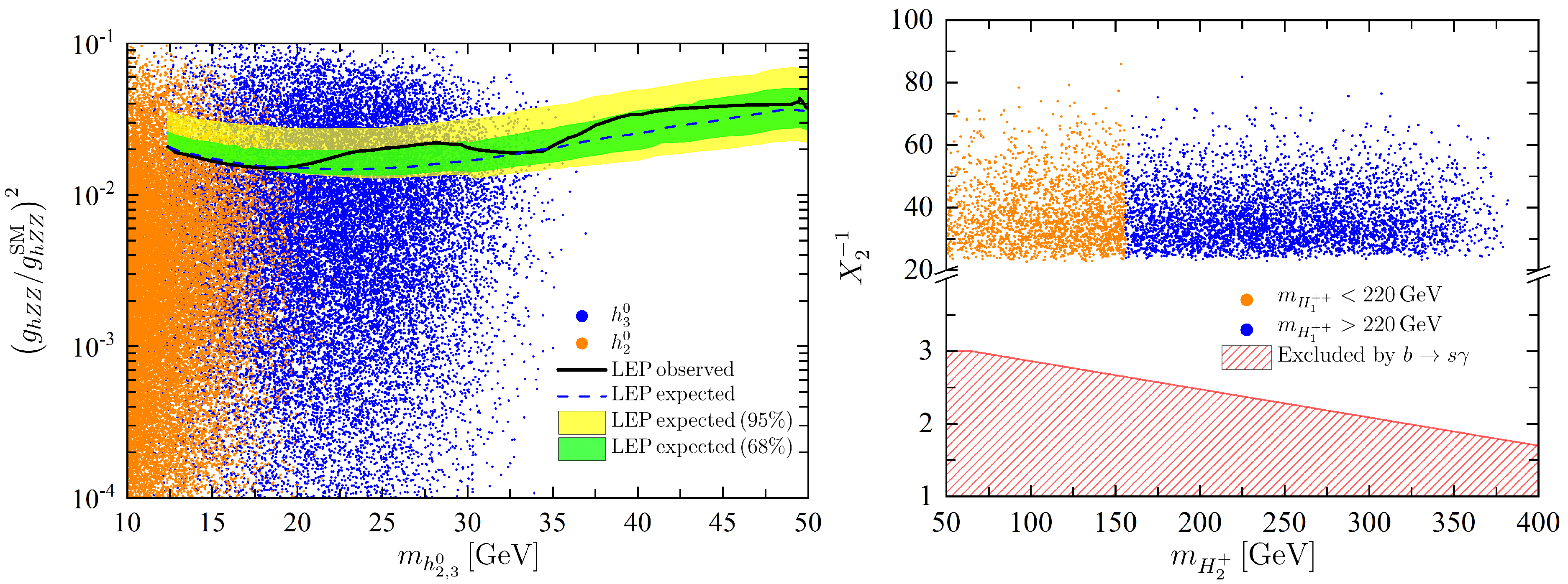
2.3.3. Scalar Triplet Model
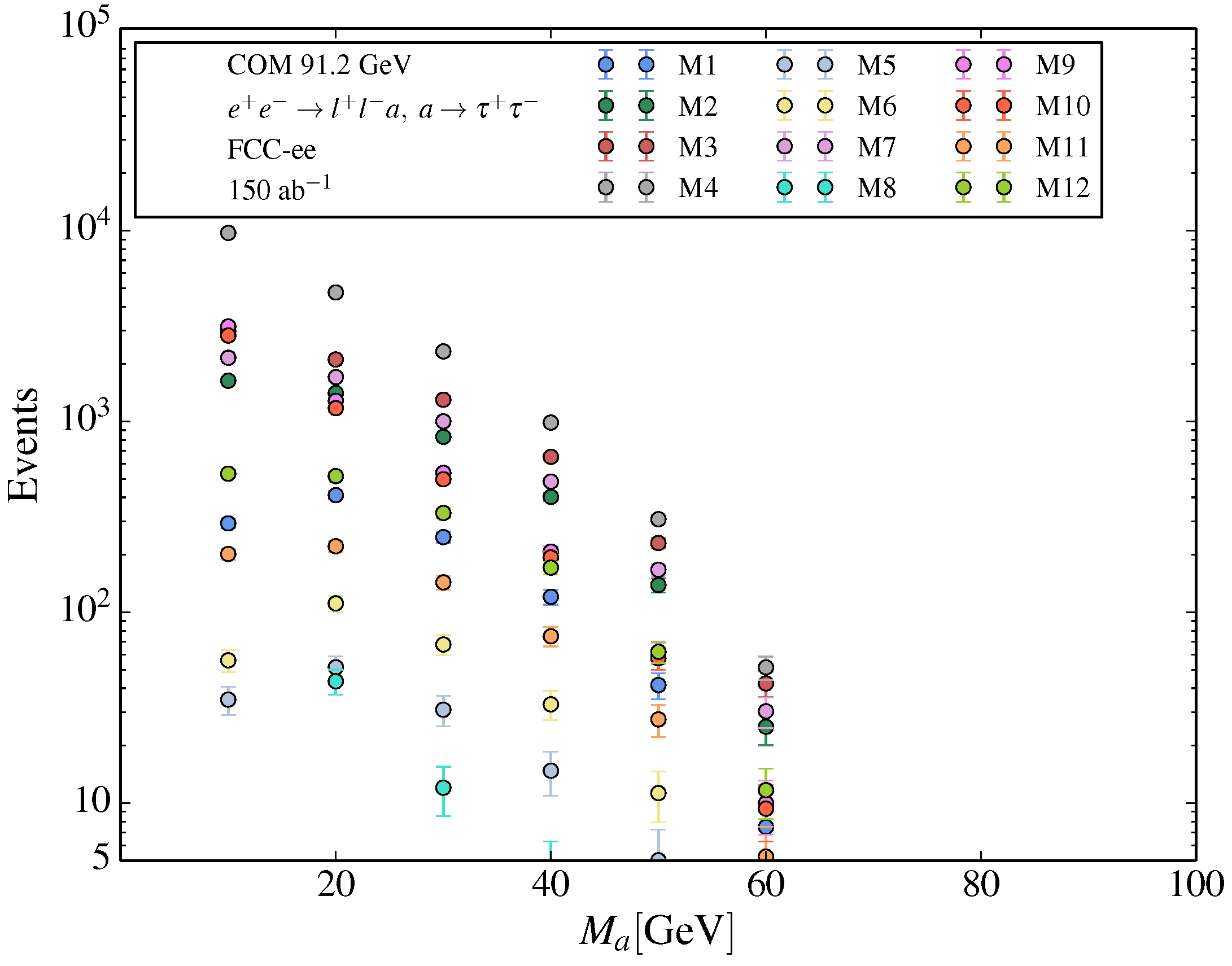
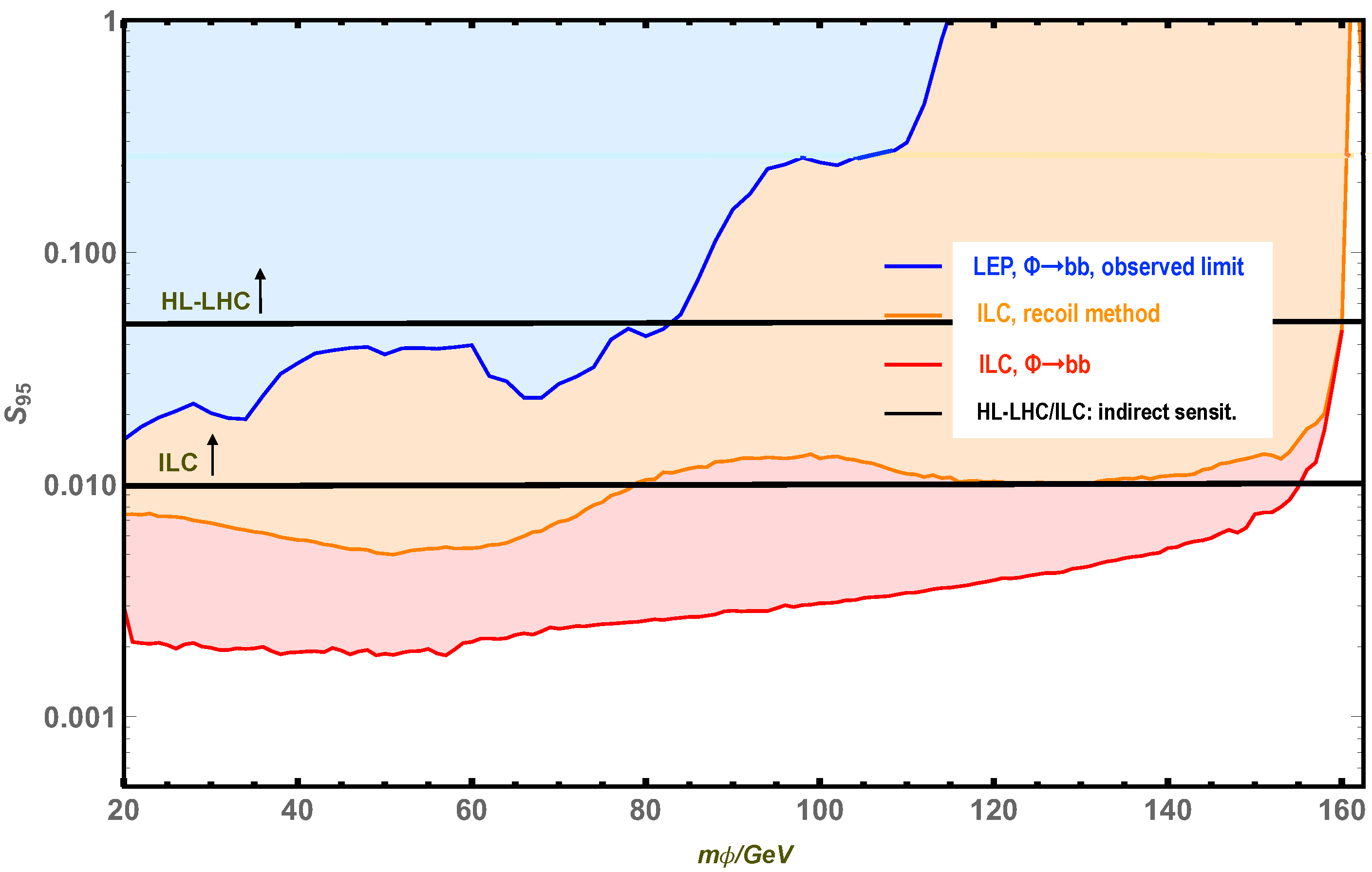
3. Studies at 90 GeV
4. Studies at 240–250 GeV
4.1. Dedicated Studies
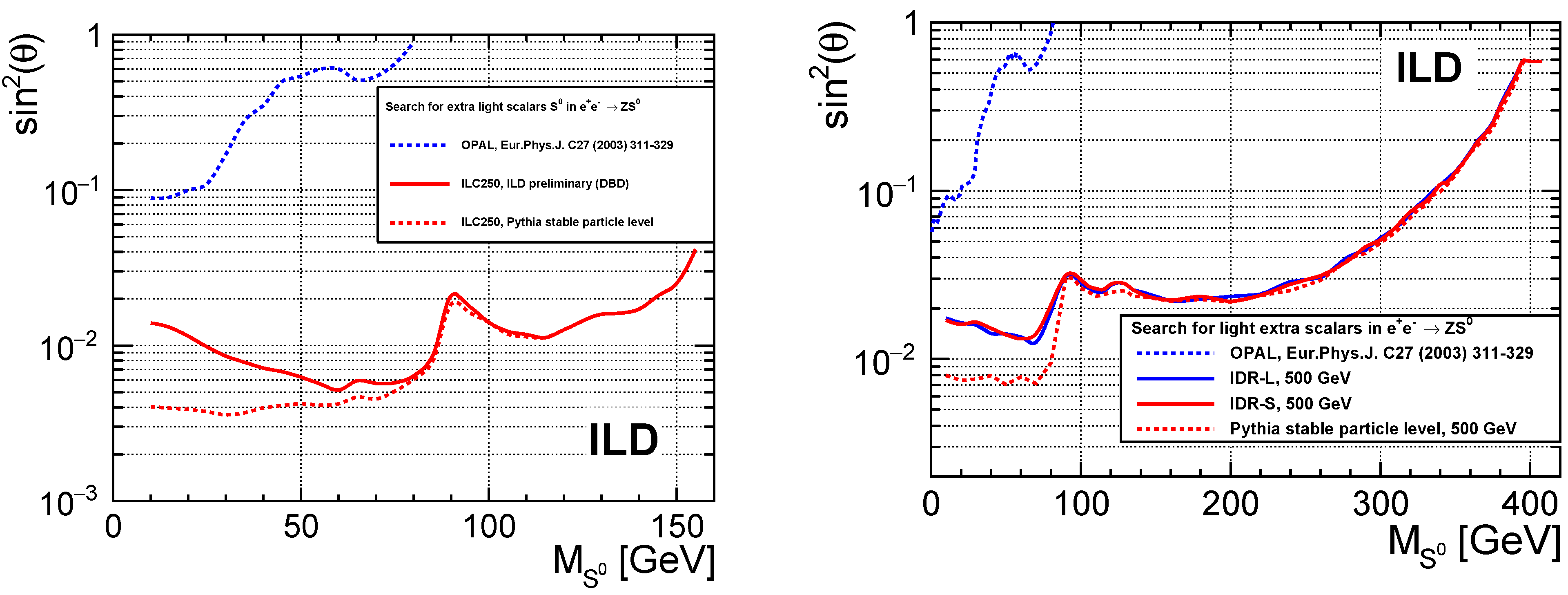
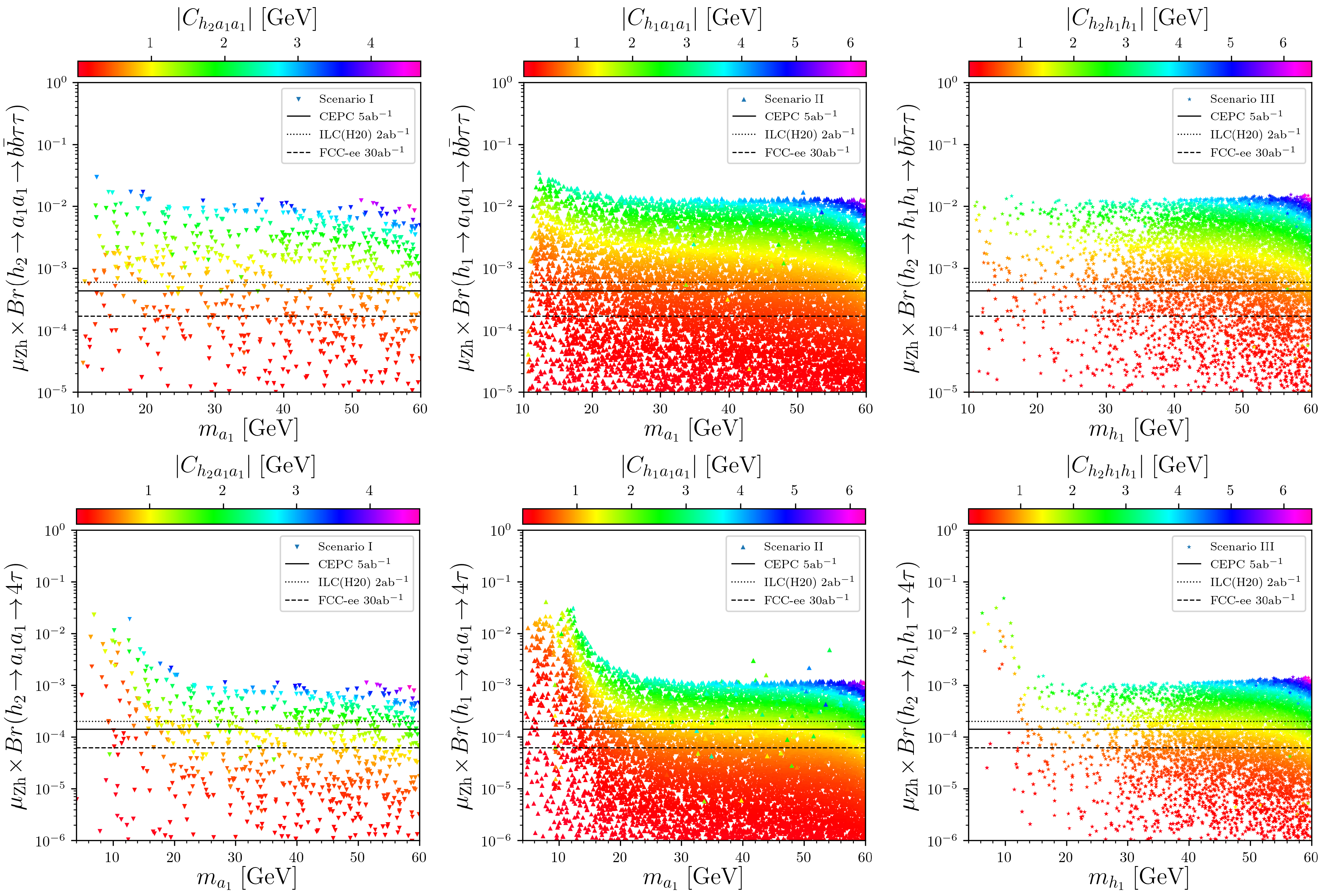
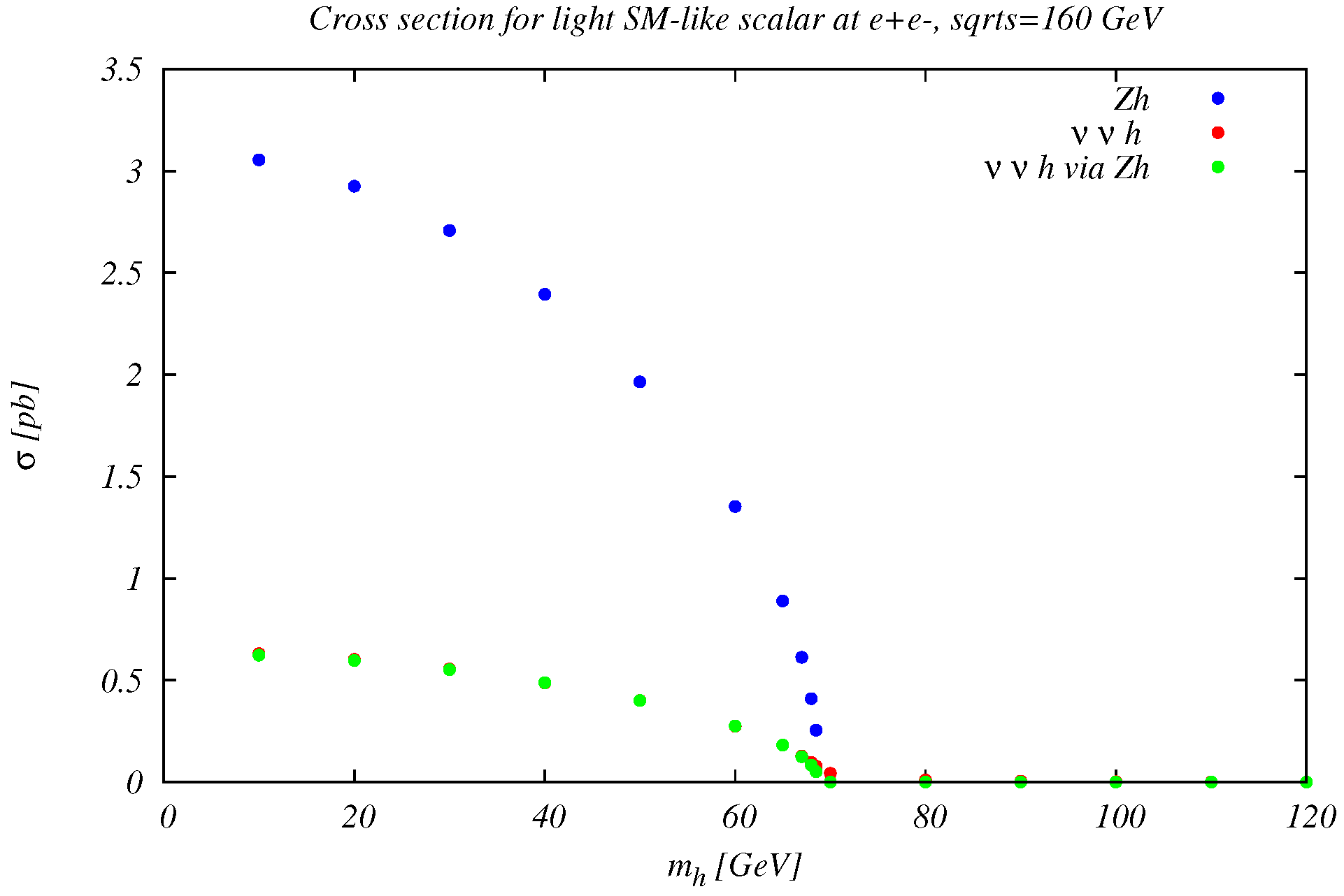
4.1.1. Light Scalars in Production
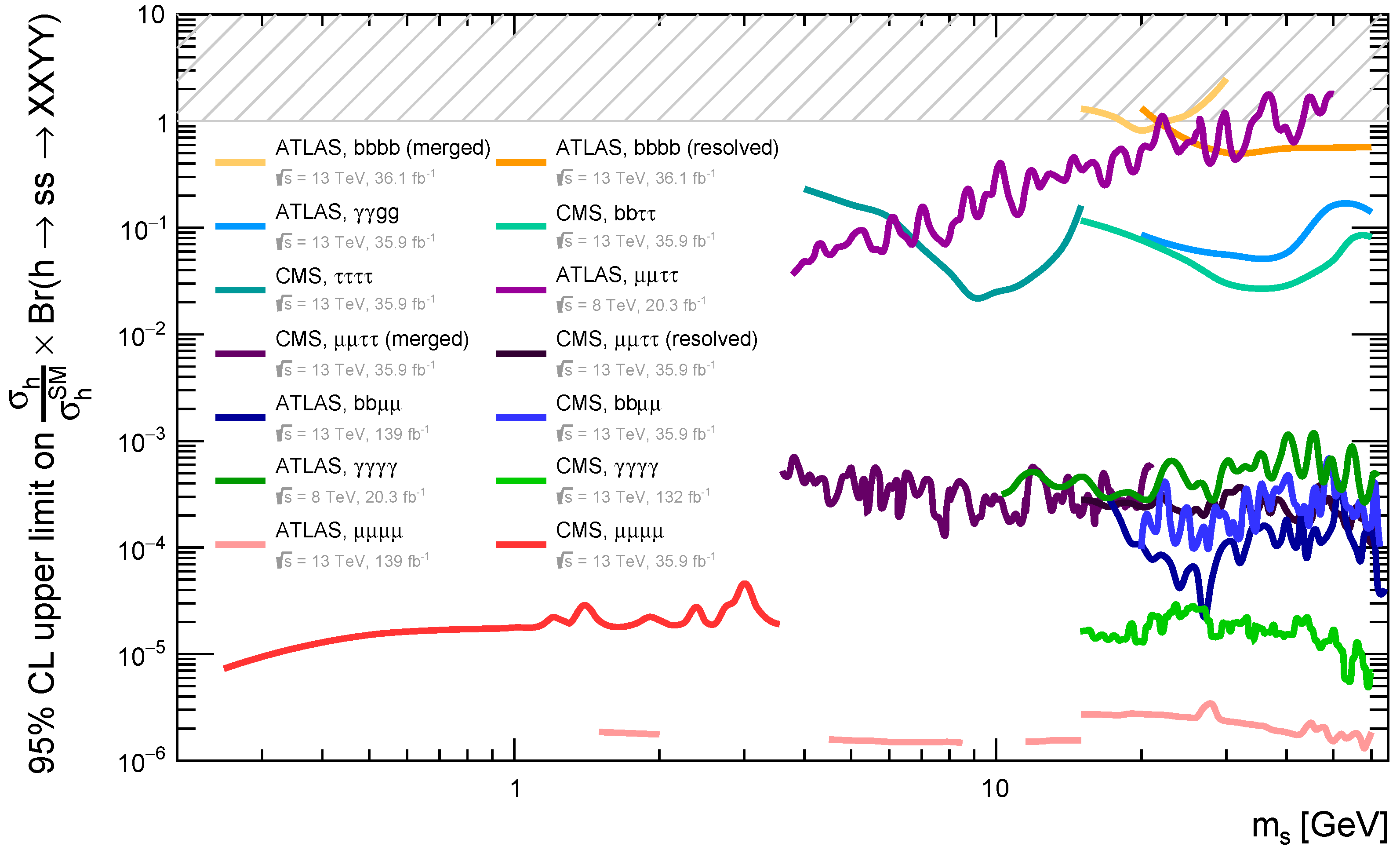
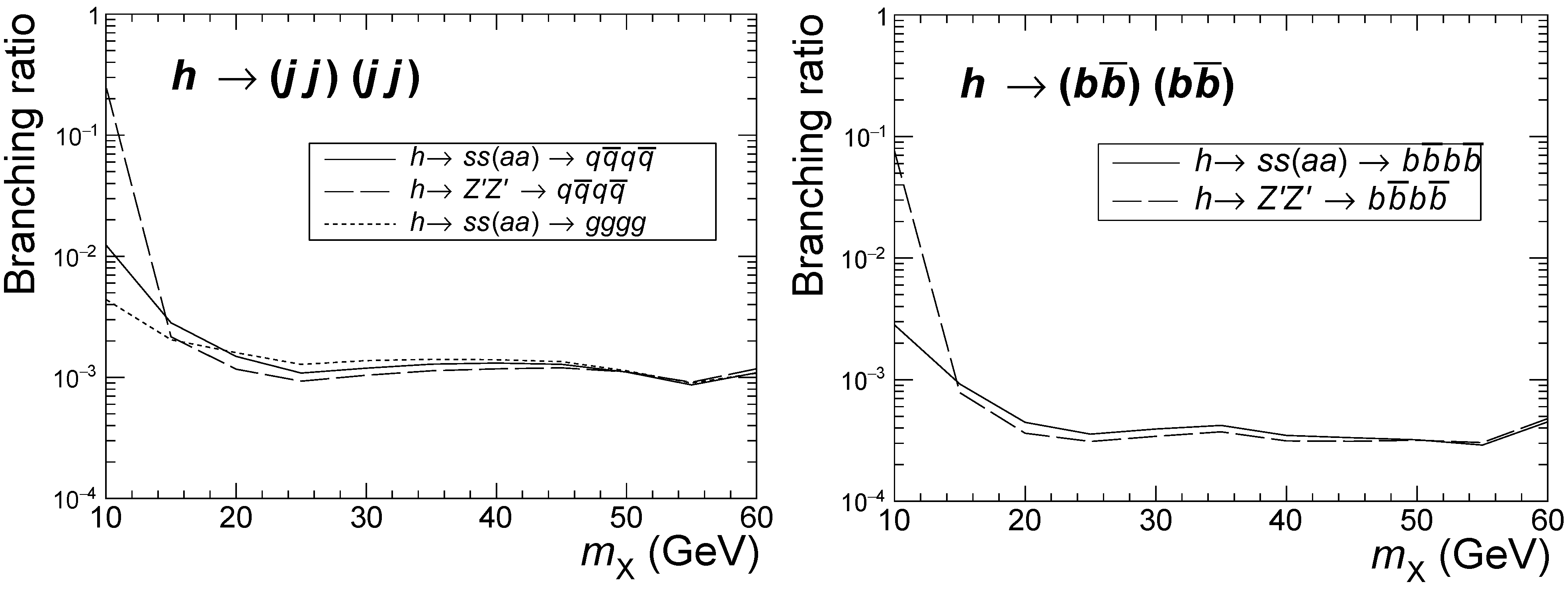
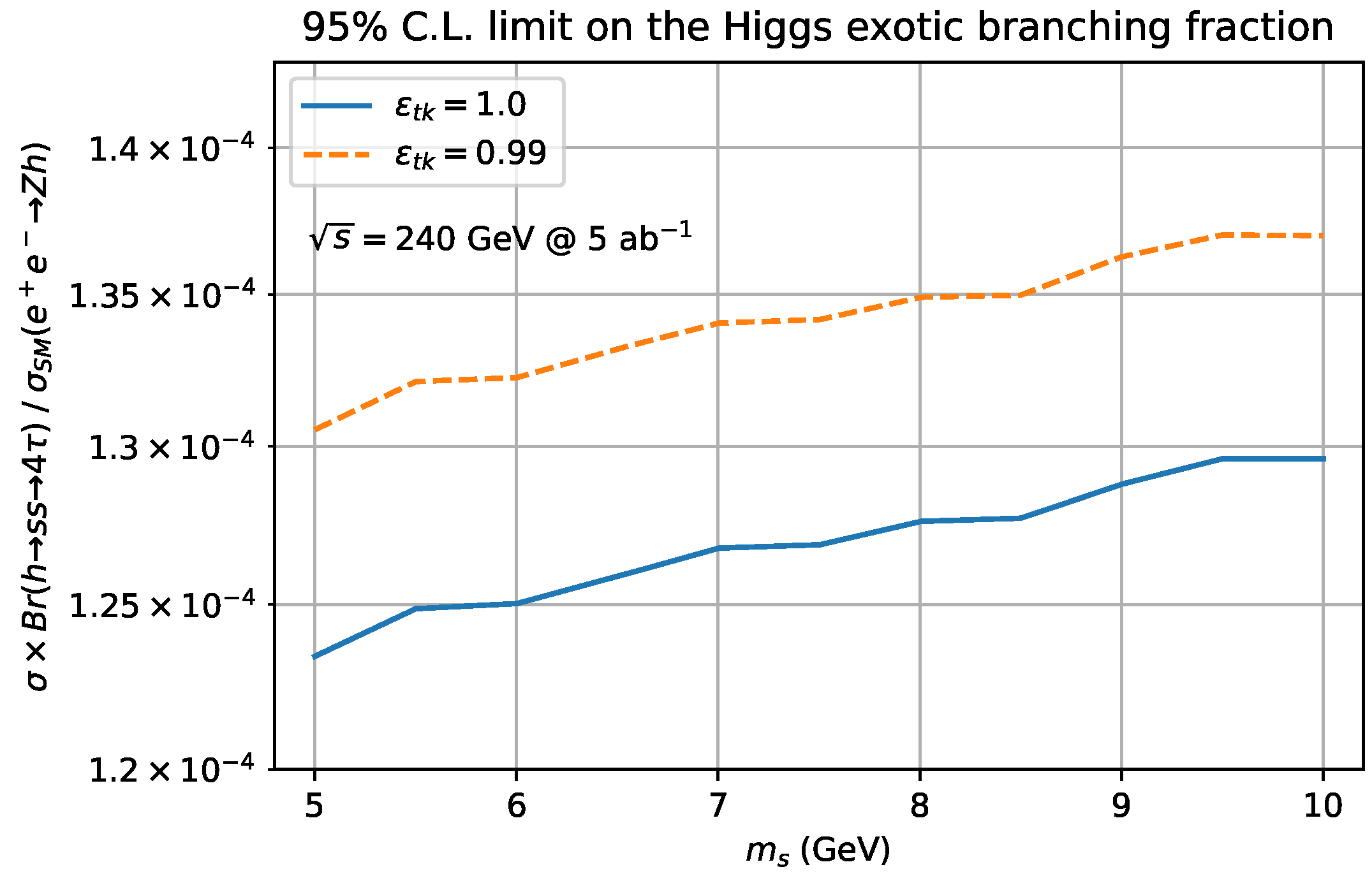
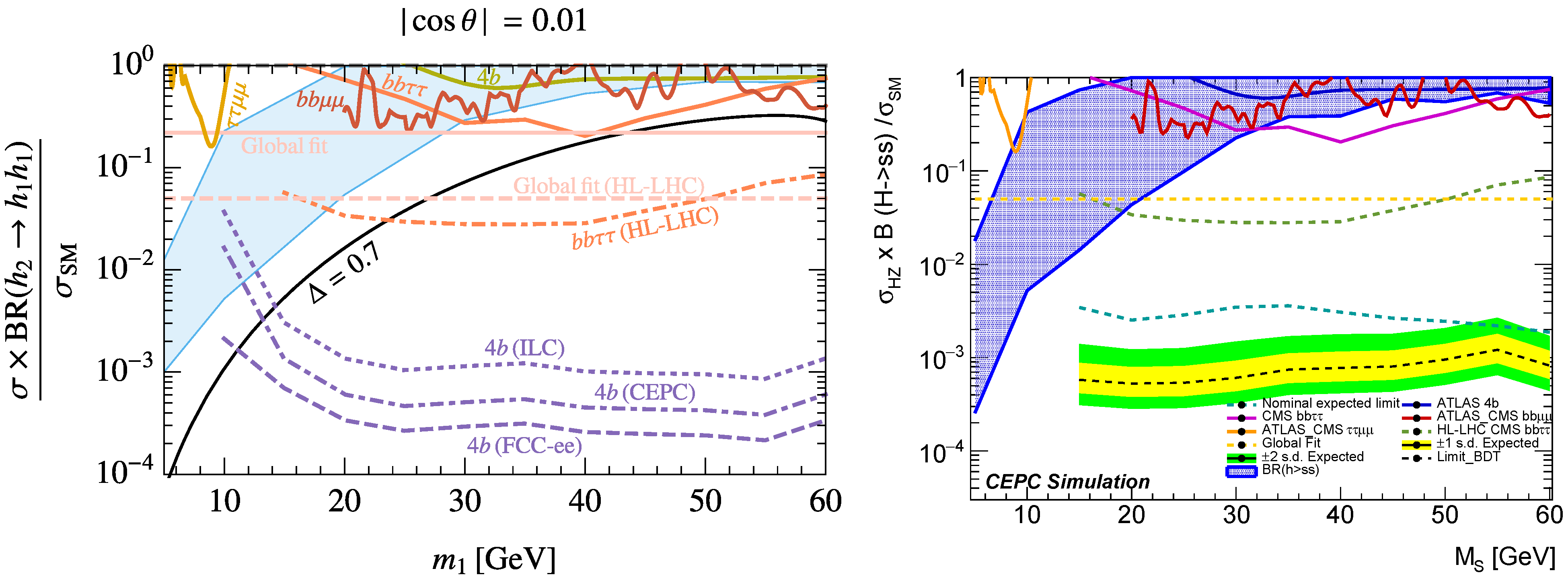
4.1.2. Higgsstrahlung and Decay into Two Light Scalars
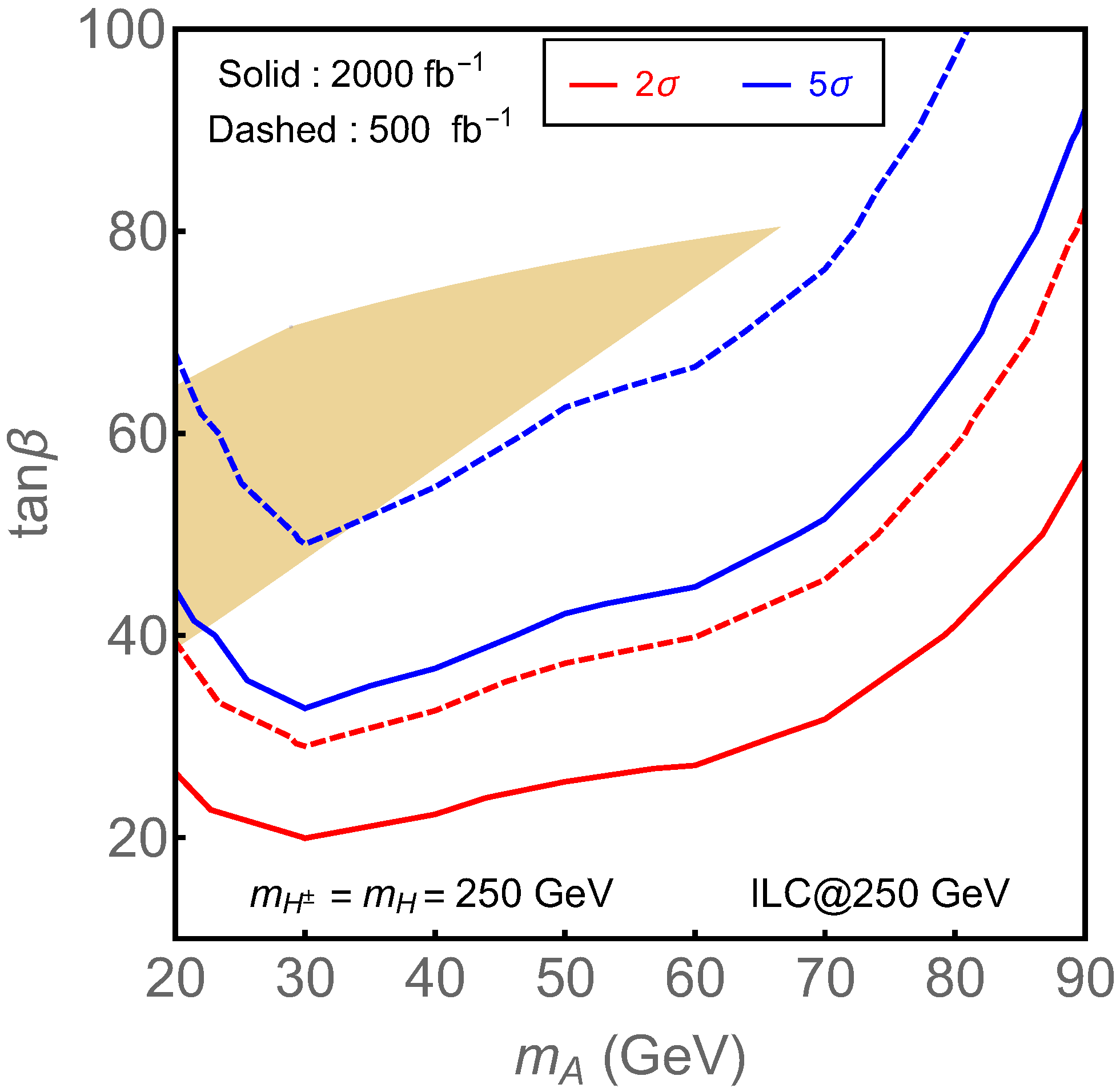
4.1.3. Other Channels
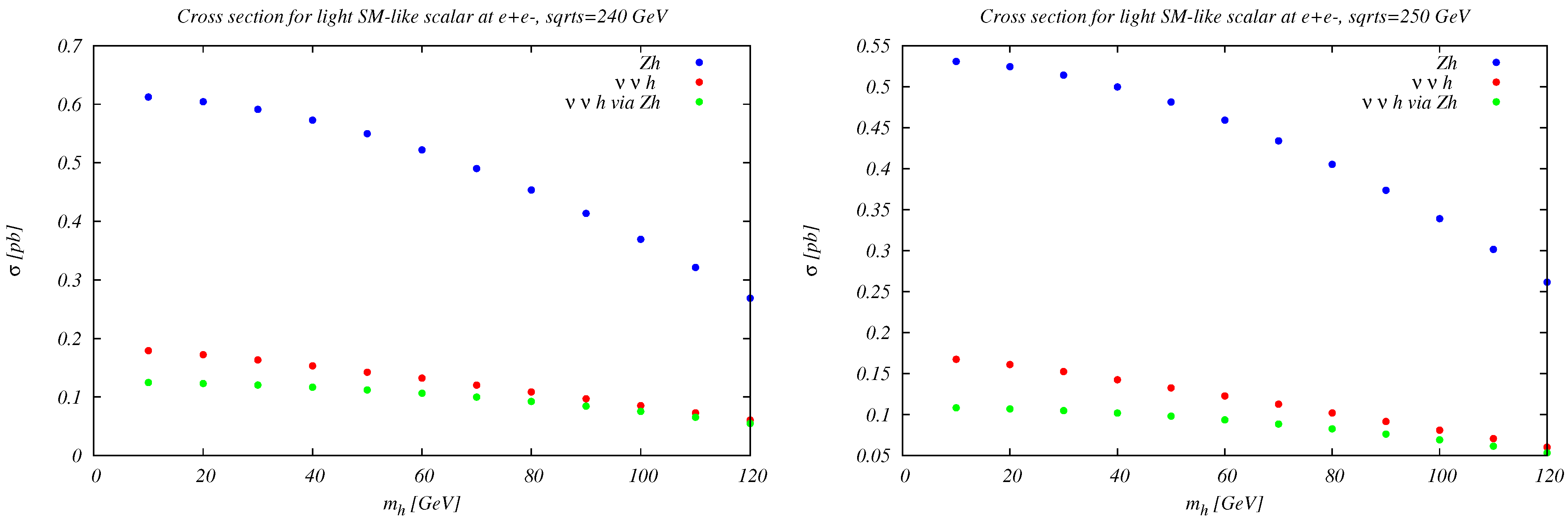
4.2. Cross Section Predictions
5. Other Center of Mass Energies
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | I thank V. Miralles for providing these plots. |
References
- Available online: https://twiki.cern.ch/twiki/bin/view/AtlasPublic/HiggsPublicResults (accessed on 14 April 2022).
- Available online: https://twiki.cern.ch/twiki/bin/view/CMSPublic/PhysicsResultsHIG (accessed on 14 April 2022).
- Ellis, R.K.; European Strategy for Particle Physics Preparatory Group. Physics Briefing Book: Input for the European Strategy for Particle Physics Update 2020. arXiv 2019, arXiv:1910.11775. [Google Scholar]
- European Strategy Group, 2020 Update of the European Strategy for Particle Physics. Technical Report, Geneva. 2020. Available online: http://cds.cern.ch/record/2720129 (accessed on 14 April 2022).
- Robens, T. A short overview on low mass scalars at future lepton colliders-Snowmass White Paper. 2022 Snowmass Summer Study. arXiv 2022, arXiv:2203.08210. [Google Scholar]
- Pruna, G.M.; Robens, T. Higgs singlet extension parameter space in the light of the LHC discovery. Phys. Rev. D 2013, 88, 115012. [Google Scholar] [CrossRef]
- Robens, T.; Stefaniak, T. Status of the Higgs Singlet Extension of the Standard Model after LHC Run 1. Eur. Phys. J. C 2015, 75, 104. [Google Scholar] [CrossRef]
- Robens, T.; Stefaniak, T. LHC Benchmark Scenarios for the Real Higgs Singlet Extension of the Standard Model. Eur. Phys. J. C 2016, 76, 268. [Google Scholar] [CrossRef]
- Ilnicka, A.; Robens, T.; Stefaniak, T. Constraining Extended Scalar Sectors at the LHC and beyond. Mod. Phys. Lett. A 2018, 33, 1830007. [Google Scholar] [CrossRef]
- Robens, T.; Stefaniak, T.; Wittbrodt, J. Two-real-scalar-singlet extension of the SM: LHC phenomenology and benchmark scenarios. Eur. Phys. J. C 2020, 80, 151. [Google Scholar] [CrossRef]
- Cepeda, M.; Gori, S.; Outschoorn, V.M.; Shelton, J. Exotic Higgs Decays. arXiv 2021, arXiv:2111.12751. [Google Scholar]
- Robens, T. Constraining extended scalar sectors at current and future colliders. arXiv 2022, arXiv:2203.17016. [Google Scholar]
- Carena, M.; Kozaczuk, J.; Liu, Z.; Ou, T.; Ramsey-Musolf, M.J.; Shelton, J.; Wang, Y.; Xie, K.P. Probing the Electroweak Phase Transition with Exotic Higgs Decays. 2022 Snowmass Summer Study. arXiv 2022, arXiv:2203.08206. [Google Scholar]
- Coimbra, R.; Sampaio, M.O.P.; Santos, R. ScannerS: Constraining the phase diagram of a complex scalar singlet at the LHC. Eur. Phys. J. C 2013, 73, 2428. [Google Scholar] [CrossRef]
- Mühlleitner, M.; Sampaio, M.O.P.; Santos, R.; Wittbrodt, J. ScannerS: Parameter scans in extended scalar sectors. Eur. Phys. J. C 2022, 82, 198. [Google Scholar] [CrossRef]
- Bechtle, P.; Brein, O.; Heinemeyer, S.; Weiglein, G.; Williams, K.E. HiggsBounds: Confronting Arbitrary Higgs Sectors with Exclusion Bounds from LEP and the Tevatron. Comput. Phys. Commun. 2010, 181, 138–167. [Google Scholar] [CrossRef]
- Bechtle, P.; Brein, O.; Heinemeyer, S.; Weiglein, G.; Williams, K.E. HiggsBounds 2.0.0: Confronting Neutral and Charged Higgs Sector Predictions with Exclusion Bounds from LEP and the Tevatron. Comput. Phys. Commun. 2011, 182, 2605–2631. [Google Scholar] [CrossRef]
- Bechtle, P.; Brein, O.; Heinemeyer, S.; Stål, O.; Stefaniak, T.; Weiglein, G.; Williams, K.E. HiggsBounds-4: Improved Tests of Extended Higgs Sectors against Exclusion Bounds from LEP, the Tevatron and the LHC. Eur. Phys. J. C 2014, 74, 2693. [Google Scholar] [CrossRef]
- Bechtle, P.; Dercks, D.; Heinemeyer, S.; Klingl, T.; Stefaniak, T.; Weiglein, G.; Wittbrodt, J. HiggsBounds-5: Testing Higgs Sectors in the LHC 13 TeV Era. Eur. Phys. J. C 2020, 80, 1211. [Google Scholar] [CrossRef]
- Bechtle, P.; Heinemeyer, S.; Stål, O.; Stefaniak, T.; Weiglein, G. HiggsSignals: Confronting arbitrary Higgs sectors with measurements at the Tevatron and the LHC. Eur. Phys. J. C 2014, 74, 2711. [Google Scholar] [CrossRef]
- Bechtle, P.; Heinemeyer, S.; Klingl, T.; Stefaniak, T.; Weiglein, G.; Wittbrodt, J. HiggsSignals-2: Probing new physics with precision Higgs measurements in the LHC 13 TeV era. Eur. Phys. J. C 2021, 81, 145. [Google Scholar] [CrossRef]
- CMS Collaboration. First evidence for off-shell production of the Higgs boson and measurement of its width. arXiv 2022, arXiv:2202.06923. [Google Scholar]
- Branco, G.C.; Ferreira, P.M.; Lavoura, L.; Rebelo, M.N.; Sher, M.; Silva, J.P. Theory and phenomenology of two-Higgs-doublet models. Phys. Rept. 2012, 516, 1–102. [Google Scholar] [CrossRef]
- Eberhardt, O.; Martínez, A.P.n.; Pich, A. Global fits in the Aligned Two-Higgs-Doublet model. J. High Energy Phys. 2021, 5, 005. [Google Scholar] [CrossRef]
- Pich, A.; Tuzon, P. Yukawa Alignment in the Two-Higgs-Doublet Model. Phys. Rev. D 2009, 80, 091702. [Google Scholar] [CrossRef]
- Pich, A. Flavour constraints on multi-Higgs-doublet models: Yukawa alignment. Nucl. Phys. B Proc. Suppl. 2010, 209, 182–187. [Google Scholar] [CrossRef]
- Combined Measurements of Higgs Boson Production and Decay Using Up to 139 fb−1 of Proton-Proton Collision Data at = 13 TeV Collected with the ATLAS Experiment. Technical Report, CERN, Geneva. 2021. Available online: https://atlas.web.cern.ch/Atlas/GROUPS/PHYSICS/CONFNOTES/ATLAS-CONF-2021-053 (accessed on 14 April 2022).
- Wang, L.; Yang, J.M.; Zhang, Y. Two-Higgs-doublet models in light of current experiments: A brief review. arXiv 2022, arXiv:2203.07244. [Google Scholar]
- Abouabid, H.; Arhrib, A.; Azevedo, D.; Falaki, J.E.; Ferreira, P.M.; Mühlleitner, M.; Santos, R. Benchmarking Di-Higgs Production in Various Extended Higgs Sector Models. arXiv 2021, arXiv:2112.12515. [Google Scholar]
- Han, X.F.; Li, T.; Wang, H.X.; Wang, L.; Zhang, Y. Lepton-specific inert two-Higgs-doublet model confronted with the new results for muon and electron g-2 anomalies and multilepton searches at the LHC. Phys. Rev. D 2021, 104, 115001. [Google Scholar] [CrossRef]
- Ferreira, P.M.; Gonçalves, B.L.; Joaquim, F.R. The hidden side of scalar-triplet models with spontaneous CP violation. arXiv 2021, arXiv:2109.13179. [Google Scholar] [CrossRef]
- OPAL Collaboration; Abbiendi, G. Decay mode independent searches for new scalar bosons with the OPAL detector at LEP. Eur. Phys. J. C 2003, 27, 311–329. [Google Scholar] [CrossRef]
- Schael, S.; Barate, R.; Brunelière, R.; De Bonis, I.; Decamp, D.; Goy, C.; Jézéquel, S.; Lees, J.P.; Martin, F.; Merle, E.; et al. Search for neutral MSSM Higgs bosons at LEP. Eur. Phys. J. C 2006, 47, 547–587. [Google Scholar] [CrossRef]
- Abada, A.; Abbrescia, M.; AbdusSalam, S.S.; Abdyukhanov, I.; Abelleira Fernandez, J.; Abramov, A.; Aburaia, M.; Acar, A.O.; Adzic, P.R.; Agrawal, P.; et al. FCC-ee: The Lepton Collider: Future Circular Collider Conceptual Design Report Volume 2. Eur. Phys. J. Spec. Top. 2019, 228, 261–623. [Google Scholar] [CrossRef]
- CEPC Study Group. CEPC Conceptual Design Report: Volume 2-Physics & Detector. arXiv 2018, arXiv:1811.10545. [Google Scholar]
- Cornell, A.S.; Deandrea, A.; Fuks, B.; Mason, L. Future lepton collider prospects for a ubiquitous composite pseudoscalar. Phys. Rev. D 2020, 102, 035030. [Google Scholar] [CrossRef]
- Alwall, J.; Herquet, M.; Maltoni, F.; Mattelaer, O.; Stelzer, T. MadGraph 5: Going Beyond. J. High Energy Phys. 2011, 06, 128. [Google Scholar] [CrossRef]
- Bambade, P.; Barklow, T.; Behnke, T.; Berggren, M.; Brau, J.; Burrows, P.; Denisov, D.; Faus-Golfe, A.; Foster, B.; Fujii, K.; et al. The International Linear Collider: A Global Project. arXiv 2019, arXiv:1903.01629. [Google Scholar]
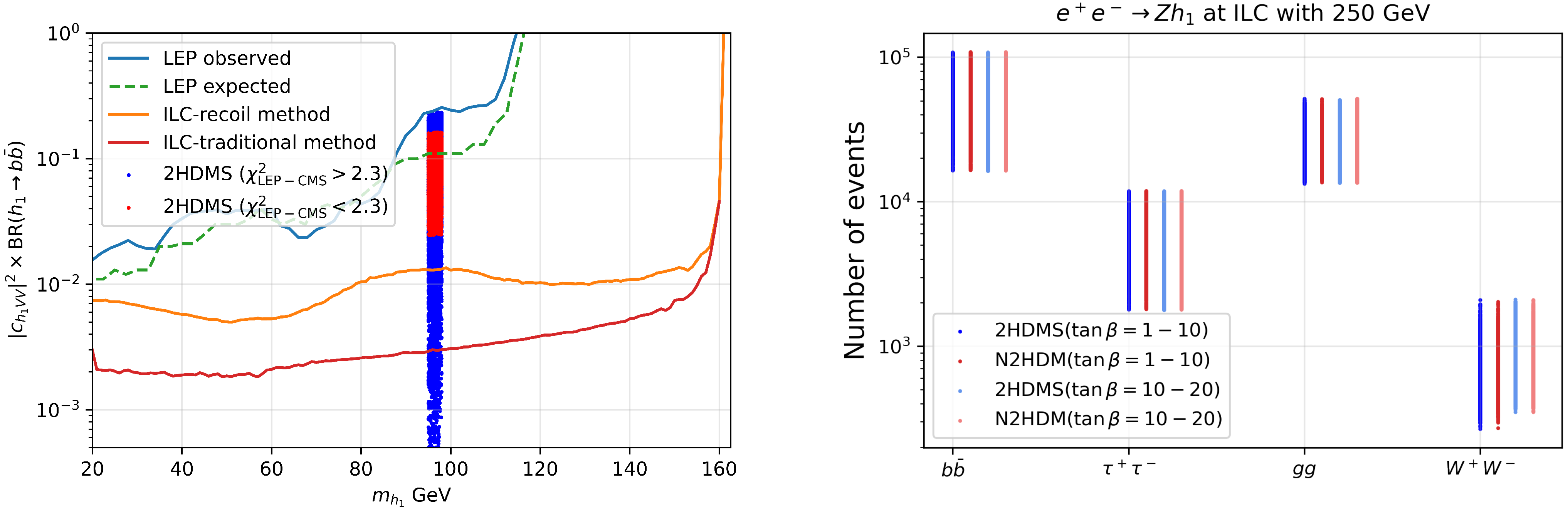
- Drechsel, P.; Moortgat-Pick, G.; Weiglein, G. Prospects for direct searches for light Higgs bosons at the ILC with 250 GeV. Eur. Phys. J. C 2020, 80, 922. [Google Scholar] [CrossRef]
- Barate, R. Search for the standard model Higgs boson at LEP. Phys. Lett. B 2003, 565, 61–75. [Google Scholar] [CrossRef]
- Wang, Y.; Berggren, M.; List, J. ILD Benchmark: Search for Extra Scalars Produced in Association with a Z boson at =500 GeV. arXiv 2020, arXiv:2005.06265. [Google Scholar]
- Liu, Z.; Wang, L.T.; Zhang, H. Exotic decays of the 125 GeV Higgs boson at future e+e− lepton colliders. Chin. Phys. C 2017, 41, 063102. [Google Scholar] [CrossRef]
- Shelton, J.; Xu, D. Exotic Higgs Decays to Four Taus at Future Electron-Positron Colliders. 2022 Snowmass Summer Study. arXiv 2021, arXiv:2110.13225. [Google Scholar]
- Ma, S.; Wang, K.; Zhu, J. Higgs decay to light (pseudo)scalars in the semi-constrained NMSSM. Chin. Phys. C 2021, 45, 023113. [Google Scholar] [CrossRef]
- Das, D.; Ellwanger, U.; Teixeira, A.M. LHC constraints on M1/2 and m0 in the semi-constrained NMSSM. J. High Energy Phys. 2013, 4, 117. [Google Scholar] [CrossRef]
- Ellwanger, U.; Hugonie, C. The semi-constrained NMSSM satisfying bounds from the LHC, LUX and Planck. J. High Energy Phys. 2014, 8, 046. [Google Scholar] [CrossRef]
- Nakamura, K.; Nomura, D. Charged Lepton Flavor Violation in the Semi-Constrained NMSSM with Right-Handed Neutrinos. Phys. Lett. B 2015, 746, 396–405. [Google Scholar] [CrossRef][Green Version]
- Wang, K.; Wang, F.; Zhu, J.; Jie, Q. The semi-constrained NMSSM in light of muon g-2, LHC, and dark matter constraints. Chin. Phys. C 2018, 42, 103109. [Google Scholar] [CrossRef]
- Kozaczuk, J.; Ramsey-Musolf, M.J.; Shelton, J. Exotic Higgs boson decays and the electroweak phase transition. Phys. Rev. D 2020, 101, 115035. [Google Scholar] [CrossRef]
- Wang, Z.; Zhu, X.; Khoda, E.E.; Hsu, S.C.; Konstantinidis, N.; Li, K.; Li, S.; Ramsey-Musolf, M.J.; Wu, Y.; Zhang, Y.E. Study of Electroweak Phase Transition in Exotic Higgs Decays at the CEPC. 2022 Snowmass Summer Study. arXiv 2022, arXiv:2203.10184. [Google Scholar]
- Aaboud, M.; Aad, G.; Abbott, B.; Abeloos, B.; Abhayasinghe, D.K.; Abidi, S.H.; AbouZeid, O.S.; Abraham, N.L.; Abramowicz, H.; Abreu, H.; et al. Search for Higgs boson decays into a pair of light bosons in the bbμμ final state in pp collision at =13 TeV with the ATLAS detector. Phys. Lett. B 2019, 790, 1–21. [Google Scholar] [CrossRef]
- Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Ambrogi, F.; Asilar, E.; Bergauer, T.; Brandstetter, J.; Brondolin, E.; Dragicevic, M.; Erö, J.; et al. Search for an exotic decay of the Higgs boson to a pair of light pseudoscalars in the final state with two muons and two b quarks in pp collisions at 13 TeV. Phys. Lett. B 2019, 795, 398–423. [Google Scholar] [CrossRef]
- Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Ambrogi, F.; Asilar, E.; Bergauer, T.; Brandstetter, J.; Brondolin, E.; Dragicevic, M.; Erö, J.; et al. Search for an exotic decay of the Higgs boson to a pair of light pseudoscalars in the final state with two b quarks and two τ leptons in proton-proton collisions at = 13 TeV. Phys. Lett. B 2018, 785, 462. [Google Scholar] [CrossRef]
- Aaboud, M.; Aad, G.; Abbott, B.; Abeloos, B.; Abhayasinghe, D.K.; Abidi, S.H.; AbouZeid, O.S.; Abraham, N.L.; Abramowicz, H.; Abreu, H.; et al. Search for the Higgs boson produced in association with a vector boson and decaying into two spin-zero particles in the H→aa→4b channel in pp collisions at =13 TeV with the ATLAS detector. J. High Energy Phys. 2018, 10, 031. [Google Scholar] [CrossRef]
- Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Ambrogi, F.; Asilar, E.; Bergauer, T.; Brandstetter, J.; Dragicevic, M.; Erö, J.; Del Valle, A.E.; et al. Search for light pseudoscalar boson pairs produced from decays of the 125 GeV Higgs boson in final states with two muons and two nearby tracks in pp collisions at = 13 TeV. Phys. Lett. B 2020, 800, 135087. [Google Scholar] [CrossRef]
- Aad, G.; Abbott, B.; Abdallah, J.; Aben, R.; Abolins, M.; AbouZeid, O.S.; Abramowicz, H.; Abreu, H.; Abreu, R.; Abulaiti, Y.; et al. Search for Higgs bosons decaying to aa in the μμττ final state in pp collisions at = 8 TeV with the ATLAS experiment. Phys. Rev. D 2015, 92, 052002. [Google Scholar] [CrossRef]
- Carena, M.; Liu, Z.; Wang, Y. Electroweak phase transition with spontaneous Z2-breaking. J. High Energy Phys. 2020, 8, 107. [Google Scholar] [CrossRef]
- Chun, E.J.; Mondal, T. Searching for a Light Higgs Boson via the Yukawa Process at Lepton Colliders. Phys. Lett. B 2020, 802, 135190. [Google Scholar] [CrossRef]
- Abi, B.; Albahri, T.; Al-Kilani, S.; Allspach, D.; Alonzi, L.P.; Anastasi, A.; Anisenkov, A.; Azfar, F.; Badgley, K.; Baeßler, S.; et al. Measurement of the Positive Muon Anomalous Magnetic Moment to 0.46 ppm. Phys. Rev. Lett. 2021, 126, 141801. [Google Scholar] [CrossRef]
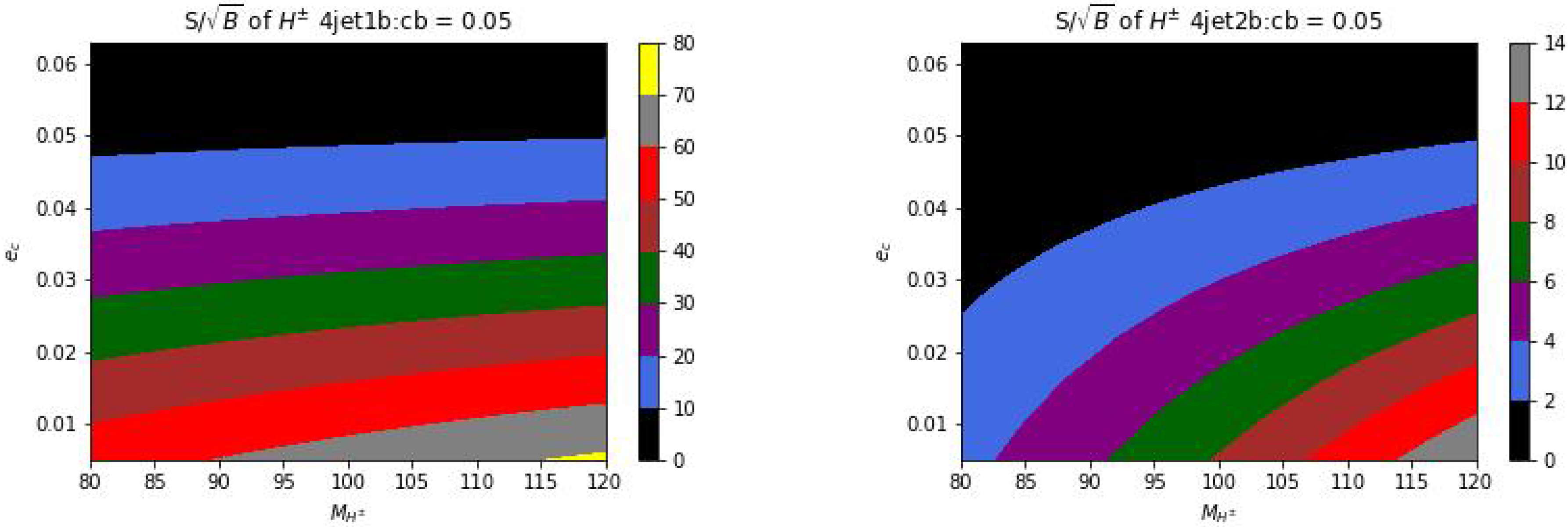
- Akeroyd, A.G.; Moretti, S.; Song, M. Light charged Higgs boson with dominant decay to a charm quark and a bottom quark and its search at LEP2 and future e+e− colliders. Phys. Rev. D 2020, 101, 035021. [Google Scholar] [CrossRef]
- Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Ambrogi, F.; Asilar, E.; Bergauer, T.; Brandstetter, J.; Brondolin, E.; Dragicevic, M.; Erö, J.; et al. Search for a standard model-like Higgs boson in the mass range between 70 and 110 GeV in the diphoton final state in proton-proton collisions at = 8 and 13 TeV. Phys. Lett. B 2019, 793, 320–347. [Google Scholar] [CrossRef]
- Heinemeyer, S.; Li, C.; Lika, F.; Moortgat-Pick, G.; Paasch, S. A 96 GeV Higgs Boson in the 2HDM plus Singlet. arXiv 2021, arXiv:2112.11958. [Google Scholar]
- Biekötter, T.; Heinemeyer, S.; Weiglein, G. Mounting evidence for a 95 GeV Higgs boson. arXiv 2022, arXiv:2203.13180. [Google Scholar]
- Azevedo, D.; Ferreira, P.; Mühlleitner, M.M.; Santos, R.; Wittbrodt, J. Models with extended Higgs sectors at future e+e− colliders. Phys. Rev. D 2019, 99, 055013. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Robens, T. A Short Overview on Low Mass Scalars at Future Lepton Colliders. Universe 2022, 8, 286. https://doi.org/10.3390/universe8050286
Robens T. A Short Overview on Low Mass Scalars at Future Lepton Colliders. Universe. 2022; 8(5):286. https://doi.org/10.3390/universe8050286
Chicago/Turabian StyleRobens, Tania. 2022. "A Short Overview on Low Mass Scalars at Future Lepton Colliders" Universe 8, no. 5: 286. https://doi.org/10.3390/universe8050286
APA StyleRobens, T. (2022). A Short Overview on Low Mass Scalars at Future Lepton Colliders. Universe, 8(5), 286. https://doi.org/10.3390/universe8050286





