1. Introduction
Weak-scale supersymmetry (SUSY), which is a leading candidate for physics beyond the standard model (SM), can solve elegantly the hierarchy problem of the Higgs boson by introducing various superpartners at the TeV scale. Moreover, the unification of gauge couplings, which cannot be exact in SM, can be successful in its SUSY extensions. The dark matter (DM) puzzle as well as the baryon asymmetry of universe, can also be explained with proper DM candidates and baryogensis mechanisms in SUSY. It is worth to note that the Higgs scalar, which was discovered by the ATALS [
1] and CMS [
2] collaborations of LHC in 2012, lie miraculously in the small ‘115–135’ GeV window predicted by the low-energy SUSY. (See [
3,
4,
5,
6,
7,
8] for excellent reviews on SUSY.)
It is well known that the soft SUSY spectrum, including the gaugino and sfermion masses, are determined by the SUSY breaking mechanism. Depending on the way the visible sector ’feels’ the SUSY breaking effects in the hidden sector, the SUSY breaking mechanisms can be classified into gravity mediation [
9,
10,
11], gauge mediation [
12], anomaly mediation [
13,
14] scenarios, etc. Gauge-mediated SUSY breaking (GMSB) scenarios, which will not cause flavor and CP problems that bother gravity mediation models, are calculable, predictive, and phenomenologically distinctive with a minimal messenger sector. However, unless additional messenger–matter interactions are introduced, minimal GMSB can hardly explain the 125 GeV Higgs with TeV scale soft SUSY breaking parameters because of the vanishing trilinear terms at the messenger scale. An interesting extension is the (extra)ordinary gauge mediation (EOGM) scenarios [
15,
16], in which the messenger sector can include all renormalizable, gauge-invariant couplings between the messengers and any number of singlet fields. In fact, many examples in the literature of OGM deformed by mass terms can fall into this category, and their generic properties can be obtained therein.
Gravity can generate the soft SUSY breaking masses by the auxiliary field of the compensator multiplet. Such a ’pure’ gravity mediation scenario with negligible contributions from direct non-renormalizable contact terms is called the anomaly-mediated SUSY breaking (AMSB). Pure anomaly mediation is bothered by the tachyonic slepton problem [
17]. Its non-trivial extensions with messenger sectors, namely the deflected AMSB [
18,
19,
20], can elegantly solve such tachyonic slepton problems through the deflection of the renormalization group equation (RGE) trajectory [
21]. There are two types of deflections in the literature, the deflection in the superpotential [
18,
20,
22,
23,
24] and the deflection in the Kahler potential [
25,
26,
27,
28,
29], respectively. However, it is difficult to determine consistently the deflection parameter ‘
d’ and soft SUSY parameters if both deflections are present. So, it is very interesting theoretically to solve such a difficulty systematically. A special example of EOGM extension of deflected AMSB had been given in [
30]. However, no systematical treatments and analytical results of the previously mentioned general case are given yet.
We find that the most general deflection scenario in deflected AMSB can be seen as a special case of the EOGM extension of deflected AMSB. We propose to introduce proper auxiliary spurion superfields and derive successfully the analytical expressions of the soft SUSY breaking parameters in the framework of EOGM extension of the deflected AMSB scenarios with both Kahler and superpotential deflections. Besides, special attentions are paid to the case with multi-scales messengers, especially the case with a vanishing beta function at an intermediate scale and the case with .
This paper is organized as follows. In
Section 2, we discuss the deflected AMSB scenario with EOGM extension for scenarios with both Kahler and superpotential deflections. In
Section 3, we discuss the analytical expressions of soft SUSY parameters in EOGM extended deflected AMSB. In
Section 4, constraints from the Landau pole, etc., with multi-scales messengers are given.
Section 5 contains our conclusions.
2. Effective EOGM Form in Deflected AMSB
To fully understand the deflected AMSB scenarios with the presence of both the superpotential and Kahler potential deflections, we need to obtain the effective deflection parameter ‘d’ to derive the full expressions of the soft SUSY breaking parameters. We find that such an effective deflection parameter ‘d’ can be obtained in the framework of EOGM extension of deflected AMSB.
In the deflected AMSB, the Kahler potential can have the following types of deflection with holomorphic terms for messengers
or the deflection from the couplings in the superpotential
with
the conformal compensator field that carries the SUSY breaking information in the SUSY breaking sector
A proper form of superpotential
is assumed for the pseudo-moduli field
to determine the deflection parameter
and the messenger threshold scale
. We should note that the messengers
can possibly be identified to be the
superfields.
To accommodate both types of deflections, we need to extract the total GMSB contributions in addition to the AMSB-type contributions, especially in the case that several SUSY breaking sources can contribute via the messenger sector. Combining both the Kahler and superpotential deflections, we have
We propose to rewrite this expression in the form
with
a new spurion superfield (
can have an R-symmetry charge
as the combination
has vanishing R-charge) introduced to incorporate the Kahler deflection effects with its VEV
and
being
or
. Knowing the spurion VEV, the GMSB contributions could be determined in the framework of EOGM to include several SUSY breaking sources.
We can rotate the spurion superfields
and
so that only one combination
X will acquire F-term VEVs while
T will acquire only the lowest component VEVs
So, the superpotential can be rewritten as
with
So, the coupling of the spurions to the messenger sector takes the form of EOGM.
It is reasonable to assume that the superpotential (
9) has a non-trivial R-symmetry
which can prevent destructive D-term contributions to sfermion masses. As noted in [
15], we can choose
without loss of generality by the mixing of the R-symmetry with the trivial
. After integrating out the messenger fields, the messenger determinant is proven by [
15] to be a monomial in
X
with
Note that the GMSB contribution of the most general deflection scenario in AMSB is quite similar to that of EOGM in GMSB, except that the VEV of
X is given by
from (
8).
The previous discussions can be generalized to the case with multiple pseudo-moduli
superfields in the superpotential, which are all very flat in the SUSY limit and can couple differently to the messengers. Each
will acquire its corresponding F-term VEV to give additional GMSB-type contributions to the soft SUSY breaking parameters in addition to AMSB contributions. We have
which can be rewritten as
After associating each dimensional parameter in the superpotential
with proper power of compensator field
and substituting the expression of the compensator VEV
, one can obtain the VEV of each
by minimizing the whole scalar potential. The VEV for each
can be parameterized as
Similar to (
8), one can perform a unitary transformation for
superfields so that only one of the combinations can have an F-term VEV, while the other combinations only have the lowest component VEVs. So, the resulting superpotential involving the messengers can again be written in the form
with similar discussions from (
11) to (
13).
We will discuss the soft SUSY breaking parameters in our scenarios. The VEV of
X, which is determined by the dynamics of
X and the unitary transformation of
, can take the following form
For multiple messenger species with the general form of the coupling
we can in principle diagonalize the non-singular mass matrix
by
, so the couplings can be recast into the form
with
the corresponding eigenvalues and
Simply, we choose
to lie in the
and
representations of SU(5), respectively. Because of the R-symmetry, the eigenvalue
has to be a monomial in
X, which can only take the following form (see the discussions in
Section 3.3):
with
and
. We can associate each dimensional parameter with a proper power of the compensator field
to obtain the deflection parameter related to the messenger
and
after substituting the VEV
and
. Without loss of generality, one can assume that the messenger thresholds satisfy
These
can be hierarchical or lie at the same order.
So, the soft SUSY breaking parameters can be obtained by the wavefunction renormalization [
31] approach.
The gaugino masses are given as
The trilinear couplings
are given as
The soft SUSY breaking scalar masses are given as
Details of the expression involving the derivatives with respect to
, etc., can be found in [
24,
32,
33].
It is well known that in the limit, the anomaly mediation contributions in the deflect AMSB are sub-leading and the gauge mediation contributions are dominant. So, we will derive the EOGM contributions first and return to deflected AMSB cases subsequently.
3. Analytical Expressions within EOGM
For multiple messengers, we assume that the mass thresholds of the
N messengers can be degenerated and separated into
groups as
with
.
The gauge couplings at a scale
below all the messenger thresholds are given as
Here we assume that the eigenvalues of the messenger mass matrix are given by
. So, the gaugino mass can be given as
Here
, which are given by
with
and
is given in Equation (
12). Besides, the previous expressions also agree with the result
with
the deflection parameter with respect to messenger threshold
, whose expression is given by (
23). The previous results can be rewritten in an alternative form by using the identity
for non-singular matrix
M. If we assume that the lowest component VEV of
vanishes and the SUSY breaking parameter
is small in comparison to the messenger scale, we have
in the basis where
is real and diagonal.
For the soft sfermion masses and trilinear couplings, we need the dependence of wavefunction
on each messenger threshold
. The derivative of
with respect to
can be obtained via
The sum over
, which depends on the messenger thresholds
, take the values
. The third term always vanishes because the anomalous dimension is continuous across the messenger thresholds (here we assume no messenger–matter interactions are present).
To obtain the expressions for wavefunction , we need the following classifications:
In the case for all , the expression will fall into class A.
In the case for some , the expression will fall into class B.
3.1. Class A: Partition without Vanishing Gauge Beta Functions
To obtain
, we can construct an invariant by surveying the anomalous dimension of
and solve the differential equation in the basis of
with
at the scale
. The expressions of the wavefunction can be solved (for example, see Appendix A in Refs. [
34,
35] for details) as
with the corresponding coefficients
given as
at the energy interval
(
), respectively.
If all the Yukawa terms within the wavefunction are neglected, the will take the value with , the quadratic Casimir invariant for the superfield .
From Equation (
37), we obtain
with the column indices
.
From the expressions of gauge coupling at scale
within each threshold interval, we can obtain an
matrix
So, we have
with the column indices corresponding to
, etc. Here we rewrite our expressions neatly by defining
within which
is just the beta function coefficient below all the messenger thresholds. From the previous expressions, we can check that each row will vanish if we neglect the scale dependence of
. This observation agrees with the ordinary conclusion that the trilinear couplings of GMSB vanish if no Yukawa deflections are present.
From the expressions in Equation (
40), we can obtain the symmetric matrix (for indices
j and
k)
with the contributions
for each gauge field
The functions within
are defined as
within which
Here we define the summation to vanish if its index lies out of its definition range. For example,
. From the previous expressions, we can check that each non-diagonal element of
will vanish if we neglect the scale dependence of
. Only the diagonal elements of
can give non-vanishing values of order
The inclusion of top-Yukawa coupling is straightforward in the analytical expressions. The scale dependence of top-Yukawa in the simplest case, in which only the leading top Yukawa
and
are kept in the anomalous dimension, takes the form
Define
, the equation can be written as
So, we can exactly solve the differential equation to obtain
Expanding the expressions and neglecting high-order terms, we finally have
It can be observed that, in the leading order approximation, the expression within the square bracket is just the beta function of top Yukawa coupling. As there are no Yukawa deflection contributions related to the introduction of messengers, the Yukawa coupling contributions will not enter the expression within the GMSB part of the generalized dAMSB.
3.2. Class B: Partition with Vanishing Gauge Beta Functions
In previous discussions, apparent poles may arise if we have vanishing gauge beta function coefficient between certain messenger scales. (Although such poles will not appear if higher loop order beta functions contributions are included, we still want to check the status of the contribution with tiny beta functions.) For example, with non-degenerate messengers in representation, the beta function for , which is given by , will vanish after decoupling family of vector-like messengers at one-loop level. (The beta function for gauge fields will not encounter such difficulties.) Such an artificial pole can be resolved by revisiting the deduction procedure of wavefunctions.
Assume that all the i-th gauge coupling beta function coefficients are non-vanishing for . After integrating out the family of vector-like messengers at the scale, the beta function coefficient is assumed to vanish (so that ).
The wavefunction at the
scale takes value
As the
i-th beta function vanishes at one-loop level
it can be seen as a constant between
. Within this range, the RGE invariant became
and we can deduce that
The value
with the value
given in
Appendix A. We will keep using
in this paper to indicate clearly the consequence of vanishing one-loop beta functions.
So, for
,
and for
,
Therefore, we have for
with the last term giving non-vanishing contributions only for
From the general expressions, we can see that the
j-th and (
j + 1)-th components will be changed into
while other columns are unchanged as Equation (
38) if
for
. The matrix
, which is given by Equation (
39), is unchanged. Then the contributions from the
i-th gauge field, which has vanishing beta functions between
, are given as
Within the deduction, we use the fact that
and
. Furthermore, we also define
within the expression
We note that when
c takes value
or
j in the summation of
, the sum skip
and begins at
.
From the previous expressions, we can see that each row will vanish if we neglect the scale dependence of
and higher-order
terms. In fact, with such an approximation, the
j-th and
-th row is given by
In the summation
the expressions for
gauge fields (which have no vanishing beta functions) are still given by
from Equation (
40).
With previous results, we can derive the expression of
from
i-th (here
) gauge fields
with
a symmetric matrix given as
The functions within
are defined as
with
From the previous expressions, we can check that each non-diagonal element of
will vanish if we neglect the scale dependence of
and higher-order
terms. The diagonal elements of
can give non-vanishing values of order
The
and
term will be given as
if we neglect the scale dependence of
and higher-order
terms.
The contributions from
gauge fields are still given by Equation (
43). The total contributions are given by the sum of
gauge fields.
3.3. Dependence of on
As noted before, with non-trivial
symmetry, the messenger determinant is proven by [
15] to be a monomial in
X
Knowing the value of the determinant, it is still non-trivial to express the eigenvalues of
in terms of
. (Here and after,
is used to denote the scalar component VEV of the superfield X.) Fortunately, the asymptotic behavior will display a simple form. In large
region,
messengers acquire masses
while the remaining
messengers acquire masses of order
with
. At small
region,
messengers acquire masses
while the remaining
messengers acquire masses of order
with
.
Depending on the singularity properties of the messenger mass matrix, we have the following discussions.
Type I: .
In the basis in which
m is diagonal, it can prove [
15] that Equation (68) takes the form
which necessarily implies
. As the matrix is upper triangular, the eigenvalues are
that do not depend on
.
So, in this case, we have
or
So, we can see that the gauginos, the trilinear couplings, and the sfermions will not receive any gauge mediation contributions.
Type II: .
Similarly, we can obtain an upper triangular matrix with eigenvalues equal to the diagonal elements of diagonalized matrix
. The determinant is
So, the eigenvalues will be and depend linearly on . We will arrange to obtain the eigenvalues .
Suppose the
are ordered so as that
, we define
For degenerate eigenvalues
with
, the matrix
reduces to a
matrix
So, the soft SUSY breaking parameters for GMSB can be given as
- -
- -
GMSB contributions to trilinear terms:
As anticipated, the trilinear term will vanish if we neglect the scale dependence of and higher-order terms.
- -
Pure GMSB contributions to soft sfermion masses:
This expression can be simplified into
if we neglect the scale dependence of
and higher-order
terms.
Such GMSB expressions can easily be extended to gauge mediation contributions in deflected AMSB.
Type III: .
As the matrix
is non-singular, its eigenvalues can be written as
, which should satisfy
and
In the large
X region in which
can be neglected, we can use linear transformation to put
into
There are messengers with mass of order X. As the trace depends linearly on X, such messengers had to have a linear dependence on X. The remaining messengers can only be proportional to an inverse power of X or be a constant. From the trace, which contains only the constant and the linear X term, the term with negative power of X should appear in pairs or vanish. It is also obvious that terms with negative power of X have to appear if . As the eigenvalues, which contain non-vanishing negative powers, are suppressed by an additional factor, they need to be the lighter eigenvalues.
As
messengers depend linearly on
X, we can approximately use
with
For degenerate eigenvalues,
with
, some constants eigenvalues of
are independent of
X. Assuming
, the matrix
reduces to a
matrix
with
The partition of N can be obtained numerically by diagonalizing to obtain its eigenvalues as functions of .
So, we can obtain the GMSB contributions
with the
taking the value in Equation (87). Again, the trilinear term will vanish if we neglect the scale dependence of
and higher-order
terms.
will reduce to
if the scale dependence of
and higher-order
terms are neglected.
If the first
j-th eigenvalues are proportional to
X while the remaining
eigenvalues are proportional to
m, the summation of the elements in the scalar matrix
will be truncated so that only the upper
terms will be taken into account. So, the sfermion soft masses will in general be lighter than that of Type II. It is phenomenologically attractive to have light slepton masses. The well-known muon
discrepancy can be solved with large contributions from slepton-electroweakino loops [
36].
The inclusion of EOGM in deflected AMSB is straightforward. The AMSB type contributions can be given as
with
the discontinuity of beta functions across the threshold
.
In [
15], the ‘
effective messenger number’ is defined as
with
So, the approximate value of
can be given as
by neglecting the scale dependence of
and higher-order terms in the expressions of soft SUSY parameters. With previous approximation, the value of
in Type II can be calculated to be
after simplification, while in Type III EOGM, it can be calculated to be
. Such a result holds for both Class A and Class B. Taking into account the scale dependence of
,
can be different to
and
N.
The framework of EOGM extension of AMSB can accommodate deflections both in the Kahler potential and in the superpotential. So, it can easily solve the notorious negative square mass problem of sleptons. As the Kahler deflection [
29] and superpotential deflection [
22,
23] in AMSB can easily accommodate the 125 GeV Higgs and be regarded as special cases of our EOGM extensions framework, this general case can also possibly accommodate the 125 GeV Higgs. With our previous setting in [
29], it can be seen in
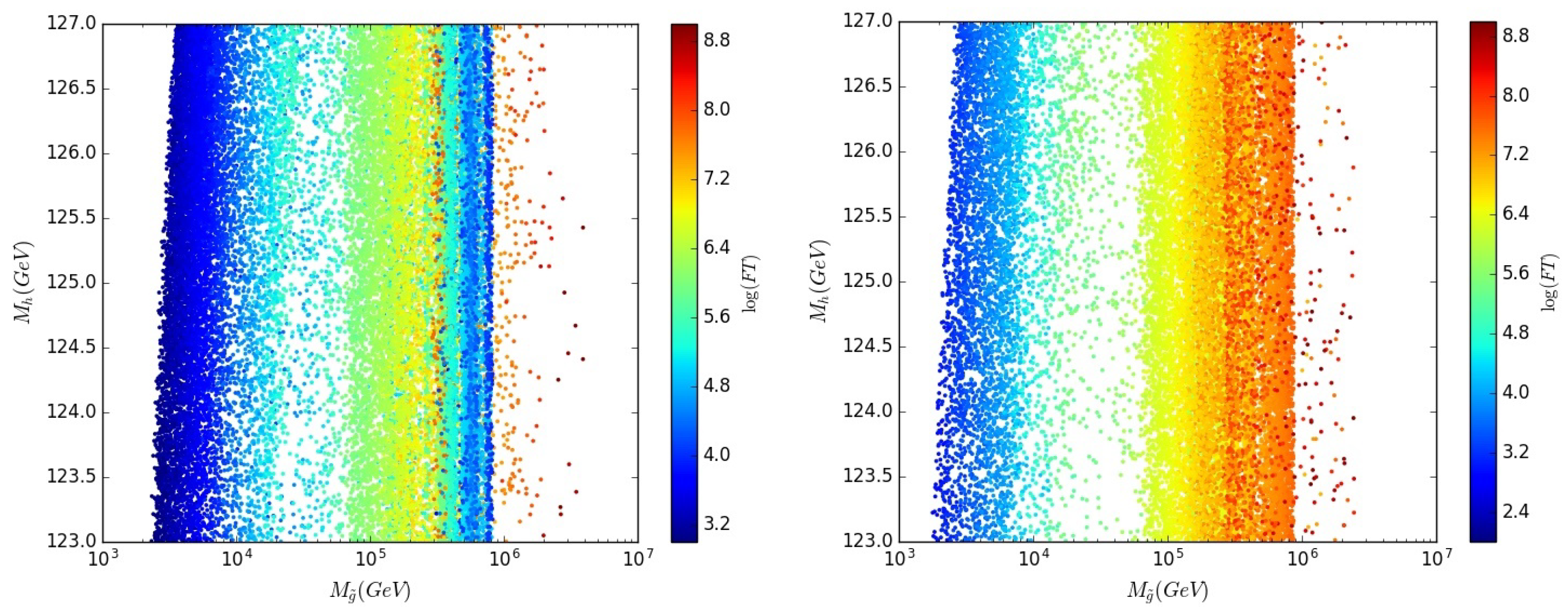
Figure 1 that our EOGM extension of AMSB can easily lead to a realistic spectrum in various constrained limits. A detailed numerical scan will be studied in our subsequent works.
EOGM extension of deflected AMSB scenarios can easily adopt light sleptons. In addition, the EOGM extension of deflected AMSB scenarios can alter the gaugino relations into at the EW scale, with n an integer satisfying and the deflection parameter. So, with proper choices for and n, light electroweakinos can easily be obtained, given the stringent LHC constraints on gluino mass.
Light sleptons and eletroweakinos are welcome to explain the recent muon
anomaly [
37] and new CDF II W-boson mass data [
38] in the SUSY framework [
39]. Such light smuons and electroweakinos can be tested at the LHC. However, some compressed regions can still survive the updated constraints. Detailed simulations on the signals and collider exclusion bounds will be given in our subsequent studies.
Large gaugino ratios, especially between
and
, can be possible in this EOGM extension of deflected AMSB scenarios. With a large hierarchy, the gluino mass should be heavy due to the stringent lower mass bounds on chargino masses. Consequently, the squarks will always be pushed to be heavy by gluino loops. The heavy first two generation squarks are welcome to evade the LHC constrains. However, heavy stops, which can be welcome to accommodate the 125 GeV Higgs, may increase the involved electroweak fine-tuning (EWFT). Fortunately, EOGM extension of deflected AMSB scenarios can always predict large
term, which can lead to small EWFT even for TeV scale stops [
40,
41]. So, EOGM extension of deflected AMSB scenarios are also interesting phenomenologically.
Wino DM is always predicted in such scenarios. For light wino smaller than approximately 3 TeV, additional DM species are necessarily present to give correct relic abundances. Relevant phenomenology for such wino DM will be given in our subsequent studies.
4. Messengers on GUT and Landau Pole
We must ensure that no Landau pole will be reached below the GUT scale. It is obvious that the gauge coupling unification will be preserved because the messengers are fitted into complete SU(5) representations. The presence of (complete GUT representation) messenger fields at an intermediate scale does not modify the value of . However, proton decay could possibly set constraints on the gauge couplings at the GUT scale.
We can define the quantity
which contributes to the inverse gauge coupling strength. The gauge couplings at the GUT scale are given at one-loop level by
The first two terms give the gauge couplings at the GUT scale with
with
GeV and the SUSY scale
TeV. So, the perturbativity of gauge couplings at the GUT scale set a bound on the quantity
to be
Proton decay experiments will also constrain the value of
. As the proton decay induced from the triplet Higgs depends on the scale of the triplets, we just take constraints from proton decay induced by heavy gauge bosons. The decay channel
has the lifetime
With updated experimental bounds from Super-Kamiokande [
42,
43]
years, we can constrain the inputs
by taking
MeV, chiral Lagrangian factor
with
,
[
44], the hadronic matrix element
(at renormalization scale
) and
, respectively. This value constrained
to be
It is known that a measure of gauge unification by experiments
agrees with the one-loop MSSM prediction
up to
accuracy. In our scenario with multi-scale messengers, the parameter is given by
with
the total species of messenger. So, in order for the deviation of
B to not exceed
, the parameters should satisfy
We should note that
, which represent the renormalization effects resulting from the anomalous dimensions of the operators, will also be amended by presence of vector-like messengers [
45]. They are defined as
with
the long and short distance factors, respectively. Here the long-distance contribution
is taken to be
. The short distance factors will be changed into
in the case that one vector-like family of messengers at scale
is present. Results with multiple messenger thresholds can be trivially extended. The relevant coefficients within the expressions are given [
46] as
with
the relevant gauge beta functions upon each threshold. The multiple factor for
in the presence of messengers is given approximately by
in which we define
. This multiple factor can be easily extended to include multiple messengers. For example, with additional messenger thresholds at
, the new multiple factor is given by
with the total multiple factor
As the coefficients
depend on the messenger scales, the proton decay constraints will feed back into the constraints on
. Detailed discussions on constraints for
will be given in our subsequent studies.
5. Conclusions
The EOGM extension of deflected AMSB scenarios can accommodate the deflected AMSB scenarios with the presence of both Kahler and superpotential deflections. We revisit the EOGM scenario and derive the analytical expressions for soft SUSY breaking parameters with wavefunction renormalization approach in EOGM extension of deflected AMSB scenarios. As EOGM extension scenarios always introduce additional messenger species, we therefore also consider the Landau pole and proton decay constraints on the messenger sector.
Minimal AMSB is always bothered by the tachyonic slepton problem. As deflections by the messengers can introduce additional positive contributions to the slepton squared masses, the slepton squared masses can be tuned to be positive small numbers. Consequently, EOGM extension of deflected AMSB scenarios can easily predict light sleptons. In addition, the EOGM extension of deflected AMSB scenarios can alter the gaugino relations at the EW scale. The gluino masses are constrained by LHC to be heavier than 2.2 TeV. So, the gaugino ratios
:
:
1:2:6 in ordinary GMSB and mSUGRA always constrain the electroweakino masses to be light. However, recent muon
anomaly [
37] and new CDF II W-boson mass data [
38] always prefer light electroweakinos [
39]. So, spoiled gaugino relations are always welcome. In EOGM extension of deflected AMSB scenarios, the gaugino ratios change approximately into
at the EW scale, with
n an integer satisfying
and
the deflection parameter. So, with proper choices for
and
n, light electrweakinos can be obtained, given the LHC constraints on gluino mass. With light sleptons and eletroweakinos (especially light wino), the muon
anomaly and new CDF II W-boson mass data can be explained in the SUSY framework. Such light smuons and electroweakinos will be tested at the LHC and set new constraints on the EOGM extension AMSB type models, although some compressed regions can still survive. Wino DM is always predicted in such scenarios. For light wino, additional DM species are necessary to give correct relic abundances. Relevant phenomenology for such EOGM extension of deflected AMSB scenarios will be discussed in our subsequent studies.