Search for Dark Higgs Inflation with Curvature Corrections at LHC Experiments
Abstract
:1. Introduction
2. Dark Higgs Model
2.1. Light Dark Higgs Mass and Mixing Angle
2.2. Reheating and Horizon Crossing
3. Dark Higgs Inflation with Curvature Corrections
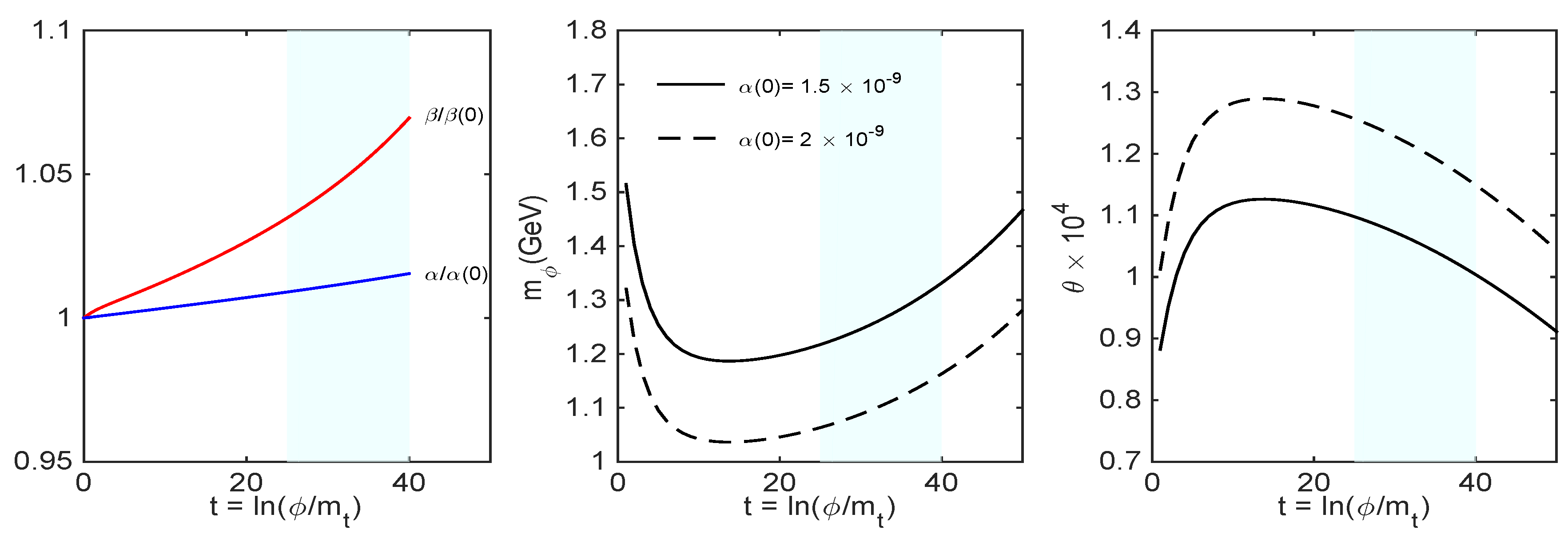
4. Cosmological Constraints
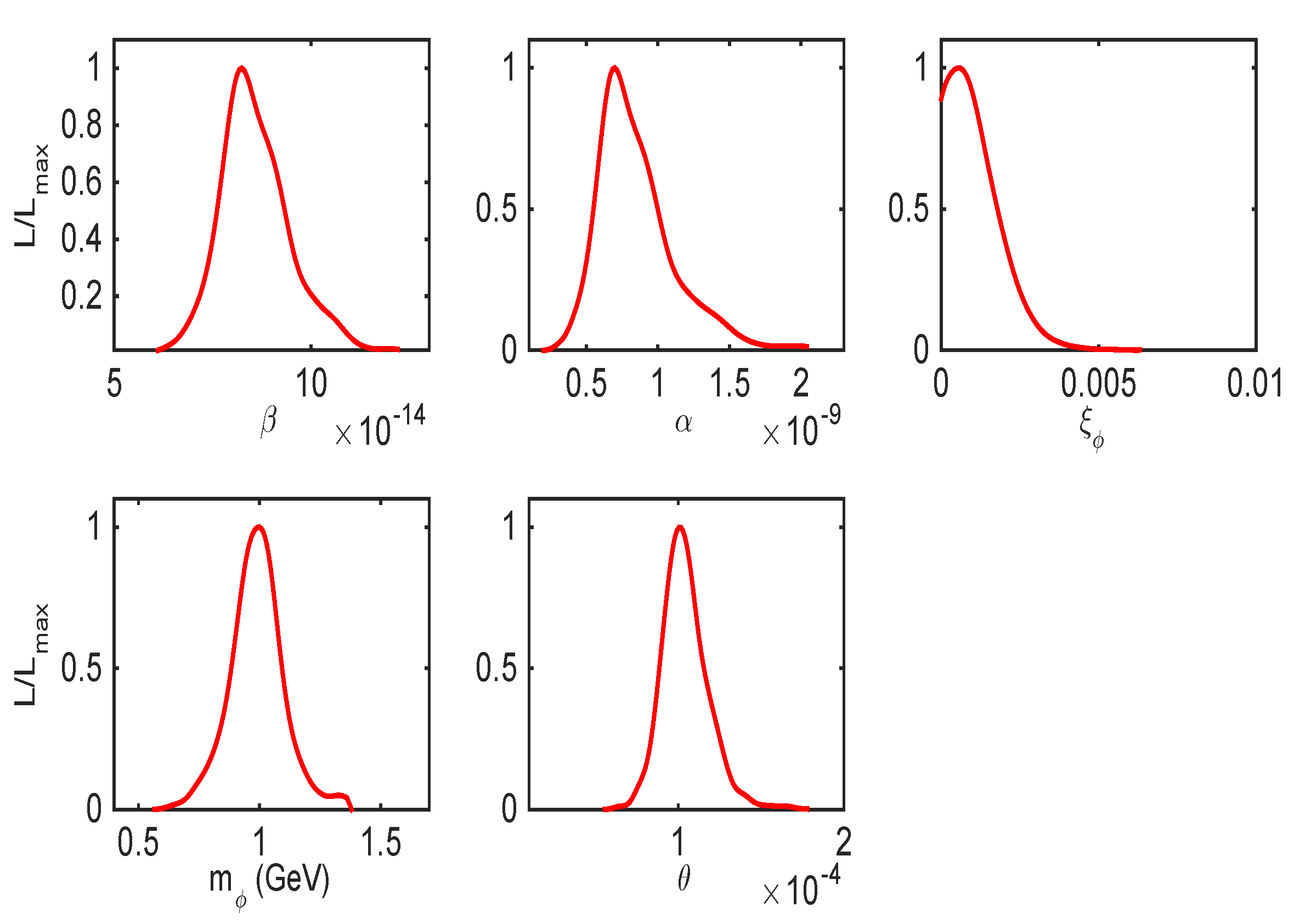
4.1. Parameterisation and Methods
4.2. Analysis
5. Search for Dark Higgs Inflation at LHC Experiments
5.1. Dark Higgs Inflation Decay
5.2. Dark Higgs Reheating Temperature and Energy Density
5.3. Dark Higgs Decay Inside Detector
- The FASER detector has a cylindrical shape centred on the LHC beam collision axis at = 480 m from IP, has an available length = 15 m and the radius R = 2 m.
- The MAPP detector is a parallelepiped at approximately from the beam collision axis at m from IP with an available length m and the parallelepiped height m.
5.4. Dark Higgs Production
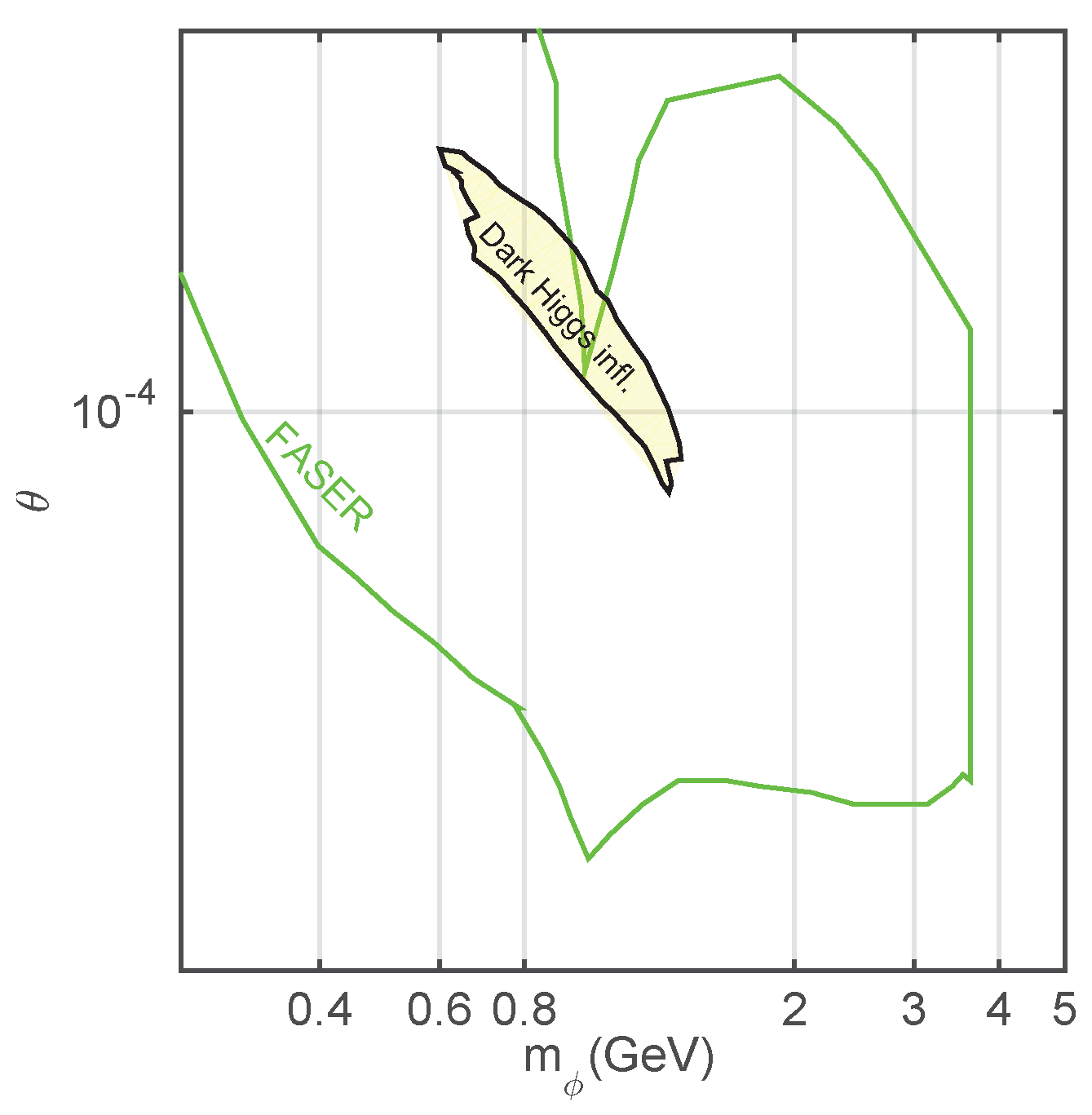
5.5. LHC Experiments Reach for Dark Higgs Inflation with Curvature Couplings
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A10. [Google Scholar]
- Akrami, Y.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. X. Constraints on inflation. Astron. Astrophys. 2020, 641, A6. [Google Scholar]
- Ade, P.A.R.; Ahmed, Z.; Aikin, R.W.; Alexander, K.D.; Barkats, D.; Benton, S.J.; Bischoff, C.A.; Bock, J.J.; Bowens-Rubin, R.; Brevik, J.A.; et al. BICEP2/Keck Array X: Constraints on Primordial Gravitational Waves using Planck, WMAP, and New BICEP2/Keck Observations through the 2015 Season. Phys. Rev. Lett. 2018, 121, 221301. [Google Scholar] [CrossRef] [Green Version]
- ATLAS Collaboration; Aad, G.; Abajyan, T.; Abbott, B.; Abdallah, J.; Khalek, S.A.; Abdelalim, A.A.; Abdinov, O.; Aben, R.; Abi, B.; et al. Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. 2012, 761, 1–29. [Google Scholar]
- Chatrchyan, S.; Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Aguilo, E.; Bergauer, T.; Dragicevic, M.; Erö, J.; Fabjan, C.; et al. Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC. Phys. Lett. 2012, 716, 30. [Google Scholar] [CrossRef]
- Beacham, J.; Burrage, C.; Curtin, D.; De Roeck, A.; Evans, J.; Feng, J.L.; Gatto, C.; Gninenko, S.; Hartin, A.; Irastorza, I.; et al. Physics Beyond Colliders at CERN Beyond the Standard Model Working Group Report. J. Phys. G 2020, 47, 010501. [Google Scholar] [CrossRef]
- Bezrukov, F.L.; Shaposhnikov, M. The Standard Model Higgs boson as the inflaton. Phys. Lett. 2008, 659, 703. [Google Scholar] [CrossRef] [Green Version]
- Futamase, T.; Maeda, K.-I. Chaotic Inflationary Scenario in Models Having Nonminimal Coupling with Curvature. Phys. Rev. 1989, 39, 399. [Google Scholar]
- Fakir, R.; Unruh, W.G. Improvement on cosmological chaotic inflation through nonminimal coupling. Phys. Rev. 1990, 41, 1783. [Google Scholar] [CrossRef]
- Germani, C.; Kehagias, A. New Model of inflation with Nonminimal Derivative Coupling of Standard Model Higgs Boson to Gravity. Phys. Rev. Lett. 2010, 105, 011302. [Google Scholar] [CrossRef] [Green Version]
- Granda, L.N. Inflation driven by scalar field with non-minimal kinetic coupling with Higgs and quadratic potentials. JCAP 2011, 04, 016. [Google Scholar] [CrossRef] [Green Version]
- Granda, L.N.; Jimenez, D.F.; Cardona, W. Higss inflation with non-minimal derivative coupling to gravity. Astropart. Phys. 2020, 121, 102459. [Google Scholar] [CrossRef]
- Tsujikawa, S. Observational tests of inflation with a field derivative coupling to gravity. Phys. Rev. 2012, 85, 083518. [Google Scholar] [CrossRef] [Green Version]
- Granda, L.N.; Jimenez, D.F. Higgs Inflation with linear and quadratic curvature corrections. arXiv 2019, arXiv:1910.11289. [Google Scholar]
- Granda, L.N.; Jimenez, D.F. Slow-Roll Inflation in Scalar-Tensor Models. JCAP 2019, 9, 7. [Google Scholar] [CrossRef] [Green Version]
- Kamada, K.; Kobayashi, T.; Yamaguchi, M.; Yokoyama, J. Higgs G-inflation. Phys. Rev. 2011, 83, 083515. [Google Scholar]
- Ohashi, J.; Tsujikawa, S. Potential-driven Galileon inflation. JCAP 2012, 1210, 035. [Google Scholar] [CrossRef] [Green Version]
- Kobayashi, T.; Yamaguchi, M.; Yokoyama, J. Inflation Driven by the Galileon Field. Phys. Rev. Lett. 2010, 105, 231302. [Google Scholar] [CrossRef] [Green Version]
- Kobayashi, T.; Yamaguchi, M.; Yokoyama, J. Generalized G-inflation: Inflation with the most general second-order field equations. Prog. Theor. Phys. 2011, 126, 511. [Google Scholar] [CrossRef]
- Bramante, J.; Cook, J.; Delgado, A.; Martin, A. Low scale inflation at high energy colliders and meson factories. Phys. Rev. 2016, 94, 115012. [Google Scholar] [CrossRef] [Green Version]
- German, G. Quartic hilltop inflation revisited. JCAP 2021, 2, 34. [Google Scholar] [CrossRef]
- Burgess, C.P.; Lee, H.M.; Trott, M. Power-counting and the Validity of the Classical Approximation During Inflation. JHEP 2009, 9, 103. [Google Scholar] [CrossRef] [Green Version]
- Bezrukov, F.; Magnin, A.; Shaposhnikov, M.; Sibiryakov, S. Higgs inflation: Consistency and generalisations. JHEP 2011, 11, 16. [Google Scholar] [CrossRef] [Green Version]
- Burgess, C.P.; Patil, S.P.; Michael, T. On the predictiveness of single-field inflationary models. JHEP 2014, 6, 10. [Google Scholar] [CrossRef] [Green Version]
- Linde, A.D. Chaotic inflation. Phys. Lett. 1983, 129, 177. [Google Scholar] [CrossRef]
- Atkins, M.; Calmet, X. Remarks on Higgs inflation. Phys. Lett. 2011, 697, 37. [Google Scholar] [CrossRef] [Green Version]
- Bhattacharjee, S.; Maity, D.; Mukherjee, R. Constraining scalar-Gauss-Bonnet Inflation by Reheating, Unitarity and PLANCK. Phys. Rev. 2017, 95, 023514. [Google Scholar] [CrossRef] [Green Version]
- Zyla, P.A.; Barnett, R.M.; Beringer, J.; Dahl, O.; Dwyer, D.A.; Groom, D.E.; Lin, C.J.; Lugovsky, K.S.; Pianori, E.; Robinson, D.J.; et al. The Review of Particle Physics. Prog. Theor. Exp. Phys. 2020, 2020, 083C01. [Google Scholar]
- Bezrukov, F.; Rubio, J.; Shaposhnikov, M. Living beyond the edge: Higgs inflation and vacuum metastability. Phys. Rev. 2015, 92, 083512. [Google Scholar] [CrossRef] [Green Version]
- Buttazzo, D.; Degrassi, G.; Giardino, P.P.; Giudice, G.F.; Sala, F.; Salvio, A.; Strumia, A. Investigating the near-criticality of the Higgs boson. JHEP 2013, 12, 89. [Google Scholar] [CrossRef] [Green Version]
- Degrassi, G.; Vita, S.D.; Elias-Miro, J.; Espinosa, J.R.; Giudice, G.F.; Isidori, G.; Strumia, A. Higgs mass and vacuum stability in the Standard Model at NNLO. JHEP 2012, 8, 98. [Google Scholar] [CrossRef] [Green Version]
- Allison, K. Higgs xi-inflation for the 125-126 GeV Higgs: A two-loop analysis. JHEP 2014, 2, 40. [Google Scholar] [CrossRef] [Green Version]
- Lebedev, O. On Stability of the Electroweak Vacuum and the Higgs Portal. Eur. Phys. J. 2012, 72, 2058. [Google Scholar] [CrossRef] [Green Version]
- Elias-Miro, J.; Espinosa, J.R.; Giudice, G.F.; Lee, H.M.; Strumia, A. Stabilization of the Electroweak Vacuum by a Scalar Threshold Effect. JHEP 2012, 6, 31. [Google Scholar] [CrossRef] [Green Version]
- Ballesteros, G.; Tamarit, C. Higgs portal valleys, stability and inflation. JHEP 2015, 9, 210. [Google Scholar]
- Ellis, J.R.; Gaillard, M.K.; Nanopoulos, D.V. A phenomenological profile of the Higgs boson. Nucl. Phys. 1976, 106, 292. [Google Scholar] [CrossRef]
- Feng, J.L.; Galon, I.; Kling, F.; Trojanowski, S. Dark Higgs bosons at the ForwArd Search ExpeRiment. Phys. Rev. 2018, 97, 055034. [Google Scholar] [CrossRef] [Green Version]
- Shaposhnikov, M.; Tkachev, I. The νMSM inflation and dark matter. Phys. Lett. 2006, 639, 414. [Google Scholar] [CrossRef] [Green Version]
- Asaka, T.; Blanchet, S.; Shaposhnikov, M. The MSM, dark matter and neutrino masses. Phys. Lett. 2005, 631, 151. [Google Scholar] [CrossRef] [Green Version]
- Asaka, T.; Shaposhnikov, M. The MSM dark matter and baryon asymmetry of the universe. Phys. Lett. 2005, 620, 17. [Google Scholar] [CrossRef] [Green Version]
- Anisimov, A.; Bartocci, Y.; Bezrukov, F.L. Inflaton mass in the νMSM inflation. Phys. Lett. 2009, 671, 211. [Google Scholar] [CrossRef]
- Lerner, R.N.; McDonald, J. Distinguishing Higgs inflation and its variants. Phys. Rev. 2011, 83, 123522. [Google Scholar] [CrossRef] [Green Version]
- Tenkanen, T.; Tuominen, K.; Vaskonen, V. A Strong Electroweak Phase Transition from the Inflaton Field. JCAP 2016, 9, 37. [Google Scholar] [CrossRef]
- Kim, J.; Ko, P.; Park, W. Higgs-portal assisted Higgs inflation with a sizeable tensor-to-scalar ratio. JCAP 2017, 2, 3. [Google Scholar] [CrossRef] [Green Version]
- Aravind, A.; Xiao, M.; Yu, J.H. Higgs Portal to Inflation and Fermionic Dark Matter. Phys. Rev. 2016, 93, 123513. [Google Scholar] [CrossRef] [Green Version]
- Okada, N.; Raut, D. Hunting inflatons at FASER. Phy. Rev. 2021, 103, 055022. [Google Scholar] [CrossRef]
- Bezrukov, F.; Gorbunov, D. Light inflaton Hunter’s Guide. JHEP 2010, 5, 10. [Google Scholar] [CrossRef] [Green Version]
- Bezrukov, F.; Gorbunov, D. Light inflaton after LHC8 and WMAP9 results. JHEP 2013, 7, 140. [Google Scholar] [CrossRef] [Green Version]
- Jiang, P.X.; Hu, J.W.; Guo, Z.K. Inflation coupled to a Gauss-Bonnet term. Phys. Rev. 2013, 88, 123508. [Google Scholar] [CrossRef] [Green Version]
- Kanti, P.; Gannouji, R.; Dadhich, N. Gauss-Bonnet Inflation. Phys. Rev. 2015, 92, 041302. [Google Scholar] [CrossRef] [Green Version]
- Odintsov, S.D.; Oikonomou, V.K. Viable Inflation in Scalar-Gauss-Bonnet Gravity and Reconstruction from Observational Indices. Phys. Rev. 2018, 98, 044039. [Google Scholar] [CrossRef] [Green Version]
- Pozdeeva, E.O.; Gangopadhyay, M.R.; Sami, M.; Toporensky, A.V.; Vernov, S.Y. Inflation with a quartic potential in the framework of Einstein-Gauss-Bonnet gravity. Phys. Rev. 2020, 102, 043525. [Google Scholar] [CrossRef]
- Pozdeevaa, E.O.; Vernov, S.Y. Construction of inflationary scenarios with the Gauss-Bonnet term and non-minimal coupling. Eur. Phys. J. C 2021, 81, 633. [Google Scholar] [CrossRef]
- Vernov, S.Y.; Pozdeeva, E.O. De Sitter solutions in Einstein-Gauss-Bonnet gravity. Universe 2021, 7, 149. [Google Scholar] [CrossRef]
- Shaposhnikov, M.; Zenhausern, D.B. Scale invariance, unimodular gravity and dark energy. Phys. Lett. 2009, 671, 187. [Google Scholar] [CrossRef] [Green Version]
- Garcia-Bellido, J.; Rubio, J.; Shaposhnikov, M.; Zenhausern, D. Higgs-Dilaton Cosmology: From the Early to the Late Universe. Phys. Rev. 2011, 84, 123504. [Google Scholar] [CrossRef] [Green Version]
- Garcia-Bellido, J.; Rubio, J.; Shaposhnikov, M. Higgs-Dilaton cosmology: Are there extra relativistic species. Phys. Lett. 2012, 718, 507. [Google Scholar] [CrossRef] [Green Version]
- Lyth, D.H.; Riotto, A.A. Particle physics models of inflation and the cosmological density perturbation. Phys. Rep. 1999, 314, 1–146. [Google Scholar] [CrossRef] [Green Version]
- Micha, R.; Tkachev, I.I. Relativistic Turbulence: A Long Way from Preheating to Equilibrium. Phys. Rev. Lett. 2003, 90, 121301. [Google Scholar] [CrossRef] [Green Version]
- Micha, R.; Tkachev, I.I. Turbulent Thermalization. Phys.Rev. 2004, 70, 043538. [Google Scholar] [CrossRef] [Green Version]
- Antoniadis, I.; Karam, A.; Lykkas, A.; Tamvakis, A.K. Palatini inflation in models with an R2 term. JCAP 2018, 11, 28. [Google Scholar] [CrossRef] [Green Version]
- Antoniadis, I.; Karam, A.; Lykkas, A.; Tamvakis, A.K. Rescuing Quartic and Natural Inflation in the Palatini Formalism. JCAP 2019, 3, 005. [Google Scholar] [CrossRef] [Green Version]
- Gorbunov, D.; Tokareva, A. Scalaron the healer: Removing the strong-coupling in the Higgs- and Higgs-dilaton inflations. Phys. Lett. 2019, 788, 37. [Google Scholar] [CrossRef]
- Lebedev, O.; Lee, H.M. Higgs Portal Inflation. Eur. Phys. J. 2011, 71, 1821. [Google Scholar] [CrossRef]
- Lebedev, O. The Higgs portal to cosmology. Prog. Part. Nucl. Phys. 2021, 120, 103881. [Google Scholar] [CrossRef]
- Cosme, C.; Rosa, J.G.; Bertolami, O. Can dark matter drive electroweak symmetry breaking? Phys. Rev. 2020, 102, 063507. [Google Scholar] [CrossRef]
- Aaffleck, I.; Dine, M. A New Mechanism for Baryogenesis. Nucl. Phys. 1985, 249, 361. [Google Scholar] [CrossRef]
- Dine, M.; Randall, L.; Thomas, S.D. Baryogenesis from flat directions of the supersymmetric standard model. Nucl. Phys. 1996, 458, 291. [Google Scholar] [CrossRef] [Green Version]
- Kinney, W.H.; Riotto, A. Theoretical uncertainties in inflationary predictions. JCAP 2006, 3, 011. [Google Scholar] [CrossRef]
- Lahiri, S. Anisotropic inflation in Gauss-Bonnet gravity. JCAP 2016, 09, 025. [Google Scholar] [CrossRef] [Green Version]
- Bruck, C.V.; Longden, C. Higgs inflation with a Gauss-Bonnet term in the Jordan frame. Phys. Rev. 2016, 93, 063519. [Google Scholar]
- Pozdeeva, E.O.; Sami, M.; Toporensky, A.V.; Vernov, S.Y. Stability analysis of de Sitter solutions in models with the Gauss-Bonnet term. Phys. Rev. 2019, 100, 083527. [Google Scholar] [CrossRef] [Green Version]
- Barvinsky, A.O.; Kamenshchik, A.Y.; Kiefer, C.; Starobinsky, A.A.; Steinwachs, C.F. Higgs boson, renormalization group, and naturalness in cosmology. JCAP 2009, 12, 003. [Google Scholar] [CrossRef]
- Lewis, A.; Challinor, A.; Lasenby, A. Efficient computation of CMB anisotropies in closed FRW models. ApJ 2000, 538, 473. [Google Scholar] [CrossRef] [Green Version]
- Lewis, A.; Bridle, S. Cosmological parameters from CMB and other data: A Monte Carlo approach. Phys. Rev. 2002, 66, 103511. [Google Scholar] [CrossRef] [Green Version]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VIII. Gravitational lensing. Astron. Astrophys. 2020, 641, A8. [Google Scholar]
- Clarke, J.D.; Foot, R.; Volkas, R.R. Phenomenology of a very light scalar (100 MeV <mh< 10 GeV) mixing with the SM Higgs. JHEP 2014, 2, 123. [Google Scholar]
- Winkler, M.W. Decay and Detection of a Light Scalar Boson Mixing with the Higgs. Phys. Rev. 2018, 99, 015018. [Google Scholar] [CrossRef] [Green Version]
- Grinstein, B.; Hall, L.J.; Randall, L. Do B meson decays exclude a light Higgs? Phys. Lett. 1988, 211, 363. [Google Scholar] [CrossRef]
- McKeen, D. Constraining Light Bosons with Radiative (1S) Decays. Phys. Rev. 2009, 79, 015007. [Google Scholar]
- Gunion, J.F.; Haber, H.E.; Kane, G.L.; Dawson, S. The Higgs Hunter’s Guide. Front. Phys. 2000, 80, 1. [Google Scholar]
- Ariga, A.; Ariga, T.; Boyd, J.; Cadoux, F.; Casper, D.W.; Favre, Y.; Feng, J.L.; Ferrere, D.; Galon, I.; Gonzalez-Sevilla, S.; et al. (FASER Collaboration). FASER’s physics reach for long-lived particles. Phys. Rev. 2019, 99, 095011. [Google Scholar]
- Anchordoqui, L.A.; Ariga, A.; Ariga, T.; Bai, W.; Balazs, K.; Batell, B.; Boyd, J.; Bramante, J.; Campanelli, M.; Carmona, A.; et al. (FASER Collaboration). The Forward Physics Facility: Sites, Experiments, and Physics Potential. arXiv 2021, arXiv:2109.10905. [Google Scholar]
- Pinfold, J.L. The MoEDAL experiment: A new light on the high-energy frontier. Phil. Trans. R. Soc. 2019, 377, 20190382. [Google Scholar] [CrossRef]
- Chivukula, R.S.; Manohar, A.V. Limits on a Light Higgs Boson. Phys. Lett. 1988, 207, 86. [Google Scholar] [CrossRef]
- Grinstein, B.; Hall, L.J.; Randall, L. Decay and Detection of a Light Scalar Boson Mixing with the Higgs. Phys. Lett. 1988, 211, 363. [Google Scholar] [CrossRef]
- LHCb Collaboration; Aaij, R.; Adeva, B.; Adinolfi, M.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; Albero, A.A.; et al. Measurement of the B production cross-sction in pp collisions at s = 7 and 13 TeV. arXiv 2017, arXiv:1710.04921. [Google Scholar]





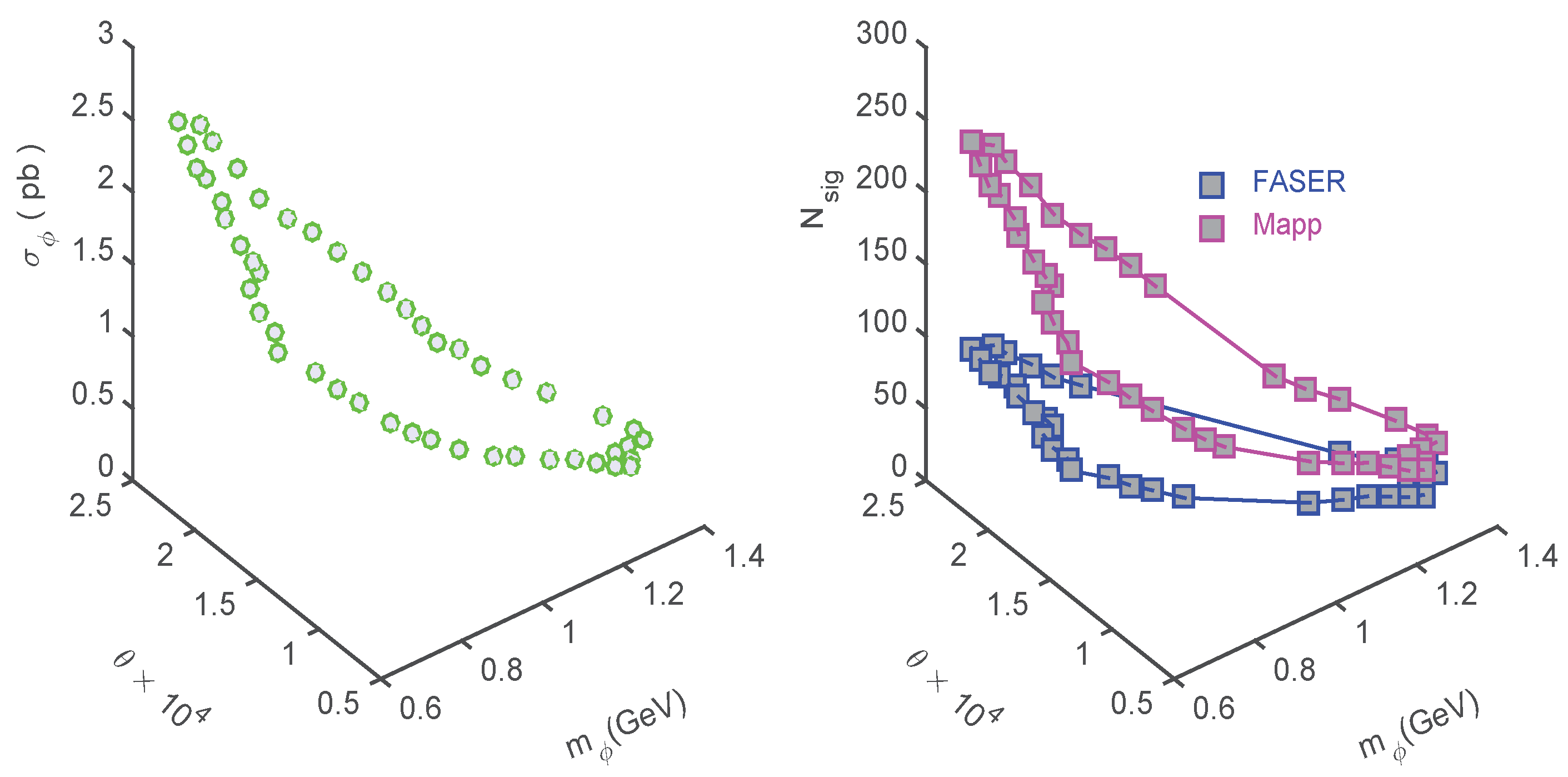
| Parameter | Prior |
|---|---|
| [0.005, 0.1] | |
| [0.001, 0.5 ] | |
| [0.5, 10] | |
| [0.01, 0.9] | |
| [54, 64] | |
| [0.007, 3] | |
| [1, 5] | |
| [0, 3] | |
| [0, 1] | |
| [20, 100] |
| Parameter | |
|---|---|
| 0.0223 ± 0.0002 | |
| 0.1194 ± 0.0011 | |
| 1.0410 ± 0.0004 | |
| 0.050 ± 0.009 | |
| <0.059 | |
| 59.4 ± 1.210 | |
| 0.892 ± 0.051 | |
| 1.021 ±0.219 | |
| 0.879±1.215 | |
| <0.0023 | |
| 67.729 ± 0.641 | |
| 3.050 ± 0.008 | |
| 0.967 ± 0.0044 | |
| (GeV) | 0.919 ± 0.211 |
| 1.291 ± 0.045 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Popa, L.A. Search for Dark Higgs Inflation with Curvature Corrections at LHC Experiments. Universe 2022, 8, 235. https://doi.org/10.3390/universe8040235
Popa LA. Search for Dark Higgs Inflation with Curvature Corrections at LHC Experiments. Universe. 2022; 8(4):235. https://doi.org/10.3390/universe8040235
Chicago/Turabian StylePopa, Lucia Aurelia. 2022. "Search for Dark Higgs Inflation with Curvature Corrections at LHC Experiments" Universe 8, no. 4: 235. https://doi.org/10.3390/universe8040235
APA StylePopa, L. A. (2022). Search for Dark Higgs Inflation with Curvature Corrections at LHC Experiments. Universe, 8(4), 235. https://doi.org/10.3390/universe8040235






