CP Violation for the Heavens and the Earth

Abstract

Electroweak baryogenesis can be driven by the top quark in a general two Higgs doublet model with extra Yukawa couplings. Higgs quartics provide the first order phase transition, while extra top Yukawa coupling ${\rho }_{tt}$ can fuel the cosmic baryon asymmetry through the ${\lambda }_t\mathrm{Im}{\rho }_{tt}$ product, with flavor-changing ${\rho }_{tc}$ coupling as backup. The impressive ACME 2018 bound on the electron electric dipole moment calls for an extra electron coupling ${\rho }_{ee}$ for exquisite cancellation among dangerous diagrams, broadening the baryogenesis solution space. The mechanism suggests that extra Yukawa couplings echo the hierarchical structure of standard Yukawa couplings. Phenomenological consequences in the Higgs search and flavor physics are discussed, with $\mu$ and $\tau$ EDM touched upon.

1. Introduction: Our Life and Times

The 125 GeV boson, h, was discovered in 2012, but No New Physics (NNP) beyond the Standard Model (BSM) has been found: not before 2012, and not in the decade since. Where is SUSY [1], the long-anticipated front-runner? Where is everybody else?

One place where people converge on is “Out-of-the-Box” searches, from [2] ALPs (Axion-Like Particles) to [3] LLPs (Long-Lived Particles), reflecting a sign of our times, as if we built the grand “boxes” called ATLAS and CMS, and so forth, out of human vanity; but really? It also reflects the lack of evidence for [4] WIMPs (Weakly Interacting Massive Particles) after a plethora of Dark Matter searches, where SUSY had provided excellent candidates.

Another general direction that is in vogue is EFT [5], or Effective Field Theory: since No New Particles (NNP) are seen other than those of SM, one assumes new states exist above some “cutoff” scale $\mathsf{\Lambda }$, far above the known SM particles such as t, h and $Z/W$ that are below the v.e.v. scale of 246 GeV. The latter give the dimension-4 terms of the SM Lagrangian, while we can only (nominally) divine minute deviations from SM with dimension-6 or higher operators as an expansion in $1/\mathsf{\Lambda }$.

However, have we truly exhausted “normal” dimension-4 terms? We wish to explore something “unconventionally-conventional”, a Road Not Taken (by most): we advocate the existence of an extra Higgs doublet [6] that carries extra Yukawa couplings, and of course the accompanying extra Higgs quartic couplings. We argue that the exotic Higgs bosons, H, A and $H^{+}$, are naturally sub-TeV in mass. Hence, the two sets of new dimension-4 couplings should be pursued at the LHC, ”within the box” of ATLAS and CMS, as well as at the flavor frontier.

An extra Higgs doublet1 sounds conventional enough, but in part influenced by SUSY, an extra Higgs doublet is usually viewed [6] as without extra, or a second set of Yukawa couplings. We will show how this is very much a prejudice, as our perspective is broadened by considering other big issues, such as electroweak baryogenesis (EWBG See for example, Ref. [12], and references therein), which calls for additional, large CP violation (CPV) sources. Since all experimentally verified CPV so far [13] come from Yukawa couplings, we place special premium on these extra Yukawa couplings. EWBG comes closer to heart as it is more testable, perhaps even at the LHC. This makes a second Higgs doublet with extra Yukawa couplings attractive, since as a cousin of the observed Higgs boson doublet, we should explore all its possible aspects at the electroweak scale. However, NNP at the LHC poses a challenge: Can one still have large CPV for EWBG? We will show that the answer is quite in the affirmative. What is more, the extra Higgs quartics are thrown in as a bonus to provide first order electroweak phase transition (EWPT), one of the three Sakharov conditions [14] for baryogenesis.

Billions and billions of stars, all those protons burning to light the Universe—but no antiprotons. The Baryon Asymmetry of the Universe (BAU), or disappearance of antimatter very shortly after the Big Bang, is indeed a problem as big as the Universe itself, and at the very core of our own existence.

CPV for the Heavens, or having extra, large sources of CPV for EWBG sounds attractive, but this brings about another problem: precision low energy (LE) experiments on Earth, such as ACME, which has recently pushed the bound on electron electric dipole moment (eEDM) down to the very impressive ${10}^{-29}e$ cm level [15]. Can an extra, large CPV source that drives EWBG survive such stringent precision frontier LE probes? Indeed, table-top experiments such as ACME are now competing directly with behemoths such as the LHC and its associated experiments at the high energy (HE) frontier.

Perhaps a bit surprisingly, we will show that extra Yukawa couplings of an extra Higgs doublet may come with the finesse to survive ACME’s check on EWBG—CPV on Earth. The finesse echoes the mysterious “flavor enigma”: the mass hierarchy between fermion generations, and the apparently correlated mixing hierarchy of the three mixing angles of the Cabibbo–Kobayashi–Maskawa (CKM) matrix [13], V. Nature even threw in the recently emerged “alignment” phenomenon, that the observed h boson does not seem to mix (much) with the exotic CP-even H boson. While unrelated to flavor per se, it helps hide this extra Higgs doublet from our view, so far. All these we shall elucidate.

Though our focus is on CPV, having touched on flavor, we have to comment on “B-anomalies”, which have been in vogue since 2012. This started with the $R_{D^{(*)}}$ anomaly by BaBar [16], where ratio of $B\to D^{(*)}\tau \nu$ to $B\to D^{(*)}\mu \nu$ rates exceeded SM expectations significantly. A similar $R_K$ anomaly, the ratio of $B^{+}\to K^{+}{\mu }^{+}{\mu }^{-}$ to $B^{+}\to K^{+}{e}^{+}{e}^{-}$ from LHCb [17] also showed deviation from SM, while $R_{D^{*}}$ anomaly turned into a sensation when LHCb concurred [18] with BaBar. Before long, LHCb came up with the $P_5^{\prime }$ anomaly [19] in two bins of the angular analysis of $B^0\to K^{*0}{\mu }^{+}{\mu }^{-}$, followed by the $R_{K^{*}}$ anomaly that is analogous to $R_K$ [20]. The experimental situation has not changed drastically since, as LHCb has been cautious in making updates. We have given our critique [21] from the experimental perspective. As these are rather large effects, g2HDM is not a front-runner explanation, and we give our comments in Section 5.

In the following, we first present the general two Higgs doublet model (g2HDM) and illustrate how it can bring about EWBG. We then show how g2HDM pulls the finesse to survive the ACME bound, which implies eEDM could be just around the corner. On the wheres and hows to verify this BSM physics, important phenomenological consequences are then discussed. Foretelling our Summary, the g2HDM is really just SM but with two Higgs doublets (SM2). It is thus quite simple, but dynamical parameters abound, providing CPV for the Heavens and the Earth—where general 2HDM offers an illustration.

2. General Two Higgs Doublet Model

Out of the three Sakharov conditions [14] for baryogenesis, his original suggestion of baryon number violation is provided by electroweak theory at high temperature, which is realized in the very early Universe. However, a first order electroweak phase transition (EWPT)? Or sufficient amount of CPV? On these two counts, SM falls short: the weak interaction, as well as the SM Higgs quartic coupling $\lambda$, are too weak; the Jarlskog invariant of SM falls way too short [22], receiving high powers of light mass as well as CKM suppression.

Adding a second Higgs doublet [6], that is, 2HDM, can help: The first order EWPT is achievable with $\mathcal{O}\left(1\right)$ Higgs quartics in the Higgs potential, $V({\Phi }_1,{\Phi }_2)$. Conventional wisdom is that one may want to keep the Higgs potential CP conserving [7], otherwise one could run into problems with electric dipole moments, such as $d_n$ of the neutron.

As we have mentioned, all measured CPV in the laboratory can be accounted for by the CKM matrix V, which originates from Yukawa couplings. Thus, for the sake of baryogenesis, extra BSM Yukawa couplings, such as due to a second Higgs doublet, should be welcome. However, having two Yukawa coupling matrices, say for up-type quarks, the linear combination that is orthogonal to the mass matrix $\mathbf{m}$${}^u$ cannot be simultaneously diagonalized. This means the presence of flavor changing neutral Higgs (FCNH) couplings, the fear of which led Glashow and Weinberg to famously propose [23] the Natural Flavor Conservation (NFC) condition, that each type of charged fermion receive mass from just one scalar doublet, thereby killing FCNH couplings. The NFC condition is usually implemented in 2HDM via a $Z_2$ symmetry, leading to 2HDM type I and type II, where the latter is automatic in minimal SUSY for separate reasons, making it rather popular.

However, if one puts a premium on extra Yukawa couplings for the sake of baryogenesis, imposing a $Z_2$ symmetry would seem ad hoc and an overkill. After all, with NNP seen at the LHC, any add-on symmetry should be suspect. We therefore wish to explore the 2HDM further without any $Z_2$ symmetry. Without a $Z_2$ to impose NFC, we have a second set of Yukawa couplings, for example, $\mathbf{\rho }$${}^u$ to accompany the SM Yukawa matrix $\mathbf{\lambda }$${}^u\equiv \sqrt{2}$$\mathbf{m}$${}^u/v$, where $v\simeq 246$ GeV is the vacuum expectation value. We call this the general 2HDM, or g2HDM.

In the next subsection, we will show that the up-type extra Yukawa coupling ${\rho }_{tt}$, expected at $\mathcal{O}\left(1\right)$ by analogy with ${\lambda }_t\cong 1$, can drive EWBG, while ${\rho }_{tc}$ provides a backup. So let us prepare for the two needed elements for EWBG: Extra Yukawa couplings as CPV source, and extra Higgs quartics to provide first order EWPT. We will address the concerns of Glashow and Weinberg later.

2.1. Extra Yukawa Couplings

With two Higgs doublets and without a $Z_2$ coupling to enforce NFC, the general Yukawa couplings for up-type quarks are:

$${\overline{u}}_{iL}(Y_{1ij}^u{\tilde{\Phi }}_1+Y_{2ij}^u{\tilde{\Phi }}_2)u_{jR}+\mathrm{h}.\mathrm{c}.$$

(1)

Although later on we would invoke the Higgs basis and put the v.e.v. to only one Higgs doublet, as the Universe cooled down from its very hot beginning and electroweak symmetry breaking develops, the evolution history can be viewed as effectively tracing through both doublets having v.e.v.s. Thus, we will take $v_1=vcos\beta$ and $v_2=vsin\beta$ where $\beta$ is temperature-dependent, and

$$Y_{\mathrm{SM}}^u=Y_1^{u}cos\beta +Y_2^{u}sin\beta ,$$

(2)

feeds the mass matrix, which is diagonalized by $U_L^{†}{Y}_{\mathrm{SM}}^u{U}_R=\mathrm{diag}({\lambda }_u,{\lambda }_c,{\lambda }_t)$ as usual. The orthogonal combination,

$${\rho }^u=U_L^{†}(-Y_1^{u}sin\beta +Y_2^{u}cos\beta )U_R,$$

(3)

then cannot be simultaneously diagonal, leading to FCNH couplings.

The ${\rho }^u$ matrix is orthogonal to the mass matrix. However, the Higgs potential would induce mixing between the light h boson from the mass giving doublet and the exotic CP-even boson H, and we arrive at the neutral up-type Yukawa interaction at $T=0$:

$$\begin{array}{c}\hfill {\overline{u}}_{iL}\left(\frac{{\lambda }_i{\delta }_{ij}}{\sqrt{2}}{s}_{\gamma }+\frac{{\rho }_{ij}^u}{\sqrt{2}}{c}_{\gamma }\right)u_{jR}h+{\overline{u}}_{iL}\left(\frac{{\lambda }_i{\delta }_{ij}}{\sqrt{2}}{c}_{\gamma }-\frac{{\rho }_{ij}^u}{\sqrt{2}}{s}_{\gamma }\right)u_{jR}H-\frac{i}{\sqrt{2}}{\overline{u}}_{iL}^u{\rho }_{ij}{u}_{jR}A+\mathrm{h}.\mathrm{c}.,\end{array}$$

(4)

where $c_{\gamma }=cos(\beta -\alpha )$ is the h-H mixing angle in SUSY notation. The recently emergent “alignment” phenomenon2 states that, if a second Higgs doublet exists, h-H mixing seems small [27]. We see that, in the alignment limit of $c_{\gamma }\to 0$, the h couplings become diagonal, even if the $\rho$ matrix is nondiagonal. This helps control processes such as $t\to ch$ decay, where CMS set recently [28] the most stringent bound. If the effect of the extra $\rho$ Yukawa matrix on h disappears in the alignment limit, its full effect is in the exotic scalar sector.

The fact that LHC experiments search for $t\to ch$ and $h\to \tau \mu$ [13] states that, whether NFC is active or not in Nature is actually an experimental question. Note also from Equation (4) that, due to the chiral nature of the weak interactions, the extra Yukawa couplings, as in SM, are complex, that is, ${\rho }_{ij}=\left|{\rho }_{ij}\right|e^{i{\varphi }_{ij}}$, which we employ towards baryogenesis.

2.2. Extra Higgs Quartic Couplings

Besides the source of CPV, the other prerequisite for EWBG is to have a first order EWPT, which SM lacks, but 2HDM can provide, if extra Higgs quartics are $\mathcal{O}\left(1\right)$ [29].

The most general CP-conserving potential of g2HDM in the Higgs basis is [8,30]

$$\begin{array}{cc}\hfill V(\Phi ,{\Phi }^{\prime })& ={\mu }_{11}^2{|\Phi |}^2+{\mu }_{22}^2|{\Phi }^{\prime }{|}^2-\left({\mu }_{12}^2{\Phi }^{†}{\Phi }^{\prime }+\mathrm{h}.\mathrm{c}.\right)+\frac{{\eta }_1}{2}{|\Phi |}^4+\frac{{\eta }_2}{2}{\left|{\Phi }^{\prime }\right|}^4\hfill \\ \hfill & +{\eta }_3|{\Phi }^2\left|\right|{\Phi }^{\prime }{|}^2+{\eta }_4{\left|{\Phi }^{†}{\Phi }^{\prime }\right|}^2+\left\{\left(\frac{{\eta }_5^{}}{2}{\Phi }^{†}{\Phi }^{\prime }+{\eta }_6^{}{|\Phi |}^2+{\eta }_7^{}{\left|{\Phi }^{\prime }\right|}^2\right){\Phi }^{†}{\Phi }^{\prime }+\mathrm{h}.\mathrm{c}.\right\},\hfill \end{array}$$

(5)

where ${\mu }_{11}^2<0$ generates v.e.v., $v\ne 0$, with a slightly different convention from SM potential. A second minimization condition, ${\mu }_{12}^2={\eta }_6{v}^2/2$, eliminates ${\mu }_{12}^2$ as a parameter, leaving ${\eta }_6$ as the sole parameter for h-H mixing, that is, $c_{\gamma }$. Note that ${\eta }_6$ and ${\eta }_7$ terms would be absent with usual $Z_2$ symmetry. We note that the potential of Equation (5) makes better sense than the usual ones under $Z_2$: by putting symmetry breaking in ${\mu }_{11}^2<0$, we have ${\mu }_{22}^2>0$ as inertial mass while ${\mu }_{12}^2$ is eliminated. In contrast, in 2HDM I & II, one has both ${\mu }_{11}^2<0$ and ${\mu }_{22}^2<0$, while ${\mu }_{12}^2$ serves the dual function as inertial mass and h-H mixing parameter.

One sees now that requiring a first order EWPT, that is, having extra Higgs quartics at $\mathcal{O}\left(1\right)$ [29] has implications on H, A, $H^{+}$ masses. One can also argue for ${\mu }_{22}^2/v^2=\mathcal{O}\left(1\right)$, for if it is much larger, it would damp away all amplitudes for baryogenesis. One therefore finds [30] that the exotic scalars are sub-TeV in mass. It is interesting to note that, having all ${\eta }_i$’s and ${\mu }_{22}^2/v^2$ at $\mathcal{O}\left(1\right)$ reflects “common” naturalness that one learned in high school, for example, one does not put one dollar and 1 million dollars on the table at the same time, whatever the currency. In any case, the sub-TeV spectrum should be fully explored at the LHC before one heads for heavier masses.

It is worthy of note that one has the approximate relation [30] near alignment,

$$\begin{array}{c}\hfill c_{\gamma }\cong \frac{{\eta }_6{v}^2}{m_H^2-m_h^2},\end{array}$$

(6)

since $s_{\gamma }$ approaches 1 faster than $c_{\gamma }$ approaches 0. With $m_h$ fixed at 125 GeV, one sees that for $m_H\lesssim 300$ GeV or so, small $c_{\gamma }$ can be sustained only by tuning ${\eta }_6$ towards zero.3 So, from the “common naturalness” perspective, $m_H$ or the exotic scalar masses below v is not favored. Thus, the target mass range for H, A, $H^{+}$ is approximately (300, 600) GeV. However, the LHC should of course leave no stone unturned.

3. The Heavens: Electroweak BaryoGenesis

It has been shown that a strongly first order EWPT can be achieved [29] by extra thermal loops in 2HDM with $\mathcal{O}\left(1\right)$ Higgs quartic couplings, fulfilling one of the prerequisites for EWBG. This we shall assume, taking in fact H, A and $H^{+}$ to be degenerate at 500 GeV to simplify. The main purpose of this section is to illustrate the CPV source [33] in g2HDM.

Let us give an account of EWBG at the semi-folklore level. Shortly after the Big Bang, one has an expanding bubble of the broken phase. Inside the bubble where $v\ne 0$, baryon number is conserved, but outside the bubble in the symmetric phase, baryon number is violated by sphalerons. To avoid baryon number $n_B$ washout, one needs ${\mathsf{\Gamma }}_B^{\left(\mathrm{br}\right)}\left(T_C\right)<H\left(T_C\right)$ in the broken phase, that is, the $n_B$ changing rate ${\mathsf{\Gamma }}_B^{\left(\mathrm{br}\right)}\left(T_C\right)$ is less than the Hubble parameter $H\left(T_C\right)$ at critical temperature $T_C$. To satisfy this condition, first order EWPT is needed to ensure [34] $v_c/T_C>{\zeta }_{\mathrm{sph}}\left(T_C\right)=\mathcal{O}\left(1\right)$, where $v_C=\sqrt{v_1^2\left(T_C\right)+v_2^2\left(T_C\right)}$ is the v.e.v. at $T_C$.

The task then is to estimate BAU, that is, the ratio of $n_B$ to entropy density s, by

$$\begin{array}{c}\hfill Y_B\equiv \frac{n_B}{s}=\frac{-3{\Gamma }_B^{\left(\mathrm{sym}\right)}}{2D_q{\lambda }_{+}s}{\int }_{-\infty }^{0}d{z}^{\prime }{n}_L\left(z^{\prime }\right)e^{-{\lambda }_{-}{z}^{\prime }},\end{array}$$

(7)

where ${\mathsf{\Gamma }}_B^{\left(\mathrm{sym}\right)}=120{\alpha }_W^{5}T$ is the B changing rate in symmetric phase, $D_q\simeq 8.9/T$ is the quark diffusion constant, and ${\lambda }_{\pm }\simeq v_w$ is the bubble wall velocity, with ${\alpha }_W$ the weak coupling constant and $v_w$ the bubble wall velocity. One integrates over $z^{\prime }$, the coordinate opposite the bubble expansion direction, and collect left-handed fermion number density $n_L$ inside the bubble as it expands to become our Universe. The observed BAU by Planck 2014 is [35] $Y_B^{\mathrm{obs}}=8.59\times {10}^{-11}$.

In g2HDM, $n_L$ is likely the left-handed top density via CPV top interactions at the bubble wall, as illustrated in Figure 1, where vertices are given in Equation (1). The bubble wall is denoted as the spacetime-dependent v.e.v.s [34], $v_a\left(x\right)$, $v_b\left(y\right)$ ($a,b=1,2$).

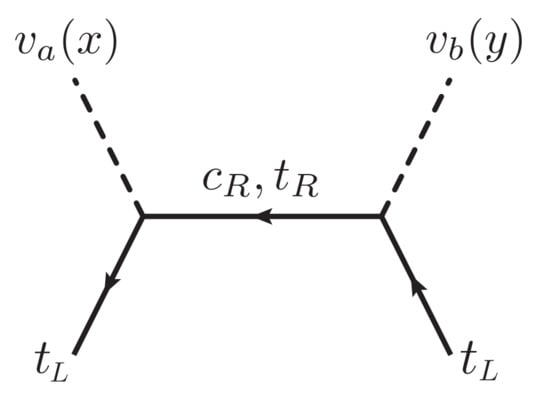
Figure 1. CPV process for generating left-handed top density $n_L$ towards BAU, where Higgs bubble wall is denoted symbolically as $v_a\left(x\right)$ and $v_b\left(y\right)$.

We skip the discussion of transport equations, for which we refer to Refs. [33,34].

3.1. Cpv Top Interactions

Skipping details, the CPV source term $S_{ij}$ [33] for left-handed fermion $f_{iL}$ induced by right-handed fermion $f_{jR}$ is,

$$\begin{array}{cc}\hfill S_{i_L{j}_R}\left(Z\right)& =N_{C}F\mathrm{Im}\left[{\left(Y_1\right)}_{ij}{\left(Y_2\right)}_{ij}^{*}\right]v^2\left(Z\right){\partial }_{t_Z}\beta \left(Z\right),\hfill \end{array}$$

(8)

where $Z=(t_Z,0,0,z)$ is the position in heat bath of the very early Universe, $N_C=3$ the color factor, and F is a function [34] of complex energies of $f_{iL}$ and $f_{jR}$ that incorporate T-dependent widths of particle/hole modes. We note that, although the angle $\beta$ is basis-dependent in g2HDM, its variation ${\partial }_{t_Z}\beta \left(Z\right)$, reflecting the departure from equilibrium, is physical. We use [33] the value $\Delta \beta =0.015$.

The essence of the CPV for BAU is clearly in $\mathrm{Im}\left[{\left(Y_1\right)}_{ij}{\left(Y_2\right)}_{ij}^{*}\right]$. From Equations (2) and (3) and reversing the diagonalization, one has:

$$\begin{array}{c}\hfill \mathrm{Im}\left[{\left(Y_1\right)}_{ij}{\left(Y_2\right)}_{ij}^{*}\right]=\mathrm{Im}\left[{\left(U_L{Y}_{\mathrm{diag}}{U}_R^{†}\right)}_{ij}{\left(U_L\rho U_R^{†}\right)}_{ij}^{*}\right].\end{array}$$

(9)

A simple exercise [36] can help one gain understanding, and reflect what may be truly happening for the up-type extra Yukawa matrix $\rho$. Suppose one picks ${\left(Y_1\right)}_{tc}\ne 0$, ${\left(Y_2\right)}_{tc}\ne 0$, and ${\left(Y_1\right)}_{tt}={\left(Y_2\right)}_{tt}\ne 0$ and all else vanishes, that is, altogether three (complex) parameters. Setting $tan\beta =1$ for convenience, one can easily show that $\sqrt{2}{Y}^{\mathrm{SM}}=Y_1+Y_2$ is diagonalized by just $U_R$ to a single nonvanishing 33 element ${\lambda }_t$, the observed SM Yukawa coupling, while the combination $-Y_1+Y_2$ is not diagonalized. Solving for $U_R$ in terms of nonvanishing elements in $Y_1$ and $Y_2$, one finds [33] (since ${\lambda }_t$ is real):

$$\begin{array}{c}\hfill \mathrm{Im}\left[{\left(Y_1\right)}_{tc}{\left(Y_2\right)}_{tc}^{*}\right]=-{\lambda }_t\mathrm{Im}{\rho }_{tt},\end{array}$$

(10)

with ${\rho }_{ct}=0$, which is part of the construction, as ${\rho }_{ct}$ is severely constrained by $B_q$–${\overline{B}}_q$ mixings [37]. The less constrained ${\rho }_{tc}$, though related to ${\rho }_{tt}$, remains a free parameter.

Equation (10) is quite remarkable. With ${\lambda }_t\cong 1$ affirmed recently by experiment [13], the best guess for ${\rho }_{tt}$, hence $\mathrm{Im}{\rho }_{tt}$, is also $\mathcal{O}\left(1\right)$. Thus, the CPV source of Equation (10) is $\mathcal{O}\left(1\right)$ in strength, which is in strong contrast to the rather suppressed Jarlskog invariant of SM [22], with the SM and extra top Yukawa couplings joining forces together.

In a similar vein of having extra Yukawa couplings, we previously advocated [22] the fourth generation (4G) as driver of EWBG. However, not only one did not find 4G while it offered no handle on the order of EWPT, the dominant Jarlskog invariant (Appendix A) still suffers $m_b^2/v^2$ as well as CKM suppression [22]. Providing both the CPV source and the first order EWPT, the g2HDM is a winner.

To illustrate the robustness of EWBG through Equation (10), we estimate $Y_B$ of Equation (7) by solving the transport equations, where more discussion can be found in Refs. [33,34]. We plot $Y_B/Y_B^{\mathrm{obs}}$ vs $|{\rho }_{tt}|$ (up to 1) in Figure 2(left), where we scan over $|{\rho }_{tc}|<1$ and the two phases ${\varphi }_{tt}$ and ${\varphi }_{tc}$ (keeping physical charm and top masses), taking $tan\beta =1$ and $c_{\gamma }\equiv c_{\beta -\alpha }=0.1$. Furthermore, we take $m_H=m_A=m_{H^{+}}=$ 500 GeV that can give rise to first order EWPT (in particular, we have $v_C=176.7$ GeV $>T_C=119.2$ GeV [33]), while ${\rho }_{tt}$ and ${\rho }_{tc}$ satisfy $B_{d,s}$ mixing and $b\to s\gamma$ constraints.

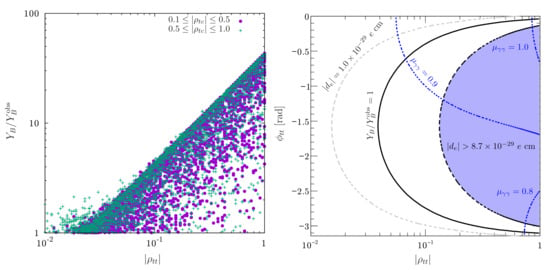
Figure 2. (Left) $Y_B$ vs $|{\rho }_{tt}|$, where one scans over the phases ${\varphi }_{tt}$ and ${\varphi }_{tc}$$\in [0,2\pi ]$, and purple (green) points are for $0.1\le |{\rho }_{tc}|\le 0.5$ ($0.5\le |{\rho }_{tc}|\le 1.0$); (Right) $Y_B$ and $|d_e|$ in the $|{\rho }_{tt}|$-${\varphi }_{tt}$ plane, where the dashed curve is the ACME’14 bound, the solid curve is for $Y_B=Y_B^{\mathrm{obs}}$, and the gray dashed curve is the ACME projected bound [44].

To discern the impact of $|{\rho }_{tt}|$ vs $|{\rho }_{tc}|$, we separate $|{\rho }_{tc}|$ into lower and higher regions: the purple dots (green crosses) are for $0.1<|{\rho }_{tc}|<0.5$ ($0.5<|{\rho }_{tc}|<1.0$). For the bulk, there is no obvious distinction between the two, so EWBG is largely $|{\rho }_{tt}|$-driven, allowing $Y_B/Y_B^{\mathrm{obs}}$ up to $\sim 40$ at $|{\rho }_{tt}|=1$. However, for $|{\rho }_{tt}|\lesssim 0.05$, $Y_B/Y_B^{\mathrm{obs}}$ peters out as $|{\rho }_{tt}|$ drops, and more “green crosses” populate $Y_B/Y_B^{\mathrm{obs}}>1$. So, interestingly, for very small $|{\rho }_{tt}|$, ${\rho }_{tc}$ can serve as a backup mechanism for EWBG. However, this is only possible [33] for $|{\rho }_{tc}|=\mathcal{O}\left(1\right)$ with near maximal CPV phase, hence it is less efficient.4

3.2. Watch Your Back: eEDM

With ${\rho }_{tt}$ being complex and sizable, it can induce electron EDM through the two-loop mechanism [42]. At the time of writing of Ref. [33], May 2017, the ACME experiment had already set the impressively stringent limit [43] of $|d_e|<8.7\times {10}^{-29}e\mathrm{cm}$ using the polar ThO molecule, which had to be faced. Keeping parameters as above, where the $t\to ch$ bound at the time [13] could be satisfied because of our low $c_{\gamma }$ value, we chose to simplify by setting ${\rho }_{ee}$ to zero. Setting a parameter to zero without a symmetry did not sound right, but we could project a range of $d_e$ for ACME to test. ACME had made the projection [44] earlier of improving by another order of magnitude, to $1.0\times {10}^{-29}e\mathrm{cm}$ or better.

In Figure 2(right) we give $Y_B$ and $|d_e|$ in the $|{\rho }_{tt}|$-${\varphi }_{tt}$ plane [33], where the shaded region is ruled out by ACME’14 [43], the solid curve is for $Y_B/Y_B^{\mathrm{obs}}=1$, and the gray dashed curve to the left is the projected ACME bound [44]. Little did we know that our projection had a shelf life of ∼a year. By October 2018, as announced in Nature [15],

$$d_e<1.1\times {10}^{-29}e\mathrm{cm},\left(\mathrm{ACME}2018\right)$$

(11)

the entire range of Figure 2(right) was ruled out by the ACME update. ACME, the Advanced Cold Molecule Electron EDM experiment, has leapt to the forefront of particle physics.

4. Under the Heavens on Earth: $\mathbf{e}$EDM

Having soared to the Heavens with an $\mathcal{O}\left(1\right)$ CPV source, $-{\lambda }_t\mathrm{Im}{\rho }_{tt}$ as in Equation (10), one has to be more attentive to eEDM back on Earth; for once, Wile E. Coyote is keeping us honest through ACME. Amazingly, ACME managed to deliver on their projected [44] order of magnitude of improvement within two years [15]. It also turned out, on our side, that things were not as complicated or intimidating as they had seemed, because all loop functions for the two-loop mechanism are known. We just have to turn ${\rho }_{ee}$ on, with its complex phase. The outcome turned out to be intriguing [45].

The dominant contributions to $d_e$ in g2HDM come from Barr–Zee diagrams [42], as depicted in Figure 3, which has three pieces,

$$\begin{array}{c}\hfill d_e=d_e^{\varphi \gamma }+d_e^{\varphi Z}+d_e^{\varphi W},\end{array}$$

(12)

where $\varphi$ can be the neutral $h,H,A$ bosons for $V=\gamma ,Z$, or the $H^{+}$ boson for $V=W$. CP is violated at the lower and/or upper vertices of the $\varphi$ line. So, how to render eEDM small? The first thing to note is that the dominant effect comes from the “$\varphi \gamma \gamma$” insertion in Figure 3 for $\varphi =h,H,A$, which is quite similar to the diagram that generates $h\to \gamma \gamma$, one of the two discovery modes of h.

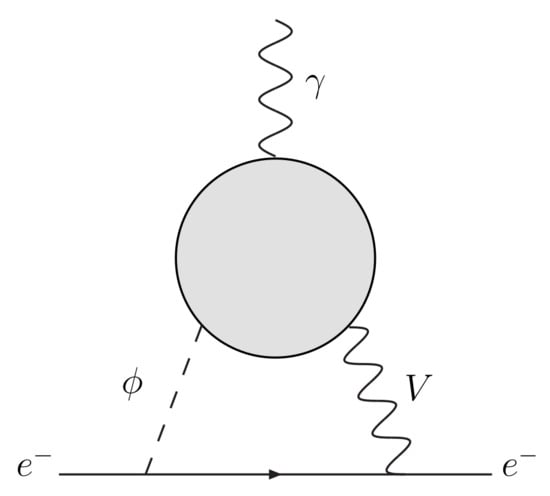
Figure 3. Two-loop Barr–Zee diagrams [42] contributing to the electron EDM, where $\varphi$ denotes neutral and charged Higgs bosons, and V denotes vector bosons $\gamma$, Z and W.

In Ref. [33], we assumed only ${\rho }_{tt}$ has a nonzero CPV phase, and set ${\rho }_{ee}$ in fact to zero. Then $d_e$ is solely due to ${\left(d_e^{\varphi \gamma }\right)}_t$, which arises from the left diagram of Figure 4. We find

$$\begin{array}{c}\hfill \frac{{\left(d_e^{\varphi \gamma }\right)}_t}{e}=\frac{{\alpha }_{\mathrm{em}}{s}_{2\gamma }}{12\sqrt{2}{\pi }^{3}v}\frac{m_e}{m_t}\mathrm{Im}{\rho }_{tt}\Delta g=-6.6\times {10}^{-29}\left(\frac{s_{2\gamma }}{0.2}\right)\left(\frac{\mathrm{Im}{\rho }_{tt}}{-0.1}\right)\left(\frac{\Delta g}{0.94}\right),\end{array}$$

(13)

where e is the positron charge, ${\alpha }_{\mathrm{em}}=e^2/4\pi$ and $\Delta g=g(m_t^2/m_h^2)-g(m_t^2/m_H^2)$, where the loop function g is given in Ref. [42]. We have put $d_e={\left(d_e^{\varphi \gamma }\right)}_t$ in a form to make clear that $d_e$ survives ACME’14 [43], but not ACME’18 [15]. Compared with the robust ${\lambda }_t\mathrm{Im}{\rho }_{tt}$ EWBG-driver of Equation (10), the ${\lambda }_e\mathrm{Im}{\rho }_{tt}$ effect of Equation (13) did not pass ACME scrutiny.

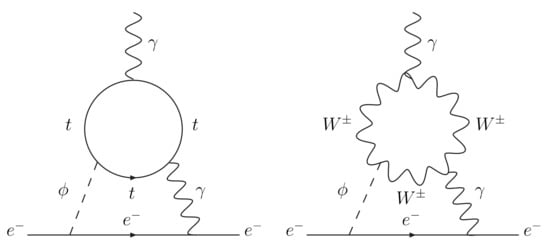
Figure 4. Two dominant diagrams for $d_e^{\varphi \gamma }$ when $\mathrm{Im}{\rho }_{ee}$ is also taken into account.

So, to survive ACME’18, one needs a cancellation mechanism for $d_e^{\varphi \gamma }$, upon turning on ${\rho }_{ee}$ with its CPV phase.

4.1. Cancellation Mechanism for Electron EDM

For a cancellation mechanism, one naturally recalls the cancellation between the top and W loops for $h\to \gamma \gamma$, the diphoton decay of h, where in fact the W loop dominates over top. Upon turning on $\mathrm{Im}{\rho }_{ee}$, a similar effect can happen to make ${\left(d_e^{\varphi \gamma }\right)}_W$ of Figure 4(right) comparable to or even bigger than ${\left(d_e^{\varphi \gamma }\right)}_t$ of Figure 4(left).

Let us separate ${\left(d_e^{\varphi \gamma }\right)}_i$ into two parts

$$\begin{array}{c}\hfill {\left(d_e^{\varphi \gamma }\right)}_i\equiv {\left(d_e^{\varphi \gamma }\right)}_i^{\mathrm{mix}}+{\left(d_e^{\varphi \gamma }\right)}_i^{\mathrm{extr}}.\end{array}$$

(14)

The first term comes from mixing both SM and extra Yukawa couplings, while the second term involves extra Yukawa couplings only. From Figure 4(left), one has for the top-loop

$$\begin{array}{cc}\hfill \frac{{\left(d_e^{\varphi \gamma }\right)}_t^{\mathrm{mix}}}{e}& =\frac{{\alpha }_{\mathrm{em}}{s}_{2\gamma }}{12\sqrt{2}{\pi }^{3}v}\left[\mathrm{Im}{\rho }_{ee}\Delta f+\frac{m_e}{m_t}\mathrm{Im}{\rho }_{tt}\Delta g\right],\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill \frac{{\left(d_e^{\varphi \gamma }\right)}_t^{\mathrm{extr}}}{e}& \simeq \frac{{\alpha }_{\mathrm{em}}}{12{\pi }^3{m}_t}\mathrm{Im}\left({\rho }_{ee}{\rho }_{tt}\right)\left[f\left({\tau }_{tA}\right)+g\left({\tau }_{tA}\right)\right],\hfill \end{array}$$

(16)

where ${\tau }_{ij}=m_i^2/m_j^2$, $\Delta X=X\left({\tau }_{th}\right)-X\left({\tau }_{tH}\right)$, and $X=f,g$ are monotonically increasing loop functions given in Ref. [42]; thus $\Delta X>0$ for $m_h<m_H$. Note that Equation (15) is an extension of Equation (13) for $\mathrm{Im}{\rho }_{ee}\ne 0$, while Equation (16) depends on the phase difference between ${\rho }_{ee}$ and ${\rho }_{tt}$. We have made the approximation of $c_{\gamma }^2\ll 1$ and $m_H\simeq m_A$ to simplify the appearance of ${\left(d_e^{H\gamma }\right)}_t^{\mathrm{extr}}$, but this is not imposed in our later numerics.

For the W-loop of Figure 4(right), the $\varphi WW$ vertex involves SM couplings modulated by h-H mixing, so ${\left(d_e^{\varphi \gamma }\right)}_W$ is solely given by ${\left(d_e^{\varphi \gamma }\right)}_W^{\mathrm{mix}}$,

$$\begin{array}{cc}\hfill \frac{{\left(d_e^{\varphi \gamma }\right)}_W^{\mathrm{mix}}}{e}& =-\frac{{\alpha }_{\mathrm{em}}{s}_{2\gamma }}{64\sqrt{2}{\pi }^{3}v}\mathrm{Im}{\rho }_{ee}\Delta {\mathcal{J}}_W^{\gamma },\hfill \end{array}$$

(17)

where $\Delta {\mathcal{J}}_W^{\gamma }={\mathcal{J}}_W^{\gamma }\left(m_h\right)-{\mathcal{J}}_W^{\gamma }\left(m_H\right)$. The function ${\mathcal{J}}_W^{\gamma }$ is given in Ref. [46], which is monotonically decreasing, hence $\Delta {\mathcal{J}}_W^{\gamma }>0$ for $m_h<m_H$.

To suppress $d_e^{\varphi \gamma }$, we consider the cancellation between top and W loops for the h-H mixing terms, ${\left(d_e^{\varphi \gamma }\right)}_t^{\mathrm{mix}}+{\left(d_e^{\varphi \gamma }\right)}_W^{\mathrm{mix}}=0$, while the purely extra Yukawa term vanishes, ${\left(d_e^{\varphi \gamma }\right)}_t^{\mathrm{extr}}=0$. We will discuss ${\left(d_e^{\varphi \gamma }\right)}_t^{\mathrm{extr}}\ne 0$ later. Comparing Equations (15) and (17) for the first condition, and Equation (16) for the second, one finds

$$\begin{array}{c}\hfill \frac{\mathrm{Im}{\rho }_{ee}}{\mathrm{Im}{\rho }_{tt}}=c\frac{{\lambda }_e}{{\lambda }_t},\frac{\mathrm{Re}{\rho }_{ee}}{\mathrm{Re}{\rho }_{tt}}=-\frac{\mathrm{Im}{\rho }_{ee}}{\mathrm{Im}{\rho }_{tt}},\end{array}$$

(18)

respectively, where $c=(16/3)\Delta g/[\Delta {\mathcal{J}}_W^{\gamma }-(16/3)\Delta f]$. For example, $c\simeq 0.71$ for $m_h,m_H=125$, 500 GeV. Combining the two conditions of Equation (18), one gets

$$\left|\frac{{\rho }_{ee}}{{\rho }_{tt}}\right|=c\frac{{\lambda }_e}{{\lambda }_t},\mathrm{Im}\left({\rho }_{ee}{\rho }_{tt}\right)\to 0,$$

(19)

with a correlated phase between ${\rho }_{tt}$ and ${\rho }_{ee}$ as indicated. Note that c is not sensitive to the detailed exotic Higgs spectrum that is consistent with first order EWPT, hence does not change drastically in the parameter range for EWBG.

4.2. Facing ACME: Thorium Oxide EDM

Having elucidated the cancellation mechanism for the dominant $d_e^{\varphi \gamma }$ term, to understand our more detailed numerics, we need to include the subdominant effects of $d_e^{\varphi W}$ and $d_e^{\varphi Z}$ in Equation (12). We also need to tune in to a little more detail in making contact with experiment, that is, how the measurement is actually performed.

As ThO is a polar molecule with a very strong internal electric field, we need to understand some “environment” effects. The effective EDM for ThO is [47]

$$\begin{array}{c}\hfill d_{\mathrm{ThO}}=d_e+{\alpha }_{\mathrm{ThO}}{C}_S,\end{array}$$

(20)

where $d_e$ is the coefficient of the dimension-5 operator $-\frac{i}{2}{d}_e\left(\overline{e}{\sigma }^{\mu \nu }{\gamma }_{5}e\right)F_{\mu \nu }$, with $F_{\mu \nu }$ the EM field strength tensor. The $C_S$ term is due to the T-violating electron–nucleon interaction, $-\frac{G_F}{\sqrt{2}}{C}_S\left(\overline{N}N\right)\left(\overline{e}i{\gamma }_{5}e\right)$, with $G_F$ the Fermi constant. The ACME’18 result of Equation (11) corresponds to $d_{\mathrm{ThO}}=(4.3\pm 4.0)\times {10}^{-30}e$ cm, but taking $C_S=0$ [15]. For our case, an estimate [48] of ${\alpha }_{\mathrm{ThO}}=1.5\times {10}^{-20}$ implies $C_S$ cannot be neglected w.r.t. $d_e^{\varphi Z}$ and $d_e^{\varphi W}$ of Equation (12), and we use $d_{\mathrm{ThO}}$ of ACME’18 to explore the constraint.

We follow the estimate for $C_S$ from Ref. [49] (consistent with Ref. [50]),

$$\begin{array}{c}\hfill C_S=-2v^2\left[6.3(C_{de}+C_{ue})+C_{se}\frac{41\mathrm{MeV}}{m_s}+C_{ce}\frac{79\mathrm{MeV}}{m_c}+0.062\left(\frac{C_{be}}{m_b}+\frac{C_{te}}{m_t}\right)\right],\end{array}$$

(21)

where $C_{qe}$ is given by: ${\mathcal{L}}_{4f}^{\mathrm{CPV}}={\sum }_q{C}_{qe}\left(\overline{q}q\right)\left(\overline{e}i{\gamma }_{5}e\right)$ after integrating out all neutral Higgs bosons. Note that quark masses are balanced by corresponding Yukawa couplings in $C_{qe}$, so all quark flavors are generally relevant. Note also that for $s_{\gamma }\to 1$ and $m_H\simeq m_A$, one has $C_{ue}\simeq \mathrm{Im}\left({\rho }_{ee}{\rho }_{uu}\right)/\left(2m_A^2\right)$ and $C_{de}\simeq \mathrm{Im}\left({\rho }_{ee}{\rho }_{dd}^{*}\right)/\left(2m_A^2\right)$, respectively, implying that $C_{qe}\simeq 0$ for ${\left(d_e^{\varphi \gamma }\right)}_q^{\mathrm{extr}}\simeq 0$.

We find [45] one-loop induced CPV mixing of neutral Higgs bosons to be minor, so we turn to the numerics. Motivated by Equation (18), we consider the simplified “Ansatz”,

$$\begin{array}{c}\hfill \frac{\mathrm{Im}{\rho }_{ff}}{\mathrm{Im}{\rho }_{tt}}=r\frac{{\lambda }_f}{{\lambda }_t},\frac{\mathrm{Re}{\rho }_{ff}}{\mathrm{Re}{\rho }_{tt}}=-r\frac{{\lambda }_f}{{\lambda }_t},\end{array}$$

(22)

which is flavor-blind. Keeping EWBG in mind, we choose ${\rho }_{tt}$ strength that is able to drive it. In Figure 5(left) we plot $|d_{\mathrm{ThO}}|$ (black, solid) and its components $|d_e|$ (red, solid), $|d_e^{\varphi \gamma }|$ (red, dashed), $|d_e^{\varphi W}|$ (red, dot-dashed), $|d_e^{\varphi Z}|$ (red, dotted), $|{\alpha }_{\mathrm{ThO}}{C}_S|$ (blue, solid) as functions of r, where we set $\mathrm{Re}{\rho }_{tt}=\mathrm{Im}{\rho }_{tt}=-0.1$, $c_{\gamma }=0.1$, and common H, A, $H^{+}$ mass at 500 GeV for illustration, which we will show below that it can generate successful EWBG. The ACME’18 [15] and previous (ACME’14) bounds are the gray and light brown shaded regions. The absence of ${\rho }_{ee}$ corresponds to $r=0$, with $d_e\simeq {\left(d_e^{\varphi \gamma }\right)}_t$ estimated in Equation (13). This specific point [33], far to the left and outside the plot, is excluded by ACME’18. However, the situation is considerably different [45] for $r\ne 0$.

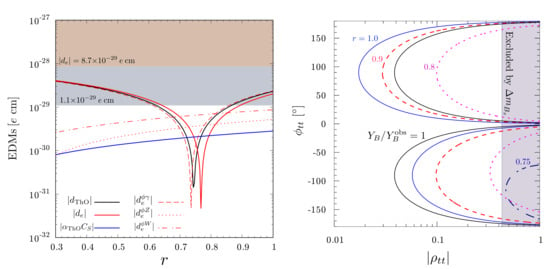
Figure 5. (Left) $|d_{\mathrm{ThO}}|$ and its components vs r, as defined in Equation (22). We take $\mathrm{Re}{\rho }_{tt}=\mathrm{Im}{\rho }_{tt}=-0.1$, $c_{\gamma }=0.1$ and $m_H=m_A=m_{H^{\pm }}=500$ GeV, with ACME bounds overlaid. (Right) 2$\sigma$-allowed region of $d_{\mathrm{ThO}}$ with $r=1.0$ (blue, solid), 0.9 (red, dashed), 0.8 (magenta, dotted) and 0.75 (navy blue, dot-dashed), respectively. The region to the right of the black solid contour, $Y_B/Y_B^{\mathrm{obs}}=1$, is allowed. The gray shaded region is nominally excluded by $B_s$–${\overline{B}}_s$ mixing.

We see strong cancellation in $d_e^{\varphi \gamma }$ around $r\simeq 0.75$, as mentioned in our discussion after Equation (18). This is due to ${\left(d_e^{\varphi \gamma }\right)}_W$ of Figure 4(right) canceling against Figure 4(left) for $\mathrm{Im}{\rho }_{ee}\ne 0$. The subdominant effects of $d_e^{\varphi W}$ and $d_e^{\varphi Z}$ then shift the cancellation point for $d_e$ upwards in r. Finally, to get $d_{\mathrm{ThO}}$, the $C_S$ contribution needs to be added, which moves $d_{\mathrm{ThO}}$ downwards a bit. The upshot is that, owing to this cancellation mechanism, $d_{\mathrm{ThO}}$ can be suppressed by two orders of magnitude below the ACME’18 bound. We remark that, in principle r can depend on the fermion flavor f (see Equation (22)), enriching the possibilities. On the other hand, even finding a preferred r value in the future, it depends on several loop functions with various input parameters to disentangle.

With electron EDM under control and with a lot of leeway to face experimental scrutiny, it is imperative now to check whether EWBG survives. The 2$\sigma$ allowed region of $d_{\mathrm{ThO}}$ is displayed in Figure 5(right) in the $|{\rho }_{tt}|$–${\varphi }_{tt}$ plane, for $r=1.0$ (blue, solid), 0.9 (red, dashed), 0.8 (magenta, dotted) and 0.75 (navy blue, dot-dashed). Regions to the left of these contours are allowed, while to the right of the black contours correspond to $Y_B>Y_B^{\mathrm{obs}}=8.59\times {10}^{-11}$, consistent with Planck 2014 [35] for EWBG. The gray shaded region for larger $|{\rho }_{tt}|$ values is excluded by $B_s$-${\overline{B}}_s$ mixing, but this is by ignoring tree diagrams due to ${\rho }_{sb}$, and so forth. In Ref. [33] we considered ${\varphi }_{tt}<0$ for BAU positive. However, one can flip the sign of $\Delta \beta$ to get ${\varphi }_{tt}>0$. Since the central value of $d_{\mathrm{ThO}}$ is positive, the allowed region is asymmetric in ${\varphi }_{tt}$. For $r=1.0$ and 0.9, only ${\varphi }_{tt}<0$ is consistent with ${\rho }_{tt}$-driven EWBG. However, ${\varphi }_{tt}>0$ becomes possible as r approaches the cancellation point at $r\sim 0.75$, enlarging the solution space for ${\rho }_{tt}$-driven EWBG.

Our results presented here are illustrative and do not exhaust the parameter space that satisfy both EWBG and eEDM. We remark that a cancellation mechanism would not be necessary if ${\rho }_{tt}$ is very small but EWBG is driven by ${\rho }_{tc}$.

4.3. The Flavor Enigma and NFC

Having survived the eEDM bound of ACME’18, and with EWBG once again demonstrated, we cannot help but exclaim (quoting a Psalm of David):

O Lord, our Lord,

How Majestic is Thy Name

in all the Earth,

Who have set Thy Splendor

above the Heavens.

There may be something to g2HDM.

Our simplified Ansatz to achieve cancellation, Equation (22), basically says that the diagonal elements of the extra Yukawa couplings ${\rho }_{ff}$ follow the same SM hierarchy, with specific correlation of CPV phases between charged leptons and up-type quarks. Although the Ansatz enters also $C_S$, the most relevant couplings are ${\rho }_{tt}$ and ${\rho }_{ee}$, reflecting the largest and smallest Yukawa couplings ${\lambda }_t$ and ${\lambda }_e$, which differ by six orders of magnitude.

We now turn to comment on how the NFC condition of Glashow and Weinberg is a prejudice in itself. At the time of their paper, they knew very well the fermion mass hierarchy, namely:

$$\begin{array}{cc}\hfill m_e\ll & m_{\mu }\ll m_{\tau },\hfill \\ \hfill m_d\ll & m_s\ll m_b,\hfill \\ \hfill m_u\ll & m_c\ll m_t,\hfill \end{array}$$

(23)

between the fermion generations. What they did not know was how heavy the top quark actually turned out to be. That is, nobody anticipated the very large ratio

$$m_t/m_b\gg 1,$$

(24)

as attested by the parade of accelerators, PEP, PETRA, TRISTAN, each holding hope to be the one to capture the top quark. However, it was the ARGUS discovery [51] of large $B^0$–${\overline{B}}^0$ mixing in 1987 that harbingered the heaviness of the top and spelled out the null search prospect at SLC/LEP beforehand. It took almost another decade for the top to be discovered [13] at the Tevatron. The large $B^0$–${\overline{B}}^0$ mixing, however, sowed the seed for the eventual B factories that confirmed the Kobayashi–Maskawa CPV mechanism of the SM quark sector.

If the fermion mass hierarchy of Equation (23) was known in 1977, except for the very large $m_t/m_b$ ratio (much larger than $m_c/m_s$), what came totally out of whack, circa 1983 [13] is the quark mixing hierarchy,

$$V_{ub}^2\ll V_{cb}^2\ll V_{us}^2\ll V_{tb}^2\cong 1,$$

(25)

which was an experimental discovery (MAC/Mark II for long b lifetime, and CLEO for absence of $b\to u$) and not anticipated at all. Note that $V_{us}^2\sim 1/20\ll 1$ was known for a long time, which led to the naming of “strangeness”. However, the quark mixing hierarchy of Equation (25) came out of the blue, which led Wolfenstein to propose his namesake parametrization [52],which influenced the placing [13] of the KM phase.

With the mass-mixing hierarchies of Equations (23) and (25), probably stimulated by the ARGUS suggestion for the heaviness of the top, Equation (24), Cheng and Sher suggested [53], a decade after the Glashow–Weinberg paper, that one may not need NFC if FCNH couplings trickle down off-diagonal $\propto \sqrt{m_i{m}_j}/v$. A few years later, we pointed out [54] that, based on the Cheng–Sher Ansatz, the decay mode to watch is $t\to ch$, if some Higgs boson h is lighter than top, or $h\to t\overline{c}$ if h is heavier. The paper also stressed that the Cheng–Sher Ansatz was too specific, and one can more broadly define a “2HDM III” just based on the quark mass-mixing hierarchies. This 2HDM III we now call g2HDM, or even SM2—SM with two scalar doublets, as the mass-mixing hierarchies are “known” to both doublets.

Nature’s design of fermion mass-mixing hierarchies—the flavor enigma—seems to hide well the extra Higgs bosons H, A, $H^{+}$ to this day. That the extra Yukawa couplings would echo this observed mass-mixing hierarchy structure, as exemplified in Equation (22) that evades ACME probe with eEDM, with a couple of order of magnitudes to spare, seems staggering. Even more perplexing is that nature seemingly sent in another unexpected “protection”: the emergent phenomenon of small $c_{\gamma }$, alignment, that can handily explain the absence of $t\to ch\left(125\right)$ so far, without requiring ${\rho }_{tc}$ to be much less than 1.

To what lengths would nature go to hide from us these extra Higgs bosons and their associated couplings?

4.4. Comments: On “The Heavens and the Earth”

In the context of EWBG driven by an extra top Yukawa coupling, the impressive ACME’18 bound suggests an extra electron Yukawa coupling that works in concert to give exquisite cancellation among dangerous diagrams. The cancellation mechanism calls for the extra Yukawas to echo the hierarchical pattern of SM Yukawa couplings.

As we quoted from Psalm 8, of David, which echoes our title, the theme of this article is to strike the contrast between the Heavens and the Earth. To explain the disappearance of antimatter from the early Universe, or the Heavens, one needs lofty, new CPV phases that are very BSM, that is, beyond the KM phase. However, with such large CPV phase, can one survive the very stringent scrutiny from LE precision frontier probes, such as ACME? The g2HDM provides an existence proof, which also illustrates the delicateness. The contrast between ${\rho }_{tt}$ and ${\rho }_{ee}$, that it echoes the ${\lambda }_t$ vs ${\lambda }_e$ pattern, is truly curious.5

A second point to make is that ACME’14 was basically confirmed by the JILA group [58] using trapped HfF${}^{+}$ ions. This is a different approach from ACME, hence fulfills the standard criterion of an independent check. However, the ACME’18 result has not been confirmed independently so far, although several groups are galvanized to join the fray. In this sense, we do not view ${10}^{-29}e$ cm as “finished business”, for we have witnessed, in our own lifetime, discovery [51] right on top of the previously set [59] bound.

It is very amusing that the largest diagonal extra Yukawa ${\rho }_{tt}$ drives B.A.U., while working in concert with the smallest diagonal extra Yukawa ${\rho }_{ee}$ to generate eEDM, which might be revealed soon by very-low-energy ultra-precision probes. It should be clear that the ${10}^{-29}$ to ${10}^{-30}e$ cm range seems ripe and fabulous. Godspeed their success.

What lies between ${\rho }_{tt}$ and ${\rho }_{ee}$, spanning 6 orders of magnitude, the various extra Yukawa couplings provide a host of phenomena that can be probed at the LHC as well as the flavor frontier, to which we now turn.

5. Phenomenological Consequences

As the extra Yukawa couplings reflect the SM Yukawa pattern, we shall take [60,61] the conservative,

$${\rho }_{ii}\lesssim \mathcal{O}\left({\lambda }_i\right);{\rho }_{1i}\lesssim \mathcal{O}\left({\lambda }_1\right);{\rho }_{3j}\lesssim \mathcal{O}\left({\lambda }_3\right)(j\ne 1),$$

(26)

since the bounds involving the third generation are the weakest. The main phenomenological consequences are searching for H, A, $H^{+}$ at the LHC, and combing the flavor frontier; our discussion will be brief. We shall also comment on the need of $\mathcal{O}\left(1\right)$ Higgs quartics, namely the issue of order of phase transition, and implications on the Landau ghost. On the side, we comment on the possible impact of the recently confirmed muon $g-2$ anomaly.

5.1. Leading Search Modes at the LHC

Shortly after our EWBG [33] and alignment [30] studies, we capitalized on the ${\rho }_{tc}$ and ${\rho }_{tt}$ couplings and proposed [62] the associated production mechanism, that is, the two diagrams on the left side of Figure 6,

$$\begin{array}{cc}\hfill cg\to tH/tA\to & tt\overline{c},\hfill \\ \hfill & tt\overline{t},\hfill \end{array}$$

(27)

where production is due to ${\rho }_{tc}$, while $A/H$ decay can go through ${\rho }_{tc}$ or ${\rho }_{tt}$, giving rise to $tt\overline{c}$ (Same-Sign Top plus c-jet), or $tt\overline{t}$ (Triple-Top) signatures. The discovery potential for $tt\overline{c}$ already looks promising [62] with LHC Run 2 data, while the more exquisite Triple-Top, at higher threshold and with tiny SM cross section, can be explored at the High-Luminosity LHC (HL-LHC). See Ref. [63] for further discussion. Note that $4t$ has a SM cross section at $\mathcal{O}\left(12\right)$ fb, which is about an order of magnitude larger than triple-top in SM, and has been fervently searched for by both ATLAS and CMS, which puts constraints [64] on ${\rho }_{tc}$ and ${\rho }_{tt}$.

Figure 6. Feynman diagrams for the $cg\to tA,tH$ and $cg\to b{H}^{+}$ associated production processes.

The down-type Yukawa interaction is analogous to Equation (4), while the corresponding charged Higgs Yukawa coupling can be found in Ref. [63]. It is curious that it took some while for us to come up with [65] the novel $H^{+}$ associated production process illustrated in the two diagrams on the right side of Figure 6, that is,

$$cg\to b{H}^{+}\to bt\overline{b},$$

(28)

where ${\rho }_{tc}$ enters the $\overline{c}b{H}^{+}$ coupling, while $H^{+}\to t\overline{b}$ goes through ${\rho }_{tt}$. It is not surprising that the latter coupling has an associated $V_{tb}$ CKM factor, but a bit counter-intuitively (compared with 2HDM II), the former also has the $V_{tb}$ CKM factor rather than $V_{cb}$, hence it is enhanced by $V_{tb}/V_{cb}$ at amplitude level [65] . Furthermore, association with the b quark means the threshold is lower than $tH,tA$ production, hence it is generally more efficient.

Our study [65] did not find severe backgrounds for the $bt\overline{b}$ signature, but we await experimental scrutiny to find out whether there are some yet unspecified background. With ${\rho }_{tc}$ and ${\rho }_{tt}$ largely unexplored, and keeping in mind each one of them could possibly drive EWBG, we urge the ATLAS and CMS experiments to make a serious effort to search for the processes of Equations (27) and (28). We note that, even if the signatures are discovered, reconstructing the H, A and $H^{+}$ bosons would be the next challenge, let alone disentangling the CPV phase of ${\rho }_{tt}$ down the line.

We remark that in our collider studies, we always use the 2HDMC package [66,67] to check parameter space, that many standard criteria such as positivity, perturbativity and unitarity, as well as electroweak precision observables, are satisfied.

5.2. Glimpse of the Coming New Flavor Era

What hides H, A, $H^{+}$ effects so well from our view?

In this subsection we will show that the conservative pattern of Equation (26), which respects the mass-mixing hierarchy of SM Yukawa couplings as revealed by the eEDM cancellation mechanism, does hide exotic Higgs effects rather well in the flavor sector.

After pointing out [54] the importance of $t\to ch$, we utilized the two-loop mechanism, analogous to Figure 3 and Figure 4, to explore $\mu \to e\gamma$ [68]; a sizable ${\rho }_{tt}$, together with ${\rho }_{\mu e}$, could make it dominate over one-loop. The same mechanism was later applied to $\tau \to \mu \gamma$.

With myriads of extra Yukawa couplings for up- and down-type quarks and charged leptons, we recently made a survey [60] of processes of interest, starting with $\mu \to e\gamma$ and $\tau \to \mu \gamma$. We saturate Equation (26) and take: $c_{\gamma }=0.05$, ${\rho }_{\mu e}={\lambda }_e$, ${\rho }_{\tau \mu }={\lambda }_{\tau }$, ${\rho }_{ii}={\lambda }_i$, except ${\rho }_{tt}\sim 0.4$, as we take the relatively low $m_{H,A}=300$GeV. We see from the left side entries of Figure 7 that both $\mu \to e\gamma$ and $\tau \to \mu \gamma$ could be discovered in the near future, by MEG II and Belle II, respectively. The $\mu \to 3e$ and $\tau \to 3\mu$ decays would be dominated by dipole transition, with $\tau \to 3\mu$ falling outside of Belle II sensitivity. Particularly interesting [60] may be $\mu N\to eN$ conversion, where COMET at KEK and Mu2e at Fermilab aim for up to 6 orders of magnitude improvement. If realized, these experiments have the potential to disentangle various extra Yukawa couplings by utilizing different nuclei.

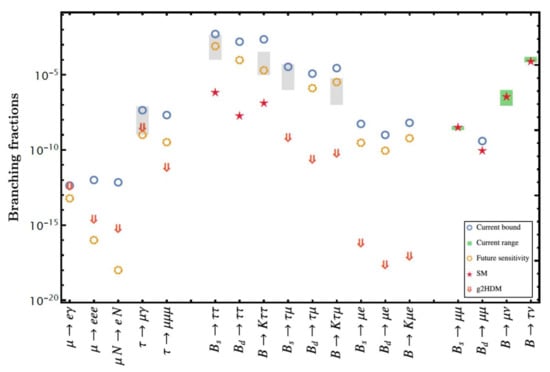
Figure 7. Pictorial table of $\mu$, $\tau$ and B decay processes: blue solid (orange dotted) circles for current bounds (future sensitivities); green shaded bands for measured ranges of $B_s\to \mu \mu$ and $B\to \tau \nu ,\mu \nu$; grey shaded bands illustrate the five leading predictions of the PS${}^3$ model for B-anomalies; red ☆ for SM predictions. The red ⇓ illustrate g2HDM benchmark projections, using $c_{\gamma }=0.05$, $m_{H,A}=300$ GeV, ${\rho }_{\mu e}={\lambda }_e$, ${\rho }_{\tau \mu }={\lambda }_{\tau }$, and ${\rho }_{ii}={\lambda }_i$, except ${\rho }_{tt}=0.4$. See text for more detail.

Turning to B decays with leptons in the final state, we contrast g2HDM with five spectacular projections [69] from leptoquarks (LQ) of the PS${}^3$ model (three copies of Pati-Salam symmetry) motivated by the “B anomalies” (for a description and critique, see Ref. [21]), which are illustrated by grey bands on the upper side of Figure 7. The B anomalies are large effects, hence lead to spectacular projections, including $\tau \to \mu \gamma$ that falls into the Belle II range. We comment on the correlated modes of $B_s\to \tau \tau$ and $B\to K\tau \tau$ below, where the studies are a bit more difficult. However, the two other modes, $B_s\to \tau \mu$ (note that it was LHCb measurement that pushed down the PS${}^3$ projection.) and $B\to K\tau \mu$ are very interesting. For the latter, BaBar has shown the way with full hadronic tag of the other B, and one can just count events in the $m_{\tau }$ window, while LHCb has demonstrated they can do something similar, that is, with full kinematic control from a decaying excited $B_s$ parent. Surprisingly, Belle has not shown anything so far, and $B\to K\tau \mu$ would be a competition between LHCb and Belle II in the future.

We note from Figure 7 that $B_{s,d}\to \tau \tau$ and $B\to K\tau \tau$ have SM projections that are orders of magnitude below experimental sensitivity, so PS${}^3$ enhancement is certainly motivating. However, for the “middle-ground” modes in Figure 7, g2HDM projections that are illustrated by the red downward arrow are even further away from experimental scrutiny. This illustrates the efficacy of Equation (26) in hiding the exotic Higgs boson effects in g2HDM, making $B_{s,d}\to \mu e$ and $B\to K\mu e$ even harder to see, although they certainly should be searched for.

Finally, we come to the last four modes on the far right of Figure 7: $B_{s,d}\to \mu \mu$ and $B^{-}\to \mu \nu ,\tau \nu$. The former two have been vigorously searched for by LHCb and CMS, with LHCb holding the upper hand so far, and with indication that $B_s\to \mu \mu$ is slightly below SM expectation, while $B_d\to \mu \mu$ is not yet measured.6 The latter two modes have been searched for at the B factories, with $B^{-}\to \tau \nu$ providing [70] one of the two important bounds on $H^{+}$ in 2HDM II, where the current result is consistent with SM expectation. The $B^{-}\to \mu \nu$ mode has been under Belle scrutiny lately [13], and will be a mode of great interest at Belle II, especially in g2HDM. It was in fact the study [71] of this decay that clarified for us some intricacies of $H^{+}$ effects in g2HDM that differs from 2HDM II. However, it still took us some time to propose [65] the $cg\to b{H}^{+}\to bt\overline{b}$ process of Equation (28), which enjoys CKM enhancement.

We had pointed out earlier [72] that g2HDM could in principle make the ratio $\mathcal{B}(B\to \mu \nu )/\mathcal{B}(B\to \tau \nu )$ deviate from the SM expectation of 0.0045, where 2HDM II shares the same value [70]. However, it was only by checking explicitly [71] that we found that, indeed, $B\to \tau \nu$ would be SM-like, but $B\to \mu \nu$ could be more easily shifted, even when one respects Equation (26). Besides a large CKM enhancement on the quark side ($b\to u$ transition), this is in part due to some intricacy that the neutrino flavor is not measured in this decay, hence allowing ${\rho }_{\tau \mu }$ to enter. It would be exciting if Belle II finds $\mathcal{B}(B\to \mu \nu )/\mathcal{B}(B\to \tau \nu )\ne 0.0045$, as it would not only be BSM, but would rule out 2HDM II as well.

These last four modes share the virtue that they have SM expectations that have been driving experimental measurement. Thus, BSM effects are more effectively probed through interference, and there is much to look forward to in the near future.

Let us comment on whether g2HDM itself could impact on the B-anomalies in general. Early on, g2HDM (called 2HDM III) was proposed [73] as a possible solution to the “BaBar anomaly”. However, as stated, the B-anomalies are large, tree-level effects. It was subsequently pointed out [74] that this approach ran into an issue with the $B_c$ lifetime by a constraint on $B_c\to \tau \nu$, hence was disfavored. The issue has recently been reopened by the loosening [75,76] of the $\mathcal{B}(B_c\to \tau \nu )$ constraint, and it remains to be seen [77,78,79] whether g2HDM can handle $R_D$, $R_{D^{*}}$ anomalies. However, in general, the conservative Equation (26), which is consistent with fermion mass-mixing hierarchies as well as eEDM constraint, cannot easily account for large tree-level effects.

5.3. Lattice Connection: Phase Transition and Landau Ghost

We have mentioned that the first order electroweak phase transition demands $\mathcal{O}\left(1\right)$ Higgs quartic couplings of the g2HDM Higgs potential. At the same time, ${\mu }_{22}^2/v^2$ also ought to be $\mathcal{O}\left(1\right)$, otherwise a large ${\mu }_{22}^2$ would damp away dynamical effects such as EWPT, as well as EWBG itself. Thus, $v\cong 246$ GeV sets the electroweak scale, and all other dimensionless parameters of the Higgs potential are $\mathcal{O}\left(1\right)$, which is why the exotic Higgs bosons populate 300 to 600 GeV, ripe for the LHC to explore.

The $\mathcal{O}\left(1\right)$ Higgs quartics are not weak, bringing in two aspects to ponder. The first is to go beyond one-loop resumed effective potential [29] and put the Higgs potential on the lattice [80], to check nonperturbatively how the first order EWPT occurs. Though there are quite a few Higgs quartic couplings in g2HDM, this is a question of interest in its own right, and it is quite timely to check the Higgs quartic coupling parameter space that support first order EWPT.

A second issue is even more dynamical: the Landau pole of these $\mathcal{O}\left(1\right)$ Higgs quartics. A simple estimate in Ref. [30] gave 10–20 TeV, which is rather interesting. It implies some strong interaction and one would have to reconsider the theoretical framework—another issue to be studied on the lattice. Establishing the strengthening of the quartic couplings with scale would imply New Physics at some higher scale beyond, which could justify the 100 TeV pp collider. Although it would be a challenge to theorists to find a theory that can accommodate this, one might bring back SUSY and reconsider it above this scale.

With enough experimental progress, one could in principle interface the lattice study with experimental development on the exotic Higgs search, for example, exploring exotic Higgs scattering processes to actually measure the increase in quartic coupling strength.

In any case, searching for sub-TeV exotic Higgs bosons at the LHC is mandatory.

5.4. Possible Implications of Muon G-2 in g2HDM

After much effort, the Fermilab Muon g-2 experiment recently confirmed [81] the previous measurement at BNL, and the combined result deviates from the “consensus” theory prediction [82] by 4.2$\sigma$. Thus, the muon $g-2$ anomaly has to be taken seriously. In fact, g2HDM can quite easily handle it, if one is willing to deviate from the conservative estimate of Equation (26). As illustrated in Figure 8, the one-loop mechanism readily handles the observed discrepancy with, for example, $m_H=300$ GeV (with $m_A=m_{H^{+}}$ heavier) and ${\rho }_{\tau \mu }={\rho }_{\mu \tau }\sim 0.2$, which is 20 times ${\lambda }_{\tau }\simeq 0.01$. The one-loop mechanism suffers chiral suppression, which is one of the reasons why the two loop mechanism could win over. However, having $\tau$ in the loop helps, as it is not so severely chiral-suppressed.

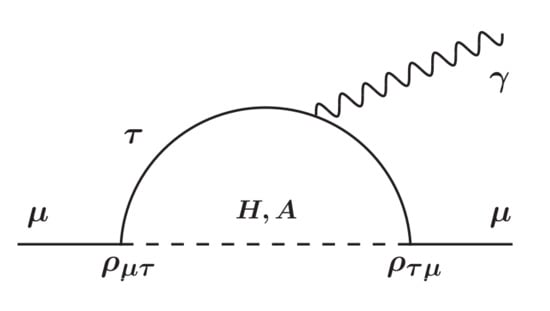
Figure 8. One-loop mechanism for muon $g-2$ anomaly, with ${\rho }_{\tau \mu }$, ${\rho }_{\mu \tau }$ much larger than Equation (26).

A large ${\rho }_{\tau \mu }$ or ${\rho }_{\mu \tau }$ would enter $\tau \to \mu \gamma$ via the two-loop mechanism with the help of ${\rho }_{tt}$, analogous to our previous discussion. However, what may be surprising [83] is that, through the production chain [84] of

$$gg\to H,A\to \tau \mu ,$$

(29)

the recent search bounds by CMS [85] turn out to be more stringent on the product ${\rho }_{tt}{\rho }_{\tau \mu }$ than from the recent Belle measurement of $\tau \to \mu \gamma$ [86]. This means that a hint could well appear with full Run 2 data, as CMS only used 36 fb${}^{-1}$ data at 13 TeV in Ref. [85].

With ${\rho }_{\tau \mu }={\rho }_{\mu \tau }\sim 0.2$ and $m_H$ as before, the present bound on ${\rho }_{tt}$ is about 0.1, which is still efficient for EWBG. A finite ${\rho }_{tc}$ value would have $t\overline{c}$ in the final state and dilute the $H\to \tau \mu$ branching fraction, hence allow ${\rho }_{tt}$ to be larger (although $\tau \to \mu \gamma$ constraint would kick in). With ${\rho }_{tc}$ and ${\rho }_{\tau \mu }$ both sizable, one could have [83] the novel signatures of $cg\to b{H}^{+}\to \mu \tau b{W}^{+}$, $tcb{W}^{+}$ via $H^{+}\to H{W}^{+}$ weak decay, showing the potential implications of the muon $g-2$ anomaly.

We found [87] further profound impact of the muon $g-2$ anomaly: a possible revival of muon physics. If one replaces the final $\mu$ in Figure 8 by e, the electron, one has a one-loop mechanism for $\mu \to e\gamma$, which would be handily suppressed by Equation (26), but now can allow MEG II to probe ${\rho }_{\tau e}$ down to ${\lambda }_e$ strength. If MEG II makes a discovery, it can be followed up by COMET/Mu2e for $\mu N\to eN$, which now can even probe ${\rho }_{qq}$ by using various different nuclei. For $\tau$ physics, Belle II can readily probe down to ${\rho }_{\tau \tau }={\lambda }_{\tau }$ with $\tau \to \mu \gamma$, while $\tau \to 3\mu$ can now probe down to ${\rho }_{\mu \mu }\sim {\lambda }_{\mu }$, which seems quite exciting.

We had already been investigating the EDM of muon and tau, assuming Equation (26). It is easy to note that the same one-loop diagram of Figure 8 would give rise to $d_{\mu }$ with complex ${\rho }_{\tau \mu }{\rho }_{\mu \tau }$. We note in passing that, while this does not help $\tau$EDM, we find that [61] $\mu$EDM can be enhanced to $6\times {10}^{-23}e$ cm, within the range of a proposed experiment at PSI, which adds to the “renaissance of muon physics”.

We stress, however, that this one-loop muon $g-2$ mechanism, though exciting (and not impossible), would actually make Nature appear rather “whimsical” [61]. Judging from the pattern of hiding exotic scalar effects so well through the fermion mass-mixing hierarchies, we think that Equation (26) is more likely to be realized.

6. Summary

Let us briefly summarize our findings. With the backdrop of No New Physics found at the LHC so far, other than the expected Higgs boson (which resembles remarkably the one expected in SM), when the whole field appears somewhat rudderless, we point out a “most likely New Physics” (by its simplicity and richness) that is in plain sight, but the majority of the field sees not: a second Higgs doublet that possesses extra Yukawa couplings, the general 2HDM. The extra Yukawa couplings can provide sufficiently strong extra CPV, in the form of ${\lambda }_t\mathrm{Im}{\rho }_{tt}$, Equation (10), that provides robust electroweak baryogenesis, while the extra Higgs quartic couplings can provide the needed first order phase transition.

With such a large CPV from the top sector, one needs to cover one’s “back” from precision CPV probes such as electron EDM. Our initial projection with ${\rho }_{ee}$ turned off was quickly ruled out by the 2018 update of the ACME experiment. Revisiting, we discovered an exquisite—and natural—cancellation mechanism, that diagonal ${\rho }_{ff}$ couplings are correlated with ${\rho }_{tt}$ (including phase) via the ${\lambda }_f/{\lambda }_t$ ratio, the Ansatz of Equation (22). This echoes the well-known charged fermion mass-mixing hierarchies, the flavor enigma, which offers further support for dropping the NFC condition of Glashow and Weinberg.

With Equation (22), extra Yukawa couplings also span a six order of magnitude range in strength, providing rich phenomena to be searched for. First things to be checked are the associated production of $tH$, $tA$ and $b{H}^{+}$, where H, A and $H^{+}$ are the exotic Higgs bosons of the second doublet. Leading search modes are $tt\overline{c}$ (same-sign top plus jet), $tt\overline{t}$ (triple-top) and $bt\overline{b}$ (single top plus high $p_T$$b\overline{b}$ pair), with the interesting note that EWBG demands H, A and $H^{+}$ to be sub-TeV in mass, which is ripe for the LHC. Second, the myriad extra Yukawa couplings, especially flavor changing ones, impact on a myriad of observables, as illustrated in the pictogram of Figure 7, where the most interesting processes are $\mu \to e\gamma$, $\mu N\to eN$, $\tau \to \mu \gamma$, $B_{s,d}\to \mu \mu$ and $B^{-}\to \mu \nu ,\tau \nu$. This plot also illustrates, with gray-shaded bands, the more tantalizing signals from the leptoquark interpretation of “B-anomalies”, with the remark that they are not mutually exclusive with g2HDM.

Worthy of mention is the lattice program. Since EWBG demands Higgs quartics to be $\mathcal{O}\left(1\right)$ in strength, this is borderline on perturbation theory; a nonperturbative study of the phase transition issue has intrinsic value. Furthermore, $\mathcal{O}\left(1\right)$ quartics imply a nearby Landau ghost scale, which may link with a future high energy collider program. We further note that the muon $g-2$ anomaly can be accounted for by the one-loop mechanism, that is, sizable ${\rho }_{\tau \mu }$. Though we do not view this favorably (compare our conservative Equation (26)), with nature the ultimate arbiter, the impact could be dramatic, as outlined in Section 4.4.

To conclude, we have presented the picture where exotic H, A, $H^{+}$ Higgs bosons exist at 500 GeV scale, which can generate baryon asymmetry of the Universe while accommodating electron EDM bound of ACME 2018—and can be verified at the LHC. This fantastic possibility is accompanied by a host of flavor physics and CPV probes.

We advocate, therefore:

A Decadal Mission

Find the extra H, A, $H^{+}$ bosons and crack the flavor code.

Go ATLAS/CMS and LHCb/BelleII (and others)

and Lattice, too.

Finally, we raise the following challenge: Having some large CPV at the electroweak scale to face “the Heavens”, how difficult is it to evade low energy precision eEDM probes on Earth? The general 2HDM with extra Yukawa couplings provides an existence proof.