Compact Objects in Alternative Gravities
Abstract
:1. Introduction
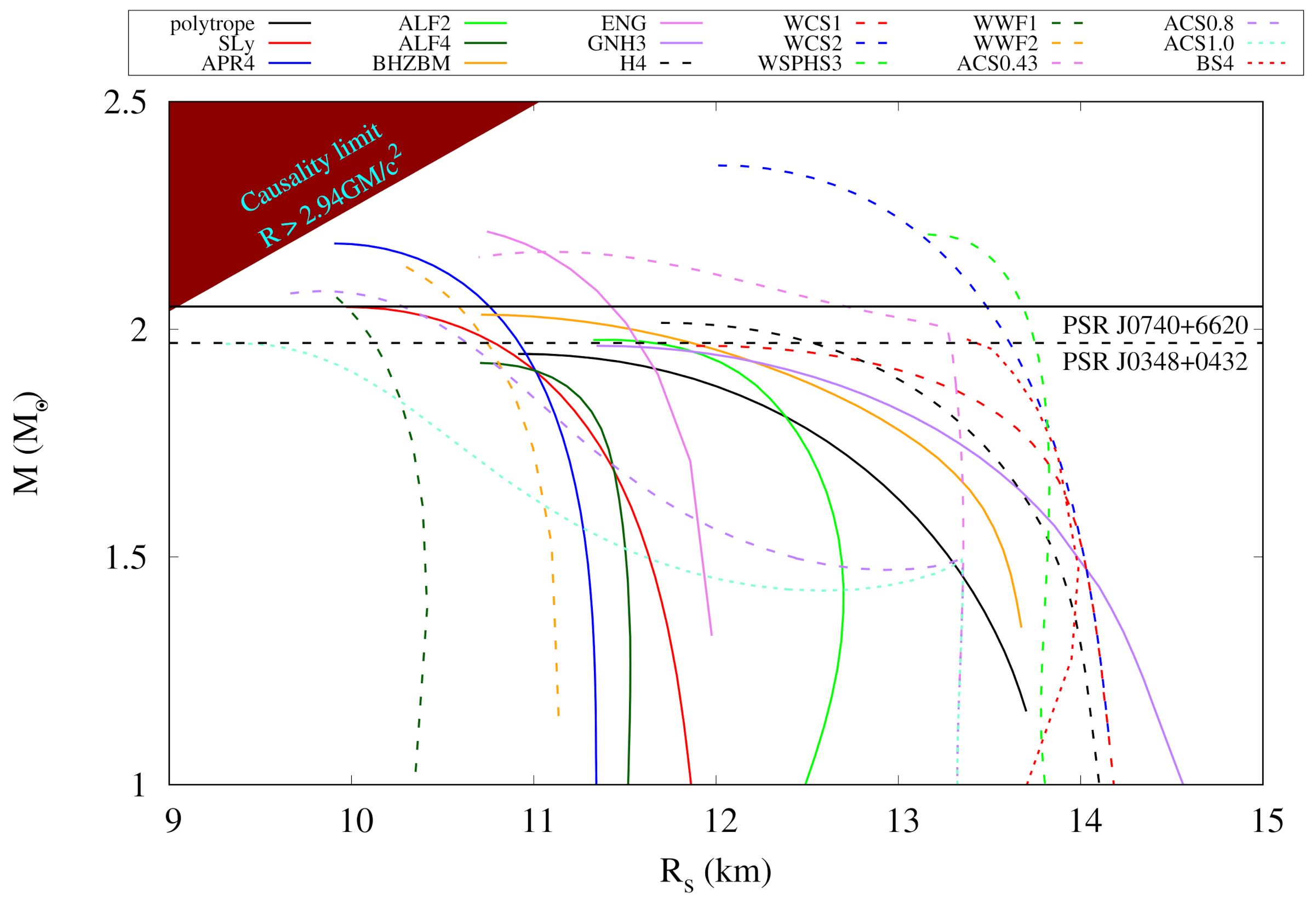
2. Neutron Stars
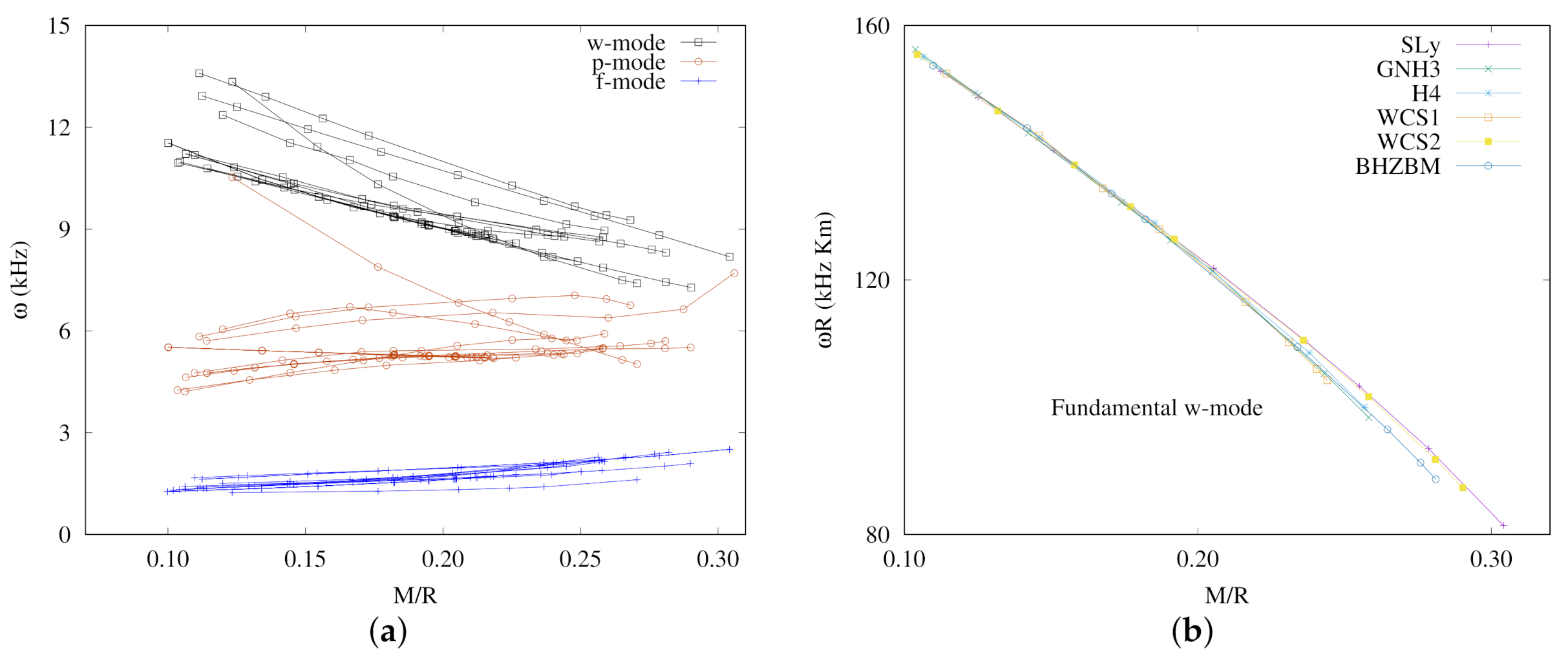
2.1. Neutron Stars in General Relativity
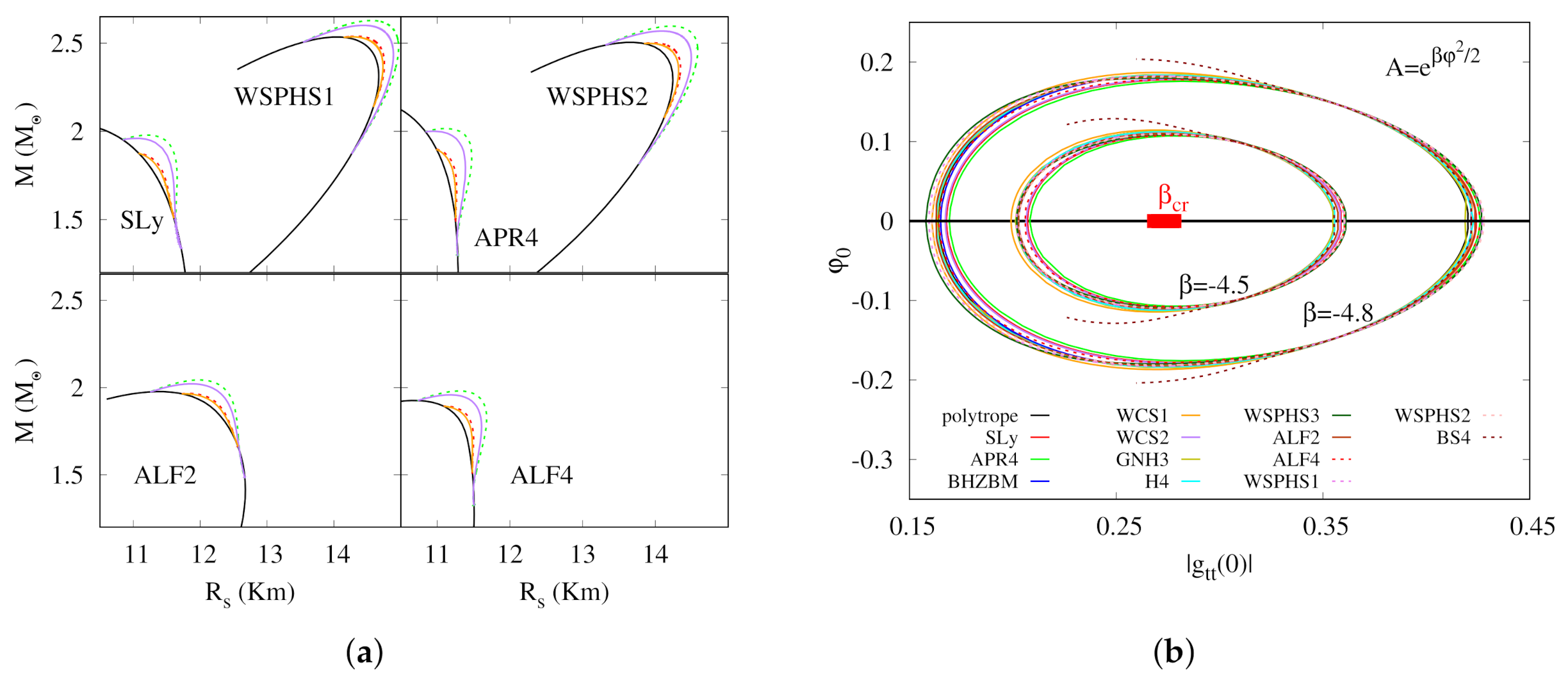
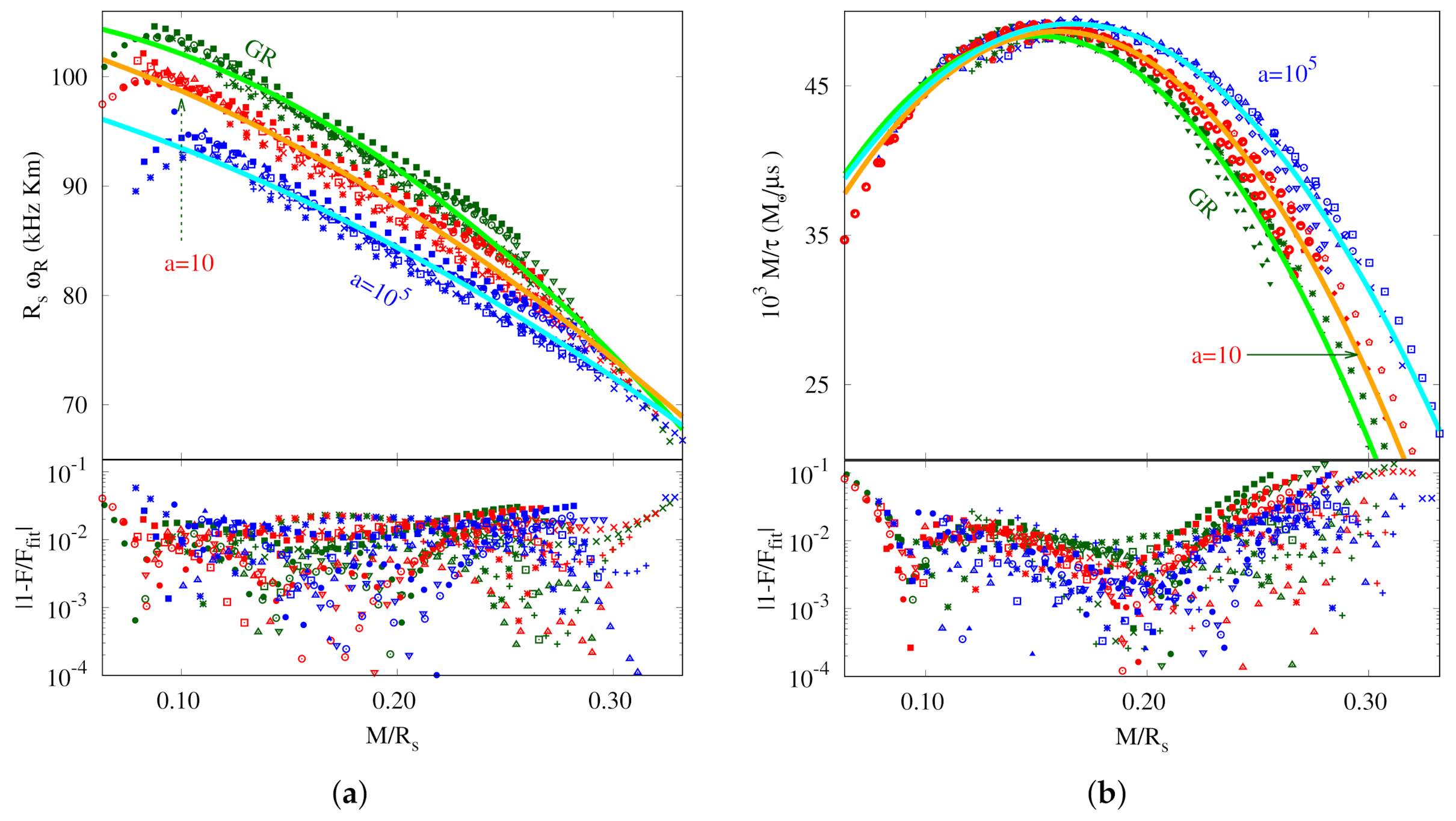
2.2. Neutron Stars beyond General Relativity
3. Black Holes
3.1. Black Holes in General Relativity
3.2. Black Holes beyond General Relativity
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Faraoni, V.; Capozziello, S. Beyond Einstein Gravity: A Survey of Gravitational Theories for Cosmology and Astrophysics. Fundam. Theor. Phys. 2010, 170. [Google Scholar] [CrossRef] [Green Version]
- Berti, E.; Barausse, E.; Cardoso, V.; Gualtieri, L.; Pani, P.; Sperhake, U.; Stein, L.C.; Wex, N.; Yagi, K.; Baker, T.; et al. Testing General Relativity with Present and Future Astrophysical Observations. Class. Quant. Grav. 2015, 32, 243001. [Google Scholar] [CrossRef]
- Saridakis, E.N.; Lazkoz, R.; Salzano, V.; Moniz, P.V.; Capozziello, S.; Jiménez, J.B.; De Laurentis, M.; Olmo, G.J. (Eds.) Modified Gravity and Cosmology: An Update by the CANTATA Network; Springer: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [Green Version]
- Abbott, B.P.; Bloemen, S.; Canizares, P.; Falcke, H.; Fender, R.P.; Ghosh, S.; Groot, P.; Hinderer, T.; Hörandel, J.R.; Jonker, P.G.; et al. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. Lett. 2017, 848, L12. [Google Scholar] [CrossRef]
- Akiyama, K. [Event Horizon Telescope]. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. Lett. 2019, 875, L1. [Google Scholar] [CrossRef]
- Will, C.M. Theory and Experiment in Gravitational Physics; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar] [CrossRef]
- Shao, L.; Stairs, I.H.; Antoniadis, J.; Deller, A.T.; Freire, P.C.C.; Hessels, J.W.T.; Janssen, G.H.; Kramer, M.; Kunz, J.; Lämmerzahl, C.; et al. Testing Gravity with Pulsars in the SKA Era. PoS AASKA14, 042 (2015). arXiv 2014, arXiv:1501.00058. [Google Scholar]
- Kramer, M.; Stairs, I.H.; Manchester, R.N.; Wex, N.; Deller, A.T.; Coles, W.A.; Ali, M.; Burgay, M.; Camilo, F.; Cognard, I.; et al. Strong-Field Gravity Tests with the Double Pulsar. Phys. Rev. X 2021, 11, 041050. [Google Scholar] [CrossRef]
- Yagi, K.; Yunes, N. Approximate Universal Relations for Neutron Stars and Quark Stars. Phys. Rep. 2017, 681, 1. [Google Scholar] [CrossRef] [Green Version]
- Doneva, D.D.; Pappas, G. Universal Relations and Alternative Gravity Theories. Astrophys. Space Sci. Libr. 2018, 457, 737–806. [Google Scholar] [CrossRef] [Green Version]
- Brans, C.; Dicke, R.H. Mach’s principle and a relativistic theory of gravitation. Phys. Rev. 1961, 124, 925. [Google Scholar] [CrossRef]
- Damour, T.; Esposito-Farese, G. Tensor multiscalar theories of gravitation. Class. Quant. Grav. 1992, 9, 2093. [Google Scholar] [CrossRef]
- Fujii, Y.; Maeda, K. The Scalar-Tensor Theory of Gravitation; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar] [CrossRef]
- Damour, T.; Esposito-Farese, G. Nonperturbative strong field effects in tensor—Scalar theories of gravitation. Phys. Rev. Lett. 1993, 70, 2220. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Faraoni, V. f(R) Theories Of Gravity. Rev. Mod. Phys. 2010, 82, 451. [Google Scholar] [CrossRef] [Green Version]
- De Felice, A.; Tsujikawa, S. f(R) theories. Living Rev. Relativ. 2010, 13, 3. [Google Scholar] [CrossRef] [Green Version]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rep. 2011, 505, 59. [Google Scholar] [CrossRef] [Green Version]
- Yazadjiev, S.S.; Doneva, D.D.; Kokkotas, K.D.; Staykov, K.V. Non-perturbative and self-consistent models of neutron stars in R-squared gravity. J. Cosmol. Astropart. Phys. 2014, 06, 003. [Google Scholar] [CrossRef] [Green Version]
- Capozziello, S.; de Laurentis, M. Extended Theories of Gravity. Phys. Rep. 2011, 509, 167–321. [Google Scholar] [CrossRef] [Green Version]
- Brax, P.; Davis, A.C.; Li, B.; Winther, H.A. A Unified Description of Screened Modified Gravity. Phys. Rev. D 2012, 86, 044015. [Google Scholar] [CrossRef] [Green Version]
- Zwiebach, B. Curvature Squared Terms and String Theories. Phys. Lett. 1985, 156, 315–317. [Google Scholar] [CrossRef]
- Gross, D.J.; Sloan, J.H. The Quartic Effective Action for the Heterotic String. Nucl. Phys. B 1987, 291, 41–89. [Google Scholar] [CrossRef]
- Metsaev, R.R.; Tseytlin, A.A. Order alpha-prime (Two Loop) Equivalence of the String Equations of Motion and the Sigma Model Weyl Invariance Conditions: Dependence on the Dilaton and the Antisymmetric Tensor. Nucl. Phys. 1987, 293, 385. [Google Scholar] [CrossRef]
- Doneva, D.D.; Yazadjiev, S.S. New Gauss–Bonnet black holes with curvature induced scalarization in the extended scalar-tensor theories. Phys. Rev. Lett. 2018, 120, 131103. [Google Scholar] [CrossRef] [Green Version]
- Silva, H.O.; Sakstein, J.; Gualtieri, L.; Sotiriou, T.P.; Berti, E. Spontaneous scalarization of black holes and compact stars from a Gauss–Bonnet coupling. Phys. Rev. Lett. 2018, 120, 131104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Antoniou, G.; Bakopoulos, A.; Kanti, P. Evasion of No-Hair Theorems and Novel Black-Hole Solutions in Gauss–Bonnet Theories. Phys. Rev. Lett. 2018, 120, 131102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dima, A.; Barausse, E.; Franchini, N.; Sotiriou, T.P. Spin-induced black hole spontaneous scalarization. Phys. Rev. Lett. 2020, 125, 231101. [Google Scholar] [CrossRef] [PubMed]
- Lattimer, J.M. The nuclear equation of state and neutron star masses. Ann. Rev. Nucl. Part. Sci. 2012, 62, 485–515. [Google Scholar] [CrossRef] [Green Version]
- Özel, F.; Freire, P. Masses, Radii, and the Equation of State of Neutron Stars. Ann. Rev. Astron. Astrophys. 2016, 54, 401–440. [Google Scholar] [CrossRef] [Green Version]
- Baym, G.; Hatsuda, T.; Kojo, T.; Powell, P.D.; Song, Y.; Takatsuka, T. From hadrons to quarks in neutron stars: A review. Rep. Prog. Phys. 2018, 81, 056902. [Google Scholar] [CrossRef] [Green Version]
- Demorest, P.; Pennucci, T.; Ransom, S.; Roberts, M.; Hessels, J. Shapiro Delay Measurement of A Two Solar Mass Neutron Star. Nature 2010, 467, 1081. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.C.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 1233232. [Google Scholar] [CrossRef] [Green Version]
- Cromartie, H.T.; Fonseca, E.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Blumer, H.; Brook, P.R.; DeCesar, M.E.; Dolch, T.; Ellis, J.A.; et al. [NANOGrav]. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nat. Astron. 2019, 4, 72–76. [Google Scholar] [CrossRef] [Green Version]
- Yagi, K.; Yunes, N. I-Love-Q. Science 2013, 341, 365–368. [Google Scholar] [CrossRef] [Green Version]
- Krastev, P.G.; Li, B.A. Nuclear constraints on gravitational waves from deformed pulsars. arXiv 2016, arXiv:1607.05373. [Google Scholar]
- Manko, V.S.; Ruiz, E. A note on hierarchy of universal relations for neutron stars in terms of multipole moments. Class. Quant. Grav. 2019, 36, 147002. [Google Scholar] [CrossRef]
- Jiang, N.; Yagi, K. Improved Analytic Modeling of Neutron Star Interiors. Phys. Rev. D 2019, 99, 124029. [Google Scholar] [CrossRef] [Green Version]
- Andersson, N.; Kokkotas, K.D. Towards gravitational wave asteroseismology. Mon. Not. R. Astron. Soc. 1998, 299, 1059–1068. [Google Scholar] [CrossRef] [Green Version]
- Kokkotas, K.D.; Schmidt, B.G. Quasinormal modes of stars and black holes. Living Rev. Relativ. 1999, 2, 1–72. [Google Scholar] [CrossRef] [Green Version]
- Andersson, N.; Kokkotas, K.D. Gravitational waves and pulsating stars: What can we learn from future observations? Phys. Rev. Lett. 1996, 77, 4134. [Google Scholar] [CrossRef] [Green Version]
- Blázquez-Salcedo, J.L.; González-Romero, L.M.; Navarro-Lérida, F. Polar quasi-normal modes of neutron stars with equations of state satisfying the 2M⊙ constraint. Phys. Rev. D 2014, 89, 044006. [Google Scholar] [CrossRef] [Green Version]
- Mendes, R.F.P. Possibility of setting a new constraint to scalar-tensor theories. Phys. Rev. D 2015, 91, 064024. [Google Scholar] [CrossRef] [Green Version]
- Mendes, R.F.P.; Ortiz, N. Highly compact neutron stars in scalar-tensor theories of gravity: Spontaneous scalarization versus gravitational collapse. Phys. Rev. D 2016, 93, 124035. [Google Scholar] [CrossRef] [Green Version]
- Motahar, Z.A.; Blázquez-Salcedo, J.L.; Kleihaus, B.; Kunz, J. Scalarization of neutron stars with realistic equations of state. Phys. Rev. D 2017, 96, 064046. [Google Scholar] [CrossRef] [Green Version]
- Alsing, J.; Berti, E.; Will, C.M.; Zaglauer, H. Gravitational radiation from compact binary systems in the massive Brans–Dicke theory of gravity. Phys. Rev. D 2012, 85, 064041. [Google Scholar] [CrossRef] [Green Version]
- Freire, P.C.C.; Wex, N.; Esposito-Farese, G.; Verbiest, J.P.W.; Bailes, M.; Jacoby, B.A.; Kramer, M.; Stairs, I.H.; Antoniadis, J.; Janssen, G.H. The relativistic pulsar-white dwarf binary PSR J1738+0333 II. The most stringent test of scalar-tensor gravity. Mon. Not. R. Astron. Soc. 2012, 423, 3328–3343. [Google Scholar] [CrossRef]
- Zhao, J.; Freire, P.C.C.; Kramer, M.; Shao, L.; Wex, N. Closing the spontaneous-scalarization window with binary pulsars. arXiv 2022, arXiv:2201.03771. [Google Scholar]
- Ramazanoğlu, F.M.; Pretorius, F. Spontaneous Scalarization with Massive Fields. Phys. Rev. D 2016, 93, 064005. [Google Scholar] [CrossRef] [Green Version]
- Yazadjiev, S.S.; Doneva, D.D.; Popchev, D. Slowly rotating neutron stars in scalar-tensor theories with a massive scalar field. Phys. Rev. D 2016, 93, 084038. [Google Scholar] [CrossRef] [Green Version]
- Doneva, D.D.; Yazadjiev, S.S. Rapidly rotating neutron stars with a massive scalar field—structure and universal relations. J. Cosmol. Astropart. Phys. 2016, 11, 019. [Google Scholar] [CrossRef]
- Motahar, Z.A.; Blázquez-Salcedo, J.L.; Doneva, D.D.; Kunz, J.; Yazadjiev, S.S. Axial quasinormal modes of scalarized neutron stars with massive self-interacting scalar field. Phys. Rev. D 2019, 99, 104006. [Google Scholar] [CrossRef] [Green Version]
- Staykov, K.V.; Doneva, D.D.; Yazadjiev, S.S.; Kokkotas, K.D. Slowly rotating neutron and strange stars in R2 gravity. J. Cosmol. Astropart. Phys. 2014, 10, 006. [Google Scholar] [CrossRef] [Green Version]
- Yazadjiev, S.S.; Doneva, D.D.; Kokkotas, K.D. Rapidly rotating neutron stars in R-squared gravity. Phys. Rev. D 2015, 91, 084018. [Google Scholar] [CrossRef] [Green Version]
- Doneva, D.D.; Yazadjiev, S.S.; Kokkotas, K.D. The I-Q relations for rapidly rotating neutron stars in f(R) gravity. Phys. Rev. D 2015, 92, 064015. [Google Scholar] [CrossRef] [Green Version]
- Blázquez-Salcedo, J.L.; Doneva, D.D.; Kunz, J.; Staykov, K.V.; Yazadjiev, S.S. Axial quasinormal modes of neutron stars in R2 gravity. Phys. Rev. D 2018, 98, 104047. [Google Scholar] [CrossRef] [Green Version]
- Blázquez-Salcedo, J.L.; Khoo, F.S.; Kunz, J. Ultra-long-lived quasi-normal modes of neutron stars in massive scalar-tensor gravity. EPL (Europhys. Lett.) 2020, 130, 50002. [Google Scholar] [CrossRef]
- Blázquez-Salcedo, J.L.; Khoo, F.S.; Kunz, J.; Preut, V. Polar Quasinormal Modes of Neutron Stars in Massive Scalar-Tensor Theories. Front. Phys. 2021, 9, 741427. [Google Scholar] [CrossRef]
- Pappas, G.; Apostolatos, T.A. Effectively universal behavior of rotating neutron stars in general relativity makes them even simpler than their Newtonian counterparts. Phys. Rev. Lett. 2014, 112, 121101. [Google Scholar] [CrossRef]
- Chakrabarti, S.; Delsate, T.; Gürlebeck, N.; Steinhoff, J. I-Q relation for rapidly rotating neutron stars. Phys. Rev. Lett. 2014, 112, 201102. [Google Scholar] [CrossRef] [Green Version]
- De Aguiar, B.F.; Mendes, R.F.P. Highly compact neutron stars and screening mechanisms: Equilibrium and stability. Phys. Rev. D 2020, 102, 024064. [Google Scholar] [CrossRef]
- Dima, A.; Bezares, M.; Barausse, E. Dynamical chameleon neutron stars: Stability, radial oscillations, and scalar radiation in spherical symmetry. Phys. Rev. D 2021, 104, 084017. [Google Scholar] [CrossRef]
- Kerr, R.P. Gravitational field of a spinning mass as an example of algebraically special metrics. Phys. Rev. Lett. 1963, 11, 237. [Google Scholar] [CrossRef]
- Teukolsky, S.A. The Kerr Metric. Class. Quant. Grav. 2015, 32, 124006. [Google Scholar] [CrossRef]
- Chrusciel, P.T.; Costa, J.L.; Heusler, M. Stationary Black Holes: Uniqueness and Beyond. Living Rev. Relativ. 2012, 15, 1–73. [Google Scholar] [CrossRef] [Green Version]
- Geroch, R.P. Multipole moments. II. Curved space. J. Math. Phys. 1970, 11, 2580–2588. [Google Scholar] [CrossRef]
- Hansen, R.O. Multipole moments of stationary space-times. J. Math. Phys. 1974, 15, 46–52. [Google Scholar] [CrossRef]
- Bambi, C. Towards the use of the most massive black hole candidates in AGN to test the Kerr paradigm. Phys. Rev. D 2012, 85, 043001. [Google Scholar] [CrossRef] [Green Version]
- Cardoso, V.; Gualtieri, L. Testing the black hole ‘no-hair’ hypothesis. Class. Quant. Grav. 2016, 33, 174001. [Google Scholar] [CrossRef] [Green Version]
- Cardoso, V.; Pani, P. Testing the nature of dark compact objects: A status report. Living Rev. Relativ. 2019, 22, 1–104. [Google Scholar] [CrossRef] [Green Version]
- Bardeen, J.M. Timelike and null geodesics in the Kerr metric. In Black Holes; DeWitt, C., DeWitt, B., Eds.; Gordon and Breach: New York, NY, USA, 1973; p. 215. [Google Scholar]
- Berti, E.; Cardoso, V.; Starinets, A.O. Quasinormal modes of black holes and black branes. Class. Quant. Grav. 2009, 26, 163001. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Zhidenko, A. Quasinormal modes of black holes: From astrophysics to string theory. Rev. Mod. Phys. 2011, 83, 793. [Google Scholar] [CrossRef] [Green Version]
- Volkov, M.S.; Gal’tsov, D.V. Gravitating nonAbelian solitons and black holes with Yang-Mills fields. Phys. Rep. 1999, 319, 1–83. [Google Scholar] [CrossRef] [Green Version]
- Kleihaus, B.; Kunz, J.; Navarro-Lerida, F. Rotating black holes with non-Abelian hair. Class. Quant. Grav. 2016, 33, 234002. [Google Scholar] [CrossRef] [Green Version]
- Herdeiro, C.A.R.; Radu, E. Kerr black holes with scalar hair. Phys. Rev. Lett. 2014, 112, 221101. [Google Scholar] [CrossRef] [Green Version]
- Herdeiro, C.; Radu, E.; Rúnarsson, H. Kerr black holes with Proca hair. Class. Quant. Grav. 2016, 33, 154001. [Google Scholar] [CrossRef] [Green Version]
- Berti, E.; Cardoso, V.; Will, C.M. On gravitational-wave spectroscopy of massive black holes with the space interferometer LISA. Phys. Rev. D 2006, 73, 064030. [Google Scholar] [CrossRef] [Green Version]
- Horndeski, G.W. Second-order scalar-tensor field equations in a four-dimensional space. Int. J. Theor. Phys. 1974, 10, 363–384. [Google Scholar] [CrossRef]
- Kanti, P.; Mavromatos, N.E.; Rizos, J.; Tamvakis, K.; Winstanley, E. Dilatonic Black Holes in Higher Curvature String Gravity. Phys. Rev. D 1996, 54, 5049. [Google Scholar] [CrossRef] [Green Version]
- Torii, T.; Yajima, H.; Maeda, K.I. Dilatonic black holes with Gauss–Bonnet term. Phys. Rev. D 1997, 55, 739. [Google Scholar] [CrossRef] [Green Version]
- Guo, Z.K.; Ohta, N.; Torii, T. Black Holes in the Dilatonic Einstein–Gauss–Bonnet Theory in Various Dimensions. I. Asymptotically Flat Black Holes. Prog. Theor. Phys. 2008, 120, 581–607. [Google Scholar] [CrossRef] [Green Version]
- Kleihaus, B.; Kunz, J.; Radu, E. Rotating Black Holes in Dilatonic Einstein–Gauss–Bonnet Theory. Phys. Rev. Lett. 2011, 106, 151104. [Google Scholar] [CrossRef] [Green Version]
- Kleihaus, B.; Kunz, J.; Mojica, S. Quadrupole Moments of Rapidly Rotating Compact Objects in Dilatonic Einstein–Gauss–Bonnet Theory. Phys. Rev. D 2014, 90, 061501. [Google Scholar] [CrossRef] [Green Version]
- Kleihaus, B.; Kunz, J.; Mojica, S.; Radu, E. Spinning black holes in Einstein–Gauss–Bonnet–dilaton theory: Nonperturbative solutions. Phys. Rev. D 2016, 93, 044047. [Google Scholar] [CrossRef] [Green Version]
- Cunha, P.V.P.; Herdeiro, C.A.R.; Kleihaus, B.; Kunz, J.; Radu, E. Shadows of Einstein–dilaton–Gauss–Bonnet black holes. Phys. Lett. B 2017, 768, 373–379. [Google Scholar] [CrossRef]
- Wald, R.M. Black hole entropy is the Noether charge. Phys. Rev. D 1993, 48, R3427. [Google Scholar] [CrossRef] [Green Version]
- Kanti, P.; Mavromatos, N.E.; Rizos, J.; Tamvakis, K.; Winstanley, E. Dilatonic black holes in higher curvature string gravity. 2: Linear stability. Phys. Rev. D 1998, 57, 6255. [Google Scholar] [CrossRef] [Green Version]
- Pani, P.; Cardoso, V. Are black holes in alternative theories serious astrophysical candidates? The Case for Einstein-Dilaton-Gauss–Bonnet black holes. Phys. Rev. D 2009, 79, 084031. [Google Scholar] [CrossRef] [Green Version]
- Ayzenberg, D.; Yagi, K.; Yunes, N. Linear Stability Analysis of Dynamical Quadratic Gravity. Phys. Rev. D 2014, 89, 044023. [Google Scholar] [CrossRef] [Green Version]
- Blázquez-Salcedo, J.L.; Macedo, C.F.B.; Cardoso, V.; Ferrari, V.; Gualtieri, L.; Khoo, F.S.; Kunz, J.; Pani, P. Perturbed black holes in Einstein-dilaton-Gauss–Bonnet gravity: Stability, ringdown, and gravitational-wave emission. Phys. Rev. D 2016, 94, 104024. [Google Scholar] [CrossRef] [Green Version]
- Blázquez-Salcedo, J.L.; Khoo, F.S.; Kunz, J. Quasinormal modes of Einstein–Gauss–Bonnet-dilaton black holes. Phys. Rev. D 2017, 96, 064008. [Google Scholar] [CrossRef] [Green Version]
- Konoplya, R.A.; Zinhailo, A.F.; Stuchlík, Z. Quasinormal modes, scattering, and Hawking radiation in the vicinity of an Einstein-dilaton-Gauss–Bonnet black hole. Phys. Rev. D 2019, 99, 124042. [Google Scholar] [CrossRef] [Green Version]
- Zinhailo, A.F. Quasinormal modes of Dirac field in the Einstein–Dilaton–Gauss–Bonnet and Einstein–Weyl gravities. Eur. Phys. J. C 2019, 79, 912. [Google Scholar] [CrossRef] [Green Version]
- Pierini, L.; Gualtieri, L. Quasi-normal modes of rotating black holes in Einstein-dilaton Gauss–Bonnet gravity: The first order in rotation. Phys. Rev. D 2021, 103, 124017. [Google Scholar] [CrossRef]
- Shiralilou, B.; Hinderer, T.; Nissanke, S.; Ortiz, N.; Witek, H. Nonlinear curvature effects in gravitational waves from inspiralling black hole binaries. Phys. Rev. D 2021, 103, L121503. [Google Scholar] [CrossRef]
- Shiralilou, B.; Hinderer, T.; Nissanke, S.M.; Ortiz, N.; Witek, H. Post-Newtonian gravitational and scalar waves in scalar-Gauss–Bonnet gravity. Class. Quant. Grav. 2022, 39, 035002. [Google Scholar] [CrossRef]
- Blázquez-Salcedo, J.L.; Doneva, D.D.; Kunz, J.; Yazadjiev, S.S. Radial perturbations of the scalarized Einstein–Gauss–Bonnet black holes. Phys. Rev. D 2018, 98, 084011. [Google Scholar] [CrossRef] [Green Version]
- Blázquez-Salcedo, J.L.; Doneva, D.D.; Kahlen, S.; Kunz, J.; Nedkova, P.; Yazadjiev, S.S. Axial perturbations of the scalarized Einstein–Gauss–Bonnet black holes. Phys. Rev. D 2020, 101, 104006. [Google Scholar] [CrossRef]
- Blázquez-Salcedo, J.L.; Doneva, D.D.; Kahlen, S.; Kunz, J.; Nedkova, P.; Yazadjiev, S.S. Polar quasinormal modes of the scalarized Einstein–Gauss–Bonnet black holes. Phys. Rev. D 2020, 102, 024086. [Google Scholar] [CrossRef]
- Macedo, C.F.B.; Sakstein, J.; Berti, E.; Gualtieri, L.; Silva, H.O.; Sotiriou, T.P. Self-interactions and Spontaneous Black Hole Scalarization. Phys. Rev. D 2019, 99, 104041. [Google Scholar] [CrossRef] [Green Version]
- Cunha, P.V.P.; Herdeiro, C.A.R.; Radu, E. Spontaneously Scalarized Kerr Black Holes in Extended Scalar-Tensor–Gauss–Bonnet Gravity. Phys. Rev. Lett. 2019, 123, 011101. [Google Scholar] [CrossRef] [Green Version]
- Collodel, L.G.; Kleihaus, B.; Kunz, J.; Berti, E. Spinning and excited black holes in Einstein-scalar–Gauss–Bonnet theory. Class. Quant. Grav. 2020, 37, 075018. [Google Scholar] [CrossRef] [Green Version]
- Hod, S. Onset of spontaneous scalarization in spinning Gauss–Bonnet black holes. Phys. Rev. D 2020, 102, 084060. [Google Scholar] [CrossRef]
- Doneva, D.D.; Collodel, L.G.; Krüger, C.J.; Yazadjiev, S.S. Black hole scalarization induced by the spin: 2+1 time evolution. Phys. Rev. D 2020, 102, 104027. [Google Scholar] [CrossRef]
- Herdeiro, C.A.R.; Radu, E.; Silva, H.O.; Sotiriou, T.P.; Yunes, N. Spin-induced scalarized black holes. Phys. Rev. Lett. 2021, 126, 011103. [Google Scholar] [CrossRef]
- Berti, E.; Collodel, L.G.; Kleihaus, B.; Kunz, J. Spin-induced black-hole scalarization in Einstein-scalar–Gauss–Bonnet theory. Phys. Rev. Lett. 2021, 126, 011104. [Google Scholar] [CrossRef]
- Witek, H.; Gualtieri, L.; Pani, P.; Sotiriou, T.P. Black holes and binary mergers in scalar Gauss–Bonnet gravity: Scalar field dynamics. Phys. Rev. D 2019, 99, 064035. [Google Scholar] [CrossRef] [Green Version]
- Witek, H.; Gualtieri, L.; Pani, P. Towards numerical relativity in scalar Gauss–Bonnet gravity: 3+1 decomposition beyond the small-coupling limit. Phys. Rev. D 2020, 101, 124055. [Google Scholar] [CrossRef]
- Kuan, H.J.; Doneva, D.D.; Yazadjiev, S.S. Dynamical formation of scalarized black holes and neutron stars through stellar core collapse. Phys. Rev. Lett. 2021, 127, 161103. [Google Scholar] [CrossRef]
- Silva, H.O.; Witek, H.; Elley, M.; Yunes, N. Dynamical scalarization and descalarization in binary black hole mergers. Phys. Rev. Lett. 2021, 127, 031101. [Google Scholar] [CrossRef]
- Doneva, D.D.; Yazadjiev, S.S. Dynamics of the nonrotating and rotating black hole scalarization. Phys. Rev. D 2021, 103, 064024. [Google Scholar] [CrossRef]
- East, W.E.; Ripley, J.L. Dynamics of spontaneous black hole scalarization and mergers in Einstein-scalar–Gauss–Bonnet gravity. Phys. Rev. Lett. 2021, 127, 101102. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blázquez-Salcedo, J.L.; Kleihaus, B.; Kunz, J. Compact Objects in Alternative Gravities. Universe 2022, 8, 153. https://doi.org/10.3390/universe8030153
Blázquez-Salcedo JL, Kleihaus B, Kunz J. Compact Objects in Alternative Gravities. Universe. 2022; 8(3):153. https://doi.org/10.3390/universe8030153
Chicago/Turabian StyleBlázquez-Salcedo, Jose Luis, Burkhard Kleihaus, and Jutta Kunz. 2022. "Compact Objects in Alternative Gravities" Universe 8, no. 3: 153. https://doi.org/10.3390/universe8030153
APA StyleBlázquez-Salcedo, J. L., Kleihaus, B., & Kunz, J. (2022). Compact Objects in Alternative Gravities. Universe, 8(3), 153. https://doi.org/10.3390/universe8030153





