The Stationary Electric Field in the Heliosphere and Its Possible Relation to Current Sheets

Abstract

The nature of the large-scale electric field in the heliosphere is discussed in this paper. The electric potential along each line of the magnetic field should be constant in the ideally conductive solar wind. A high electric potential is supposed to be maintained by the rapidly flowing solar wind far from the Sun and, near the Sun, by the unipolar effect caused by the rotation of the Sun. Meanwhile, there is a discrepancy between observations and theoretical concepts. The ratio of the observed electric field and that calculated from a model employing the unipolar effect at the Sun was obtained for the 1994–2008 Ulysses data. It was found that the unipolar effect is insufficient to maintain equipotentiality of magnetic field lines throughout the heliosphere, suggesting the existence of additional sources of the electric field at the Sun. Since the strong electric field is stably observed at high heliolatitudes, its previously unknown sources may be associated with polar conic current sheets and current sheets at the edges of coronal holes.

1. Introduction

The existence of the electric field in the heliosphere is determined by many processes and structures with various spatial and temporal scales. The large-scale electric field in the solar wind is created by an inhomogeneous motion of the plasma relative to an observer. Since the conductivity of the solar wind is high, the electric field is equal to zero in the frame of reference in which the considered plasma element is at rest. As a consequence of the Lorentz transformations in the limit of low velocities, an observer motionless relative to the Sun will measure an electric field equal to:

E = −c⁻¹[v, B],

(1)

where v is the solar wind speed and B is the interplanetary magnetic field (IMF). Equation (1) is known as the equation describing the magnetic field frozen into the plasma (the so-called frozen-in equation). It follows from this that even if there are no high-speed processes or spatial inhomogeneities, an unperturbed solar wind will still have a stationary electric field, since there is a velocity and a magnetic field that is not parallel to it [1,2]. Moreover, if the velocity components depend on heliolatitude, the electric field cannot be removed everywhere by a transition to a non-inertial reference frame.

Small-scale fast plasma processes can lead to local variations in the electric field. For example, magnetic reconnection in current sheets can occur at the scale of the ion inertial length (d_i ≈ 100 km at the Earth’s orbit) and be accompanied by an increase in the electric field [3,4,5]. The characteristic reconnection time, in this case, turns out to be in the order of tens of seconds, and depends on the ratio of d_i and the speed of the plasma inflow. In the folds of the large-scale current sheets, such as the heliospheric current sheet (HCS), magnetic islands can form [6];interacting with one another, they can change their size and also merge. Both processes are accompanied by the powerful induction of the electric field due to the magnetic flux changes in the interaction domain [3,4,5,6,7,8,9]. The characteristic scale of the changes in the electric field in such a case is of the order of the magnetic island size, which is from hundreds to thousands of times the ionic Larmor radius r_ci. The variability of the electric field depends on the Alfvén plasma speed. In the vicinity of the HCS, this can occur at a time scale in the order of minutes or hours. Both of these examples are related to small-scale non stationary processes, but some large-scale current sheets can be stationary; they carry a self-consistent electric field, the typical scale of which is close to the layer thickness, which is a few or tens of r_ci [10].

There are other non stationary large-scale sources of the electric field, such as interplanetary coronal mass ejections (ICMEs) and co-rotating interaction regions (CIRs), which cause perturbations in regions larger than 1 AU. The typical time scale of these perturbations depends on the ICME/CIR rate, and usually exceeds a day [6,11]. Meanwhile, there are no systematic observational studies of the quasi-stationary and non stationary electric fields in the heliosphere, and this topic still remains beyond the main scope of space physics investigations.

The observational aspect of this task is very important. Precise values of the electric field in the solar wind can only be obtained from multipoint in situ observations performed by constellation-type spacecraft, while the majority of spacecraft in the solar wind are of the single type. Such spacecraft are equipped with instruments for measuring the IMF and the solar wind speed, enabling estimation of the electric field. There are few examples when the electric field was measured directly with the Cluster and Magnetospheric Multiscale Mission (MMS) satellites [12,13,14]. The process of correct determination of the electric field is very complicated due to the heavy influence of spacecraft rotation on the measurement, the existence of its own electric field, and all kinds of induction and plasma instabilities. Attempts to measure the electric field at a single spacecraft using the potential difference have been unsuccessful. For example, for technical reasons, in the Ulysses case, it was possible to extract the signal from the noise in only a small number of cases [15]. The Cassini spacecraft gave no opportunity to determine which part of the data corresponded to the unperturbed solar wind [16]. Cluster and MMS are able to measure the electric field in the heliosphere for only short periods of time when they leave the magnetosphere [17]. Therefore, the frozen-in Equation (1) may serve to find the electric field from observations using v and B, whilealso taking into account the spacecraft’s velocity. In the abovementioned works, Kellogg et al. [16,17] showed that the electric field in the solar wind can be described using the frozen-in Equation (1).

The latter was expected, because the frozen-in equation corresponds to the application of the ideal one-fluid MHD approximation. For its applicability, it is required that (1) the plasma is collisionless, and (2) the scale of the magnetic field change exceeds d_i and r_ci [18]. Most models from the 1960s and 1970s described the solar wind at scales much larger than d_i and r_ci, but much less than the mean free path of ions; they were based on the application of Equation (1) to the description of axisymmetric MHD equilibria [1,2,19,20,21,22].

Equation (1) implies that the IMF lines are electrically equipotential. This means that a constant electric potential Ψ must be maintained along any line of force—even near the Sun, and at the boundaries of the heliosphere. In the solar wind, the electrical potential depends on speed of the plasma. Meanwhile, at small distances from the Sun’s surface, the solar wind is not yet formed. In the solar turbosphere, the speed of individual streams and perturbations exceeds the average speed of radial expansion of plasma [23,24]. At larger distances (a few solar radii), where the solar wind begins to form, the plasma velocity is low and nearly parallel to the magnetic field [25,26]. Therefore, the conservation of the electric potential in these regions becomes unobvious, despite the applicability of Equation (1). Thus, the electric potential maintained near the Sun is no less than in the solar wind. The question then arises: what is the source of the enhanced electric potential near the Sun? Are there possibly any layers in the corona at which a jump of the potential occurs?

Classical solar wind models ignore these questions because they aim at solving other problems [1,2,19,20,21,22]. These are 1D hydrodynamic or MHD models that demonstrate the impossibility of hydrostatic equilibrium near the Sun, and describe acceleration of the solar wind, the origin of the IMF spiral, and the large-scale structure of the IMF. It is believed that (i) the nature of the electric potential near the Sun is determined by a unipolar effect, and (ii) the rotation of the Sun as a conducting sphere in its own magnetic field is sufficient to explain the observed magnitude of the electric potential without taking into account more complex plasma flows.

Despite the simplicity of this task, the real situation may differ from expectations. It is easy to imagine a situation when the electric field is reinforced due to the impact of its local sources, including strong current sheets and fast solar wind flows/streams (both ICMEs and flows from coronal holes that follow turbulent stream interaction regions (SIRs) and CIRs). In that case, there may be deviations from calculations based on assumptions (i) and (ii).

Most spacecraft measurements are carried out at low heliolatitudes, where the low-speed solar wind dominates during the period of solar minimum to which most of the models mentioned above are applied. Meanwhile, there have not been studies of temporal variations in the heliospheric electric field near the ecliptic plane. As a consequence of Equation (1), the electric field in these regions should not be very strong. Assumptions (i) and (ii) used in earlier works make it possible to estimate the magnitude of the low-latitude electric field by calculating it from available observations, as was done in this work.

Regarding higher heliolatitudes, there have not been systematic studies of the electric field there either. The only spacecraft to orbit through the polar heliosphere was Ulysses, with the help of which it has been found that a faster solar wind is more characteristic ofhigh heliolatitudes than of low ones at the minimum of solar activity. As a consequence, one can expect a strengthening of the electric field during this period (Equation (1)). While the rotation of the Sun maintains the electrical potential at low latitudes, it may be not sufficient to maintain it in the polar solar wind. In this case, assumptions (i) and (ii) are inapplicable to high heliolatitudes, where there should be additional sources of the electric field.

Recently, polar conic current sheets (CCSs) confining huge magnetic tornadoes have been discovered based on Ulysses data [27]. The electric field undergoes strong variations at their boundaries. In addition, accelerated high-energy particles have been detected at their borders and inside CCSs. One can suggest that many CCSs are of solar origin and connected with non stationary processes occurring inside coronal holes. As a rule, such processes are accompanied by an increase in the electric field, which entails an increase in the average electric potential. Because of this, the effective stationary electric potential will also increase. Since the magnetic field lines are equipotential, the electric potential can be amplified away from the Sun as well. The latter can be measured in situ by Ulysses.

This work raises a question concerning the temporal and spatial variability and the nature of the stationary electric field in the heliosphere, as well as the possible impact of large-scale current-carrying structures on its magnitude. Using Ulysses observations, it is shown that it is impossible to explain an observed picture by the unipolar effect caused by the rotation of the Sun. It seems to be insufficient to maintain a constant electric potential along the lines of the interplanetary magnetic field at high heliolatitudes. The role of the unipolar effect in polar conic current sheets in solving this problem is discussed. At low heliolatitudes, the situation is far from predictions, and one may suggest that some screening of the electric field (the sources of which remain unknown) is possible.

2. The Unipolar Effect

Let us recall what the so-called unipolar effect is, and how to apply it to the heliospheric electric field. Conducting plasma rotates with the Sun in its magnetic field. With an increasing distance from the Sun, the angular speed of the plasma decreases, so there will be a difference in angular speed between adjacent layers of plasma. In the limit v/c << 1, the electric field E* in the frame of reference in which one layer is at rest is related to the electric field E in the rest frame of the second layer, according to the following law:

E* = E + c⁻¹[δv, B],

(2)

where δv is the difference in velocity between the layers. Due to the difference in electrical fields, a potential difference arises between the contacting layers. The generation of this potential difference is exactly the unipolar effect. In the case of ideal conductivity, when E* = 0, Equation (2) is reduced to the frozen-in Equation (1). More generally, E* and its associated electric potential are dependent on conduction currents and any other sources.

In axisymmetric self-consistent models [2,22,28], the electric potential is taken into account using the angular speed of Ferraro’s isorotation Ω = cdΨ/dΦ, where Φ is the magnetic flux and Ψ is the electric potential. This means that the potential difference between adjacent flow surfaces and Ω is constant along the magnetic field lines. In all models where it was used, the function Ω was equal to the angular speed of the footpoints of the magnetic field lines at the Sun [2,22,28,29,30]. Other situations were almost never considered, although it is clear from the definition of Ω that they are possible. For example, the potential associated with E* in Equation (2) can be included in the definition of Ω. This makes it possible to take into account the sources of the electric field that are not associated with the motion of an ideally conducting medium. For example, Alfvén [31] was able to account for double layers in the solar atmosphere when describing the heliospheric current circuit (he directly used the electric potentials, not Ω). Another example is that large magnetic vortices are possible in the solar atmosphere—the motion of plasma that resembles terrestrial tornadoes [32,33]. In this case, the plasma’s rotation around the axis of the vortex can be much faster than around the axis of the Sun. Then, the value of Ω along the bundle of magnetic field lines associated with the vortex will be different from the angular velocity of the Sun. The recent discovery of CCSs in the heliosphere makes it relevant to study the electric field in the polar heliosphere [27]. According to the available observations of Ulysses, it can be seen that there is a rotational motion of the plasma in the CCSs. However, according to observations of the Sun, it is difficult to say for certain whether there is a vortex flow in the polar zone that is not associated with the star’s rotation. The estimates of the parameter Ω from the Ulysses observations can serve as an argument in favor of their presence/absence, since Ω provides information about the source of the structure at the Sun.

3. Verification Factors

In order to find out whether the unipolar effect at the Sun is the source of the observed electric field in the heliosphere, we compared the estimates for the electric field in the framework of axisymmetric models E_th and on the basis of observations E_obs.

Let us choose a cylindrical coordinate system (r, φ, z) with it sorigin at the center of the Sun and the z-axis along its rotation axis. Let ω_ʘ be the angular speed of the Sun in the region, where the frozen-in Equation (1) is applicable. Thus, the unipolar electric field caused by the rotation of the Sun is equal to:

E = −c⁻¹[ω_ʘre_φ, B] = (−ω_ʘr B_z/c, 0, ω_ʘr B_r/c),

(3)

where e_φ is the unit vector in the azimuthal direction. If there are no other sources, then the electric field (Equation (3)) determines the potential distribution on the solar surface and, as a consequence, in the entire heliosphere. In this case, the electric potential distribution in the heliosphere follows from Equation (3), taking into account the shape of the magnetic field lines, and cannot be described by Equation (3) directly.

Let us consider the electric field in any axisymmetric ideal MHD models (such as [2,28,34]). We are discussing large-scale stationary electric fields; therefore:

rotE = 0,

whence it follows that:

E = −∇Ψ = −(∂Ψ/∂r, ∂Ψ/r∂φ, ∂Ψ/∂z),

(4)

where Ψ is the electrical potential. The magnetic field is divergence-free:

divB = 0.

(5)

Let us assume the presence of axial symmetry, i.e., ∂/∂φ = 0. Thus, E_φ = 0. In the presence of axial symmetry, any magnetic field of the following form satisfies Equation (5):

B = (−∂Φ/r∂z, B_φ, ∂Φ/r∂r),

(6)

where Φ is the magnetic flux between the north pole and the considered surface of rotation of the lines of force, divided by 2π. The equalities Φ = const set the lines of force of the poloidal component of the magnetic field. The frozen-in Equation (1):

E + c⁻¹[v, B] = 0,

yields that the magnetic field lines are equipotential. In the case of axial symmetry, this means that the electric potential is a single-valued function of the magnetic flux Ψ(Φ). From this, and from Equations (4) and (6), it follows that:

E = −(dΨ/dΦ)∇Φ = (−Ω r B_z/c, 0, Ω r B_r/c),
E = Ω r B_p/c,

(7)

where:

Ω = c dΨ/dΦ

is the angular speed of Ferraro’s isorotation, B_p is the modulus of the poloidal component of the magnetic field, and E is the modulus of the electric field.

Comparing the unipolar electric field near the Sun (Equation (3)) and the expression for the axisymmetric electric field (Equation (7)), it can be noted that in the case of the unipolar effect:

Ω = ω_ʘ,

(8)

where ω_ʘ is the angular speed of the Sun. Therefore, Ω is considered to be equal to the angular speed of the footpoints of the magnetic field lines at the Sun, in the photosphere, or at the source surface [2,22,28,29]. The dependence of ω_ʘ on latitude can be taken into account [30,35,36]; however, latitudinal variations in ω_ʘ are small (less than 20–30%) [37,38].

According to Equations (7) and(8), the final theoretical estimate of the modulus of the electric field is as follows:

E_th = Ω r B_p/c = ω_ʘr B_p/c.

(9)

Based on observations, the modulus of the electric field can be estimated using the frozen-in Equation (1). In other words:

E_obs = c⁻¹vB sinα,

(10)

where α is the angle between IMF and the solar wind velocity. Let the unipolar coefficient be:

k = E_obs/E_th.

(11)

Then, from Equations (9)–(11), we get:

k = (v/ω_ʘr) (B|sinα|/B_p) = (Ω_obs/ω_ʘ)(B|sinα|/B_p),

(12)

where Ω_obs = v/r is the estimation of the angular speed of Ferraro’s isorotation based on the modulus of the solar wind speed derived from observations. The introduced coefficient k in Equation (12) consists of two factors: The factor Ω_obs/ω_ʘ describes to what extent the real mechanisms more efficiently generate the electric field in the considered region in comparison with the unipolar effect from the rotation of the Sun as a whole. The factor:

Γ = B|sinα|/B_p

(13)

is a geometric factor; it takes into account how the azimuthal magnetic field component and plasma flow across the IMF lines affect the unipolar coefficient. We can also interpret Equation (13) as the influence of the direction of the magnetic field and velocity on the value of k. We emphasize that we are talking about real flows; any parameters in Equations (12) and (13) can be determined from observations.

The observational estimate of the angular speed of Ferraro’s isorotation Ω_obs is not equal to the local angular speed v_φ/r of the plasma even in the axisymmetric model (in other words, if we take the results of the same model instead of observational data). Since the speed in the models depends on the boundary conditions, the ratio can assume various values, but it turns out to be equal to 1/Γ if the unipolar effect is the electric field source. When using any observations, Ω_obs/ω_ʘ ≠ 1/Γ. Therefore, when checking real sources of the electric field, it is convenient to precisely consider coefficient k, but not its parts.

The geometric factor Γ should be close to 1 in both models and observations. Indeed, Bsinα is the magnetic field’s magnitude across the velocity. In the solar wind, for the most part, the velocity is directed radially. In this case, B_r >> B_z, on the Earth’s orbit B_r ~ B_φ, according to observations and models [2,39,40,41]. Therefore, B sinα ≈ B_φ. Then, for B_p ≈ B_r, it will turn out that Γ ≈ 1. Γ may differ significantly from 1 far from the Earth’s orbit. Observations may show k >> 1 or k << 1. If a strong deviation of k from 1 is caused by the value of Γ—i.e., Γ << 1 or Γ >> 1—then it can be explained by the local complication of the structure of the magnetic field and plasma flow (moreover, Γ >> 1 does not look like a typical unperturbed solar wind in observations);hence, one cannot say anythingdefinite about the sources on the Sun. Therefore, one should consider the value of Γ.

Strong variations in Γ can occur with the entanglement of magnetic field lines—especially with three-dimensional reconnection [5], and in current sheets. As is known, the rotation of the magnetic field relative to the velocity direction is one of the observational signs of current sheets in the solar wind. In current sheets, the quantity |sinα| can approach 1 [6], leading to an increase in Γ. From the theoretical point of view, near the neutral lines of IMF there can be zones where the curvature radius of the magnetic field lines is comparable to the Larmor radius. Plasma demagnetization occurs in these regions and, as a consequence, the separation of particles from the magnetic field lines [42,43]. Large-scale current sheets are connected with magnetic neutral lines at the Sun. Conditions for magnetic reconnection and nonstationary processes often arise near them [6]. As a consequence, the function Ω can grow near the neutral lines. Thus, an increase in the parameter k can be a sign of a large-scale current sheet.

Equations (11)–(13) can be used in two ways: The first is to use only observational data in calculating both E_obs and E_th, as shown below. The second way is to substitute the results of calculations for any model as E_th,without involving observations (in this case, Equations (12) and(13) are inapplicable). In the first method, the discrepancies between k and 1 can be explained by both unknown sources of the electric field on the Sun and model errors in determining the direction of the magnetic field and velocity. The latter takes place if the difference between k and 1 is due to the fact that Γ ≠ 1. In the second method, one can only find the reason why k ≠ 1 with the help of additional analysis of the model.

4. Unipolar Coefficient and Geometric Factor according to Ulysses Data. Dependence of the Electric Field on the Phase of the 11-Year Cycle of Solar Activity

One of the achievements of the Ulysses mission is the detection of the latitudinal dependence of solar wind speed. A fast wind with v ~ 450–900 km/s dominates in the minimum solar activity at high latitudes; a slow solar wind with speeds of 300–450 km/s dominates at low latitudes. At the maximum solar activity, the difference between latitudes is partially smoothed out, and outliers of a different nature appear. Since the unipolar coefficient depends on the speed (Equation (12)), it can differ for the polar and equatorial solar winds, as well as for different phases of solar activity.

Working with Ulysses data is not an easy task. The spacecraft visited different latitudes, longitudes, and distances from the Sun, and performed measurements over parts of two minima and a full maximum of solar activity. When analyzing changes in solar wind parameters, it is necessary to take into account the influence of all of the above factors. For example, it would be incorrect to take the Ulysses data, plot the speed or magnetic field versus latitude, and from this immediately draw a conclusion about how the measured value depends on latitude θ—it also depends on the heliocentric distance R, azimuthal angle φ, and time t (not only on θ).

Strictly speaking, we cannot accurately draw conclusions about the structure of the IMF and solar wind based only on the Ulysses measurements, since the heliosphere is three-dimensional and evolving with time, and the trajectory of the spacecraft is a line. However, there are no other extensive in situ data outside the ecliptic plane. The fact is often applied that not all variables in the quartet (R, θ, φ, t) are of equal significance. For example, the dependence of IMF on φ is caused by inhomogeneities at the Sun and its rotation. When it comes to large-scale IMF or solar wind speed, the ultimate goal of many studies is the regularity that is valid for times in the order of a month or more. During this time, the spacecraft travels a distance of ~1 AU, while the Sun makes at least one rotation around its axis. Therefore, inhomogeneities associated with the axial asymmetry of the speed and magnetic field of the star become unimportant. At such time scales, the measurements of the spacecraft at the point (R, θ, t) can be considered typical for all φ.

Thus, the dependence on φ can be excluded from consideration. The time dependence of t remains, since conditions in the heliosphere change throughout the solar cycle; to exclude it, the periods of minima and maxima can be considered separately. In this case, the dependence on (R, θ) characterizes the structure of the solar wind typical for a given minimum or maximum. Note that the dependences on (R, θ) obtained from observations may not correspond to axisymmetric stationary models. For example, the presence of a long-lived co-rotating interaction region can lead to an increase in the solar wind speed at low and middle latitudes, as can be seen in the v(R, θ) dependence.

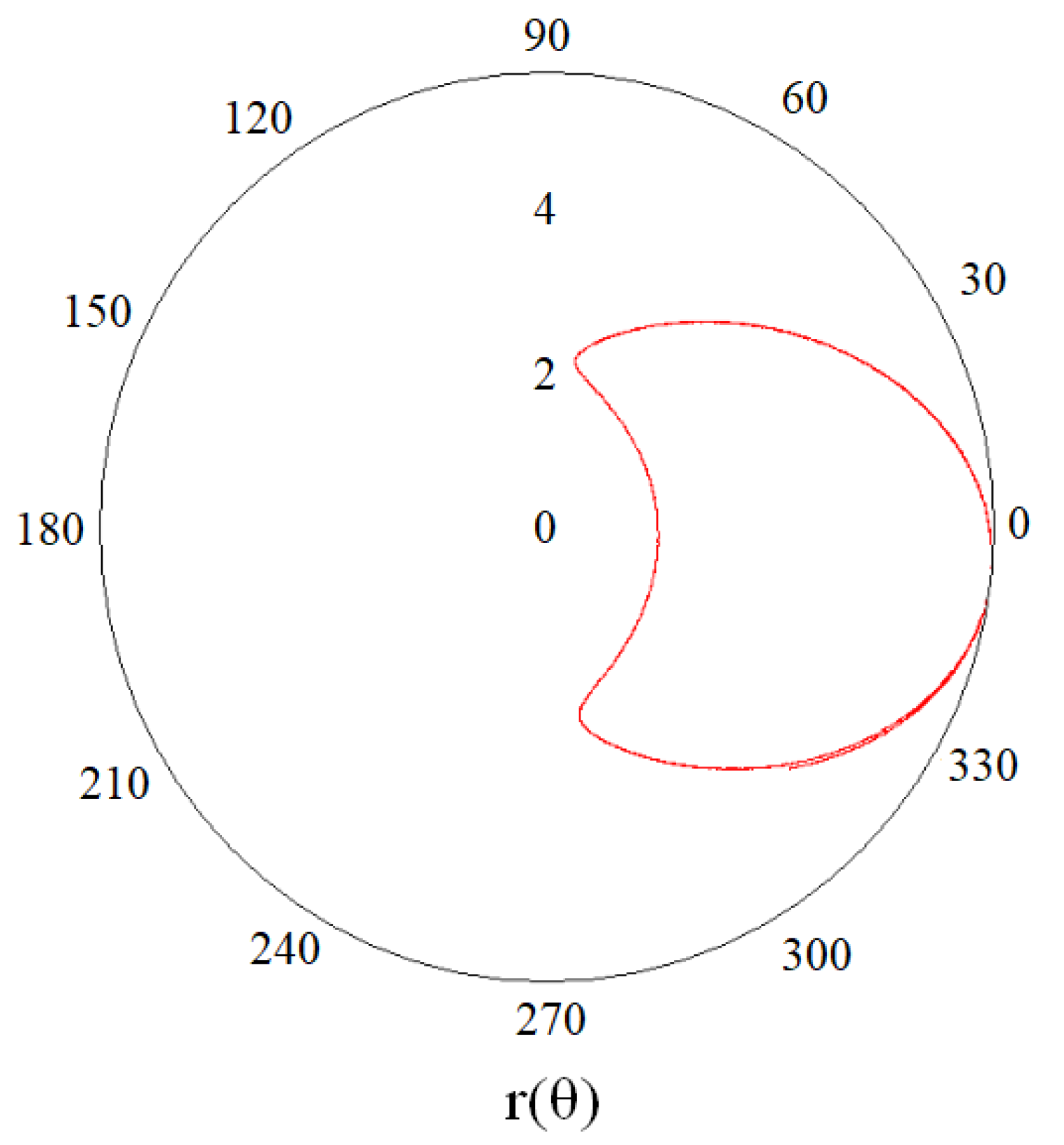
Acting in the way described above, we considered the dependences of the verification factors on two variables: (R, θ), as in Figure 1, and (r, z) for all of the others. We used daily averaged Ulysses data for the years 1994–2008—5479 points altogether (with the addition of 1 January 2009). The data are in the public domain: https://cdaweb.gsfc.nasa.gov/istp_public/ (accessed on 19 January 2022). To visualize the verification factors as functions of (r, z), we considered them along the spacecraft’s trajectory in the variables (r, z), as shown in Figure 1. The trajectory resembles a cat’s face with ears. The “ears” correspond to the maximum latitudes that the spacecraft reached; the “crown” and “chin” correspond to the intersections of the equator near and far from the Sun, respectively, while the cat’s “cheeks” correspond to mid-latitudes far from the star. Note that the axis of symmetry of the trajectory deviates slightly from the equator.

We did not only use graphs for analysis.

Table 1. Cases of large and small values of the parameters k and Γ for various time intervals.

№	Time Period, dd.mm.yy	Days	k > 2	Γ > 2	k < 0.5	Γ < 0.5	k > 5	Γ > 5
1	01.01.1994–01.01.2009	5479	2187 (39.9%)	3350 (61.1%)	894 (16.3%)	49 (0.9%)	746 (13.6%)	746 (13.6%)
2	01.01.1994–31.12.1994	365	301 (82.5%)	168 (46%)	0	0	122 (33.4%)	3 (0.8%)
3	01.01.1995–31.12.1995	365	309 (84.7%)	136 (37.3%)	0	0	115 (31.5%)	12 (3.3%)
4	01.01.2007–31.12.2007	365	319 (87.4%)	202 (55.3%)	1 (0.3%)	0	150 (41.1%)	22 (6%)
5	01.01.2008–31.12.2008	366	219 (59.8%)	210 (57.4%)	11 (3%)	13 (3.6%)	104 (28.4%)	22 (6%)
6	01.01.1994–26.10.1997	1394	747 (53.6%)	811 (58.2%)	121 (8.7%)	6 (0.4%)	247 (17.7%)	137 (9.8%)
7	20.04.2005–01.01.2009	1350	780 (57.8%)	809 (59.9%)	100 (7.4%)	15 (1.1%)	300 (22.2%)	123 (9.1%)
8	27.10.1997–19.04.2005	2732	660 (24.2%)	1730 (63.3%)	673 (24.6%)	28 (1%)	199 (7.3%)	486 (17.8%)
9	06.07.1994–03.12.1994	151	151 (100%)	53 (35.3%)	0	0	106 (70.2%)	1 (0.7%)
10	27.05.1995–17.11.1995	176	175 (99.4%)	74 (42.3%)	0	0	103 (58.5%)	0
11	30.10.2006–24.04.2007	176	176 (100%)	95 (54.3%)	0	0	119 (67.6%)	4 (2.3%)
12	09.11.2007–04.05.2008	176	176 (100%)	114 (65.1%)	0	0	127 (72.2%)	5 (2.9%)
13	03.09.2000–30.01.2001	151	123 (81.5%)	74 (49.3%)	0	2 (1.3%)	41 (27.2%)	20 (13.3%)
14	18.08.2001–15.01.2002	151	144 (95.4%)	67 (44.7%)	0	1 (0.7%)	94 (62.3%)	6 (4%)
15	intervals № 9–14	981	944 (96.2%)	477 (48.9%)	0	3 (0.3%)	590 (60.1%)	36 (3.7%)

shows how many times the verification factors took on values greater than or less than a certain quantity. We counted the number of cases when k > 2, k < 0.5, k > 5, and Γ > 2, Γ< 0.5, and Γ < 5. The numbers 2, 0.5, and 5 were chosen in order to qualitatively divide the large, small, and very large values of the parameters in the graphs below. These values are of interest, since significant deviations of k from 1 can be associated with unknown sources of electric potential and electric field. The values k > 5 turned out to be typical for polar passages of Ulysses; therefore, they are considered separately. Each line of Table 1 corresponds to a certain time interval. The intervals considered may overlap. Their choice was dictated by the presence of features in the values of k, Γ, which can be seen in the summary figures for all analyzed years.

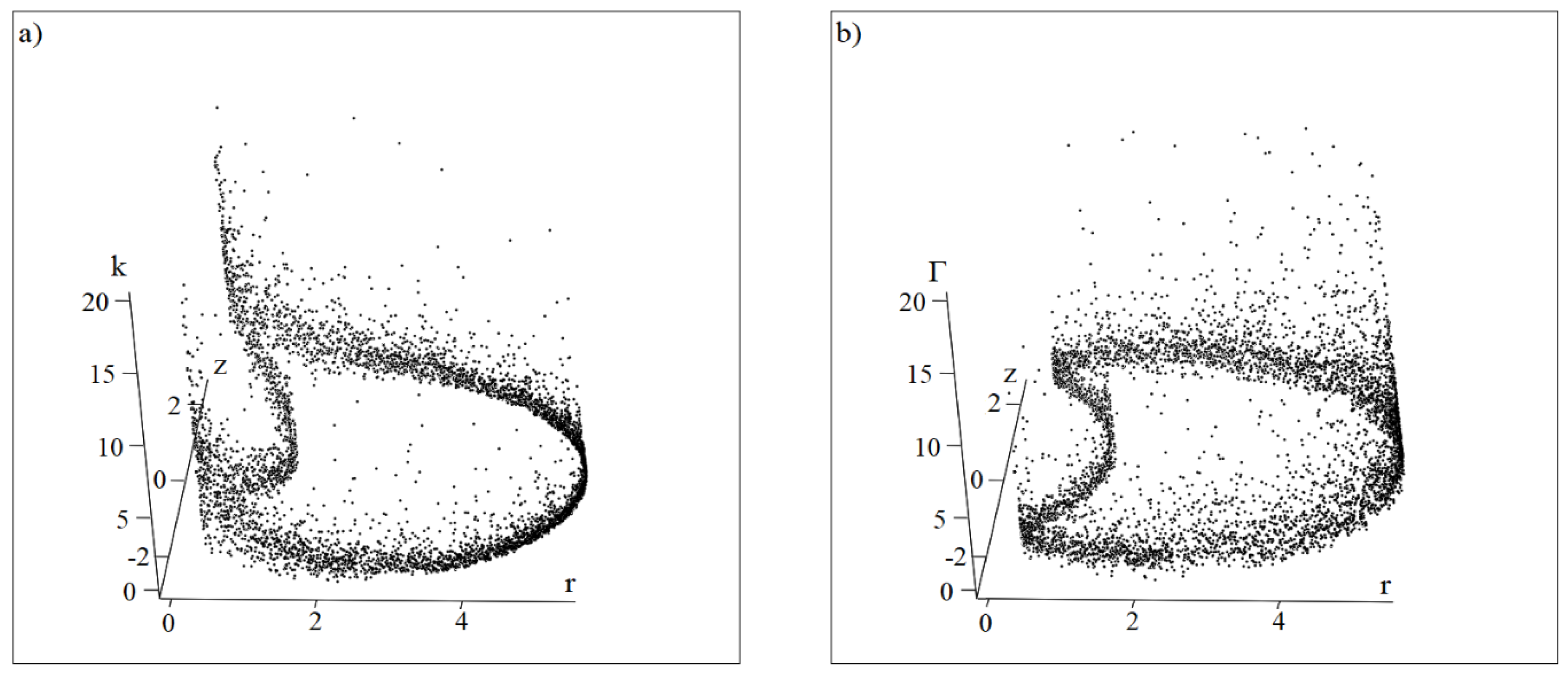
Figure 2 shows the dependences of the unipolar coefficient k (Figure 2a) and the geometric factor Γ (Figure 2b) for all (r, z) visited by Ulysses from 1 January 1994 to 1 January 2009, for a total of 5479 days. The parameters k and Γ were calculated using Equations (12) and (13). All values in them, except for the angular speed of the Sun, are taken from the observations of Ulysses. Figure 2a shows that the unipolar coefficient k reaches its maximum values in the parts of the trajectory corresponding to high latitudes. Here, typical values of k exceed 5 (>50% cases); individual outliers of k reach 10–20. In the region in which Ulysses passed closest to the star, the values of k are diverse, but rarely exceed 5. For large distances from the Sun, values of k in the order of 1 are typical, and cases where k < 1 are common. Individual outliers exceeding 5 are noticeable. It follows from Figure 2a that there are many points at which k differs markedly from 1. Therefore, situations where the unipolar effect does not provide a sufficiently high electric potential on the magnetic field lines may not be isolated in such cases.

Figure 2b depicts the dependence of the geometric factor Γ according to the data from 1 January 1994 to 1 January 2009. The first thing that catches the eye when comparing Figure 2a, b is their opposite nature. In Figure 2b, there are no multipoint peaks at high latitudes. The geometric factor is slightly higher at low latitudes near the Sun, and experiences strong variations with frequent outliers far from the Sun. In this case, Γ is slightly larger than 2 almost everywhere (see Table 1, line 1). Therefore, the increase in k in the polar zones is not related to the geometric factor, i.e., the reason is precisely the insufficiency of the unipolar effect at the Sun. A large number of outliers of Γ at large distances indicates the complication of the IMF structure with increasing r, since outliers occur at all latitudes. Note that the cases Γ >> 1 are grouped in Figure 2b in the form of peculiar columns. Since Γ does not depend on the velocity modulus, they can be associated with the presence of large-scale magnetic structures.

Cases of an increase in Γ at large distances from the Sun can be associated with at least two reasons: The first reason is the increase in the ratio of B_φ/B_p because of the existence of the Parker spiral [1]. The second reason is the possible presence of large-scale magnetic structures, whichcan be associated with large-scale turbulence and remnants of SIRs/CIRs and ICMEs [6,44,45,46,47].

The values of k and Γ for the years 1994–2008 are given in Table 1, line 1. It can be seen that the cases of k close to 1 and k > 2 are equally widespread. Among the latter, about one-third are k > 5. For the geometric factor, days with Γ > 2 dominate. However, near the Sun and in the polar zones, the percentage of cases is different. In the years 1994, 1995, 2007, and 2008 (lines 2–5 of Table 1), the spacecraft was near the Sun at a minimum of activity. In these years, small k values are almost absent and k > 2 dominates. Moreover, the share of days with the values k > 5 is above the average for all years. The cases Γ > 2 are as common as k > 2; however, among them, there are very few Γ > 5. Thus, the events of k > 5 cannot be explained by the increase in Γ; that is, they are not related to the geometry of the magnetic field and the angle between the magnetic field and velocity, and probably depend on the presence of unknown sources on the Sun.

Let us pay attention to the considerable number of cases of k < 0.5 (16.3%) with a negligible proportion of Γ < 0.5 (0.9%, Table 1, line 1). Thus, the situations where k < 0.5 are not connected with the specific features of the magnetic field geometry. It follows from this that there is an unknown process that leads to the screening of the electric field caused by the unipolar effect.

The year 2008 differs from other flights by the greater proportion of time away from the Sun, and by the presence of hardware interference in the last months of the Ulysses mission. Note that the numbers of k and Γ values exceeding 5 for 1994–2008 (Table 1, line 1) coincide accidentally; this can be seen from the discrepancies in the other lines of Table 1.

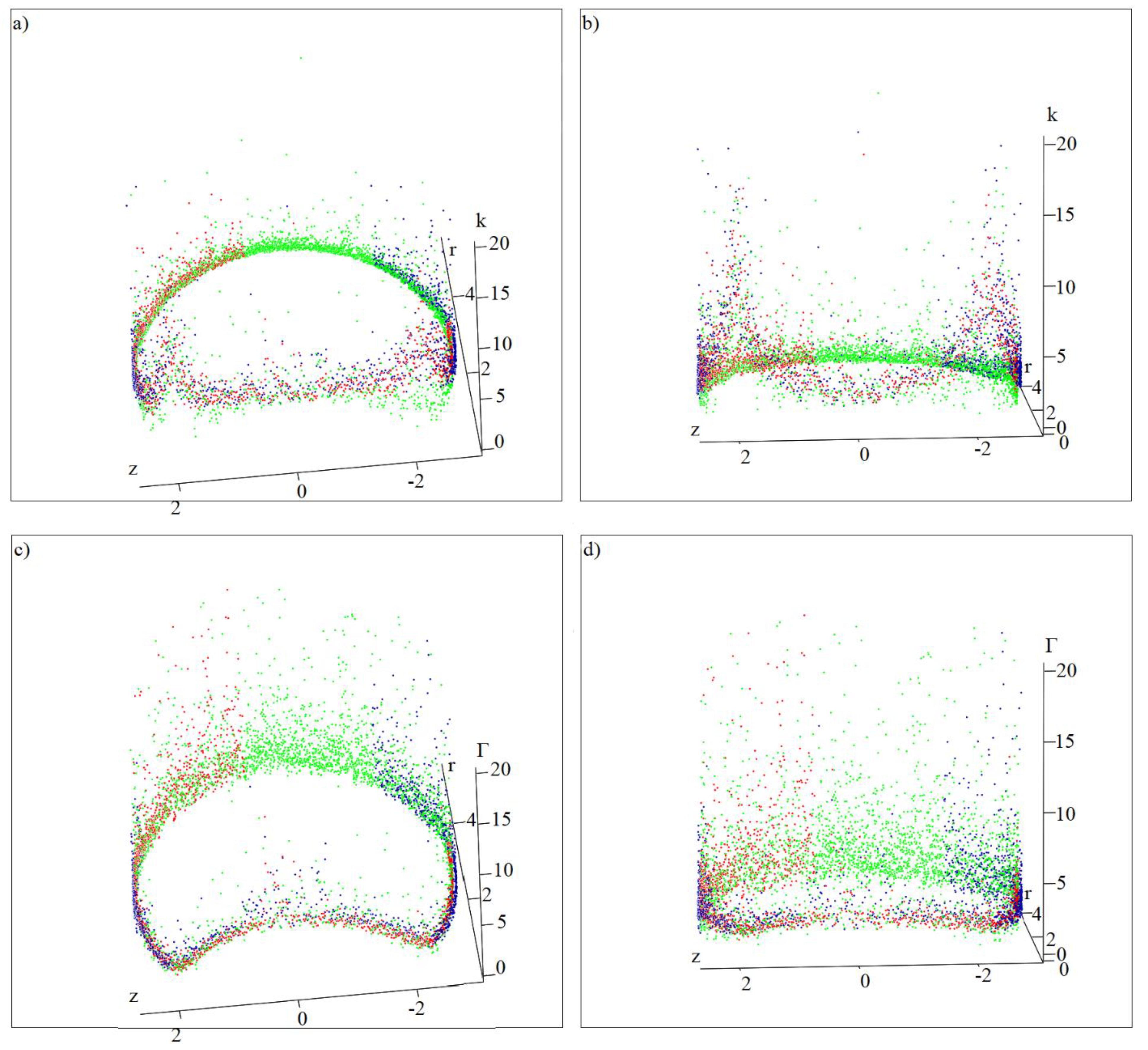
The coefficients in Figure 2 are for a 15-year period, and may have been influenced by solar activity. Information on the course of the solar cycle can be found in a number of publications [48,49]. Figure 3 shows the parameters k and Γ, found on the basis of Ulysses data for three time intervals. The data that include part of the minimum solar activity from 1 January 1994 to 26 October 1997 (also Table 1, line 6) are highlighted in red; the beginning of the solar activity minimum, from 20 April 2005 to 31 December 2008 (also Table 1, line 7), is in blue. The green color marks the interval, including the maximum of solar activity from 27 October 1997 to 19 April 2005 (also Table 1, line 8). The total duration of the first two intervals is close to the duration of the third. Figure 3a, b show the values of the unipolar coefficient for different angles of rotation of the axes in relation to the reader. It can be seen that the k peaks in the northern and southern polar regions differ for all phases of activity, indicating a north–south asymmetry. There is abundant observational evidence for the existence of asymmetry [50,51,52,53]; when simulated, it arises as a consequence of the non-dipole harmonics of the solar magnetic field [35,36,54,55]. Therefore, the north–south asymmetry is unlikely to be related to the inclination of Ulysses’ orbit. Far from the Sun, the behavior of k is approximately the same as near the minimum of solar activity and near the maximum of solar activity. In the sum over all latitudes, the values of k > 2 are found near the minimum of solar activity more often than near the maximum. In this case, k < 0.5 is observed near the maximum of solar activity several times more often than near the minimum of solar activity (see Table 1, lines 6–8); that is, near the maximum of solar activity, screening of the unipolar electric potential is observed relatively often. Moreover, near the maximum of solar activity, the strengthening of the unipolar electric potential and field occurs no more often than screening. Up to 50% of the days of the interval 27.10.1997–19.04.2005 near the maximum of solar activity correspond to 0.5 < k < 2, i.e., to the cases where the unipolar effect can provide the equipotentiality of the lines. At the intervals near the minima of solar activity, ~50% of the time is days when k > 2, i.e., the unipolar electric potential is possibly increased due to unknown sources.

Since the parameter k is proportional to the solar wind speed, the observed discrepancies between the solar minima and solar maxima can be explained by the influence of stream interaction regions (SIRs), which are greater in the solar minimum than in the solar maximum [6]. Data for two solar minima and one solar maximum are shown in Table 1, lines 6–8, and are consistent with visual analysis.

Figure 3c,d are similar to Figure 3a,b, but they show the geometric factor Γ. It can be seen that the scatter of the values of Γ far from the Sun is greater than near the Sun. Moreover, near the Sun it is greater at low latitudes than at high latitudes. Extreme cases of Γ > 5 occur at the maximum of solar activity almost twice as often as at the minimum of solar activity. The visual analysis is supported by the data in Table 1 for solar minima and maxima (lines 6–8); thus, the dependence of k and Γ on the cycle phase is opposite. This can be explained by the fact that Γ characterizes the complexity of the magnetic field structure, which increases during the years of maximum solar activity. The value of k decreases at the maximum of solar activity due to a decrease in the SIR number and a decrease in speed at high and middle latitudes. At the same time, ICMEs often occur at the maximum solar activity, but they do not have a permanent source at the Sun and, therefore, do not contribute more to speed than SIRs [6]; therefore, they do not have a decisive influence on k.

As we mentioned, growth of k and Γ in current sheets is possible. In the study [27], it was shown that at the minimum of solar activity, Ulysses crossed the CCS, flying over the South Pole region of the Sun in 1994 and 2007. An increase in the electric field was observed at the edges of the current sheets. Therefore, it is interesting to consider k and Γ only in the high-latitude parts of the trajectory. In total, Ulysses flew six times in the polar zone above ±60°. The data are shown in lines 9–15 of Table 1, showing that the unipolar coefficient is always greater than 2 at high latitudes at the minimum (678 days out of 679). Moreover, the cases of k > 5 exceed 50%. At the same time, the share of Γ > 2 rarely exceeds 50%, whereas the number of cases of Γ > 5 does not exceed a few percent.

This means that in order to explain the effect, it is necessary to recognize the existence of unknown sources of the electric field and potential at high latitudes of the Sun. Unlike low latitudes, at high latitudes there is no screening of the unipolar electric potential. The difference between the northern and southern passages at the maximum solar activity is also noticeable—this difference is especially significant when comparing k > 5 and Γ > 5 (Table 1, lines 13, 14). This can be explained by the north–south asymmetry caused by the Sun’s non-dipole magnetic field, although the exact reasons for the discovered difference are worthy of a separate study. In general, it can be seen that most of the extreme values of k > 5 correspond to high latitudes (590 cases out of 746, 79%; Table 1, line 15).

There are clear discrepancies between the values of the parameter Γ in lines 9–10 and lines 11–12 of the Table 1.This can be explained by the fact that the magnetic field could be rather more twisted and have relatively stronger meridional components in the latter two periods than in the first two.

Let us consider in more detail the cases of passing across the polar conic current sheets from [27]. To do this, we move on to the Ulysses hourly data, because IMF signatures of CCSs can be unclear if one analyzes the low-resolution data only [27]. The parameters k and Γ in the hourly data are characterized by significant discrepancies between adjacent points. However, the k/Γ ratio does not have this shortcoming, since it depends only on the speed of the solar wind and the spacecraft coordinates. The parameter k/Γ is convenient for studying polar conic current sheets, since they are located at the edges of regions with sharp dips in the solar wind speed corresponding to the axis of the cone or cylinder carrying the current [27]. According to (12), k/Γ = Ω_obs/ω_ʘ, where Ω_obs is the observational estimate of the angular speed of Ferraro’s isorotation. If Γ ~ 1, then k/Γ shows how many times faster the Sun should rotate in order to ensure the equipotentiality of the IMF lines using the unipolar effect. As follows from Table 1 (lines 9–14) and Figure 2b and Figure 3c,d, the typical value of Γ in the polar regions lies between 1 and 2. Therefore, the proposed interpretation of k/Γ is suitable for qualitative explanation.

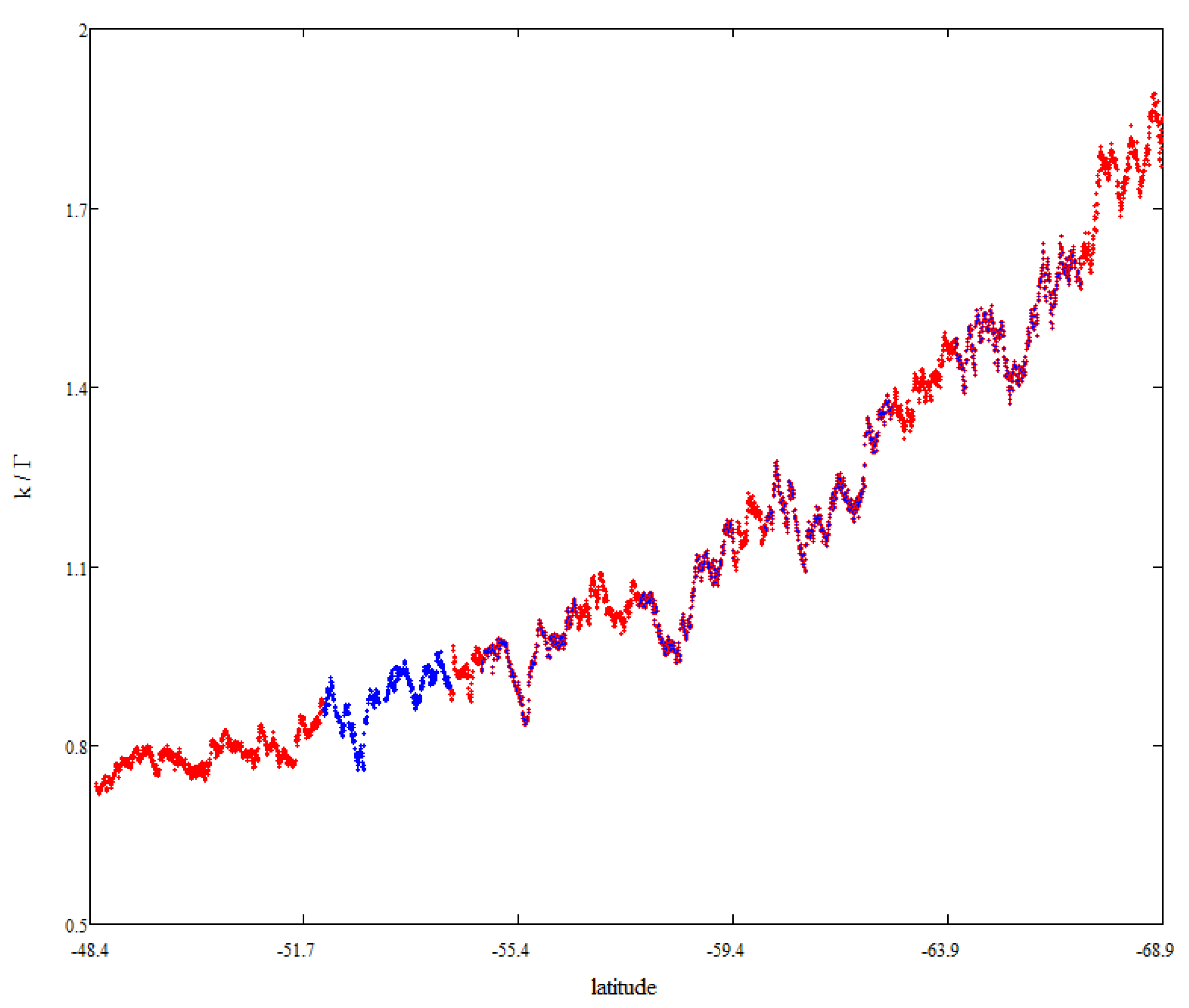
Figure 4 shows the values of the ratio k/Γ in the first 170 days of the year 1994, and the heliolatitudes are indicated. In this time period, Ulysses was in the south polar heliosphere, and made the first five crossings of the regions containing polar conic current sheets (CCSs);in the figure, these are shown in blue, in agreement with the work of [27]. The first crossing of the polar conic current sheet occurred near the edge of the coronal hole; in Figure 4, it is marked with intense blue. The rest of the current sheets were discovered inside the high-speed stream from the coronal hole. Note that the probable reason for the recurrence of regions with polar conic current sheets is their co-rotation with the Sun and a smooth change in the latitude of Ulysses. Moreover, the zone with polar conic current sheets is not the only one (current sheets were also observed at higher latitudes). The rotation hypothesis is supported by the repeatability of the structure shape at time intervals close to the solar rotation [27].

Figure 4 shows that the regions with polar conic current sheets can be located by sharp dips in the values of k/Γ. In other words, polar conic current sheets can be identified by the variations ink/Γ. At the same time, there is no unambiguous relationship between the value of k/Γ and the presence of polar conic current sheets, since the average values of k/Γ at the edges of regions with polar conic current sheets follow the general trend. Thus, in order to detect polar conic current sheets, variations in the value of k/Γ are important, but not the value itself. The latter is determined by the parameters of the surrounding plasma, in which the polar conic current sheets are located. It follows from this that high values of k (for Γ ~ 1–2) inside flows from polar coronal holes are a consequence of processes at the base of coronal holes of the Sun, and not a consequence of the existence of conic current sheets and their sources.

Note that k/Γ ~ 1–2 in Figure 4. Since polar conic current sheets can lie at high heliolatitudes, where this ratio is much higher (see Figure 5), k/Γ ≈ 1 is not a sign of them. However, the zone of k/Γ ≈ 1 is interesting in itself, since it approximately corresponds to the boundary of the coronal hole, and in it the values of k are determined by the magnitude of the geometric factor Γ. In other words, in this zone, the discrepancies between the estimates of the electric field from theory and from observations can be explained by the complexity of the shape of the IMF lines. At the same time, it remains true that polar conic current sheets are connected with solar sources, since (1) a sign of polar conic current sheets is variations in the value of k/Γ, independent of Γ, and (2) it is not possible to detect polar conic current sheets by the value of Γ.

5. Conclusions and Discussion

Temporal and spatial variations in the stationary large-scale electric field in the solar wind were analyzed using the data from the Ulysses spacecraft for 1994–2008. Estimates of the electric field values derived from the observations were compared with the predictions of ideal axisymmetric models that take into account the unipolar effect on the Sun. Possible explanations of mismatches between model expectations and observations, as well as a possible connection between polar electric fields and conic current sheets, were discussed. The question was raised as to the nature of the electric field in the heliosphere and the ways of maintaining a constant electric potential along the IMF lines. The following results were obtained:

• There are regions in the heliosphere in which the magnitude of the electric field computed from the Ulysses spacecraft data cannot be explained by the unipolar effect at the Sun. A quantitative measure of the difference between observations and theory is the unipolar coefficient k = E_obs/E_th, where E_obs is the estimate of the electric field modulus from observations and E_th is the estimate of the electric field modulus according to the Equation (11). It was shown that E_obs significantly exceeded E_th for half of the Ulysses observations from1994–2008;
• It was shown that the discrepancies found between the theory and observations can be explained by the presence of unknown sources of the electric field at the Sun, but not by errors in theoretical estimates of the direction of the magnetic field and the solar wind speed. The unknown sources can both enhance the electric field and weaken it in comparison with model estimates; in the latter case, one can talk about the screening of the unipolar electric field;
• High heliolatitudes are characterized by observations of the strongly enhanced electric field above the predicted level in almost 100% of cases. To generate it only with the help of the unipolar effect, the Sun would have to rotate several times faster than in reality;
• A north–south asymmetry and dependence on the solar activity cycle can be seen in the spatial distribution of the unipolar coefficient. Therefore, the sources of the electric field at the Sun can also be located asymmetrically, and depend on the solar cycle phase;
• The shielding of the unipolar electric field occurs mainly away from the solar minima, at low heliolatitudes;
• The ratio of the unipolar coefficient (Equation (12)) and the geometric factor (Equation (13)) can be used to identify polar conic current sheets [27]. Most of the known polar conic current sheets lie in a specific zone within the coronal hole boundaries, in which k/Γ ≈ 1, and the rate of the electromagnetic energy transfer is equal to the solar wind speed;
• Variations in the unipolar coefficient far from the Sun (beyond Mars’ orbit) are determined by the variations in the geometric factor (Equation (13)), which may indicate that the interplanetary magnetic field structure becomes more and more complex with increasing heliocentric distance.

It was found that the electric field calculated from in situ observations of the magnetic field and the solar wind speed cannot be explained only by the unipolar effect at the Sun. It was possible to find this by analyzing variations in the unipolar coefficient (Equation (12)) and the geometric factor (Equation (13)) at different points of Ulysses’ trajectory.

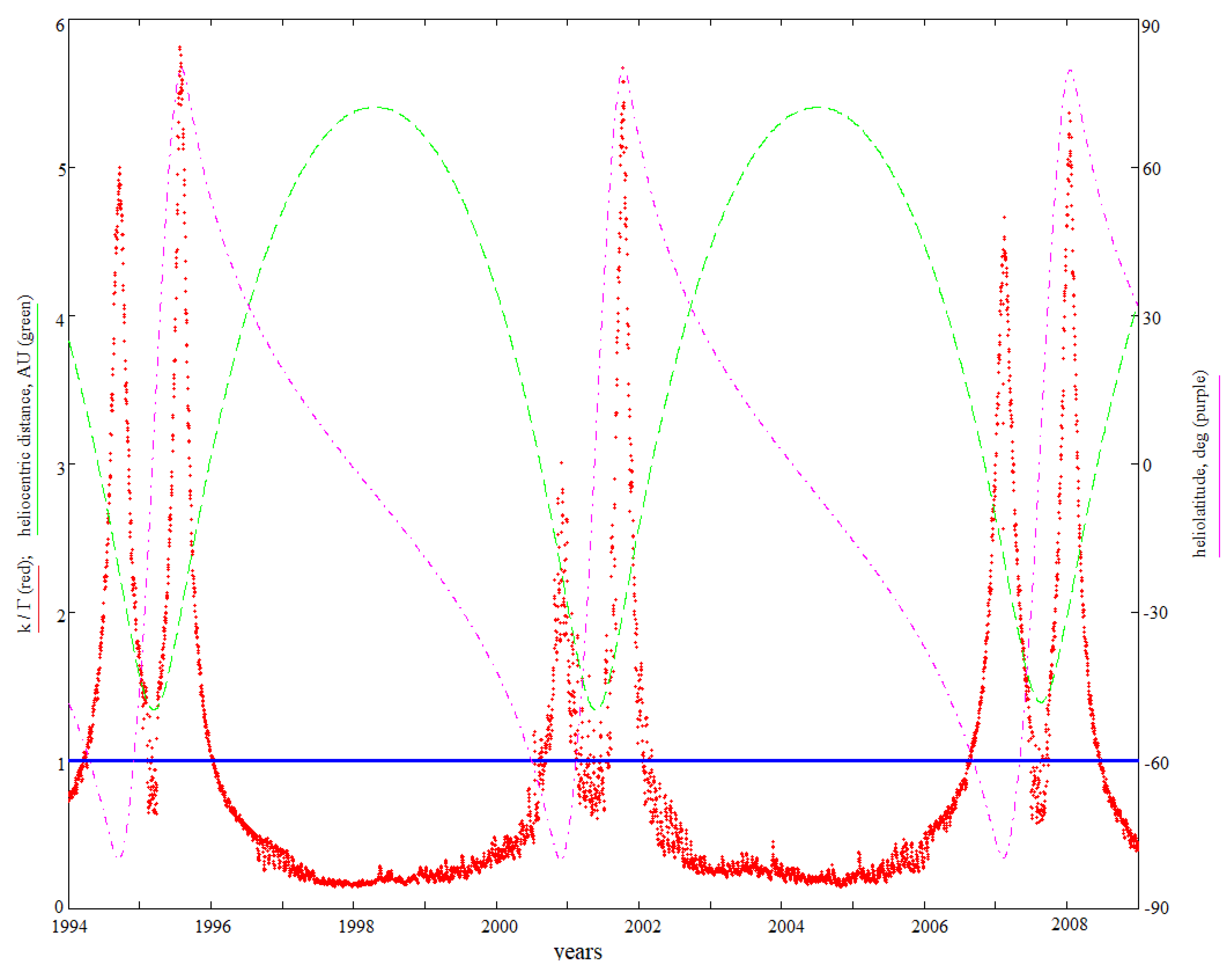
Discussing the results, let us note that our star rotates too slowly to enable the motion of ideal conducting plasma in the corona and coronal holes to maintain a constant electric potential along the IMF lines. This can be understood by estimating the value of k/Γ, since k/Γ is equal to the ratio of the angular speed of Ferraro’s isorotation calculated from observations and the angular speed of the Sun. The values of k/Γ for 1994–2008 are shown in Figure 5. As one can see, the ratio k/Γ ≠ 1, and reaches 5–6 in polar regions. There is also another effect in the heliosphere: far from the Sun (beyond Mars’ orbit), and at low heliolatitudes, the electric field is weaker than suggested by the unipolar effect (see Figure 5).

Figure 4 shows the intersections of polar current sheets, and corresponds to the left-hand side of Figure 5, where k/Γ first reaches values from 1 to 2. This region contains most of the known polar conic current sheets. As one can see from Figure 5, all regions where k/Γ ≈ 1 are observed for an insignificant part of the time. Six of them correspond to the boundaries of coronal holes, and three zones correspond to the perihelions of Ulysses orbit located at low heliolatitudes. The regions of k/Γ ≈ 1 have unique properties. The equality k ≈ Γ means that Ω_obs ≈ ω_ʘ, and deviations of the observational values of the electric field from the theoretical ones are determined by the geometric factor. In other words, there are regions with a complex geometry of the magnetic field in which these deviations are observed, and there is no other explanation of the effect because the solar wind speed cannot be responsible for this, since it always remains predominantly radially directed away from the Sun [27,50]. The equality Ω_obs ≈ ω_ʘoften takes place when the angle between the magnetic field and the speed is close to 90 degrees. It follows from this that the Poynting vector is equal to vB²/4π, i.e., the speed of the solar wind coincides in magnitude and direction with the transfer speed of the electromagnetic energy. The latter can be used when simulating polar conic current sheets.

In Figure 2, Figure 3 and Figure 4, the most noticeable effects are those connected with the latitudinal dependences of the parameters. As can be seen from Figure 5, the ratio k/Γ is minimal between 1997 and 1999, as well as between 2003 and 2006. During these time intervals, Ulysses was at its maximum distance from the Sun at medium and low heliolatitudes. At the end of 1997 and at the beginning of 2004, the spacecraft crossed the helioequator, approaching the aphelion. Other equatorial crossings occurred near the Sun in 1995, 2001, and 2007. In Figure 5, these correspond to the M-shaped dips of k/Γ, located between two closely situated maxima. One can observe that the typical values of k/Γ at equatorial crossings in 1995, 2001, and 2007 are several times larger than in 1997 and 2004. In addition, the absolute minima of k/Γ lie near the aphelions in the beginning of 1998 and during the second half of 2004. Therefore, k/Γ decreases with distance, as expected from Equations (12) and (13). Note that the distance dependence of the coefficients k and Γ is less obvious, since they experience strong variations far from the Sun (Figure 2 and Figure 3). As the k/Γ ratio has a regular shape (Figure 5), variations in the unipolar coefficient far from the Sun are associated with the geometric factor Γ. This may indicate a complication of the IMF structure with an increasing heliocentric distance. In other words, variations in k far from the Sun are most probably associated with inhomogeneities in the direction of the magnetic field, which may represent small-scale current sheets and magnetic islands.

In some periods of Ulysses’ observations, a small influence of comet tails on plasma parameters is possible—specifically, comet Hyakutake for few hours in May 1996 [56], comet McNaught–Hartley for two days in the beginning of October 2000 [57], and comet McNaught for five days in February 2007 [27,58]. These intervals are not long enough to change the numbers in Table 1; however, as indicated in [27], when crossing the cometary tail in February 2007, the conic current sheets became more clearly identified than in 1994. The influence of cometary ions on k and Γ is an interesting problem for future studies.

In recent works, it has been shown that the necessary conditions for the α- and Ω-dynamos are satisfied in the outer heliosheath [59,60]. According to observations from the Voyager-1,2 spacecraft, a jump in the magnetic field is observed at spatial scales in the order of 0.005–0.02 AU, which may be associated with the dynamo effect. The kinetic energy of the plasma transmitted by the rotation of the Sun is converted into magnetic energy [59,60]. Then, in the outer heliosheath, an increase in the electric field and a change in the electric potential distribution are possible. Let us consider the magnetic field lines that are located between the Sun and the outer heliosheath; by virtue of the frozen-in equation, these magnetic field lines are equipotential. At the same time, there are sources of the electric field both in the outer heliosheath and near the Sun. Generally speaking, these can create different potentials at the ends of the magnetic field lines. To prevent this from happening, the values of the potential at the ends of the IMF lines should be self-consistent. In other words, mutual influence between the corona, coronal holes, and heliosheath is possible. Note that this idea is mentioned in [61]. The details of this effect are the subject of further research. It should be noted that when studying the sources of the electric field in the solar wind, it may be necessary to consider conditions not only near the Sun, but also near the boundaries of the heliosphere.

In the present work, we did not touch on the problem of identifying the sources of the additional electric field at the Sun, or of determining the nature of its possible screening; this is a direction for further studies. To understand the nature of the sources of the electric field, it is necessary to develop models of the solar corona and photosphere, taking into account nonstationary processes and the applicability of the frozen-in equation. Electric fields arising in these cases will affect the potential distribution in the corona, including the places where the plasma is ideally conducting. Using this distribution, one can potentially find the electric field in the entire heliosphere.

The results obtained in this study show the importance of understanding the nature of large-scale electric fields in the heliosphere and their possible connections with the processes occurring both at the Sun and in the solar wind. The question of the nature of the sources of the electric field on the Sun remains open, and its answering requires further systematic investigations. In this study, we test the applicability of large-scale electric field description based on the ideal MHD approximation and the unipolar effect at the Sun. It was shown that there should be other unknown sources of the electric field, or this approximation will not be applicable. In the latter case, the accounting for non-ideal terms in Ohm’s law can eliminate the discrepancies between theory and observations. In such a case, the problem of the electric field’s nature can be solved. However, the solution requires the use of a non-ideal global MHD solar wind model and, perhaps, a complicated solar corona model. Clearly, this is a challenging and interesting problem for future studies.

Any effects associated with small-scale turbulence do not affect the large-scale stationary electric field. If there is a large-scale quasi-stationary turbulence that can strengthen or weaken the electric field several times over several Carrington rotations, then this can solve the problem stated in the manuscript.