Warm Dark Matter Galaxies with Central Supermassive Black Holes

Abstract

We generalize the Thomas–Fermi approach to galaxy structure to include central supermassive black holes and find, self-consistently and non-linearly, the gravitational potential of the galaxy plus the central black hole (BH) system. This approach naturally incorporates the quantum pressure of the fermionic warm dark matter (WDM) particles and shows its full power and clearness in the presence of supermassive black holes. We find the main galaxy and central black hole magnitudes as the halo radius $r_h$, halo mass $M_h$, black hole mass $M_{BH}$, velocity dispersion $\sigma$, and phase space density, with their realistic astrophysical values, masses and sizes over a wide galaxy range. The supermassive black hole masses arise naturally in this framework. Our extensive numerical calculations and detailed analytic resolution of the Thomas–Fermi equations show that in the presence of the central BH, both DM regimes—classical (Boltzmann dilute) and quantum (compact)—do necessarily co-exist generically in any galaxy, from the smaller and compact galaxies to the largest ones. The ratio $\mathcal{R}\left(r\right)$ of the particle wavelength to the average interparticle distance shows consistently that the transition, $\mathcal{R}\simeq 1$, from the quantum to the classical region occurs precisely at the same point $r_A$ where the chemical potential vanishes. A novel halo structure with three regions shows up: in the vicinity of the BH, WDM is always quantum in a small compact core of radius $r_A$ and nearly constant density; in the region $r_A<r<r_i$ until the BH influence radius $r_i$, WDM is less compact and exhibits a clear classical Boltzmann-like behavior; for $r>r_i$, the WDM gravity potential dominates, and the known halo galaxy shows up with its astrophysical size. DM is a dilute classical gas in this region. As an illustration, three representative families of galaxy plus central BH solutions are found and analyzed: small, medium and large galaxies with realistic supermassive BH masses of ${10}^5{M}_{\odot }$, ${10}^7{M}_{\odot }$ and ${10}^9{M}_{\odot }$, respectively. In the presence of the central BH, we find a minimum galaxy size and mass $M_h^{min}\simeq {10}^7{M}_{\odot }$, larger ($2.2233\times {10}^3$ times) than the one without BH, and reached at a minimal non-zero temperature $T_{min}$. The supermassive BH heats up the DM and prevents it from becoming an exactly degenerate gas at zero temperature. Colder galaxies are smaller, and warmer galaxies are larger. Galaxies with a central black hole have large masses $M_h>{10}^7{M}_{\odot }>M_h^{min}$; compact or ultracompact dwarf galaxies in the range ${10}^4{M}_{\odot }<M_h<{10}^7{M}_{\odot }$ cannot harbor central BHs. We find novel scaling relations $M_{BH}=D{M}_h^{\frac{3}{8}}$ and $r_h=C{M}_{BH}^{\frac{4}{3}}$, and show that the DM galaxy scaling relations $M_h=b{\Sigma }_0{r}_h^2$ and $M_h=a{{\sigma }_h}^4/{\Sigma }_0$ hold too in the presence of the central BH, ${\Sigma }_0$ being the constant surface density scale over a wide galaxy range. The galaxy equation of state is derived: pressure $P\left(r\right)$ takes huge values in the BH vicinity region and then sharply decreases entering the classical region, following consistently a self-gravitating perfect gas $P\left(r\right)={\sigma }^2\rho \left(r\right)$ behavior.

1. Introduction and Results

Dark matter (DM) is the main component of galaxies: the fraction of DM over the total galaxy mass goes from 90% for large diluted galaxies to 99.99% for dwarf compact galaxies. Therefore, as a first approximation, DM alone should explain the main basic magnitudes of galaxies (as masses and sizes) as well as main structural properties of density profiles and rotation curves. Baryons should give corrections to the pure DM results. For such reasons, we consider here warm dark matter galaxies with central supermassive black holes without including baryons as a first approximation.

Warm dark matter (WDM), that is, dark matter formed by particles with masses of the order of kiloelectron volt (keV) scale has received increasing attention in the last years (see, for example, [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20] and references therein). At intermediate scales, ∼100 kpc, WDM gives the correct abundance of substructures and solves the cold dark matter (CDM) overabundance of structures at small scales [21,22,23,24,25,26,27,28,29]. For scales larger than $100$ kpc, WDM yields the same results as CDM. Hence, WDM agrees with the small-scale as well as large-scale structure observations and CMB anisotropy observations.

Astronomical observations show that the DM galaxy density profiles are cored to scales below the kiloparsec (kpc) [30,31,32,33,34,35,36,37,38]. On the other hand, N-body CDM simulations exhibit cusped density profiles with a typical $1/r$ behavior near the galaxy center $r=0$. Inside galaxy cores, below ∼100 pc, N-body classical physics simulations do not provide the correct structures for WDM because quantum effects are important in WDM at these scales. Classical, that is, non-quantum physics N-body WDM simulations which do not take into account the quantum WDM pressure, exhibit cusps or small cores with sizes smaller than the observed cores [39,40,41,42]. WDM predicts correct structures and cores with the right sizes for small scales (below kiloparsec) when the quantum nature of the WDM particles, that is, the quantum pressure of the fermionic WDM, is taken into account [9,10,11,12].

We follow here the Thomas–Fermi approach to galaxy structure for self-gravitating fermionic WDM [9,10,11,12]. This approach is especially appropriate to take into account the quantum properties of systems with a large number of particles, namely, macroscopic quantum systems as neutron stars, white dwarf stars [43] and galaxies [9,10,11,12].

Fermionic dark matter is appropriate because dark matter particles do not interact with the standard or electromagnetic forces; a typical example is the sterile neutrino. Fermionic statistics is totally valid for dark matter, and the kiloelectron volt fermionic dark matter has become popular in the last years. The DM particles composing the self-gravitating Fermi gas only interact through gravitation.

In this paper, we generalize the Thomas–Fermi approach to galaxies, including their central supermassive black holes.

In this approach, the central quantity to derive is the DM chemical potential $\mu \left(r\right)$, which is the free energy per particle. For self-gravitating systems, the potential $\mu \left(r\right)$ is proportional to the gravitational potential $\varphi \left(r\right)$, $\mu \left(r\right)={\mu }_0-m\varphi \left(r\right)$, ${\mu }_0$ being a constant, and obeys the self-consistent and non-linear Poisson equation

$${\nabla }^2\mu \left(r\right)=-4\pi gG{m}^2\int \frac{d^{3}p}{{(2\pi \hslash )}^3}f\left(\frac{p^2}{2m}-\mu \left(r\right)\right).$$

(1)

Here, G is Newton’s gravitational constant, g is the number of internal degrees of freedom of the DM particle, m is the DM particle mass, p is the DM particle momentum and $f\left(E\right)$ is the energy distribution function. This is a semiclassical gravitational approach to determine self-consistently the gravitational potential of the quantum fermionic WDM, given its distribution function $f\left(E\right)$.

In the Thomas–Fermi approach, DM-dominated galaxies are considered in a stationary state. This is a realistic situation for the late stages of structure formation since the free-fall (Jeans) time $t_{ff}$ for galaxies is much shorter than the age of galaxies. $t_{ff}$ is at least one or two orders of magnitude smaller than the age of the galaxy.

We consider spherical symmetric configurations where Equation (1) becomes an ordinary nonlinear differential equation that determines self-consistently the chemical potential $\mu \left(r\right)$ and constitutes the Thomas–Fermi approach [9,10,11,12]. We choose for the energy distribution function a Fermi–Dirac distribution

$$f\left(E\right)=\frac{1}{e^{E/T_0}+1},$$

where $T_0$ is the characteristic one-particle energy scale. As we see below, except near the central black hole, we can take the $T_0$ constant. $T_0$ plays the role of an effective temperature scale and depends on the galaxy mass [11,12].

The Fermi–Dirac distribution function is justified in the inner regions of the galaxy, inside the halo radius where we find that the Thomas–Fermi density profiles perfectly agree with the observations [11,12]. These results are supported by our work [13], where, within an Eddington-like approach for galaxies, it is shown that the observed galaxy density profiles describe a self-gravitating thermal gas for $r\lesssim R_{virial}$.

Our theoretical results follow by solving the self-consistent and non-linear Poisson equation Equation (1), which is solely derived from the purely gravitational interaction of the WDM particles and their fermionic nature.

The central quantity in the Thomas–Fermi Equation (1) is the chemical potential $\mu \left(r\right)$. The boundary condition of the chemical or gravitational potential $\mu \left(r\right)$ at the center $r\to 0$ in the Thomas–Fermi approach is extended here to allow for the presence of the central black hole, namely,

$$\mu \left(r\right)\stackrel{{}_{r\to 0}}{=}\frac{Gm{M}_{BH}}{r}+Const.+\mathcal{O}\left(r\right).$$

(2)

$M_{BH}$ being the black hole mass. That is, the presence of a galactic central black hole implies near the center $r\to 0$, a behavior proportional to $1/r$ in $\mu \left(r\right)$, while in the absence of the black hole, let us recall that $\mu \left(r\right)$ is bounded for $r\to 0$ [9,10,11,12].

Positive values of $\mu \left(r\right)$ correspond to a self-gravitating quantum gas regime, while negative values of $\mu \left(r\right)$ describe the self-gravitating classical (Boltzmann) regime [44]. As we see below, one of the results of this paper is that in galaxies possessing central black holes, both regimes do appear. The strong gravitational field of the central black hole makes the WDM chemical potential large and positive near the center. This implies that the WDM behaves quantum mechanically inside a small quantum core with a nearly constant density.

We summarize in what follows the main results of this paper:

(i)

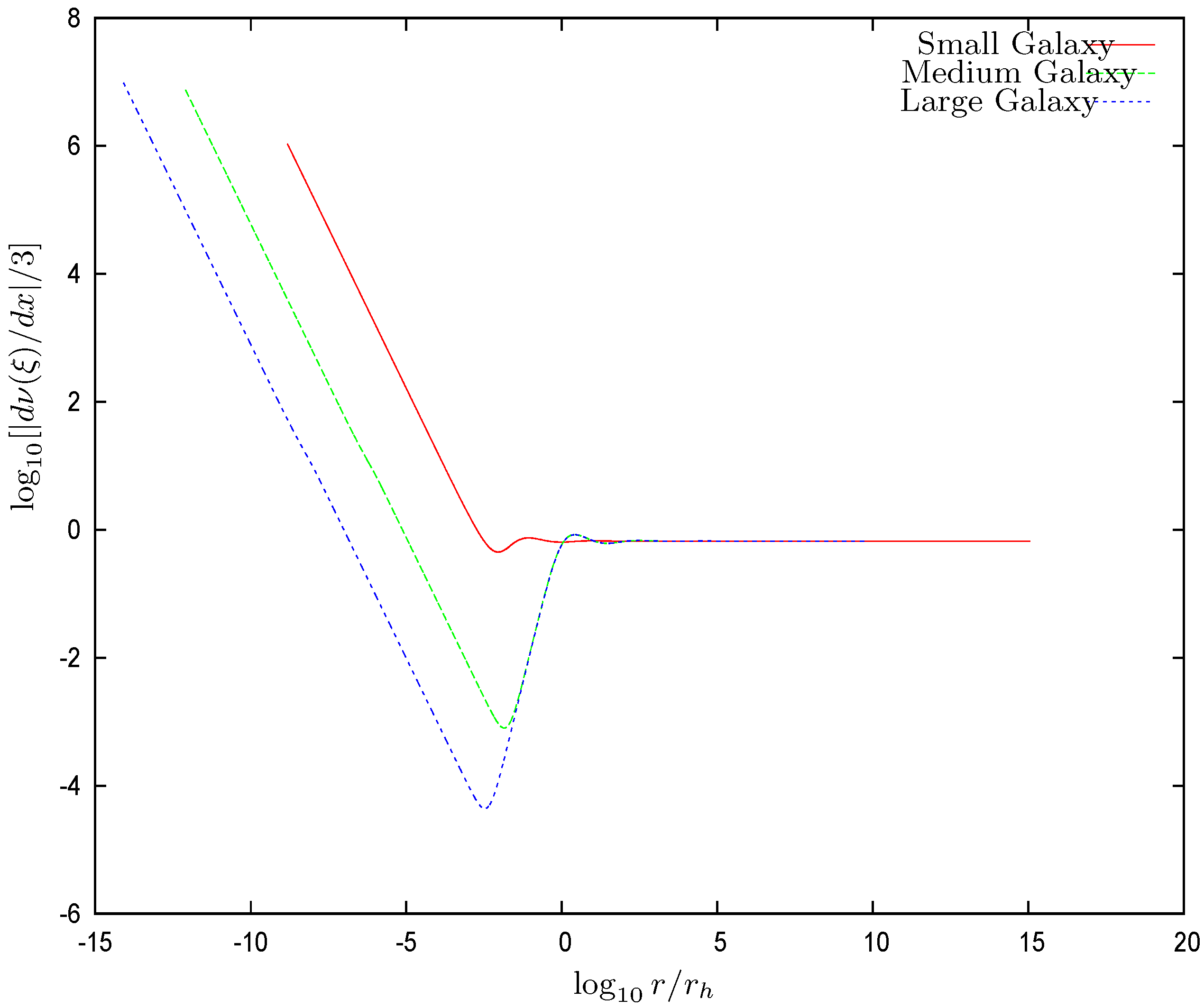
We find that $\mu \left(r\right)$ takes large positive values in the inner regions as implied by Equation (28), then decreases until vanishing at $r=r_A$, and becomes negative for $r>r_A$, as shown by our detailed resolution of the Thomas–Fermi equation (Section 3.3 and Figure 1). Therefore, $r_A$ is precisely the transition between the quantum and classical DM behaviors; $r_A$ plays the role of the quantum DM radius of the galaxy for galaxies exhibiting a central black hole. Namely, inside $r_A$, the WDM gas is a self-gravitating quantum gas, while for $r\gtrsim r_A$ the WDM gas is a self-gravitating classical Boltzmann gas. The size $r_A$ of the quantum WDM core turns to be smaller for increasing galaxy masses and black hole masses. WDM inside a small core of radius $r_A$ is in a quantum gas high-density state, namely a Fermi nearly degenerate state with nearly constant density ${\rho }_A$. For the three representative families of galaxy solutions we find here, the values of $r_A$ and ${\rho }_A$ are given by Equations (75)–(77). The density ${\rho }_A$ is orders of magnitude larger than its values for $r>r_A$, where the WDM is in the classical Boltzmann regime. $r_A$ runs between 0.07 and 1.90 pc for galaxies with virial masses from ${10}^{16}{M}_{\odot }$ to ${10}^7{M}_{\odot }$ (as shown in Section 3.3). In any case, $r_A$ is much larger than the Schwarzschild radius of the central black hole, which runs from ${10}^{-4}$ to ${10}^{-8}$ pc.

This is an important result: in the vicinity of the central black hole, the fermionic WDM is always in a quantum regime, while far from the central black hole, the WDM follows a classical Boltzmann regime [12]. This is natural to understand: the strong attractive gravitational force near the central BH compacts the WDM, and its high density makes it to behave quantum mechanically. On the contrary, far from the BH, the gravitational forces are weak, the WDM is diluted, and it is then described by a classical Boltzmann gas. Ultracompact dwarf galaxies also exhibit WDM in a quantum regime [9,10,12].

(ii)

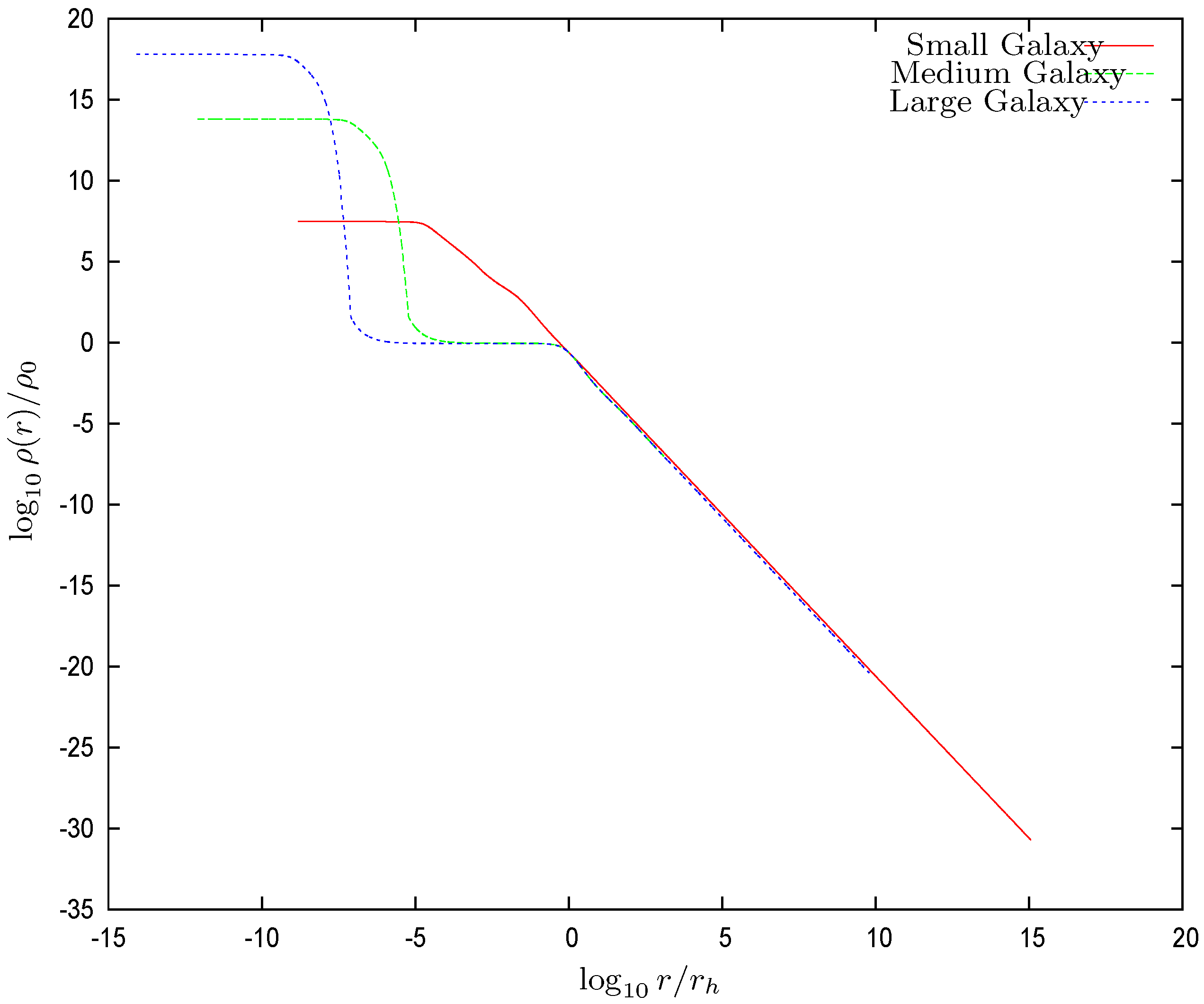
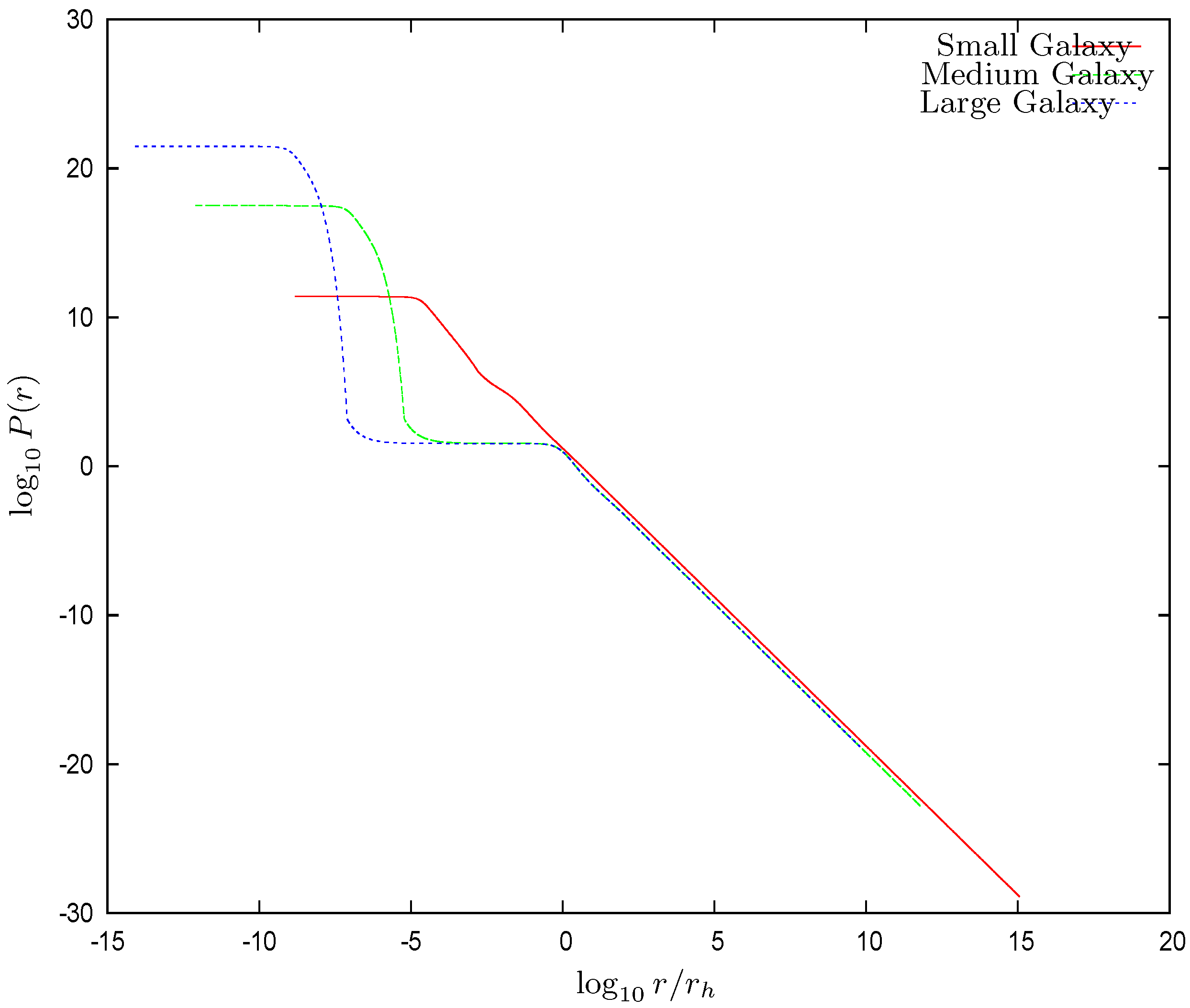
In addition, the black hole has an influence radius $r_i$. In the vicinity of the black hole, the gravitational force, due to the black hole, is larger than the gravitational force exerted by the dark matter. The influence radius of the black-hole $r_i$ is defined as the radius where both forces are of equal strength. Both forces point inward and always sum up. $r_i$ turns out to be larger than the radius $r_A$ where the chemical potential vanishes, $r_i>r_A$. The region $r_A<r<r_i$ is dominated by the central black hole, and the WDM exhibits there a classical behavior. For $r\lesssim r_i$, we see from Figure 1 and Figure 2 that both $\mu \left(r\right)$ and $\left|d\mu \right(r)/dr|$ (or equivalently, the dimensionless potential $\nu \left(\xi \right)$ and its derivative $\left|d\nu \right(\xi )/dx|$, x= ln $r/r_h$), follow the behavior dictated by the central black hole Equation (32), which produce straight lines on the left part of the logarithmic plots Figure 1 and Figure 2. Consistently, for $r\gtrsim r_i,\nu \left(\xi \right)$ and $\left|d\nu \right(\xi )/dx|$ are dominated by the WDM and exhibit a similar behavior to that of the Thomas–Fermi solutions without a central black hole [9,10,11,12].

Figure 3 shows that the local density behavior is dominated by the black hole for $r\lesssim r_i$. For $r_i\lesssim r\lesssim r_h$, the WDM gravitational field dominates over the black hole field, and the galaxy core shows up. For medium and large galaxies, the core is seen as a plateau. At the same time, the chemical potential is negative for $r\gtrsim r_i>r_A$, and the WDM is a classical Boltzmann gas in this region.

The surface density

$${\Sigma }_0\equiv r_h{\rho }_0\simeq 120M_{\odot }/{\mathrm{pc}}^2\mathrm{up}\mathrm{to}10–20\%,$$

(3)

has the remarkable property of being nearly constant and independent of luminosity in different galactic systems (spirals, dwarfs irregular and spheroidal, and ellipticals) spanning over 14 magnitudes in luminosity and over different Hubble types [36,37]. It is therefore a useful physical characteristic scale in terms of which galaxy magnitudes are expressed.

(iii)

We find the main galaxy magnitudes as the halo radius $r_h$, halo mass $M_h$, black hole mass $M_{BH}$, velocity dispersion, circular velocity, density, pressure and phase space density. Analytic formulae are derived for them and expressed in terms of the reference surface density ${\Sigma }_0$. Moreover, we can express the black hole mass as

$$M_{BH}=2.73116\times {10}^4{M}_{\odot }\frac{{\xi }_0}{{\left[{\xi }_h{I}_2\left({\nu }_0\right)\right]}^{\frac{3}{5}}}{\left(\frac{{\Sigma }_0{\mathrm{pc}}^2}{120M_{\odot }}\right)}^{\frac{3}{5}}{\left(\frac{2\mathrm{keV}}{m}\right)}^{\frac{16}{5}}$$

(4)

${\xi }_0$ being the dimensionless central radius and $I_2\left({\nu }_0\right)$ the 2nd momentum of the distribution function Equation (21). The black hole mass $M_{BH}$ grows when ${\xi }_0$ grows. Notice that $M_{BH}$ does not simply grow linearly with ${\xi }_0$ due to the presence of the factor ${\left[{\xi }_h{I}_2\left({\nu }_0\right)\right]}^{-\frac{3}{5}}$.

(iv)

We find in this approach explicit realistic galaxy solutions with central supermassive black holes and analyze three representative families of them: small size (mass) galaxies, intermediate size (mass) galaxies, and large size (mass) galaxies.

For a fixed value of the surface density ${\Sigma }_0$, the solutions are parametrized by two truly physical parameters: the dimensionless central radius ${\xi }_0$ and the constant A characteristic of the chemical potential behavior Equation (32) at the center $\xi \to 0$. The dimensionless central radius ${\xi }_0$ is explicated in Equation (28). This is the ratio of the relevant physical parameters $(m,M_{BH},T)$ which appear in the chemical potential at the center. The constant A is truly physical too and characterizes the boundary condition of the chemical potential at the center in the presence of the central supermassive black hole, Equation (32). In the absence of the central SMBH: ${\xi }_0=0$, and the boundary condition at the center without BH, $\nu \left(0\right)=A$ is recovered.

We derive an illuminating expression for the central radius $r_0$ for large galaxies $M_h\gtrsim {10}^6{M}_{\odot }$ explicitly in terms of the black hole mass $M_{BH}$, the halo mass $M_h$ and the reference surface density ${\Sigma }_0$. It follows from Equations (41), (43) and (66) that,

$$r_0=l_0{\xi }_0=126.762\sqrt{\frac{{10}^6{M}_{\odot }}{M_h}}\frac{M_{BH}}{{10}^6{M}_{\odot }}\sqrt{\frac{120M_{\odot }}{{\Sigma }_0{\mathrm{pc}}^2}}\mathrm{pc}$$

(5)

(v)

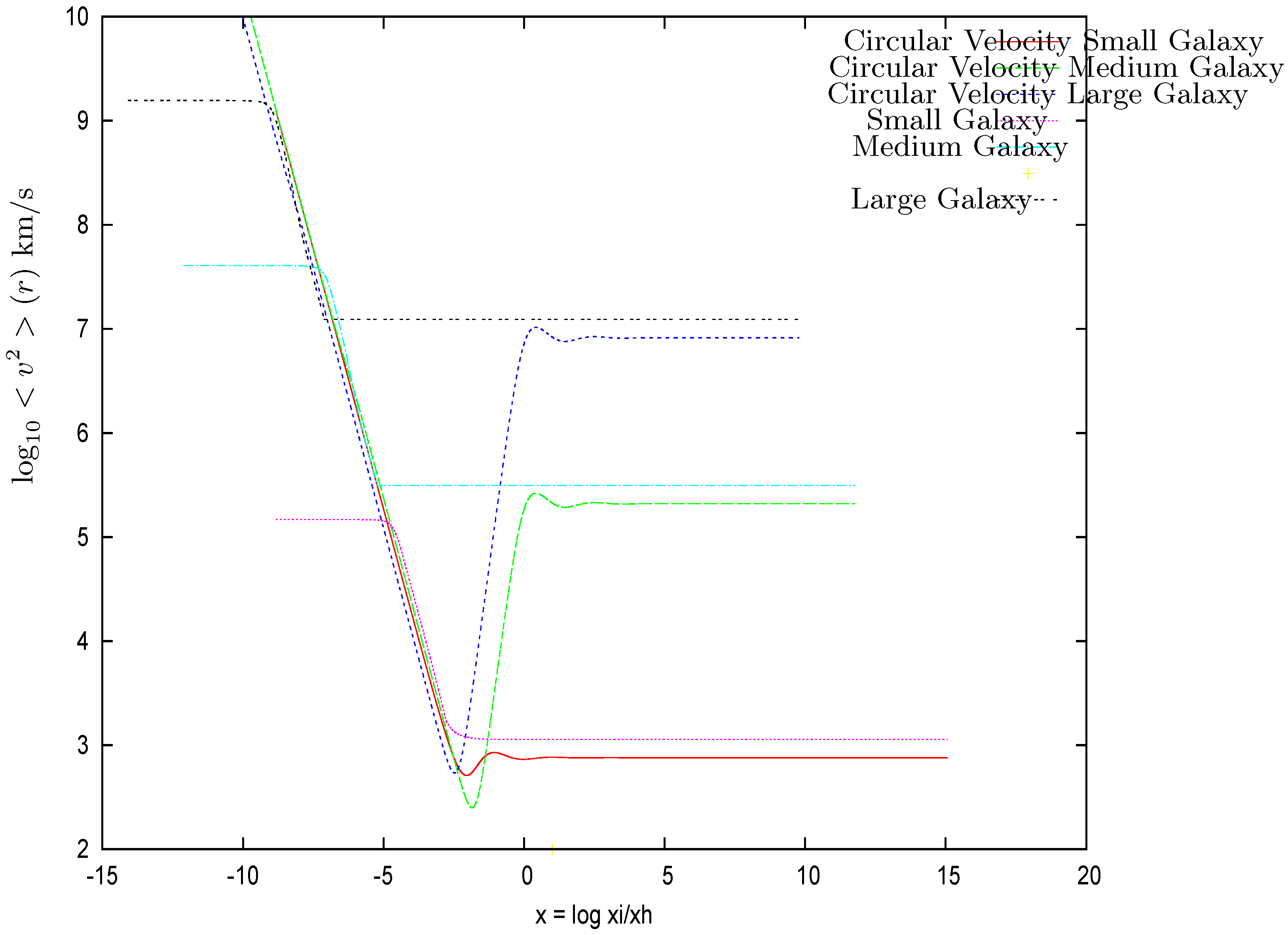
We find from our extensive numerical calculations that the halo is thermalized at the uniform temperature $T_0$ and matches the circular temperature $T_c\left(r\right)$ by $r\sim 3r_h$. This picture is similar to the picture found in the absence of the central black hole which follows from the observed density profiles in the Eddington-like approach to galaxies [13]. We obtain here in the Thomas–Fermi approach and in the presence of a central supermassive black hole that the halo is thermalized at a uniform temperature $T_0$ inside $r\lesssim 3r_h$, which tends to the circular temperature $T_c\left(r\right)$ at $r\sim 3r_h$ as illustrated in Figure 4. The circular temperature is defined in terms of the circular velocity as $T_c\left(r\right)=\frac{m}{3}{v}_c^2\left(r\right)$. The circular temperature is discussed in Section 3. We introduce the circular temperature $T_c\left(r\right)$ in terms of the circular (virial) velocity $v_c^2\left(r\right)$ in the same way the temperature $T\left(r\right)$ is defined in terms of the velocity dispersion $T\left(r\right)=m{v}^2\left(r\right)/3$. The circular velocity $v_c^2\left(r\right)$ is defined and found in Section 2. Near the central black hole, the space dependent temperature $T_c\left(r\right)$ is given by an equipartition and the virial theorem, as shown by Equations (68)–(70).

From our extensive numerical calculations, we find that the galaxy mass increases and the galaxy size increases when the constant $\left|A\right|$ characteristic of the the central behavior of $\nu \left(\xi \right)$ for $\xi \to 0$ Equation (32) increases. This is similar to the case with the absence of central black holes, where $A=\nu \left(0\right)$ [9,10,12].

(vi)

We plot in Figure 4 the circular velocity given by Equation (58) vs. ${log}_{10}r/r_h$. For $r>r_h$, the circular velocity tends to the velocity dispersion as obtained from the Eddington equation for realistic density profiles [13]. For $r\to 0$, the circular velocity grows as in Equation (59) due to the central black hole field.

(vii)

We find in Equations (75)–(77) the WDM mass $M_A$ inside the quantum galaxy radius $r_A$. $M_A$ represents only a small fraction of the halo or virial mass of the galaxy but it is a significant fraction of the black hole mass $M_{BH}$. We see from Equations (75)–(77) that $M_A$ amounts to 20% of $M_{BH}$ for the medium and large galaxies and 45% for the small galaxy.

(viii)

We also measure the classical and quantum gas character of the galaxy plus the black hole system by means of the ratio $\mathcal{R}\left(r\right)$ between the particle de Broglie wavelength and the average interparticle distance. For $\mathcal{R}\lesssim 1$, the system is of a classical dilute nature while for $\mathcal{R}\gtrsim 1$, it is a macroscopic quantum system. We find $\mathcal{R}\left(r\right)$ in terms of the surface density and momenta of the gravitational or chemical potential in dimensionless units $\nu \left(\xi \right)$ Equations (80) and (81). Figure 5 shows ${log}_{10}\mathcal{R}$ vs. ${log}_{10}(r/r_h)$ for the three representative galaxy solutions. The transition from the quantum to the classical regime occurs precisely at the same point $r_A$ where the chemical potential vanishes (see Figure 1), as it must be, showing the consistency and powerful of our treatment. This point defines the transition from the quantum to the classical behavior.

(ix)

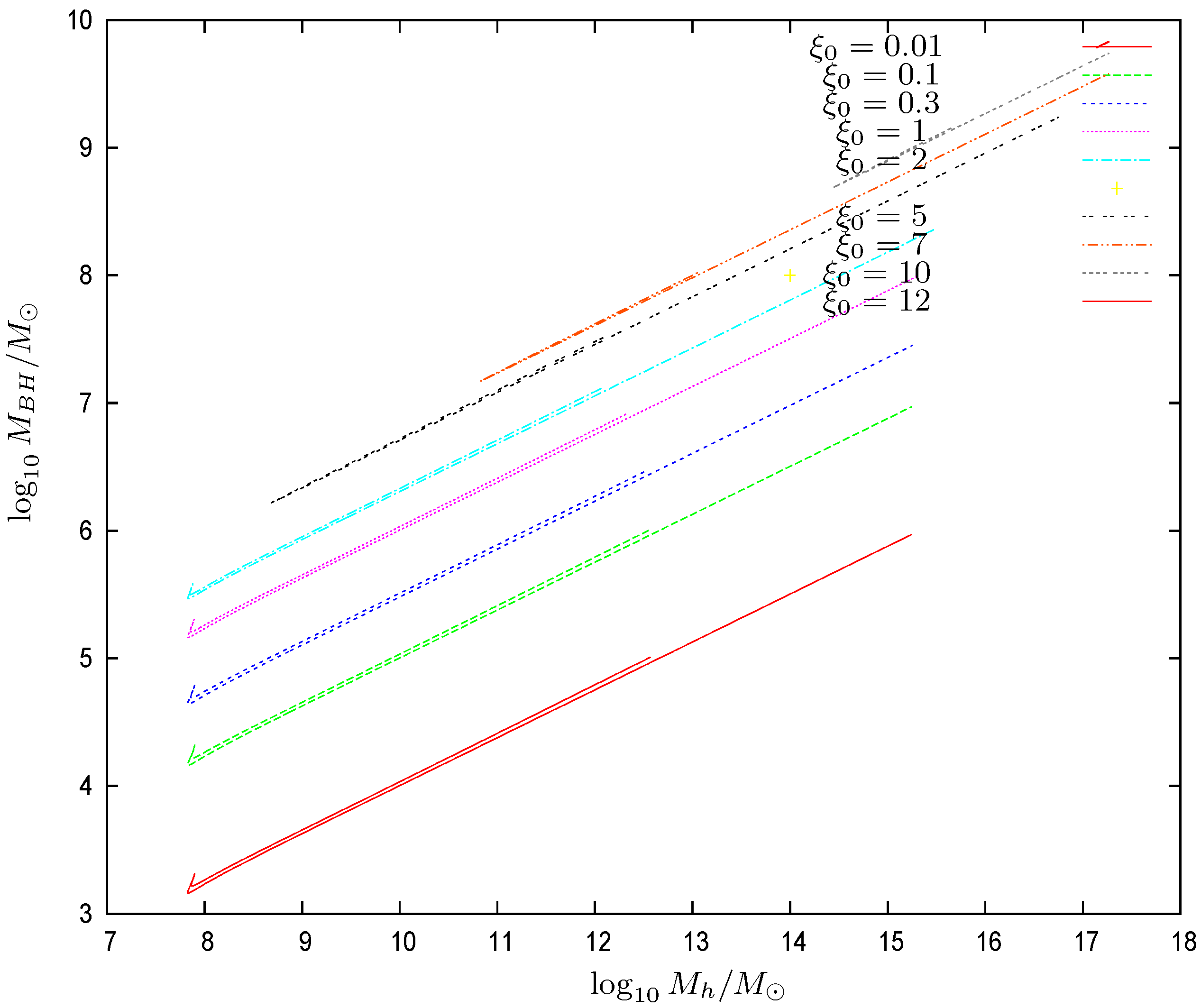
There is an important qualitative difference between galaxy solutions with a black hole (${\xi }_0>0$), and galaxy solutions without a black hole (${\xi }_0=0$). In the absence of the central black hole, the halo mass $M_h$ reaches the minimal value $M_h^{min}$ Equation (82), which is the degenerate quantum limit at zero temperature $T_0^{min}=0$ [9,10,12]. In the presence of a central black hole, we find that the minimal temperature $T_0^{min}$ is always non-zero and that the halo mass takes as a minimal value

$$M_h^{min}=6.892\times {10}^7{\left(\frac{2\mathrm{keV}}{m}\right)}^{\frac{16}{5}}{\left(\frac{{\Sigma }_0{\mathrm{pc}}^2}{120M_{\odot }}\right)}^{\frac{3}{5}}{M}_{\odot },\mathbf{with}\mathbf{central}\mathbf{black}\mathbf{hole}.$$

(6)

$$M_h^{min}=3.0999\times {10}^4{\left(\frac{2\mathrm{keV}}{m}\right)}^{\frac{16}{5}}{\left(\frac{{\Sigma }_0{\mathrm{pc}}^2}{120M_{\odot }}\right)}^{\frac{3}{5}}{M}_{\odot },T_0^{min}=0,\mathbf{without}\mathbf{central}\mathbf{black}\mathbf{hole}.$$

(7)

The presence of the supermassive black hole heats up the dark matter gas and prevents it from becoming an exact degenerate gas at zero temperature. The minimal galaxy mass and size and most compact galaxy state with a central black hole is a nearly degenerate state at very low but non-zero temperature as seen from Equation (84). All matter studied in this paper is dark matter, and the only DM interaction is the gravitational interaction. The presence of the black hole naturally makes the DM particles acquire a higher velocity (and thus, a higher associated temperature), and in this sense, the SMBH does “heat” the dark matter around it. Gravitation self-consistently acts on such DM, and the SMBH adds too to such gravitational action. This is a very clean physical process, with a clean framework and clean conclusive results.

This situation is clearly shown in Figure 6. The value of $M_h^{min}$ with a central black hole is $2.2233\times {10}^3$ times larger than without the black hole. Notice that the small galaxy solution Equation (75) is just 11% larger in halo mass than the minimal galaxy Equation (83) with a central black hole. We conclude that galaxies possessing a central black hole are in the dilute Boltzmann regime because of their large mass $M_h>{10}^6{M}_{\odot }>M_h^{min}$ [12]. On the contrary, compact galaxies, in particular, ultracompact galaxies in the quantum regime $M_h<2.3\times {10}^6{M}_{\odot }$ [12], cannot harbor central black holes because the minimal galaxy mass with central black hole Equation (83) is always larger than $2.3\times {10}^6{M}_{\odot }$. In other words, galaxies with masses $M_h<M_h^{min}$, namely ultracompact dwarfs, necessarily do not possess central black holes.

The mass of the supermassive black hole $M_{BH}$ monotonically increases with the central radius $r_0$ or equivalently the dimensionless one ${\xi }_0$ at fixed A. In addition, for ${\xi }_0<0.3$, that is, for small supermassive black holes, and all A, the galaxy parameters, such as halo mass $M_h$, halo radius $r_h$, virial mass $M_{vir}$ and galaxy temperature $T_0$, become independent of ${\xi }_0$, showing a limiting galaxy solution. Only the BH mass depends on ${\xi }_0$ in this regime.

Figure 7displays our results for $T_0$. Figure 8 displays our results for the black hole mass ${log}_{10}{M}_{BH}$ vs. the halo mass ${log}_{10}{M}_h$. We see that $M_{BH}$ is a two-valued function of $M_h$. For each value of $M_h$, there are two possible values for $M_{BH}$, which are quite close to each other. This two-valued dependence on $M_h$ is a direct consequence of the dependence of $M_h$ on A shown in Figure 6. The branch points on the left in Figure 8 correspond to the minimal galactic halo mass $M_h^{min}$ Equation (83) when the central supermassive black hole is present. At fixed ${\xi }_0$, as shown in Figure 8, the central black hole mass $M_{BH}$ scales with the halo mass $M_h$ as

$$M_{BH}=D\left({\xi }_0\right)M_h^{\frac{3}{8}},$$

where $D\left({\xi }_0\right)$ is an increasing function of ${\xi }_0$. We plot in Figure 9 the halo galaxy mass ${log}_{10}{M}_h$ vs. the galaxy temperature ${log}_{10}{T}_0/\mathrm{K}$. The halo mass $M_h$ grows when $T_0$ increases. Colder galaxies are smaller. Warmer galaxies are larger. We see at the branch points in Figure 9 the minimal galaxy temperature $T_0^{min}$ in Equation (84) when a supermassive black hole is present.

We find galaxy solutions with central black holes for arbitrarily small values of ${\xi }_0>0$ and a correspondingly, arbitrarily small central BH mass. There is no minimal central BH mass. The only minimal central BH mass possibility is zero (for $\xi =0$).

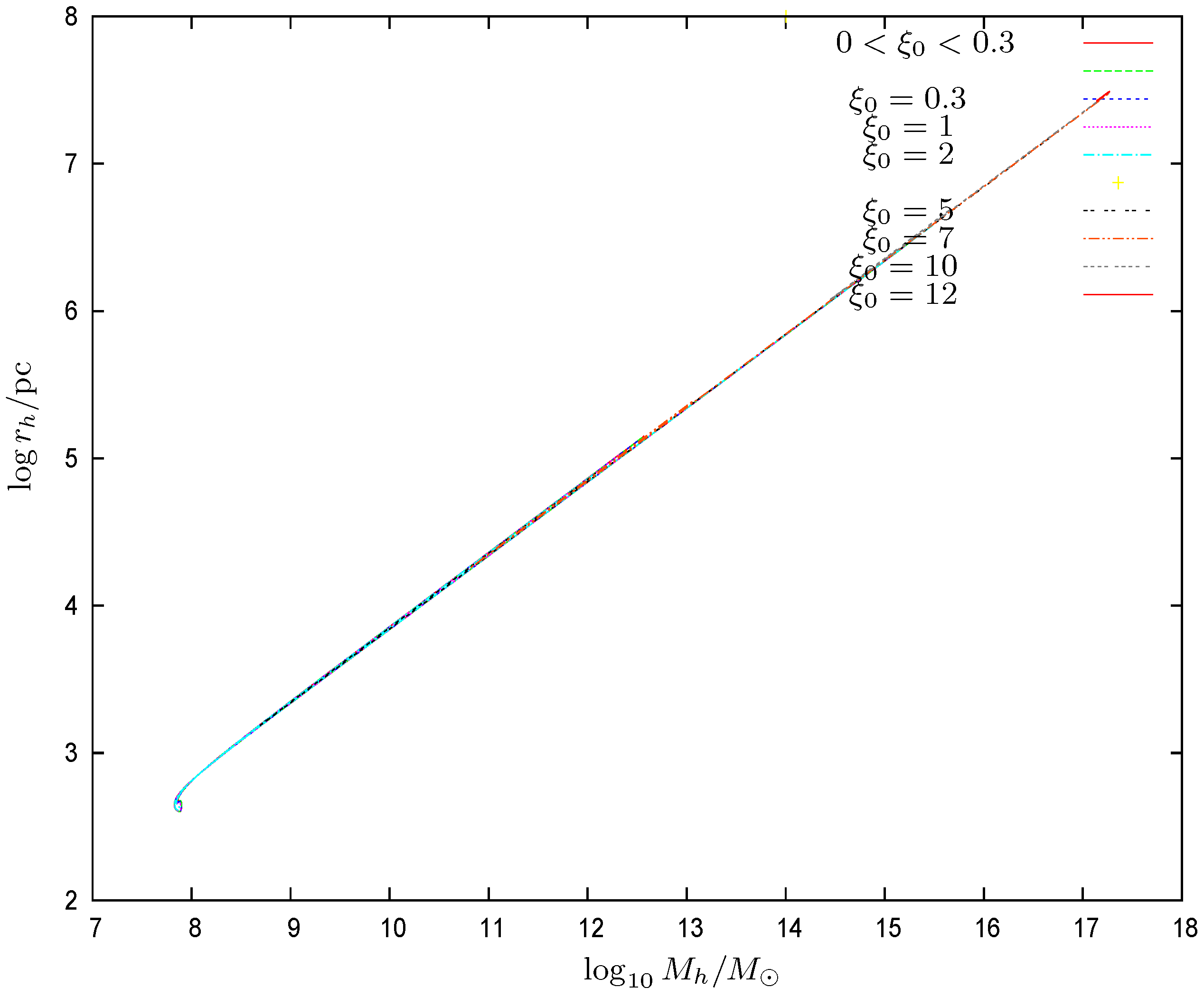
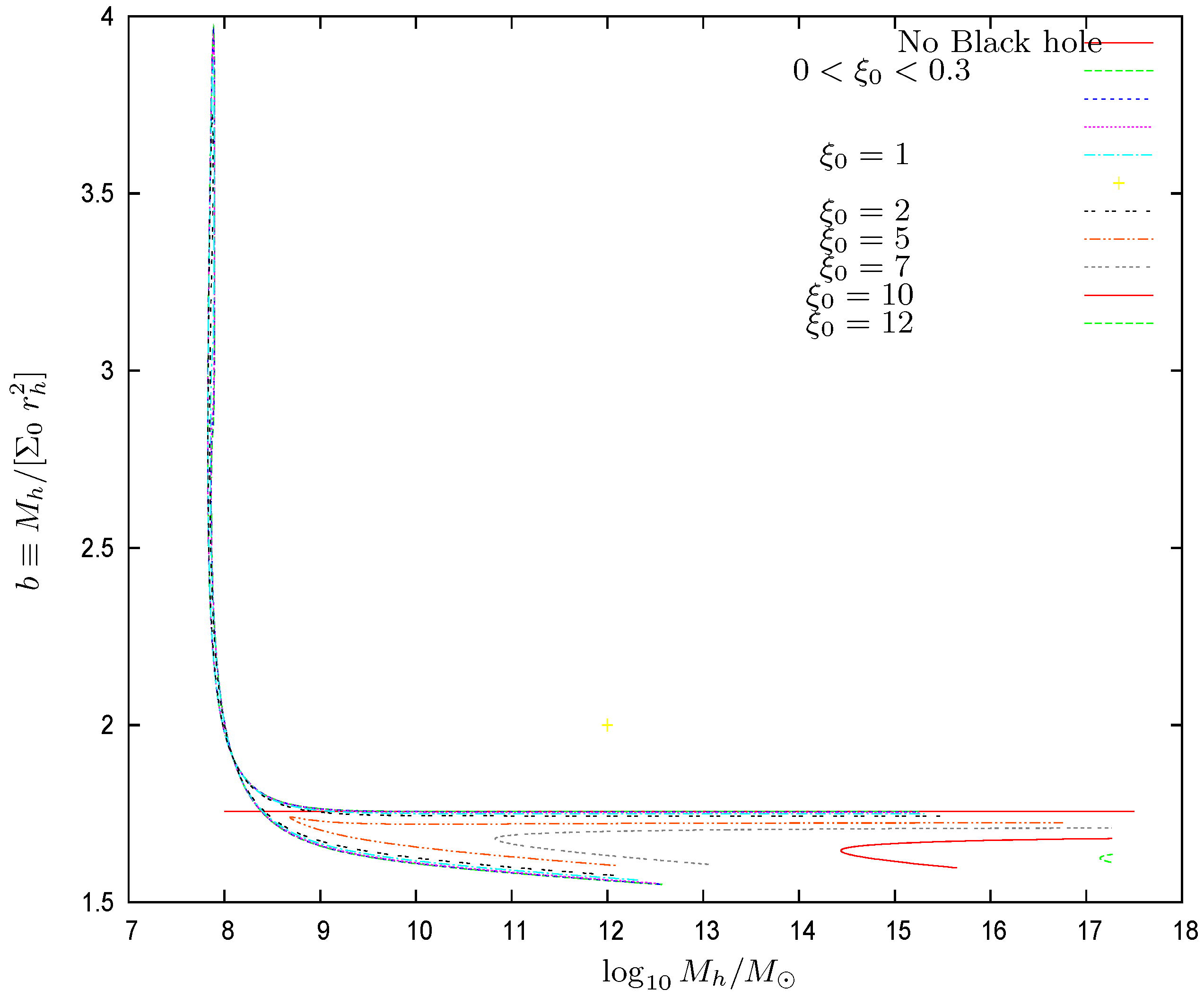
(x)

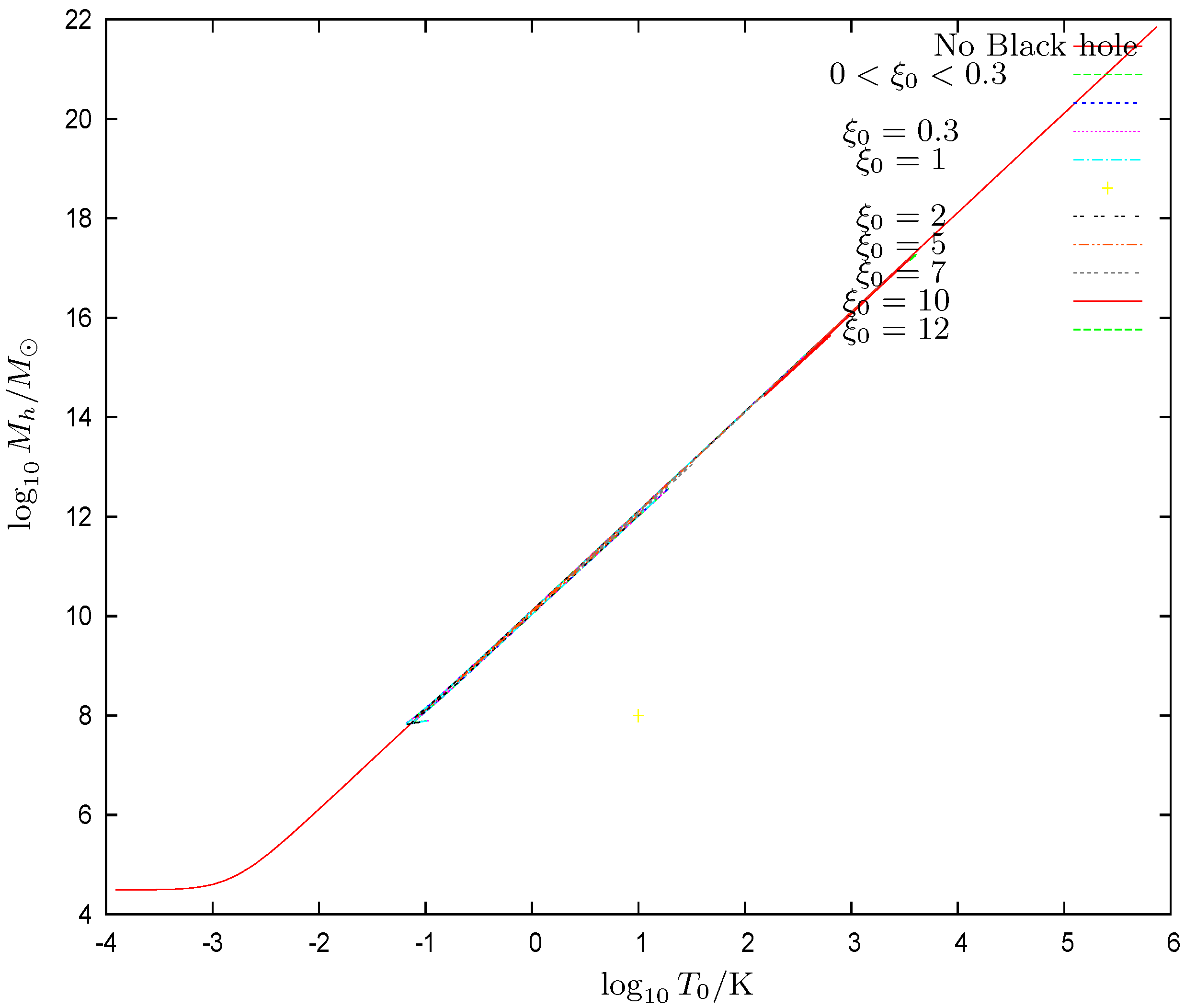
We find that $M_h$ scales as $r_h^2$, which is the same scaling found in the Thomas–Fermi approach to galaxies in the absence of black holes [9,10,12]. We plot in Figure 10 the ordinary logarithm of the halo radius ${log}_{10}{r}_h$ vs. the ordinary logarithm of the halo mass ${log}_{10}{M}_h$ for galaxies with central black holes of many different masses. The halo mass in the absence of a central black hole behaves in the Thomas–Fermi approach as [12]

$$M_h=1.75572{\Sigma }_0{r}_h^2,\mathbf{without}\mathbf{central}\mathbf{black}\mathbf{hole}.$$

(8)

The proportionality factor in this scaling relation is confirmed by the galaxy data [12]. In the presence of a central black hole, we find in the Thomas–Fermi approach an analogous relation

$$M_h=b{\Sigma }_0{r}_h^2,\mathbf{with}\mathbf{central}\mathbf{black}\mathbf{hole}.$$

(9)

where the coefficient b turns to be of order unity. We plot in Figure 11 the coefficient b as a function of the halo mass $M_h$. We see that, except for halo masses near the minimum halo mass $M_h^{min}$, b in the presence of a central black hole takes values up to 10% below its value in the absence of a central black hole Equation (85). For halo masses near $M_h^{min},b$ increases, reaching values $b\le 4$. For very large halos and central black holes, b could be as small as about $1.6$. b changes at most by a factor from $1/2$ up to 2 while the halo mass $M_h$ varies by ten orders of magnitude. As shown by Figure 11, b is a two-valued function of $M_h$. b turns out to be independent of the precise value of the WDM particle mass m, which is due to the fact that the scaling relation Equation (86) as well as Equation (85) apply in the classical Boltzmann regime of the galaxy ($M_h\gtrsim {10}^6{M}_{\odot }$). In summary, the scaling relation Equation (86) and the coefficient b turn out to be remarkably robust.

(xi)

We plot in Figure 12 the ordinary logarithm of the halo radius ${log}_{10}{r}_h$ versus the ordinary logarithm of the central black hole mass ${log}_{10}{M}_{BH}$ for many galaxy solutions. The halo radius $r_h$ turns out to be a double-valued function of $M_{BH}$. Remarkably, $r_h$ for fixed ${\xi }_0$ scales as

$$r_h=C\left({\xi }_0\right)M_{BH}^{\frac{4}{3}}.$$

(10)

The constant $C\left({\xi }_0\right)$ turns out to be a decreasing function of ${\xi }_0$.

(xii)

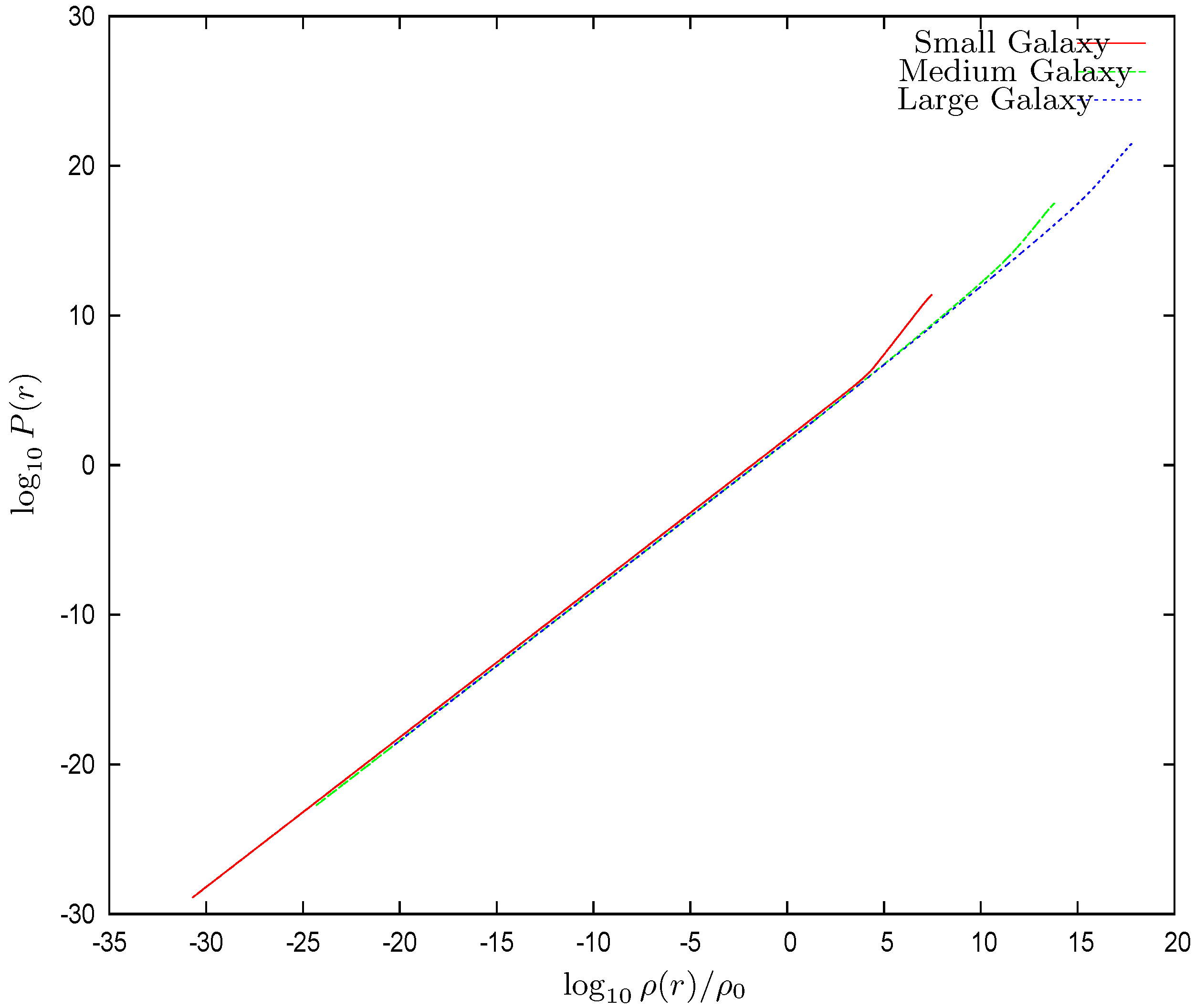
We find the local pressure $P\left(r\right)$ as given by Equation (53). In Figure 13, we plot ${log}_{10}P\left(r\right)$ vs. ${log}_{10}(r/r_h)$ for the three representative galaxy solutions. $P\left(r\right)$ monotonically decreases with r. The pressure $P\left(r\right)$ takes huge values in the quantum (high density) region $r<r_A$ and then it sharply decreases entering the classical (dilute) region $r>r_A$. In Figure 14, we plot the derived equation of state ${log}_{10}P\left(r\right)$ vs. ${log}_{10}\rho \left(r\right)/{\rho }_0$ for the three galaxy solutions we find here with central SMBH. The three curves almost coincide and are almost straight lines of unit slope. That is, the equation of state is in very good approximation of a perfect gas equation of state $P\left(r\right)={\sigma }^2\rho \left(r\right)$, which stems from the fact that galaxies with central black holes have halo masses $M_h>M_h\gtrsim {10}^6{M}_{\odot }>M_h^{min}$, Equation (83), and therefore necessarily belong to the dilute Boltzmann classical regime [12]. The equation of state turns out to be a local (r-dependent) perfect gas equation of state because of the gravitational interaction (WDM self-gravitating perfect gas). Indeed, for galaxies with central black holes, the WDM is in a quantum (highly compact) regime inside the quantum radius $r_A$. However, because $r_A$ is in the parsec scale or smaller (see Equations (75)–(77)), the bulk of the WDM is in the Boltzmann classical regime, which is consistently reflected in the perfect gas equation of state behavior.

In summary, the results of this paper show the power and cleanliness of the Thomas–Fermi theory and WDM to properly describe the galaxy structures and the galaxy physical states with and without supermassive central black holes. We consider in this paper pure WDM galaxies with central supermassive black holes. Adding baryons will introduce corrections, but the picture of galaxies with central supermassive black holes presented here should not change essentially. This approach is independent of any WDM particle physics model. It depends only on the fermionic WDM nature and gravity. The results presented in this paper do not depend on the precise value of the WDM particle mass m but only on the fact that m is in the kiloelectron volt scale, namely keV $2\lesssim m\lesssim 10$ keV, for example.

This paper is organized as follows.

In Section 2, we formulate the problem of galaxy structure with central supermassive black holes in the WDM Thomas–Fermi approach and find the main physical magnitudes and properties of the galaxy plus the black hole system. In Section 3, we solve the corresponding equations with the boundary conditions, find three representative families of galaxy solutions (small, medium and large size galaxies) with central supermassive black holes and analyze the new quantum and classical physics properties of the system. In Section 4, we perform an extensive study of the galaxy solutions with a central supermassive black hole, find the main important differences between galaxies with and without the presence of a central black hole, derive universal galaxy scaling relations in the presence of a central supermassive black hole (halo mass $M_h$ and halo size $r_h$ relation, black hole mass $M_{BH}$ and halo radius $r_h$ relation) and find the galaxy local pressure and equation of state in the presence of central supermassive black holes and their different regimes. In Section 5 we provide remarks and Conclusions. In Appendix A we provide the analytical computation of the density and pressure integrals.

2. Galaxy Structure with Central Supermassive Black Holes in the WDM Thomas–Fermi Approach

We consider DM-dominated galaxies in their late stages of structure formation when they are relaxing to a stationary situation, at least not too far from the galaxy center.

This is a realistic situation since the free-fall (Jeans) time $t_{ff}$ for galaxies is much shorter than the age of galaxies:

$$t_{ff}=\frac{1}{\sqrt{G{\rho }_0}}=1.49\times {10}^7\sqrt{\frac{M_{\odot }}{{\rho }_0{\mathrm{pc}}^3}}\mathrm{yr}.$$

(11)

The observed central densities of galaxies yield free-fall times in the range from 15 million years for ultracompact galaxies to 330 million years for large diluted spiral galaxies. These free-fall (or collapse) times are small compared with the age of galaxies running in billions of years.

Hence, we can consider the DM described by a time-independent and energy distribution function $f\left(E\right)$, where $E=\sqrt{p^2+m^2}-m-\mu$ is the relativistic single-particle energy, m is the mass of the DM particle, and $\mu$ is the chemical potential [9,10,12] related to the gravitational potential $\varphi \left(r\right)$ by

$$\mu \left(r\right)={\mu }_0-m\varphi \left(r\right),$$

(12)

where ${\mu }_0$ is a constant. We consider here relativistic kinematics because the WDM particles in the vicinity of the central black hole can be relativistic. In the non-relativistic limit, we recover the relations used in Refs. [9,10,12].

In the Thomas–Fermi approach, $\rho \left(r\right)$ is expressed as a function of $\mu \left(r\right)$ through the standard integral of the DM phase–space distribution function over the momentum

$$\rho \left(r\right)=\frac{g}{2{\pi }^2{\hslash }^3}{\int }_0^{\infty }dp{p}^2\sqrt{p^2+m^2}f\left[{\displaystyle \sqrt{p^2+m^2}-m-\mu \left(r\right)}\right],$$

(13)

where g is the number of internal degrees of freedom of the DM particle, with $g=1$ for Majorana fermions and $g=2$ for Dirac fermions. Equation (13) is valid in general for relativistic fermions, and generalizes the non-relativistic framework of Refs. [9,10,12].

We consider spherical symmetric configurations. Then, the Poisson equation for $\varphi \left(r\right)$ takes the self-consistent form

$$\frac{d^2\mu }{d{r}^2}+\frac{2}{r}\frac{d\mu }{dr}=-4\pi Gm\rho \left(r\right)=-\frac{2gGm}{\pi {\hslash }^3}{\int }_0^{\infty }dp{p}^2\sqrt{p^2+m^2}f\left[{\displaystyle \sqrt{p^2+m^2}-m-\mu \left(r\right)}\right],$$

(14)

where G is Newton’s constant and $\rho \left(r\right)$ is the DM mass density.

Equation (14) provides an ordinary nonlinear differential equation that determines self-consistently the chemical potential $\mu \left(r\right)$ and constitutes the Thomas–Fermi approach [9,10,12] (see also Refs. [45,46,47]). This is a semi-classical approach to galaxy structure in which the quantum nature of the DM particles is taken into account through the quantum statistical distribution function $f\left(E\right)$.

The DM pressure and the velocity dispersion can also be expressed as integrals over the DM phase–space distribution function as

$$P\left(r\right)=\frac{1}{3}\rho \left(r\right)<v^2\left(r\right)\ge \frac{g}{6{\pi }^2{\hslash }^3}{\int }_0^{\infty }dp\frac{p^4}{\sqrt{p^2+m^2}}f\left[{\displaystyle \sqrt{p^2+m^2}-m-\mu \left(r\right)}\right].$$

(15)

We see that $\mu \left(r\right)$ fully characterizes the DM halo structure in this Thomas–Fermi framework.

In this semi-classical framework, the stationary energy distribution function $f\left(E\right)$ must be given. We consider the Fermi–Dirac distribution

$$f\left(E\right)={\Psi }_{\mathrm{FD}}(E/T_0)=\frac{1}{e^{E/T_0}+1},$$

(16)

where the characteristic one-particle energy scale $T_0$ in the DM halo plays the role of an effective temperature. $T_0$ can be taken as constant, except near the central black hole.

In neutron stars, where the neutron mass is about six orders of magnitude larger than the WDM particle mass, the temperature can be approximated by zero.

As shown in Ref. [12], the value of $T_0$ depends on the galaxy mass. In galaxies, $T_0\sim m<v^2>$ turns out to be non-zero but small in the range of ${10}^{-3}\mathrm{K}\lesssim T_0\lesssim 10$ K for all halo galaxy masses in the range ${10}^5-{10}^{12}{M}_{\odot }$, which reproduce the observed velocity dispersions for $m\simeq 2$ keV. The smaller values of $T_0$ correspond to compact dwarf galaxies, and the larger values of $T_0$ are for large and diluted galaxies [12].

More precisely, large positive values of the chemical potential correspond to the degenerate fermions limit, which is the extreme quantum state, and oppositely, large negative values of the chemical potential at the origin give the diluted states, which are in the classical regime. The quantum-degenerate regime describes dwarf and compact galaxies, while the classical diluted regime describes large and diluted galaxies. In the classical regime, the Thomas–Fermi Equation (14) becomes the equation for a self-gravitating Boltzmann gas.

Galaxies possessing central black holes exhibit both quantum and classical regions as we see below.

The units used in this paper are those appropriate to the kiloelectron volt mass of the dark matter particle in the context of galaxy structure. The expression and conversion of units in terms of the kiloelectron volt includes the Planck constant h. Relevant conversion relations in terms of kiloelecron volt in this context are

$$\mathrm{keV}kpc=1.563738\times {10}^{29}$$

(17)

$$M_{\odot }=1.115468\times {10}^{63}\mathrm{keV}$$

(18)

2.1. Thomas–Fermi Equations with a Central Black Hole

It is useful to introduce dimensionless variables $\xi ,\nu \left(\xi \right)$

$$r=l_0\xi ,\mu \left(r\right)=T_0\nu \left(\xi \right),f\left(E\right)=\Psi (E/T_0),$$

(19)

where $l_0$ is the characteristic length that emerges from the dynamical Equation (14):

$$l_0\equiv \frac{\hslash }{\sqrt{8G}}{\left(\frac{2}{g}\right)}^{\frac{1}{3}}{\left[\frac{9\pi I_2\left({\nu }_0\right)}{m^8{\rho }_0}\right]}^{\frac{1}{6}}=R_0{\left(\frac{2\mathrm{keV}}{m}\right)}^{\frac{4}{3}}{\left(\frac{2}{g}\right)}^{\frac{1}{3}}{\left[\frac{I_2\left({\nu }_0\right)}{{\rho }_0}\frac{M_{\odot }}{{\mathrm{pc}}^3}\right]}^{\frac{1}{6}},R_0=7.425\mathrm{pc},$$

(20)

and

$$I_2\left(\nu \right)\equiv 3{\int }_0^{\infty }{y}^{2}dy\sqrt{1+\frac{2y^2}{\tau }}{\Psi }_{FD}\left({\displaystyle \tau \left[\sqrt{1+\frac{2y^2}{\tau }}-1\right]-\nu }\right),$$

(21)

$$\tau \equiv \frac{m}{T_0},{\nu }_0\equiv \nu \left({\xi }_i\right),{\rho }_0=\rho \left({\xi }_i\right)$$

(22)

where we use the integration variable $y\equiv p/\sqrt{2m{T}_0}$. ${\xi }_i$ stands for the influence radius of the black hole, which is defined below by Equation (31).

We consider in Equation (21) the case of a constant temperature $T_0$. The case of a r-dependent temperature is analyzed in Section 3.2.

For definiteness, we will take $g=2$, Dirac fermions in the sequel. One can easily translate from Dirac to Majorana fermions, changing the WDM fermion mass as

$$m\Rightarrow \frac{m}{2^{\frac{1}{4}}}=0.8409m.$$

Then, in dimensionless variables, the self-consistent Thomas–Fermi Equation (14) for the chemical potential $\nu \left(\xi \right)$ takes the form

$$\frac{d^2\nu }{d{\xi }^2}+\frac{2}{\xi }\frac{d\nu }{d\xi }=-I_2\left(\nu \right).$$

(23)

The presence of the central black hole is introduced through the boundary conditions, Equation (32), given below for the chemical potential $\nu \left(\xi \right)$ at $\xi \to 0$.

2.2. Central Galactic Black Hole and Its Influence Radius

In the presence of a central galactic black hole, the gravitational potential and the chemical potential near the center take the form

$$\varphi \left(r\right)\stackrel{{}_{r\to 0}}{=}-\frac{G{M}_{BH}}{r},\mu \left(r\right)-{\mu }_0\stackrel{{}_{r\to 0}}{=}\frac{Gm{M}_{BH}}{r},$$

(24)

where $M_{BH}$ is the black hole mass.

Integrating Equation (14) from $r=0$ to r yields

$$r^2\frac{d\mu }{dr}-\left[{\left.r^2\frac{d\mu }{dr}\right|}_{r\to 0}\right]=-GmM\left(r\right)$$

(25)

where

$$M\left(r\right)=4\pi {\int }_0^{r}d{r}^{\prime }{r^{\prime }}^2\rho \left(r^{\prime }\right),$$

(26)

is the total WDM mass $M\left(r\right)$ enclosed in a sphere of radius r, not including the central black hole mass.

Inserting the $r\to 0$ behavior of Equation (24) into Equation (25) yields, for the derivative of the chemical potential,

$$\frac{d\mu }{dr}=-\frac{Gm}{r^2}\left[M\left(r\right)+M_{BH}\right],$$

(27)

showing that the chemical potential is monotonically decreasing in r.

From Equations (12) and (19), the dimensionless chemical potential $\nu \left(\xi \right)$ takes the form

$$\nu \left(\xi \right)\stackrel{{}_{\xi \to 0}}{=}\frac{Gm{M}_{BH}}{T_0{l}_0\xi }\equiv \frac{{\xi }_0}{\xi }=\frac{r_0}{r},{\xi }_0\equiv \frac{Gm{M}_{BH}}{T_0{l}_0}=\frac{r_0}{l_0}.$$

(28)

That is, the presence of a galactic central black hole implies near the center $\xi \to 0$, a ${\xi }_0/\xi$ behavior in $\nu \left(\xi \right)$. ${\xi }_0$ is proportional to the black hole mass $M_{BH}$. Recall that in the absence of the black hole, $\nu \left(\xi \right)$ is bounded for $\xi \to 0$ [9,10,12].

We see from Equation (28) that in the vicinity $\xi \lesssim {\xi }_0$ of the central black hole, the chemical potential $\nu \left(\xi \right)$ is dominated by its boundary expression Equation (28), and therefore, $\nu \left(\xi \right)$ takes positive values $\nu \left(\xi \right)\gtrsim 1$. Values of $\nu \left(\xi \right)$ larger than unity correspond to a fermionic WDM gas in a quantum regime [43]. This is an important result: in the vicinity of the central black hole, the fermionic WDM is always in a quantum regime, while far from the central black hole, the WDM follows a classical Boltzmann regime [12]. This is natural to understand: the strong attractive gravitational force near the central BH compacts the WDM, and its high density makes it to behave quantum mechanically. On the contrary, far from the BH, the gravitational forces are weak, the WDM is diluted, and it is then described by a classical Boltzmann gas.

Ultracompact dwarf galaxies also exhibit WDM in a quantum regime [9,10,12].

$\nu \left(\xi \right)$ takes large positive values for $\xi \ll {\xi }_0$ as implied by Equation (28), then decreases until vanishing at $\xi ={\xi }_A$, $\nu \left({\xi }_A\right)=0$ and becomes negative for $\xi >{\xi }_A$, as shown by our detailed resolution of the Thomas–Fermi equation (Section 3.3 and Figure 1).

Therefore, $r_A=l_0{\xi }_A$ plays the role of the quantum DM radius of the galaxy for galaxies exhibiting a central black hole. Namely, inside $r_A$, the WDM gas is a quantum gas, while for $r\gtrsim r_A$, the WDM gas is a classical Boltzmann gas.

That is, a small quantum core of DM forms around the central black hole. The size $r_A$ of the quantum core turns to be smaller for increasing galaxy masses and black-hole masses, because the larger the black hole mass, the larger its gravitational attraction on the WDM, which is thus more compact, and, hence, the smaller the quantum radius core $r_A$.

$r_A$ runs between 0.07 and 1.90 pc for galaxies with virial masses from ${10}^{16}$ to ${10}^7{M}_{\odot }$ (see Section 3.3). In any case, $r_A$ is much larger than the Schwarzschild radius of the central black hole which runs from ${10}^{-4}$ to ${10}^{-8}$ pc.

In the vicinity of the black hole, the gravitational force due to the black hole is larger than the gravitational force exerted by the dark matter. The influence radius of the black hole $r_i$ is defined as the radius where both forces are of equal strength. Notice that both forces point inward and always sum up.

The total gravitational potential $V\left(r\right)$ and its derivative $V^{\prime }\left(r\right)$ are given by

$$V\left(r\right)=-\frac{G{M}_{BH}}{r}+\varphi \left(r\right),V^{\prime }\left(r\right)=\frac{G{M}_{BH}}{r^2}-\frac{1}{m}{\mu }^{\prime }\left(r\right)$$

(29)

where we used Equation (12). In dimensionless variables, $V^{\prime }\left(r\right)$ becomes

$$V^{\prime }\left(r\right)=\frac{T_0}{m{l}_0\xi }\left[\frac{{\xi }_0}{\xi }-\xi \frac{d\nu }{d\xi }\right]$$

(30)

The black hole and dark matter gravitational forces become equal at $\xi ={\xi }_i$. ${\xi }_i$ is the solution of the equation

$${\xi }_i^2{\left.\frac{d\nu }{d\xi }\right|}_{{\xi }_i}={\xi }_0.$$

(31)

In the Thomas–Fermi approach to galaxies with a central supermassive black hole, the boundary condition for $\nu \left(\xi \right)$ at $\xi \to 0$ imposes the black hole presence according to Equation (28). That is,

$$\nu \left(\xi \right)\stackrel{{}_{\xi \to 0}}{=}\frac{{\xi }_0}{\xi }+A+\mathcal{O}\left(\xi \right)$$

(32)

where ${\xi }_0$ is the dimensionless radius defined in Equation (28) and A is a constant that determines the properties of the corresponding galaxy solution as the galaxy mass and galaxy radius. In the absence of the central BH, we have ${\xi }_0=0,\nu \left(0\right)=A$, and the boundary condition used in Refs. [9,10,12] is recovered.

2.3. Main Physical Magnitudes of the Galaxy plus Central Black Hole System

We find the main physical galaxy magnitudes, such as the mass density $\rho \left(r\right)$, the velocity dispersion ${\sigma }^2\left(r\right)=v^2\left(r\right)/3$ and the pressure $P\left(r\right)$, which are all r-dependent, as

$$\begin{array}{ccc}\hfill & & \rho \left(r\right)=\frac{m^{\frac{5}{2}}}{3{\pi }^2{\hslash }^3}{\left(2T_0\right)}^{\frac{3}{2}}{I}_2\left(\nu \left(\xi \right)\right)={\rho }_0\frac{I_2\left(\nu \left(\xi \right)\right)}{I_2\left({\nu }_0\right)},{\rho }_0=\frac{m^{\frac{5}{2}}}{3{\pi }^2{\hslash }^3}{\left(2T_0\right)}^{\frac{3}{2}}{I}_2\left({\nu }_0\right)\hfill \end{array}$$

(33)

$$\begin{array}{ccc}& & P\left(r\right)=\frac{m^{\frac{3}{2}}}{15{\pi }^2{\hslash }^3}{\left(2T_0\right)}^{\frac{5}{2}}{I}_4\left(\nu \left(\xi \right)\right)=\frac{1}{5}{\left(9{\pi }^4\right)}^{\frac{1}{3}}{\left(\frac{{\hslash }^6}{m^8}\right)}^{\frac{1}{3}}{\left[\frac{{\rho }_0}{I_2\left({\nu }_0\right)}\right]}^{5/3}{I}_4\left(\nu \left(\xi \right)\right)\hfill \end{array}$$

(34)

$$\begin{array}{ccc}& & I_4\left(\nu \right)\equiv 5{\int }_0^{\infty }\frac{y^{4}dy}{\sqrt{1+\frac{2y^2}{\tau }}}{\Psi }_{FD}\left({\displaystyle \tau \left[\sqrt{1+\frac{2y^2}{\tau }}-1\right]-\nu }\right).\hfill \end{array}$$

(35)

The integrals $I_2$ and $I_4$ are analytically computed in Appendix A. As a consequence, from Equations (19), (20), (27) and (33) the total WDM mass $M\left(r\right)$ enclosed in a sphere of radius r (not including the central black hole mass) turns out to be

$$M\left(r\right)=4\pi \frac{{\rho }_0{l}_0^3}{I_2\left({\nu }_0\right)}{\int }_0^{\xi }dx{x}^2{I}_2\left(\nu \left(x\right)\right).$$

(36)

That is, $M\left(r\right)$ is the mass enclosed inside a sphere of radius r not including the mass of the central black hole mass.

The integral Equation (36) can be computed in closed form by integrating both sides of Equation (23)

$$M\left(r\right)=4\pi \frac{{\rho }_0{l}_0^3}{I_2\left({\nu }_0\right)}\left\{{\xi }^2\left|{\nu }^{\prime }\left(\xi \right)\right|-\left[{\left.{\xi }^2\left|{\nu }^{\prime }\left(\xi \right)\right|\right|}_{\xi \to 0}\right]\right\}$$

(37)

The contribution here from $\xi \to 0$ is obtained from the boundary condition Equation (32) with the result

$$\begin{array}{ccc}\hfill & & M\left(r\right)=M_0{\xi }^2\left|{\nu }^{\prime }\left(\xi \right)\right|{\left(\frac{\mathrm{keV}}{m}\right)}^4\sqrt{\frac{{\rho }_0}{I_2\left({\nu }_0\right)}\frac{{\mathrm{pc}}^3}{M_{\odot }}}-M_{BH},\hfill \\ & & M_0=4\pi M_{\odot }{\left(\frac{R_0}{\mathrm{pc}}\right)}^3=0.8230\times {10}^5{M}_{\odot }.\hfill \end{array}$$

(38)

In the absence of the central black hole, we recover the expression for the total mass $M\left(r\right)$ obtained in Ref. [12].

In these expressions, we have systematically eliminated the energy scale $T_0$ in terms of the central density ${\rho }_0$ through Equation (33).

We define the core size $r_h$ of the halo by analogy with the Burkert density profile as

$$\frac{\rho \left(r_h\right)}{{\rho }_0}=\frac{1}{4},r_h=l_0{\xi }_h.$$

(39)

It must be noticed that the surface density

$${\Sigma }_0\equiv r_h{\rho }_0,$$

(40)

is found to be nearly constant and independent of luminosity in different galactic systems (spirals, dwarfs irregular and spheroidal, and ellipticals) spanning over 14 magnitudes in luminosity and over different Hubble types. More precisely, all galaxies seem to have the same value for ${\Sigma }_0$, namely ${\Sigma }_0\simeq 120M_{\odot }/{\mathrm{pc}}^2$ up to 10–20% [36,37,38]. It is remarkable that, at the same time, other important structural quantities, such as $r_h,{\rho }_0$, the baryon fraction and the galaxy mass vary by orders of magnitude from one galaxy to another.

The constancy of ${\Sigma }_0$ seems unlikely to be a mere coincidence and probably reflects a physical scaling relation between the mass and halo size of galaxies. It must be stressed that ${\Sigma }_0$ is the only dimensionful quantity which is practically constant among the different galaxies.

It is then useful to take here the dimensionful quantity ${\Sigma }_0$ as physical scale to express the galaxy magnitudes in the Thomas–Fermi approach. That is, we replace the central density ${\rho }_0$ in the above galaxy magnitudes Equations (20)–(38) in terms of ${\Sigma }_0$ Equation (40) with the following results:

$$\begin{array}{cc}& l_0={\left(\frac{9\pi }{2^9}\right)}^{\frac{1}{5}}{\left(\frac{{\hslash }^6}{G^3{m}^8}\right)}^{\frac{1}{5}}{\left[\frac{{\xi }_h{I}_2\left({\nu }_0\right)}{{\Sigma }_0}\right]}^{\frac{1}{5}},\hfill \\ \\ & l_0=4.2557{\left[{\xi }_h{I}_2\left({\nu }_0\right)\right]}^{\frac{1}{5}}{\left(\frac{2\mathrm{keV}}{m}\right)}^{\frac{8}{5}}{\left(\frac{120M_{\odot }}{{\Sigma }_0{\mathrm{pc}}^2}\right)}^{\frac{1}{5}}\mathrm{pc}\hfill \end{array}$$

(41)

$$\begin{array}{cc}& T_0={\left(18{\pi }^6\frac{{\hslash }^6{G}^2}{m^3}\right)}^{\frac{1}{5}}{\left[\frac{{\Sigma }_0}{{\xi }_h{I}_2\left({\nu }_0\right)}\right]}^{\frac{4}{5}},\hfill \\ \\ & T_0=\frac{7.12757{10}^{-3}}{{\left[{\xi }_h{I}_2\left({\nu }_0\right)\right]}^{\frac{4}{5}}}{\left(\frac{2\mathrm{keV}}{m}\right)}^{\frac{3}{5}}{\left(\frac{{\Sigma }_0{\mathrm{pc}}^2}{120M_{\odot }}\right)}^{\frac{4}{5}}\mathrm{K}.\hfill \end{array}$$

(42)

The dimensionless quantum radius of the galaxy ${\xi }_0$ Equation (28) can be expressed as

$${\xi }_0={\left(\frac{2^8}{3^4{\pi }^7}\right)}^{\frac{1}{5}}{\left[\frac{{\xi }_h{I}_2\left({\nu }_0\right)}{{\Sigma }_0}\right]}^{\frac{3}{5}}{G}^{\frac{6}{5}}{m}^{\frac{16}{5}}{M}_{BH},$$

(43)

$${\xi }_0=36.6145{\left[{\xi }_h{I}_2\left({\nu }_0\right)\frac{120M_{\odot }}{{\Sigma }_0{\mathrm{pc}}^2}\right]}^{\frac{3}{5}}{\left(\frac{m}{2\mathrm{keV}}\right)}^{\frac{16}{5}}\frac{M_{BH}}{{10}^6{M}_{\odot }}.$$

(44)

Moreover, we can express from here the black hole mass as

$$M_{BH}=2.73116\times {10}^4{M}_{\odot }\frac{{\xi }_0}{{\left[{\xi }_h{I}_2\left({\nu }_0\right)\right]}^{\frac{3}{5}}}{\left(\frac{{\Sigma }_0{\mathrm{pc}}^2}{120M_{\odot }}\right)}^{\frac{3}{5}}{\left(\frac{2\mathrm{keV}}{m}\right)}^{\frac{16}{5}}.$$

(45)

Furthermore, we obtain

$$\begin{array}{ccc}\hfill & & r=4.2557\xi {\left[{\xi }_h{I}_2\left({\nu }_0\right)\right]}^{\frac{1}{5}}{\left(\frac{2\mathrm{keV}}{m}\right)}^{\frac{8}{5}}{\left(\frac{120M_{\odot }}{{\Sigma }_0{\mathrm{pc}}^2}\right)}^{\frac{1}{5}}\mathrm{pc}\hfill \end{array}$$

(46)

$$\begin{array}{ccc}& & \rho \left(r\right)={\left(\frac{2^9{G}^3{m}^8}{9\pi {\hslash }^6}\right)}^{\frac{1}{5}}{\left[\frac{{\Sigma }_0}{{\xi }_h{I}_2\left({\nu }_0\right)}\right]}^{\frac{6}{5}}{I}_2\left(\nu \left(\xi \right)\right),\hfill \end{array}$$

(47)

$$\begin{array}{ccc}& & \rho \left(r\right)=18.1967;\frac{I_2\left(\nu \left(\xi \right)\right)}{{\left[{\xi }_h{I}_2\left({\nu }_0\right)\right]}^{\frac{6}{5}}}{\left(\frac{m}{2\mathrm{keV}}\right)}^{\frac{8}{5}}{\left(\frac{{\Sigma }_0{\mathrm{pc}}^2}{120M_{\odot }}\right)}^{\frac{6}{5}}\frac{M_{\odot }}{{\mathrm{pc}}^3}\hfill \end{array}$$

(48)

$$\begin{array}{ccc}& & M\left(r\right)+M_{BH}=4\pi {\left(\frac{9\pi {\hslash }^6}{2^9{G}^3{m}^8}\right)}^{\frac{2}{5}}{\left[\frac{{\Sigma }_0}{{\xi }_h{I}_2\left({\nu }_0\right)}\right]}^{\frac{3}{5}}{\xi }^2\left|{\nu }^{\prime }\left(\xi \right)\right|,\hfill \end{array}$$

(49)

$$\begin{array}{ccc}& & M\left(r\right)+M_{BH}=\frac{27312{\xi }^2}{{\left[{\xi }_h{I}_2\left({\nu }_0\right)\right]}^{\frac{3}{5}}}\left|{\nu }^{\prime }\left(\xi \right)\right|{\left(\frac{2\mathrm{keV}}{m}\right)}^{\frac{16}{5}}{\left(\frac{{\Sigma }_0{\mathrm{pc}}^2}{120M_{\odot }}\right)}^{\frac{3}{5}}{M}_{\odot }\hfill \end{array}$$

(50)

$$\begin{array}{ccc}& & {\sigma }^2\left(r\right)=\frac{1}{3}{v}^2\left(r\right)=\frac{11.0402}{{\left[{\xi }_h{I}_2\left({\nu }_0\right)\right]}^{\frac{4}{5}}}\frac{I_4\left(\nu \left(\xi \right)\right)}{I_2\left(\nu \left(\xi \right)\right)}{\left(\frac{2\mathrm{keV}}{m}\right)}^{\frac{8}{5}}{\left(\frac{{\Sigma }_0{\mathrm{pc}}^2}{120M_{\odot }}\right)}^{\frac{4}{5}}{\left(\frac{\mathrm{km}}{\mathrm{s}}\right)}^2,\hfill \end{array}$$

(51)

$$\begin{array}{ccc}& & P\left(r\right)=\frac{8\pi }{5}G{\left[\frac{{\Sigma }_0}{{\xi }_h{I}_2\left({\nu }_0\right)}\right]}^2{I}_4\left(\nu \left(\xi \right)\right),\hfill \end{array}$$

(52)

$$\begin{array}{ccc}& & P\left(r\right)=\frac{200.895}{{\left[{\xi }_h{I}_2\left({\nu }_0\right)\right]}^2}{I}_4\left(\nu \left(\xi \right)\right){\left(\frac{{\Sigma }_0{\mathrm{pc}}^2}{120M_{\odot }}\right)}^2\frac{M_{\odot }}{{\mathrm{pc}}^3}{\left(\frac{\mathrm{km}}{\mathrm{s}}\right)}^2.\hfill \end{array}$$

(53)

That is, $M\left(r\right)+M_{BH}$ is the total mass inside a sphere of radius r including the mass of the central black hole.

Notice that both $M\left(r\right)$ and $M_{BH}$ at fixed ${\Sigma }_0$ do scale with the WDM particle mass as $m^{-\frac{16}{5}}$.

In particular, the halo galaxy mass $M_h$ follows from Equation (50) at $r=r_h$:

$$M_h\equiv M\left(r_h\right)+M_{BH}=\frac{27312{\xi }_h^{\frac{7}{5}}}{{\left[I_2\left({\nu }_0\right)\right]}^{\frac{3}{5}}}\left|{\nu }^{\prime }\left({\xi }_h\right)\right|{\left(\frac{2\mathrm{keV}}{m}\right)}^{\frac{16}{5}}{\left(\frac{{\Sigma }_0{\mathrm{pc}}^2}{120M_{\odot }}\right)}^{\frac{3}{5}}{M}_{\odot }.$$

(54)

The phase–space density $Q\left(r\right)$ follows from Equations (48) and (51) as

$$Q\left(r\right)\equiv \frac{\rho \left(r\right)}{{\sigma }^3\left(r\right)}=3\sqrt{3}\frac{\rho \left(r\right)}{<v^2{>}^{\frac{3}{2}}\left(r\right)}=\frac{\sqrt{125}}{3{\pi }^2}\frac{m^4}{{\hslash }^3}\frac{I_2^{\frac{5}{2}}\left(\nu \left(\xi \right)\right)}{I_4^{\frac{3}{2}}\left(\nu \left(\xi \right)\right)}.$$

(55)

Notice that $Q\left(r\right)$ turns out to be independent of $T_0$ and ${\Sigma }_0$. In addition, $Q\left(r\right)/m^4$ has no explicit dependence on the DM particle mass.

For a fixed value of the surface density ${\Sigma }_0$, the solutions of the Thomas–Fermi Equation (23) are parametrized by two parameters: the dimensionless central radius ${\xi }_0$ and the constant A characteristic of the chemical potential behavior of Equation (32) at the center $\xi \to 0$.

Additionally, at fixed surface density ${\Sigma }_0$, the halo mass $M_h$, the black hole mass $M_{BH}$, the characteristic length $l_0$, the density ${\rho }_0$ and the effective temperature $T_0$ are only functions of ${\xi }_0$ and the constant A.

The circular velocity $v_c\left(r\right)$ is defined through the virial theorem as

$$v_c\left(r\right)\equiv \sqrt{\frac{G\left[M\left(r\right)+M_{BH}\right]}{r}},$$

(56)

and it is directly related by Equation (27) to the derivative of the chemical potential as

$$v_c\left(r\right)=\sqrt{-\frac{r}{m}\frac{d\mu }{dr}}=\sqrt{-\frac{T_0}{m}\frac{d\nu }{dln\xi }}.$$

(57)

Expressing $T_0$ in terms of the surface density ${\Sigma }_0$ using Equation (42), we have, for the circular velocity, the explicit expression

$$v_c\left(r\right)=5.2537\frac{\sqrt{-\xi {\nu }^{\prime }\left(\xi \right)}}{{\left[{\xi }_h{I}_2\left({\nu }_0\right)\right]}^{\frac{2}{5}}}{\left(\frac{2\mathrm{keV}}{m}\right)}^{\frac{4}{5}}{\left(\frac{{\Sigma }_0{\mathrm{pc}}^2}{120M_{\odot }}\right)}^{\frac{2}{5}}\frac{\mathrm{km}}{\mathrm{s}}.$$

(58)

For $r\to 0$, the circular velocity $v_c\left(r\right)$ grows due to the black hole field as

$$v_c\left(r\right)\stackrel{{}_{r\to 0}}{=}\sqrt{\frac{T_0}{m}\frac{r_0}{r}},$$

(59)

where we used Equations (24) and (57).

2.4. Galaxy Properties in the Diluted Boltzmann Regime

In the diluted Boltzmann regime, ${\nu }_0\lesssim -5$ corresponding to large galaxies $M_h\gtrsim {10}^6{M}_{\odot }$, we find for the main galaxy magnitudes, the following analytic expressions:

$$\begin{array}{ccc}\hfill & & M_h=1.75572{\Sigma }_0{r}_h^2,r_h=68.894\sqrt{\frac{M_h}{{10}^6{M}_{\odot }}\frac{120M_{\odot }}{{\Sigma }_0{\mathrm{pc}}^2}}\mathrm{pc}\hfill \end{array}$$

(60)

$$\begin{array}{ccc}& & T_0=8.7615\times {10}^{-3}\sqrt{\frac{M_h}{{10}^6{M}_{\odot }}}\frac{m}{2\mathrm{keV}}\sqrt{\frac{{\Sigma }_0{\mathrm{pc}}^2}{120M_{\odot }}}\mathrm{K}\hfill \end{array}$$

(61)

$$\begin{array}{ccc}& & \rho \left(r\right)=5.19505{\left(\frac{M_h}{{10}^4{M}_{\odot }}\frac{{\Sigma }_0{\mathrm{pc}}^2}{120M_{\odot }}\right)}^{\frac{3}{4}}{\left(\frac{m}{2\mathrm{keV}}\right)}^4{e}^{\nu \left(\xi \right)}\frac{M_{\odot }}{{\mathrm{pc}}^3}\hfill \end{array}$$

(62)

$$\begin{array}{ccc}& & v_c^2\left(r\right)=33.9297\sqrt{\frac{M_h}{{10}^6{M}_{\odot }}\frac{{\Sigma }_0{\mathrm{pc}}^2}{120M_{\odot }}}\left|\frac{d\nu \left(\xi \right)}{dln\xi }\right|{\left(\frac{\mathrm{km}}{\mathrm{s}}\right)}^2,\hfill \end{array}$$

(63)

$$\begin{array}{ccc}& & v_c^2\left(r_h\right)=62.4292\sqrt{\frac{M_h}{{10}^6{M}_{\odot }}\frac{{\Sigma }_0{\mathrm{pc}}^2}{120M_{\odot }}}{\left(\frac{\mathrm{km}}{\mathrm{s}}\right)}^2\hfill \end{array}$$

(64)

$$\begin{array}{ccc}& & M\left(r\right)+M_{BH}=7.88895\left|\frac{d\nu \left(\xi \right)}{dln\xi }\right|\frac{r}{\mathrm{pc}}\sqrt{\frac{M_h}{{10}^6{M}_{\odot }}\frac{{\Sigma }_0{\mathrm{pc}}^2}{120M_{\odot }}}.\hfill \end{array}$$

(65)

Equations (42) and (61) allow us to express the quantity ${\xi }_h{I}_2\left({\nu }_0\right)$ in terms of the observable galaxy magnitudes $M_h$ and ${\Sigma }_0$ for large galaxies $M_h\gtrsim {10}^6{M}_{\odot }$ in the diluted regime. We obtain from Equations (42) and (61)

$${\xi }_h{I}_2\left({\nu }_0\right)=0.772598{\left(\frac{{10}^6{M}_{\odot }}{M_h}\right)}^{\frac{5}{8}}{\left(\frac{2\mathrm{keV}}{m}\right)}^2{\left(\frac{{\Sigma }_0{\mathrm{pc}}^2}{120M_{\odot }}\right)}^{\frac{3}{8}}$$

(66)

It is illuminating to express the radius $r_0$ Equation (28) in terms of $M_{BH}$ and ${\Sigma }_0$ for large galaxies $M_h\gtrsim {10}^6{M}_{\odot }$. It follows from Equations (41), (43) and (66) that

$$r_0=l_0{\xi }_0=126.762\sqrt{\frac{{10}^6{M}_{\odot }}{M_h}}\frac{M_{BH}}{{10}^6{M}_{\odot }}\sqrt{\frac{120M_{\odot }}{{\Sigma }_0{\mathrm{pc}}^2}}\mathrm{pc}$$

(67)

This explicitly provides the value of the radius $r_0$ in terms of the black hole mass $M_{BH}$, the halo mass $M_h$, and the reference surface density ${\Sigma }_0$.

In summary, we see the power of the WDM Thomas–Fermi approach to describe the structure and the physical state of galaxies in a clear way and in very good agreement with the observations.

3. Explicit Thomas–Fermi Galaxy Solutions with Central Supermassive Black Holes

We solve here the Thomas–Fermi Equation (23) with the boundary conditions (32) for a galaxy with a central black hole.

3.1. Local Thermal Equilibrium in the Galaxy

In Ref. [13], using the Eddington equation for dark matter in galaxies and observed density profiles, it is shown that the DM halo is realistically a self-gravitating thermal gas for $r\lesssim R_{virial}$. More precisely, the DM halo can be consistently considered in a local thermal equilibrium situation with (i) a constant temperature $T_0$ for $r\lesssim 3r_h$, and (ii) a space-dependent temperature $T\left(r\right)$ for $3r_h<r\lesssim R_{virial}$, which slowly decreases with r. $T\left(r\right)$ outside the halo radius nicely follows the decrease in the circular velocity squared $T_c\left(r\right)$ [13]. These results are physically understood because thermalization is more easy achieved in the inner regions due to the fact that the gravitational interaction is stronger than in the external regions where instead virialization occurs. The slow decreasing in the temperature $T\left(r\right)$ with the halo radius consistently corresponds to a transfer flux of the kinetic energy into potential energy. These results were derived from empirical observed density profiles, which do not have information of the regions near the central black hole.

The constant temperature $T_0$ for $r\lesssim 3r_h$ turns out to be in the Kelvin scale for a DM particle mass in the kiloelectron volt scale [12].

To implement the Thomas–Fermi approach for a galaxy plus a central black hole, we take into account the results of Ref. [13]. We simply set the WDM temperature to be a constant $T_0$, except in the vicinity of the central black hole. We do not assume WDM thermalization near the central black hole where the black hole force is strong but we assume virialization. Namely, the WDM square velocity is determined by the black hole gravitational field through virialization.

In summary, we have the following:

• Near the central black hole, the space-dependent temperature is given by equipartition and the virial theorem

  $$T_c\left(r\right)=\frac{m}{3}{v}_c^2\left(r\right)=\frac{Gm}{3r}{M}_{BH}=\frac{T_0{\xi }_0}{3\xi }$$

  (68)

  where we used Equations (19) and (28). We use this temperature $T_c\left(r\right)$ for $\xi \le {\xi }_0/3$. $T_0$ is given by Equation (42).
• For $\xi \ge {\xi }_0/3$ we set

  $$T_c\left(r\right)=T_0.$$
  Here, the circular temperature $T_c\left(r\right)$ associated to the velocity squared is given by

  $$T_c\left(r\right)=\frac{m}{3}\frac{G[M\left(r\right)+M_{BH}]}{r},$$

  (69)

  where $M\left(r\right)+M_{BH}$, the mass of the galaxy inside the radius r including the BH mass $M_{BH}$, is given by Equation (50). Inserting Equation (50) into Equation (69) and using Equation (42) yields

  $$T_c\left(r\right)=\frac{1}{3}\xi \left|{\nu }^{\prime }\left(\xi \right)\right|T_0.$$

  (70)
  Near the central black hole, that is, for $\xi \le {\xi }_0/3$, the chemical potential $\nu \left(\xi \right)$ is given by Equation (28). Inserting Equation (28) into Equation (70) yields Equation (68) as it must be.
• We find from our extensive numerical calculations that the halo is thermalized at the uniform temperature $T_0$ and matches the circular temperature $T_c\left(r\right)$ by $r\sim 3r_h$. This picture is similar to the picture found in the absence of the central black hole which follows from the observed density profiles in the Eddington-like approach to galaxies [13]. We obtain here in the Thomas–Fermi approach and in the presence of a central supermassive black hole that the halo is thermalized at a uniform temperature $T_0$ inside $r\lesssim 3r_h$ which matches the circular temperature $T_c\left(r\right)$ at $r\sim 3r_h$ (see Figure 4).
• In summary, each galaxy solution with a central black hole depends only on two free parameters: the dimensionless constants ${\xi }_0$ and A in Equation (32). We have a two-parameter family of Thomas–Fermi galaxy solutions with a central supermassive black hole parametrized by ${\xi }_0$ and A.
  The black hole mass $M_{BH}$ grows when ${\xi }_0$ grows as shown by Equation (45). Notice that $M_{BH}$ does not simply grow linearly with ${\xi }_0$ due to the presence of the factor

  $${\left[{\xi }_h{I}_2\left({\nu }_0\right)\right]}^{-\frac{3}{5}},$$

  in Equation (45).

From our extensive numerical calculations, we find that the galaxy mass increases and the galaxy size increases when the constant $\left|A\right|$, characteristic of the the central behavior of $\nu \left(\xi \right)$ for $\xi \to 0$ Equation (32) increases. This is similar to the case in the absence of central black holes, where $A=\nu \left(0\right)$ [9,10,12].

3.2. Thomas–Fermi Equations with r-Dependent Temperature Tc(r)

For a r-dependent temperature $T_c\left(r\right)$, the normalized energy density $I_2\left(\nu \right)$ (recall Equation (21)) takes the form

$$I_2\left(\nu \right)=3{\int }_0^{\infty }{y}^{2}dy\sqrt{1+\frac{2y^2}{\tau }}{\Psi }_{FD}\left({\displaystyle \frac{T_0}{T_c\left(r\right)}\left[\tau \left(\sqrt{1+\frac{2y^2}{\tau }}-1\right)-\nu \right]}\right),$$

(71)

which becomes Equation (21) for a constant temperature $T_c\left(r\right)=T_0$, that is in the region $\xi \ge {\xi }_0/3$, i.e., $r\ge r_0/3$.

Near the BH, for $\xi \le {\xi }_0/3$, we have from Equation (68),

$$\frac{T_0}{T_c\left(r\right)}=\frac{3\xi }{{\xi }_0}.$$

(72)

Beyond $r=3r_h$, using Equation (70), these quantities take the values

$$\frac{T_0}{T_c\left(r\right)}=\frac{3}{\xi |{\nu }^{\prime }\left(\xi \right)|}$$

(73)

Notice that $T_c\left(r\right)$ grows for $r\to 0$ as $1/r$ due to the BH presence; Equation (68). On the contrary, $T_c\left(r\right)$ decreases with increasing $r>3r_h$.

For a density profile scaling at large r, $r>3r_h$, as $r^{-2\alpha }$ we find $T_c\left(r\right)\sim r^{2(1-\alpha )}$. Because observations favor $\alpha \sim 1.5>1$, $T_c\left(r\right)$ decreases with increasing $r>3r_h$, as in the case where the black hole is absent [13].

3.3. Examples of Thomas–Fermi Galaxy Solutions with a Central Supermassive Black Hole

We consider here three realistic examples: a small mass galaxy, a medium mass and a large mass galaxy. We choose as boundary conditions in Equation (32)

$$\begin{array}{ccc}\hfill & & {\xi }_0=1,A=0,\mathrm{small}\mathrm{size}\mathrm{galaxy}\hfill \\ & & {\xi }_0=7,A=-10,\mathrm{medium}\mathrm{size}\mathrm{galaxy}\hfill \\ & & {\xi }_0=9,A=-15,\mathrm{large}\mathrm{size}\mathrm{galaxy}.\hfill \end{array}$$

(74)

These values are illustrative and yield realistic galaxies with a supermassive central black hole as we see below.

Indeed, we find realistic solutions for a large manifold of boundary conditions.

To compute these solutions, we set as reference values $m=2$ keV and ${\Sigma }_0=120M_{\odot }/{\mathrm{pc}}^2$.

The present solutions allow to characterize the WDM properties that show up in the different halo regions according to the distance to the central black hole.

For the three representative galaxy solutions Equation (74), we plot in Figure 1 the dimensionless chemical potential ${log}_{10}\nu \left(\xi \right)$ versus the dimensionless radius ${log}_{10}(\xi /{\xi }_h)={log}_{10}(r/r_h)$, $r_h$ being the halo radius (and ${\xi }_h$ the dimensionless one); in Figure 2, we plot the derivative ${log}_{10}|d\nu \left(\xi \right)/dx|$ vs. ${log}_{10}(r/r_h)$; and in Figure 3, we plot the density profiles ${log}_{10}[\rho \left(\xi \right)/{\rho }_0]$ vs. ${log}_{10}(r/r_h)$, (recall that ${\rho }_0\equiv \rho \left({\xi }_i\right)$, ${\xi }_i$ being the dimensionless influence radius of the black hole Equation (31), that is, when the black hole and dark matter gravitational forces become equal).

Notice that the curves for the three galaxy solutions are of similar size thanks to the use of the rescaled variable $r/r_h=\xi /{\xi }_h$ in the abscissa. The dimensionless halo radius ${\xi }_h$ increases by five orders of magnitude going from the small to the large size galaxy.

For the relevant parameters of the solutions, we obtain the following results:

$$\begin{array}{ccc}\hfill & & \mathbf{Small}\mathbf{size}\mathbf{galaxy}:\hfill \\ & & r_i=221\mathrm{pc},r_h=452\mathrm{pc},T_0=0.0978\mathrm{K},\hfill \\ & & \sqrt{<v^2>}(r\gtrsim r_A)=35.48\mathrm{km}/\mathrm{s},\sqrt{<v^2>}(r\lesssim r_A)=383.75\mathrm{km}/\mathrm{s},\hfill \\ & & M_h=7.678\times {10}^7{M}_{\odot },M_{vir}=8.582\times {10}^8{M}_{\odot },\hfill \\ & & M_{BH}=1.947\times {10}^5{M}_{\odot },r_{BH}^{Schw}=1.863\times {10}^{-8}\mathrm{pc},\hfill \\ & & {\rho }_0=1.797\times {10}^{-23}\mathrm{g}/{\mathrm{cm}}^3,\hfill \\ & & {\rho }_A=0.9878\times {10}^{-19}\mathrm{g}/{\mathrm{cm}}^3,M_A=8.767\times {10}^4{M}_{\odot },r_A=1.91\mathrm{pc}.\hfill \end{array}$$

(75)

$$\begin{array}{ccc}& & \mathbf{Medium}\mathbf{size}\mathbf{galaxy}:\hfill \\ & & r_i=54.3\mathrm{pc},r_h=210\mathrm{kpc},T_0=26.97\mathrm{K},\hfill \\ & & \sqrt{<v^2>}(r\gtrsim r_A)=559.8\mathrm{km}/\mathrm{s},\sqrt{<v^2>}(r\lesssim r_A)=6370.9\mathrm{km}/\mathrm{s},\hfill \\ & & M_h=9.022\times {10}^{12}{M}_{\odot },M_{vir}=8.222\times {10}^{13}{M}_{\odot },\hfill \\ & & M_{BH}=9.224\times {10}^7{M}_{\odot },r_{BH}^{Schw}=8.828\times {10}^{-6}\mathrm{pc},\hfill \\ & & {\rho }_0=3.867\times {10}^{-26}\mathrm{g}/{\mathrm{cm}}^3,\hfill \\ & & {\rho }_A=7.182\times {10}^{-15}\mathrm{g}/{\mathrm{cm}}^3,M_A=1.932\times {10}^7{M}_{\odot },r_A=0.2\mathrm{pc}.\hfill \end{array}$$

(76)

$$\begin{array}{ccc}& & \mathbf{Large}\mathbf{size}\mathbf{galaxy}:\hfill \\ & & r_i=21.66\mathrm{pc},r_h=8.237\times {10}^3\mathrm{kpc},T_0=1061\mathrm{K},\hfill \\ & & \sqrt{<v^2>}(r\gtrsim r_A)=3511.2\mathrm{km}/\mathrm{s},\sqrt{<v^2>}(r\lesssim r_A)=39591\mathrm{km}/\mathrm{s},\hfill \\ & & M_h=1.3753\times {10}^{16}{M}_{\odot },M_{vir}=3.3482\times {10}^{16}{M}_{\odot },\hfill \\ & & M_{BH}=1.8632\times {10}^9{M}_{\odot },r_{BH}^{Schw}=1.783\times {10}^{-4}\mathrm{pc},\hfill \\ & & {\rho }_0=0.9860\times {10}^{-27}\mathrm{g}/{\mathrm{cm}}^3,\hfill \\ & & {\rho }_A=2.9163\times {10}^{-12}\mathrm{g}/{\mathrm{cm}}^3,M_A=3.873\times {10}^8{M}_{\odot },r_A=0.074\mathrm{pc}.\hfill \end{array}$$

(77)

$M_A$ stands for the mass inside the radius $r_A$.

Notice that the obtained galaxy solutions have halo masses $M_h>{10}^6{M}_{\odot }$ and, therefore, belong to the dilute Boltzmann regime [12].

Let us now analyze Figure 1, Figure 2 and Figure 3. We start from the galaxy center and go toward the halo tail.

• Quantum to classical behavior: The central black hole strongly attracts the WDM and makes its density very high for $r<r_A$, where a compact quantum core gets formed. The dimensionless chemical potential $\nu \left(\xi \right)$ vanishes at $r=r_A$ and becomes negative for $r>r_A$. The density $\rho \left(r\right)$ drops several orders of magnitude immediately after $r_A$ as shown in Figure 3. $\nu \left(\xi \right)$ is negative for $r>r_A$, and the WDM exhibits there a classical Boltzmann behavior while the WDM exhibits a quantum behavior for $r<r_A$, where the chemical potential is large and positive. Therefore, the point $r_A$ where the chemical potential vanishes defines the transition from the quantum to classical behavior. In the quantum region $r<r_A$, the density exhibits a constant plateau as shown in Figure 3. Notice from Equation (75) that $r_A$ turns to be much larger than the Schwarzschild radius of the central black hole $r_A\gg r_{BH}^{Schw}$.
• Black hole influence radius $r_i$: For $r<r_i$, the black hole gravitational field dominates over the dark matter gravitational field. The influence radius $r_i=l_0{\xi }_i$ is defined by Equation (31). The black hole influence radius turns out to be larger than the radius $r_A$ where the chemical potential vanishes, $r_i>r_A$. The region $r_A<r<r_i$ is dominated by the central black hole and the WDM exhibits there a classical behavior. For $r\lesssim r_i$, we see from Figure 1 and Figure 2 that both $\nu \left(\xi \right)$ and $\left|d\nu \right(\xi )/dx|$ follow the behavior dictated by the central black hole. That is, from Equation (32)

  $$\nu \left(\xi \right)\simeq {\xi }_0{e}^{-x}+A={\xi }_0\frac{r_h}{r}+A,|d\nu \left(\xi \right)/dx|\simeq {\xi }_0{e}^{-x}={\xi }_0\frac{r_h}{r},x\equiv ln\frac{r}{r_h},$$

  which produce straight lines on the left part of the logarithmic plots of Figure 1 and Figure 2. $r\gtrsim r_i,\nu \left(\xi \right)$ and $\left|d\nu \right(\xi )/dx|$ are dominated by the WDM and exhibit a similar behaviour to that of the Thomas–Fermi solutions without a central black hole [9,10,11,12].
  Figure 3 shows that the local density behavior is dominated by the black hole for $r\lesssim r_i$. Coherently, for $r\gtrsim r_i$ the WDM gravitational field dominates over the black hole field and the galaxy core shows up for $r_i\lesssim r\lesssim r_h$ in Figure 3. For medium and large galaxies, the core is seen as a plateau. At the same time, the chemical potential is negative for $r\gtrsim r_i>r_A$, and the WDM is a classical Boltzmann gas in this region.
• Halo radius $r_h$: Finally, we see in Figure 3 the tail of the WDM density profile for $r\gtrsim r_h$, which exhibits a similar shape for all three galaxy solutions.
• WDM thermalization: As shown by Figure 4, the velocity dispersion $<v^2>\left(r\right)$ is constant as a function of r, indicating a thermalized WDM with temperature

  $$T_0=\frac{1}{3}m<v^2>.$$
  WDM is thermalized as in the absence of the central black hole [12]. This is consistent with the use of a thermal Fermi–Dirac distribution function for $r\ge r_0/3$.
• We also plot in Figure 4 the circular velocity given by Equation (58) vs. ${log}_{10}r/r_h$. For $r>r_h$, the circular velocity tends to the velocity dispersion as obtained from the Eddington equation for realistic density profiles [13]. For $r\to 0$, the circular velocity grows as in Equation (59) due to the central black hole field.
• WDM inside a small core of radius $r_A$ is in a quantum gas high density state, namely, a Fermi nearly degenerate state with nearly constant density ${\rho }_A$. For the three galaxy solutions, the values of $r_A$ and ${\rho }_A$ are given by Equations (75)–(77). Notice that the density ${\rho }_A$ is orders of magnitude larger than its values for $r>r_A$, where the WDM is in the classical Boltzmann regime.
• We also give in Equations (75)–(77) the WDM mass $M_A$ inside $r_A$. $M_A$ represents only a small fraction of the halo or virial mass of the galaxy, but it is a significant fraction of the black hole mass $M_{BH}$. We see from Equations (75)–(77) that $M_A$ amounts to 20% of $M_{BH}$ for the medium and large galaxies and 45% for the small galaxy.

3.4. Quantum Physics in Galaxies

In order to determine whether a physical system has a classical or quantum nature, one has to compare the average distance between particles d with their de Broglie wavelength ${\lambda }_{dB}$.

The de Broglie wavelength of DM particles in a galaxy can be expressed as

$${\lambda }_{dB}\left(r\right)=\frac{h}{mv\left(r\right)},$$

(78)

where h stands for the Planck constant and $v\equiv \sqrt{<v^2>}$ is the velocity dispersion, while the average interparticle distance d at r can be estimated as

$$d\left(r\right)={\left(\frac{m}{\rho \left(r\right)}\right)}^{\frac{1}{3}}$$

(79)

Here, $\rho \left(r\right)$ is the local density in the galaxy core.

We can measure the classical or quantum character of the system by considering the ratio

$$\mathcal{R}\left(r\right)\equiv \frac{{\lambda }_{dB}\left(r\right)}{d\left(r\right)}$$

For $\mathcal{R}\lesssim 1$, the system is of a classical dilute nature, while for $\mathcal{R}\gtrsim 1$, it is a macroscopic quantum system.

By using the phase–space density Equation (55),

$$Q\left(r\right)=\frac{\rho \left(r\right)}{{\sigma }^3\left(r\right)},$$

and Equations (78) and (79), $\mathcal{R}\left(r\right)$ can be expressed solely in terms of the phase–space density $Q\left(r\right)$ as [9,10,12]

$$\mathcal{R}\left(r\right)=\frac{2\pi }{\sqrt{3}}\hslash {\left(\frac{Q\left(r\right)}{m^4}\right)}^{\frac{1}{3}}.$$

(80)

Inserting the phase–space density Equation (55) into Equation (80) yields, for the ratio $\mathcal{R}\left(r\right)$,

$$\mathcal{R}\left(r\right)=2\sqrt{5}{\left(\frac{\pi }{81}\right)}^{\frac{1}{3}}\frac{I_2^{\frac{5}{6}}\left(\nu \left(\xi \right)\right)}{I_4^{\frac{1}{2}}\left(\nu \left(\xi \right)\right)}=1.513805\frac{I_2^{\frac{5}{6}}\left(\nu \left(\xi \right)\right)}{I_4^{\frac{1}{2}}\left(\nu \left(\xi \right)\right)}.$$

(81)

In Figure 5, we plot ${log}_{10}\mathcal{R}$ vs. ${log}_{10}(r/r_h)$ for the three representative galaxy solutions.

Comparing now Figure 1 and Figure 5, we see that $\nu \left(\xi \right)$ changes sign, indicating the transition from the quantum to the classical galaxy regime precisely at the same point where $\mathcal{R}\simeq 1$, as it must be. This result shows the power and consistency of our treatment.

4. Systematic Study of the Thomas–Fermi Galaxy Solutions with a Central Supermassive Black Hole

We present in this section our extensive study of the Thomas–Fermi galaxy solutions with a central supermassive black hole.

As stated in Section 3.1, each galaxy solution with a central black hole depends only on two free parameters: ${\xi }_0$ and A defining the boundary conditions near the center (see Equation (32)), ${\xi }_0$ being the dimensionless central radius and A characterizing the central chemical potential behavior.

We plot in Figure 6 the halo mass ${log}_{10}{M}_h$ vs. A for fixed values of ${\xi }_0$.

We see that the halo mass $M_h$ increases with ${\xi }_0$ at fixed A. In addition, at fixed ${\xi }_0>0$, $M_h$ increases when the absolute value of A increases.

There is an important qualitative difference between galaxy solutions with a black hole (${\xi }_0>0$ ), and galaxy solutions without a black hole (${\xi }_0=0$). In the absence of the central black hole, the halo mass $M_h$ monotonically decreases when A increases until $M_h$ reaches a minimal value, which is the degenerate quantum limit at zero temperature [9,10,12]:

$$M_h^{min}=3.0999\times {10}^4{\left(\frac{2\mathrm{keV}}{m}\right)}^{\frac{16}{5}}{\left(\frac{{\Sigma }_0{\mathrm{pc}}^2}{120M_{\odot }}\right)}^{\frac{3}{5}}{M}_{\odot },T_0^{min}=0,\mathbf{without}\mathbf{central}\mathbf{black}\mathbf{hole}.$$

(82)

In the presence of a central black hole, we find that the halo mass takes as minimal value

$$M_h^{min}=6.892\times {10}^7{\left(\frac{2\mathrm{keV}}{m}\right)}^{\frac{16}{5}}{\left(\frac{{\Sigma }_0{\mathrm{pc}}^2}{120M_{\odot }}\right)}^{\frac{3}{5}}{M}_{\odot },\mathbf{with}\mathbf{central}\mathbf{black}\mathbf{hole}.$$

(83)

This situation is clearly shown in Figure 6. The value of $M_h^{min}$ with a central black hole is $2.2233\times {10}^3$ times larger than without the black hole. Notice that the small galaxy solution Equation (75) is just 11% larger in halo mass than the minimal galaxy Equation (83) with a central black hole.

We conclude that galaxies possessing a central black hole are in the dilute Boltzmann regime because of their large mass $M_h>M_h^{min}$ [12]. In addition, compact galaxies with $M_h<M_h^{min}$, in particular, ultracompact galaxies in the quantum regime $M_h<2.3\times {10}^6{M}_{\odot }$ [12], cannot harbor central black holes.

We plot in Figure 7 the galaxy temperature ${log}_{10}{T}_0/\mathrm{K}$ vs. the characteristic central chemical potential constant A for fixed values of ${\xi }_0$.

Similarly to the halo mass $M_h$, the galaxy temperature $T_0$ increases with ${\xi }_0$ at fixed A. On the other hand, at fixed ${\xi }_0>0$, $T_0$ increases when the absolute value of A increases.

In the absence of a black hole, the galaxy temperature $T_0$ tends to zero for $A\to \infty$, while in the presence of a central black hole, we find that $T_0$ is always larger than the non-zero minimal value:

$$T_0^{min}=0.06928{\left(\frac{2\mathrm{keV}}{m}\right)}^{\frac{3}{5}}{\left(\frac{{\Sigma }_0{\mathrm{pc}}^2}{120M_{\odot }}\right)}^{\frac{4}{5}}\mathrm{K},\mathbf{with}\mathbf{central}\mathbf{black}\mathbf{hole}.$$

(84)

The presence of the supermassive black hole heats up the dark matter gas and prevents it from becoming an exact degenerate gas at zero temperature. The minimal mass and size and most compact galaxy state with a supermassive black hole is a nearly degenerate state at very low temperature as seen from Equation (84).

The mass of the supermassive black hole $M_{BH}$ monotonically increases with ${\xi }_0$ at fixed A. In addition, for ${\xi }_0<0.3$, that is, for small supermassive black holes, and all A, the galaxy parameters, such as halo mass $M_h$, halo radius $r_h$, virial mass $M_{vir}$ and galaxy temperature $T_0$, become independent of ${\xi }_0$, showing a limiting galaxy solution. Only the BH mass depends on ${\xi }_0$ in this regime.

We depict in Figure 8 the black hole mass ${log}_{10}{M}_{BH}$ vs. the halo mass ${log}_{10}{M}_h$. We see that $M_{BH}$ is a two-valued function of $M_h$. For each value of $M_h$, there are two possible values for $M_{BH}$. These two values of $M_{BH}$ for a given $M_h$ are quite close to each other. This two-valued dependence on $M_h$ is a direct consequence of the dependence of $M_h$ on A shown in Figure 6.

We see at the branch points on the left in Figure 8 the minimal galactic halo mass $M_h^{min}$ Equation (83) when a supermassive black hole is present.

At fixed ${\xi }_0$, as shown in Figure 8, the central black hole mass $M_{BH}$ scales with the halo mass $M_h$ as

$$M_{BH}=D\left({\xi }_0\right)M_h^{\frac{3}{8}},$$

where $D\left({\xi }_0\right)$ is an increasing function of ${\xi }_0$.

• We plot in Figure 9 the halo galaxy mass ${log}_{10}{M}_h$ vs. the galaxy temperature ${log}_{10}{T}_0/\mathrm{K}$. The halo mass $M_h$ grows when $T_0$ increases. Colder galaxies are smaller. Warmer galaxies are larger.
  We see at the branch points in Figure 9 the minimal galaxy temperature $T_0^{min}$ Equation (84) when a supermassive black hole is present.
• We find galaxy solutions with central black holes for arbitrarily small values ${\xi }_0>0$ and correspondingly arbitrarily small central BH mass. There is no emergence of a minimal mass for the central black hole.

4.1. Universal Scaling Relations in the Presence of Central Black Holes

We plot in Figure 10 the ordinary logarithm of the halo radius ${log}_{10}{r}_h$ vs. the ordinary logarithm of the halo mass ${log}_{10}{M}_h$ for galaxies with central black holes of many different masses. We see in all cases that $M_h$ scales as $r_h^2$. The same scaling was found in the Thomas–Fermi approach to galaxies in absence of black holes [9,10,12].

The halo mass in the absence of a central black hole behaves in the Thomas–Fermi approach as [12]

$$M_h=1.75572{\Sigma }_0{r}_h^2,\mathbf{without}\mathbf{central}\mathbf{black}\mathbf{hole}.$$

(85)

The proportionality factor in this scaling relation is confirmed by the galaxy data [12].

In the presence of a central black hole, we find in the Thomas–Fermi approach an analogous relation

$$M_h=b{\Sigma }_0{r}_h^2,\mathbf{with}\mathbf{central}\mathbf{black}\mathbf{hole},$$

(86)

where the coefficient b turns to be of order unity.

We plot in Figure 11 the coefficient b as a function of the halo mass $M_h$. We see that except for halo masses near the minimum halo mass $M_h^{min}$, b in the presence of a central black hole takes values up to 10% below its value in the absence of a central black hole Equation (85). For halo masses near $M_h^{min},b$ increases, reaching values $b\le 4$. For very large halos and central black holes, b could be as small as about $1.6$.

That is, the coefficient b changes at most by a factor from $1/2$ up to 2, while the halo mass $M_h$ varies by ten orders of magnitude. As shown by Figure 11, the coefficient b turns out to be a two-valued function of $M_h$.

The coefficient b turns out to be independent of the precise value of the WDM particle mass m. This is due to the fact that the scaling relation Equation (86) as well as Equation (85) apply in the classical Boltzmann regime of the galaxy.

In summary, the scaling relation Equation (86) and the coefficient b turn out to be remarkably robust.

We plot in Figure 12 the ordinary logarithm of the halo radius ${log}_{10}{r}_h$ versus the ordinary logarithm of the central black hole mass ${log}_{10}{M}_{BH}$ for many galaxy solutions. The halo radius $r_h$ turns to be a double-valued function of $M_{BH}$. Remarkably, $r_h$ scales for fixed ${\xi }_0$ as

$$r_h=C\left({\xi }_0\right)M_{BH}^{\frac{4}{3}}.$$

(87)

The constant $C\left({\xi }_0\right)$ turns out to be a decreasing function of ${\xi }_0$.

4.2. Pressure and Equation of State in the Presence of Central Black Holes

The local pressure $P\left(r\right)$ is given by Equation (53). In Figure 13, we plot ${log}_{10}P\left(r\right)$ vs. ${log}_{10}(r/r_h)$ for the three representative galaxy solutions. We see that $P\left(r\right)$ monotonically decreases with r. The pressure $P\left(r\right)$ takes huge values in the quantum (high density) region $r<r_A$, and then it sharply decreases entering the classical (dilute) region $r>r_A$.

In Figure 14, we plot ${log}_{10}P\left(r\right)$ vs. ${log}_{10}\rho \left(r\right)/{\rho }_0$ for the three galaxy solutions with central SMBH. We see that the three curves almost coincide and that they are almost straight lines of the unit slope. That is, the equation of state is in very good approximation of a perfect gas equation of state. This perfect gas equation of state stems from the fact that galaxies with central black holes have halo masses $M_h>M_h^{min}$, Equation (83), and therefore belong to the dilute Boltzmann classical regime [12]. The equation of state turns out to be a local (r-dependent) perfect gas equation of state because of the gravitational interaction (WDM self-gravitating perfect gas).

Indeed, for galaxies with central black holes, the WDM is in a quantum (highly compact) regime inside the quantum radius $r_A$. However, because $r_A$ is in the parsec scale or smaller (see Equations (75)–(77)), the bulk of the WDM is in the Boltzmann classical regime, which is consistently reflected in the perfect gas equation of state behavior.

5. Conclusions

• We presented here a novel study of galaxies with central supermassive black holes, which shows itself as fruitful and enlightening. This framework stresses the key role of gravity and warm dark matter in structuring galaxies with their central supermassive black holes and provides correctly the major physical quantities to be first obtained for the galaxy–black-hole system: the masses, sizes, densities, velocity dispersions, and their internal physical states. This also yields a physical and precise characterization of whether they are compact, ultracompact, low density or large dilute galaxies, encompassed with their classical physics and quantum gas physical properties.
• We thus found different regions structuring internally the halo of the galaxy from the vicinity of the supermassive central black hole region to the external regions or virial radius. For all galaxies harboring a central black hole, there is a transition from the quantum to the classical regime going from the more compact inner regions, which are in a quantum gas state, to the classical dilute regions in a Boltzmann-like state. This is accompanied by a decreasing in the local temperature from the central warmer regions to the colder external ones. The SMBH heats the DM near around and prevents it from becoming exactly degenerated at zero temperature. Although the inner DM quantum core is highly compact in a nearly degenerate quantum gas state, it is not at zero temperature. Inside $r\lesssim 3r_h$, the halo is thermalized at a uniform or slowly varying local temperature $T_0$, which tends to the circular temperature $T_c\left(r\right)$ at $r\sim 3r_h$.
• We formulated the problem of galaxy structure with central supermassive black holes in the WDM Thomas–Fermi approach and found the main physical magnitudes and properties of the galaxy plus black hole system. We solved the corresponding equations and boundary conditions, found three representative families of realistic galaxy solutions (small, medium and large size galaxies) with central supermassive black holes, and provided a systematic analysis of the new quantum and classical physics properties of the system. The approach naturally incorporates the quantum pressure of the self-gravitating dark matter fermions, showing its full power and clearness to treat the galaxy plus supermassive black hole system. The realistic astrophysical masses of supermassive black holes are naturally obtained in this framework.
• We found the main important physical differences between galaxies with and without the presence of a central black hole. In the presence of a central black hole, both the quantum and classical behaviors of the dark matter gas do co-exist generically in any galaxy from the compact small galaxies to the dilute large ones, and a novel galaxy halo structure with three regions show up.
• The transition from the quantum to classical regime occurs at the point $r_A$, where the chemical potential vanishes and which is, in addition, precisely and consistently, the point where the particle wavelength and the interparticle distance are equal (their ratio being a measure of the quantum or classical properties of the system). The quantum radius $r_A$ is larger for the smaller and more compact galaxies and diminishes with increasing galaxy and black hole masses for the large dilute galaxies. The WDM mass $M_A$ inside the quantum galaxy radius $r_A$ represents only a small fraction of the halo mass $M_h$ or virial mass of the galaxy, but it is a significant fraction of the black hole mass $M_{BH}$. $M_A$ amounts to 20% of $M_{BH}$ for the medium and large galaxies and 45% for the small galaxies.
• The minimal mass $M_h^{min}$ that a galaxy should have in order to harbor SMBHs was found, which shows, among other features, why compact or ultracompact galaxies (in the range ${10}^4{M}_{\odot }<M_h<{10}^7{M}_{\odot }$) cannot harbor necessarily central black holes.
• Novel universal scaling relations in the presence of a central supermassive black hole were derived: black hole mass $M_{BH}$, halo radius $r_h$ and halo mass $M_h$ relations. The black hole mass $M_{BH}$ turned out to be a two-valued function of the halo mass $M_h$ and size $r_h$, and we found the local pressure and equation of state of the galaxy–black-hole system and its different regimes.
• A more detailed quantitative account of the main features and results of this paper is presented in the Introduction, Section 1.
• The circular velocities, galactic rotation curves in the WDM halo with central SMBH are discussed, self-consistently computed and plotted in Section 2, Equations (56)–(59), (63) and (64) and Figure 4 of this paper, together with the obtained velocity dispersions. These results are presented for the three family of galaxy solutions with SMBHs obtained here with this approach: small or dwarf galaxies, medium galaxies and large galaxies. They remarkably encompass the other relevant physical magnitudes obtained for these systems in this paper with the same approach. Toward the central regions, the circular velocity grows as in Equation (59) due to the central black hole field. As seen from Figure 4, the dispersion velocity is constant in the Boltzmann (outer or classical) region and in the quantum (inner or compact) region, indicating WDM thermalization. For $r>r_h$, the circular velocity tends to the velocity dispersion. Remarkably, this result confirms the same behavior we obtained independently with a different approach (the inverse problem or the Eddington integral equation for galaxies which we developed in Ref. [13]), namely, given the observed density profiles as input, the velocities, pressure and other galaxy magnitudes are obtained and analyzed as output. The observed density profiles being, by definition, real realistic data, the obtained results from them are valid, realistic magnitudes. Moreover, another robust verification of the kiloelectron volt WDM Thomas–Fermi approach is the 10 independent sets of observational data we used in Ref. [11] for galaxy masses from $5\times {10}^9{M}_{\odot }$ to $5\times {10}^{11}{M}_{\odot }$. And also for many other different observational data sets [48,49,50,51,52,53,54,55,56,57,58,59,60]. The theoretical and observational rotation curves do agree. In addition, they agree extremely well with the observational rotation curves described by the empirical Burkert profile for $r\ge 2r_h$ (they differ from each other by only $2.4$ percent). These results show the success of the kiloelectron volt WDM Thomas–Fermi approach to correctly describe the galaxy structures.
• We first investigated pure WDM galaxies with their central black holes because DM is, on average, the over-dominant component in galaxies, and it is reasonable then to investigate first the effects of gravity plus WDM. This is thus a first approximation, more precisely the zero order of a first approximation in which the visible matter component, baryons, can be incorporated to provide a most accurate and complete picture. We observed that these zero order results found here are already realistic, very good and robust results, and they set the basis and the direction for improvements and a more complete understanding.
• Baryons will provide corrections to this picture and will allow to study other processes in which ordinary matter naturally plays a role as the gas and star components, but baryons will not change drastically the pure WDM results found here, which are the structural galaxy and black hole properties, masses, sizes, their scaling and relations, density profiles, the classical and quantum natures of the halo regions and their physical, high-density, medium-density or dilute states, the halo thermalization and virialization.
• This predictive theory and the obtained classes of solutions include very well the different galaxy types through their generic and important physical quantitive properties, such as the pressure, density, equation of state, mass, halo structure, and central black holes. Thus, we have primarily three galaxy classes: large dilute galaxies, intermediate galaxies, and small compact galaxies, whatever their astronomical empirical/historical name. The Milky Way galaxy is one of the galaxies in the large dilute galaxy class we found with all the specific properties of this class, mass, structure and central SMBH. Messier 87 is a larger (“supergiant”) galaxy within the large class of galaxies we found, hosting, consequently, a bigger central SMBH (M87).
• As explained in the paper, the central quantum WDM gaz is relevant for the presence of the obtained central non-cusped cores and their correct sizes, and for the presence of the central SMBHs and their realistic mass values without any ad hoc prescription. Recall, for instance, Figure 3 of the paper, which displays the density $\rho \left(r\right)$ normalized at the influence radius $r_i$, vs. $r/r_h$ for the three family of galaxy solutions with central SMBHs we found, large dilute galaxies, intermediate galaxies, and small compact galaxies, covering the different types of galaxies with their central SMBHs. The Milky Way is within the large dilute galaxy class we found with all the characteristic properties of this class: mass, structure and central SMBH, namely $M_{BH}=4.100\times {10}^6{M}_{\odot }$, galaxy mass $M=(0.8-1.5)\times {10}^{12}{M}_{\odot }$ and $r_h=580+/-120\mathrm{kpc})$. Notice that in the quantum WDM gas region $r<r_A$, the density is constant, clearly exhibiting a plateau behavior corresponding to the quantum macroscopic Fermi DM gas behavior in such a region. Figure 3 shows that the local density behavior is dominated by the black hole for $r\lesssim r_i$. Coherently, for $r_i\lesssim r\lesssim r_h$, the WDM gravitational field dominates over the black hole field, and the galaxy core shows up. For medium and large galaxies, such as the Milky Way, the core is seen as a plateau. At the same time, the chemical potential is negative for $r>r_i>r_A$ and the WDM is a Boltzmann gas in this region.
  The first or primary “signatures” are the set of galactic physical magnitudes and structural properties: sizes, masses, cored density profiles and their correct sizes. In particular, dwarf galaxies appear to be a full quantum macroscopic system. Dwarf galaxies are really interesting to observe in this respect, as tracers of the quantum kiloelctron volt WDM nature in nearly degenerated states, their temperatures and properties. These are important features all found and provided by the same and one single approach, without tailored prescriptions, and without considering different approaches for each of the different computed magnitudes. Therefore, these are all “signatures” for this approach.
  These results consistently encompass the ones shown in Figure 2: the derivative of the chemical potential vs. $(r/rh)$ for the three families of galaxy solutions with central SMBH. For $r\lesssim r_i$, the behavior is dictated by the central black hole. For $r>r_i$, they are dominated by the WDM and in this region exhibit a similar behavior to the Thomas-Fermi galaxy solutions without a central SMBH [9,10,11,12]. For galaxies with central black holes, the WDM is in a quantum (highly compact) regime inside the quantum radius $r_A$. Because $r_A$ is in the parsec scale or smaller (see Equations (75)–(77)), the bulk of the WDM is then in the Boltzmann regime, e.g., Figure 13 and Figure 14. In the quantum gas (dense) region, the equation of state becomes steeper than the perfect gas. Notice the huge values of $P\left(r\right)$ in the quantum (high density) region $r<r_A$ and its sharp decrease entering the classical (dilute) region $r>r_A$, all consistent with the other results we found.
• In all the obtained results, and in the Introduction, we carefully compared the results and solutions we obtained in this paper for galaxy systems with a central black hole and without a central black hole. From our results here, we recover, in particular, the galaxy structures, the cores of quantum WDM and their right sizes, the velocity dispersions, the scaling relations, the equation of state and the other related results in the absence of black holes, which we already discussed in our previous works [9,10,11,12,13] in which the careful check for rotation curves, masses, scaling relations, velocities, are in full agreement with observations for the whole set of properties.
  Cored density profiles and their right size, halo masses, are in full agreement with the observations. The quantum DM nature in the central regions is not an exotic property: it is the quantum nature of the degenerate or nearly degenerate gaz of DM particles. Interaction is fully gravitational, namely, a self-gravitating and self-consistent WDM gas. The first or primary “ signatures” are, therefore, the set of galactic physical magnitudes and structural properties—the sizes, masses, central cored profiles, velocity distributions, and surface density we found and confronted to real astronomical observations. Other effects, such as the influence of such DM structures, could in turn exert on the propagation of generated gravitational waves, on the accretion processes, which are superimposed effects, or on the secondary dark matter processes or secondary signatures, a problem which would require individual analysis and is clearly beyond the scope of the present paper, which is devoted to the primary dark matter effects, namely the dark matter galactic structures. Those secondary effects, such as the orbits, diffusion and absorption in the different regions and regimes around the BH require the interaction in propagation with other non dark matter components, as electromagnetic effects and accretion plasmas are not the subject of this paper.
• For the primary objectives of obtaining the galaxy structural magnitudes, e.g., the realistic astrophysical masses of the galaxies, the realistic SMBH central masses, their sizes, velocities, cored density and pressure profiles, the Newtonian treatment is largely enough. Recall that the Thomas–Fermi approach is a statistical many body approach. Near the black hole horizon, there will appear effects of spiraling, orbiting, or a glory effect (180 degrees backscattering) but it does not truly affect the properties and magnitudes of the galaxy–black-hole system (and this paper is not devoted to test GR black hole, horizon or baryonic effects). The values of the relevant radii are as follows (besides the halo radius): the quantum galaxy radius $r_A$, the BH influence radius $r_i$, and the horizon black hole radius $r_{BH}^{Schw}$ are given by Equations (75)–(77). The horizon radius is always extremely small with respect to the other radii. For galaxies with virial masses from ${10}^{16}$ to ${10}^7{M}_{\odot }$, $r_A$ runs between $0.07$ and $1.90$ pc, respectively (as shown in Section 3.3), while the horizon radius of the central black hole runs from ${10}^{-4}$ to ${10}^{-8}$ pc for such range of galaxy masses, respectively; $r_i$ is larger than $r_A$:$r_i>r_A>>r_{BH}^{Schw}$. The important point in order to account for both the realistic galaxy and their central SMBH masses, their sizes, velocities, pressure profiles, density profiles and the core sizes, is the DM nature: kiloelectron volt WDM with its quantum and its relativistic treatment.
  Newtonian black holes have many common properties with general relativity black holes, and most importantly, they both have the same size. Recall that Newtonian and post-Newtonian approximation have proven to be remarkably effective, even in describing strong-field systems and astrophysical black hole systems (e.g., binary bhs) in spiraling toward a final merger (e.g., Ref. [61] and references therein). Of course, a fully GR treatment is needed to account for a causal space–time structure, central classical space–time curvature singularity, and precise tests of GR of the horizon or of the “no hair theorems”, for which inner orbits at milliparsec (mpc) distances need to be considered but not for the magnitudes of the galactic masses, sizes, or of their central SMBHs. The GR treatment minimally affects the obtained huge mass magnitude values. A high merit of the kiloelectron volt WDM approach is that it accounts naturally (with dark matter only) for the realistic astrophysical masses, sizes, density and velocity profiles, rotation curves, equation of state and structural properties of both galaxies and their central SMBHs.