Constraints on a Tidal Charge of the Supermassive Black Hole in M87* with the EHT Observations in April 2017
Abstract
1. Introduction
2. Motivation
3. An Analytical Expression for Shadow Radius as a Function of Charge
4. Constraints on a Tidal Charge
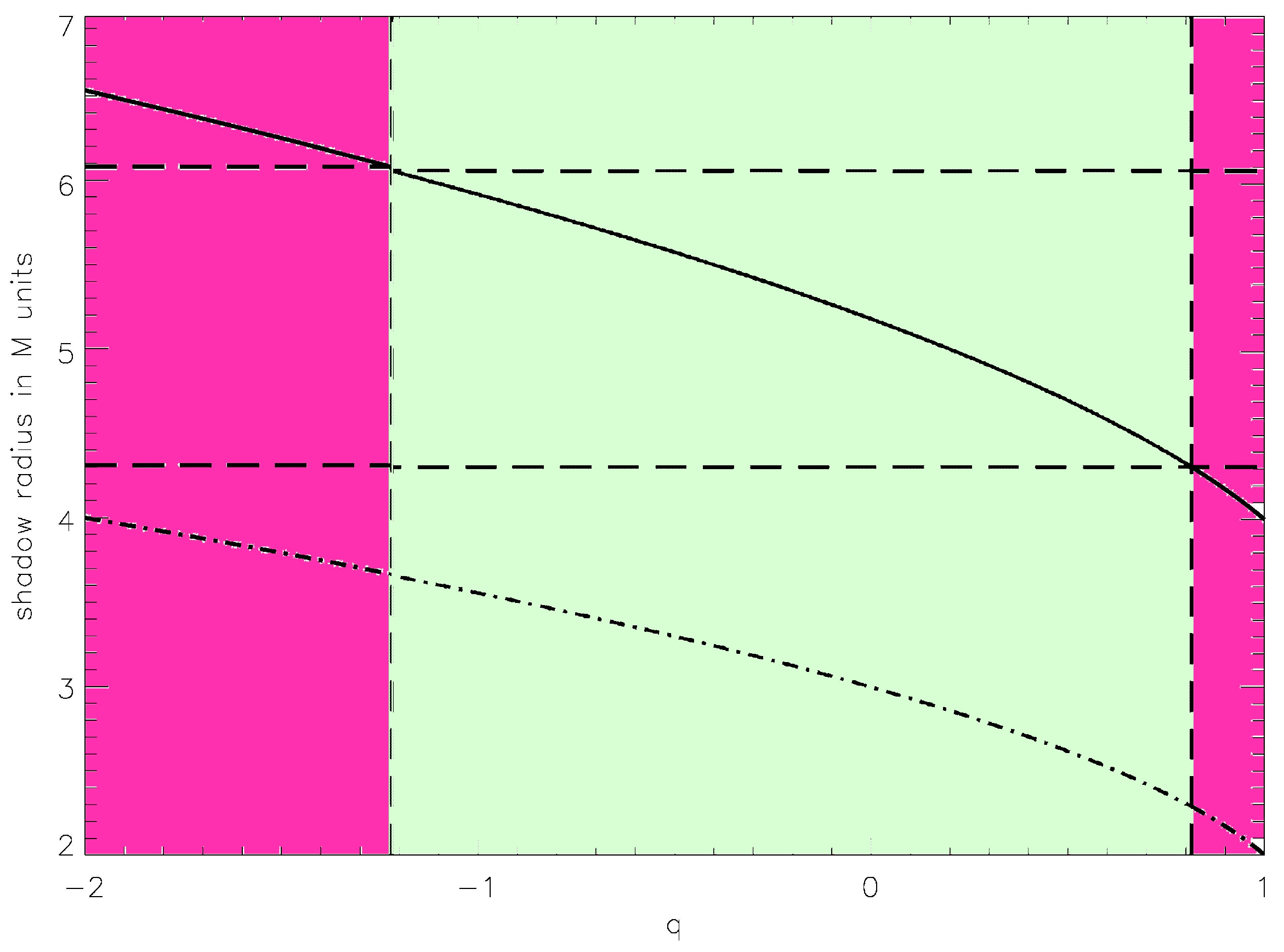
4.1. Constraints from Observations of M87*
4.2. Constraints from Observations of Sgr A*
5. Discussion
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | The space–ground interferometer Radioastron was effectively operating in 2011–2019. |
| 2 | Based on results of their computer simulations and available estimates of the black hole mass in Sgr A* the authors concluded that the shadow size for the Galactic Center is around 30 as [14,15,16] and it is necessary to use a wavelength around 1 mm to reduce ray scattering and to improve the angular resolution of a VLBI network. Currently, the predicted shadow size for Sgr A* is slightly more than 50 as. An angular resolution of the ground based interferometer Event Horizon Telescope (EHT) is around 25 as [17] and it can not be improved significantly since now the EHT arm lengths are comparable with the Earth diameter. |
References
- Matveenko, L.I. Early VLBI in the USSR. Astron. Nachr. 2007, 328, 411. [Google Scholar] [CrossRef]
- Kellermann, K.I. Reflections on the Soviet-American VLBI program. In Astrophysics on the Threshold of the 21st Century; Kardashev, N.S., Ed.; Gordon & Breach Science Publisher: Philadelphia, PA, USA, 1992; p. 37. [Google Scholar]
- Lovell, B. Out of the Zenith; Jodrell Bank 1957–1970; Oxford University Press: London, UK, 1973. [Google Scholar]
- Kardashev, N.S.; Slysh, V.I. The Radioastron Project, in The Impact of VLBI on Astrophysics and Geophysics. In Proceedings of the 129th IAU Symposium; Reid, M.J., Moran, J.M., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1988; p. 433. [Google Scholar]
- Kardashev, N.S. AGN’s Central Machine Physics from Space VLBI. In ESO Astrophysics Symposia, Quasars, AGNs and Related Research Across 2000: Conference on the Occasion of L. Woltjer’s 70th Birthday Held at the Accademia Nazionale dei Lincei, Rome, Italy, 3–5 May 2000; Setti, G., Swings, J.-P., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; p. 66. [Google Scholar]
- Kardashev, N.S.; Langston, G.I. RadioAstron Space VLBI: Micro-Arc Second Resolution. Bull. Am. Soc. 2004, 36, 1550. [Google Scholar]
- Zakharov, A.F.; Nucita, A.A.; Paolis, F.D.; Ingrosso, G. Measuring the black hole parameters in the galactic center with RADIOASTRON. New Astron. 2005, 10, 479. [Google Scholar] [CrossRef]
- Zakharov, A.F.; Nucita, A.A.; Paolis, F.D.; Ingrosso, G. Shadow shapes around the black hole in the galactic centre. In Dark Matter in Astro- and Particle Physics, Proceedings of the International Conference DARK 2004; Klapdor-Kleingrothaus, H.-V., Arnowitt, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; p. 77. [Google Scholar]
- Bardeen, J.M. Timelike and null geodesics in the Kerr metric. In Black Holes, Les Astres Occlus; deWitt, C., deWitt, B.S., Eds.; Gordon and Breach Science Publishers: New York, NY, USA, 1973; p. 216. [Google Scholar]
- Luminet, J.-P. Image of a spherical black hole with thin accretion disk. Astron. Astrophys. 1979, 75, 228. [Google Scholar]
- Luminet, J.-P. Black Holes; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Young, P. Capture of particles from plunge orbits by a black hole. Phys. Rev. D 1976, 14, 3281. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Mathematical Theory of Black Holes; Clarendon Press: Oxford, UK, 1983. [Google Scholar]
- Falcke, H.; Melia, F.; Agol, E. Viewing the Shadow of the Black Hole at the Galactic Center. Astrophys. J. 2000, 528, L13. [Google Scholar] [CrossRef]
- Falcke, H.; Melia, F.; Agol, E. The shadow of the black hole at the galactic center. In AIP Conference Proceedings, Cosmic Explosions: Tenth Astrophysics Conference; American Institute of Physics Publishing: New York, NY, USA, 2000; Volume 522, p. 317. [Google Scholar]
- Melia, F.; Falcke, H. The Supermassive Black Hole at the Galactic Center. Ann. Rev. Astron. Astrophys. 2001, 39, 309. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azuly, R. [Event Horizon Telescope Collaboration]. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. Lett. 2019, 875, L1. [Google Scholar]
- Rubakov, V.A. Large and infinite extra dimensions. Phys. Usp. 2001, 44, 871. [Google Scholar] [CrossRef]
- Randall, L.; Sundrum, R. Large Mass Hierarchy from a Small Extra Dimension. Phys. Rev. Lett. 1999, 83, 3370. [Google Scholar] [CrossRef]
- Randall, L.; Sundrum, R. An Alternative to Compactification. Phys. Rev. Lett. 1999, 83, 4690. [Google Scholar] [CrossRef]
- Dadhich, N.; Maartens, R.; Papadopoulos, P.; Rezania, V. Black Holes on the Brane. Phys. Lett. B 2000, 487, 1. [Google Scholar] [CrossRef]
- Bin-Nun, A.Y. Relativistic images in Randall-Sundrum II braneworld lensing. Phys. Rev. D 2010, 81, 123011. [Google Scholar] [CrossRef]
- Bin-Nun, A.Y. Gravitational lensing of stars orbiting Sgr A* as a probe of the black hole metric in the Galactic center. Phys. Rev. D 2010, 82, 064009. [Google Scholar] [CrossRef]
- Bin-Nun, A.Y. Strong gravitational lensing by Sgr A*. Class. Quant. Grav. 2011, 28, 114003. [Google Scholar] [CrossRef]
- Doeleman, S.S.; Weintroub, J.; Rogers, A.E.; Plambeck, R.; Freund, R.; Tilanus, R.P.; Friberg, P.; Ziurys, L.M.; Moran, J.M.; Woody, D.; et al. Event-horizon-scale structure in the supermassive black hole candidate at the Galactic Centre. Nature 2008, 455, 78. [Google Scholar] [CrossRef]
- Zakharov, A.F.; Nucita, A.A.; Paolis, F.D.; Ingrosso, G. Shadows as a tool to evaluate black hole parameters and a dimension of spacetime. New Astron. Rev. 2012, 56, 64. [Google Scholar] [CrossRef]
- Horndeski, G.W. Second-order scalar–tensor field equations in a four-dimensional space. Int. J. Theor. Phys. 1974, 10, 363. [Google Scholar] [CrossRef]
- Ishak, M. Testing general relativity in cosmology. Liv. Rev. Relativ. 2019, 22, 1. [Google Scholar] [CrossRef]
- Babichev, E.; Charmousis, C.; Lehébel, A. Asymptotically flat black holes in Horndeski theory and beyond. J. Cosmol. Astropart. Phys. 2017, 4, 27. [Google Scholar] [CrossRef]
- Zakharov, A.F. Constraints on tidal charge of the supermassive black hole at the Galactic Center with trajectories of bright stars. Eur. Phys. J. C 2018, 78, 689. [Google Scholar] [CrossRef] [PubMed]
- Abuter, R.; Amorim, A.; Bauböck, M.; Berger, J.P.; Bonnet, H.; Brandner, W.; Cardoso, V.; Clénet, Y.; de Zeeuw, P.T.; Zins, G.; et al. Detection of the Schwarzschild precession in the orbit of the star S2 near the Galactic centre massive black hole. Astron. Astrophys. 2020, 636, L5. [Google Scholar]
- Borka, D.; Jovanović, V.B.; Capozziello, S.; Zakharov, A.F.; Jovanović, P. Estimating the Parameters of Extended Gravity Theories with the Schwarzschild Precession of S2 Star. Universe 2021, 7, 407. [Google Scholar] [CrossRef]
- Touboul, P.; Rodrigues, M.; Bergé, J. Einstein rules at a precision of 2 × 10-14. Nat. Astron. 2018, 2, 174. [Google Scholar] [CrossRef]
- Touboul, P.; Métris, G.; Rodrigues, M.; André, Y.; Baghi, Q.; Bergé, J.; Boulanger, D.; Bremer, S.; Chhun, R.; Visser, P.; et al. Space test of the equivalence principle: First results of the MICROSCOPE mission. Class. Quantum Grav. 2019, 36, 225006. [Google Scholar] [CrossRef]
- Tino, G.M.; Cacciapuoti, L.; Capozziello, S.; Lambiase, G.; Sorrentino, F. Precision gravity tests and the Einstein Equivalence Principle. Progr. Part Nucl. Phys. 2020, 112, 103772. [Google Scholar] [CrossRef]
- Ruffini, R.; Argüelles, C.R.; Rueda, J.A. On the core-halo distribution of dark matter in galaxies. Mon. Not. R. Astron. Soc. 2015, 451, 622. [Google Scholar] [CrossRef]
- Becerra-Vergara, E.A.; Argüelles, C.R.; Krut, A.; Rueda, J.A.; Ruffini, R. Hinting a dark matter nature of Sgr A* via the S-stars. Mon. Not. R. Astron. Soc. Lett. 2021, 505, L64. [Google Scholar] [CrossRef]
- Zakharov, A.F. Testing the Galactic Centre potential with S-stars. Mon. Not. R. Astron. Soc. Lett. 2021; in press. [Google Scholar]
- Abuter, R.; Aimar, N.; Amorim, A.; Ball, J.; Bauböck, M.; Berger, J.P.; Bonnet, H.; Bourdarot, G.; Brandner, W.; Cardoso, V.; et al. [The GRAVITY Collaboration]. Mass distribution in the Galactic Center based on interferometric astrometry of multiple stellar orbits. Astron. Astrophys. 2022, 657, L12. [Google Scholar]
- Zakharov, A.F.; Nucita, A.A.; Paolis, F.D.; Ingrosso, G. Direct measurements of black hole charge with future astrometrical missions. Astron. Astrophys. 2005, 442, 795. [Google Scholar] [CrossRef]
- Zakharov, A.F. Constraints on a charge in the Reissner-Nordström metric for the black hole at the Galactic Center. Phys. Rev. D 2014, 90, 062007. [Google Scholar] [CrossRef]
- Kocherlakota, P.; Rezzolla, L.; Falcke, H.; Fromm, C.M.; Kramer, M.; Mizuno, Y.; Nathanail, A.; Olivares, H.; Younsi, Z.; Akiyama, K.; et al. [Event Horizon Telescope Collaboration]. Constraints on black-hole charges with the 2017 EHT observations of M87*. Phys. Rev. D 2021, 103, 104047. [Google Scholar] [CrossRef]
- Wald, R. General Relativity; The University of Chicago Press: Chicago, IL, USA, 1984. [Google Scholar]
- Zakharov, A.F. Capture Cross Sections for a Charged Reissner-Nordstrom Black-Hole-Photons Ultrarelativistic Uncharged Particles and Slow Uncharged Particles. Sov. Astron. 1991, 35, 147. [Google Scholar]
- Zakharov, A.F. Particle capture cross sections for a Reissner–Nordström black hole. Class. Quant. Grav. 1994, 11, 1027. [Google Scholar] [CrossRef]
- Reissner, H. Über die Eigengravitation des elektrischen Feldes nach der Einsteinschen Theorie. Ann. Phys. 1916, 355, 106. [Google Scholar] [CrossRef]
- Nordström, G. On the Energy of the Gravitation field in Einstein’s Theory. K. Ned. Akad. Vanwetenschappen Proc. 1918, 20, 1238. [Google Scholar]
- Misner, C.; Thorne, K.S.; Wheeler, J.A. Gravitation; W.H. Freeman and Company: San Francisco, CA, USA, 1973. [Google Scholar]
- Zakharov, A.F. On the hotspot near a Kerr black hole: Monte Carlo simulations. Mon. Not. R. Astron. Soc. 1994, 269, 283. [Google Scholar] [CrossRef]
- Kostrikin, A.I. Introduction to Algebra; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1982. [Google Scholar]
- Shaikh, R.; Kocherlakota, P.; Narayan, R.; Joshi, P.S. Shadows of spherically symmetric black holes and naked singularities. Mon. Not. R. Astron. Soc. 2018, 482, 52. [Google Scholar] [CrossRef]
- Psaltis, D.; Medeiros, L.; Christian, P.; Özel, F.; Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Ball, D.; et al. [Event Horizon Telescope Collaboration]. Gravitational Test beyond the First Post-Newtonian Order with the Shadow of the M87 Black Hole. Phys. Rev. Lett. 2020, 125, 141104. [Google Scholar] [CrossRef] [PubMed]
- Lu, R.S.; Krichbaum, T.P.; Roy, A.L.; Fish, V.L.; Doeleman, S.S.; Johnson, M.D.; Akiyama, K.; Psaltis, D.; Alef, W.; Ziurys, L.M. Detection of Intrinsic Source Structure at 3 Schwarzschild Radii with Millimeter-VLBI Observations of SAGITTARIUS A*. Astrophys. J. 2018, 859, 60. [Google Scholar] [CrossRef]
- D’Inverno, R. Introducing Einstein’s Relativity; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Deser, S.; Franklin, J. Schwarzschild and Birkhoff a la Weyl. Am. J. Phys. 2005, 73, 261. [Google Scholar] [CrossRef]
- Zajaček, M.; Tursunov, A.; Eckart, A.; Britzen, S.; Hackmann, E.; Karas, V.; Stuchlík, Z.; Czerny, B.; Zensus, J.A. Constraining the charge of the Galactic centre black hole. J. Phys. Conf. Ser. 2019, 1258, 012031. [Google Scholar] [CrossRef]
- Böhmer, C.G.; Harko, T.; Lobo, F.S.N. Solar system tests of brane world models. Class. Quantum Grav. 2008, 25, 045015. [Google Scholar] [CrossRef][Green Version]
- Banerjee, I.; Chakraborty, S.; SenGupta, S. Silhouette of M87*: A new window to peek into the world of hidden dimensions. Phys. Rev. D 2020, 101, 041301. [Google Scholar] [CrossRef]
- Neves, J.C.S. Constraining the tidal charge of brane black holes using their shadows. Eur. Phys. J. C 2020, 80, 717. [Google Scholar] [CrossRef]
- Johnson, M.D.; Narayan, R.; Psaltis, D.; Blackburn, L.; Kovalev, Y.Y.; Gwinn, C.R.; Zhao, G.; Bower, G.C.; Moran, J.M.; Sironi, L.; et al. The Scattering and Intrinsic Structure of Sagittarius A* at Radio Wavelengths. Astrophys. J. 2018, 865, 104. [Google Scholar] [CrossRef]
- Issaoun, S.; Johnson, M.D.; Blackburn, L.; Brinkerink, C.D.; Mościbrodzka, M.; Chael, A.; Goddi, C.; Martí-Vidal, I.; Wagner, J.; Zhao, G.Y.; et al. The Size, Shape, and Scattering of Sagittarius A* at 86 GHz: First VLBI with ALMA. Astrophys. J. 2019, 871, 30. [Google Scholar] [CrossRef]
- Issaoun, S.; Johnson, M.D.; Blackburn, L.; Broderick, A.; Tiede, P.; Wielgus, M.; Doeleman, S.S.; Falcke, H.; Akiyama, K.; Wagner, J.; et al. Persistent Non-Gaussian Structure in the Image of Sagittarius A* at 86 GHz. Astrophys. J. 2021, 915, 99. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zakharov, A.F. Constraints on a Tidal Charge of the Supermassive Black Hole in M87* with the EHT Observations in April 2017. Universe 2022, 8, 141. https://doi.org/10.3390/universe8030141
Zakharov AF. Constraints on a Tidal Charge of the Supermassive Black Hole in M87* with the EHT Observations in April 2017. Universe. 2022; 8(3):141. https://doi.org/10.3390/universe8030141
Chicago/Turabian StyleZakharov, Alexander F. 2022. "Constraints on a Tidal Charge of the Supermassive Black Hole in M87* with the EHT Observations in April 2017" Universe 8, no. 3: 141. https://doi.org/10.3390/universe8030141
APA StyleZakharov, A. F. (2022). Constraints on a Tidal Charge of the Supermassive Black Hole in M87* with the EHT Observations in April 2017. Universe, 8(3), 141. https://doi.org/10.3390/universe8030141





