Multi-Messenger Astrophysics of a Millisecond Pulsar Orbiting around a Massive Black Hole

Abstract

Extreme-mass-ratio and intermediate-mass-ratio binaries with a millisecond pulsar are gravitational-wave sources that emit also electromagnetic radiation. The millisecond pulsars in these binaries have complex orbital and spin dynamics, which are observable because of spin–orbit and spin–spin coupling (through spin–curvature interaction). The strengths of the couplings generally depends on the mass ratio between the pulsar and the black hole. The narrow mass range of neutron stars gives an advantage in parameter extraction as it greatly reduces the search space, in particular, in the determination of the black-hole mass, in gravitational wave experiments and radio pulsar timing observations. Extreme-mass-ratio and intermediate-mass-ratio binaries with a millisecond pulsar will help to resolve the astrophysical problems, concerning the applicability of the $\mathcal{M}$-$\sigma$ relation for galactic spheroids extending to the very low-mass galaxies and whether or not low-mass dwarf galaxies and globular clusters would harbour a nuclear intermediate-mass black hole. The high-precision that can be achieved in gravitational wave experiments and radio pulsar timing observations will provide an opportunity to directly detect gravitational clock effects that are arisen from spin couplings. Radio monitoring of the orbital and spin evolution of the millisecond pulsar in an extreme-mass-ratio binary can be used as a bootstrap method for correcting the drifts in the phases in the gravitational waves from the extreme-mass-ratio and intermediate-mass-ratio binaries caused by self-force.

1. Introduction

Extreme-mass-ratio binarys (EMRBs) and intermediate-mass-ratio binarys (IMRBs) are gravitational wave (GW) sources that are expected to be detected by the future space GW observatory Laser Interferometric Space Antenna (LISA) (see [1,2]). EMRBs and IMRBs containing a millisecond pulsar (MSP) are particular important, as the presence of the pulsar (a neutron star) guarantees an electromagnetic counterpart of these GW sources.

These binaries are a useful apparatus for the studies of various astrophysics and fundamental physics due to the stability of the MSPs’s rotation (see, e.g., [3]), which provides a reliable local timing reference. Information regarding the system dynamics can be extracted from the GWs and independently from the MSP’s pulsed radio emission. Certain system parameters, such as the black hole (BH) mass, can also be determined from the GWs and the MSP’s pulsed radio emission in high precision.

Studies of test objects orbiting around a BH (as in the EMRB, IMRB, extreme-massratio-inspiral (EMRI) and intermediate-mass-ratio-inspiral (IMRI) systems) often put focus on the relativistic dynamics or on the GWs of the system (e.g., [4,5,6]). The test object is often generic, without specifying whether it is a BH, a neutron star or simply a “particle”. BHs are usually not directly observable when they are not accreting gas. In contrast, neutron stars can be observed across the electromagnetic spectrum ranging from radio wavelengths to gamma-ray wavelengths.

MSPs have rotational periods of ∼(1.4–30) ms (see [3,7]), and PSR J1748−2446ad, the fastest spinning MSP known to date, has a rotational angular speed of $2\pi \left(716\right){\mathrm{s}}^{-1}$ [8], corresponding to a speed almost 20% of the speed of light at the pulsar’s rotational equator. In a EMRB, the MSP and the BH are in close proximity, and strong spin couplings facilitate the exchange of angular momentum between the MSP, the BH and the binary orbit. The angular-momentum exchange will lead to complex orbital and spin dynamics of the MSP, and, in some situations, the orbit and spin precessions of the MSPs will show chaotic patterns (see [9,10,11]). These dynamical behaviours of the system will be reflected in the beaming of the pulsed radiation from the MSP (see, e.g., [12,13]).

While the terms spin–spin and spin–orbit couplings have captured some aspects of the spin–curvature interaction between the MSP and the BH, the two objects are subject to a joint gravity and the spin–curvature interaction cannot always be linearly separated into independent components. Nonetheless, the spin couplings will generate forces/torques on the MSP that cannot be eliminated via co-ordinate transformation.

In the presence of these forces/torques, the motion of MSP is no longer along a geodesic in space-time. It is described by a world line instead, though the equations of motion (EOMs) of the MSP are still obtained from the conservation laws. If the self-gravity is ignored, the orbital and spin evolution of MSP under the gravity of a massive BH, can be determined using the Mathisson-Papapetrou-Dixon (MPD) equations [14,15,16], with an appropriate choice of spin supplementary condition (SSC).

In astrophysics, measuring the masses of the nuclear BH in galaxies or stellar systems is often non-trivial, and in fundamental physics, measuring time accurately in a non-stationary gravitational field is enormously challenging. The multi-messenger studies of EMRBs containing a MSP would provide new opportunities to resolve these astrophysics and fundamental physics problems.

This work examines how the multi-messenger studies of EMRBs with a MSP would help to verify the extension of the M-$\sigma$ relation for galactic spheroids to the very low-mass dwarf galaxies and whether or not intermediate-mass nuclear BHs reside in low-mass galaxies and globular clusters. It also accesses the observability of gravitational clock effects arisen from spin couplings in EMRBs and IMRBs and the possibility of obtaining a bootstrap scheme to correct self-force effects in the GWs from EMRBs that contain a MSP using radio pulsar monitoring observations.

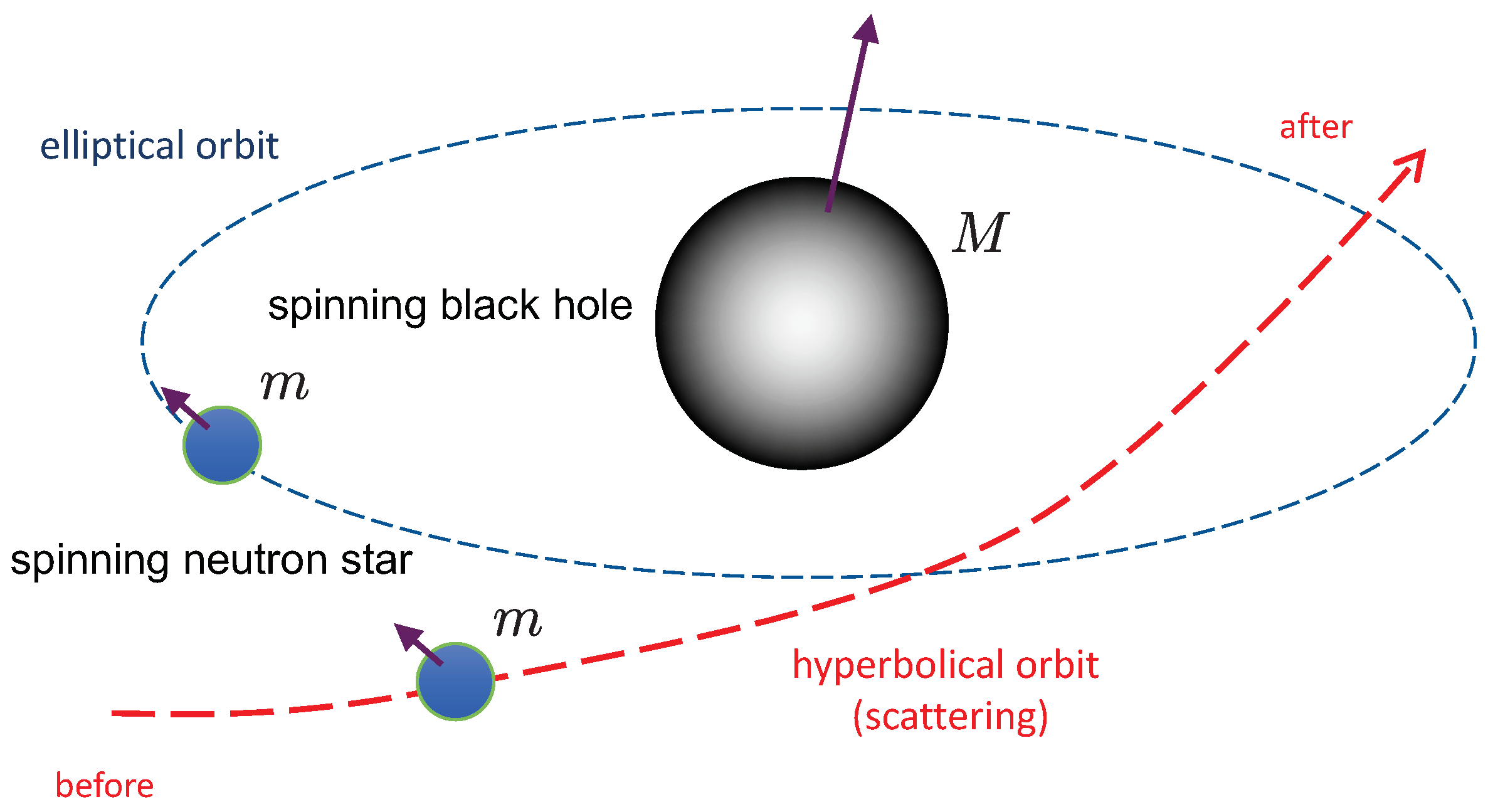
2. Orbital and Spin Dynamics of Extreme-Mass-Ratio Binaries

The $[-+++]$ metric signature and, unless otherwise stated, a natural unit system with unity speed of light c and gravitational constant G, i.e., $c=G=1$, are adopted. The Schwarzschild radius of a BH, with a mass M, is therefore $r_{\mathrm{s}}=2M$. The mass of the pulsar is fixed to be $m=1.5{\mathrm{M}}_{\odot }$ and the radius of the pulsar is assumed to be $R_{\mathrm{ns}}=10\mathrm{km}$ (see, e.g., [17]). The dimensionless spin of the pulsar with spin period $P_{\mathrm{ns}}$ is

$$\widehat{s}=\frac{s}{mM}=5.68\times {10}^{-7}\left(\frac{1\mathrm{ms}}{P_{\mathrm{ns}}}\right)\left(\frac{{10}^6{\mathrm{M}}_{\odot }}{M}\right)$$

(1)

(with the pulsar treated as a uniform solid sphere). Without losing generality, the spin period of the pulsar is fixed to be $P_{\mathrm{ns}}=1\mathrm{ms}$ in the calculations. Pulsars with this spin period are referred to as MSPs hereafter, unless otherwise stated. The configuration of the binary is shown in Figure 1.

In EMRB and EMRI systems, $m\ll M$, and the MSP can be considered as a spinning test mass interacting with a stationary background gravitational field provided by a rotating (Kerr) BH. In a stationary Kerr space-time, the line element is

$$\begin{array}{cc}\hfill -\mathrm{d}{\tau }^2=& -\left(1-\frac{2Mr}{\Sigma }\right)\mathrm{d}{t}^2-\frac{4aMr{sin}^2\theta }{\Sigma }\mathrm{d}t\mathrm{d}\varphi +\frac{\Sigma }{\Delta }\mathrm{d}{r}^2+\Sigma \mathrm{d}{\theta }^2\hfill \\ \hfill & +\left(r^2+a^2+\frac{2a^{2}Mr{sin}^2\theta }{\Sigma }\right){sin}^2\theta \mathrm{d}{\varphi }^2\hfill \end{array}$$

(2)

in Boyer–Lindquist coordinates, where $\Sigma =r^2+a^2{cos}^2\theta$, $\Delta =r^2-2Mr+a^2$, $a(\equiv J/M)$ is the Kerr parameter of the BH, J is the angular momentum of the BH and $(r,\theta ,\varphi )$ is the spatial 3-vector in (pseudo-)spherical polar coordinates with the BH centre as the origin. The point-mass approximation is generally used in the calculations in this work, except in explicitly stated situations, where higher-order interactions or self-force effects are discussed.

2.1. Mathisson-Papapetrou-Dixon Formulation

The orbital motion of a test object in a stationary gravitational field is a free fall, i.e., represented by a geodesic in space-time. If the test object is rotating, there will be forces/torques on the object, arisen from spin couplings. These forces/torques will cause the object to deviate from a geodesic motion. The spin–orbit and spin–spin couplings (as the leading orders of spin–curvature coupling [18]) may be explained in terms of a gravito-electromagnetic ananlogue (see, e.g., [19,20,21,22]), although the spins coupling, taking account of the non-zero size of the object and the higher-order effects, would require a more proper treatment (see, e.g., [23,24,25]).

The MPD formulation (see, e.g., [26]), which is constructed from Einstein’s equation based on the conservation law, is often used to determine the orbital and spin dynamics of rotating test objects in a stationary gravitating field. This gives the EOMs a MSP in a gravitational field provided by a Kerr BH:

$$\begin{array}{cc}\hfill {\dot{p}}^{\mu }& =-\frac{1}{2}{R^{\mu }}_{\nu \alpha \beta }{u}^{\nu }{s}^{\alpha \beta }+{\mathcal{F}}^{\mu };\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill {\dot{s}}^{\mu \nu }& =p^{\mu }{u}^{\nu }-p^{\nu }{u}^{\mu }+{\mathcal{T}}^{\mu \nu }\hfill \end{array}$$

(4)

Refs. [14,15,16], with the Dixon force ${\mathcal{F}}^{\mu }$ and the Dixon torque ${\mathcal{T}}^{\mu \nu }$

$$\begin{array}{cc}\hfill {\mathcal{F}}^{\mu }& \equiv -\frac{1}{6}{J}^{\alpha \beta \gamma \sigma }{\nabla }^{\mu }{R}_{\alpha \beta \gamma \sigma };\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill {\mathcal{T}}^{\mu \nu }& \equiv \frac{4}{3}{J}^{\alpha \beta \gamma [\mu }{R}^{\nu ]}{}_{\gamma \alpha \beta }\hfill \end{array}$$

(6)

(see, e.g., [27]). Here, $u^{\mu }=\mathrm{d}{x}^{\mu }/\mathrm{d}\tau$ is the unit tangent vector along the worldline of the centre of mass of the MSPs, and the “over-dot” above the variables represents a covariant derivative along this worldline (i.e., ${\dot{p}}^{\mu }\equiv u^{\nu }{\nabla }_{\nu }{p}^{\mu }$), and $J^{\alpha \beta \gamma \sigma }$ is the quadrupole tensor of the MSPs. For the quadrupole induced by spin-coupling with gravity,

$$\begin{array}{cc}\hfill J^{\alpha \beta \gamma \sigma }& =4{\upsilon }^{[\alpha }\chi {\left(\upsilon \right)}^{\beta \left]\right[\gamma }{\upsilon }^{\sigma ]}\hfill \end{array}$$

(7)

(see [28]), and

$$\begin{array}{cc}\hfill \chi {\left(\upsilon \right)}^{\beta \gamma }& =\frac{3}{4}\frac{C_Q}{m}\left[s^{\beta }{s}^{\gamma }-\frac{1}{3}{s}^2\left(g^{\beta \gamma }+{\upsilon }^{\beta }{\upsilon }^{\gamma }\right)\right],\hfill \end{array}$$

(8)

where ${\upsilon }^{\alpha }=p^{\alpha }/m$ and $\sqrt{-p^{\mu }{p}_{\mu }}=m$. The polarisability constant $C_Q$ is determined by the structure, and hence the equation of state, of the MSPs. It is normalised such that $C_Q=1$ corresponds to a BH. For neutron stars, $C_Q\sim$ (3.1–7.4) (see [29,30]), and $C_Q=6$, appropriate for strong spin-couplings, was adopted by Li et al. [27] in the study of hyperbolic EMRB systems (see also Kimpson, Wu and Zane [31] for the systems with bounded orbits with the inclusion of the mass quadrupole).

In the MPD formulation, the EOMs are not a set of close first order differential equations. There are 18 variables but only 14 independent equations. Four additional independent equations are therefore required, and they can be provided by introducing a SSC. A commonly used SSC is the Tulczyjew–Dixon (TD) condition (see [32,33,34]), which states

$$\begin{array}{c}\hfill s^{\mu \nu }{p}_{\nu }=0,\end{array}$$

(9)

and it is adopted in the calculations shown in this work. This projection yields

$$\begin{array}{cc}\hfill s_{\mu }& =-\frac{1}{2m}{ϵ}_{\mu \nu \alpha \beta }{p}^{\nu }{s}^{\alpha \beta };\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill s^{\mu \nu }& =\frac{1}{m}{ϵ}^{\mu \nu \alpha \beta }{p}_{\alpha }{s}_{\beta },\hfill \end{array}$$

(11)

in which the ${\sigma }_{0123}=+1$ permutation is adopted for the Levi–Civita tensor, i.e., ${ϵ}_{\mu \nu \alpha \beta }=\sqrt{-g}{\sigma }_{\mu \nu \alpha \beta }$. With the implement of TD SSC, the dynamic equations for the orbital and spin evolution of the MSP may then be expressed as

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{p}^{\alpha }}{\mathrm{d}\tau }=& -{{\Gamma }^{\alpha }}_{\mu \nu }{p}^{\mu }{u}^{\nu }+\lambda \left(-\frac{1}{2}{R^{\alpha }}_{\beta \mu \nu }{u}^{\beta }{s}^{\mu \nu }+{\mathcal{F}}^{\alpha }\right);\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{s}^{\alpha }}{\mathrm{d}\tau }=& -{{\Gamma }^{\alpha }}_{\mu \nu }{s}^{\mu }{u}^{\nu }\hfill \\ \hfill & +\lambda \left[\left(-\frac{1}{2m^2}{R}_{\gamma \beta \mu \nu }{u}^{\beta }{s}^{\mu \nu }+{\mathcal{F}}_{\gamma }\right)s^{\gamma }{p}^{\alpha }-\frac{1}{2m}{{ϵ}^{\alpha }}_{\beta \mu \nu }{p}^{\beta }{\mathcal{T}}^{\mu \nu }\right].\hfill \end{array}$$

(13)

The dynamics equations above contain a parameter switch $\lambda$, which was introduced by Singh [35] to suppress spin–curvature coupling and was also used by in some later studies, (see, e.g., [36,37]) for demonstrative purposes. Spin-curvature coupling is fully considered when $\lambda$ is set to unity, and spin–curvature coupling is ignored when $\lambda$ is set to zero. Quadrupole-curvature coupling is included when both $C_Q$ and $\lambda$ are both non-zero, and quadrupole-curvature coupling is ignored when $C_Q$ equals zero regardless of the value of $\lambda$ (see [27]).

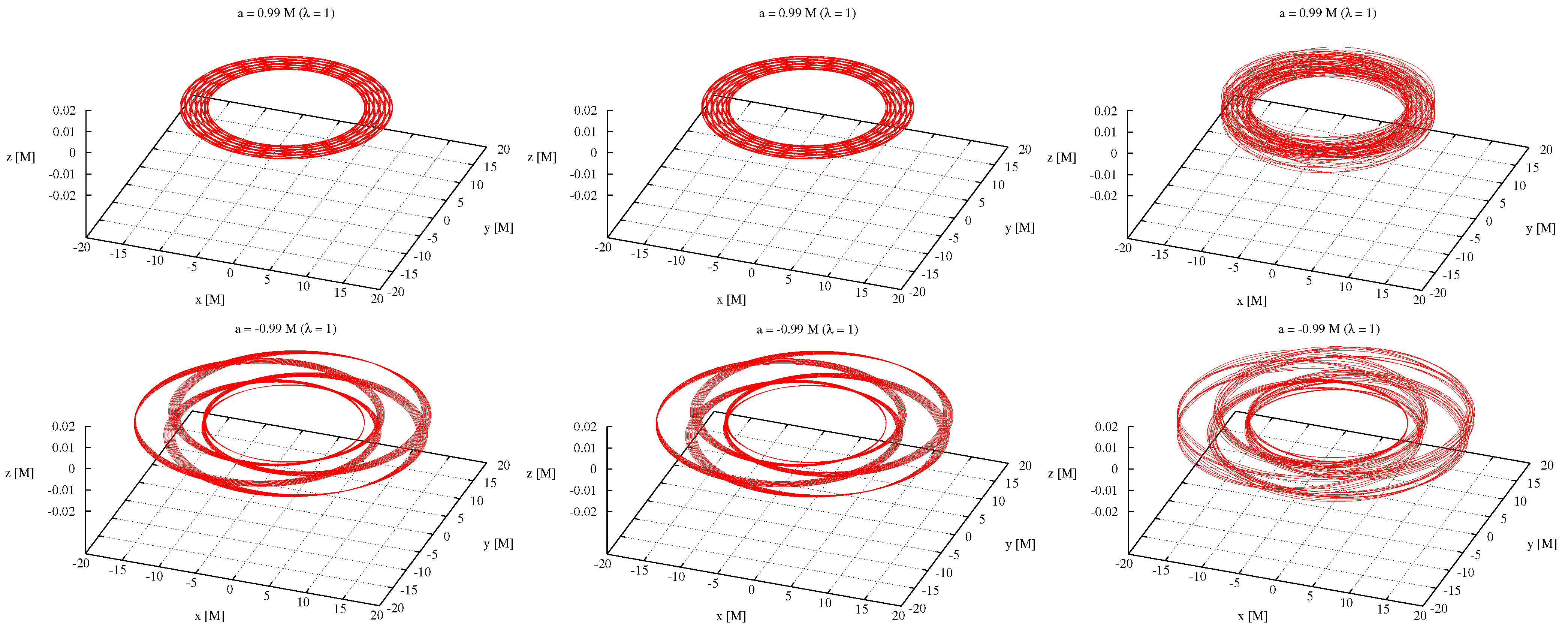
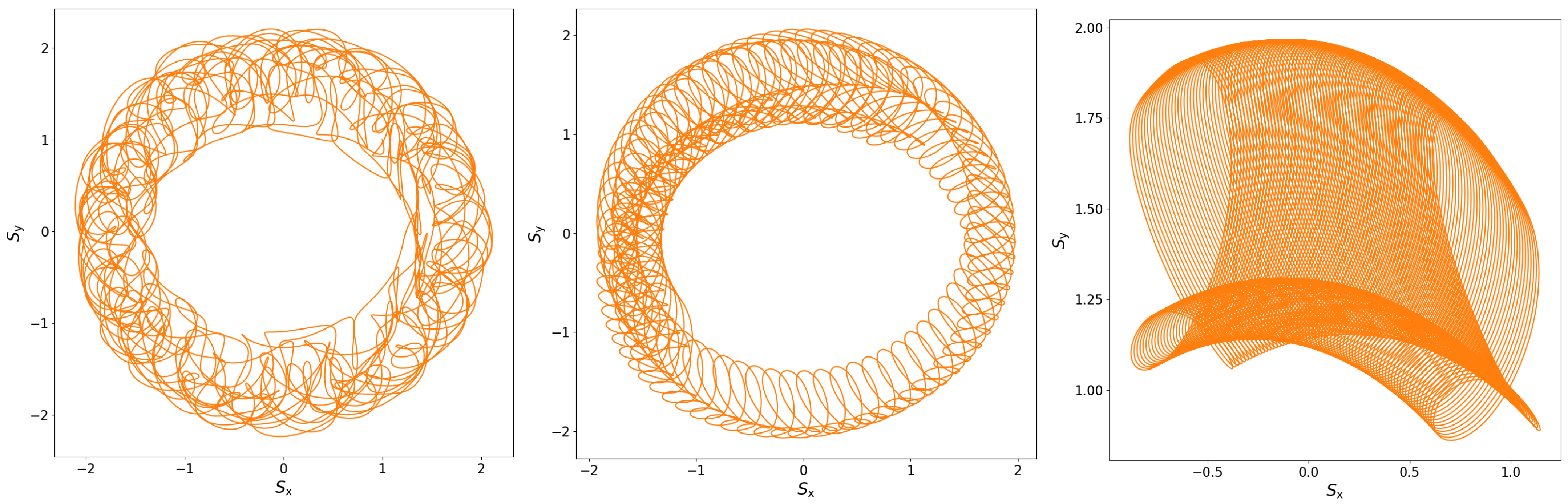
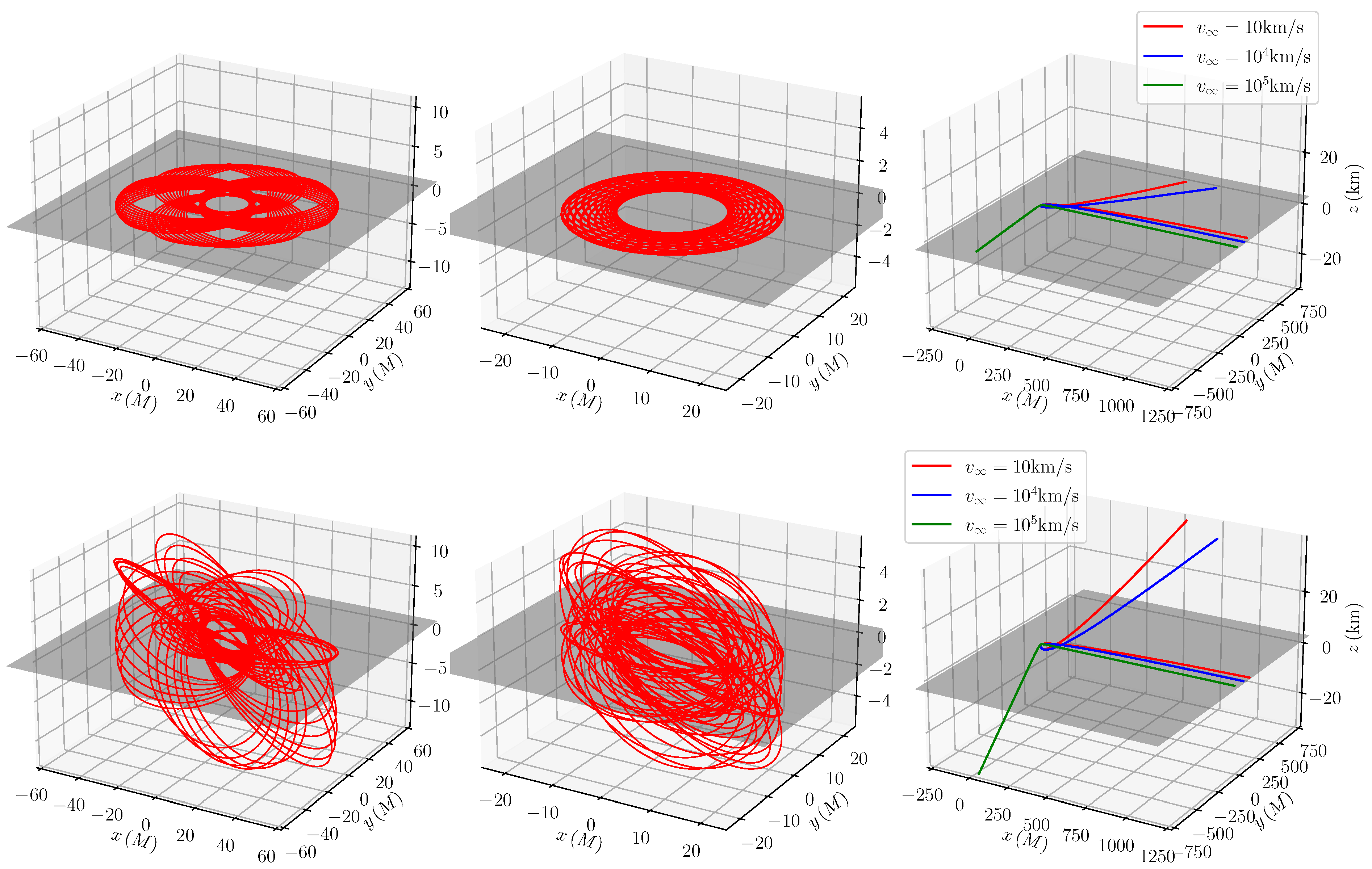
2.2. Orbital and Spin Dynamics of Bound and Unbound Systems

A non-rotating test object revolving around a BH follows geodesics in space-time, if the gravitational radiation and its back reaction are ignored, and its dynamic is described by Equation (12) with $\lambda =0$. The motion of the test object is confined in a plane, i.e., a consequence of conservation of orbital angular momentum (as measured by a distant observer). The above would not hold if the test object is rotating, and test object will interact with the binary system through spin–orbit and spin–spin (via spin–curvature coupling).

Orbital angular momentum is no longer a conserved quantity in the presence of spin-couplings, and, as a consequence, the MSP’s orbit becomes non-planar and non-circular. Figure 2 and Figure 3 show the orbits of a MSP (with a spin period of $1\mathrm{ms}$) around a more massive Kerr BH (of a mass $M=2\times {10}^6{\mathrm{M}}_{\odot }$, ${10}^5{\mathrm{M}}_{\odot }$ and ${10}^3{\mathrm{M}}_{\odot }$) with a spin parameter $|a/M|=0.99$.

As shown, the orbits are non-circular and not close. They do not lie on a plane. The orbits appear to show more complex patterns when for larger $m/M$ ratios. Moreover, orbits that are retrograde with respect to the BH spin, ($a/M=-0.99$) show stronger deviations from circular motion than orbits that are prograde with respect to the BH spin ($a/M=+0.99$). The MSP’s spin would precess and nutate when the MSP revolves around a black hole. Figure 4 shows the precession and nutation of the MSP’s spin. The spin precession and nutation depend on the strength of the spin–curvature coupling and hence on the separation between the MSP and the BH. However, the trend of dependence is not obvious.

The orbit and spin dynamics of a rotating object around a massive gravitating object is intrinsically chaotic, because of the effective gravitational potential, even considering only spin–orbit coupling (see, e.g., [22]), i.e., ignoring the spin–spin and higher-order spin couplings. Thus, a MSP orbiting around Kerr BH is expected to show complex and even chaotic patterns in the precession of the MSP’s orbit and spin.

Figure 5 shows the comparison of the orbital dynamics of EMRBs in the presence and in the absence of spin couplings for both elliptical and hyperbolic orbits. The spin couplings, when present, are considered up to a quadrupole order (with $C_Q=6$). As shown, the orbits are planar when spin couplings are absent (top panels, Figure 5). In the cases of elliptical orbits, the complex orbital patterns is a manifestation of general relativistic precession (cf. the precession of Mercury’s orbit around the Sun). When the spin–curvature couplings are present, the orbits of the MSP are not confined to a plane in both the elliptic and hyperbolic cases (bottom panels, Figure 5). The orbit also precesses, i.e., the orientation of the normal vector of the orbital plane is no longer fixed.

Some Remarks on the Spin Supplementary Conditions

The Mathisson–Pirani SSC [15,38] is an alternative to the Tulczyjew–Dixon SSC [33,34] adopted above. It assumes that $s^{\mu \nu }{u}_{\nu }=0$, instead of $s^{\mu \nu }{p}_{\nu }=0$. Examples of other commonly used conditions are the Cornaldesi–Papapetrou SSC [39], the Newton–Wigner SSC [40] and the Ohashi–Kyrian–Smerák SSC [41,42]. These SSCs generally take the form: $s^{\mu \nu }{V}_{\nu }=0$, where $V_{\nu }$ is a time-like vector, and they generally give acceptable physics solutions to the MPD equations (see [5,43,44,45] for discussions of various SSCs).

The momentum of the test object is

$$\begin{array}{cc}\hfill p^{\mu }& =m{u}^{\mu }-u_{\nu }\frac{\mathrm{D}{s}^{\mu \nu }}{\mathrm{d}\tau }.\hfill \end{array}$$

(14)

The quantity $m=-p_{\nu }{u}^{\mu }$ will become the ordinary rest mass of the test object when the spin of the object approaches zero (see, e.g., [46]). Spin-curvature couplings will generate forces/torques on a spinning object, which has a non-zero physical extent, and the object will be pushed away from geodesic motion. If omitting the effects caused by the emission of GW and the presence of self-forces, then

$$\begin{array}{c}\hfill \frac{\mathrm{D}{s}^{\mu \nu }}{\mathrm{d}\tau }\approx 0,\end{array}$$

(15)

keeping on the first leading order term (see, e.g., [5]). Thus, m is a constant of motion. It follows that $p^{\mu }\approx m{u}^{\mu }$, and $s^{\mu \nu }$ is parallel transported along $u^{\mu }$, i.e., $s^{\mu \nu }{u}_{\nu }\approx 0$, and hence, the Mathisson–Pirani condition and the Tulczyjew–Dixon condition reconcile.

3. Multi-Messenger Astrophysics and Physics

3.1. Millisecond Pulsars as High-Precision Clocks

MSPs are extremely stable gyros, with the drift of their spin periods about 1 cycle over the Hubble time (see, e.g., [3] for a review). The rotational stability makes the MSPs among the most reliable, high-precision clocks in the Universe [3,47,48,49]. The predictability of the spin evolution of MSPs, at least for most of them, implies that tracking the spin evolution of MSPs requires only infrequent monitoring [47]. Combining high-precision pulsar timing analyses and high-precision measurements in GW observations, the extreme-mass-ratio systems will be a means for us to tackle some of the challenging important problems in astrophysics and fundamental physics.

Timing analysis of MSPs generally requires the integration of streams of signals over a large number (∼${10}^4$) of pulsation cycles, i.e., not relying on the arrival of single individual pulses (see, e.g., [50] for the determination of the complex orbital dynamics of the triple system containing the 2.73-ms MSP PSR B1620-26). Thus, a sufficient number of pulse cycles are required to be registered over the period of the GWs, so that we construct meaningful joint analysis in high timing precision, using the information extracted from the GWs and electromagnetic waves.

The orbital period of the MSP around the BH

$$\begin{array}{c}\hfill P_{\mathrm{o}}\approx 9.8\pi {\left(2\chi \right)}^{3/2}\left(\frac{M}{{10}^6{\mathrm{M}}_{\odot }}\right)\mathrm{s},\end{array}$$

(16)

with $\chi =R_{\mathrm{o}}/r_{\mathrm{s}}$, where $R_{\mathrm{o}}$ is the orbital radius of the MSP, and $r_{\mathrm{s}}$ (=2 M) is the Schwarzschild radius of the BH. Thus, for $M={10}^6{\mathrm{M}}_{\odot }$ and $\chi =10$, the number of pulses from a 1-ms MSP to be tracked in one orbital revolution will be about $2.75\times {10}^6$.

For a quasi-circular orbit, the ratio of time scale of GW loss to the orbital period is roughly given by

$$\begin{array}{c}\hfill \frac{{\tau }_{\mathrm{gw}}}{P_{\mathrm{o}}}\sim \frac{5{\varpi }^{5/2}}{192\pi }\left(\frac{M}{m}\right){\left(\frac{M}{m+M}\right)}^{1/2},\end{array}$$

(17)

where $\varpi =\overline{r}/M$ and $\overline{r}$ is the mean orbital separation [37]. For $(M/{\mathrm{M}}_{\odot })\sim$10${}^4$–10${}^6$ and $(\overline{r}/M)\sim$10–100, ${\tau }_{\mathrm{gw}}/P_{\mathrm{o}}\sim$10${}^4$–10${}^9$. Thus, the fraction of orbital energy loss to emission of GW is insignificant, for the purposes of the astrophysical problems considered below.

3.2. $\mathcal{M}$-$\sigma$ Relation of Galaxies and Intermediate-Mass Black Holes in Galactic Spheroids

Observations showed that large galaxies (those with masses above ∼${10}^{10}{\mathrm{M}}_{\odot }$) generally harbour a massive BHs at their centres. The masses of these nuclear BHs are found to correlate with the dynamical properties of the galaxies, and hence the mass of their galactic spheroid components (see [51,52,53]). This correlation is manifested in an empirical $\mathcal{M}-\sigma$ relation, which suggests a co-evolution of galactic spheroids and their nuclear BH. (Here $\mathcal{M}$ is the mass of the nuclear BH, and $\sigma$ is velocity dispersion of stars in the galactic spheroid).

Studies have indicated that this empirical relation may not uniformly hold for all types of galaxies, and it seems to deviate at the low-mass end where the dwarf galaxies are located (see, e.g., [54]). Some low-mass galaxies are found to have a dense stellar cluster at their centre instead of a nuclear BH (see [55]), though some fraction of dwarf galaxies would contain a nuclear BH. If the $\mathcal{M}-\sigma$ can be extrapolated beyond the very low-mass galactic spheroids to the globular clusters (see [56,57,58]), then the nuclear BHs should have masses ∼10${}^2$–${10}^4{\mathrm{M}}_{\odot }$ [59,60].

BHs in this mass range are generally referred to as the intermediate mass BH (IMBHs), distinguishing them from the stellar-mass BHs in X-ray binaries, e.g., GRO J1655-40 (see [61]), and the supermassive BH in AGN, e.g., the M87 AGN [62]. It is still under debates if most of the very low-mass galactic spheroids and and some globular clusters would contain an IMBH or not at their centres.

A BH can grow its mass by accreting gas. It can also gain mass by coalescing with another BH or by capturing stars in its neighbourhood, and the latter would occur in dense stellar environments, e.g., the central regions of ultra-compact dwarf galaxies or the cores of globular clusters, if a nuclear BH is present. LIGO observations have shown that the merging of two neutron stars can produce a BH [63] and the coalescence of two BHs will form a more massive single BH (see [64]). The recent LIGO discovery of a remnant BH of mass $\approx 142 {\mathrm{M}}_{\odot }$ from the coalesce of two BHs [65] provide an unambiguous evidence for the existence of IMBHs, at least in the mass range of ∼100–200 ${\mathrm{M}}_{\odot }$.

Determining the masses of BHs is a challenging task. There are substantial uncertainties, especially in deriving the stellar kinematics associated with the nuclear BHs in the low-mass galaxies using optical/IR spectroscopic data (see, e.g., [52,54,66]). Accurate determination of the nuclear BH masses in the low-mass galaxies is crucial for establishing a proper $\mathcal{M}$-galaxy relations (including the $\mathcal{M}-\sigma$ relation) across the mass spectrum of galaxies and for verifying the presence of nuclear IMBHs, at least in a fraction of the very low-mass galaxies, and perhaps also in the globular clusters.

GW experiments can determine the masses of the objects in a binary system. In the context of measuring the masses of nuclear BHs in galaxies, the accuracy would maintain at similar levels across the BH mass spectrum from the IMBHs to the supermassive BH. If a pulsar is present, orbiting around the BH, i.e., forming an EMRB or an IMRB, the BH mass can also be determined independently from pulsar timing observations. Spin couplings depend on the mass ratio between the two components in a binary (see, e.g., [22,67,68]). A MSP will provides an advantage over a BH in the EMRB or IMRB, because of its narrow mass range around $1.5 {\mathrm{M}}_{\odot }$ would greatly reduce the parameter space of consideration.

Figure 6 shows the variation in the time dilation factor of the pulsed emission from a pulsar revolving around a non-rotating BH over the pulsar’s orbital cycle (see [69]). The orbital variations in the time dilation factor of the pulse emission and the orbital period are measurable, and hence the BH mass and the viewing inclination of the pulsar orbit can be determined in the pulsar timing observations. For the rotating BH, the orbital variations in time dilation factor is affected by frame dragging and spin couplings. This introduces additional variations in the time dilation factor. The BH mass can still be determined, together with the BH spin as an additional undetermined variable.

The variations associated with the off-plane orbital motion caused by spin couplings (see Figure 3 and Figure 5) will alter in the arrival time of the pulses in the radio emission from the pulsar. The off-plane variations shown in Figure 3 are of the order of $10\mathrm{km}$, corresponding to a light travelling time of ∼30 $\mathsf{\mu }$s. Variations of such time scales can be easily resolved in the pulsar timing observations.

3.3. Gravitational Physics—Possibilities and Opportunities

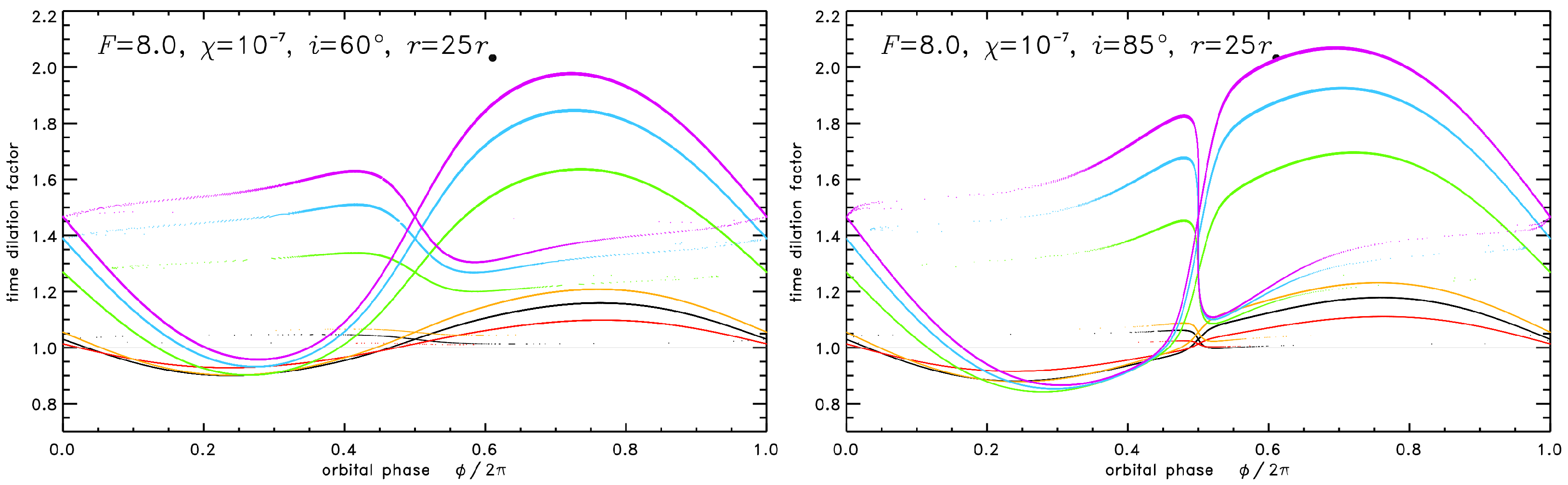
3.3.1. Time Dilation and Gravitational Clock Effects

Radiation emitted from the vicinity of a BH will be redshifted when it reaches a distant observer. It is a time dilation effect, caused by difference between the time measured by the clock of the emitter deep in the BH’s gravitational well and the time measured by the clock of the observer far away. This clock effect implies that the spin period measured by a distant observer is longer than the proper spin period of a pulsar orbiting around a BH as that in an EMRB or IMRB. In relativistic binary systems, additional gravitational clock effects can also be caused by spin couplings. These effects can be illustrated as follows.

Consider first the case in which the neutron star is slowly rotating such that the couplings related to its spin is less significant than to the other gravitational couplings. The neutron star is then a point test mass (in contrast to the pole-dipole mass as the MSP in the MPD formulation discussed in the previous sections). The interaction between the neutron star’s orbital motion and the BH’s rotation leads to a difference in the periods for the neutron star to complete a prograde orbit and a retrograde orbit, with respect to the BH’s spin, when measured by a distant observe. The difference of the two periods is

$$\begin{array}{cc}\hfill {\mathcal{T}}_{+}-{\mathcal{T}}_{-}& =\frac{4\pi }{\left[c\right]}\left(\frac{Jcosi}{M\left[c\right]}\right)\left[\frac{4-2{tan}^{2}i{cos}^2{\phi }_0}{{\left[1+ecos({\phi }_0-g)\right]}^2}-\frac{3}{{(1-e^2)}^{1/2}}\right],\hfill \end{array}$$

(18)

as given by Mashhoon, Iorio and Lichtenegger [70], where the prograde orbit is denoted by “+” and the retrograde orbit by “−”, J is the proper angular momentum of the BH, e is the orbital eccentricity, i is orbital inclination relative to the BH’s spin axis, $(\phi -g_0)$ is the true anomaly, ${\phi }_0$ is value of the azimuthal angle $\phi$ at $t=0$, and $g_0=(g-f)$. The explicit form of f can be found in Mashhoon, Iorio and Lichtenegger [70]1. In the above expression and in this subsubsection, unless otherwise stated, we keep the gravitational constant G and the speed of light c explicitly, instead imposing the convention of the natural unit system, for clarity in physics.

In terms of the dimensionless BH spin parameter $a^{*}$, which is related to a BH’s angular momentum as $J=\left[G\right]M^2{a}^{*}/\left[c\right]$,

$$\begin{array}{cc}\hfill {\mathcal{T}}_{+}-{\mathcal{T}}_{-}& =\frac{4\pi }{\left[c\right]}\left(\frac{J}{M\left[c\right]}\right)=2\pi a^{*}\left(\frac{r_{\mathrm{s}}}{\left[c\right]}\right)=2\pi a^{*}{t}_{\mathrm{s}},\hfill \end{array}$$

(19)

for a circular orbit with an inclination $i=0$, where $t_{\mathrm{s}}(=r_{\mathrm{s}}/\left[c\right])$ is the time for light to traverse across the Schwarzschild radius $r_{\mathrm{s}}$ of the BH. The time difference depends only on the parameters of the Kerr BH, the spin and the mass, but not the orbital radius of the neutron star, indicating that the effect is topological. It vanishes, if the BH is not rotating (i.e., $a^{*}=0$) or the traverse time $t_{\mathrm{s}}$ approaches zero (when either $M\to 0$ or $\left[c\right]\to \infty$). For the BHs relevant to the astrophysical systems considered here,

$$\begin{array}{cc}\hfill {\mathcal{T}}_{+}-{\mathcal{T}}_{-}& \approx 31\left(\frac{a^{*}}{0.5}\right)\left(\frac{M}{{10}^3{\mathrm{M}}_{\odot }}\right)\mathrm{ms}.\hfill \end{array}$$

(20)

This time difference is non-negligible. It is about a few min for an extreme Kerr BH with a mass similar to that of the BH in the Galactic Centre and ∼$1\mathrm{d}$ for an extreme Kerr BH with mass similar to that of the supermassive BH in the M87 galaxy.

This clock effect may be understood in the context gravito-electromagnetism. Without losing generality, consider that the pulsar’s orbit is circular, with a radius $r_{\mathrm{o}}$ in Schwarzschild radial coordinate, and has a zero orbital inclination. The periods of the prograde and retrograde orbits can then be expressed as

$$\begin{array}{cc}\hfill {\mathcal{T}}_{\pm }& =P_{\mathrm{k}}(1+{\mathcal{G}}_{\mathrm{ge}}\pm {\mathcal{G}}_{\mathrm{gm}}),\hfill \end{array}$$

(21)

where $P_{\mathrm{k}}$ the Kepkerian period, given by $P_{\mathrm{k}}=2\pi /{\Omega }_{\mathrm{k}}=2\pi {({r_{\mathrm{o}}}^3/\left[G\right]M)}^{1/2}$, and ${\Omega }_{\mathrm{k}}$ is the Keplerian frequency. The deviations from the Keplerian motion is represented by a gravito-electric correction factor ${\mathcal{G}}_{\mathrm{ge}}$ and a gravito-magnetic correction factor ${\mathcal{G}}_{\mathrm{ge}}$. The gravito-electric effect is the same for prograde and retrograde orbits. The gravito-electric correction factor is given by

$$\begin{array}{cc}\hfill {\mathcal{G}}_{\mathrm{ge}}& =\frac{3}{2}\left(\frac{\left[G\right]M}{c^2{r}_{\mathrm{o}}}\right)=\frac{3}{4}\left(\frac{r_{\mathrm{s}}}{r_{\mathrm{o}}}\right)\hfill \end{array}$$

(22)

(see [70] for the derivation). On the other hand, the gravito-magnetic correction factor is given by

$$\begin{array}{cc}\hfill {\mathcal{G}}_{\mathrm{gm}}& =\left(\frac{{\Omega }_{\mathrm{k}}J}{M{\left[c\right]}^2}\right)=\frac{1}{2}\left(\frac{{\Omega }_{\mathrm{LS}}}{{\Omega }_{\mathrm{k}}}\right)=\frac{1}{2}\left({\Omega }_{\mathrm{k}}{t}_{\mathrm{s}}\right)a^{*},\hfill \end{array}$$

(23)

but the sign of the gravito-magnetic factor is opposite for the prograde orbit and for the retrograde orbit. The gravito-magnetic effect is caused by the BH’s rotation. It is therefore associated with the reference-frame dragging in space time (see, e.g., [20]). As shown in Equation (23) the gravito-magnetic correction factor can be expressed in terms of the Lense–Thirring frequency,

$$\begin{array}{cc}\hfill {\Omega }_{\mathrm{LS}}& =\frac{2\left[G\right]J}{{r_{\mathrm{o}}}^3{\left[c\right]}^2}=\left({{\Omega }_{\mathrm{k}}}^2{t}_{\mathrm{s}}\right)a^{*}.\hfill \end{array}$$

(24)

The gravito-electric and gravito-magnetic corrections alter the gravitational potential, which is otherwise as that given in the Newtonian–Keplerian formulation. These alternations will induce a gravitational redshift/blueshift, i.e., the amount of time dilation, depending on interacting angular momenta—the orbital of the neutron star, $\mathit{L}$, and that of the rotation of the BH, $\sigma$.

The effects of these angular-momentum couplings are similar to those in atoms (see [71,72,73,74]), where the Coulomb potential is perturbed by the interactions between the orbits and spins of the electrons and nuclei, e.g., Zeeman and hyperfine splittings (cf. contunuous Stern–Gerlach effect, see [75]). Analogous to Zeeman and hyperfine splittings, the gravito-magnetic corrections are contributed by the ($\mathit{s}·\mathit{L}$) and ($\mathit{s}·\mathit{\sigma }$) couplings, together with the ($\mathit{L}·\mathit{\sigma }$) coupling (see Figure 7), where $\mathit{s}$ is the spin of the MSP, $\mathit{L}$ is the orbital angular momentum of the MSP and $\mathit{\sigma }$ is the spin of the BH.

Measuring the timing difference between ${\mathcal{T}}_{+}$ and ${\mathcal{T}}_{-}$ arisen from spin-couplings is challenging (see [70,76,77]). Firstly, we need a system with two test masses orbiting in two identical but opposite orbits around a rotating gravitating object. Secondly, we need two stable and reliable timing references, one within the system and another associated with the observer. However, these difficulties can be overcome if we could idenify a suitable EMRB containing a MSP.

The MSP, which is a highly stable gyro, will provide a reliable local timing reference within the system. The complex and chaotic nature of the MSP’s orbital motion implies that the flipping of the angular momentum $\mathit{L}$ will lead to different combinations of ($\mathit{s}·\mathit{L}$) and ($\mathit{L}·\mathit{\sigma }$) coupling, and hence detectable change in the combined gravito-magnetic correction factor. While the proper spinning period of the MSP is stable, the spinning period of the MSP measured by the observer will depend on gravito-magnetic correction arisen from the combination of ($\mathit{s}·\mathit{L}$), ($\mathit{s}·\mathit{\sigma }$) and ($\mathit{L}·\mathit{\sigma }$) couplings. This could lead to measurable period differences (see Equation (20)) in EMRB and IMRB, and the presence of a MSP, which provides the timing reference, makes possible the measurements of such gravitational clock effect.

3.3.2. Self-Force in Gravitational Waves

The MPD formulation has assumed that the orbiting MSP is in a stationary space time provided by the BH, ignoring that the space time is dynamical with the gravity contributed also by the spinning MSP, i.e., the presence of a self-force. The dynamics of the MSP is determined by a non-linear combination of gravity due to the MSP and the BH. Studies of self-force in EMRI systems and the comparison of its effect with those arisen from spin–orbit coupling have been conducted in many studies (e.g., [78,79,80,81]).

The self-forces may be broadly divided into two categories, one associated with dissipative processes and another associated with non-dissipative processes. The leading order of dissipative self-force is the radiative reaction (see [80]) caused by the emission of GWs, which carry away energy and angular momentum from the system (see [82,83,84,85,86]). The dissipative self-force is in general stronger than the non-dissipative self-forces such as those caused by spin couplings.

For a MSP in quasi-circular orbits with an effective radius $\overline{r}$, the precession period of the MSP spin is given by

$$\begin{array}{cc}\hfill P_{\mathrm{sp}}& \approx \frac{2\pi }{\langle {\omega }_{L_{\mathrm{N}}}\rangle }\sim \frac{4\pi }{3}\frac{{\overline{r}}^{5/2}}{M^2}{\left(m+M\right)}^{1/2}\hfill \end{array}$$

(25)

in terms of the system parameters. Here ${\omega }_{L_{\mathrm{N}}}=(3/2)(M/{\overline{r}}^3)\left(\right|{\mathit{L}}_{\mathrm{N}}|/m)$ is the precession frequency (see [36,72,87]), $\langle {\omega }_{L_{\mathrm{N}}}\rangle$ is the average of it over a MSP orbital cycle, ${\mathit{L}}_{\mathrm{N}}$ is the Newtonian angular momentum. The ratio of time scale of radiative loss due to the emission of GW to the MSP’s spin precession period is therefore

$$\begin{array}{cc}\hfill \frac{{\tau }_{\mathrm{gw}}}{P_{\mathrm{sp}}}& \sim \frac{3{\varpi }^{3/2}}{128\pi }\left(\frac{M}{m}\right){\left(\frac{M}{m+M}\right)}^{3/2},\hfill \end{array}$$

(26)

where $\varpi =\overline{r}/M$. For $m=1.5{\mathrm{M}}_{\odot }$, $M/m>$ 10${}^6$–10${}^9$ and $\varpi \sim$50–100, the ratio ${\tau }_{\mathrm{GW}}/P_{\mathrm{sp}}>{10}^5$. This analysis shows that the MPD equations are justified for the calculations of orbital and spin dynamics of the MSP, despite the presence of the dissipiative self-force.

The effect of dissipative self-force would, however, be detectable in the monitoring observations of the MSP, when tracking its spin precession over a substantial number (∼${10}^5$) of cycles. As timing analysis of pulsed radio emission from MSP does not require knowing pre-requisite knowledge of the emission wave-forms and their drifts such as those arisen from radiative reaction, unlike in the GW experiments, observations of evolution of the orbital and spin dynamics would give us a means to empirically derive a correction scheme for the dissipative self-force on the wave-form drift in the GWs from the EMRBs containing an observable MSP.

The non-dissipative self-force, to the first order, is comparable to the equivalent force arisen from the spin–orbit coupling (see [78,86,88]), in terms of mass ratio $m/M$. For the EMRB and EMRI binaries considered here, the leading term of the correction to the precession rate of the MSP’s spin, due to the conservative part of the first order self-force, is roughly given by

$$\begin{array}{cc}\hfill {\omega }_{1\mathrm{st}}& \sim \left(\frac{m}{M}\right)\frac{M}{\overline{r}}{\omega }_{L_{\mathrm{N}}}\hfill \end{array}$$

(27)

(see [67,89]). Comparing this with Equation (25), we may conclude it is smaller than that due to MSP’s spin ${\omega }_{\mathrm{sp}}$ by a factor of $M/\overline{r}$ in addition to mass-ratio factor (see [36]).

The rough analysis above has assumed a quasi-circular MSP orbit, and the effects of the self-forces depends on the orbital eccentricity. It is important to include the effects of the self-force when modelling the secular evolution of the orbital and the spin dynamics of MSP in an EMRB or IMRB, in particular, for generating the GW templates.

In addition to the time shift and width variation of the pulses due to the precession and nutation of the spin, and the orbital deviation from geodesic motion (studied in [37]), the bending of light (i.e., gravitational lensing) due to the black hole’s gravity can be non-negligible. Nonetheless, monitoring of the evolution of pulsed radio emission from the MSPs in EMRBs and IMRBs will give us a useful empirical tools to gauge and adjust the theoretical modelling of the GWs from these binaries in the presence of spin-coupling and self-forces.

4. Summary and Conclusions

EMRBs and IMRBs containing a MSP are GW sources with an observable electromagnetic counterpart. The spin–spin and spin–orbit coupling (via spin–curvature interaction) between the MSP and the BH lead to non-planar orbital motion and precessions in the spin and the orbit of the pulsar. The couplings have observational signatures that can be identified in the GWs from the binary and pulsed radio radiation from the MSP. With the high-precision that can be achieved in GW experiments and radio pulsar timing observations, the EMRBs and IMRBs containing a MSP provide us a useful mean to tackle some challenging problems in astrophysics and in fundamental physics.

An accurate determination of the mass of the nuclear BH in the low-mass galactic spheroids will better establish the applicability of the $\mathcal{M}-\sigma$ relation for spheroids of low-mass dwarf galaxies. The identification of nuclear BH with masses of ∼10${}^3$–10${}^4{\mathrm{M}}_{\odot }$ in low-mass galaxies or globular clusters will confirm the presence of IMBHs. It will also provide estimates to the occupancy of nuclear BH in these stellar systems. The radio pulsar timing and GW observations of EMRBs with a MSP will give us the opportunity to detect gravitational clock effects arisen from spin couplings directly.

Monitoring of the evolution orbital and spin dynamics of the MSP in EMRBs using radio observations will track the phase drifts in the orbital motion of MSP caused by self-force effects. This will provide a means to derive an empirical scheme to correct for the self-force effects in the GW observations of EMRBs and IMRBs. In summary, the presence of a MSP (a fast spinning neutron star) in the EMRBs and EMRIs places this group of binaries into a special class of relativistic systems, and we can take advantage of high precision multi-messenger observations to tackle various challenging problems in astrophysics and fundamental physics.