1. Introduction
The brown dwarf TVLM 513-46546 is currently one of the most studied among ultracool stars of spectral types M > 7, L, T, and Y. Radio, X-ray, ultraviolet, and optical spectroscopic observations have revealed rather unusual properties of TVLM 513-46546 radiation (see, for example, [
1,
2,
3]). In addition to the surprising radio to X-ray luminosity ratio (
LR/
LX ≈ 3.3
10
−12 Hz
−1), by a factor of 10
4 larger than expected [
2,
4], a persistent (on a multiyear timescale) quiescent nonthermal radio emission from the brown dwarf TVLM 513-46546 is observed, which assumes a continuous source of accelerated electrons. The persistent quiescent radio emission is accompanied by long-term X-ray emission. By now, in low-mass dwarf stars, two thermal components of X-ray emission are observed: the “soft” one, with the temperature
T ≈ (1–6)
10
6 K, and the “hard” one, corresponding to the source temperature
T ≈ 10
7 K [
5].
The current models of the microwave [
1] and multiwavelength radiation sources in TVLM 513-46546 [
2] provide no explanation for the nature of the accelerator of electrons producing the quiescent nonthermal gyrosynchrotron emission for several years. Moreover, the microwave radiation source was represented either by the dipole magnetic field of the dwarf [
1] or as a large-scale magnetic structure with a “covering factor” of about 50% [
2].
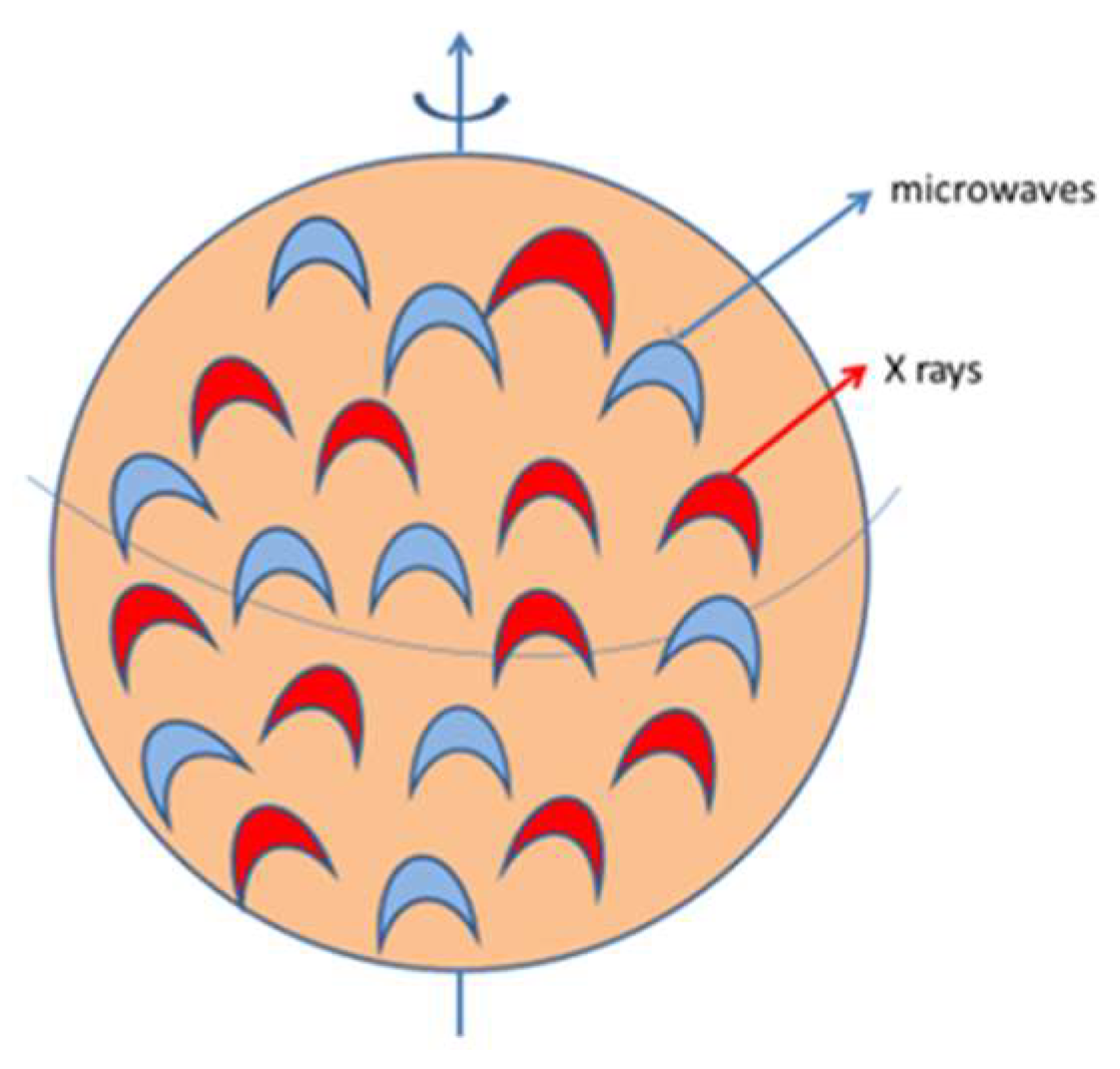
Here, we show that the sources of radio and X-ray emission of TVLM 513-46546 consist of a few ×100 coronal magnetic loops quasi-uniformly distributed over the dwarf surface. We propose the heating mechanism of coronal loop plasma driven by dissipation of electric current generated by photospheric convection and the mechanism of long-term particle acceleration in the atmosphere of a brown dwarf supporting the persistent nature of the radio flux. Electric currents required for the heating of the loop up to T ≈ 107 K are determined. Therefore, the magnetic loops responsible for the persistent microwave emission can also be the sources of the “soft” X-ray component.
2. Radio Emission from TVLM 513-46546
The M8.5V ultracool dwarf TVM 513-46546 (hereafter, TVLM 513) has an effective temperature of the photosphere
Teff = 2200 K, the mass
= 0.07
M⊙, the radius
= 0.1
R⊙, and is located at a distance of 10.6 pc from the Sun. The gravitational acceleration on the star surface is
g = 2 × 10
5 cm/s
2, and rotation velocity
v sin i ≈ 60 km/s. In the case of brown dwarfs, energy is transferred from the star core to its surface by convection. On the photosphere level, the convection velocity for the stars of M ≥ 7 spectral type varies from
V ≈ 10
310
4 cm/s [
6] to
V ≈ 1.4
10
5 cm/s [
7]. The size of granulation cells for M8.5V stars approximately coincides with that of supergranulation cells,
D ≈ 1.4
10
7 cm [
8].
TVLM 513 displays two components of microwave radiation in the range of 4.8
8.5 GHz. The first one consists of periodic bursts with high brightness temperature ≥10
11 K, highly beamed emission, and 100% circular polarization [
3]. The periodicity presented in burst emission (
≈1.96 h) is due to the rotation of the dwarf. The peculiarity of the microwave emission was explained in terms of the Electron Cyclotron Maser [
9] or the plasma radiation mechanism [
10]. The second component, which is called “quiescent”, displays a brightness temperature of about 10
9 K and a small degree of circular polarization (<15%) [
1,
2]. The weak modulation of the quiescent component under the dwarf rotation means that the sources are distributed uniformly in the TVLM 513 atmosphere, and their total area is comparable with the area of the dwarf’s surface. In addition, the respective sources of the radio emission should be supplied continuously by energetic particles, to compensate the losses caused by particles precipitation into the loss-cone and to provide the observed brightness temperature. Microwave observations of the TVLM 513 indicate that the quiescent component is stable on a multiyear timescale [
2].
Observations with Very Large Array revealed the spectral index α in quiescent radio flux
Fν~ν
α for the wavelengths 20–3.6 cm [
1]. It is positive between 20 and 6 cm and equal to α = 0.1
0.2. For the wavelengths 6–3.6 cm, the spectral index is negative and equal to α =
0.4
0.1. A change in the sign of the spectral index implies that the spectrum of quiescent emission has a maximum and the maximum frequency ν
max is in the range of ν
max = 1.4–4.8 GHz (i.e., 20–6 cm) [
1]. The change in the frequency index’s sign in the gyrosynchrotron mechanism means that the radiation mode transits from optically thick to optically thin. In other words, the source of radiation in the range 4.8–8.4 GHz is most probably optically thin, which is important for further estimations.
We will use the information on the flux of the quiescent component at 8.4 GHz, i.e., where the emission source is optically thin. For the power-law distribution of energetic electrons
ne(ε) ∝ ε
−δ, the flux of gyrosynchrotron emission from an optically thin source at the frequency ν is [
11]
Here,
ϑ is the angle between the magnetic field
B and the direction toward the observer,
νe = 2.8
10
6 B is electron gyrofrequency,
is the number density of energetic electrons,
d is the source thickness in the projection to the observer, S is the source area, and
= 10.6 pc is the distance to the source. For the maximum frequency in the gyrosynchrotron spectrum and the polarization degree, we use the following formulas [
11]:
Equations (1)–(3) are true in the angle range
and for the optical thickness
, where
For the model of quiescent component, we determine the visible area of the source as
, where
is the number of elementary radiation sources (magnetic loops) on the visible hemisphere (
Figure 1), and
d and
l are a typical thickness and length of a single loop.
Using the relation
from the spectral index of the optically thin radio emission α = −0.4
0.1, one can determine the spectral index of energetic electrons
, indicating a rather hard spectrum of emitting particles. Equation (3) for the degree of circular polarization (15%) was used to estimate the magnetic field in coronal magnetic loops, the sources of gyrosynchrotron radiation of TVLM 513, B ≈ 100 G [
2].
It should be noted that one of the problems with multi-loop radio source is the estimation of the magnetic field using the observed degree of circular polarization, since various orientations of magnetic loops with different magnetic polarity should lead to a decrease in the Stokes V parameter. We assume here that despite this some predominant average polarity is retained in set of the loops, which gives a final degree of observed circular polarization (about 15%) that is rather low as compared to the polarization degree of gyrosynchrotron emission from solar loops (about 30%). The predominant average magnetic polarity can be associated with the large-scale magnetic field of the dwarf, which is partially fragmented into loops by the photospheric convection. A good example of the conservation of the magnetic field polarity in the loop set one can find from the observations of solar magnetic loops with the Solar and Heliospheric Observatory (SOHO) [
12]. Among 30 loops recorded on 1999 August 30 in AR 7986, in 21 loops the negative magnetic polarity was retained. This example means that our estimates of the magnitude of the magnetic field from the observed polarization of microwave radiation from TVLM 513 give a lower average magnitude of the magnetic field in the loops.
The values of the magnetic field and the spectral index of energetic electrons, together with the condition of optically thin sources at 8.4 GHz, impose a limitation on the value
≤ 2 × 10
16 cm
−2, which determines the microwave flux. Assuming the loop thickness of the order of the granulation cell,
d ≈ 10
7 cm,
cm, we obtain the area of all elementary sources
S ≈ (2.5–5)
10
16 Nloop cm
2; from the microwave flux (Equation (1))
one can estimate the number of sources of quiescent radio emission in the visible hemisphere required to explain the observed microwave flux,
≈ (0.4–1.0)
10
19/(
) ≈ 200
500. The filling factor of the stellar surface with the sources is about 3
16%. The number density of energetic particles is found from the condition of an optically thin source (Equations (1) and (4)) at 8.4 GHz,
, which yields
.
3. Long-Term X-ray Emission of TVLM 513 and the Coronal Heating Problem
The information collected by Chandra ACIS-S3 shows that the quiescent radio emission from the brown dwarf TVLM 513 is accompanied by soft X-ray radiation in the energy range 0.3
2 keV [
2]. To estimate the plasma temperature from 0.3
2 keV spectrum, the authors of [
2] have shown that the best-fit temperature of TVLM 513 is 0.9 keV, or
T ≈ 10
7 K. The X-ray flux in the 0.3
2 keV range is
Fx ≈ 6.3
10
−16 ergs/cm
2 s and the total luminosity
Lx = 4π
Fx ≈ 8.4
10
24 erg/s. This value of luminosity corresponds to the emission measure
=
Lx/
P(
T), where [
5]
putting
T = 10
7 K in Equation (6), we obtain
≈ 9
10
47 cm
−3.
There is the problem of heating of the entire corona of TVLM 513. Indeed, if the source of the quasi-stationary X-ray radiation is a corona with a temperature of
T ≈ 10
7 K, then the emitting volume is V ≈ 4π
H, where
,
is the Boltzmann constant,
is the gravitational constant. The X-ray luminosity from corona is
where
is determined by Equation (6),
is the average number density of electrons (ions) in the volume V. Using Equation (7), we determine the volume of the emitting corona V and the average values of the number density of particles in the corona from the observed values of the radiation luminosity and coronal temperature. For TVLM-513, we find V ≈ 2.5
10
30 cm
3, the height scale
H ≈ 4
10
9 cm, and the average plasma density in the corona
≈ 6
10
8 cm
−3.
As a result of hot coronae, brown dwarfs noticeably increase their energy losses due to thermal conductivity. The radiation losses for TVLM-513 are
[
13], while the energy losses due to thermal conductivity [
14,
15]
significantly exceed similar losses in the solar corona,
. Therefore, to maintain the corona of TVLM 513 with
T ≈ 10
7 K, more powerful heating sources are required than those in the Sun. Let us assume that in the atmospheres of brown dwarfs, as is the case in the solar corona, there are hot Type II spicules, which in the last decade have been considered to be a probable source of solar corona heating [
15,
16,
17]. Then the heat flux from the single spicule into the corona due to electron thermal conductivity along the magnetic field of the spicule is [
15]
For the radius of the spicule (magnetic flux tube) of brown dwarfs, the size of the granulation cell can be taken to be ≈ 107 cm. Then for T = 107 K and a spicule length ∆z = 109 cm, from Equation (8) we obtain ergs/s. Therefore, to compensate for the energy losses from the TVLM 513 corona, ~4 105 hot spicules covered persistently the dwarf surface are required. Moreover, the total foot-points area of spicules should be of the order of the dwarf surface area (1.5 1020 cm2), which significantly differs from the Sun, where spicules occupy ≈1% of the surface.
4. Generation of Electric Current and Plasma Heating in a Magnetic Loop: The Role of Photospheric Convection
Energy is transferred from the TVLM 513 core to the surface by the convection. At the photosphere level, the convection velocity is V ≈ 10
410
5 cm/s [
6,
7]. The half-thickness of the magnetic loops is of the order of the size of a granulation cell
cm [
8]. When the radial component of the convection velocity
Vr interacts with the azimuthal component of the magnetic field of the loop
, an EMF arises, which generates an electric current flowing from one foot point of the loop through the coronal part to the other, and closing in the photosphere, where the inequality
is satisfied and the conductivity becomes isotropic. Here,
are gyrofrequencies of electrons and ions,
are electron-atom and ion-atom collision frequencies. Thus, the coronal magnetic loop with the photospheric current channel is an equivalent RLC-circuit [
18,
19,
20]. In the self-consistent equation of the equivalent electric circuit, the resistance
R and capacitance
C are found to be dependent on the electric current [
21]:
where
y(
t) =
,
L is a loop inductance. EMF is in the photospheric foot point of the loop and is equal to
where
l1 is the height of the RLC-circuit section in the area of EMF action,
I is the longitudinal electric current,
. Estimates show that the main contribution to the loop resistance is made by the region of photospheric EMF, where the Cowling conductivity due to ion-atom collisions plays a decisive role. The resistance value in this case [
22]
where
is the relative density of neutrals,
n is the density of electrons,
Hz is the effective frequency of collisions of ions with neutrals. The steady-state value of the current in the loop is determined from the condition
R(
I) = Ξ(
I), hence at
we obtain
For the brown dwarf considered, in the height interval
z~
l1, the atomic density
,
,
T ≈ 2200 K. In this case, for the rate of photospheric convection
cm/s and
, we obtain the estimates of the current value:
. At the coronal level for an optically thin medium at temperatures
, hydrogen makes the main contribution to the neutral component, while the relative content of neutrals is determined by the formula [
23]
where
. In the temperature range of interest,
, the approximation
F ≈ 0.15/
T is valid. The rate of Joule dissipation of the current per unit volume of the loop, taking into account Equation (11), is determined by the formula [
22]
In the coronal part of the loop, the main contribution to the current dissipation is made by the second term in Equation (14). Despite the relatively low density of neutral atoms,
F ≪ 1, an effective dissipation channel associated with Cowling conductivity is switched on. This is due to a decrease in the effective plasma conductivity
because in the corona the second term in the denominator of Equation (15) is ≫1. The heating of the magnetic loop is determined by the balance of Joule dissipation, thermal conductivity, and radiation losses:
Here,
,
s is the coordinate along the loop,
Equation (15) is solved under the following boundary conditions at the foot point (
s = 0) and at the loop top (
s =
l/2):
at
s = 0 and
at
s =
l/2. It is assumed that
. From Equation (16), we find the distribution of temperature and density along the loop [
22]
It can be seen from Equation (17) that the temperature at the top of the loop reaches its maximum, and the plasma density its minimum. Both values vary slightly over most of the length of the loop, and at the foot points they reach the equilibrium values. Let us determine the number of hot loops in the corona of TVLM 513, which provide the observed measure of X-ray emission
≈ 9 × 10
47 cm
−3. By analogy with the solar corona, we assume that the thickness of the loops does not change with height, i.e.,
≈ 10
7 cm. Then from Equation (17) we find the electric current required to heat the loop plasma,
, the plasma density
and the measure of the emission of an individual loop
. To ensure the observed emission measure of “hard” X-ray radiation, it is necessary that
200 hot loops should be presented in the TVLM 513 corona. As shown in
Section 2, to explain the persistent microwave emission from TVLM 513 as well as the “soft” X-ray radiation, about 200–500 loops are needed (
Figure 1).
5. Mechanism of Long-Term Acceleration of Electrons in a Magnetic Loop—An Equivalent Electric Circuit
The persistent microwave emission generated in the TVLM 513 corona by a set of magnetic loops suggests that magnetic loops must be constantly replenished with energetic particles to compensate for the losses associated with the escape of particles into the loss-cone. In [
24,
25] a mechanism of long-term acceleration of electrons, caused by oscillations of the electric current in the loop, generated by photospheric convection, was proposed and developed. Let us show that even with a relatively small electric current, the acceleration of electrons by current oscillations in the loop is effective. From Equation (9) it follows that the current oscillations of the loop as an equivalent electric circuit are excited when the negative resistance of the photospheric EMF exceeds the loop resistance,
. The eigen-frequency of the equivalent RLC-circuit depends on the loop radius
, density
n, and length
l of the coronal part of the loop [
21,
22]:
Assuming
from Equation (18) we obtain an estimate for the eigen-frequency of the electric circuit:
(that is, a period of 50 s). Oscillations of the electric current are associated with those of the azimuthal component of the magnetic field in the magnetic loop,
. These oscillations, in turn, according to the equation
lead to the generation of an electric field directed along the loop axis. Assuming
, we obtain the electric field averaged over the loop cross section [
24]
Then from Equation (19) we obtain at
the value of the electric field:
In such an electric field at a distance of
l = 6
10
9 cm, electrons can acquire energy
ε ≈ 160 keV. At
= 0.02 more energetic electrons,
ε≈ 320 keV, will be accelerated. For the plasma density
n = 10
10 cm
−3 and the temperature
T = 10
6 K, the Dreicer field is [
26]
and the ratio of the Dreicer field to the accelerating field is
The kinetic theory gives the rate of electron acceleration per unit volume [
27]:
where
≈ 60n
s
−1. Substituting the values of
n and
T into Equation (21), we find the acceleration rate
e ≈ 3
. The condition for the generation of microwave radiation (
Section 2) requires
< 2 × 10
16 cm
−2, which for
d =
= 2
10
7 cm gives
ne < 10
9 cm
−3. The developing small-scale turbulence (whistlers for example) prevents the free escape of particles from the magnetic loop and contributes to the accumulation of accelerated particles in coronal magnetic loops.
The regimes of pitch-angle diffusion of accelerated particles into the loss-cone depend on the ratio of the following time scales [
28]: the diffusion time
, which corresponds to the mean time for the change in the pitch-angle of a fast electron at π/2 due to the wave-particle interaction, the time of filling the loss-cone
/
σ, and the time of flight when escaping into the loss-cone,
=
l/
v ≈ 0.3 s. Here,
σ =
Bfoot/
Btop is the mirror ratio of a magnetic loop. In the case of intermediate diffusion, when the condition
<
<
σ is satisfied, the loss-cone is filled faster than the particles escape into the loss-cone. In this case, the lifetime of a particle in a magnetic trap is of the order of
σt0 and the number density of accelerated electrons is [
29]
Substituting into Equation (22) = 3 , σ = 3, l = 6 109 cm, and ε = 160 keV, we obtain ≈ 2.3 107 cm−3. In the case of strong diffusion, when the condition < is satisfied, the density of accelerated electrons is by about an order of magnitude higher. Therefore, the proposed acceleration mechanism will provide the persistent microwave emission.
6. Discussion
In the problem of the origin of X-ray radiation and heating of stellar coronae, the question arises: what is emitting? Is it the entire hot corona or its local regions, such as coronal magnetic loops, and what are the constant sources of the heating for the corona or the local regions? We have shown that plasma heating to the temperature T~10 MK provided by electric current in several hundred magnetic loops quasi-uniformly distributed over the surface of the brown dwarf TVLM 513, which explains the X-ray emission luminosity of ~1 keV, is energetically more favorable than heating the entire corona. The second population of colder, with T~1 MK, coronal loops is a source of persistent nonthermal microwave radiation explained by gyrosynchrotron radiation of ~150300 keV electrons in a magnetic field of ~100 G. The proposed mechanism of long-term acceleration of electrons by induced electric fields is based on small oscillations of electric current in the coronal loops supported by photospheric convection.
In the model proposed by Osten et al. [
1], the source of microwave radiation is represented by the dipole magnetic field of the dwarf. Berger et al. [
2] suggested that the source of microwave radiation is a large-scale magnetic structure with a “covering factor” of about 50%. Both models cannot provide a long-term supply of sub-relativistic electrons to the radiation sources. In addition, the Berger’s model does not identify the X-ray source in the brown dwarf corona.
It follows from Equation (17) that the plasma heating temperature is proportional to
T~
I4/9. For a current
I = 10
8 A, at which the acceleration of electrons is sufficiently efficient, the plasma in the loop heats up only to a temperature of 4 × 10
5 K, and at
I = 10
9 A up to 10
6 K, i.e., the “microwave” loops are also sources of a softer X-ray component with a maximum in the spectrum of ≈0.2 keV. With an increase in the current value, the lumped-loop approach used by us is invalid, since the period of the RLC oscillations becomes shorter than the propagation time of the Alfvén disturbance along the loop
tA =
l/
VA ≈ 30 s. During this time, the current oscillations change direction many times and the acceleration of electrons is ineffective. This circumstance can explain the absence of noticeable nonthermal radio emission from hot coronal loops with the plasma temperature
T = 10 MK. In this work, we did not consider the origin of the intense, with the brightness temperature
Tb ≥ 10
11 K, flare component of microwave radiation from TVLM 513, the nature of which was discussed in [
9,
10]
7. Conclusions
Photospheric convection, interacting with the magnetic field at the foot points of the magnetic loops, leads to generation of an electric current, , the dissipation of which under the conditions of partially ionized plasma causes the loop plasma heating up to a temperature of T ≈ 107 K. Hot plasma of ~200 loops, quasi-uniformly distributed over the dwarf’s surface, is a source of ~1 keV X-ray emission from TVLM 513.
Photospheric convection maintains continuous oscillations of electric current in the magnetic loops as an equivalent RLC circuit, generating the induced electric fields that accelerate electrons up to 150300 keV in magnetic loops distributed over the dwarf’s surface. This provides the persistent quiescent microwave radiation of a few ×100 loops of TVLM 513 by the gyrosynchrotron mechanism.
Effective acceleration of electrons by the electric current oscillations is possible even at relatively low values of electric current, A. At currents , the loop plasma heats up only to temperature T ≈ 106 K, i.e., magnetic loops emitting microwave radiation can simultaneously be the sources of ~0.2 keV X-ray emission.
Thus, photospheric convection not only forms numerous magnetic loops in the corona of TVLM 513, but also generates an electric current leading to heating of the loop plasma and acceleration of electrons. As a result, two populations of loops quasi-distributed over the TVLM 513 surface are formed, one of which is a source of “hard” X-ray radiation, and the other is simultaneously a source of microwave and “soft” X-ray radiation.