Abstract
Recent discovery of fast blue optical transients (FBOTs)—a new class of energetic transient sources—can shed light on the long-standing problem of supernova—long gamma-ray burst connections. A distinctive feature of such objects is the presence of modestly relativistic outflows which place them in between the non-relativistic and relativistic supernovae-related events. Here we present the results of kinetic particle-in-cell and Monte Carlo simulations of particle acceleration and magnetic field amplification by shocks with the velocities in the interval between 0.1 and 0.7 c. These simulations are needed for the interpretation of the observed broad band radiation of FBOTs. Their fast, mildly to moderately relativistic outflows may efficiently accelerate relativistic particles. With particle-in-cell simulations we demonstrate that synchrotron radiation of accelerated relativistic electrons in the shock downstream may fit the observed radio fluxes. At longer timescales, well beyond those reachable within a particle-in-cell approach, our nonlinear Monte Carlo model predicts that protons and nuclei can be accelerated to petaelectronvolt (PeV) energies. Therefore, such fast and energetic transient sources can contribute to galactic populations of high energy cosmic rays.
1. Introduction
The time domain astronomy operating now at all wavebands from radio to gamma rays has provided unique information on highly energetic processes in transient astrophysical objects such as supernovae (SNe), gamma-ray bursts (GRBs), fast radio bursts and others. The pioneer program of a dedicated search for supernovae in the optical band started by Fritz Zwicky in 1936, which has later allowed, in particular, obtaining fundamental results on the accelerated expansion of the Universe via spectroscopy of SN type Ia, is now ongoing with great perspectives [1]. The capabilities of fast and sensitive wide field imaging suggested for the forthcoming Large Synoptic Survey Telescope (LSST) would allow detecting many thousands of luminous SNe and tidal disruption events (TDEs) per year as well as studying other types of transient sources [2]. Together with the LSST, the currently operating wide field [3] and survey [4] X-ray observatories along with the future high energy missions [5,6,7], gravitational wave and neutrino observatories will allow revealing the physical nature of various types of energetic space transients.
The fast blue optical transients (FBOTs) [8,9,10,11] are among the most interesting recent discoveries. Their appearance is somewhat different from most of the core-collapse SNe [8,12]. Together with the low-luminosity GRBs they possibly belong to the intermediate class of phenomena filling the gap between non-relativistic SNe and “standard” long duration gamma-ray bursts, and which could have volumetric rates well above that of the GRBs [13,14]. The duration of both the energy-momentum release from the central engine and the interaction of the anisotropic ejecta with the outer layers of the progenitor star and its circumstellar matter determine the transient appearance (see, e.g., [15]).
Three recently studied powerful FBOT sources AT2018cow [9], CSS161010 [10] and ZTF18abvkwla [11] were characterized by a low ejected mass and fast outflows. Indeed, Margutti et al. [9] found that to explain the fast rise of the optical and radio emission together with the persistent photosphere appearance in AT2018cow a wide range of velocities in the range from about 0.02 c to 0.2 c is needed, where c is the speed of light. The aspherical ejecta with the range of velocities had the estimated mass ∼0.1–1 [9]. The long low frequency radio observations [16] allowed estimating the shock radius to be cm and the speed of the fast ejecta to be above 0.2 c at 257 days after the shock breakout. The mass loss rate of the progenitor star was found to be a few times during the period of 20–50 years assuming the wind velocity ∼, while it was possibly 100 times higher in a period of a few years just before the event [16].
Another interesting FBOT source is CSS161010 located in a dwarf galaxy at a distance about 150 Mpc [10]. On the basis of the synchrotron interpretation of its radio emission, which is peaked at about 100 days after the FBOT event, the authors suggested a presence of a mildly relativistic outflow of four-velocity 0.55 c driving a blast wave. They estimated the ejected mass to be in the range of 0.01–0.1 . The outflow is faster than that estimated for AT2018cow and is similar to that in ZTF18abvkwla. The origin of the bright X-ray luminosity is attributed to an emission component, which is likely different from the primary one, which produced the synchrotron radio emission. Recent radio, millimeter wave and X-ray observations [17,18] of a short-duration luminous FBOT transient ZTF20acigmel (AT2020xnd) located at z = 0.2433 indicated a presence of a fast ejecta with a ∼0.2 c speed shock with estimated energy above 10 ergs. AT2020xnd has shown high radio luminosity of ergs Hz at 20 GHz almost 75 days after the event [18]. The observational data suggested a shock driven by a fast outflow of velocity 0.1–0.2 c interacting with the dense circumstellar matter shaped by an intense wind of with velocity of km s from the progenitor star [18]; the presence of a steep density profile of in the wind was suggested by [17]. Similar to AT2018cow, the detected X-ray emission is in excess compared to the extrapolated synchrotron spectrum and constitutes a different emission component, possibly powered by accretion onto a newly formed black hole or neutron star.
The distinctive features of the four FBOT transients discovered so far are their high peak bolometric luminosity L 1043 erg s−1 and a rapid timescale of a few days duration. Multi-wavelength observations of these objects uncovered the presence of powerful subor mildly relativistic outflows which are likely originated from either rare SN-type or TDE-type events with intermediate or stellar mass black holes (see, e.g., [19]). The kilonova type sources with the neutron stars mergers typically eject the masses in the range of 10−4–10−2 M⊙ (and even ~ for the black hole—neutron star mergers) with velocities ∼0.1–0.3 c [20]. It is interesting that the recent model of a supernova from a primordial population III star of a 55,500 mass with general relativistic instability [21] predicts the ejecta velocities of about 0.3 c. Earlier mildly and moderately relativistic ejecta outflows were found in a few broad line type Ic SNe (e.g., [22,23]). The geometry and structure of the outflows producing FBOTs depend on the source of their power and it is a subject of modeling [9]. Relativistic mass ejection in spherically symmetric shock outflows of core-collapse supernovae was studied in detail in [24,25,26]. Their high-velocity solutions demonstrated rather a steep dependence of the deposited kinetic energy as a function of the ejecta four-speed . Much flatter energy—ejecta velocity distribution can be obtained for engine-driven asymmetric supernovae with a powerful activity of compact stellar remnants [27,28,29,30]. Recently, numerical models of supernova explosions where the supernova ejecta interacts with the relativistic wind from the central engine were constructed in [31]. The formation of relativistic flows in the interaction of the powerful non-thermal radiation produced by the central machine with the supernova ejecta was considered in the papers [32,33].
Very luminous optical FBOT events with light curves extending to a couple of weeks can be expected in the case of shock breakout into a dense circumstellar shell produced by the dense progenitor wind a few years before the SN event [34,35,36]. The presence of an hour timescale central engine activity with a luminosity of about 10 producing mildly relativistic jet was proposed in [15] to model SN 2006aj associated with a low-luminosity GRB. The bright high frequency radio emission of FBOTs and, possibly, the hard X-ray component detected in some events of this type, is produced by relativistic electrons accelerated by shocks driven by fast moderately relativistic outflows from the central engine. Moreover, the synchrotron self-absorption effects [37] are apparent in some FBOT spectra.
The SN shock breakout is usually accompanied by a bright ultraviolet (UV) flash, and it is likely that afterwards the shock enters a collisionless regime [38] with the X-ray dominated spectrum. Some models of relativistic shock breakout which consider a multifluid structure of a relativistic shock mediated by radiation in a cold electron-proton plasma are currently under discussion [39,40]. A MeV gamma-ray flash of the total energy ∼ erg lasting from a few seconds to a few hours was predicted in [41,42] for some SN events. At the later SN stages (after a few days from the event) the radiative shock is transforming into a collisionless plasma shock regulated by kinetic plasma instabilities. A specific feature of the collisionless shocks is their ability to create a powerful non-thermal particle population and to accelerate relativistic particles [43]. The collisionless shock structure and the efficiency of particle acceleration depend on the shock speed, on magnetic field inclination to the shock normal and on the plasma magnetization parameter [44,45]. Modeling of particle acceleration by non-relativistic shocks of velocities below 0.1 c in supernova remnants was discussed in [46] while studies of relativistic shocks was presented in [47].
Kinetic simulations of the efficiencies of the shock ram pressure conversion to magnetic fluctuations and relativistic particles are needed to provide an adequate interpretation of the observed non-thermal radiation. The mildly relativistic magneto-hydrodynamic (MHD) flows were shown (see, e.g., [48,49]) to be the most efficient environment providing the maximum energies of the accelerated nuclei for a given magnetic/kinetic luminosity of the power engine. Recent models suggested a possibility of cosmic ray acceleration to ultra high energies in the low-luminosity GRBs associated with SNe (see, e.g., [50,51]) and in relativistic SNe [52]. Fast outflows from SNe with dense circumstellar shells could accelerate cosmic rays up to the high energy regime on a few weeks timescale (e.g., [53,54]).
The structure and particle acceleration in the fast collisionless shocks can be successfully modeled with the kinetic particle-in-cell (PIC) technique [43,55] at many thousands of the particle gyro-scales. On the other hand, as the observed multi-wavelength spectra of supernova remnants and GRBs compellingly demonstrated that the spectra of accelerated particles extend to many decades in the particle momentum, a combination of both microscopic (see Section 2) and macroscopic kinetic models (see Section 3) is necessary to construct realistic models of such sources. Cosmic ray acceleration by supernova remnants is a subject of extensive modeling [46,52,56,57,58,59]. One of the most uncertain points is at what stage PeV regime cosmic rays can be accelerated. We discuss in Section 3 high energy cosmic ray acceleration in FBOT-type sources as potential pevatrons.
Here we will present 2D PIC simulation of sub and mildly relativistic shocks within the shock speed interval 0.1–0.7 c in proton-electron plasmas which could be applied to FBOT sources modeling. The fiducial case in our work is 0.3 c.
Earlier, Park et al. [60] presented a set of 1D PIC models of shocks in a range of velocities up to 0.1 c. They performed in the 1D case long simulation runs up to . For higher shock speed of 0.75 c Crumley et al. [61,62] published 2D PIC simulation results. In the quasi-parallel shock of a velocity 0.75 c simulation of about 4100 duration allowed them to model Bell-mediated shock. In particular, they noted that acceleration of electrons is likely initially associated with the shock drift acceleration and then switches to diffusive shock acceleration regime as it was seen in [60].
To model radio emission observed from CSS161010, where the shock velocity of about 0.3 c was suggested by observations, we make 2D PIC simulations with ratio of 100, which are limited to the timescale ∼7 . We discuss possible extrapolations of electron spectra to the energy range needed to model the radio emission.
2. Particle-in-Cell Simulations of Fast Mildly Relativistic Shocks
In this section, we present the results of particle-in-cell simulations of mildly relativistic shocks at gyro-scales with application to the observed non-thermal emission from FBOTs.
To simulate the structure and non-thermal particle acceleration by a mildly relativistic collisionless shock wave we have employed the publicly available code Smilei developed by Derouillat et al. [63]. This code is based on explicit Finite Differences Time Domain approach for solving Maxwell equations and on a relativistic solver for particle movement with charge-conserving algorithm proposed by [64].
For model shock initialization we employ a common approach: a homogeneous plasma flow collides with an ideal reflecting wall. The simulation box is two-dimensional, with the number of cells = 204,800 in the direction along the flow velocity and in the transverse direction, while particle velocities and the electromagnetic field are represented by full 3D vectors. Homogeneous plasma flows in through the right boundary and the reflecting wall is placed at the left boundary. Boundary conditions in the transverse direction are periodic. The initial magnetic field lies in the plane of the simulation inclined by the angle to the velocity of the flow. The electric field is initialized to compensate the Lorentz force in the laboratory frame . The velocity of plasma flow is 0.3 c and its Lorentz-factor is . The magnetization , where is upstream concentration and is mass of proton, in all the modeled configurations is about . The electron mass is artificially increased up to in order to save computational resources. All the quantities obtained from the simulation can be scaled with respect to the plasma concentration, which can be chosen arbitrary during the data analysis. The spatial grid step is and the time step is , where is electron plasma frequency , is the absolute value of the electron charge. Within such a setting the simulation box size along the -axis corresponds to gyroradii of protons in plasma flow and along the -axis—to 1 gyroradius. The maximum simulation time is or about inverse proton gyrofrequencies. For plasma concentration cm, this corresponds to timescale about 1 s, which is much smaller than the typical activity period of FBOTs.
The efficiency of particle acceleration depends on the inclination angle , especially in the case of relativistic flows [44,61,62,65]. To participate in the diffusive acceleration process, a particle needs to escape from the shock front and if it moves along the magnetic field, the maximum velocity along the -axis is , and it should be larger than the shock velocity (all quantities here are measured in the upstream frame). As one can see in Figure 1, the high energy tail of the electron distribution is much higher for a quasiparallel shock. Such an angle dependence may lead to the presence of different electron distributions within one object, and this may possibly explain the difference between the spectral indices of synchrotron radio and inverse Compton X-ray radiation observed in FBOT AT2018cow [9].
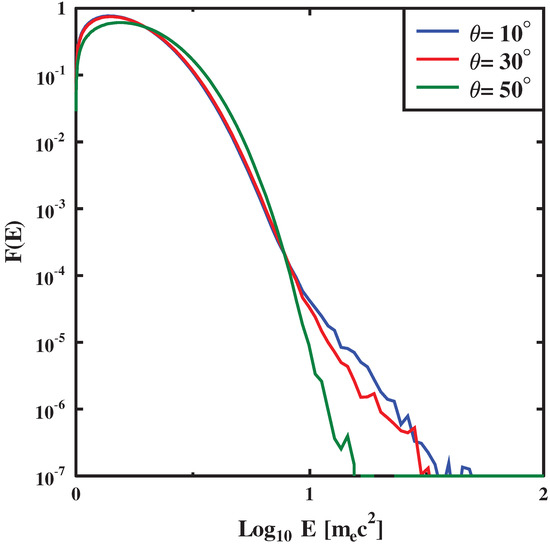
Figure 1.
Electron distribution function in the shock downstream with initial parameters c, and different inclination angles.
For further modeling of synchrotron radiation from FBOT CSS161010 we have used a setup with parameters 0.3 c, and (a quasiparallel shock). Time evolution of the concentration profile in such a shock averaged in the transverse direction is shown in Figure 2 and the corresponding magnetic field at the moment is shown in Figure 3.
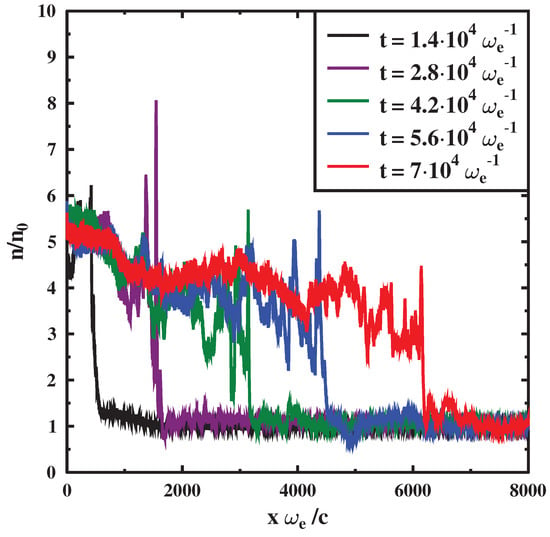
Figure 2.
Time evolution of concentration normalized to the far upstream concentration.
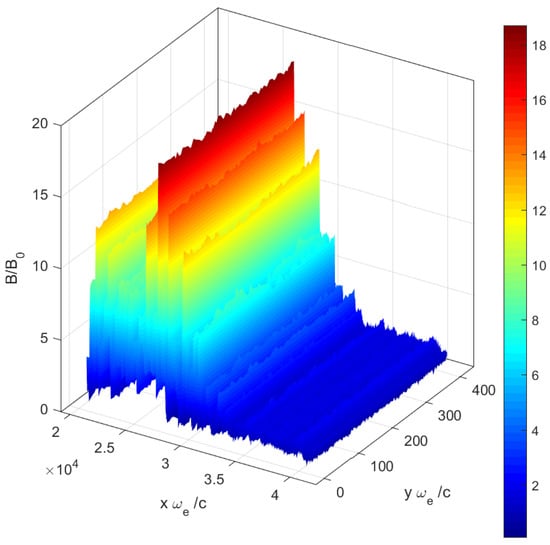
Figure 3.
Magnetic field normalized to the far upstream magnetic field.
With the computed concentration profile we can determine the coordinate of the shock front: we consider that is the first point from the right where the concentration is two times larger than that in the far upstream. The average shock velocity is the ratio of the shock coordinate and the simulation time . At later times the shock wave propagation is close to a stationary regime. The shock velocity measured in the downstream frame is close to the constant value 0.085 c. In the upstream (observer) frame it corresponds to 0.38 c.
The simulations have allowed us to compute model distributions of electrons. In the downstream region such distributions have a complex shape, where one can see two main components: a thermal peak and a power law tail at high energies. At low energies () we approximate the distribution with a Maxwell-Juttner function: an iterative process is employed to minimize the functional , where is simulated electron distribution function and is Maxwell-Juttner distribution function, and find the effective temperature. For high energies () we follow a least squares approach for linear regression in double logarithmic coordinates and obtain the power law spectral index. The electron spectrum in a close downstream of the shock (5000 grid cells behind the shock) at time = 70,000 for the setup with and and its approximation with temperature K and spectral index are shown in Figure 4.
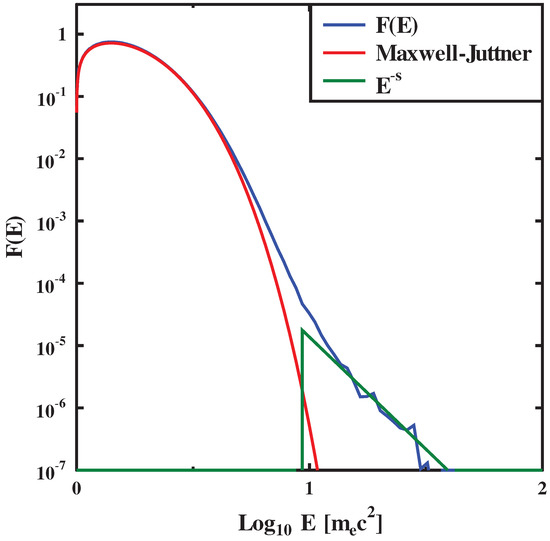
Figure 4.
The electron distribution function in the shock downstream with initial parameters c, and .
Time dependence of electron distribution function at later stages of simulation is shown in Figure 5. Distribution is not stationary and one can see the oscillation of the electron spectral distribution due to the influence of magneto-hydrodynamic instabilities, as described in [61,66]. So we have chosen the electron distribution at time = 70,000 for the further modeling.
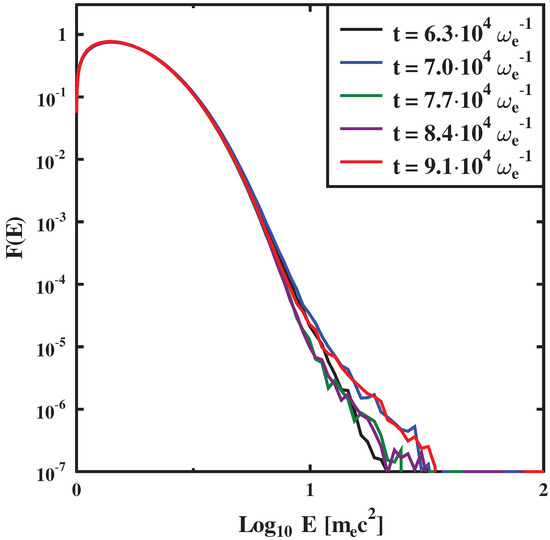
Figure 5.
The electron distribution function in the shock downstream at different time moments.
Recent observations of FBOTs [8,9,10,11] discussed above have shown that their synchrotron spectra are strongly influenced by synchrotron self-absorption. At the given time moment, observable radio fluxes rise as for low frequencies, then have a peak and fade with a power law tail, which depends on the particular electron distribution function. Additionally, the time dependence of such spectrum is very specific and its details could be used to imply a number of source parameters: the magnetic field and the shock radius can be determined from the measured maximum of the light-curve at given frequency , once the fractions of energy in accelerated electrons and magnetic field and are established, with the relations derived by Chevalier [37].
where is the electron spectral index, derived from the power law tail of emissivity spectrum and its time dependence, , , are the Pacholczyk constants [67], depending on , is the minimum energy of the electron power law distribution, which usually equals to the electron rest energy, is the filling factor—the emitting fraction of the source volume, and is the distance to the source. A problem of this method is that it needs a lot of assumptions about the shock structure and electron distribution. In this model the emitting region is considered to be a homogeneous flat disk with the radius and depth . There is also a model modification for a spherical source with an account for source inhomogenuity [17]. The electron distribution is considered to be a power law. Additionally, fractions of energy and are unknown and are often chosen according to the equipartition rule . However the simulation results show, that these values are unlikely to be that large. Following Chevalier [68] we define the energy fractions in terms of the upstream kinetic energy density , where is the upstream concentration. In this notation and , is the accelerated electron energy evaluated by subtracting from the total electron energy, that corresponds to the Maxwell–Juttner fit of the distribution function. The values obtained by particle-in-cell simulations in our fiducial setup are and . They depend on the initial conditions, but for a wide variety of parameters we see that the fraction of energy in magnetic field is lower than . Particle-in-cell simulations have rather small scales and cannot describe the influence of long wave upstream instabilities caused by high energy particles, but Monte Carlo simulations show similar values, as described below.
Using the electron distribution function obtained from the PIC simulation we can evaluate the spectral density of the energy flux of synchrotron radiation from the source, taking into account the effect of synchrotron self absorption. Standard formulae for that effect are described in detail in [69]. Emitted power per unit frequency per unit volume is
where is the angle between the magnetic field and the line of sight, is the critical frequency , and is the modified Bessel function. The absorption coefficient is
The obtained spectral density is further integrated over the volume of the source, which is described as a spherical shell, whose volume is determined by a filling factor . Hence the total emissivity and observable flux at distance can be derived. The magnetic field is considered constant and perpendicular to the line of sight. The concentration in the stellar wind depends on radius as , but in the downstream of the shock we assume it constant. The electron distribution function is also constant in the volume of the source. This modeling is further applied to explain the spectrum of the FBOT transient CSS161010. As described in [10] at time days after explosion its shock velocity was , which corresponds to the modeled upstream plasma flow velocity , measured in the downstream frame. At this moment, parameters derived with Equations (1) and (2), assuming the equipartition regime , are as follows: the magnetic field G, the outer radius cm, the concentration cm, the electron spectral index , which is similar to that obtained from a PIC simulation, and the minimum energy .
The thermal electrons may contribute substantially to the observed synchrotron spectrum and it was shown in [70] that models with the power law electron distribution might be oversimplified. Additionally, equipartition regime is not very reasonable assumption. Thus, the use of the realistic kinetic simulations is important to model broad band radiation spectra of FBOTs. We have compared the observed fluxes to three models of source emission, evaluated with power law electron distribution and two distributions obtained from PIC simulation: with extrapolation of power law tail to higher energies () and without it. For the first case, we have used the parameters described above. In order to evaluate parameters and of the simulated particle distribution, we minimized the functional , where are the observed frequencies, are the observed fluxes and —the modeled fluxes, using the gradient descent algorithm. We employed six measurements from [10]: four made with VLA at day 357 at frequencies 1.5, 3.0, 6.05 and 10 GHz and two made by GMRT at day 350 at frequencies 0.33 and 0.61 GHz. Concentration in these equations is determined by the magnetic field , obtained from the PIC simulation. One can see that distribution, obtained directly from particle-in-cell simulation, cannot correctly fit the power law tail in observational data, so we had to extrapolate the simulated electron distribution to higher energies because the PIC approach requires a lot of computational resources and thus is not suitable to simulate the considered system up to timescales long enough to form a long tail of accelerated particles. The modeled parameters for extrapolated distribution are G, cm and concentration cm. The values of the magnetic field and radius are rather close to the values from [10], while the concentration is much higher. These results are illustrated in Figure 6.
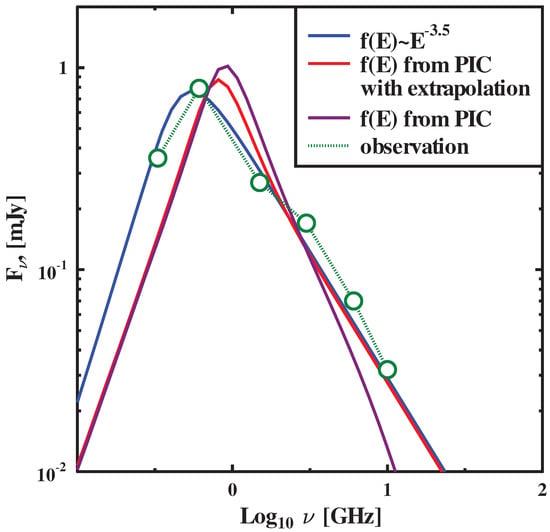
Figure 6.
Observed (green circles) and modeled spectral energy distribution of CSS161010 at day 357 for various model electron distributions.
One can see that the parameters of the shock (especially the concentration), obtained from the radiation model strongly depend on the electron distribution function. This should be kept in mind during interpretation of the observational data.
3. A Monte Carlo Model of Cosmic Ray Acceleration in Fast Transient Sources
We have developed a Monte Carlo model of particle acceleration by collisionless shock waves. Acceleration occurs according to the first-order Fermi mechanism when particles are scattered by magnetic fluctuations and cross the shock front many times—the so-called diffusive shock acceleration (DSA). The distribution function of the accelerated particles has a significant anisotropy in the upstream of the shock, and this anisotropy leads to development of plasma instabilities in the upstream. The development of plasma instabilities also leads to a magnetic field amplification (MFA) in the upstream. The pressure of the accelerated particles can be on the order of the total momentum flux flowing onto the shock. In this case, the pressure gradient of the accelerated particles leads to modification of the plasma flow in the upstream.
The Monte Carlo code employed to describe the DSA and MFA is one-dimensional, stationary, nonlinear and plane-parallel. We consider acceleration of protons. The non-relativistic model described in [71] has been modified to be applicable for the case of relativistic shocks. Within this model all the particles are divided into background and accelerated ones: the accelerated particles are those that have crossed the shock front from the downstream to the upstream at least once. The accelerated particles are treated individually. Background particles are described via macroscopic parameters under the assumption of their local Maxwell distribution function up to the injection point near the shock front in the upstream. After this point, the background particles are described as particles, which allows us not to add any additional parameters to describe the injection of particles into the acceleration process. During the propagation of particles, they are scattered elastically and isotropically in the rest frame of the scattering centers according to the pitch-angle scattering approach [72,73,74,75,76]. The reference frame of the scattering centers for background particles moves with a speed relative to the rest frame of the shock. The rest frame of the scattering centers for accelerated particles moves with a speed relative to the rest frame of the shock. is the speed of the background plasma flow. The presence of is due to the fact that with the development of resonant instability, the modes propagating only in a certain direction relative to the background plasma are amplified. will be determined below.
Between the scatterings the particles uniformly move straightforward. The distance between particle scatterings is proportional to its mean free path, which we define as:
where is the absolute value of the wavenumber of modes that make up magnetic fluctuations, is the particle momentum, is the particle coordinate that is counted from the front of the shock wave. Negative values of correspond to the upstream, positive values correspond to the downstream.
where is the spectral density of the turbulence energy.
is the large-scale magnetic field:
where is the constant longitudinal magnetic field. The particle propagates until it gets outside of the model box to the far downstream or crosses the free escape boundary (FEB) located at in the far upstream.
The iterative scheme of the employed numerical model allows us to keep the conservation laws of momentum and energy fluxes near the shock front. In the stationary relativistic case these are are formulated as follows. The law of conservation of particle flux (automatically kept here) has the form:
where is the Lorentz factor of the background plasma flow, , is the background plasma number density, is the particle flux in the far upstream.
The conservation law of momentum flux takes the form:
where is the background plasma pressure, , is the background plasma adiabatic index, is the turbulence pressure, , , is the momentum flux in the far unperturbed upstream, is the momentum flux carried away by the accelerated particles through the FEB (), is the momentum flux of the accelerated particles.
The conservation law of energy flux takes the form:
where is the energy flux in the far unperturbed upstream, is the energy flux carried away by accelerated particles through the FEB (), is the energy flux of the accelerated particles.
To keep the conservation laws (12) and (13), it is necessary to determine the profile of the background plasma flow in the upstream and the full compression by the shock by means of an iterative process. At the initial iteration, approximate profiles , in the upstream, and the full shock compression are set. Then the particles are propagated and their distribution function is calculated accordingly. In the far downstream, the momentum distribution function of all the particles in the rest frame of the flow is isotropic. Thus, it is possible to determine the adiabatic index of the entire plasma in the downstream based on the obtained particle distribution function. Here and below, the subscript 0(2) denotes the values in the far upstream (downstream). In these designations .
To find the full compression, we write down the flux conservation laws (11), (12) and (13) for the far upstream and for the downstream.
where is the pressure of the entire plasma in the downstream, . We determine the current values , and at this iteration of the quantities from the distribution function obtained after particle propagation. The value is also calculated based on the equation given below. Thus, three unknowns , and remain in the Equations (14)–(16). Solving these equations, we find a new value of . The value for the next iteration is found by averaging the new value and the old one.
A new profile of the flow velocity in the upstream is determined according to the formula based on (12):
where the values obtained after propagation of particles are in the right part of the expression. The background plasma momentum flux is . The turbulence momentum flux is . is determined by the flow profile at the previous iteration. Selection of the flow profile based on the expression (17) in the area where the background flow is described in the form of particles, works well in the case of non-relativistic motion, when calculating in this area based on the distribution function of background particles. In the relativistic case, as shown in [77], the momentum flow in the iterative process converges to a greater value than in the far upstream, when using (17) near the shock wave front. Hence, following [77] we smooth out the flow profile near the shock front. The new speed profile is then averaged with the old one. Below we describe the equations that are used to calculate the values included in and .
The turbulence energy spectrum defining is found based on the solution of the following equation:
where is the turbulent energy dissipation. The spectral flux of the turbulent energy (turbulent cascade) is:
where is the background plasma density,
where is the Kolmogorov’s constant, which is here taken equal to . The expression (19) is derived from [78]. is the growth rate of the turbulent energy in the background plasma rest frame due to plasma instabilities. Similar to [71], here we considered the growth rate of current instabilities—the Bell’s non-resonant [79] and resonant instability. The accelerated particle current, which determines the growth rates, is calculated in the rest frame of the scattering centers, after propagation of particles.
Differentiating the Equations (12) and (13) by , using (11), and excluding from the equations the term proportional to we get the following relation:
If we assume that each of the components of the system is affected only by the change of , that is, the change in energy and momentum flux occurs adiabatically due to the change of the flow velocity, we can divide the Equation (21) into separate adiabatic equations for the components:
The Equation (23) in this case is equivalent to the Equation (18) integrated by in the absence of MFA and dissipation. In the presence of MFA and dissipation after integration by , the Equation (18) will take the form (similar to (23)):
where the dissipation term is . Here we use the following expression for the turbulent energy dissipation:
where is the Boltzmann’s constant, is the background plasma temperature (). In this model, it is assumed that in the downstream and .
From the comparison of Equations (23) and (25) one can see that there are two additional terms in the right side of (25). To fulfill the total energy conservation Equation (21), these terms must be compensated by introducing additional terms into the equations for the remaining components of the system. We assume that the dissipation of the turbulent energy flow leads to heating of the background plasma. An increase in the energy flow turbulence due to MFA can be compensated by scattering accelerated particles in the frame of scattering centers moving with the speed . Then the equation for the energy flux of the accelerated particles will take the form:
Within the considered geometry we introduce as follows:
up to the injection point of the background particles in the upstream. After the injection point and before the shock front . In the downstream . In this model, we assume that part of the energy flux taken from the accelerated particle flux in the region where , goes to heat the background plasma. Thus, the equation determining the change in the energy flux of the background plasma has the form:
where if , in the opposite limit . After the injection point of background particles and in the downstream .
Substituting the expression for into the Equation (34), we obtain the following equation for the background plasma pressure:
To solve the Equation (18), one needs to set the profile on the FEB . We define —the Kolmogorov’s spectrum at the FEB with the energy-carrying scale . is normalized as follows:
Based on the developed Monte Carlo model, we have performed calculations of proton acceleration by mildly relativistic shocks, which are thought to come out during explosions of some SN kinds. In this case, the shocks often propagate into the wind of the pre-supernova star. The number density of particles (protons) in the stellar wind can be estimated as:
where is the mass-loss rate of the pre-supernova, is the speed of the stellar wind, is the distance from the center of the star. For yr, = 1000 km s and cm: cm. This estimate is used to estimated the number density in the far upstream. cm in all the calculations. We assume that the free escape boundary is at 0.2 of the current radius of the shock. The calculation parameters and their results are presented in Table 1.

Table 1.
The grid of Monte Carlo calculation parameters.
The spatial coordinate x in the figures is measured in . For the model A1: .
As can be seen from Figure 7, with an increase of the shock speed, the maximum momentum of accelerated particles increases. The value also increases with an increase in the velocity of the shock wave in the range of simulated shock velocities 0.1–0.5 c and it decreases slightly for the shock velocity of (see Table 1) where the transition to relativistic shock regime occurs. Particle-in-cell simulations of electron and proton spectra in the trans-relativistic regime were discussed in [61,62].
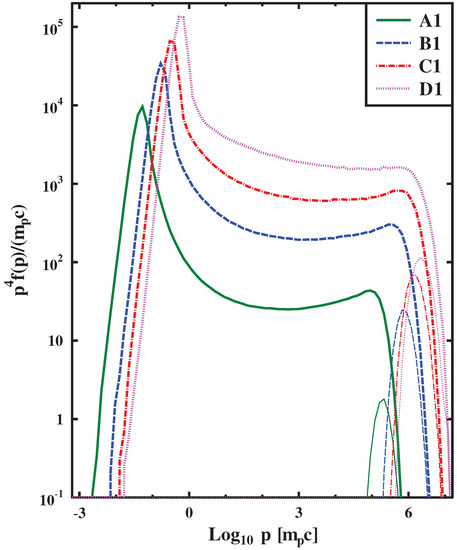
Figure 7.
Particle distribution function in the shock rest frame, thick curves correspond to the point (the front shock), thin curves correspond to a point . The correspondence of the certain model Table 1 is reflected in the legend.
Figure 8 shows particle distribution functions used for evaluations of the models A1, A2 and A3, with varying values of and the magnetic field at the FEB. Note, that with an increase of the FEB distance, the strength of the magnetic field on the FEB decreases proportionally. It can be seen that in these configurations the maximum momenta of the accelerated particles are almost the same. The current of the highest energy particles near the FEB amplify turbulent fluctuations due to the small-scale Bell’s instability on scales much smaller than their own gyroradius. In Figure 9, the spectral energy density of the turbulence is shown at various upstream points for the model A1. Furthermore, it takes time to significantly amplify the magnetic field, and thus, the amplitude of the amplified turbulent field in a significant part of the upstream differs slightly from its value at the FEB (see Figure 10). The gyroradius of the highest energy particles near the FEB turns out to be significantly larger than the scale of the amplified fluctuations, which leads to a small contribution of the expression (8) to the free path (5). Thus, the free path (5) of the highest energy particles in a significant part of the upstream is determined by the contribution (6) with the initial turbulent field. That is, the free path (5) of the highest energy particles in a significant part of the upstream is according to the normalization (36). The non-relativistic theory of DSA gives a simple estimate of the maximum momentum in the case of an upstream path independent of the coordinate: . Accordingly, our model has a good estimate: . In Figure 11, the independence of the maximum particle momentum from the number density in the far upstream is illustrated. In Figure 12, it is shown, that with an increase of the magnetic field with the other parameters kept constant, the maximum particle momentum increases.
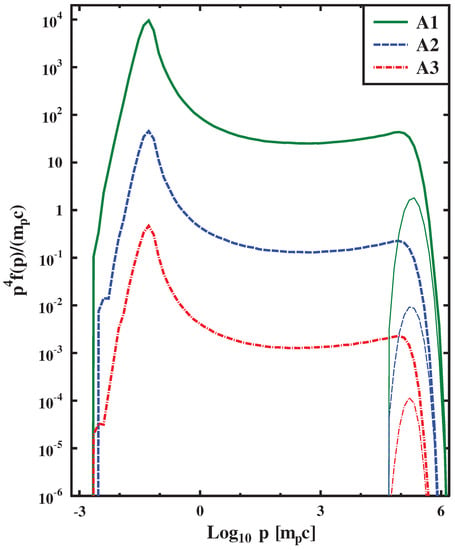
Figure 8.
The particle distribution function in the shock rest frame, the thick curves correspond to the point (the front shock), the thin curves correspond to the point . The correspondence to Table 1 is reflected in the legend.
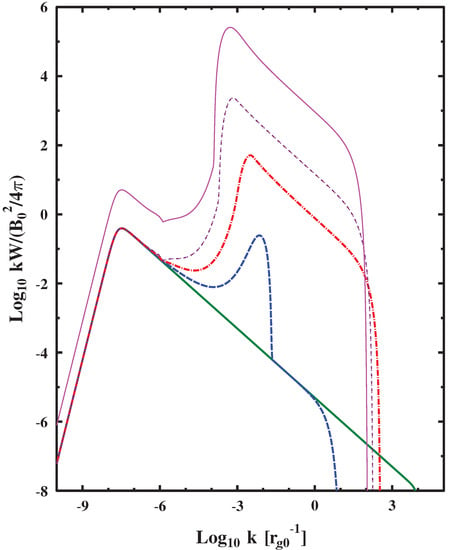
Figure 9.
Spectral turbulent energy density for the model A1. The green solid curve corresponds to the point . The blue dashed curve corresponds to the point . The red dash-point curve corresponds to the point . The thin purple dashed curve corresponds to the point . The thin magenta solid curve corresponds to the point (the shock front).
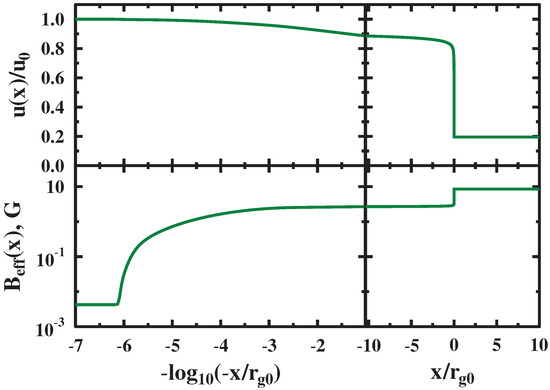
Figure 10.
Background plasma velocity profile (upper panel) and magnetic field profile (bottom panel) for the model B1.
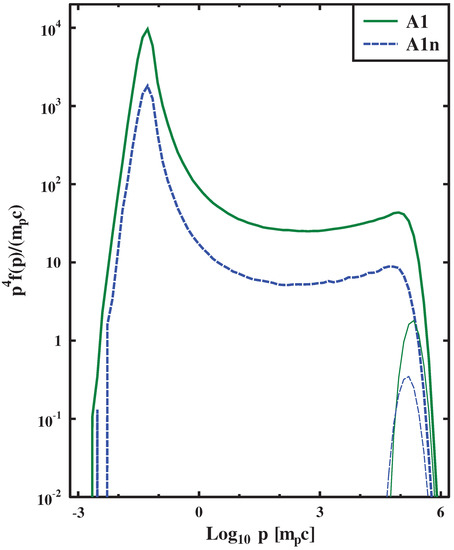
Figure 11.
Particle distribution function in the shock rest frame, the thick curves correspond to the point (the front shock), the thin curves correspond to the point . The correspondence to Table 1 is reflected in the legend.
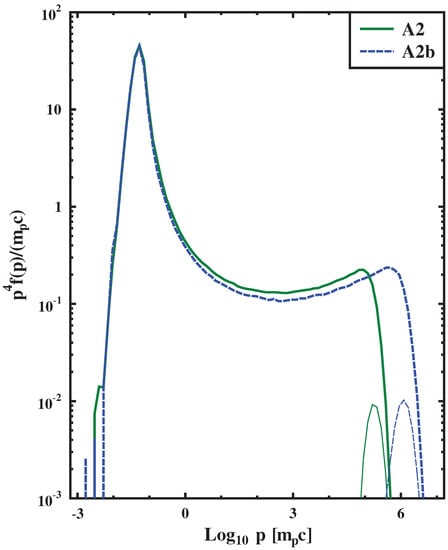
Figure 12.
Particle distribution function in the shock rest frame, the thick curves correspond to the point (the front shock), the thin curves correspond to the point . The correspondence to Table 1 is reflected in the legend.
We have made the following estimate of the acceleration time of the particles to their maximum momentum. In the estimation, we assume that the mean free path of the highest energy particles with momentum in most of the upstream can be estimated by the gyroradius in the magnetic field . Thus, taking into account that the magnetic field in the downstream is much stronger and, accordingly, the diffusion coefficient of particles is much smaller than in the upstream , where is the diffusion coefficient of the highest energy particles in the upstream. Accordingly, the estimate of the particle acceleration time to the momentum has the form:
In the considered models we assume that the current radius of the shock is . The expansion time of the supernova remnant can be estimated as the ratio of the current shock radius to the shock velocity. Accordingly, the estimate for the expansion time has the form:
4. Discussion and Conclusions
In order to understand the processes of non-thermal particle acceleration at work in fast and energetic transients we have carried out and presented above a microscopic gyro-scale modeling of the collisionless shock structure and non-thermal particle spectra, which show a strong dependence of both electron and proton acceleration efficiency on the shock obliquity.
In this context one should keep in mind that the particle-in-cell simulation assumed a fixed homogeneous magnetic field and cold flow of the incoming particles in the shock upstream at the boundary of the simulation box. On the other hand, fast non-thermal particles can penetrate into the upstream plasma flow. It is clear from the results of the Monte Carlo modeling presented in Section 3 (see, in particular, Figure 10) that the efficient cosmic ray acceleration at the shock may provide a strong magnetic field amplification and modification of the upstream plasma flow. The cosmic ray pressure gradient in the shock upstream decelerates the incoming plasma flow and the cosmic ray driven instabilities may highly amplify the fluctuating magnetic fields well outside the particle-in-cell simulation box which is limited by a few hundred of the proton gyroradii around the plasma sub-shock. Such simulations show the potential importance of the feedback effects which cannot be modeled with the microscopic particle-in-cell simulations so far. Therefore we have used here the particle-in-cell model to simulate the electron injection and acceleration in sub and mildly relativistic shocks of fast energetic transients together with Monte Carlo modeling. While the Monte Carlo technique describes the structure of upstream flow modified by the accelerated particles at scales well above the proton gyro-scales, it cannot be used to simulate the electron injection where particle-in-cell approach is required. Thus, we used the combination of the two techniques to model radio emission.
In our study, of electron spectrum convergence in quasi-parallel shock of speed we observed some non-monotonic temporal behavior of the electron spectra as it is shown in Figure 5. This could be due to the development of Bell’s instability as it was found earlier in [61] and which mediate the quasi-parallel shock structure at proton gyro-scales. The maximum electron energy achievable in our simulation was about 50 and we extrapolate the spectral slope to larger energy. We extended the spectra from 50 to 500 using the same spectral slope, it is enough to model radio spectra. This is an assumption in our case. However, the extrapolation seems to be justified by the presence of a power-law such as a spectral component with a similar slope right after the thermal peak in Crumley et al. simulation (see the electron spectra presented in Figure 7 [61] in the electron momentum range between 0.1 and 30 ). A similar spectral component is also apparent right after the peak of the spectrum in our steady Monte Carlo simulations (see, e.g., our Figure 8).
We applied 2D kinetic PIC simulations for sub-relativistic flows with velocity of 0.3 c to model the spectra of electrons and protons. The dynamical range of the full kinetic PIC simulations is limited but the electron spectrum extrapolated with account for the results of Monte Carlo simulations is enough to model the observed radio emission in the fast transients where such fast outflows were found. In the Monte Carlo model the particle-in-cell simulated domain where the electron injection occurs correspond to the sub-shock structure which is apparent at in Figure 10. The plasma compression ratio at the sub-shock of the cosmic ray modified shock is about 3 and the spectra of particles accelerated at the sub-shock in the low energy regime (c.f. the proton spectral slope right after the peak in Figure 8) are consistent with the ones obtained within the particle-in-cell simulation dynamical range. The gyroradius of electrons with Lorentz-factor of in our simulations is about the gyroradius of protons with Lorentz-factor of . The spectral index of proton distribution simulated with Monte Carlo model at Lorentz-factor of is consistent with the PIC electron spectrum extrapolated to ∼500 .
This allows to model the non-thermal emission and to understand the origin of the synchrotron radio emission of FBOTs. Additionally, one may assume an explanation of their hard X-ray spectrum using the dependence of the electron power law distribution index on the shock obliquity. As can be seen in Figure 1 it leads to the presence of relativistic electron populations of comparable intensities within a range of spectral indices along the curved shock surface expected in a wide angle outflow. In this case the synchrotron radio emission could have rather steep spectral indices, while the X-ray component produced by the inverse Compton scattering of the intense optical radiation by the relativistic electrons with the harder spectral index may appear to be flatter.
The simplified macroscopic Monte Carlo kinetic model was used in Section 3 to estimate the maximum energies of the accelerated cosmic ray nuclei. The model accounted for both the nonlinear feedback effects of the flow modification by the cosmic ray pressure gradient and magnetic turbulence amplification by cosmic ray driven instabilities in the upstream of a plain mildly relativistic shock. The model demonstrated a possibility of PeV regime proton acceleration in the shocks driven by mildly relativistic outflows of fast energetic transients on a few weeks timescale.
Transient objects of different types such as gamma-ray bursts and tidal disruption events [80,81,82] are widely discussed as possible sources of the observed high energy neutrinos. The search of PeV gamma-ray sources have recently revealed a number of potential galactic pevatron sources (see, e.g., [83,84,85,86]). The analysis presented in [59] allowed the authors to conclude that the extended galactic supernova remnants are not likely to be pevatrons, while some other types of galactic sources associated with the SN events in the compact clusters of young massive stars [87] and gamma-ray binaries with compact relativistic stars [88,89] can produce PeV photons and neutrinos. While PeV photons undergo strong attenuation and can be detected mostly from the galactic sources, high energy neutrinos from extragalactic energetic transients can be detected with currently operating and future neutrino observatories simultaneously with LSST optical transients detection.
Author Contributions
All of the authors have equally contributed into the paper. A.B. constructed the model concept. PiC simulations were performed by V.R. Monte Carlo simulations were performed by S.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research received funding from Russian Science Foundation grant 21-72-20020.
Institutional Review Board Statement
The study did not involve humans or animals.
Informed Consent Statement
The study did not involve humans.
Acknowledgments
We are honored to dedicate this paper to the memory of professor Yury Nikolaevich Gnedin (1935–2018). His great scientific enthusiasm, competence and the unfailing goodwill for many years were extremely important for us. We are grateful to the referees for constructive comments and suggestions. The authors were supported by the RSF grant 21-72-20020. Some of the modeling was performed at the Joint Supercomputer Center JSCC RAS and some—at the “Tornado” subsystem of the Peter the Great Saint-Petersburg Polytechnic University Supercomputing Center.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kulkarni, S.R. Towards An Integrated Optical Transient Utility. arXiv 2020, arXiv:2004.03511. [Google Scholar]
- Abell, P.A.; Allison, J.; Anderson, S.F.; Andrew, J.R.; Angel, J.R.P.; Armus, L.; Arnett, D.; Asztalos, S.; Axelrod, T.S.; Bailey, S.; et al. LSST Science Book, Version 2.0. arXiv 2009, arXiv:0912.0201. [Google Scholar]
- Gehrels, N.; Chincarini, G.; Giommi, P.e.; Mason, K.; Nousek, J.; Wells, A.; White, N.; Barthelmy, S.; Burrows, D.; Cominsky, L.; et al. The Swift Gamma-Ray Burst Mission. Astrophys. J. 2004, 611, 1005–1020. [Google Scholar] [CrossRef]
- Sunyaev, R.; Arefiev, V.; Babyshkin, V.; Bogomolov, A.; Borisov, K.; Buntov, M.; Brunner, H.; Burenin, R.; Churazov, E.; Coutinho, D.; et al. The SRG X-ray orbital observatory, its telescopes and first scientific results. arXiv 2021, arXiv:2104.13267. [Google Scholar]
- Greiner, J.; Mannheim, K.; Aharonian, F.; Ajello, M.; Balasz, L.G.; Barbiellini, G.; Bellazzini, R.; Bishop, S.; Bisnovatij-Kogan, G.S.; Boggs, S.; et al. GRIPS—Gamma-Ray Imaging, Polarimetry and Spectroscopy. Exp. Astron. 2012, 34, 551–582. [Google Scholar] [CrossRef]
- De Angelis, A.; Tatischeff, V.; Argan, A.; Brandt, S.; Bulgarelli, A.; Bykov, A.; Costantini, E.; Silva., R.C.d.; Grenier, I.A.; Hanlon, L.; et al. Gamma-ray astrophysics in the MeV range. Exp. Astron. 2021, 51, 1225–1254. [Google Scholar] [CrossRef]
- Mereghetti, S.; Balman, S.; Caballero-Garcia, M.; Del Santo, M.; Doroshenko, V.; Erkut, M.; Hanlon, L.; Hoeflich, P.; Markowitz, A.; Osborne, J.; et al. Time Domain Astronomy with the THESEUS Satellite. arXiv 2021, arXiv:2104.09533. [Google Scholar] [CrossRef]
- Drout, M.R.; Chornock, R.; Soderberg, A.M.; Sanders, N.E.; McKinnon, R.; Rest, A.; Foley, R.J.; Milisavljevic, D.; Margutti, R.; Berger, E.; et al. Rapidly Evolving and Luminous Transients from Pan-STARRS1. Astrophys. J. 2014, 794, 23. [Google Scholar] [CrossRef]
- Margutti, R.; Metzger, B.; Chornock, R.; Vurm, I.; Roth, N.; Grefenstette, B.; Savchenko, V.; Cartier, R.; Steiner, J.; Terreran, G.; et al. An Embedded X-ray Source Shines through the Aspherical AT 2018cow: Revealing the Inner Workings of the Most Luminous Fast-evolving Optical Transients. Astrophys. J. 2019, 872, 18. [Google Scholar] [CrossRef]
- Coppejans, D.L.; Margutti, R.; Terreran, G.; Nayana, A.; Coughlin, E.; Laskar, T.; Alexander, K.; Bietenholz, M.; Caprioli, D.; Chandra, P.; et al. A Mildly Relativistic Outflow from the Energetic, Fast-rising Blue Optical Transient CSS161010 in a Dwarf Galaxy. Astrophys. J. Lett. 2020, 895, L23. [Google Scholar] [CrossRef]
- Ho, A.Y.; Perley, D.A.; Kulkarni, S.; Dong, D.Z.; De, K.; Chandra, P.; Andreoni, I.; Bellm, E.C.; Burdge, K.B.; Coughlin, M.; et al. The Koala: A Fast Blue Optical Transient with Luminous Radio Emission from a Starburst Dwarf Galaxy at z = 0.27. Astrophys. J. 2020, 895, 49. [Google Scholar] [CrossRef]
- Nicholl, M.; Blanchard, P.K.; Berger, E.; Chornock, R.; Margutti, R.; Gomez, S.; Lunnan, R.; Miller, A.A.; Fong, W.-f.; Terreran, G.; et al. An extremely energetic supernova from a very massive star in a dense medium. Nat. Astron. 2020, 4, 893–899. [Google Scholar] [CrossRef]
- Weiler, K.W.; Panagia, N.; Montes, M.J.; Sramek, R.A. Radio Emission from Supernovae and Gamma-Ray Bursters. Ann. Rev. Astron. Astrophys. 2002, 40, 387–438. [Google Scholar] [CrossRef]
- Soderberg, A.M.; Kulkarni, S.R.; Nakar, E.; Berger, E.; Cameron, P.; Fox, D.; Frail, D.; Gal-Yam, A.; Sari, R.; Cenko, S.; et al. Relativistic ejecta from X-ray flash XRF 060218 and the rate of cosmic explosions. Nature 2006, 442, 1014–1017. [Google Scholar] [CrossRef]
- Irwin, C.M.; Chevalier, R.A. Jet or shock breakout? The low-luminosity GRB 060218. Mon. Not. R. Astron. Soc. 2016, 460, 1680–1704. [Google Scholar] [CrossRef]
- Nayana, A.J.; Chandra, P. uGMRT Observations of a Fast and Blue Optical Transient—AT 2018cow. Astrophys. J. Lett. 2021, 912, L9. [Google Scholar]
- Ho, A.Y.; Margalit, B.; Bremer, M.; Perley, D.A.; Yao, Y.; Dobie, D.; Kaplan, D.L.; O’Brien, A.; Petitpas, G.; Zic, A. Luminous Millimeter, Radio, and X-ray Emission from ZTF20acigmel (AT2020xnd). arXiv 2021, arXiv:2110.05490. [Google Scholar]
- Bright, J.S.; Margutti, R.; Matthews, D.; Brethauer, D.; Coppejans, D.; Wieringa, M.H.; Metzger, B.D.; DeMarchi, L.; Laskar, T.; Romero, C.; et al. Radio and X-ray observations of the luminous Fast Blue Optical Transient AT2020xnd. arXiv 2021, arXiv:2110.05514. [Google Scholar]
- Kremer, K.; Lu, W.; Piro, A.L.; Chatterjee, S.; Rasio, F.A.; Claire, S.Y. Fast Optical Transients from Stellar-mass Black Hole Tidal Disruption Events in Young Star Clusters. Astrophys. J. 2021, 911, 104. [Google Scholar] [CrossRef]
- Metzger, B.D. Kilonovae. Living Rev. Relat. 2019, 23, 1. [Google Scholar]
- Moriya, T.J.; Chen, K.J.; Nakajima, K.; Tominaga, N.; Blinnikov, S.I. Observational properties of a general relativistic instability supernova from a primordial supermassive star. Mon. Not. R. Astron. Soc. 2021, 503, 1206–1213. [Google Scholar] [CrossRef]
- Soderberg, A.; Chakraborti, S.; Pignata, G.; Chevalier, R.; Chandra, P.; Ray, A.; Wieringa, M.; Copete, A.; Chaplin, V.; Connaughton, V.; et al. A relativistic type Ibc supernova without a detected γ-ray burst. Nature 2010, 463, 513–515. [Google Scholar] [CrossRef]
- Corsi, A.; Gal-Yam, A.; Kulkarni, S.; Frail, D.; Mazzali, P.; Cenko, S.; Kasliwal, M.; Cao, Y.; Horesh, A.; Palliyaguru, N.; et al. Radio Observations of a Sample of Broad-line Type IC Supernovae Discovered by PTF/IPTF: A Search for Relativistic Explosions. Astrophys. J. 2016, 830, 42. [Google Scholar] [CrossRef]
- Imshennik, V.S.; Nadezhin, D.K. Supernova 1987A in the Large Magellanic Cloud: Observations and theory. Sov. Sci. Rev. Sect. E 1989, 8, 1–147. [Google Scholar]
- Matzner, C.D.; McKee, C.F. The Expulsion of Stellar Envelopes in Core-Collapse Supernovae. Astrophys. J. 1999, 510, 379–403. [Google Scholar] [CrossRef]
- Tan, J.C.; Matzner, C.D.; McKee, C.F. Trans-Relativistic Blast Waves in Supernovae as Gamma-Ray Burst Progenitors. Astrophys. J. 2001, 551, 946–972. [Google Scholar] [CrossRef]
- MacFadyen, A.I.; Woosley, S.E.; Heger, A. Supernovae, Jets, and Collapsars. Astrophys. J. 2001, 550, 410–425. [Google Scholar] [CrossRef]
- Lazzati, D.; Morsony, B.J.; Blackwell, C.H.; Begelman, M.C. Unifying the Zoo of Jet-driven Stellar Explosions. Astrophys. J. 2012, 750, 68. [Google Scholar] [CrossRef]
- Margutti, R.; Milisavljevic, D.; Soderberg, A.; Guidorzi, C.; Morsony, B.; Sanders, N.; Chakraborti, S.; Ray, A.; Kamble, A.; Drout, M.; et al. Relativistic Supernovae have Shorter-lived Central Engines or More Extended Progenitors: The Case of SN 2012ap. Astrophys. J. 2014, 797, 107. [Google Scholar] [CrossRef]
- Corsi, A.; Lazzati, D. Gamma-ray burst jets in supernovae. New Astron. Rev. 2021, 92, 101614. [Google Scholar] [CrossRef]
- Suzuki, A.; Maeda, K. Supernova ejecta with a relativistic wind from a central compact object: A unified picture for extraordinary supernovae. Mon. Not. R. Astron. Soc. 2017, 466, 2633–2657. [Google Scholar] [CrossRef]
- Suzuki, A.; Maeda, K. Three-dimensional Hydrodynamic Simulations of Supernova Ejecta with a Central Energy Source. Astrophys. J. 2019, 880, 150. [Google Scholar] [CrossRef]
- Suzuki, A.; Maeda, K. Two-dimensional Radiation-hydrodynamic Simulations of Supernova Ejecta with a Central Power Source. Astrophys. J. 2021, 908, 217. [Google Scholar] [CrossRef]
- Grassberg, E.K.; Imshennik, V.S.; Nadyozhin, D.K. On the Theory of the Light Curves of Supernovae. Astroph. Space Sci. 1971, 10, 28–51. [Google Scholar] [CrossRef]
- Chevalier, R.A.; Irwin, C.M. Shock Breakout in Dense Mass Loss: Luminous Supernovae. Astrophys. J. Lett. 2011, 729, L6. [Google Scholar] [CrossRef]
- Tolstov, A.G.; Blinnikov, S.I.; Nadyozhin, D.K. Coupling of matter and radiation at supernova shock breakout. Mon. Not. R. Astron. Soc. 2013, 429, 3181–3199. [Google Scholar] [CrossRef]
- Chevalier, R.A. Synchrotron Self-Absorption in Radio Supernovae. Astrophys. J. 1998, 499, 810–819. [Google Scholar] [CrossRef]
- Waxman, E.; Katz, B. Shock Breakout Theory. In Handbook of Supernovae; Alsabti, A.W., Murdin, P., Eds.; Springer: New York, NY, USA, 2017; p. 967. [Google Scholar]
- Budnik, R.; Katz, B.; Sagiv, A.; Waxman, E. Relativistic Radiation Mediated Shocks. Astrophys. J. 2010, 725, 63–90. [Google Scholar] [CrossRef]
- Levinson, A. Plasma kinetic effects in relativistic radiation-mediated shocks. Phys. Rev. E 2020, 102, 063210. [Google Scholar] [CrossRef] [PubMed]
- Granot, A.; Nakar, E.; Levinson, A. Relativistic shock breakout from a stellar wind. Mon. Not. R. Astron. Soc. 2018, 476, 5453–5463. [Google Scholar] [CrossRef]
- Ito, H.; Levinson, A.; Nakar, E. Monte Carlo simulations of fast Newtonian and mildly relativistic shock breakout from a stellar wind. Mon. Not. R. Astron. Soc. 2020, 499, 4961–4971. [Google Scholar] [CrossRef]
- Marcowith, A.; Bret, A.; Bykov, A.; Dieckman, M.E.; Drury, L.O.C.; Lembège, B.; Lemoine, M.; Morlino, G.; Murphy, G.; Pelletier, G.; et al. The microphysics of collisionless shock waves. Rep. Prog. Phys. 2016, 79, 046901. [Google Scholar] [CrossRef] [PubMed]
- Sironi, L.; Spitkovsky, A. Particle Acceleration in Relativistic Magnetized Collisionless Pair Shocks: Dependence of Shock Acceleration on Magnetic Obliquity. Astrophys. J. 2009, 698, 1523–1549. [Google Scholar] [CrossRef]
- Pelletier, G.; Bykov, A.; Ellison, D.; Lemoine, M. Towards Understanding the Physics of Collisionless Relativistic Shocks. Relativistic Collisionless Shocks. Space Sci. Rev. 2017, 207, 319–360. [Google Scholar] [CrossRef]
- Bell, A.R.; Schure, K.M.; Reville, B.; Giacinti, G. Cosmic-ray acceleration and escape from supernova remnants. Mon. Not. R. Astron. Soc. 2013, 431, 415–429. [Google Scholar] [CrossRef]
- Bell, A.R.; Araudo, A.T.; Matthews, J.H.; Blundell, K.M. Cosmic-ray acceleration by relativistic shocks: Limits and estimates. Mon. Not. R. Astron. Soc. 2018, 473, 2364–2371. [Google Scholar] [CrossRef]
- Lemoine, M.; Waxman, E. Anisotropy vs. chemical composition at ultra-high energies. J. Cosmol. Astropart. Phys. 2009, 2009, 009. [Google Scholar] [CrossRef]
- Bykov, A.; Gehrels, N.; Krawczynski, H.; Lemoine, M.; Pelletier, G.; Pohl, M. Particle Acceleration in Relativistic Outflows. Space Sci. Rev. 2012, 173, 309–339. [Google Scholar] [CrossRef]
- Zhang, B.T.; Murase, K. Ultrahigh-energy cosmic-ray nuclei and neutrinos from engine-driven supernovae. Phys. Rev. D 2019, 100, 103004. [Google Scholar] [CrossRef]
- Samuelsson, F.; Bégué, D.; Ryde, F.; Pe’er, A.; Murase, K. Constraining Low-luminosity Gamma-Ray Bursts as Ultra-high-energy Cosmic Ray Sources Using GRB 060218 as a Proxy. Astrophys. J. 2020, 902, 148. [Google Scholar] [CrossRef]
- Bykov, A.M.; Ellison, D.C.; Marcowith, A.; Osipov, S.M. Cosmic Ray Production in Supernovae. Space Sci. Rev. 2018, 214, 41. [Google Scholar] [CrossRef]
- Zirakashvili, V.N.; Ptuskin, V.S. Type IIn supernovae as sources of high energy astrophysical neutrinos. Astropart. Phys. 2016, 78, 28–34. [Google Scholar] [CrossRef]
- Murase, K.; Franckowiak, A.; Maeda, K.; Margutti, R.; Beacom, J.F. High-energy Emission from Interacting Supernovae: New Constraints on Cosmic-Ray Acceleration in Dense Circumstellar Environments. Astrophys. J. 2019, 874, 80. [Google Scholar] [CrossRef]
- Sironi, L.; Keshet, U.; Lemoine, M. Relativistic Shocks: Particle Acceleration and Magnetization. Space Sci. Rev. 2015, 191, 519–544. [Google Scholar] [CrossRef]
- Ptuskin, V.; Zirakashvili, V.; Seo, E.-S. Spectra of Cosmic-Ray Protons and Helium Produced in Supernova Remnants. Astrophys. J. 2013, 763, 47. [Google Scholar] [CrossRef]
- Blasi, P. The origin of galactic cosmic rays. Astron. Astrophys. Rev. 2013, 21, 70. [Google Scholar] [CrossRef]
- Amato, E. The origin of galactic cosmic rays. Int. J. Mod. Phys. D 2014, 23, 1430013. [Google Scholar] [CrossRef]
- Cristofari, P. The Hunt for Pevatrons: The Case of Supernova Remnants. Universe 2021, 7, 324. [Google Scholar] [CrossRef]
- Park, J.; Caprioli, D.; Spitkovsky, A. Simultaneous Acceleration of Protons and Electrons at Nonrelativistic Quasiparallel Collisionless Shocks. Phys. Rev. Lett. 2015, 114, 085003. [Google Scholar] [CrossRef]
- Crumley, P.; Caprioli, D.; Markoff, S.; Spitkovsky, A. Kinetic simulations of mildly relativistic shocks—I. Particle acceleration in high Mach number shocks. Mon. Not. R. Astron. Soc. 2019, 485, 5105–5119. [Google Scholar] [CrossRef]
- Romansky, V.I.; Bykov, A.M.; Osipov, S.M. Electron and ion acceleration by relativistic shocks: Particle-in-cell simulations. J. Phys. Conf. Ser. 2018, 1038, 012022. [Google Scholar] [CrossRef]
- Derouillat, J.; Beck, A.; Pérez, F.; Vinci, T.; Chiaramello, M.; Grassi, A.; Flé, M.; Bouchard, G.; Plotnikov, I.; Aunai, N.; et al. SMILEI: A collaborative, open-source, multi-purpose particle-in-cell code for plasma simulation. Comput. Phys. Commun. 2018, 222, 351–373. [Google Scholar] [CrossRef]
- Esirkepov, T.Z. Exact charge conservation scheme for Particle-in-Cell simulation with an arbitrary form-factor. Comput. Phys. Commun. 2001, 135, 144–153. [Google Scholar] [CrossRef]
- Guo, X.; Sironi, L.; Narayan, R. Non-thermal Electron Acceleration in Low Mach Number Collisionless Shocks. I. Particle Energy Spectra and Acceleration Mechanism. Astrophys. J. 2014, 794, 153. [Google Scholar] [CrossRef]
- Romansky, V.I.; Bykov, A.M.; Osipov, S.M. On electron acceleration by mildly-relativistic shocks: PIC simulations. J. Phys. Conf. Ser. 2021, 2103, 012009. [Google Scholar] [CrossRef]
- Pacholczyk, A.G. Radio Astrophysics. Nonthermal Processes in Galactic and Extragalactic Sources; Freeman: San Francisco, CA, USA, 1970. [Google Scholar]
- Chevalier, R.A.; Fransson, C. Thermal and Non-thermal Emission from Circumstellar Interaction. In Handbook of Supernovae; Alsabti, A.W., Murdin, P., Eds.; Springer: New York, NY, USA, 2017; p. 875. [Google Scholar]
- Ghisellini, G. Radiative Processes in High Energy Astrophysics; Springer International Publishing: Cham, Switzerland, 2013; Volume 873. [Google Scholar]
- Margalit, B.; Quataert, E. Thermal Electrons in Mildly Relativistic Synchrotron Blast Waves. Astrophys. J. Lett. 2021, 923, L14. [Google Scholar] [CrossRef]
- Bykov, A.M.; Ellison, D.C.; Osipov, S.M.; Vladimirov, A.E. Magnetic Field Amplification in Nonlinear Diffusive Shock Acceleration Including Resonant and Non-resonant Cosmic-Ray Driven Instabilities. Astrophys. J. 2014, 789, 137. [Google Scholar] [CrossRef]
- Jones, F.C.; Ellison, D.C. The plasma physics of shock acceleration. Space Sci. Rev. 1991, 58, 259–346. [Google Scholar] [CrossRef]
- Ellison, D.C.; Baring, M.G.; Jones, F.C. Nonlinear Particle Acceleration in Oblique Shocks. Astrophys. J. 1996, 473, 1029. [Google Scholar] [CrossRef]
- Vladimirov, A.E.; Bykov, A.M.; Ellison, D.C. Turbulence Dissipation and Particle Injection in Nonlinear Diffusive Shock Acceleration with Magnetic Field Amplification. Astrophys. J. 2008, 688, 1084–1101. [Google Scholar] [CrossRef]
- Vladimirov, A.E.; Bykov, A.M.; Ellison, D.C. Spectra of Magnetic Fluctuations and Relativistic Particles Produced by a Nonresonant Wave Instability in Supernova Remnant Shocks. Astrophys. J. Lett. 2009, 703, L29–L32. [Google Scholar] [CrossRef][Green Version]
- Vladimirov, A. Modeling Magnetic Field Amplification in Nonlinear Diffusive Shock Acceleration. Ph.D. Thesis, North Carolina State University, Raleigh, NC, USA, 2009. [Google Scholar]
- Ellison, D.C.; Warren, D.C.; Bykov, A.M. Monte Carlo Simulations of Nonlinear Particle Acceleration in Parallel Trans-relativistic Shocks. Astrophys. J. 2013, 776, 46. [Google Scholar] [CrossRef]
- Matthaeus, W.H.; Oughton, S.; Zhou, Y. Anisotropic magnetohydrodynamic spectral transfer in the diffusion approximation. Phys. Rev. E 2009, 79, 035401. [Google Scholar] [CrossRef]
- Bell, A.R. Turbulent amplification of magnetic field and diffusive shock acceleration of cosmic rays. Mon. Not. R. Astron. Soc. 2004, 353, 550–558. [Google Scholar] [CrossRef]
- Farrar, G.R.; Piran, T. Tidal disruption jets as the source of Ultra-High Energy Cosmic Rays. arXiv 2014, arXiv:1411.0704. [Google Scholar]
- Murase, K.; Waxman, E. Constraining high-energy cosmic neutrino sources: Implications and prospects. Phys. Rev. D 2016, 94, 103006. [Google Scholar] [CrossRef]
- Murase, K.; Kimura, S.S.; Zhang, B.T.; Oikonomou, F.; Petropoulou, M. High-energy Neutrino and Gamma-Ray Emission from Tidal Disruption Events. Astrophys. J. 2020, 902, 108. [Google Scholar] [CrossRef]
- Aharonian, F.; Yang, R.; de Oña Wilhelmi, E. Massive stars as major factories of Galactic cosmic rays. Nat. Astron. 2019, 3, 561–567. [Google Scholar] [CrossRef]
- Amenomori, M.; Bao, Y.; Bi, X.; Chen, D.; Chen, T.; Chen, W.; Chen, X.; Chen, Y.; Cui, S.; Ding, L.; et al. First Detection of sub-PeV Diffuse Gamma Rays from the Galactic Disk: Evidence for Ubiquitous Galactic Cosmic Rays beyond PeV Energies. Phys. Rev. Lett. 2021, 126, 141101. [Google Scholar] [CrossRef] [PubMed]
- Cao, Z.; Aharonian, F.; An, Q.; Bai, L.; Bai, Y.; Bao, Y.; Bastieri, D.; Bi, X.; Bi, Y.; Cai, H.; et al. Ultrahigh-energy photons up to 1.4 petaelectronvolts from 12 γ-ray Galactic sources. Nature 2021, 594, 33–36. [Google Scholar] [CrossRef]
- Dzhappuev, D.; Afashokov, Y.Z.; Dzaparova, I.; Dzhatdoev, T.; Gorbacheva, E.; Karpikov, I.; Khadzhiev, M.; Klimenko, N.; Kudzhaev, A.; Kurenya, A.; et al. Observation of Photons above 300 TeV Associated with a High-energy Neutrino from the Cygnus Region. Astrophys. J. Lett. 2021, 916, L22. [Google Scholar] [CrossRef]
- Bykov, A.M.; Ellison, D.C.; Gladilin, P.E.; Osipov, S.M. Ultrahard spectra of PeV neutrinos from supernovae in compact star clusters. Mon. Not. R. Astron. Soc. 2015, 453, 113–121. [Google Scholar] [CrossRef]
- Kimura, S.S.; Sudoh, T.; Kashiyama, K.; Kawanaka, N. Magnetically Arrested Disks in Quiescent Black Hole Binaries: Formation Scenario, Observable Signatures, and Potential PeVatrons. Astrophys. J. 2021, 915, 31. [Google Scholar] [CrossRef]
- Bykov, A.M.; Petrov, A.E.; Kalyashova, M.E.; Troitsky, S.V. PeV photon and neutrino flares from galactic gamma-ray binaries. Astrophys. J. Lett. 2021, 921, L10. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).